固定情形Logistic回歸模型誤差方差的經(jīng)驗(yàn)似然估計(jì)*

胡學(xué)葉張正家

(廣西師范大學(xué) 數(shù)學(xué)與統(tǒng)計(jì)學(xué)院,廣西 桂林 541004)

0 引言

經(jīng)驗(yàn)似然是由Owen[1-3]提出的一種非參數(shù)統(tǒng)計(jì)推斷方法,石堅(jiān)[4]研究了線性模型誤差方差的經(jīng)驗(yàn)似然估計(jì).廣義線性模型是經(jīng)典線性模型的推廣,陳希孺[5]對(duì)廣義線性模型的數(shù)學(xué)原理進(jìn)行系統(tǒng)的闡述.而Logistic回歸模型是常用的廣義線性模型之一.舒常江[6]在隨機(jī)設(shè)計(jì)情形研究了Logistic回歸模型誤差方差的經(jīng)驗(yàn)似然估計(jì).考慮到固定設(shè)計(jì)情形在應(yīng)用領(lǐng)域中亦有廣泛的應(yīng)用,本文利用經(jīng)驗(yàn)似然方法得到了固定設(shè)計(jì)情形下Logistic回歸模型誤差方差的經(jīng)驗(yàn)似然估計(jì),結(jié)果表明其方差比傳統(tǒng)殘差平方和方法得到的估計(jì)更小.考慮Logistic回歸模型

且連接函數(shù)g滿足,其中,x∈R p是固定設(shè)計(jì)矩陣,Y∈R1是響應(yīng)變量,β∈R p是參數(shù)向量,e∈R1是隨機(jī)誤差.這里,只有(x,Y)是可觀測的.

令ωi=ηi(1-ηi),1≤i≤n,記W(n)=diag(ω1,…,ωn),并作如下假定:

(A.1)e1,…,e n為獨(dú)立同分布的隨機(jī)變量,且

(A.2)存在ε＞0,使得E│e1│4+ε＜∞,記

(A.3)存在正定矩陣S0,S1,使得當(dāng)n→∞,有,且存在常數(shù)C＞0,使得,其 中未知,║·║是R p上的歐式模;

(A.5)當(dāng)n→0,→∞,其中,易知對(duì)某個(gè)常數(shù)C＞0有

注1:為敘述方便,始終假設(shè)C表示一不依賴于n的大于0的常數(shù),且C每次出現(xiàn)可以取不同的值.

設(shè)有來自模型的獨(dú)立同分布樣本(x1,Y1),…,(x n,Y n),其中x i=(x i1,…,x ip)′,1≤i≤n,相應(yīng)地有一組不可觀測的隨機(jī)誤差e1,…,e n,使得Y i=η(x i)+e i,1≤i≤n.記x(n)=(x1,…,x n)′,Y(n)=(Y1,…,Y n)′,E(n)=(e1,…,e n)′,E(nn)=(e n1,…,e nn)′.在廣義線性模型中,對(duì)于參數(shù)估計(jì)常用的方法是極大似然估計(jì).Logistic回歸模型中響應(yīng)變量Y服從二項(xiàng)分布,其概率分布列為:

其中ηi=η(x i),似然函數(shù)為

相應(yīng)地對(duì)數(shù)似然函數(shù)為

對(duì)其取導(dǎo)數(shù),從而得到似然方程的解:

由于上式?jīng)]有顯示解,我們采用牛頓迭代方法[7]求解,得到滿足(3)式的β^為β的極大似然估計(jì).具體操作如下:

3)由上述公式得到,若收斂即為所求;否則返回上一步,用代替得到,如此反復(fù)迭代直至收斂,即為所求.

為了得到誤差方差σ2的估計(jì),利用殘差平方和得到:

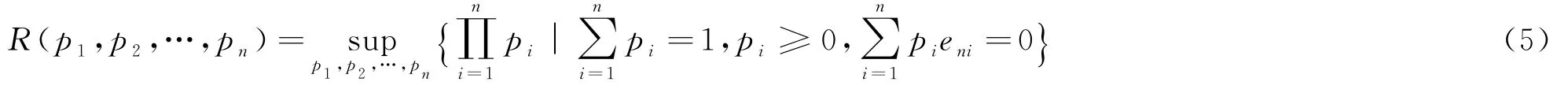
由拉格朗日數(shù)乘法得到:

其中λ滿足:

因此可以得到誤差方差σ2新的估計(jì),記為

1 主要結(jié)論

定理1 若條件(A.1)～(A.6)成立,當(dāng)n→∞,有

且

由定理知,經(jīng)驗(yàn)似然得到的誤差方差的漸近方差比傳統(tǒng)殘差平方和得到的漸近方差小.

2 定理的證明

引理1 設(shè)B1,B2,…,B n為獨(dú)立同分布的隨機(jī)變量序列,若存在α＞0,使得E(│B1│α)＜∞,則有

證明:見Ghosh[8]的引理3.

引理2 若條件(A.1)～(A.5)成立,則有:

證明:(12)式的證明:由于滿足(3)式,即

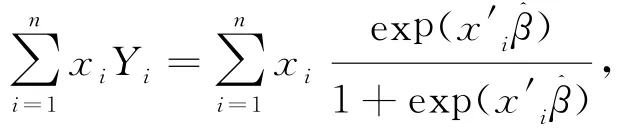
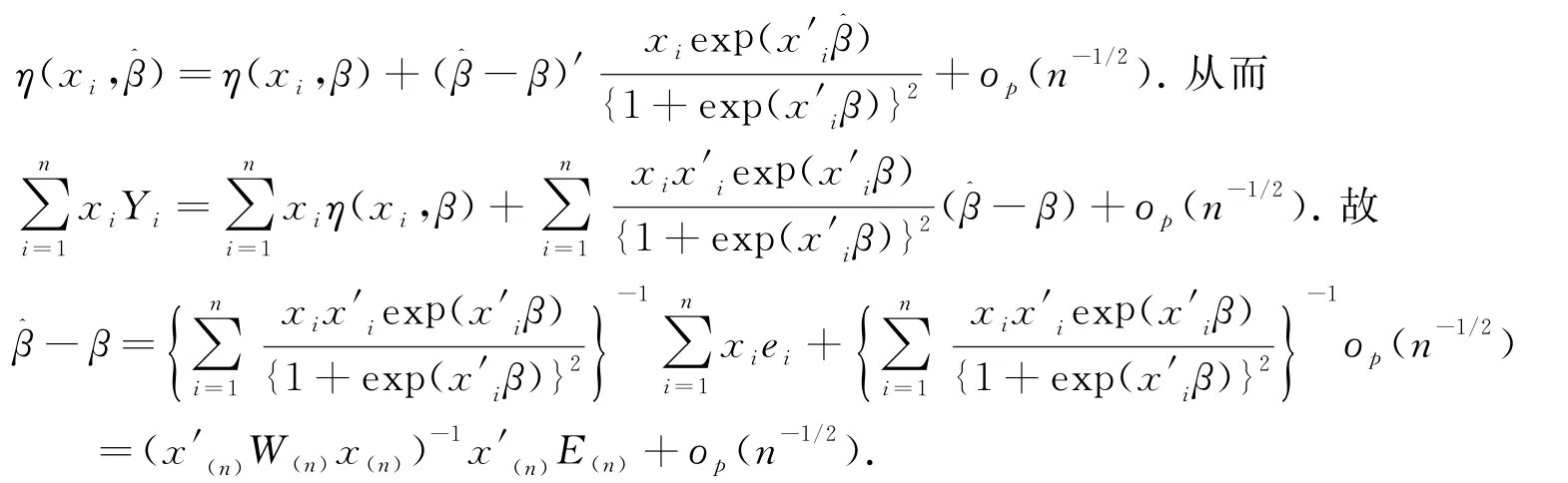
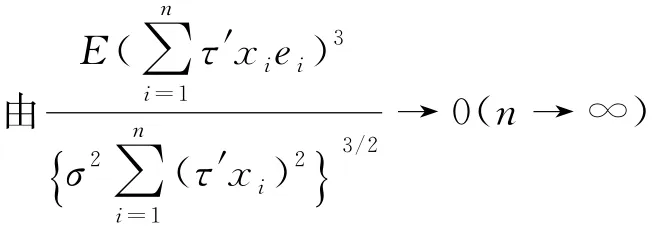
即(12)式得證.

由│e ni│≤│e i│+║x i║│β^-β│,得到

即(13)式得證.

引理3 若條件(A.1)～(A.5)成立,則有

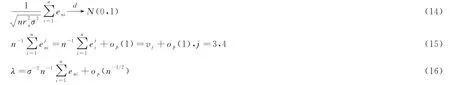
其中v j=E(e ji),j=3,4.

證明:(14)式的證明.因?yàn)?/p>

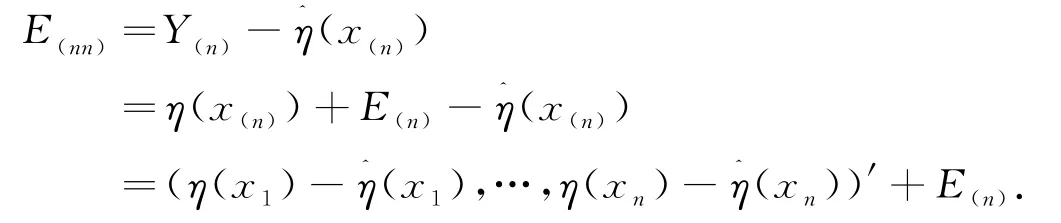
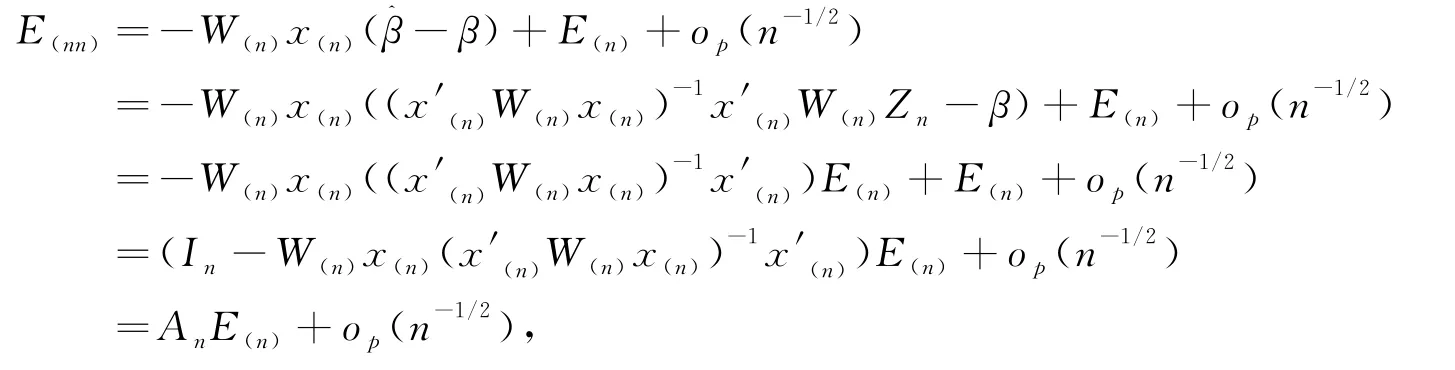
其中A n=(I n-W(n)x(n)(x′(n)W(n)x(n))-1x′(n))=(a ij),其中

由獨(dú)立隨機(jī)變量求和的矩不等式得到

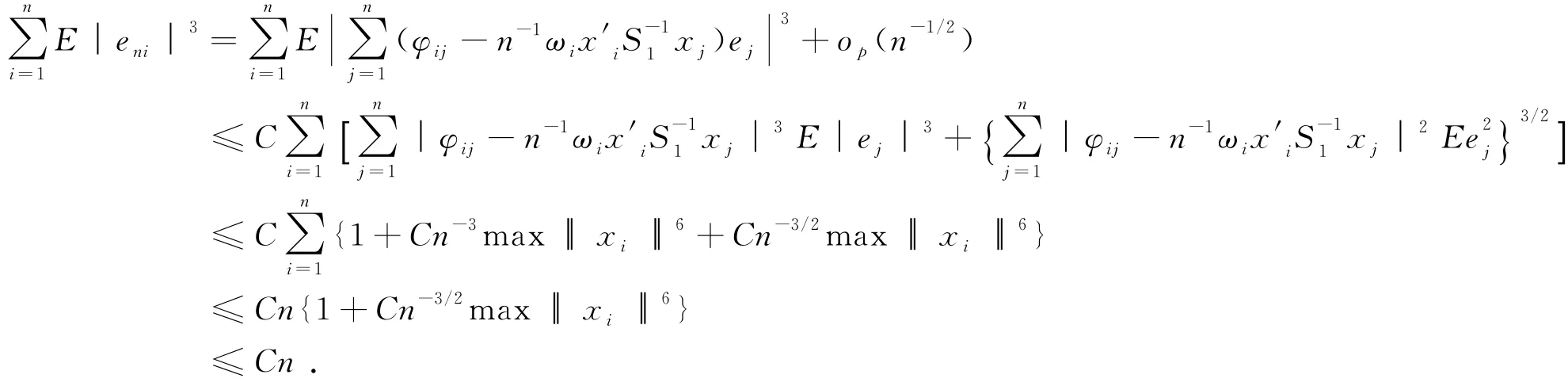
(15)式的證明:

由于0≤ωi≤1,

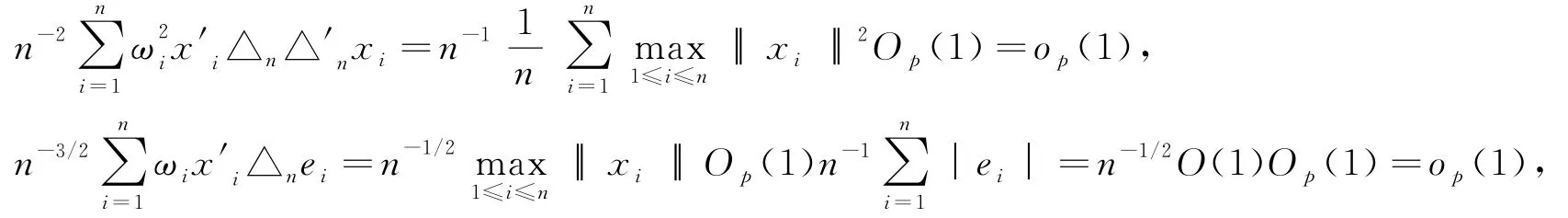
令ζi=λe ni,那么,max|ζi|=max|λe ni|=|λ|max|e ni|=n-1/2r nO p(1)o p(n1/(4+ε))=o p(1),

即max|ζi|=o p(1).

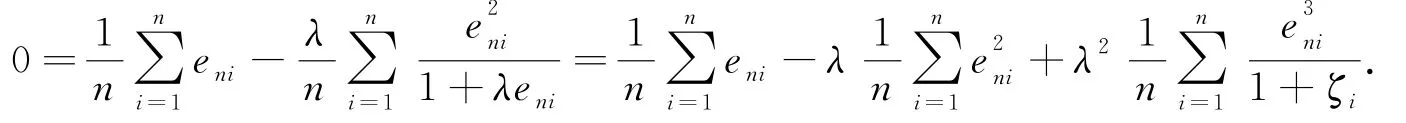
定理1中(9)式的證明:

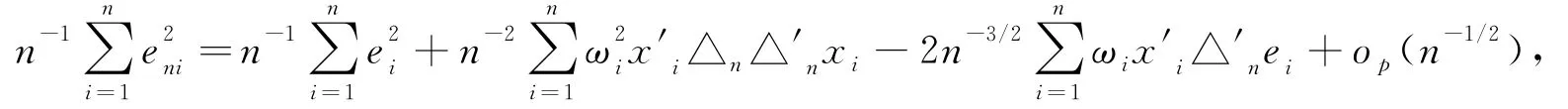
定理1中(10)式的證明:

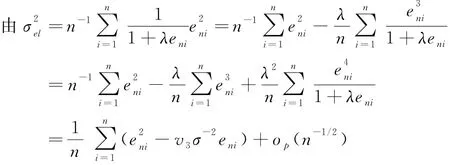
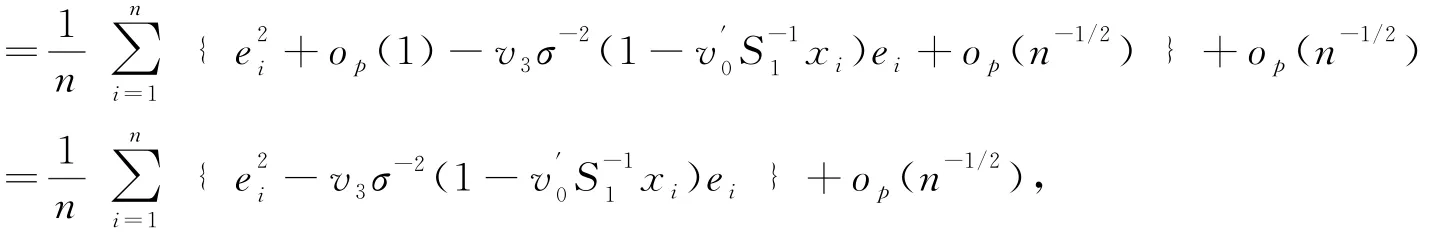
即(10)式成立.從而定理1得證.