Tracking Control of Uncertain Nonlinear Systems With Unknown Constant Input Delay
Ashish Kumar Jain and Shubhendu Bhasin,
Abstract—A robust delay compensator has been developed for a class of uncertain nonlinear systems with an unknown constant input delay. The control law consists of feedback terms based on the integral of past control values and a novel filtered tracking error, capable of compensating for input delays. Suitable Lyapunov-Krasovskii functionals are used to prove global uniformly ultimately bounded (GUUB) tracking, provided certain sufficient gain conditions, dependent on the bound of the delay, are satisfied. Simulation results illustrate the performance and robustness of the controller for different values of input delay.
I. Introduction
MANY physical systems and control engineering applications are affected by time delay, e.g., chemical processes, shared communication networks, teleoperations, coordination of unmanned vehicles, combustion controls, rolling mills, and road traffic systems [1], [2]. Delays are primarily caused due to time required for gathering information from sensors, processing the information determining what decision to make and finally executing the decision using actuators. Time delays, while sometimes beneficial, are often a source of instability and performance degradation [3]. Stability and stabilization of time delay systems is thus an ongoing area of research [4], [5].
Since the development of the Smith predictor for time delay compensation of stable linear systems, several modifications have been proposed, which extend the work to unstable linear systems [6], uncertain linear systems [7], and nonlinear systems [8]. The Arstein reduction [9] transforms a linear input delay system into a delay free system, for which a state feedback controller can be subsequently designed. Stability analysis based on Lyapunov-Razumikhin [4], [10] and Lyapunov-Krasovski (LK) [4], [11] theorems have been extensively used for such delay systems.
While delay can occur in the state, the input, and/or the measurement process, this paper focuses on unknown input delays for uncertain nonlinear systems. A common theme in most results found in the literature on stabilization of these input delays involves the use of reduction model approaches or predictor feedback for delay compensation [12]–[16]. Most results on predictor feedback assume complete knowledge of the system dynamics and delay [17]–[19]. The results in [17]represent the input delay system as an ordinary differential equation-partial differential equation (ODE-PDE) cascade and use a backstepping transformation to convert the delay system to a delay-free system. A backstepping design is considered in[20], [21] for nonlinear systems with a known input delay, and uniform global asymptotic stability and input-to-state stability(ISS) properties are proved using LK functionals. Using a reduction method approach, an asymptotically stable controller, is developed based on past values of the control,for a chain of integrators with delayed input and different types of nonlinearities [22]. In [23], ISS is proved using ISSLK functionals for a class of control-affine nonlinear systems with time delays and actuator errors in the feedback. Delay independent stability conditions for a class of nonlinear systems is derived using the Lyapunov-Razumikhin approach in [24].
Few results exist in the literature on stabilization of input delayed nonlinear systems with parametric uncertainties,unmodeled dynamics, external disturbances, and unknown delays. Recent efforts have focused on addressing these challenges [25]–[32]. A predictor feedback approach based on backstepping boundary controls has been considered for linear uncertain time delay systems with unknown delays [26], [27],[29]. In [30], a robust controller is designed for uncertain linear systems with unknown input delays, and delay dependent linear matrix inequality (LMI) conditions are derived for the stability. Robust controllers are designed in[25], [28] to compensate for input delayed uncertain Euler-Lagrange systems.
Several challenges exist when designing compensators for uncertain nonlinear systems subjected to unknown input delays. For instance, in the presence of an unknown input delay, it may not be possible to transform the time-delay system to a delay-free system. Further, classical delaydependent LK functionals are not directly amenable for stability analysis. To address these challenges, in this paper, a robust controller is developed for a class of nonlinear systems to yield global uniformly ultimately bounded (GUUB)stability despite unknown constant input delay, uncertain dynamics, and external disturbances. The control law includes a feedback term which consists of the integral of past values of the control input. The results in [33], [34] require the input delay to be exactly known. As compared to [35], the controller structure proposed in this work is fundamentally different, in that the control input consists of a filtered tracking error and a filtered integral of past values of the control, which are required for robust compensation of the unknown delay. The upper bound of delay, however, must be known, making it a milder condition as compared to the requirements in [35],where only a sufficiently close estimate of delay is needed.The proposed result assumes an additional growth condition on the dynamics, which ensures that the system does not exhibit finite escape time during the finite time where there are no control actions due to the delay. The growth condition assumption, together with the novel control design and delay bound dependent LK functionals, are used to prove a global UUB stability result, unlike recent works [25], [28], [31], [35]where only a local stability result could be obtained. Using Lyapunov stability analysis, sufficient gain conditions dependent on the delay bound are derived, which impose a restriction on the delay bound (and hence, the length of the delay). An illustrative example of an uncertain nonlinear system with unknown input delay is considered to demonstrate the efficacy of the controller. Performance of the controller with different values of input delay are also studied.
II. System Dynamics
Consider a second order nonlinear system1For simplicity of presentation, a second order system is considered in the paper, however, the development can be trivially extended to higher order system of the same form as (1).described by

The subsequent development is based on the following assumptions.
Assumption 1:The desired trajectoryis designed such that3The no tation denotes the space of bounded Lebesgue measurable func-tions on.
Assumption 2:The unknown delayhas an upper bound which is a known constant
Assumption 3:The system functionsatisfies the following growth condition

Assumption 4:The functionis bounded as
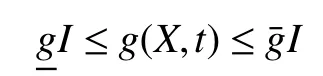
Assumption 5:The disturbance termis bounded by a known constant, i.e.,where
Lemma 1:The growth condition on(Assumption 3)and the bound on external disturbances (Assumption 5) ensure that system (1) satisfies the forward completeness property,and hence, does not exhibit a finite escape time for
Proof:See Appendix. ■
III. Control Development
The position tracking error denoted byis defined as

To quantify the control objective, a measurable filtered tracking erroris defined as
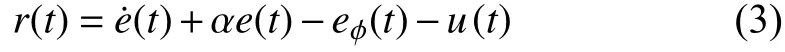
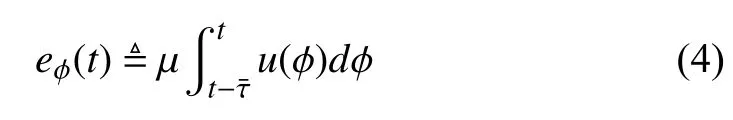
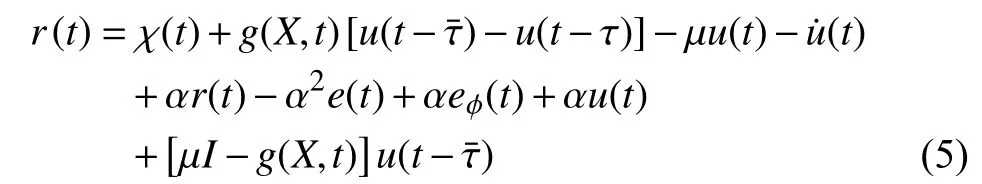
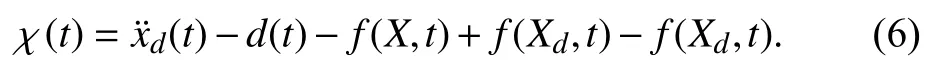
Using Assumptions 1, 3 and 5, the expression given in (6)can be upper bounded as
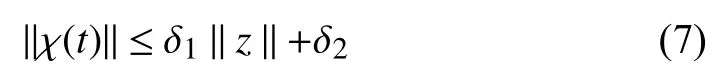
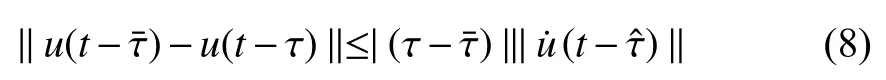

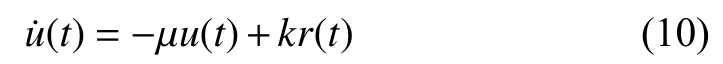
Remark 1:Using (3) and (10), the control law can be represented as
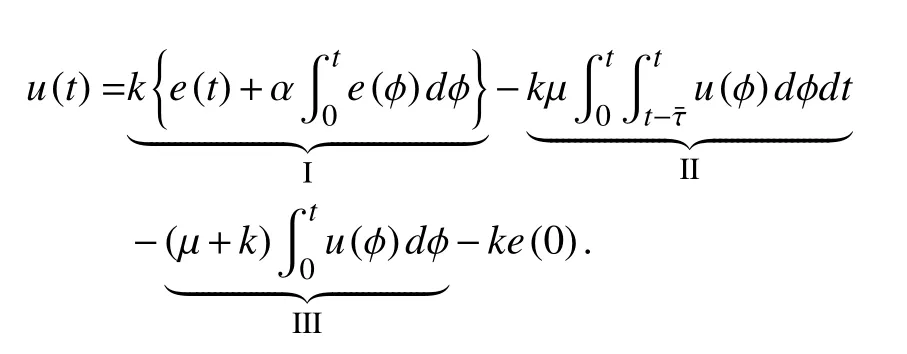
Substituting (10) into (5), the closed-loop error dynamics is given by
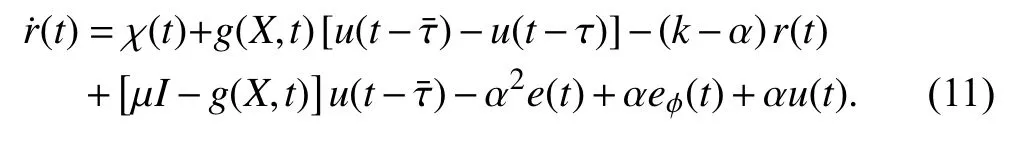
IV. Stability Analysis
Theorem 1:The controller derived from (10) ensures global uniformly ultimately bounded (GUUB) tracking for the dynamics given in (1), in the sense that
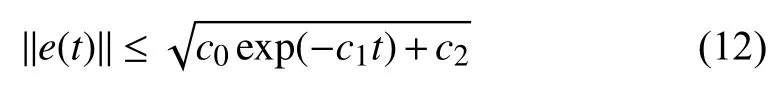

Proof:Consideras a continuously differentiable positive definite Lyapunov functional candidate, defined as
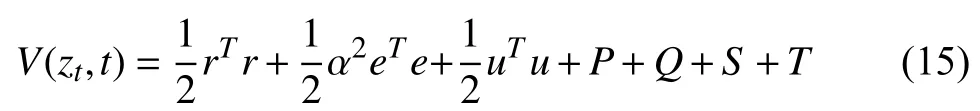

Taking the time derivative from (15), using (3), (10), and(11), the following expression is obtained
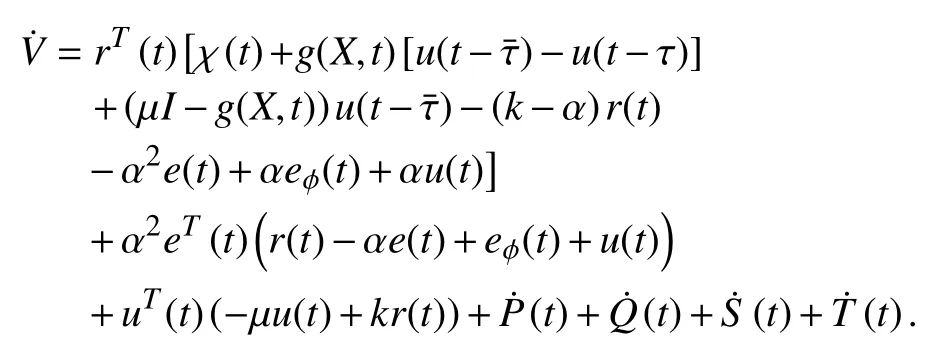
Using (16)–(19) and applying the Leibniz rule, the following derivatives are obtained as
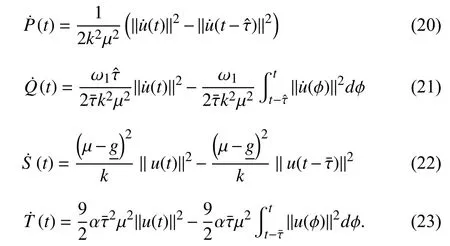
Canceling common terms, using Assumption 4, (7), (8),(10), and (20)–(23),can be upper bounded by
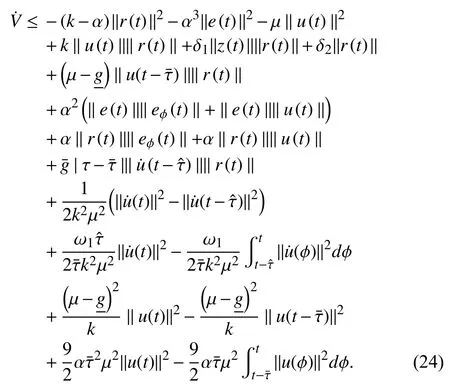
Based on Assumption 2 and using the Young’s inequality,the following terms in (24), can be upper bounded by
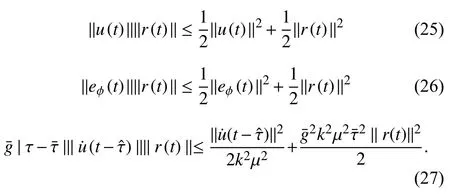
Using (25)–(27) and completing the squares, the inequality in (24) can be further upper bounded by
Based on (10) and Young’s inequality, the following inequality is obtained as
Using (29), the following inequalityand by applying the Cauchy-Schwarz inequalitythe expression in (28)can be further upper bounded by

Provided the sufficient gain conditions in (13) and (14) are satisfied, (30) can be simplified to


Using (15), it can be shown that

Using (31) and (33), the inequality in (31) is expressed as

provided

The solution of differential inequality in (35) can be obtained as
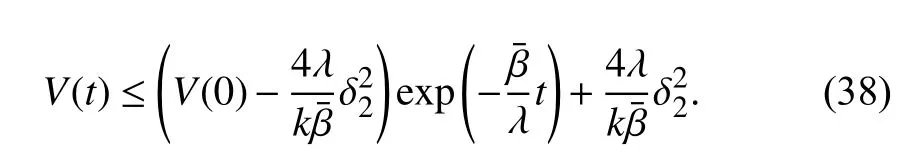
Using (15) and (38), the errorcan be expressed as
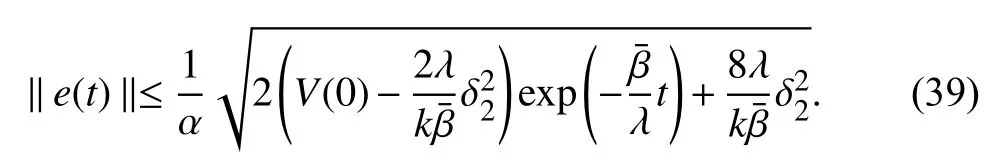
The expression in (39) can be used to prove the GUUB result in (12) withBased on (34), it is concluded thatSinceindicates that■
Remark 2:The design of the control law in (10) is motivated by the Lyapunov stability analysis, which requires us to inject the feedback signalsandinto the closed-loop error dynamics, since these components yield negative termsandrespectively, in the stability analysis. However, much insight can be gained from inspecting the expression of the control law as provided in Remark 1. The term I is a standard PI (proportional integral) controller where the integral action provides robustness to the external disturbances, including time delays as proposed in [37]. Term II corresponds to the delay compensation term as it includes a finite integral of past control values in the intervalThis term is responsible for canceling the input delay termin the stability analysis. Term III is used purely for stability purposes; specifically to cancel the left-over positive terms from the LK functional derivative, in the stability analysis.Overall, the controller is composed of a PI controller + delay compensator (based on a finite integral of the past control values).Remark 3:The gain conditions in (13) and (14) are nonlinear and coupled. For a given(lower bound ofa systematic method to choose the gains involves first selectingandto be sufficiently large as compared toandsuch that (13) holds. Then, these control gains can be used in (14) to obtain an upper bound on the delay boundSuffice it to say that for a given plant (specifically, the knowledge ofthe gain conditions in (13) and (14) impose a limit on how large aand consequentlycan be handled by the proposed controller.
V. Simulation
The dynamics of an input-delayed single link robot manipulator is considered as
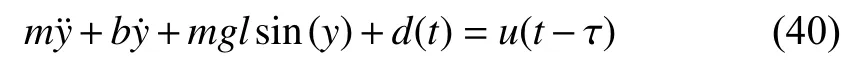
The values of system parameters are considered asm= 1 kg,b= 1,g= 9.8 m/s2and l = 0.1 m. The simulation is performed for different values of delay, i.e., 0.1 s, 0.5 s. and 0.8 s. The errors and control response are obtained for the dynamics given in (40) with a delay bound of 1 s. The tracking performance gradually degrades as the delay increases, as shown in Fig. 1. The control gainsand RMS value of errors are mentioned in 1. To test the robustness of the closed-loop system to variations in input delay,different types of variable delay, i.e.,(an example of sinusoidal delay), and normally distributed random delays are considered with the proposed controller for the dynamics given in (40). The error and control plots in Fig. 2 show that the tracking errors remain bounded for slowly timevarying delay.
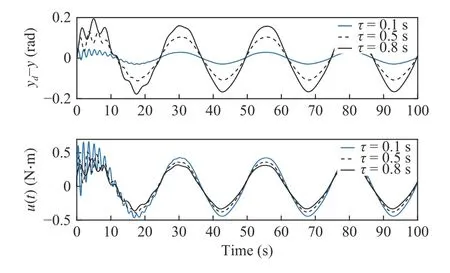
Fig. 1. Tracking error and control input response for the delay bound of 1 s.

Fig. 2. Tracking error and control input response for different values of variable delay and the delay bound of 1 s.
VI. Conclusions
This paper presents a novel input delay compensator to solve the problem of unknown constant input delay for a class of uncertain nonlinear systems. The proposed robust controller utilizes the knowledge of delay bounds to compensate input delays. Modified LK functionals, dependent on the delay bound, are used to derive sufficient gain conditions for GUUB tracking. Simulation results indicate that a less conservative delay bound leads to better tracking performance. This work can be extended to the case of unknown time-varying input delays, multiple input delays, and simultaneous state and input delays. The proposed result is not applicable to the case of arbitrary long unknown input delay, which remains a challenging problem for future research.
Appendix Proof for Lemma I

The filtered tracking error is defined as



The Lyapunov function candidate is considered as
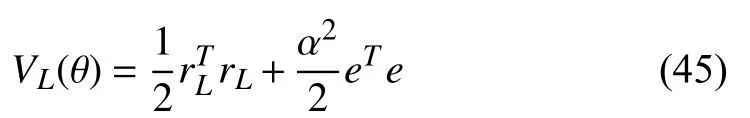
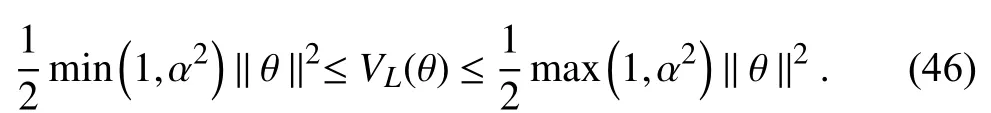
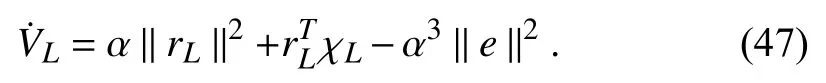
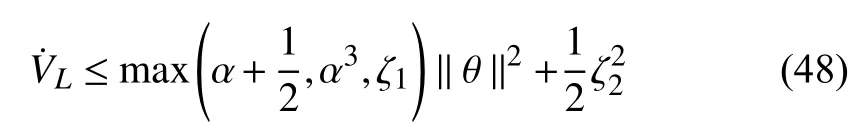

The expression in (49) is a linear differential inequality which proves that (41) does not exhibit finite escape time.
Acknowledgements
Ashish Kumar Jain gratefully acknowledges TEQIP-III,NPIU, MHRD, a world bank sponsored project for providing infrastructure and support throughout this work.
 IEEE/CAA Journal of Automatica Sinica2020年2期
IEEE/CAA Journal of Automatica Sinica2020年2期
- IEEE/CAA Journal of Automatica Sinica的其它文章
- Parallel Reinforcement Learning-Based Energy Efficiency Improvement for a Cyber-Physical System
- Flue Gas Monitoring System With Empirically-Trained Dictionary
- Post-Processing Time-Aware Optimal Scheduling of Single Robotic Cluster Tools
- Unified Smith Predictor Based H∞ Wide-Area Damping Controller to Improve the Control Resiliency to Communication Failure
- Optimal Neuro-Control Strategy for Nonlinear Systems With Asymmetric Input Constraints
- Adaptive Output Regulation of a Class of Nonlinear Output Feedback Systems With Unknown High Frequency Gain
