Optimal Neuro-Control Strategy for Nonlinear Systems With Asymmetric Input Constraints

Xiong Yang, and Bo Zhao,

Abstract— In this paper, we present an optimal neuro-control scheme for continuous-time (CT) nonlinear systems with asymmetric input constraints. Initially, we introduce a discounted cost function for the CT nonlinear systems in order to handle the asymmetric input constraints. Then, we develop a Hamilton-Jacobi-Bellman equation (HJBE), which arises in the discounted cost optimal control problem. To obtain the optimal neurocontroller,we utilize a critic neural network (CNN) to solve the HJBE under the framework of reinforcement learning. The CNN’s weight vector is tuned via the gradient descent approach. Based on the Lyapunov method, we prove that uniform ultimate boundedness of the CNN’s weight vector and the closed-loop system is guaranteed. Finally, we verify the effectiveness of the present optimal neuro-control strategy through performing simulations of two examples.

I. Introduction

REINFORCEMENT learning (RL), known as a research branch of machine learning, has been an effective tool in solving nonlinear optimization problems [1]. The main idea behind RL is to create an architecture to learn optimal policies without systems’ information. A well-known architecture used in RL is the actor-critic structure, which is comprised of two neural networks (NNs), that is, actor and critic NNs. The mechanism of implementing the actor-critic structure is as follows: The actor NN generates a control policy to surroundings or plants, and the critic NN (CNN) estimates the cost stemming from that control policy and gives a positive/negative signal to the actor NN [2]. Owing to this mechanism of actor-critic structure, one is able to not only obtain optimal policies without knowing systems’ prior knowledge, but also avoid “the curse of dimensionality” occurring [3]. According to [4], adaptive dynamic programming (ADP) also takes the actor-critic structure as an implementation architecture and shares similar spirits as RL. Thus, researchers often use ADP and RL as two interchangeable names. During the past few years, quite a few ADP and RL approaches emerged, such as goal representation ADP [5], policy/value iteration ADP [6],[7], event-sampled/triggered ADP [8], [9], robust ADP [10],integral RL [11], [12], online RL [13], [14], off-policy RL[15], [16].

Doubtlessly, the actor-critic structure utilized in RL has achieved great success in solving nonlinear optimization problems (see aforementioned literature). However, when tackling optimal control problems of nonlinear systems with available systems’ information, researchers found that the actor-critic structure could be reduced to a structure with only the critic, i.e., the critic-only structure [17]. The early research on solving optimization problems via a critic-only structure can be tracked to the work of Widrowet al.[18]. Later,Prokhorov and Wunsch [19] named this critic-only structure as a kind of adaptive critic designs (ACDs), which were originated from RL. After that, Padhiet al.[20] suggested a single network ACD to learn an optimal control policy for input-affine discrete-time (DT) nonlinear systems. Recently,Wanget al.[21] introduced a data-based ACD to acquire the robust optimal control of continuous-time (CT) nonlinear systems. Apart from the identifier NN used to reconstruct system dynamics, Wanget al.[21] proposed a unique CNN to implement the data-based ACD. Later, Luoet al.[22] reported a critic-onlymethod to derive an optimal tracking control of input-nonaffine DT nonlinear systems with unknown models. Following the line of [20]–[22], this paper aims at presenting a single CNN to obtain an optimal neurocontrol law of CT nonlinear systems with asymmetric input constraints.

System’s inputs/actuators suffering from constraints are common phenomena. This is because the design of stabilizing controllers must take safety or the physical restriction of actuators into consideration. In recent years, many scholars have paid their attention to nonlinear-constrained optimization problems. For DT nonlinear systems, Zhanget al.[23]presented an iterative ADP to derive an optimal control of nonlinear systems subject to control constraints. To implement the iterative ADP, they employed the model NN, the CNN,and the actor NN. By using a similar architecture as [23], Haet al.[24 ] suggested an event-triggered ACD to solve nonlinear-constrained optimization problems. The key feature distinguishing [23] and [24] is whether the optimal control was obtained in an event-triggering mechanism. For CT nonlinear systems, Abu-Khalaf and Lewis [25] first proposed an off-line policy iteration algorithm to solve an optimal control problem of nonlinear systems with input constraints.To implement the policy iteration algorithm, they employed aforementioned actor-critic structure. By using the same structure, Modareset al.[26 ] reported an online policy iteration algorithm together with the experience replay technique to obtain an optimal control of nonlinear constrained-input systems with totally unavailable systems’information. After that, Zhuet al.[27] suggested an ADP combined with the concurrent learning technique to design an optimal event-triggered controller for nonlinear systems with input constraints as well as partially available systems’knowledge. Recently, Wanget al.[28] reported various ACD methods to obtain the time/event-triggered robust (optimal)control of constrained-input nonlinear systems. Later, Zhanget al.[29] proposed an ADP-based robust optimal control method for nonlinear constrained-input systems with unknown systems’ prior information. More recently, unlike [28] and[29] studying nonlinear-constrained regulation problems, Cuiet al.[30] solved the nonlinear-constrained optimal tracking control problem via a single network event-triggered ADP.

Though nonlinear-constrained optimization problems were successfully solved in aforementioned literature, all of them assumed that the system’s input/actuator suffered fromsymmetricinput constraints. Actually, in engineering industries, there exist many nonlinear plants subject toasymmetricinput constraints [31]. Thus, one needs to develop adaptive control strategies, especially adaptive optimal neurocontrol schemes for such systems. Recently, Konget al.[32]proposed an asymmetric bound adaptive control for uncertain robots by using NNs and the backstepping method together.They tackled asymmetric control constraints via introducing a switching function. In general, it is challengeable to find such a switching function owing to the complexity of nonlinear systems. More recently, Zhouet al.[33] presented an ADP-based neuro-optimal tracking controller for continuous stirred tank reactor subject to asymmetric input constraints. They analyzed the convergence of the proposed ADP algorithm.But they did not discuss the stability of the closed-loop system. Moreover, they designed the optimal tracking controller for DT nonlinear systems, not for CT nonlinear systems. To the best of authors’ knowledge, there lacks the work on designing optimal neuro-controller for CT nonlinear systems with asymmetric input constraints. This motivates our investigation.

In this study, we develop an optimal neuro-control scheme for CT nonlinear systems subject to asymmetric input constraints. First, we introduce a discounted cost function for the CT nonlinear systems in order to deal with asymmetric input constraints. Then, we present the Hamilton-Jacobi-Bellman equation (HJBE) originating from the discountedcost optimal control problem. After that, under the framework of RL, we use a unique CNN to solve the HJBE in order to acquire the optimal neuro-controller. The CNN’s weight vector is updated through the gradient descent approach.Finally, uniform ultimate boundedness (UUB) of the CNN’s weight vector and the closed-loop system is proved via the Lyapunov method.

The novelties of this paper are three aspects.

1) In comparison with [25]–[30], this paper presents an optimal neuro-control strategy for CT nonlinear systems with asymmetric input constraints rather than symmetric input constraints. Thus, the present optimal control scheme is suitable for a wider range of dynamical systems, in particular,those nonlinear systems subject to asymmetric input constraints.

2) Unlike [32] handling asymmetric input constraints via proposing a switching function, this paper introduces a modified hyperbolic tangent function into the cost function to tackle such constraints (Note: here “the modified hyperbolic tangent function” means that the equilibrium point of the hyperbolic tangent function is nonzero). Thus, the present optimal control scheme can obviate the challenge arising in constructing the switching function.

3) Though both this paper and [31], [33] study optimal control problems of nonlinear systems with asymmetric input constraints, an important difference between this paper and[31], [33] is that, this paper develops an optimal neruo-control strategy for CT nonlinear systems rather than DT nonlinear systems. In general, control methods developed for DT nonlinear systems are not applicable to those CT nonlinear systems. Furthermore, in comparison with [31] and [33], this papers provided stability analyses of the closed-loop system,which guarantee the validity of the obtained optimal neurocontrol policy.

Notations:anddenote the set of real numbers,the Euclidean space of realand the space ofreal matrices, respectively.is a compact subset ofrepresents theidentity matrix.means the function with continuous derivative.anddenote the norms of the vectorand the matrixrespectively.denotes the set of admissible control on

II. Problem Formulation

We consider the following CT nonlinear systems

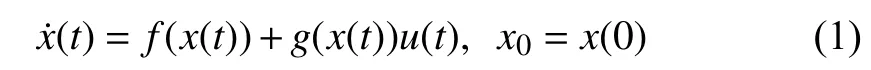
Remark 1:Generally speaking, the knowledge of system dynamics is not necessary to be known when one applies RL to design neuro-controllers for nonlinear systems, such as [34]and [35]. Here we need the prior information of system (1)(i.e.,andThis is because the neuro-controller will be designed only using a unique critic NN rather than the typical actor-critic dual NNs.

Assumption 1:is the equilibrium point of system (1) if lettingIn addition,satisfies the Lipschitz condition guaranteeing thatis the unique equilibrium point on

Assumption 2:For everywiththe known constant. Moreover,

Considering that system (1) suffers from asymmetric input constraints, we propose a discounted cost function as follows

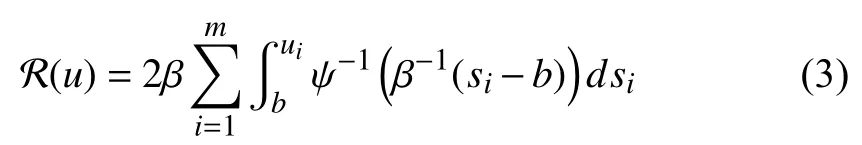
where

Remark 2:Two notes are provided to make (2) and (3)better for understanding, i.e.,

b) Owing to the asymmetric input constraints handled via(3), the optimal control will not converge to zero when the steady states are obtained (Note: According toin later(8), we can findMoreover, simulation results also verify this conclusion). Therefore, if letting(i.e., no the decay termthenmight be unbounded. That is why we introduce the discounted cost function (2).

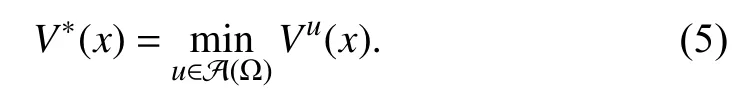
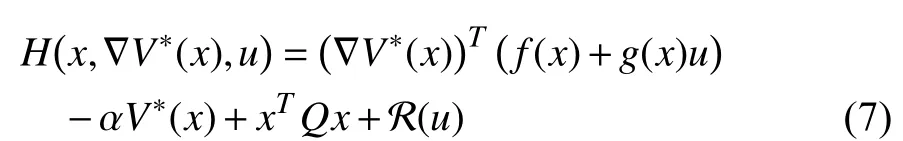
Applying the stationary condition [36, Theorem 5.8] to (7)(that is,we have the optimal control formulated as

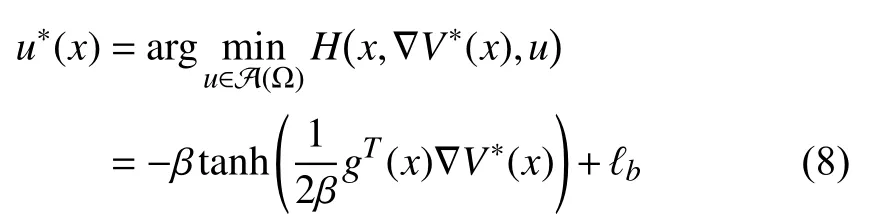
where

Inserting (8) into (6), we are able to rewrite the HJBE as

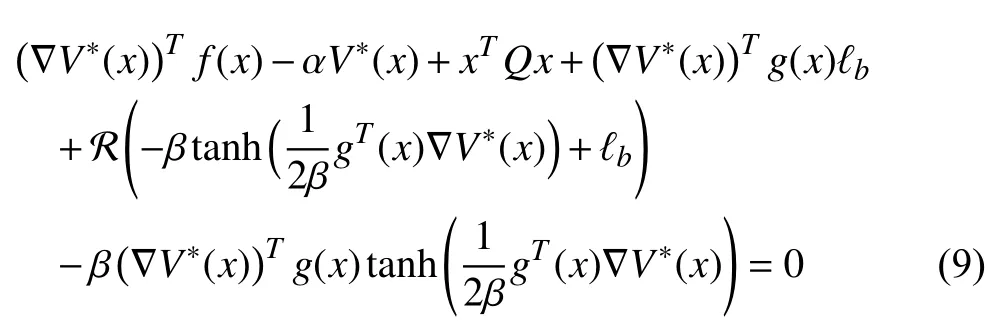
III. Optimal Neuro-control Strategy

The approximation characteristic of NNs indicated in [37]guarantees thatin (5) can be restated onin the form whereis the ideal weight vector often unavailable,denotes the number of neurons used in the NN,is the vector activation function comprised oflinearly independent elementsandandis the error originating from reconstructing

Then, we obtain from (10) that

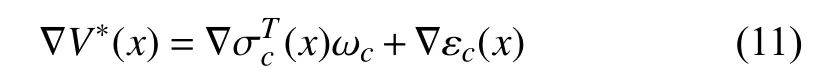
Inserting (11) into (8), it follows:

where

Remark 3:To make (12) easy for understanding, we present the detailed procedure as follows. Let

where

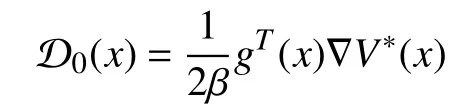
Then, using the mean value theorem [36, Theorem 5.10], we find

This verifies that (12) holds.

So, the estimated control policy ofcan be expressed as

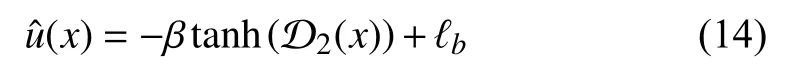
where

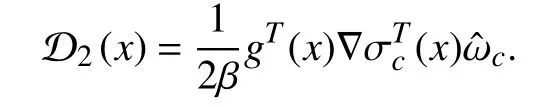
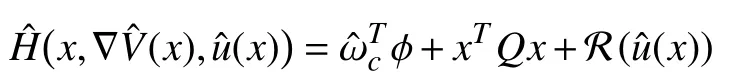
where

Then, we can describe the error betweenandas

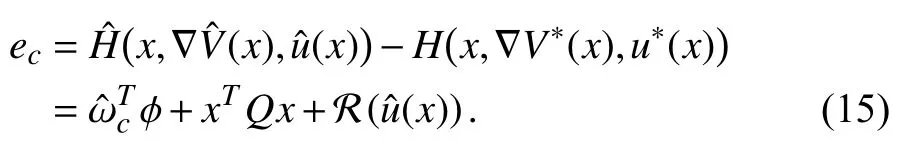
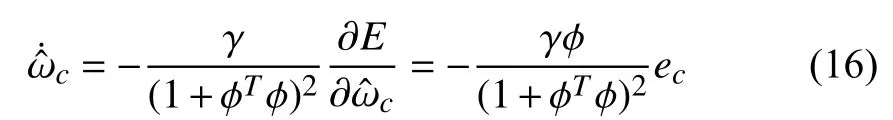
To summarize aforementioned descriptions of the proposed optimal control scheme, we present a block diagram in Fig. 1.

IV. Stability Analysis

Before proceeding further, we give two indispensable assumptions, which were employed in [38] and [39].

Assumption 3:For allthere areandwhereandare positive constants.

Fig. 1. Block diagram of the present optimal control scheme.

Assumption 4:in (17) satisfies the persistence of excitation (PE) condition. Specifically, we have constantsandsuch that, for arbitrary time

Theorem 1:Consider system (1) with the related control(14). Given that Assumptions 1–4 hold and the update rule for CNN’s weight vector is described as (16). Meanwhile, let the initial control for system (1) be admissible. Then, UUB of all signals in the closed-loop system is guaranteed.

Proof:Let the Lyapunov function candidate be

Considering the derivative ofalong the solution ofwe have

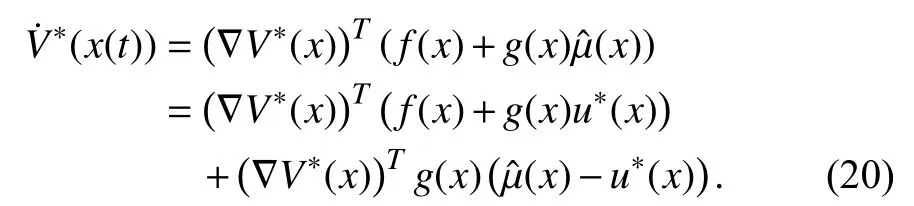
According to (6)–(8), there holds

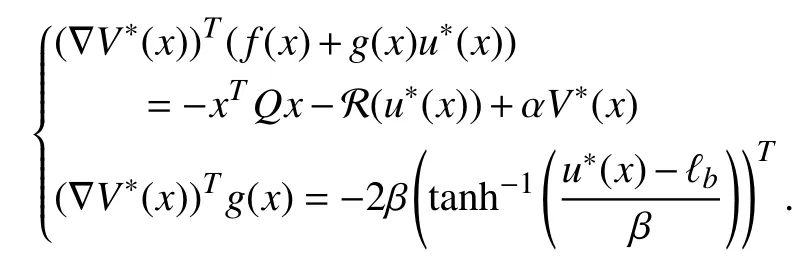
Then, after performing calculations, (20) can be restated as

with

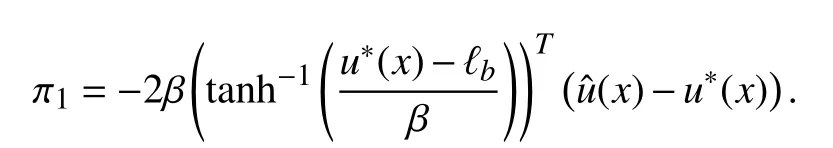
holds. Then, using (12) and (14), we havein (21) satisfied

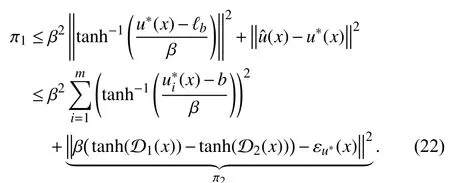
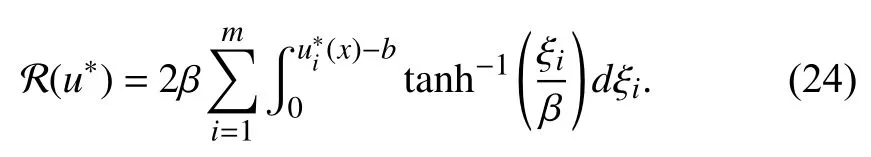
Similar to the proof of [42, Theorem 1], after performing some calculations, we can restatein (24) as

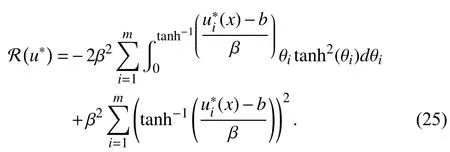
Thus, combining (22), (23), and (25), we find that (21)yields

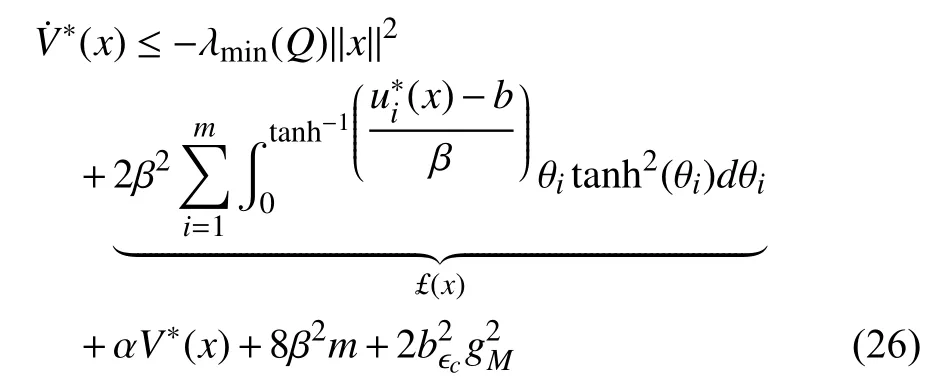
where

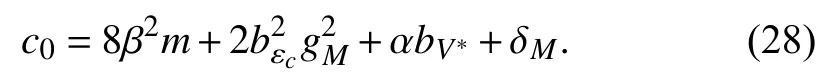
Second, we consider the time derivative ofUsing (17), we can see thatbecomes

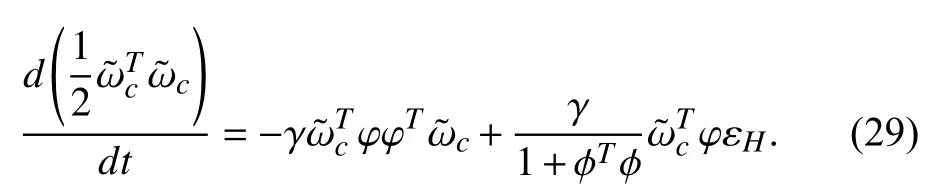
Based on aforementioned inequalityand the fact thatwe get

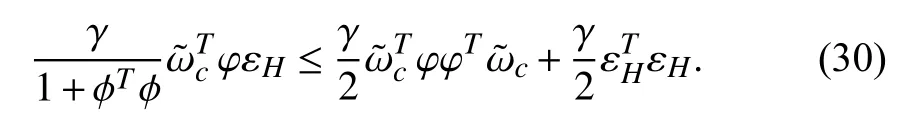
Then, using Assumptions 3 and 4 as well as (30), we can further write (29) as

Combining (27) and (31), it can be observed thatin(19) satisfies

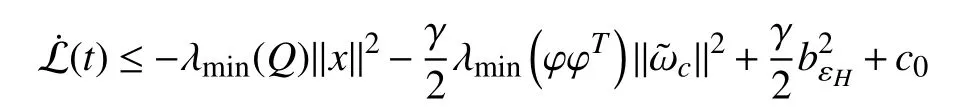
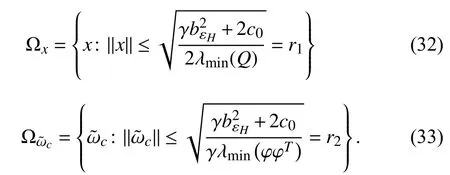
Remark 4:The key to making the inequality (31) valid lies in that there isObviously, (18) guarantees thatholds. That is why we needto satisfy the PE condition in Assumption 4.

Theorem 2:With the same condition as Theorem 1, the estimated control policyin (14) can converge toin(12) within an adjustable bound.

Proof:According to (12) and (14) and using the mean value theorem [36, Theorem 5.10], it follows

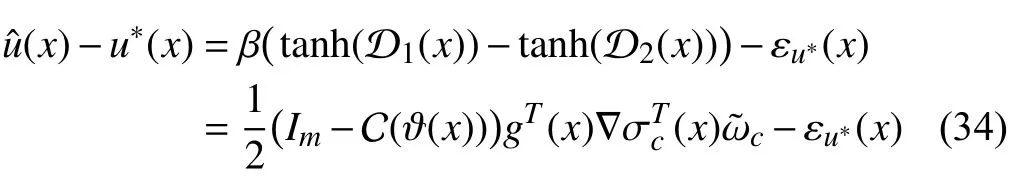
where

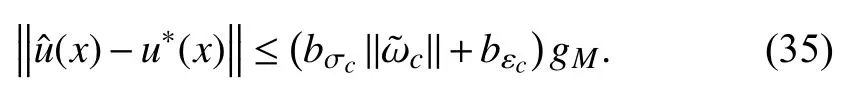
According to Theorem 1, the ultimate bound ofisin(33). Hence, from (35), we have

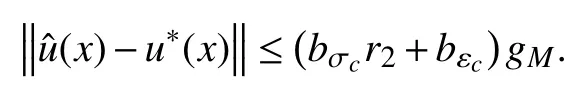
V. Simulation Results

To test the effectiveness of established theoretical results,we perform simulations of two examples in this section.

A. Example 1

We study the plant described by

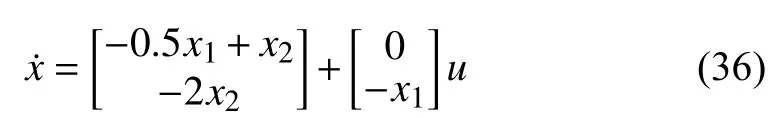
where (Note: according to (4),and

Remark 5:In this example, we determine the value of the discount factorvia experiment studies. In fact, there is no general method to determine the accurate range ofWe find that selectingin this example can lead to satisfactory results.

To approximate (37), we use the CNN described as (13)withMeanwhile, we choose the vector activation function asand denote its associated weight vector asThe initial weight vector is set asin order to guarantee the initial control policy for system (36) to be admissible (Note: according to (14), the initial control is associated with the initial weight vector. Thus, we can choose an appropriate initial weight vector to make the initial control admissible). The parameter used in (16) isMeanwhile, an exponential decay signal is added to system’s input to guaranteein (17) to be persistently exciting.

By performing simulations via the MATLAB (2017a)software package, we obtain Figs. 2–4. As displayed in Fig. 2,is convergent after the first 6 s. Here we denote the converged value ofThen, from Fig. 2,we findThe evolution of system statesandis shown in Fig. 3. Meanwhile,the control policyis illustrated in Fig. 4 . It can be observed from Figs. 3 and 4 that the system states converge to the equilibrium point (i.e.,while the control policy converges to a nonzero value (i.e.,This feature is in accordance with the analyses provided in Remark 2-b). In addition, Fig. 4 indicates that the asymmetric control constraints are overcome.

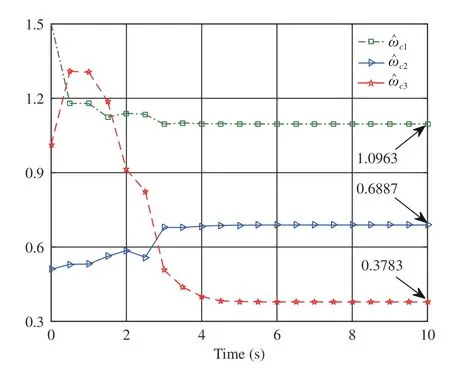
Fig. 2. Performance of

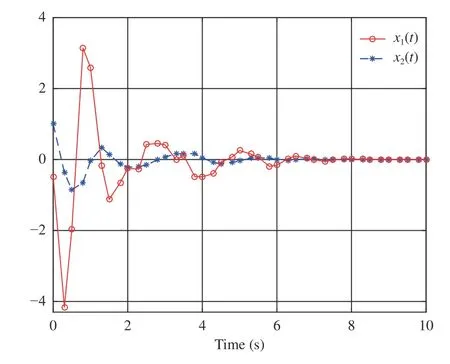
Fig. 3. System states and in Example 1.

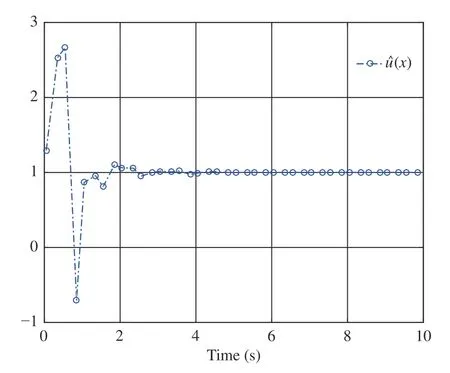
Fig. 4. Control in Example 1.

B. Example 2

We investigate the nonlinear system given as

Fig. 5. Performance of

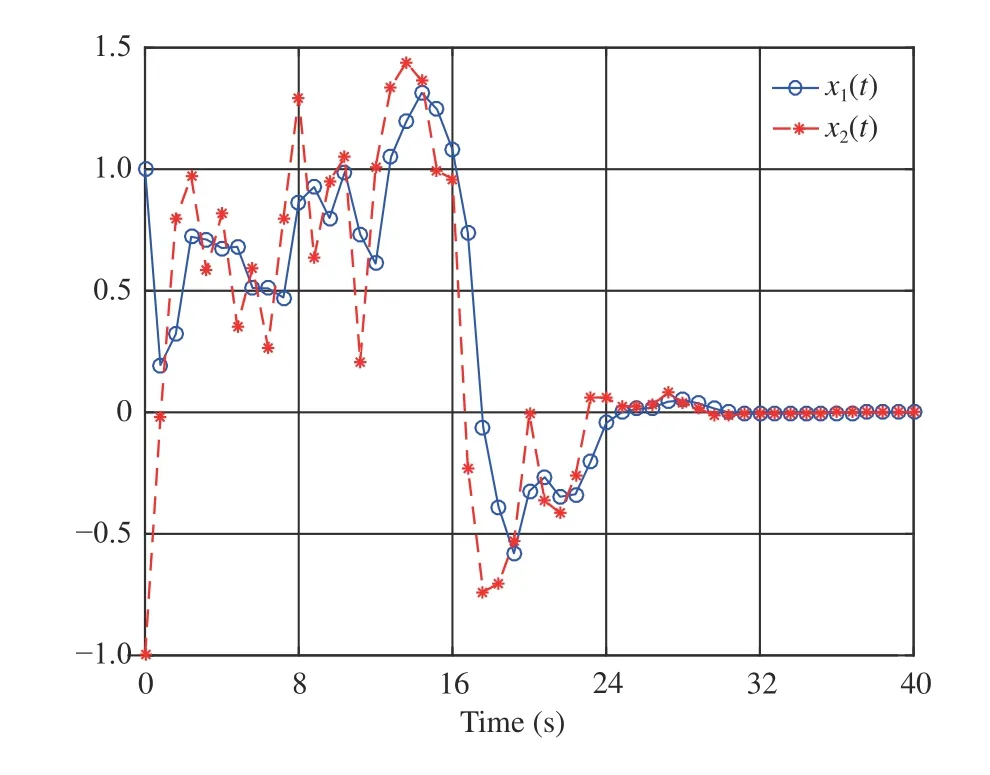
Fig. 6. System states and in Example 2.

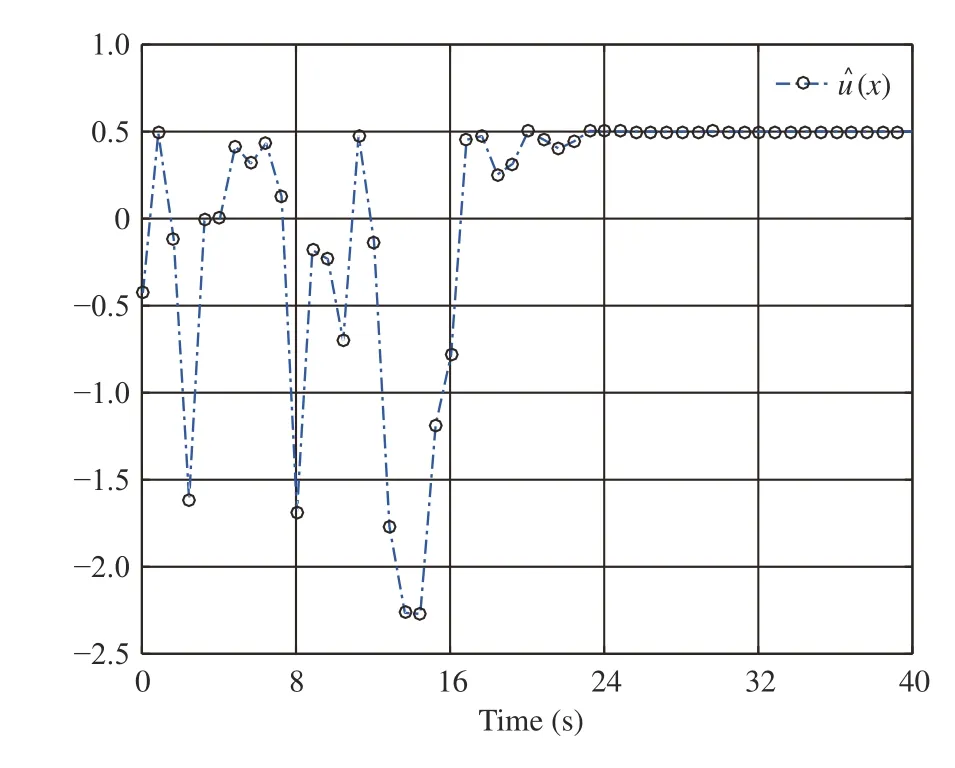
Fig. 7. Control in Example 2.

We perform simulations via the MATLAB (2017a) software package and then obtain Figs. 5–7. Fig. 5 shows that the CNN’s weight vectorconverges toafter the first 24 s. Figs. 6 and 7 present the evolution of system statesandand the control policyrespectively. We can see from Figs. 6 and 7 that the system states converge to the equilibrium pointwhile the control policy converges to a nonzero value (i.e.,This verifies the analyses provided in Remark 2-b). Moreover, Fig. 7 indicates that the asymmetric control constraints are conquered.

VI. Conclusion

An optimal neuro-control scheme has been proposed for CT nonlinear systems with asymmetric input bounds. To implement such a neuro-control strategy, only a CNN is employed, which enjoys a simpler implementation structure compared with the actor-critic structure. However, the PE condition is needed to implement the present neuro-optimal control scheme. Indeed, the PE condition is a strict limitation because of it difficult to verify. Recently, the experience replay technique was introduced to relax the PE condition[43], [44]. In our consecutive work, we shall work on combining RL with the experience replay technique to obtain optimal control policies for nonlinear systems.

On the other hand, it is worth emphasizing here that the steady states generally do not stay at zero, when the optimal control policy does not converge to zero. That is why we need the control matrix in system (1) to satisfy(see Assumption 2). Thus, this assumption excludes those nonlinear systems with the control matrixTo remove this restriction, a promising way is to allow the equilibrium point to be nonzero. Accordingly, our future work also aims at developing optimal nuero-control laws for nonlinear systems with nonzero equilibrium points. More recently, ACDs have been introduced to derive the optimal tracking control policy and the optimal fault-tolerant control policy for DT nonlinear systems, respectively [45], [46]. Therefore, whether the present optimal neuro-control strategy can be extended to solve the nonlinear optimal tracking control problems or the nonlinear optimal fault-tolerant control problems is another issue to be addressed in our consecutive study.