Effective Elastic Modulus Characteristics of Buoyancy Materials of Full-ocean-depth Manned Submersible
,,-,2,
(1.Shanghai Engineering Research Center of Hadal Science and Technology,College of Marine Sciences,Shanghai Ocean University,Shanghai 201306,China;2.School of Engineering,Westlake University,Hangzhou 310024,China;3.College of Food Science and Technology,Shanghai Ocean University,Shanghai 201306,China)
Abstract:In order to develop a high-performance full-ocean-depth buoyancy material,the meso-mechanical model of the body-centered cubic unit cell composed of glass microballoons and epoxy resin matrix is established, and the finite element program of ANSYS is used to evaluate the models which consist of different microballoon volume fraction and different wall thickness. The results show that:(1)the maximum stress is mainly concentrated on the inner surface of the glass microballoons and has a significant stress gradient; (2) when the volume fractions of microballoons are the same, as the r/R decreases,the maximum stress gradually expands from the boundary point of the equatorial position of the microballoons to the band of equatorial position. As the r/R further decreases, the stress begins to shift to the matrix; (3) the effective elastic modulus curves intersect at r/R=0.962, the larger the volume fraction of glass microballoons is, the faster the effective elastic modulus decreases with the increasing of r/R; (4) when t/R>0.04, the relative elastic modulus increases with the increase of the microballoons volume fraction; (5) the relationship among the thickness, the volume fraction of glass microballoons,the effective elastic modulus and specific gravity of buoyancy materials is obtained,which provides a theoretical basis for the development of high-performance full-ocean-depth buoyancy materials.
Key words:full ocean depth;buoyancy material;effective elastic modulus;finite element analysis
0 Introduction
Syntactic foams are lightweight closed-pore foams synthesized by dispersing hollow microspheres, called microballoons, in a matrix material[1]. Such composites are found to be highly damage-tolerant and energy-absorbent under a variety of loading conditions[2-4].
Syntactic foams are used as core materials in sandwich composites for aerospace and marine structural applications[5-7]. Hollow Glass Microspheres (HGM) filled polymer has been developed as buoyancy-aid materials in deep-sea applications as early as in 1950s[8].Materials to be used for deep-sea application must have[9]:(1)low compressibilities at high hydrostatic pressure; (2) low thermal expansion coefficients; (3) low water absorption; and (4) good fire resistance.Syntactic foam is known to possess low density,high stiffness,excellent compressive and hydrostatic strength and good impact behavior[10].
Buoyancy blocks are key components of a submersible. In order to ensure that the structure has a sufficient safety margin, a safety factor of 1.5 for buoyancy materials is required according to the latest version of CCS rule[11]. If this requirement is satisfied, the crushing pressure of the buoyancy material used in the full-ocean-depth manned submersible‘the Challenger Deep’should be greater than 170.7MPa[12].Currently only few companies claimed to be able to provide the buoyancy material for the full ocean depth, such as Trelleborg Offshore[13], Engineered Syntactic Systems[14], Ron Allum Deepsea Services (RADS)[15]and so on. Samples from these companies have been tested by the authors’group and the main discovery is that buoyancy materials fully satisfying the rule requirement of 1.5 safety factor do not exist.In order to use this buoyancy material in the full-ocean-depth manned submersible which does not meet the rule requirement,a better failure mechanism should be investigated.
At present, research on deep-sea buoyancy materials is still underway. Good mechanical properties and light weight are two aspects of balance.Better understanding the relationship between internal composition of the material and its mechanical properties is one of the foundations for developing buoyancy materials with excellent performance.
Several experimental studies can be found in the published literature characterizing syntactic foams for tensile, compressive, and flexural loadings[16-20]. Test results show that presence of stiff hollow inclusions can enhance the composite effective elastic modulus as compared to the neat resin material[21].These lightweight composite materials are finding applications in marine structures, where buoyancy is an important consideration. Studies specific to vinyl ester matrix syntactic foams have been reported,such as Tagliavia[22]and Gupta[23].
Except for experimental studies,a few theoretical models that relate mechanical properties with composition of syntactic foams are also available. A thorough overview of modeling efforts for particulate composites has been presented by Pal[24]. The Hashin’s technique, see Ref.[25],has been extended to syntactic foams by Lee and Westmann[26]to obtain a single equation for the bulk modulus and bounds for the shear modulus. Huang and Gibson estimated the elastic moduli by computing the change in strain energy due to a single hollow sphere in an infinite matrix material[3]. Results from both these approaches are accurate only for syntactic foams containing low volume fractions of microballoon. Application of self-consistent schemes to syntactic foams has also been proposed[27-29].
Available theoretical studies have clearly shown the effect of microballoons volume fraction and wall thickness on the stress distribution and modulus of syntactic foams[30-32]. Numerical methods have been extensively used for modeling composite materials, including syntactic foams[33-34]. However, such understanding is still insufficient for high volume fraction of microballoons.
In order to meet the needs of the development and utilization of marine resources, in recent years, Chinese scholars have also conducted a lot of research on buoyancy materials. One of the research fields focuses on improving the formulation of buoyancy materials for better performance. Yan et al[35]prepared chopped carbon fiber/hollow glass microballoons (K46)/epoxy composites by molding process, and studied the compressive strength and water absorption of composites.Pei et al[36]conducted an experimental study on the density,compression properties and water absorption of carbon-nanotube-reinforced solid buoyancy materials. Zhou Yun et al[37]prepared the buoyancy materials which mixed with a suitable ratio of carbon-fiber-reinforced polymer hollow spheres, epoxy resin, microballoons, and carried out experimental research on compressive strength and water absorption.Two types of buoyancy material were successfully prepared by Tianjing University[38-39], but the compressive strength is still difficult to meet the needs of the deep-sea application.
In addition, some scholars have focused on improving the coupling of the interface between the filler and the matrix to optimize the performance of buoyancy material. Chen et al[40]used epoxy resin cured by different curing agents as the matrix, and studied the effect of the amount of silane coupling agent on the water absorption and compressive strength of buoyancy materials. Liu et al[41]used epoxy resin as the matrix material to modify the surface of glass microspheres,and studied the density and compressive strength of solid buoyancy materials. Li et al[42]performed an interface activation treatment on hollow glass microspheres, and the hollow glass microspheres/epoxy solid buoyancy material prepared by the method has greatly improved the compressive strength.
Domestic research on similar composite materials mainly focuses on aviation and other fields. For the model research of buoyancy materials, it is still mainly in the exploration stage.Ni et al[43]used ANSYS to simulate the stress distribution cloud diagram of epoxy-based solid buoyancy materials with glass mircoballoon volume fraction of 50%. But the error between the intensity value obtained by the results of simulation calculation and the experimental value is large. The interface debonding and damage progression from voids in glass/epoxy syntactic foams are two of the most common types of detrimental processes that have significant negative impact on the composites strength[44].
The understanding of the mechanics of these materials is largely based on experimental studies. Predictive models capable of estimating the elastic properties of these materials over a wide variation of particle wall thickness, size, and volume fraction are not yet fully developed.In this paper, the micromechanics models were built to analyze the effect of microballoon volume fraction to the Young’s modulus,which contain high volume fraction of microballoons.Finite element method is used to obtain stress distribution in the matrix and in the hollow microballoons. Effective Young’s modulus is calculated for different loading cases and the effects of microballoon size and wall thickness on the mechanical properties of the composites are determined.
1 Analysis parameters
1.1 Model geometry
The binder (or matrix) used in syntactic foams can be polymers, metals, or ceramics. The important thermosetting polymers used in syntactic foams are epoxies, phenolics, cyanate esters, etc.[12]. Due to the limitation of environmental conditions, buoyancy materials are required to have high strength, light weight and low water absorption, etc.. So in this paper, we focus on the syntactic foam which consists of glass microballoons and epoxies.The microstructure of syntactic foam is presented in Fig.1(a), where glass microballoons are dispersed in an epoxy resin matrix.In previous studies,many unit cells were used to express the syntactic foams[12],such as Simple cubic (SC), Face centered cubic (FCC), Body centered cubic (BCC) unit cells[45]. Gupta et al[46]also created a model in which 50 glass mircoballoons were randomly distributed in the matrix. In this paper, the body centered cubic unit cells will be used to express the syntactic foam.This microstructure is the basis for developing a unit cell model shown in Fig.1(b).

Fig.1 (a)Microstructure of a syntactic foam,and(b)Body centered cubic(BCC)unit cells[45]
Two microballoons are embedded in the matrix on average, of dimensions 48.16 μm×48.16 μm×48.16 μm, to construct the unit cell shown in Fig.2(a).A microballoon is located in the center of the unit cell and eight eighth glass microballoons are located at the eight vertices of the cube. A regular arrangement of particles is considered in order to reduce the model to a unit cell. The wall thickness of the microballoon is varied from a thin-walled to a thick-walled particle. The size of the particle is varied in order to obtain different volume fractions from 10%to 60%.In the present geometry,the maximum microballoon volume of 60%can be obtained. Due to symmetry, one eighth of the unit cell, shown in Fig.2(b), is analyzed to reduce the computational resource usage. A commercial code Ansys 15.0 is used for the analysis.
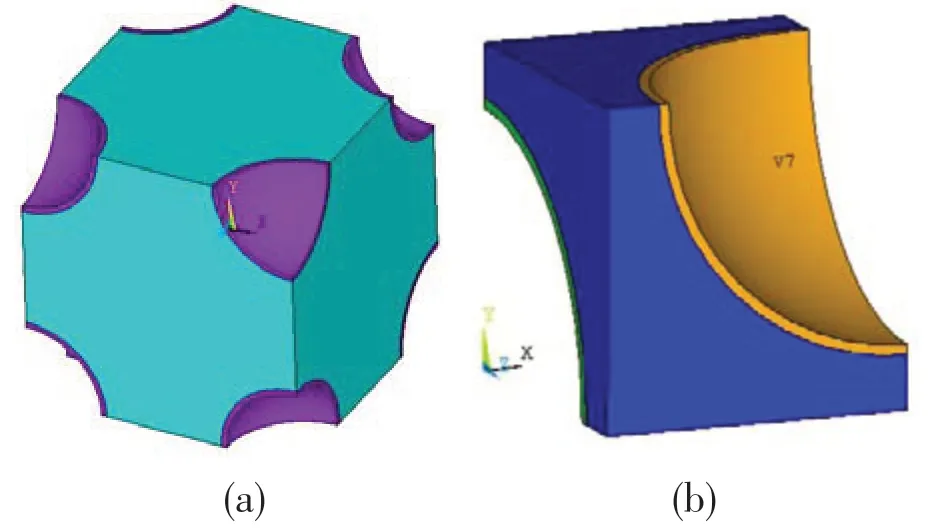
Fig.2 (a)Body centered cubic(BCC)unit cell of syntactic foam with 20% microballoon volume fraction and (b) Reduced model used in the analysis with 60% microballoon volume fraction
1.2 Element type and material properties
SOLID187 element is a higher order three-dimensional, 10-node element, which has a quadratic displacement behavior and is well suited to modeling irregular meshes (such as those produced from various CAD/CAM systems). The element is defined by 10 nodes having three degrees of freedom at each node: translations in the nodalx,y,andzdirections.The element has plasticity, hyperelasticity, creep, stress stiffening, large deflection, and large strain capabilities. It also has mixed formulation capability for simulating deformations of nearly incompressible elastoplastic materials, and fully incompressible hyperelastic materials.
The convergence of the solution is ensured by extensive mesh size analysis. The meshed model is shown in Fig.3(a). The material properties are selected based on widely studied glass microballoon/epoxy matrix syntactic foams. The elastic constants of the constituents used in the analysis are given in Tab.1. All the constituent materials are assumed to be linearly elastic and isotropic.
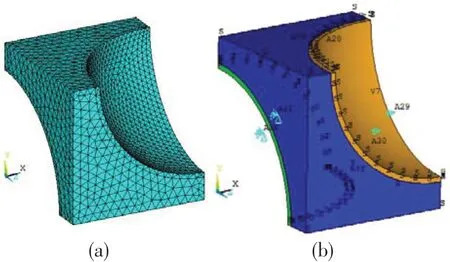
Fig.3 (a)Meshed model used in FEM and(b)With boundary conditions
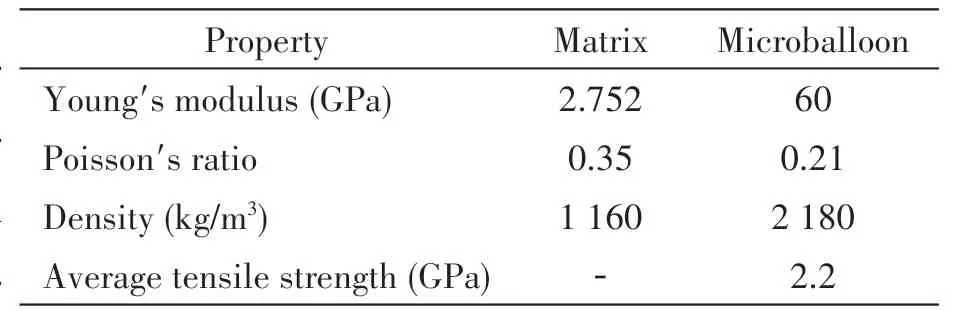
Tab.1 Material properties used in FEM[47]
1.3 Boundary conditions
Analysis of one eighth of the unit cell requires applying symmetry boundary conditions on surfaces which parallel to the loading axis. Three loading cases are analyzed in each model of this study, respectively. In each case, displacement load is applied on the unit cell surface along one of the coordinate axes, and the fixed surface is paralleled to the surface on which the displacement load is applied. Displacement load is applied along one axis and the modulus is calculated in that direction and then the process is repeated for the other two directions to independently determine modulus values in all three directions. Contacts at the microballoon-matrix interfaces are assumed to be perfect. During the analysis process, the convergence is ensured while the buoyancy material is in the stage of elastic deformation.
2 Results and discussion
In order to calculate the effective elastic modulus of the composite,the models with microballloon volume fraction from 10% to 60% were analyzed, and the microballloons radius ratior/Rwas increased from 0.75 to 0.99 (whererrepresents internal radius of sphere,Rrepresents outer radius of sphere, the following is the same). A displacement load is applied to the directions ofX,Y,Zfor each one-eighth cell model during the analysis process.
The effective elastic modulus is calculated as follows,

whereErepresents the effective elastic modulus of the buoyancy material;σstands for average stress;εstands for average stress.

whereFrepresents the force of loading direction;Astands for area.

whereu'represents the length after deformation;ustands for the length before deformation.
After solution, the force on the displacement loading surface in the direction of the displacement load was extracted, and the elastic modulus was calculated by the above formulas.Here we randomly selected nine sets of data from three models to analyze the modulus,tstands for thickness of sphere,as shown in Tab.2.
It can be seen from Tab.2 that in the case where the volume fraction and thickness of the glass microballoons are the same,the displacement loading direction has substantially no influence on the elastic modulus. Since the body cell model has symmetry, the glass microballoons and epoxy resin matrix can be regarded as a homogenous material. The average of these three Young’s modulus is calculated to characterize the effective elastic modulus of the buoyancy material.
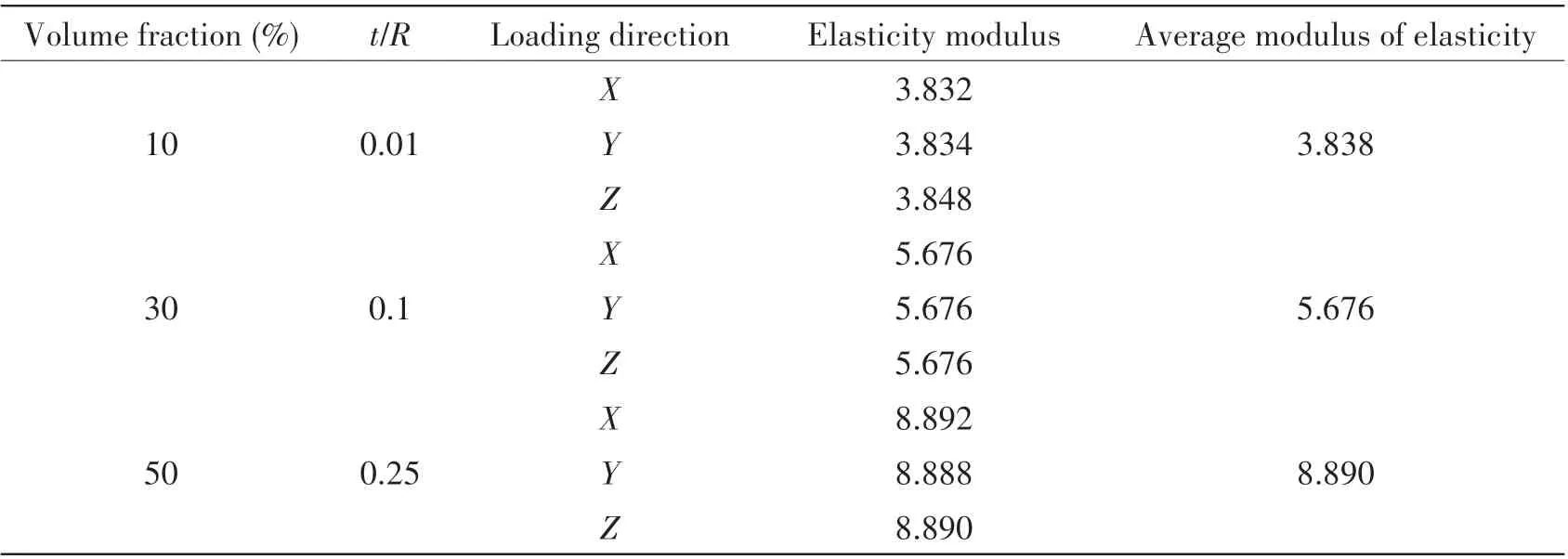
Tab.2 Randomly selected three sets of analysis results
Fig.4 compares the von-Mises stress distribution in composites containing microballoons of relative wall thicknessr/R=0.939 when the load is applied in theY-direction. Although the microballoon volume fraction is changing over a wide range in these models,the stress distribution is comparable.In each case the highest stress value is observed on the inner surface of the microballoon. At the ratior/R=0.939, the maximum stress value decreases at first and then increases as the volume fraction of microballoons increases (Fig.5). Therefore, the maximum stress is related to the thickness and volume fraction of the glass microballoons.
The stress distribution presented in Fig.4 can be compared with that in Fig.6,which shows the effect of change inr/Rat a constant volume fraction under the same applied loading conditions. Fig.4 also shows that the highest stress is on the inner surface of the thin-walled particle.
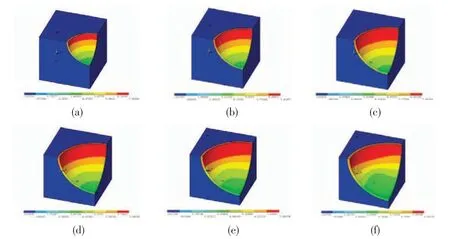
Fig.4 von-Mises stress in Y-direction loading of unit cell with r/R=0.939 and microballoon volume fractions of(a)10%,(b)20%,(c)30%,(d)40%,(e)50%,and(f)60%
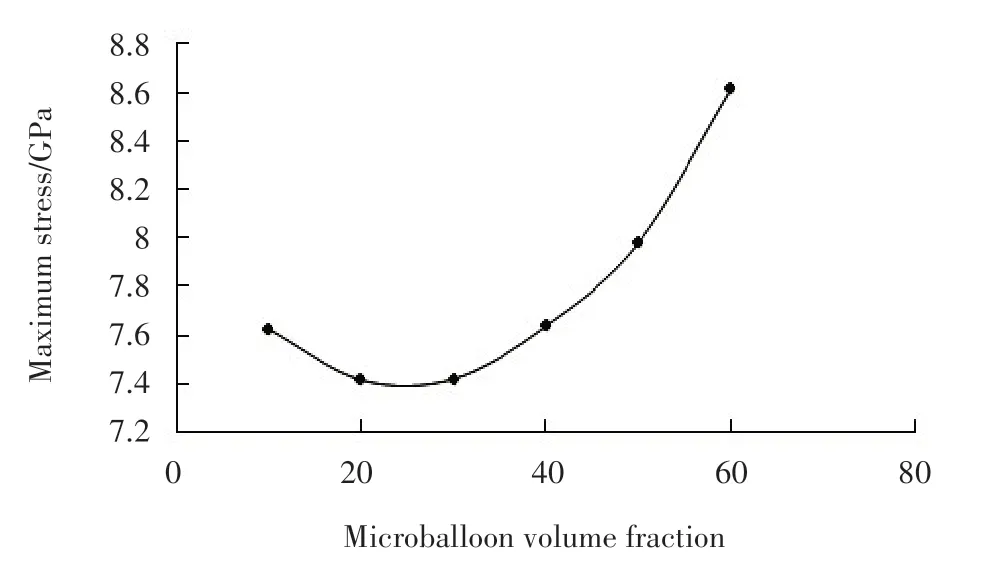
Fig.5 Maximum stress in Y-direction loading of unit cell with r/R=0.939
Although the maximum stress is still on the inner surface of the glass microspheres as the ratio ofr/Rdecreases, the stress gradually shifts to the matrix. Whenr/R=0.99, the maximum stress is concentrated near the two edge points at the equatorial position of the glass microspheres,as shown in Fig.6(a);asr/Rdecreases,the range of the maximum stress gradually expands to more areas around the equatorial position of glass microspheres,as shown in Fig.6(b).
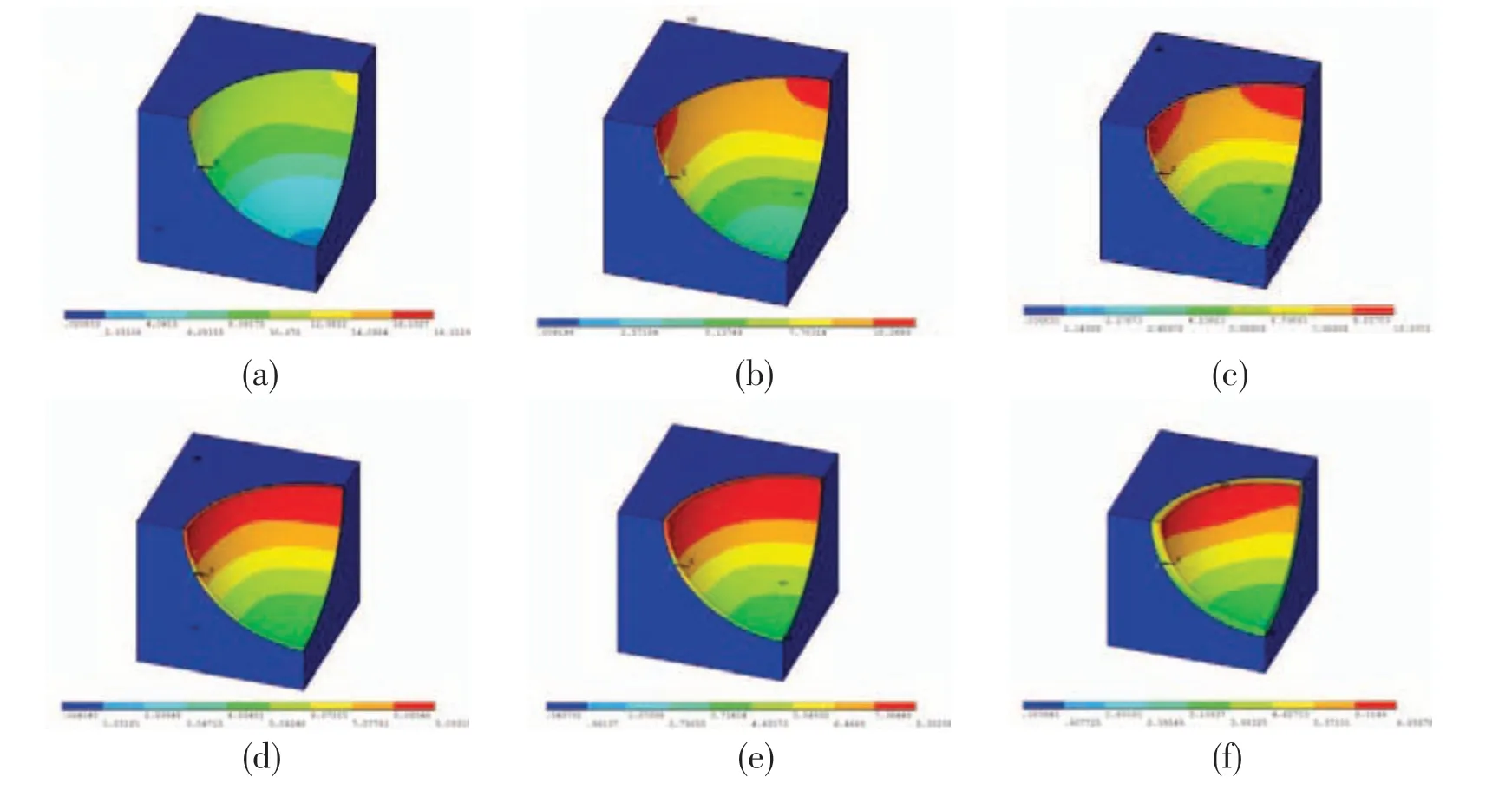

Fig.6 von-Mises stress in Y-direction loading of unit cell with particle volume fraction of 40%andr/R(a)0.99,(b)0.98,(c)0.97,(d)0.96,(e)0.95,(f)0.90,(g)0.85,(h)0.80 and(i)0.75
The value of maximum stress is lower for stiffer composite systems having thick walled microballoons. Fig.6 shows that the microballoon wall thickness can be used to manage the deformation and fracture behavior of syntactic foams.It also shows the possibility of fracture of thinwalled microballoons, which can be used as an energy absorption mechanism in these composites.
In both these loading conditions the location of maximum stress lies on the inner surface of the microballoons when thin-walled particles are used in the composite. In addition, severe stress gradient can exist within the mircoballoons walls.

Fig.7 The effective elastic modulus of the composite foam under different ratios of r/R
Fig.4 and Fig.6 show the same ratio ofr/Rand the same volume fraction of glass microballoons, respectively. Fig.7 and Fig.8 are drawn in order to show the effect of the glass microballoon volume fraction and the ratio ofr/Ron the effective elastic modulus of the composite more clearly.
It can be seen from Fig.7 that as the ratio of the inner and outer radii of the glass microballoons increases,the effective elastic modulus of the composite decreases gradually;the larger the microballoon volume fraction is, with the increase ofr/R, the sharper the effective elastic modulus decreases; on the contrary, the smaller the volume fraction of the glass microballoons,the slower the change of the effective elastic modulus with the increase ofr/R.The results of this study are consistent with the results of Porfiri[30].
Function fittings were performed on the curves, and the intersection point of the curves was calculated by the dichotomy method to be 0.962.As the increases ofr/R,the effective elastic modulus curves of different glass microballoon volume fractions intersect at a point where ther/Rvalue is 0.962. For composites with a glass microballoon volume fraction of 10%, the change of effective elastic modulus is relatively small whenr/R<0.956;whenr/R>0.962,the effective elastic modulus changes significantly. But the degree of the change is more pronounced as the mircoballoon volume fraction increases.
The position of the intersection point for each curve is about 0.962. This can be explained by the stress calculation formula of the perfect spherical shell. The perfect spherical shell has two possible failure modes. One is the maximum stress reaching the tensile strength (the same as the yield strength since glass is a very brittle material)and the other is elastic buckling leading to collapse.
The stressesσin a perfect spherical shell under uniform external pressure can be calculated by the following formula:

wherermrepresents the mean and middle radius of sphere;tstands for thickness of sphere;prepresents constant external pressure.
If the yield strength is regarded to be the maximum stress allowed in the sphere, the pressure at yielding of the sphere can be expressed as

wherepyrepresents yield load,σyrepresents yield strength.
For perfect spherical shells, the critical elastic buckling load of a complete sphere under external pressure was first derived by Zoelly in 1915[48].His equation is

wherePcrrepresents critical elastic buckling load ,μrepresents Poisson's ratio,Egrepresents Young’s modulus of sphere.
From Eq.(5) and Eq.(6), one can see that the minimal external pressure from the two failure modes depends on material property and the ratio oft/rm. Taking glass as an example, and assuming the mechanical properties of Tab.1,two curves ofpy~t/rmandpcr~t/rmcan be plotted as shown in Pan and Cui[48].Ift/rmsatisfies the following condition,

From Ref.[12],one can see the relationship amongrm,t,randRis as follows:

whererrepresents internal radius of sphere,andRrepresents outer radius of sphere.
When the tensile strength is higher than the elastic buckling strength, it is required that the critical value ofr/Rof the two failure modes should not exceed 0.939(the data in Tab.1 are used for calculation). The intersection of the effective elastic modulus curves is 0.962, very close to 0.939.The possible reason is that the glass microballoons are treated as ideal spherical shells in the present study.
The matrix may have some influence on the glass microballoons,which makes the theoretical formulas and simulation results of ANSYS slightly different.
Studies show that the interface properties play a major role in the failure behavior of syntactic foams, while the voids can reduce their tensile strength. In addition, the tensile strength decreases with the volume fraction of hollow particles, but increases with the particle shell thickness[44]. The effect of particle-matrix debonding on the tensile response of syntactic foams has been studied through the analysis of a single inclusion problem. Debonding and particle wall thickness also contribute to determining the composite properties[49].Therefore,the study of deep-sea buoyancy materials is relatively complex and requires research based on a series of questions.
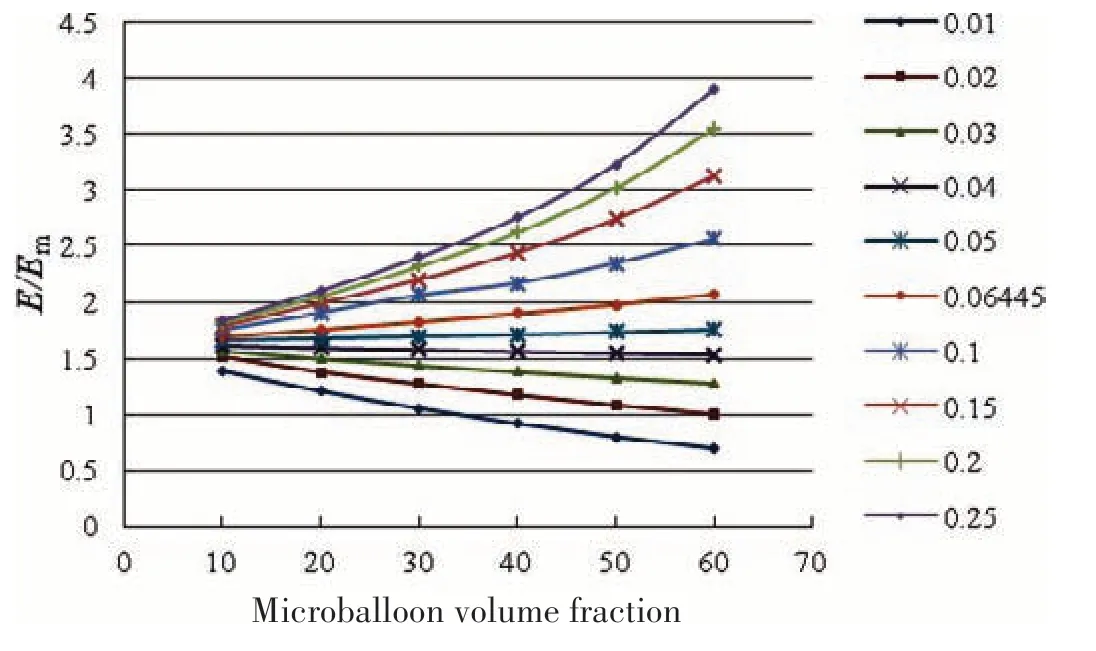
Fig.8 The ratios of the effective elastic modulus(E)of the composite foam to the elastic modulus of the matrix(Em)under different ratios of t/R
Fig.8 shows the relationship between the relative elastic modulus and the volume fraction of glass microballoons. The relative elastic modulus is the ratio of the elastic modulus of the composite to the elastic modulus of matrix. For the ideal two-phase composite material, in addition to the material properties of the matrix and the glass microballoons, the factors affecting the effective elastic modulus of the composite material are mainly the volume fraction and the ratio of the inner and outer radii of the glass microballoons.When the ratio of the wall thicknesstto the outer radiusRof the glass microballoons is close to 0.04,the relative elastic modulus of the composite does not change much with the increase of the microballoon volume fraction;whent/R<0.04,the volume fraction of the glass microballoons increases, the relative elastic modulus shows a decreasing trend; however,when the ratio oft/R>0.04,the relative elastic modulus tends to increase as the volume fraction of glass microballoons increases.
It is known that increasing the concentration of thin-walled particles results in reduced effective modulus of the composites. In comparison, thick walled particles result in increased composite modulus with the increase of the microballoon volume fraction.It can be seen that an appropriate increase in the thickness of the glass microballoons can increase the effective elastic modulus of the composite.
Fig.9(a) expresses the relationship among the volume fraction of the glass microballoons,the wall thickness and the effective elastic modulus more clearly.For full-ocean-depth buoyancy materials,increasing the effective elastic modulus of the composite material can enhance the ability to resist external seawater pressure and increase the material strength. However, as the ratio of the inner and outer radii of the glass microballoons decreases,the specific gravity of the deep-sea buoyancy material (the ratio of the density of the buoyancy material to the seawater density) is also increased, as shown in Fig.9(b). The development of full-ocean-depth buoyancy materials requires the search for areas with high effective elastic modulus and low specific gravity. It provides a reference for the development of full-ocean-depth buoyancy materials with a high performance according to Fig.9.
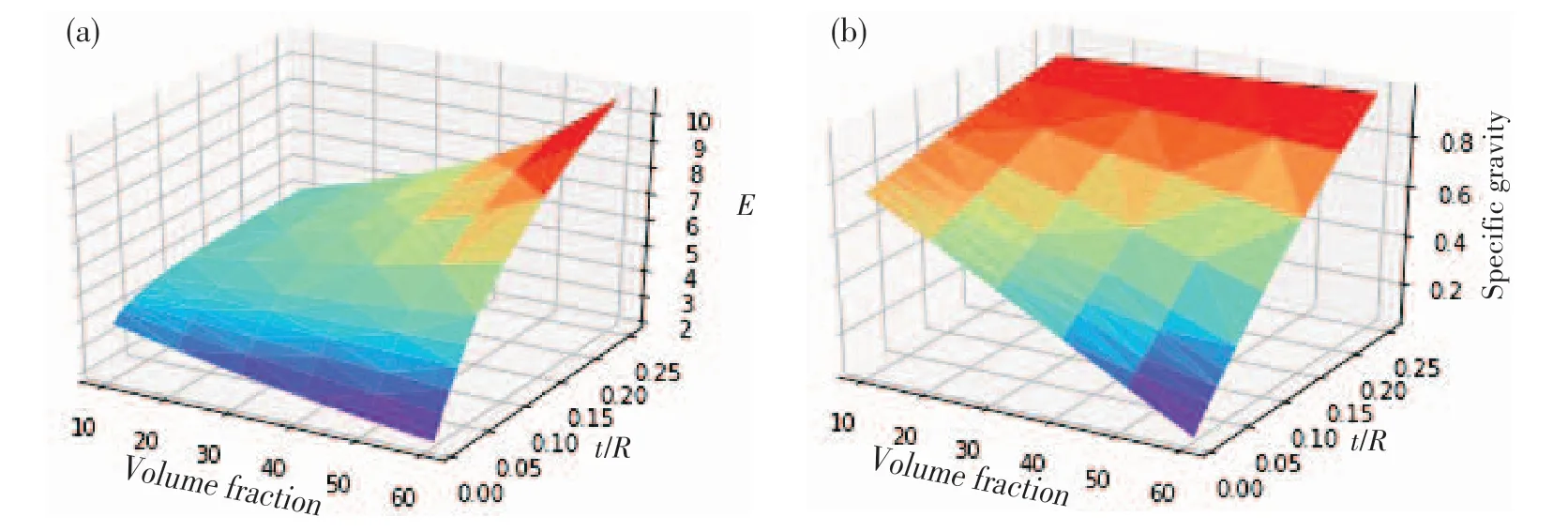
Fig.9 (a)Relationship among volume fraction,t/R and E and(b)Relationship among volume fraction,t/R and specific gravity(the normalized specific gravity)
3 Conclusions
In this paper, a series of simulation studies are carried out to study the performance of full-ocean-depth buoyancy materials. The contact interface between the glass microballoons and the matrix is approximated as a perfect contact, regardless of the influence of the air bubbles on the elastic modulus of the buoyancy material. The microscopic model of the body-centered cubic unit cell of buoyancy material is established.The models of buoyancy material with different glass microballoon volume fractions and different wall thicknesses are estimated by finite element analysis. A parametric study is conducted to observe the effect of microballoon volume fraction and wall thickness on the modulus of the composites. Through this preliminary study,the following conclusions can be drawn:
(1) A study of the stress distribution in the composite material reveals that the location of maximum von-Mises stress lies on the inner surface of the glass microballoons when thinwalled particles are used in the composite. In addition, severe stress gradient can exist within the mircoballoon walls.
(2) Although the maximum stress is still on the inner surface of the glass microspheres, asr/Rincreases, the stress has gradually shifted to the matrix. Increasing the concentration of thin-walled microballoons results in reduced effective modulus of the composites. To the contrary, thick- walled microballoons result in increased composite effective modulus with the increase of the microballoon volume fraction.The larger the microballoon volume fraction is,with the increase ofr/R,the sharper the effective elastic modulus decreases.
(3) The curves of the effective elastic modulus under different microballoon volume fraction intersect at 0.962,which is near the critical value 0.939 of the collapse of perfect spherical shell.
(4) For the study in this paper, whent/R=0.04, the relative elastic modulus does not change significantly with the increase of the glass microballoon volume fraction.
(5) Through the evaluation of ANSYS program, the relationships among the thickness, volume fraction of glass microballoons with the effective elastic modulus and the specific gravity of buoyancy materials were obtained, which provided a basis for the development of full-oceandepth buoyancy materials that meet the rule requirements of China Classification Society.
However,the present study is based on the two-phase structures in a syntactic foam material. Some further study can be done on the three-phase structures, water absorption, failure model and the effect of particle-matrix debonding in the future.
- 船舶力學(xué)的其它文章
- Fatigue Strength Assessment of Welded Joints Using Strain Energy Density Method Based on NSIF
- Hydrodynamic Analysis of a Spar Platform under Asymmetrical Mooring System
- Effects of Inflow and Outflow of Floodwater on the Parametric Roll of a Damaged Ship
- Analysis of Drilling Riser in Re-entry Operation Under Complex Currents
- Nonlinear Numerical Simulation for Flexible Pipes Carcass Wet Collapse
- Numerical and Experimental Study for SCR with Cable3D

