一類根式函數(shù)的最小值的解法與變式

武漢職業(yè)技術(shù)學(xué)院商學(xué)院(430074) 鄒 峰

安徽省和縣第一中學(xué)(238200) 蔣寶童

題目已知a,b＞0且2a+b=1,求f(a,b)=的最小值.

這是一道常見(jiàn)的根式函數(shù)的最值問(wèn)題,問(wèn)題簡(jiǎn)潔明了,本文利用柯西不等式及二次待定系數(shù)法給出其解法,并對(duì)其進(jìn)行拓展,給出一些變式,希望對(duì)讀者有所幫助、啟發(fā).

解由

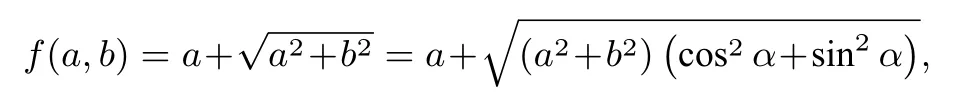
問(wèn)題1已知a,b＞0且2a+9b=1,求f(a,b)=的最小值.

解由

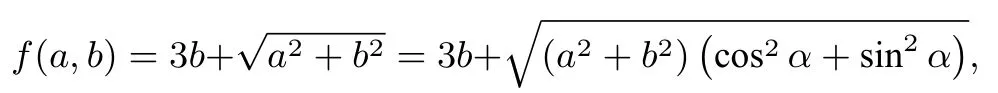
問(wèn)題2已知a,b＞0且3a+4b=1,求f(a,b)=的最小值.

解由

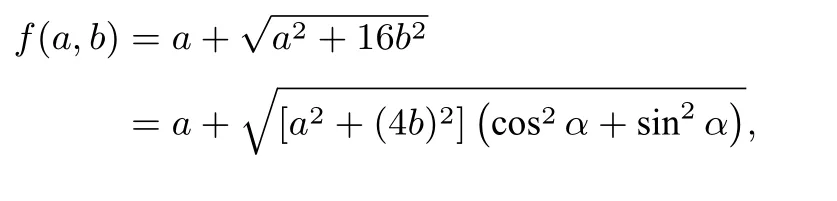
問(wèn)題3已知a,b＞0且a+b=1,求f(a,b)=的最小值.

解由

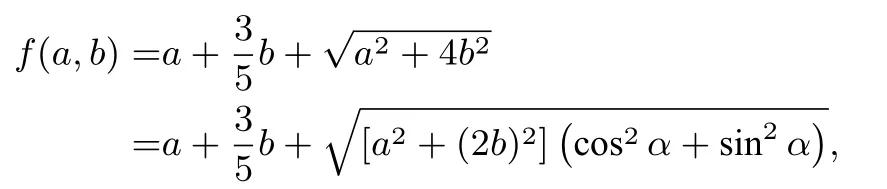
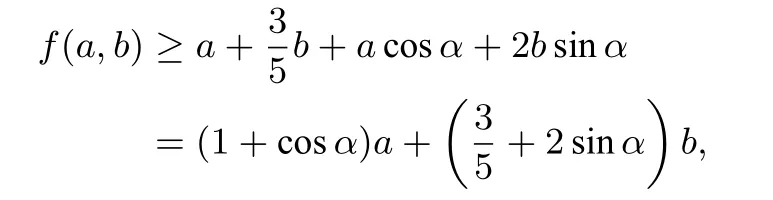
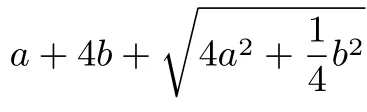
解由

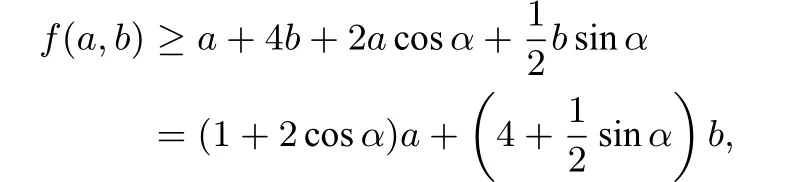
變式1已知a,b＞0且=1,求f(a,b)=的最小值.

解由

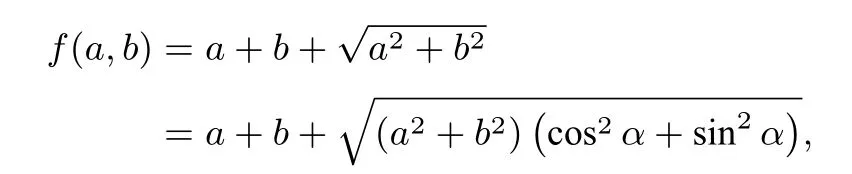
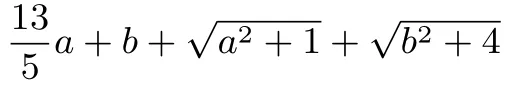
解由

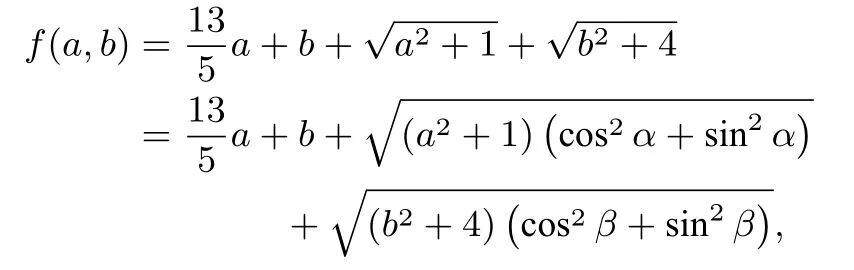
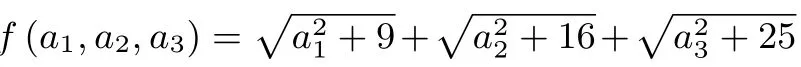
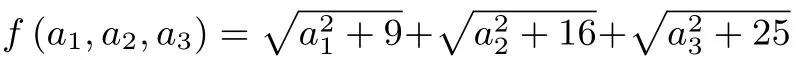
推廣1設(shè)ai,bi(i=1,2,3,···,n)均為正實(shí)數(shù),給定n∈N*,k∈R+且k為常數(shù),滿足則的最 小 值為當(dāng)n=1,k=1時(shí),問(wèn)題即為上文的題目.

推廣2設(shè)ai,bi(i=1,2,3,···,n)均為正實(shí)數(shù),給定n∈N*,滿足則的最小值為當(dāng)n=1時(shí),問(wèn)題即為變式1.

推廣3設(shè)ai,bi(i=1,2,3,···,n)均為正實(shí)數(shù),給定n∈N*,滿足則的最小值為當(dāng)n=1,k=1時(shí),問(wèn)題即為變式2.

推廣4設(shè)ai,bi(i=1,2,3,···,n)均為正實(shí)數(shù),給定n∈N*,k∈R+且k為常數(shù),滿足

以上幾個(gè)推廣給有興趣的讀者去完成.