SymTopo: An automatic tool for calculating topological properties of nonmagnetic crystalline materials?

Yuqing He(賀雨晴), Yi Jiang(蔣毅), Tiantian Zhang(張?zhí)锾?,He Huang(黃荷), Chen Fang(方辰), and Zhong Jin(金鐘)

1Computer Network Information Center,Chinese Academy of Sciences,Beijing 100190,China

2University of Chinese Academy of Sciences,Beijing 100049,China

3Beijing National Laboratory for Condensed Matter Physics,and Institute of Physics,Chinese Academy of Sciences,Beijing 100190,China

4Center of Scientific Computing Applications&Research,Chinese Academy of Sciences,Beijing 100190,China

Keywords: topological insulators, topological semimetals, topological invariants, high-throughput research mode

1. Introduction

Topology is a branch of modern mathematics that studies the features of shapes that are invariant under continuous deformation. It has found wide applications in the study of condensed matter physics in the recent years. For example,the entire field of topological insulators derives from the intricate interplay of topology and symmetry[1-4]and gives birth to many topological materials with exotic properties, such as surface states free from back-scattering[5]and Majorana zero modes[6]that may play a key role in fault-tolerant quantum computation.[7]The first step of discovering a new topological material is typically the numerical prediction of its potential topological properties,[8-12]which is a difficult step because of the involved expression of the topological invariants.

Recent theoretical progress, including theory of topological quantum chemistry,[13]symmetry-based indicators,[14]and the following works of mapping the irreducible representations (irreps) of valence bands onto topological invariants[15-17]and topological nodes,[18]has greatly relieved the workload needed for predicting the nontrivial topology in materials. According to these theories, only the irreps of the valence bands at the high-symmetry points(HSPs)in the Brillouin zone(BZ)(at most 8 in 230 space groups)are required to diagnose the topological properties,which significantly reduce the amount of first-principles calculation,making it possible to scan through large material databases to search for topological materials.Three independent works published in Nature[19-21]adopted similar algorithms and found thousands of new topological materials. A brief comparison of these three works is given in Appendix A.

In our article titled “Catalogue of topological electronic materials”,[19]we developed a fully automatic algorithm and scanned approximately 4×104crystalline materials, finding more than 8000 of them (approximately 9000 if ignoring the spin-orbital coupling effect) being topologically nontrivial.We classified these topological materials into“high-symmetry point semimetal”(HSPSM),“high-symmetry line semimetal”(HSLSM), “generic-momenta semimetal” (GMSM), “topological insulator”(TI),and“topological crystalline insulator”(TCI).The first three are topological semimetals with topological nodes at HSPs,high-symmetry lines(HSLs),and generic points in the BZ, respectively, whereas the last two are topological gapped systems protected by time-reversal symmetry and crystalline symmetries, respectively. All the results from the sweeping scan can be found at http://materiae.iphy.ac.cn.

Here, we give a thorough description of the algorithm used in the sweeping scan and elucidate important technical details that are missing in the previous article because of a limited article length of Nature. Meanwhile,we report the development of an automated package named SymTopo based on the algorithm. The package interfaces with two widely used first-principles calculation software Vienna ab initio simulation package(VASP)[22-25]and ABINIT,[26-29]enabling users with or without expertise in the symmetry-based indicators theory to easily diagnose the topological properties of materials using our algorithm.

2. Algorithm

Figure 1 summarizes the automatic algorithm for determining the topological classification of a nonmagnetic crystalline material. Starting from an arbitrary nonmagnetic crystalline material,the main steps of the algorithm are as follows:

(i)Check the number of electrons per unit cell.The material is labeled as a conventional metal if it has an odd number of electrons per unit cell,and no further analysis is performed.

(ii) Identify the space group of the crystal structure and standardize the structure for the convenience of further calculations.

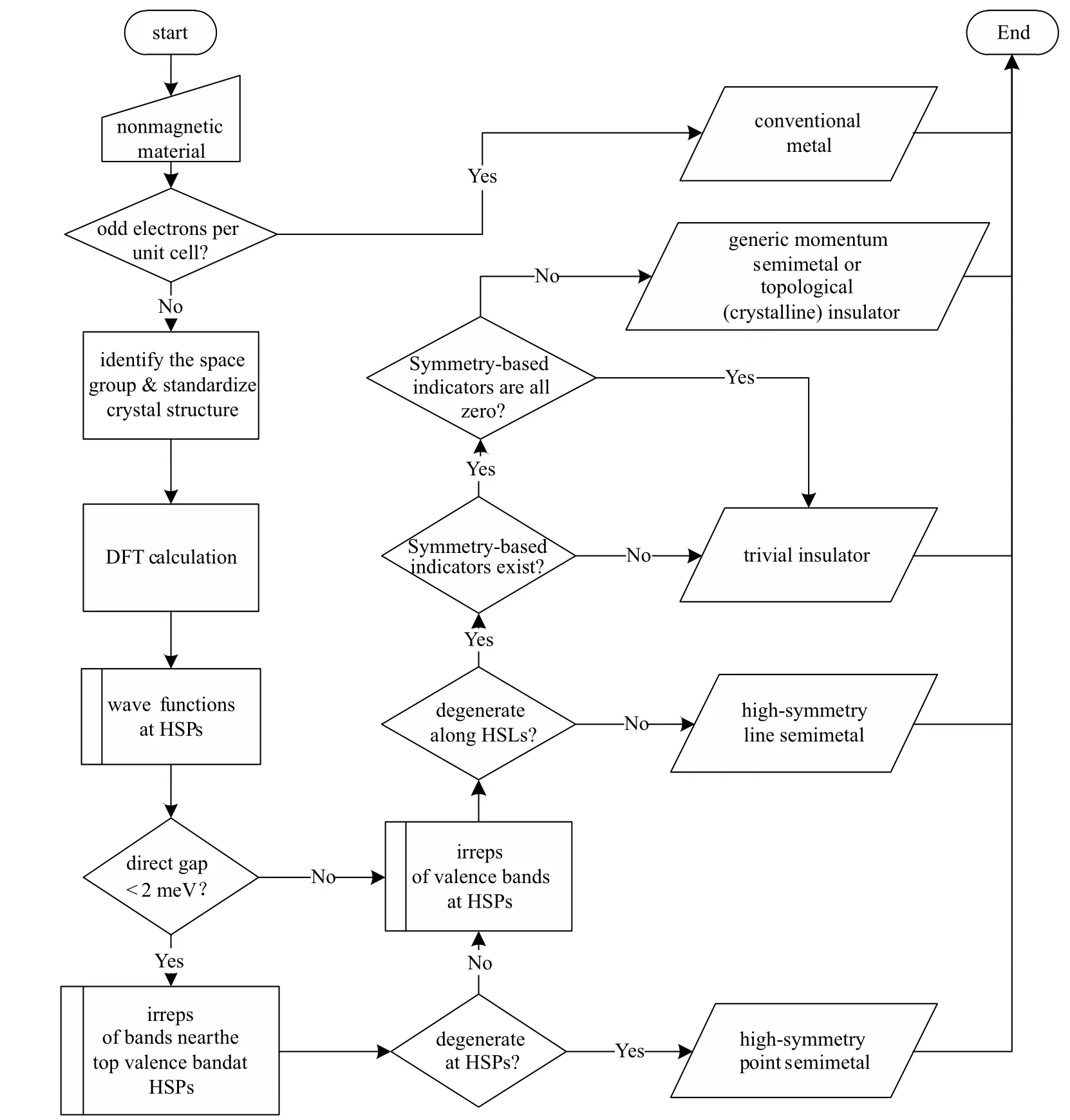
Fig.1. Flowchart of the algorithm.

(iii)Perform the density functional theory(DFT)calculation for the standardized structure to obtain the wavefunctions and energy eigenvalues at each HSP in the BZ.The calculation is typically performed using selected first-principles software.

(iv) Check the degeneracy between valence and conduction bands at the HSPs. This step is only performed if the material has a direct band gap smaller than 2 meV.The material is labeled as an HSPSM if such degeneracy exists,and no further analysis is performed.

(v)Calculate the irreps of all valence bands at each HSP.

(vi) Check the band crossings between the valence and conduction bands along the HSLs. To do so, the irreps of all valence bands are checked against the compatibility conditions. The violation of the compatibility conditions indicates the existence of band crossings along HSLs,in which case the material is labeled as an HSLSM, and no further analysis is performed;otherwise,proceed into the next step.

(vii) Calculate the symmetry-based indicators. Materials with nonzero indicators are labeled as GMSM in the nsoc setting and TI or TCI in the soc setting. This concludes the algorithm.

In the following subsections, we walk through the diagnosis process with two well-known topological materials,namely SnTe and HgTe, as examples. The technical issues involved in the implementation are described in detail.

2.1. Space group identification and crystal structure standardization

In the preparation step,we first identify the space group of the crystal structure for a nonmagnetic material with an even number of electrons per unit cell and standardize it using an open-source computational material science package, called Phonopy.[30]

The structure data of a material may have numerical errors and different choices of coordinate axes and origin. We use Phonopy to standardize the structure to facilitate highthroughput calculations.Given an input structure and error tolerance, Phonopy will identify its corresponding space group,minimize the error of the atomic positions with respect to the space group,and transform the coordinate system to a consistent primitive cell basis convention. This consistent convention provides a basis to define the matrix forms of the symmetry operations in each space group that are used to calculate the irreps of the wavefunctions later.

We set a default error tolerance of 10-4?A for Phonopy to identify the space group. If the input crystal structure is already associated with a space group and the designation is different from Phonopy’s result, we increase the error tolerance until Phonopy finds the designated space group or the error tolerance reaches 0.1 ?A,in which case the input data are considered to have large numerical errors and should be replaced by a more accurate structure.

Take SnTe of space group 225 as an example.Table 1 lists its primitive cell basis vectors of the original and standardized structures. Notice that the coordinate system is transformed.

Table 1.Primitive cell basis vectors of SnTe in the soc setting(unit: ?A).

2.2. DFT calculation

The standardized crystal structure is fed to the firstprinciples calculation software once obtained. Following the standard DFT calculation procedure, the self-consistent electron density is first calculated and used in the second step to compute the wavefunctions along with the energy eigenvalues at a given list of HSPs in the BZ.The lowest N bands(N being the number of electrons per unit cell)at each HSP are defined as the valence bands.

An HSP is a k-point in the BZ with the highest symmetry in its neighborhood. The positions of the HSPs are determined by the space group with a maximum number of 8 in all 230 space groups. The coordinates of the HSPs for each space group can be found at “The k-vector types and Brillouin zones of Space Groups”on the Bilbao Crystallographic Server (BCS).[31,32]Two HSPs related by time-reversal symmetry (with opposite coordinates and one with a suffix “A,”e.g.,“K”and“KA”)are both listed on this page,and we only use one of them.

The HSPs and the symmetry operations of the 230 space groups on the BCS are given in its conventional cell basis convention. They must be transformed into Phonopy’s primitive cell basis convention to be consistent with the crystal structure and the DFT calculation results. These two sets of convention differ by a similarity transformation of the coordinate axes and a shift of origin,which are listed in Appendix B.In either case,the coordinates of the HSPs are given as fractions of the reciprocal lattice basis,with the reciprocal lattice basis vector being defined by the standard formulas

where a1,a2,a3are the basis vectors of the primitive cell.

SnTe of space group 225 only has four HSPs in the BZ,namely Γ =[0,0,0],L=[1/2,1/2,1/2],W =[1/2,1/4,3/4],and X=[1/2,0,1/2],with the fractional number being the coordinates under the reciprocal lattice basis in Phonopy’s primitive cell convention.

We conducted the calculation with the generalized gradient approximation of the Perdew-Burke-Ernzerhof (PBE)-type exchange-correlation potential using the pseudopotential files of the projector augmented-wave atomic dataSubsection 3.1 lists the other important input parameters. The calculation may be performed with the spin-orbit coupling turned on and off,which are briefly called the“soc setting”and the“nsoc setting,”respectively.Note that although spin-orbit coupling always exists in realistic materials,ignoring it is a more physically relevant approximation for systems consisting of small atoms. For materials with a large spin-orbit coupling, the results obtained in the nsoc setting can be used as a reference and may help diagnose the origin of topological properties in the soc setting.

2.3. Irreducible representations extraction

Extracting the irrep of each(multiplet of)valence band(s)is one of the core modules of the algorithm.In the case of onedimensional irreps (the higher dimensional case will be discussed later),the wavefunction of each band at each HSP has the corresponding little group symmetry and is a basis function of one of the little group’s irreps. For such a wavefunction, its corresponding irrep is extracted in two steps. First,we calculate its character with each symmetry operation in the little group. Second,we compare these characters to the character tables on the BCS to identify the irreps. Our algorithm for extracting irreps currently only supports wavefunctions in a plane wave basis. We discuss the main steps in the following paragraphs.

Assume that the wavefunction in the nsoc setting is expanded in the plane wave basis:

where k denotes the k-point; G denotes the reciprocal lattice vectors; and CkGstands for the plane wave expansion coeff icients. The band index n is omitted here for convenience. The plane wave coeff icients can be readily read from the DFT results.

In the case of one-dimensional irreps, the character of|ψk(r)〉 under a certain symmetry operation {R|τ} is simply the eigenvalue λ:

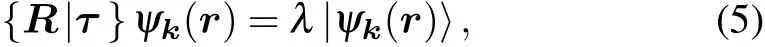
which can be reformulated as follows(assuming that|ψk(r)〉is normalized,and the volume V =1):

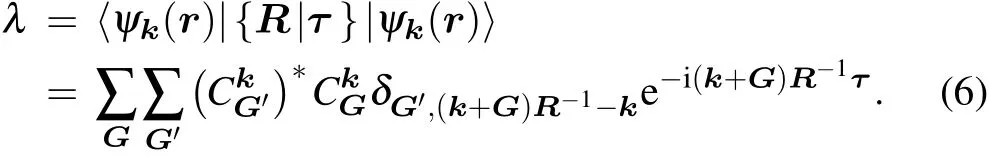
The situation with high-dimensional irreps is similar. Assume that｛ψk,j,j=1,2,...,n｝are degenerate and transform under a symmetry operation as follows:

where C is the representation matrix, R is the O(3) rotation matrix,and τ is the translation part. The character is the trace

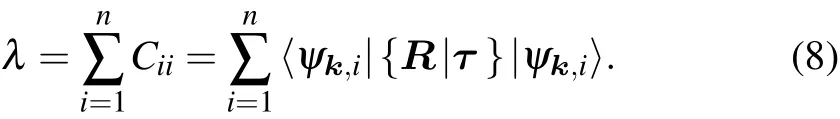
The wavefunction in the soc setting has two components,one spin-up and one spin-down:

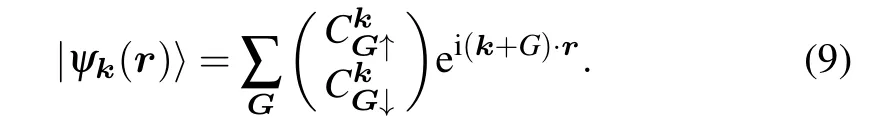
A symmetry operation acts on the wavefunction as

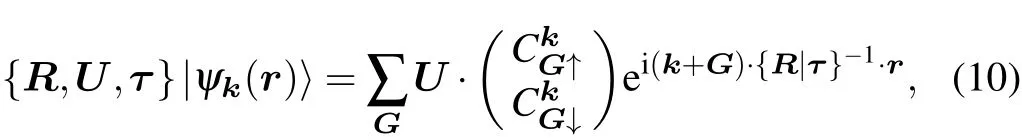
where U is the SU(2)matrix corresponding to the O(3)matrix R.

However, the representation of the translation subgroup of each space group on BCS takes the convention instead of the usual form

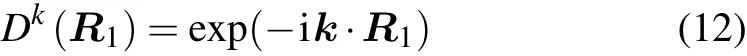
at point k. Accordingly,we must modify the acting rule when applying the symmetry operation onto the Bloch wavefunction as

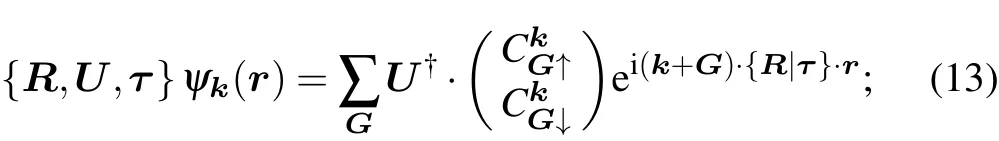
the representation matrix transforms the basis functions as

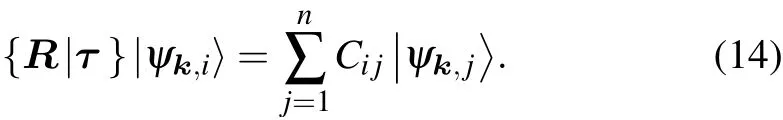
The wavefunction typically has tens of thousands of plane wave components, and calculating the character can be very time consuming. However, the O(3)matrix is isometric(i.e.,it preserves the norm of vectors);hence,in principle,we only need to useoneshell of plane wave components with constant|k+G|.In real calculations,we use|k+G|＜5 A?-1as a truncation condition, which corresponds to several hundreds or thousands of plane waves. Such a truncation may fail in some extreme cases(e.g.,when the primitive cell is extremely small). In these cases, we redo the calculation without the truncation.

We identify the irrep of the wavefunction when the characters of all the symmetry operations are calculated. This step uses the orthogonal theorem in group representation theory:

where G is a group, and χiand χjare two group representations. We calculate the inner product between the obtained characters and those of each irrep of the little group to identify that with a result of 1. The inner product in real calculations is not strictly 1 because of numerical errors, and we set a maximum error of 0.05. Failing to f ind the irrep within the error range implies a low convergence quality. Hence, increasing the convergence threshold and redoing the DFT calculation are recommended.

Note that although a set of bands belonging to a single high-dimensional irrep is,in principle,degenerate,a small energy difference between such bands may be observed because of numerical errors. As a result,we set a degeneracy error of min(0.5 meV,0.1Δk),where Δkis the direct band gap at the k-point. We split the valence bands into small sets, in which bands have an energy difference smaller than this error, and calculate the irrep for each set of bands separately.

Moreover, time-reversal symmetry always exists in nonmagnetic materials,thereby causing an additional degeneracy between the original irreps of the space groups. An irrep at a high-symmetry momentum is generally mapped under time reversal to either(i)itself or(ii)another different irrep or(iii)another same irrep. As a result, time-reversal symmetry puts different constraints on the occupation numbers of different types of irreps in the valence bands: For type-(i) irreps, the occupation numbers do not have additional constraints; for type-(ii)irreps, the occupation numbers for the two irreps related by time-reversal symmetry are constrained to equal;and for type-(iii)irreps,the occupation number of a type-(iii)irrep must be even.The compatibility relations are given in terms of the linearly independent occupation numbers;hence,we must extract them after considering these constraints.

The symmetry operations and the character tables of the 230 space groups are obtained from the“Irreducible representations of the double space groups”database on the BCS.Note that two tables can be found on the page,and we only use the first one(i.e.,representation matrices of the little group). The additional degeneracy caused by the time-reversal symmetry is not included in this page,and we extract this information separately from the “Band representations and elementary band representations of double space groups”database on the BCS,in which the irreps written together like“Γ1Γ2(4)”are degeneracies caused by time-reversal symmetry(the number 4 in the parentheses denotes the dimension of the whole degenerate irrep).

As mentioned in Subsection 2.2,the symmetry operations on the BCS are given in its conventional cell convention. We transform their coordinate axes and origin to make them consistent with Phonopy’s primitive cell convention. A change of the coordinate axes transforms the O(3)matrix of the symmetry operation,whereas a different choice of origin changes the translation part by the formula

where τ and τ′denote the translation part in the old and new coordinate systems,respectively;R is the corresponding rotation matrix; and s denotes the shift vector of the origin. The derivation of this formula can be found in Appendix C.

The SU(2)part of the symmetry operations is directly calculated using the standard formula as follows:

where n and w ∈[0,2π)are the rotation axis and the angle obtained from the corresponding O(3)matrix in Cartesian coordinates, respectively, and {σ0,σ} denotes the Pauli matrices.The SU(2) matrices on the BCS use different spin basis convention choices and differ from the SU(2)matrices calculated in Cartesian coordinates by a similarity transformation and a phase factor of±1. Note that in double space group representations,each O(3)operator corresponds to two SU(2)matrices differing by±1, and these two SU(2) matrices correspond to two rows in the character table that also differ by ±1. As a result,the calculated SU(2)matrices must be aligned with the SU(2) matrices on the BCS such that one can use the character table of the double space groups on the BCS. Although the similarity transformation is unimportant because it does not affect the irreps, the uncertainty of the±1 factor must be eliminated. This step is done by adding±1 factors to the calculated SU(2)matrices until identical multiplication tables of the two sets of SU(2)matrices are obtained.

Table 2 lists the calculated irreps of SnTe in the soc setting, with the number in the parentheses denoting the irrep dimension. Notice that SnTe has 20 electrons per unit cell(i.e.,it has 20 valence bands);this number of electrons equals the sum of the number of irreps weighted based on their dimensions at each HSP. The time-reversal symmetry will pintogether. SnTe has the same number of these two irreps.

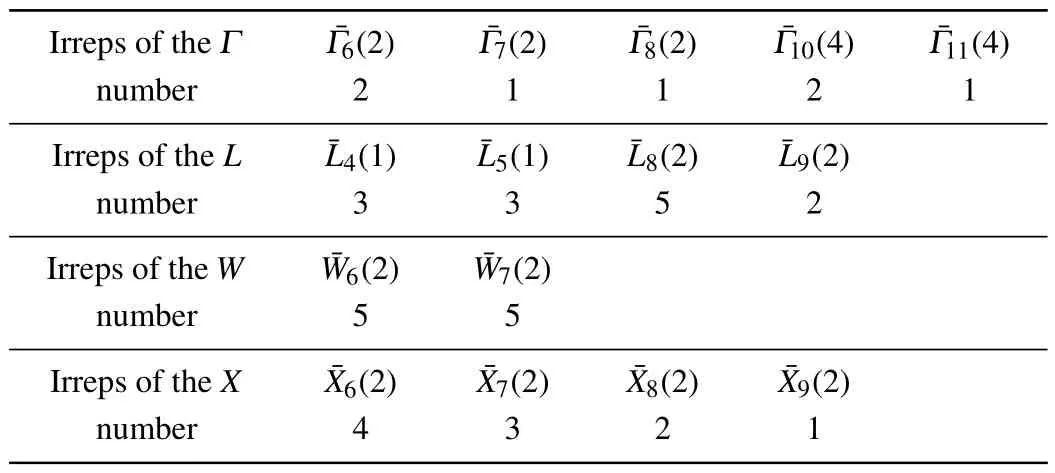
Table 2. Irreps of SnTe in the soc setting.

2.4. HSP degeneracy examination

The procedure for extracting the band irreps described earlier is applicable to both valence and conduction bands. In our algorithm, we first calculate the irreps of the bands near the top of the valence band after obtaining the wavefunctions and energy eigenvalues at the HSPs from the DFT calculations to determine if the material is an HSPSM.

A material with partially filled irreps at some HSPs is labeled as an HSPSM. In other words, the material has degeneracy between valence and conduction bands at some HSPs,and this degeneracy is protected by the HSP’s symmetry,making the material a robust topological semimetal. Note that the degeneracy can be caused by space group symmetry and timereversal symmetry.

In principle, an HSPSM is gapless at each degenerate HSP, but a small direct gap may exist because of the numerical errors of the first-principle calculations. We perform an HSPSM examination for all materials with a direct gap less than 2 meV.An energy tolerance for degeneracy starting from 0 is set starting from the N-th band (N being the number of electrons per unit cell). The lower and upper bands of the N-th band within this tolerance are found, and their irreps are calculated. If the integer number of the irreps is successfully identified,we check whether the N-th and(N+1)-th band belong to the same irrep. If so, the material is labeled as an HSPSM;otherwise,we proceed to the next phase of the algorithm. By contrast, if we fail to obtain the integer number of the irreps, the energy tolerance is increased to include more bands. If this tolerance reaches 2 meV,and the integer number of the irreps still cannot be identified, the material is considered to be poorly converged and should be re-calculated in the DFT phase using a higher-convergence threshold. The highest dimension of irreps in all the space groups is 8;therefore,we only need to examine at most eight bands in this step.

Note that in principle,only the information on the valence bands is required to determine the HSPSMs because the of the top valence band is always degenerate with at least one conduction band in an HSPSM if (i) the linear decomposition of the valence bands into the irreps has a non-integer coefficient or if (ii) the coefficients of the irreps that are related to each other(i.e.,the type-(ii)irreps)are not equal or if(iii)the coefficient of a type-(iii)irrep is odd. These factors can be used as the criteria for determining the HSPSMs(i.e.,whether all the valence bands form an integer number of symmetry-enforced degenerate multiplets). However,we also include several lowconduction bands in our algorithm to obtain the degeneracy dimension.

The direct gaps for SnTe at the four HSPs in the soc setting are 4.4196,0.0939,1.6635,and 5.6673 eV,with the smallest one being larger than 2 meV,thereby excluding the possibility for SnTe to be an HSPSM.

Take HgTe of space group 216 as another example. It has a zero direct gap at Γ in the soc setting and has 18 electrons per unit cell. Our algorithm confirms that the 17th,18th,19th,and 20th bands at Γ belong to the same four-dimensional irrepmaking HgTe an HSPSM in the soc setting.

2.5. Degeneracy along the HSL examination

We continue to extract the irreps of all the valence bands and check them against the compatibility conditions on each HSL if a material has no degeneracy between the valence and conduction bands at any HSP (i.e., it is not an HSPSM).The material is considered to be a band insulator and the algorithm proceeds into the next step if all the compatibility conditions are satisfied; otherwise, the material is labeled as an HSLSM, indicating that symmetry-enforced band crossings exist between the conduction and valence bands along the HSLs,where the compatibility conditions are violated.

The little group of an HSL is a subgroup of the little group of any HSP on it;this means that each irrep of the little group at an HSP can be decomposed into the direct sum of the irreps of the little group at a joining HSL.The decomposition coefficients are described by the so-called compatibility relations.For a system to be gapped along an HSL AB that connects two HSPs A and B, the valence bands of A and B must be continuous;thus,their irreps at A and B must be decomposable into the same set of irreps of AB’s little group with exactly the same coefficients. We call such a condition the compatibility condition, which can be represented as a set of linear equations involving the total number of each irrep for all valence bands at A and B. The compatibility condition being satisfied along all the HSLs is a necessary condition for a system to have a direct gap.Note that if a material satisfies all the compatibility conditions, band crossings may still exist at some HSLs between the valence and conduction bands; however, the crossing point(s)are not symmetry-enforced and may be gapped by tuning the Hamiltonian without breaking the symmetry.Moreover,note that the HSL mentioned herein is not necessarily a line. It can also be a surface. The generic points in the BZ are also named as an HSL“GP”for convenience,which only gives trivial compatibility conditions(i.e.,conservation of the number of bands between two k points).

The compatibility relations for the 230 space groups have been explicitly derived and are available at the “Compatibility Relations between representations of the Double Space Groups”database on the BCS.For each space group,the BCS lists these relations between each HSP/HSL and the HSP/HSL connected to it. We use these data to construct two matrices of compatibility conditions for each HSL,that is,for the soc and nsoc settings, respectively. Element (i, j) of the matrix gives the decomposition coefficient of the j-th HSP irrep into the i-th HSL irrep,with a minus sign if the irrep belongs to the second HSP.The irrep vector of a material is generated by collecting the irreps of all valence bands at both HSPs, with each entry being the total number of occurrences of one irrep arranged in the same order matching the columns of the compatibility condition matrix.We obtain a vector,whose nonzero elements indicate the violated compatibility conditions,by multiplying the compatibility condition matrix to the irrep vector.

As an example, figure 2 illustrates one page of the compatibility relations of space group 225 on the BCS, which lists the compatibility relations between HSL Q = (1/2,v,1-v) and the three HSP/HSLs connected to it, namely L=(1/2,1/2,1/2),W =(1/2,1,0),and generic points GP.

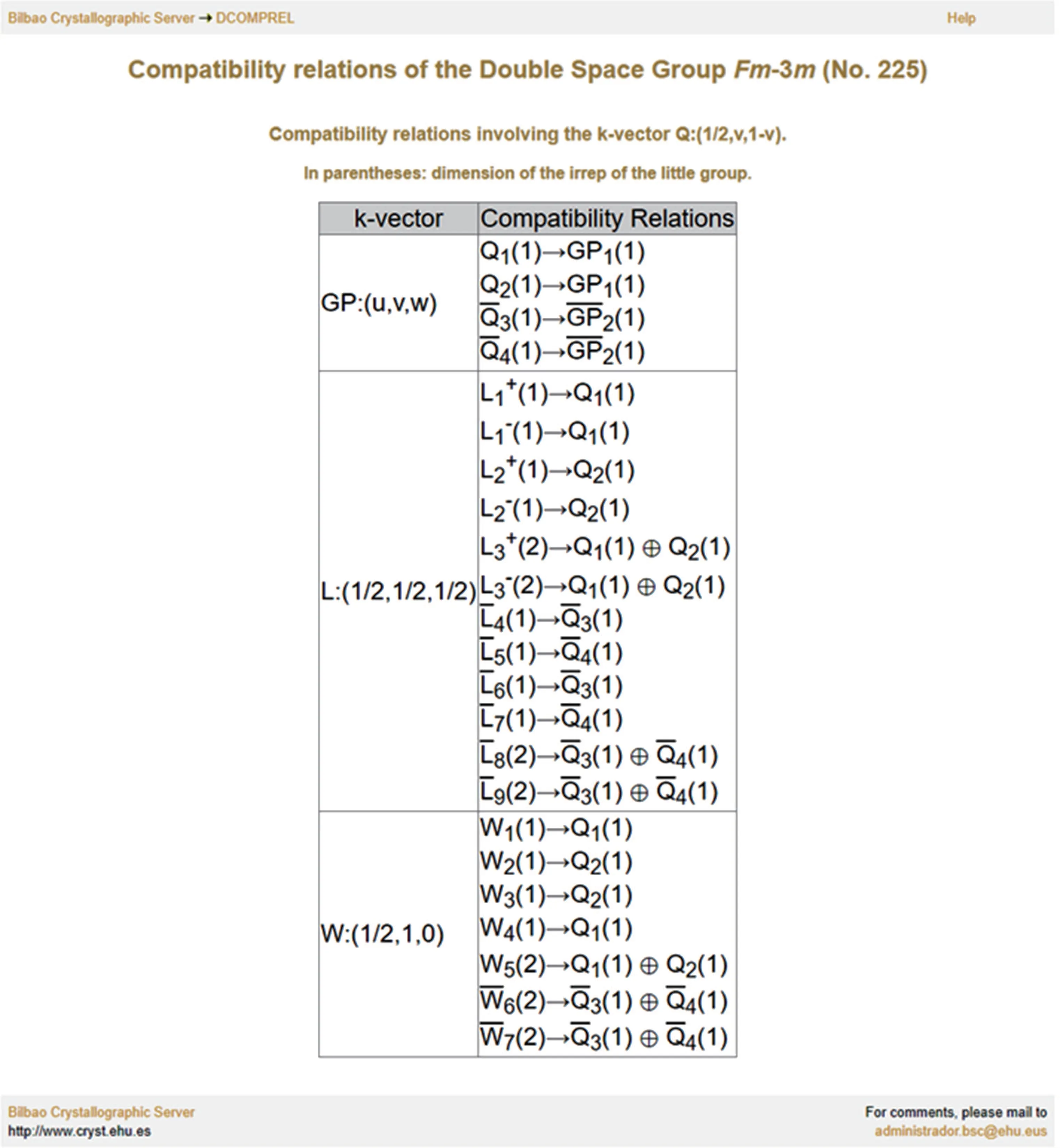
Fig. 2. Compatibility relations involving the k-vector Q (No. 225) on the BCS.

They can be written in a matrix form,as presented in Table 3.

Table 3. Compatibility condition matrix between L and W.

The whole compatibility condition matrix can be constructed similarly,with each row being one such linear equation where coefficients for all irrelevant irreps are set to 0.

The irreps of SnTe satisfy all the compatibility conditions in the soc setting but not in the nsoc setting. Table 4 lists the irreps of SnTe at L and W in the nsoc setting.

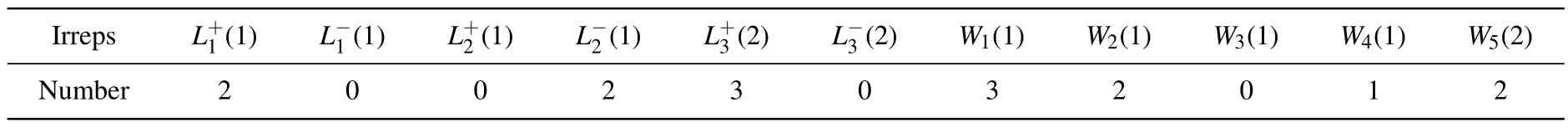
Table 4. Irreps of SnTe in the nsoc setting.

They violate both the L-Q1-W and L-Q2-W compatibility conditions,making SnTe an HSLSM in the nsoc setting.

2.6. Symmetry-based indicator calculation

We calculate the symmetry-based indicators for a material if its band structure satisfies all the compatibility conditions of the space group. The nonzero calculated indicators are labeled as a GMSM in the nsoc setting or a TI or TCI in the soc setting. The parity of the last number in the indicators in the soc setting determines whether the material is a TI or a TCI, with an odd number corresponding to a TI and an even one to a TCI. Note that not all space groups have symmetrybased indicators(117 space groups in the soc setting and 53 in the nsoc setting). A material is labeled as a trivial insulator if it has zero-valued indicators or belongs to a space group with no indicator.

The group structures of the symmetry-based indicators are given in Ref. [14], and their explicit formulas in terms of the corresponding space group irreps used in our algorithm are derived in Refs. [15]and [18]. As demonstrated by Ref. [18], the nonzero indicators in the nsoc setting correspond to the topological semimetals with topological nodes at the non-high-symmetry momenta. The possible configurations of these nodes can be found in the same article.The mapping between the symmetry indicators and the possible sets of topological invariants is tabulated in Ref.[15].The mapping is generally one-to-many, with one set of indicators mapping to several possible nonequivalent sets of topological invariants.

Note that materials with zero indicators or belonging to the space groups with no indicators are not necessarily topologically trivial. This only indicates that their band topology,if existing,cannot be detected using any symmetry eigenvalue diagnosis approach because considering only the symmetry information at the HSPs is naturally incomplete.

The symmetry-based indicator formula of space group 225 in the soc setting is[15]

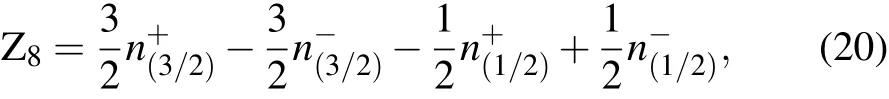
where

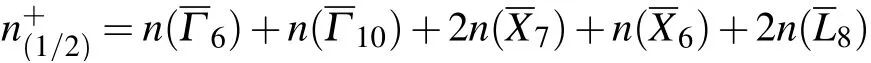
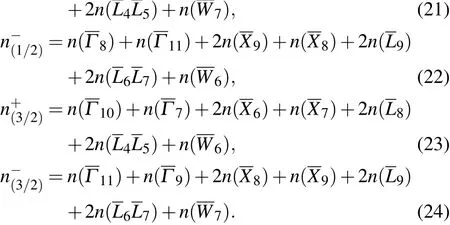
Notice that the notation of irreps here follows the notation on the BCS, which is different from the original notation.[15]The correspondence tables of these two notations of irreps are given in Appendix D.

The SnTe indicator is calculated as Z8=4,indicating that SnTe is a TCI,by substituting the number of irreps of the valence bands of SnTe listed in Subsection 2.3.

3. The SymTopo package

Based on the algorithm described in Section 2,we developed a package named SymTopo to automatically predict the topological property of an arbitrary nonmagnetic crystalline material. The package only requires the user to provide the structure data and the spin-orbital coupling setting of the material. It currently interfaces with two first-principle calculation software, namely VASP and ABINIT. The package is freely available with installation and usage instructions detailed at http://materiae.iphy.ac.cn/symtopo.

The package includes two main modules. The first module generates the standard input files for the structure data and the spin-orbital coupling setting provided by the user for the designated first-principle code,with which the band structure of the material can be readily calculated. After the wavefunctions and the energy eigenvalues are obtained by running the DFT calculations,the second module of the package analyzes these results and reports the material’s topological properties.The implementation details of these two modules are given in the following subsections.

3.1. Input file preparation for the first-principle calculation

The input generation module standardizes the structure file provided by the user,as mentioned in Subsection 2.1,and prepares all the necessary input files for VASP or ABINIT to run the DFT calculation. Several computational material science packages,including Pymatgen,[33]AbiPy[28,34](only for ABINIT),and Phonopy,are used by the module to accomplish the task.

The DFT calculation involves a self-consistent electron density calculation and a subsequent step to compute the wavefunctions and eigenvalues at all relevant HSPs. For VASP,the input files for these two steps are stored separately in two folders named“scf”and“wave,”with each folder containing four files “POSCAR,” “INCAR,” “KPOINTS,” and“POTCAR,”which store the structure,parameter,k points,and pseudopotential information in a VASP-native format,respectively.

For ABINIT,both steps are defined in the same set of input files, including a “.in” file that summarizes the structure,parameter,and k-point information and a“.files”file that designates the name and the location of the pseudopotential files,the“.in”file,and several output files.

Table 5 presents a summary of the important default input parameters for VASP and ABINIT assumed by the input generation module. These default setup yields satisfying results in most cases. Users can also manually adjust these input files to tune the parameters for the DFT calculation when necessary. For example,in case the first-principle calculations do not converge, users could retry the calculation with a different integral method for the k points or a different convergence scheme.

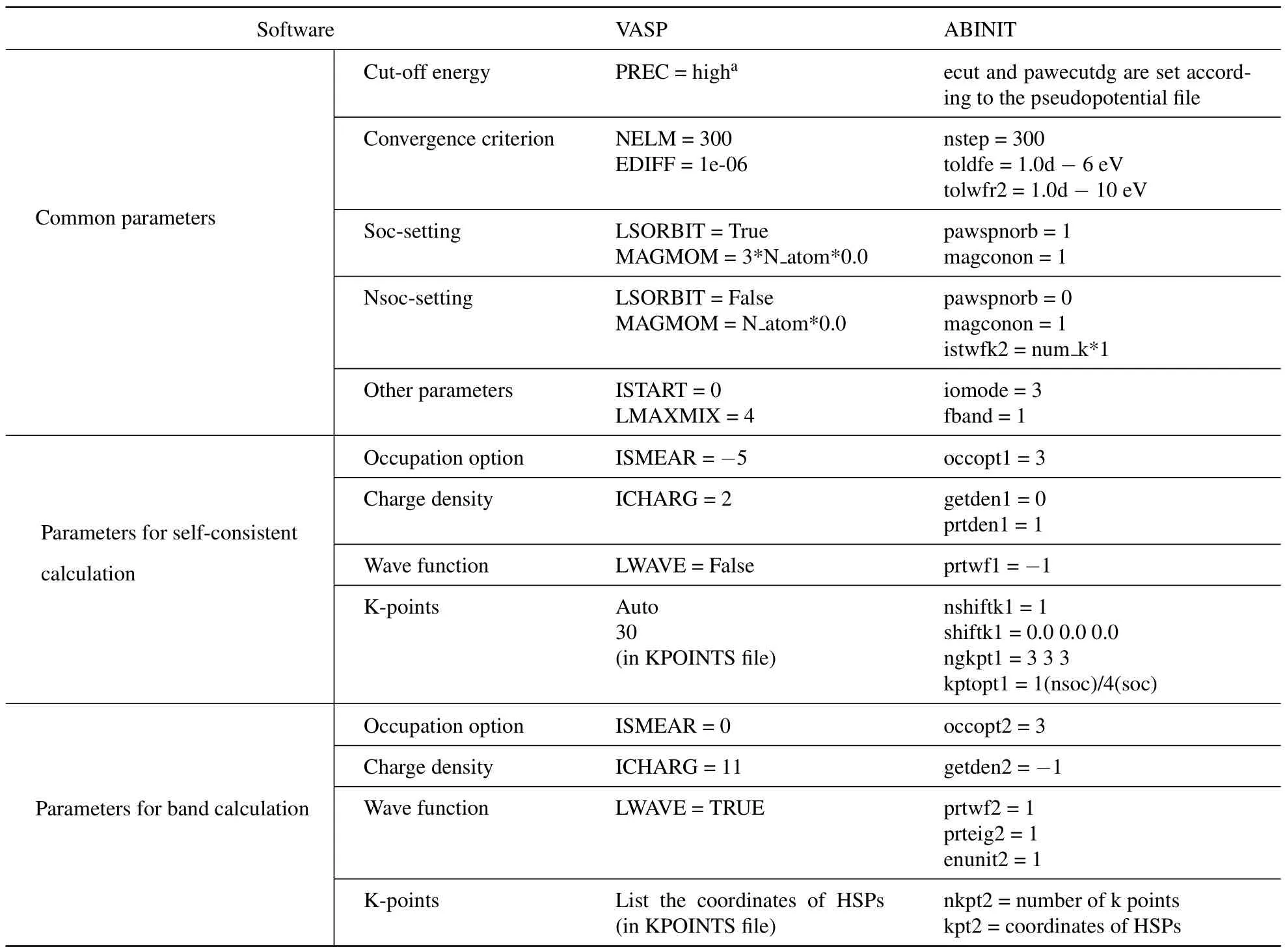
Table 5. Key input parameter template for VASP and ABINIT.

The module currently works with thetype pseudopotential files. Users need to configure the package with the location of the proper pseudopotential files before using the module. In using the other types of pseudopotential files, the user could use the structure and k-point information automatically generated by the module and manually edit the input files to fill in the correct values for the other parameters.

3.2. Topological property analysis

The analysis module of the package takes in the output files of the first-principle calculation and reports the topological classification of the material. For VASP, the output files from the band calculation, including “OUTCAR,” “WAVECAR,” and “EIGENVAL,” are analyzed. For ABINIT, the” flie that stores the wavefunction in NetCDF for-mat is analyzed.

Aside from a classification, the module also reports relevant details for the topological class. For an HSPSM, the module lists the HSPs and the corresponding irreps, where degeneracy exists between the valence and conduction bands.For an HSLSM,the module lists the pairs of HSPs,where the band crossings between the valence and conduction bands exist at some HSLs connecting these two HSPs, and the irreps of all valence bands at each HSP. For a GMSM/TI/TCI, the symmetry-based indicators and the irreps of all valence bands are given. Lastly,only the triviality and band irreps are listed for a trivial insulator.

4. Conclusion

We have given herein a thorough description of the automated algorithm for calculating the symmetry representations and topological properties used in the sweeping scan of nonmagnetic crystalline materials that were previously reported.[19]The technical issues involved in the implementation were explained in detail. Based on the algorithm,we developed a software tool named SymTopo,which can be used to automatically generate input files for first-principle codes and analyze the output to report the topological properties. The tool is freely available at http://materiae.iphy.ac.cn/symtopo.We hope this package can help discover more topological materials in the future.

Appendix A:Brief comparison of the three topological materials search articles

The three articles,[19-21]published together in Nature,all performed a high-throughput calculation in search of novel topological materials. The authors of these papers adopted similar methods and achieved generally consistent results.The crystal structures of the materials they used all came from the Inorganic Crystal Structure Database(ICSD)[35]with different filtering methods. Zhang, et al.[19]and Vergniory, et al.[20]used VASP for the first-principle calculations,whereas Tang, et al.[21]used WIEN2K[36]and performed a modified Becke-Johnson calculation[37]for crosschecking. The small differences in the structural data and the different choice of first-principle calculation software may account for the inconsistencies between the topological material predictions in the three articles.

Zhang,et al.and Tang,et al.used symmetry-based indicator theory,whereas Vergniory,et al. used topological quantum chemistry to predict topological materials. Zhang, et al.and Vergniory,et al.calculated more than 2.5×104nonmagnetic materials and found that approximately 30% of them were actually topological,whereas Tang,et al.selected several hundreds of topological materials with relatively clean Fermi surfaces.Zhang,et al.and Vergniory,et al.also calculated the indicators based on research by Song,et al.,[15]with which the topological invariants can be easily extracted. What is special about Zhang,et al. is that they also did a calculation with the nsoc setting and calculated the indicators based on research by Song, et al.,[18]whereas Vergniory, et al. calculated the topological properties of a material when the symmetry was lowered into subgroups.

Appendix B: Coordinate transformation matrix and origin point shift vectors

We list herein the similarity transformation matrices of the coordinate axes and the shift vector of the origin point between the BCS’s conventional cell convention and Phonopy’s primitive cell convention.

Table B1. Crystal system and Bravais lattice of the 230 space groups.

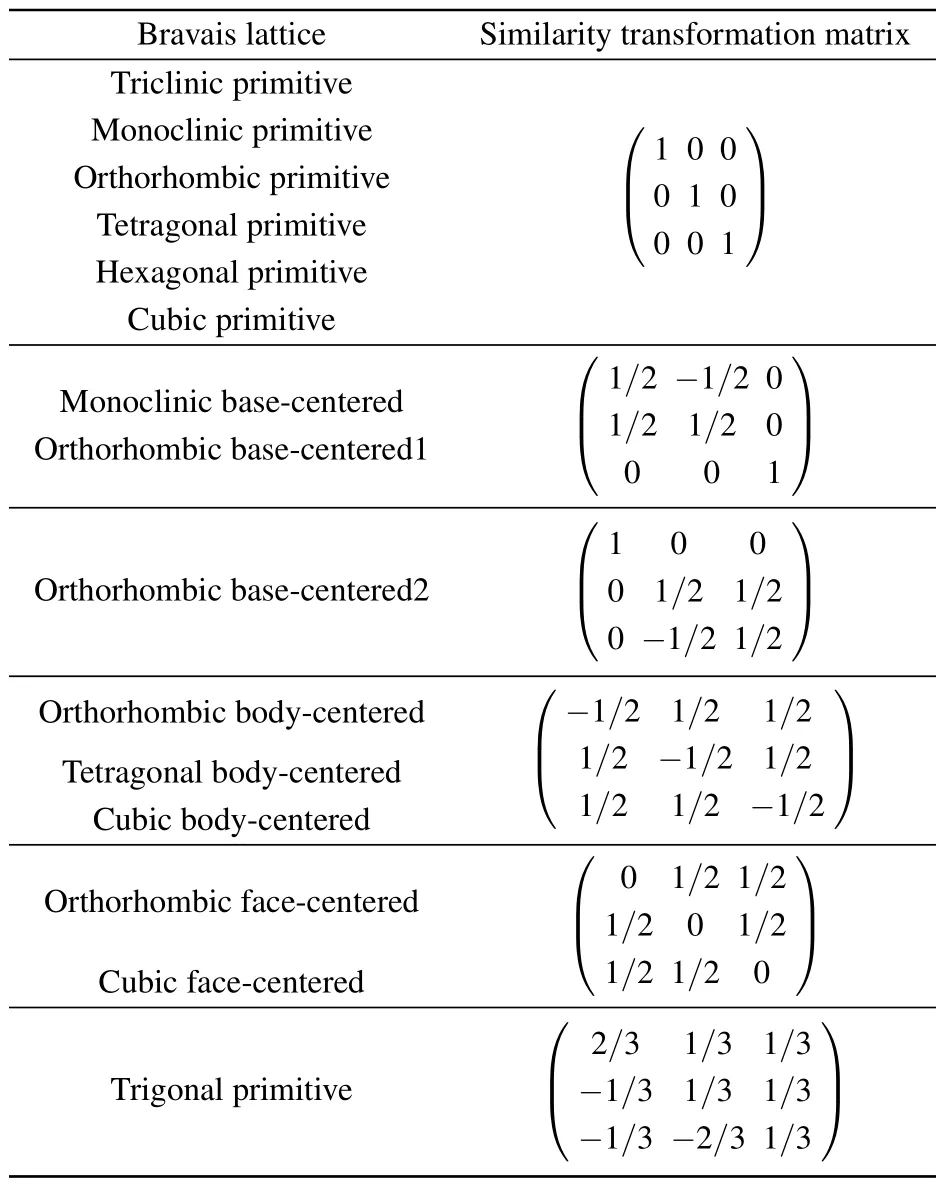
Table B2. Similarity transformation matrices of the Bravais lattices.

Table B3. Shift vector of the space groups.

Appendix C:Derivation of the shift formula

We derive herein how the translation part of a symmetry operation will change when two coordinate systems differ only by a shift of the origin.

Assume that two coordinate systems O and O1differ by an origin shift vector s(i.e.,r1=r+s). Assume that a symmetry operation has forms {R|τ} and {R|τ1} in O and O1,respectively,where R is the same rotation matrix,while τ and τ1are the translation parts. We have the following four relations:

where r′and r1′are the transformed points of r and r1respectively. We arrive at the following shift formula by eliminating these four temporary variables:

In the opposite case,this formula can be used to calculate the shift vectors when we know that a set of symmetry operations{R|τ}and{R|τ1}in two coordinate systems differs only by a shift of origin. The shift vector is not unique, and we only take one of them.

Appendix D: Correspondence table of the two different notations of the point group irreducible representations(irreps)

The notation of the space group irreps by Song,et al.[15]is different from that on the BCS.[38]It follows the notation of the point group irreps by Altmann,et al.[39]We list herein the correspondence tables of these two notations. In these tables,the first row corresponds to the irreps by Altmann,et al.,and the second row corresponds to those on the BCS.Notice that for the space group irreps,one must add the k-point label to the point group irreps when the k-point has the same point group symmetry.

Table D1. Correspondence table of two different notations of the point group irreps.

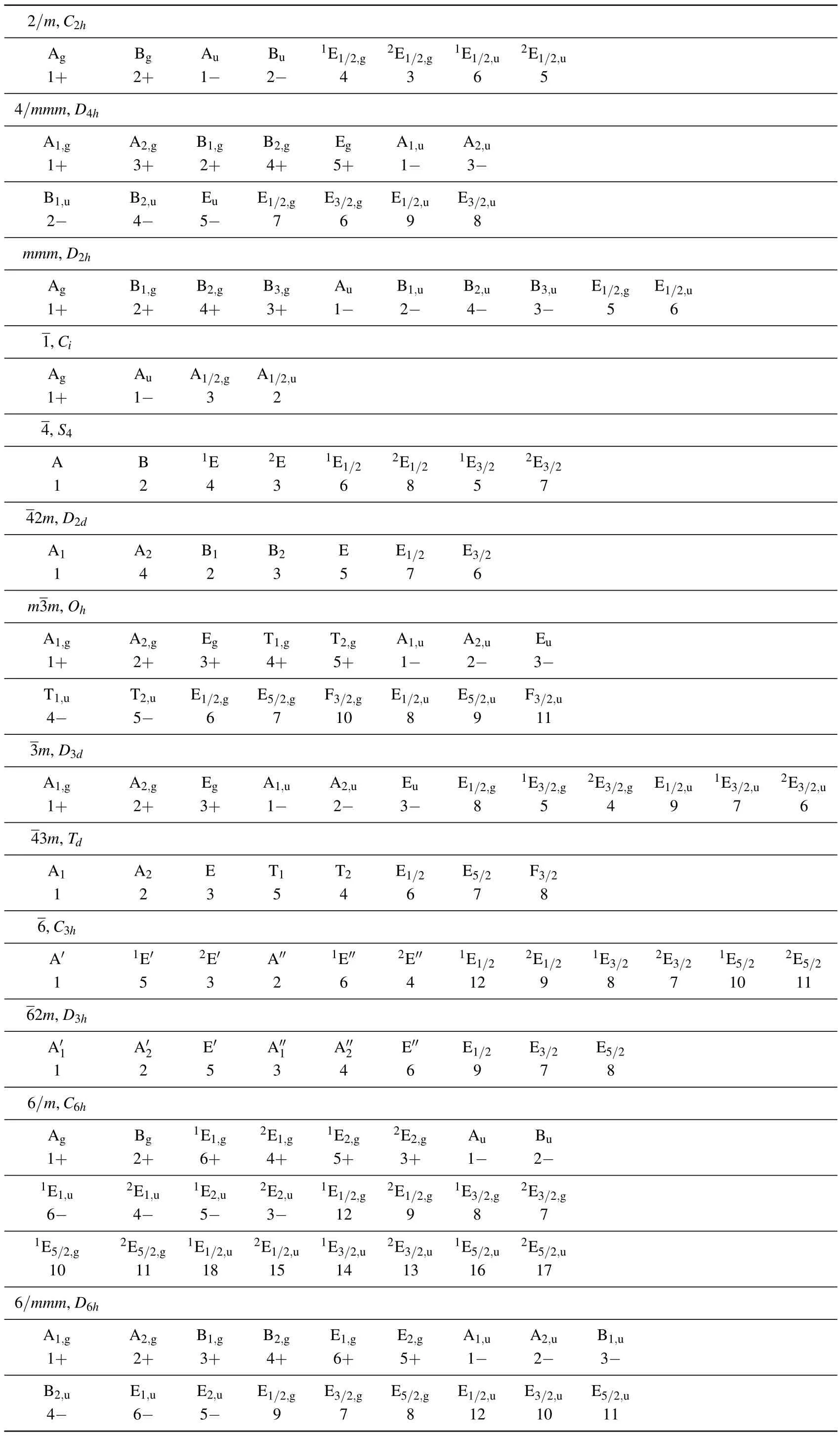
Table D1. (Continued).