Tetrapartite entanglement measures of W-class in noninertial frames?

Ariadna J.Torres-Arenas, Edgar O.L′opez-Z′u?niga,2, J.Antonio Salda?na-Herrera,2,

Qian Dong1, Guo-Hua Sun3, and Shi-Hai Dong1,?

1Laboratorio de Informaci′on Cu′antica,CIDETEC,Instituto Polit′ecnico Nacional,UPALM,CDMX 07700,Mexico

2Facultad de Ciencias F′?sico Matem′aticas,Universidad Aut′onoma de Nuevo Le′on,San Nicol′as de los Garza NL,66450,Mexico

3Catedr′atica CONACyT,Centro de Investigaci′on en Computaci′on,Instituto Polit′ecnico Nacional,UPALM,CDMX 07738,Mexico

Keywords: W-class,tetrapartite entanglement,Dirac field,noninertial frames,nonuniform acceleration

1. Introduction

Entanglement plays an important role in quantum information as a resource for quantum teleportation, communication,and cryptography.[1-3]Since relativity allows us to have a fundamental understanding of the theoretical model,it is relevant to study entanglement in a noninertial frame as a physical property of multipartite states.[4]

Fuentes-Schuller and Mann first studied the entanglement of two qubits in noninertial frames and showed that the maximal bipartite entanglement decreases when one of two observers is accelerated. When the acceleration increases, the entanglement decreases until they reach infinite acceleration reducing the state to a separable one.[5]In the case of the tripartite state, examined by Hwang et al., it has been shown that just as the bipartite case,the entanglement degrades when one of the observers is accelerated, but the accelerated observer entanglement does not completely vanish, even when the observer is moving with an infinite acceleration. Also,they found the interesting result that entanglement is observer dependent.[6]

Li et al. analyzed the entanglement of a tetrapartite GHZstate from one to four accelerated observers with a uniform acceleration a using π4-and Π4-tangles,which are the whole entanglement calculations.[7]It should be addressed that other relevant contributions have been made in tripartite entangled systems.[8-18]

Rindler coordinates are used to describe the viewpoint of uniformly accelerated observers. There are two different sets of coordinates necessary to map field states in Minkowski space-time to Rindler coordinates, which define two disconnected regions in Rindler space-time.[19,20]

In this work,we will investigate the tetrapartite entanglement of the Dirac fields when one observer is accelerated and when two observers are accelerated for the W-class of the 4-particle case. Let Alice,Bob,Charlie,and David share a fourmode W-class entangled state when they are initially not moving. First,we suppose that David moves with a uniform acceleration with respect to Alice, Bob, and Charlie. Second, we suppose that Charlie and David are moving with nonuniform acceleration. We compute the π4-tangle and the Π4-tangle as functions of David’s acceleration and Charlie’s and David’s accelerations, respectively. We show that, just as the bipartite and tripartite entanglement cases, the π-tangle decreases with the increasing acceleration, but unlike the bipartite entanglement case, when one observer reaches infinite acceleration, the entanglement does not completely vanish, but remains nonzero π4-tangle and Π4-tangle. This result implies the possibility of quantum information processing even when David reaches the Rindler horizon. Also, we are concerned with the study of von Neumann entropy to quantify this tetrapartite entangled system.

The rest of this work is organized as follows. In Section 2, we give a description of the system and the considerations are made. We then discuss the tetrapartite entanglement of the W-class when one observer is accelerated. In Section 3, we discuss the tetrapartite entanglement of the W-class when two observers are accelerated. We make calculations on negativities and show whole entanglement measurements. We will study von Neumann entropy in section 4. Finally, some discussions and concluding remarks are given in Section 5.

2. Tetrapartite entanglement when one observer is accelerated

As shown by Verstraete et al., there are nine different ways to entangle 4 qubits.[21]The vast majority of papers on this subject focus on two main states:the Greenberger-Horne-Zeilinger(GHZ)state and the W-class state. The last one often gets less attention than the first one because its calculations frequently get much more complex. There have already been a lot of treatments on the matter of the contributions for one,two,three,and four acceleration qubits for an initial GHZ state.So our attention in this work will be for an initial W-class entangled state.

The W-class entangled state we will be considering is composed of fermions, which in this case are 4 qubits with the names Alice, Bob, Charlie, and David, each of them living in a different Hilbert space. Now, we consider the case in which three of them, namely, Alice, Bob, and Charlie, are stationary while David moves with a uniform acceleration.

A generalization for N qubits of the W-class state has the form[22]

where|N-1,1〉is the state involving N-1 zeros and a one.In this work,we take N=4 and use the subscripts A,B,C,and D to represent the fermions Alice,Bob,Charlie,and David,respectively. With this,the W-class entangled state(N=4)can be written as follows:

As discussed above,the most suitable way to describe an entangled state in a noninertial frame is using the Rindler coordinates. By that,we need to make the transformation between the two coordinated systems. For the fermion field,we use the following transformation:[23]

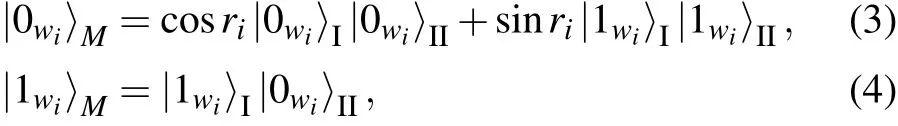
with cosri=(e-2πωic/ai+1)-1/2, aibeing the acceleration of the i-th accelerated observer and wiits corresponding frequency. One has ri∈[0,π/4]for ai∈[0,∞). The subscripts I and II in the kets represent the Rindler modes for regions I and II in the Rindler space-time diagram.

Applying Eqs.(3)and(4)to our|W〉state,we obtain the following state:

Usually, region II is considered to be the corresponding antiparticle region in the same frame.[24,25]When David moves with a uniform acceleration in Rindler region I,he is causally disconnected from region II.This means that he has no access to field modes in region II.Thus,the observer has to trace over this inaccessible region so that region II will not be considered.

2.1. Negativity

The main equation defined for negativity was made for a bipartite state. This allows us to measure the entanglement of a system and is defined as

Equation (6) represents the general form to measure the negativity. We extend the formula to the four-qubits case,and obtain[7,26]

which describe the entanglements 1-3 tangle and 1-2 tangle,respectively. When calculating the negativities Nκ(ξ?ζ)and Nκ(ξ?)in terms of the rightmost formula of Eq.(6),the matrices M are taken as)andrespectively.

In order to begin negativity computations, we trace over the inaccessible Rindler modes in region II,and then we proceed to calculate the density matrix with the following forms:

where and hereafter we use the substitutions sinrc→α,sinrd→β, cosrc→γ, and cosrd→δ. The corresponding density matrices with transposed qubits are given in Appendix A.

We now proceed to calculate the negativities,which will help us to find all the entanglement measurements. We make use of Eq.(6)to calculate the 1-3 entanglement with the following form:

As we can see in Eq. (10), the measurements when the observer is stationary, no matter whether it is Alice, Bob, or Charlie are equal to each other(Fig.1(a)). Due to their complicated expressions,we do not attempt to write them out explicitly. Fortunately, the expression for NDI(ABC)is simpler and can be obtained analytically.

Now,we proceed to calculate the 1-1 tangle using Eq.(6)and obtain the corresponding density matrices by tracing over two of the four qubits in the system respectively for each case.Because of the symmetry among Alice,Bob,and Charlie,we have the 1-1 tangle expressed as a combination of pairs of the elements{A,B,C}

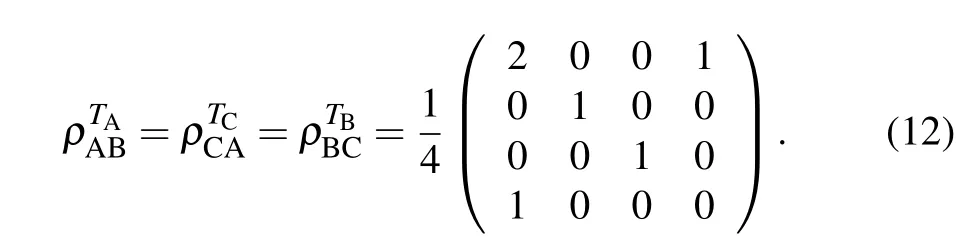
On the other hand, due to symmetry, the 1-1 tangle between two sets i={A,B,C}and j={DI}is expressed as

We can see that NABin Eq.(14)is a constant. While the observed decrement Nijin Eq.(15)is due to the rdparameter(Fig. 1(b)). It is worth noting that while the 1-1 tangle vanishes at infinite acceleration for the accelerated observer, it is not the case for the 1-3 tangle. On the other hand,it is found that NDI(ABC)decreases more quickly than NA(BCDI)with the increasing acceleration parameter rd, but they never arrive at zero even in the infinite acceleration limit.

Fig. 1. (a) The 1-3 tangle of Alice NA(BCDI) and David NDI(ABC), respectively as a function of the acceleration parameter rd, (b) the 1-1 tangle NAB and Nij as a function of the acceleration parameter rd.

2.2. The π-tangle entanglement measures

Two important entanglement measurements are defined for tripartite states, which are the whole entanglement measurements π3and Π3. Both of them depend on the negativities and we can make a tetrapartite extension of the latter equations,yielding[26]

Now,we are able to obtain the π4-tangle,which is given by taking the average of πκ,πξ,π?,and πζ[7]

Also, we use another whole entanglement measure defined as[27]

For the present case,one has

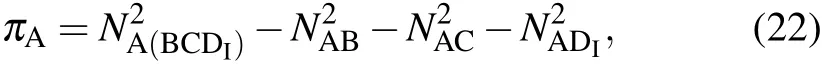
from which we are able to calculate π4=()/4 and Π4=)1/4.

For the case we are studying, we have==＞W(wǎng)e plot) andresidual entanglements in Fig. 2 and πABCDI-tangle andwhole entanglements in Fig. 3. Similarly, we notice thatdecreases more quickly thanfor the same reason as that for negativitiesndMoreover,we also find that the algebraic average residualis slightly greater than the geometric average Π4. In particular, they are almost the same when rd＜0.3.

Fig.2.Residual entanglement of Alice πA(Bob and Charlie)and David πDI as a function of the acceleration parameter rd.

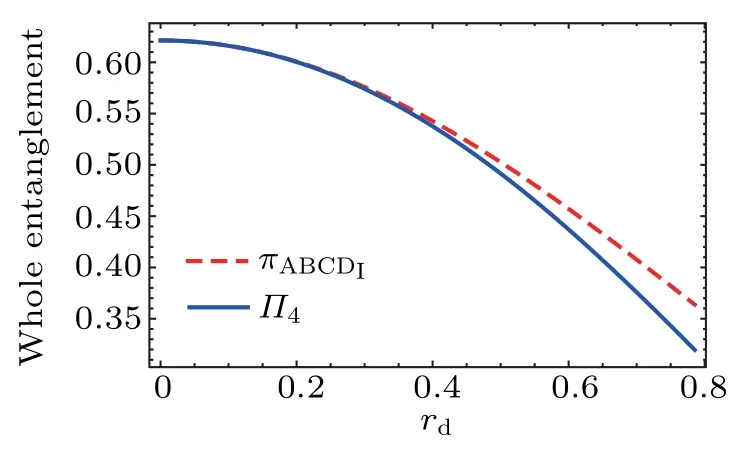
Fig. 3. The π4-tangle and Π4 whole entanglement as functions of the acceleration parameter rd.

3. Tetrapartite entanglement when two observers are accelerated

In this case,similar to the above approach,we are about to study the tetrapartite entanglement measurements of the system. Computations become more complex due to the multiqubit state. We are working with the double Rindler transformations in the state,leading to a bigger dependence of the trigonometric functions. Now, we suppose that Charlie and David are the accelerated observers. Applying Eqs. (3) and(4)to our initial|W〉state,we obtain

where rcand rdare the acceleration parameters for Charlie and David, respectively. Notations CI, CII, DI, and DIIrepresent that Charlie and David move with an acceleration in Rindler regions I and II.Just as in the previous calculations,we are not going to consider region II.

3.1. Negativity

We will,one more,use time Eq.(6)to determine the degree of entanglement for the 1-3 and 1-1 tangles.After tracing over the inaccessible Rindler modes CIIand DII,we obtain the density matrix

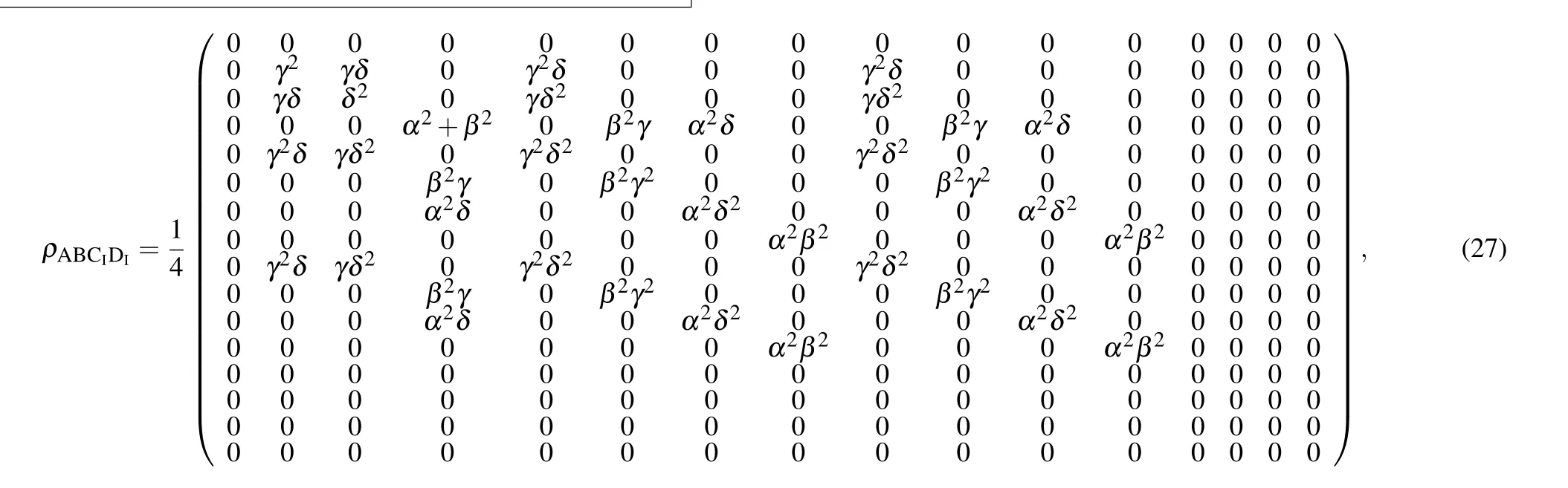
where we have also used the same notations for α,β,γ,δ as above.

For the 1-3 entanglement, we once again find that there exists some symmetry, i.e., NA(BCIDI)= NB(ACIDI). In the case of NCI(ABDI)and NDI(ABCI), it does not appear the same(Fig.4). It is seen that the negativities NCI(ABDI)and NDI(ABCI)are antisymmetric. This means that they can be obtained from each other via replacing rc?rd. It is also interesting to find that both of them increase with increasing rcbut decrease with increasing rd.

Fig. 4. (a) Entanglement measure (1-3 tangle) from the viewpoint of Alice(Bob)as a function of acceleration parameters rc and rd,(b)Entanglement measure (1-3 tangle) from the viewpoint of Charlie and David as a function of acceleration parameters rc and rd.

On the other hand, in the 1-1 tangle, we can observe in a more particular sense the entanglement between two particles, as we can see that the maximum entanglement is achieved when both particles are stationary, the lower entanglement is obtained when both accelerated particles are measured (Fig. 5). We rename the sets that based on symmetry,the 1-1 tangle can be expressed in combinations of pairs with the following sets κ ={A,B}and ξ ={C,D},

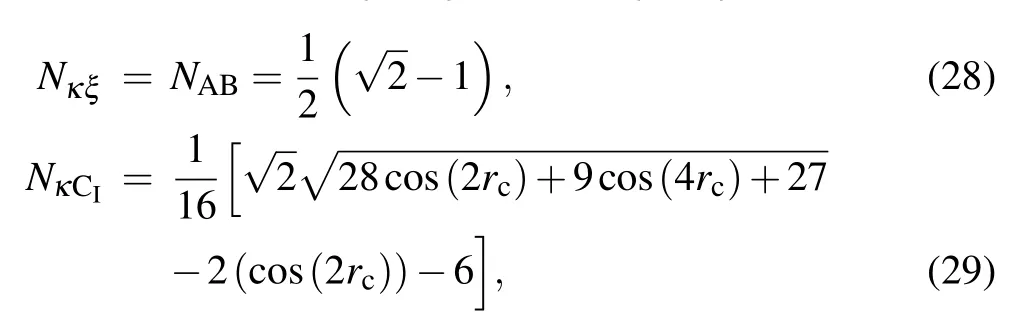
The quantity NκDIcan be obtained easily by replacing rcin NκCIwith rd.Let us analyze Fig.5 in detail.It should be noted that NCIDIdecreases to zero when r=0.472473 and NACI=0 in the infinite acceleration limit r=π/4.

Fig.5. Entanglement measure(1-1 tangle)as a function of rc=rd.

3.2. The π-tangle entanglement measure

Again, using the method required for a tetrapartite state,[26]we use Eqs. (16)-(27) to obtain the residual entanglement for the W-class state. For this case,we have a similar expressions to Eq.(22)except for notation C is replaced by CI.Thus,we have π4=(πA+πB+πCI+πDI)/4 and the geometric average(21)Π4=(πAπBπCIπDI)1/4.

Since the obtained results are not easy to express in a short term,we shall only present their representative graph in Fig.6.We remark the antisymmetry between πCIand πDI, although πAand πBremain the same. As we know,it is very difficult to plot πCIand πDIas 3D graphics since the negativity NCIDIis equal to zero when r ＞0.472473. The graphics of πCIand πDIare plotted in two segmentation intervals of the variable r,i.e.,r ∈[0,0.472473]∪[0.472473,π/4]. We find that both πCIand πDIdecrease with the acceleration parameters rcand rd.

Finally,we present in Fig.7 the π4-tangle and the whole entanglement calculated with Eqs.(20)and(21). It is interesting to find that the difference between the geometric average value π4and the geometric average value Π4is almost zero.This means that we can use any of them to describe this entangled system.

Fig.6. (a)Residual entanglement(π-tangle)for Alice and Bob as well as their comparison with their 1-3 tangle. (b)Residual entanglement(π-tangle)for Charlie and David.

Fig.7. (a)Whole entanglement(b)measures π4 and Π4 as functions of acceleration parameters rc.The π4 and Π4 as functions of the parameter rd are the same as above.

4. The von Neumann entropy

Another useful measurement for entanglement was inspired by von Neumann, establishing the analogous in quantum mechanics of the Shannon entropy for classical probability nowadays called von Neumann entropy.[28-30]It is defined as S=-Tr(ρ lnρ). Another definition is developed and provided by Bengtsson and ˙Zyczkowski[31]

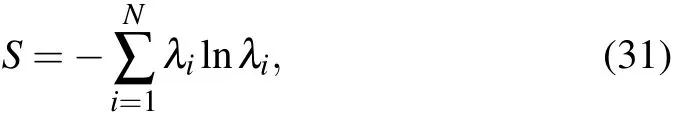
where λidenotes the i-th eigenvalue of the density matrix ρ.Using this definition, we are able to calculate the von Neumann entropy. Since for the case when only David is accelerated (Fig. 8), all eigenvalues except for two are zero, and for the case when Charlie and David are moving, all eigenvalues except for four are zero,we are able to obtain the explicit analytical expression for the von Neumann entropy in both cases,but for the case when two qubits are accelerated, the expression will be omitted due to long-polynomial nature. Nevertheless, we show the behavior of the entropy for this case in Fig.9

We find that the von Neumann entropy for these two cases increases when the acceleration is increasing. That is to say,SDincreases with rd, but the von Neumann entropy SABCIDIincreases with both the acceleration parameters rcand rd.

Fig.8. The von Neumann entropy as David’s acceleration parameter rd increases.

Fig.9.The von Neumann entropy as a function of Charlie’s and David’s acceleration parameters rc and rd.

5. Discussion and conclusion

In conclusion, it is found that the negativity and whole entanglement computations of the 4-particle W-class state decrease the entanglement when we measure in a noninertial frame. As we can see,the entanglement measures that depend on the acceleration parameters will decrease with increasing accelerations. In contrast, the entanglement measures that do not depend on the acceleration parameter will remain a constant in the acceleration limit. It is worth noting that no matter which qubit is selected from computations,we can choose any qubit or any pair of qubits from the system and switch it from inertial to noninertial,without expecting different results in any case. For the case of the 1-1 tangle, the entanglement begins to disappear for the case of one accelerated qubit. We can see that when we measure the bipartite negativity, (NAB)never can reach infinite accelerations. The lost of entanglement is due to the 4 total partial traces that we are preforming yielding to a ripping off information. The NCIDIdisappears for r ＞0.472473. This result is contrary to the cases reported for tripartite systems in which the entanglement has never been reduced to zero. For the case of the 1-3 tangle, when we are studying the one accelerated observer case,it is shown that the entanglement measure from the point of view of the noninertial qubit decreases faster than that when the other stationary qubits perform the measure. Furthermore,when we study the second case, we can see that the negativity for the stationary qubits behaves the same over all the accelerations, but when the negativities are measured for the accelerated ones,we can see their entanglement is different.It is remarkable to say that,for this measure, the entanglement never reaches zero. The whole entanglement measurements π4and Π4do not change their initial entanglement,no matter if we are studying the first or the second case,the arithmetic mean is greater than the geometric mean. Our results also suggest that,due to the growth of von Neumann entropy, our system becomes more disordered as we vary the acceleration parameter. Special cases were treated for the two noninertial case when rc=rb,having a bigger entropy than the fist case.Before ending this work,we give a useful remark about the tetrapartite entanglement measurements for the W-class state. In noninertial frames,we will predict the difficulty of studying these entanglement measures when three fermions,say Bob,Charlie,and David,are moving with nonuniform accelerations rb, rc, and rd. This is because it is impossible to illustrate them in graphics with three variables.Similarly,it will become more difficult to study the case when all particles are moving with nonuniform accelerations.

Appendix A: Density matrices for one accelerated observer

The explicit expressions of the density matrices with the partial transposed qubit when one observer, say David, is accelerated are as follows:

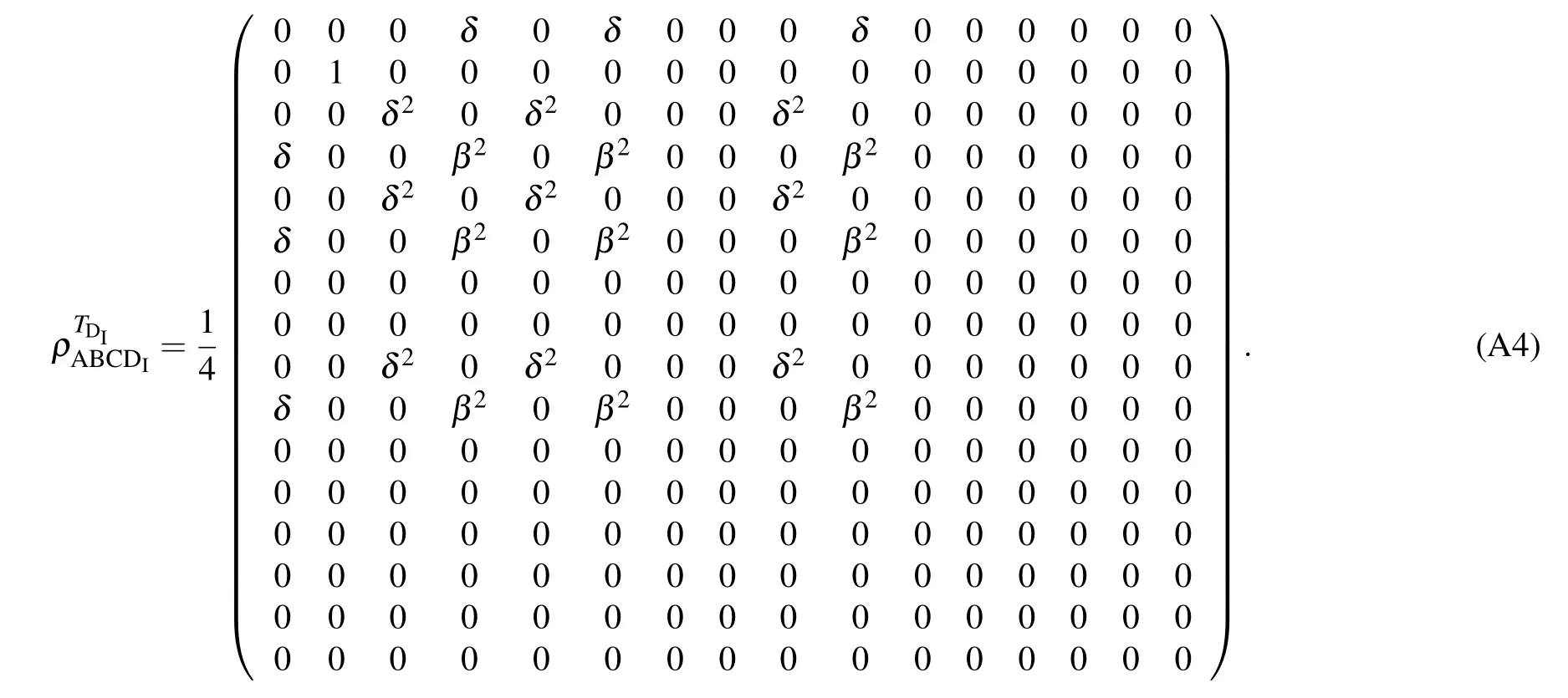
Appendix B:Density matrices for two accelerated observers

Now, we show the explicit expressions of the density matrices with the partial transposed qubit when two observers, say Charlie and David are accelerated as follows: