A primary model of decoherence in neuronal microtubules based on the interaction Hamiltonian between microtubules and plasmon in the neurons
Zuoxian Xiang(向左鮮),Chuanxiang Tang(唐傳祥),and Lixin Yan(顏立新)
Department of Engineering Physics,Tsinghua University,Beijing 100084,China
1.Introduction
Quantum theory is one of the greatest discoveries of the twentieth century. In recent years,quantum effects in biological systems have been discovered in several areas,including olfaction,[1,2]avian magnetoreception,[3,4]photosynthesis,[5–9]quantum entanglement in living bacteria,[10]and so on.[11]Theoretical study of quantum effect in bio-systems and its possible relevance to explaining the functional properties of these systems are also drawing rapid attention,such as consciousness in the brain.
How to explain consciousness? Classical or quantum? It is so mysterious and researchers have proposed many models.[12–24]Some studies suggested that the quantum effect might play an important role in the functioning of the brain.[16–24]Penrose and Hameroff proposed the orchestrated objective reduction(Orch OR)model,which suggests that microtubules(MTs)in neurons act as a quantum computer,[18–20,24]Fisher proposed that quantum entanglement may exist between two neurons.[23]
Decoherence is an important phenomenon in quantum information.The“warm,wet,and noisy”environment might destroy the quantum state,[26–29]thus the decoherence time scale τ is an important parameter to the quantum model.
To study the decoherence process in MTs,researchers determined this parameter according to different mechanisms of decoherence,including quantum gravity,[18]cavity quantum electrodynamics(QED)model,[25,26]and single ion-MT interactions;these results are listed in Table 1 and the value of decoherence time varies greatly.
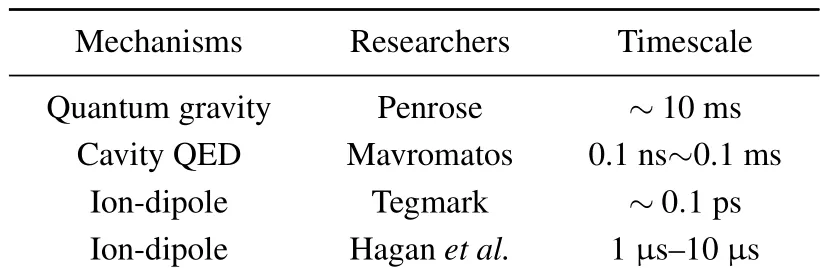
Table 1.Decoherence time scales and their mechanisms.
Decoherence mainly derives from the interaction between quantum systems and the environment.There are 4 basic interactions that have been discovered in nature;in the range of molecule interactions,the main interaction between environment and tubulin dimers is electromagnetic interaction.In this paper,a model based on the electromagnetic interaction Hamiltonian between microtubules and plasmon in the neurons is proposed.Previous studies considered the effect of a single ion on the decoherence process in MTs;however,cells are known to contain different kinds of ions that have different charges and masses,i.e.,some ions have positive charge,whereas others have negative charge.Over a long time scale,cells can be considered to be electrically neutral;however,this is not true over very short time scales.Therefore,the decoherence rates cannot be calculated only considering the effect of a single ion since decoherence is a result of the interaction between tubulin dimers and cellular fluid environment.In this paper,the interaction Hamiltonian is constructed by using the second quantization method,and the decoherence time is estimated according to the interaction Hamiltonian.
This article is organized as follows.Section 2 includes the introduction for decoherence mechanisms in our model,as well as the total Hamiltonian of tubulin dimers and cell fluid environment;the decoherence timescale τ are computed and howτ changes with environment parameters will be discussed.In Section 3,other mechanisms of decoherence will be discussed,and some important formulas and their derivations are given in the appendix.
2.Decoherence rates
In this section,the decohenrence mechanisms in MTs will be discussed.MT is a hollow cylinder with an outer diameter of 24 nm and an inner diameter of 15 nm.The basic unit of MT is tubulin dimer which has two subunits(denoted by α and β);all of the tubulin dimers form MT crystal lattice by helical encircle.The tubulin dimers have different kinds of conformational states which are regarded as quantum bit in Orch model,and MTs can store information owing to different combinations of these conformational states.Electron transition in each tubulin dimer could change the conformational states,and the MT is a polar molecule and has intrinsic electric dipole moment(Fig.1).[25]

Fig.1.The structure diagram of MTs.
2.1.Mechanisms of decoherence
The cellular fluid is considered to have both positive and negative charges(similar to plasma),and thus two basic and very important parameters are used to describe the it,namely Debye length λDand plasma frequency ωp;these two parameters will be discussed compendiously and their range will be given.
The Debye length λDrepresents the space scale when the plasma is kept as a neutral state and is determined by
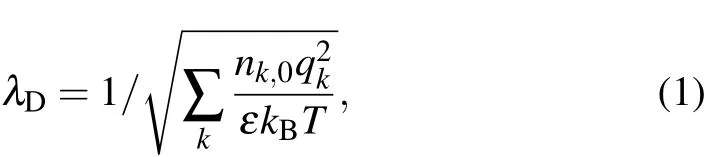
where nk,0is the average density of the k-th kind of ion,qkis the quantity of charge,ε=80ε0is the dielectric constant of water,kBis the Boltzmann constant,and T is the temperature of the cellular fluid.For physiological Ringer solution,λD~0.7 nm,[29]and in the following calculation,the value of λDis set to be around 0.7 nm.
The surface of tubulin dimers have net charge,[30]so a counterion layer will be formed because of the Debye shielding.The thickness of the counterions is approximately λD,as shown in Fig.2.The counterions could shield the interaction between MTs and the environment,as shown in Appendix C,the coupling coefficient is decreased if the shielding effect is considered.
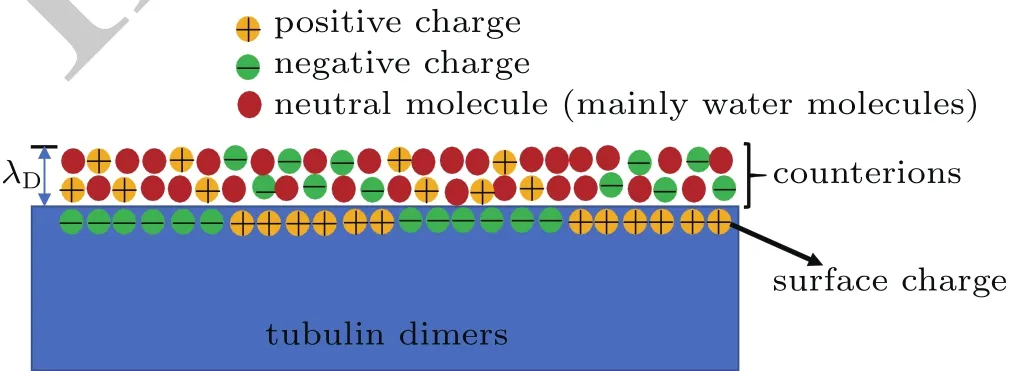
Fig.2.Schematic diagram of counterion layer with a thickness of λD.
The second parameter is called plasma frequency,which describes the collective oscillations of ions and is determined by
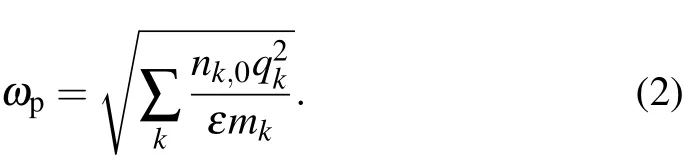
For typical parameters in a cell,[29][K+]in=400 mmol/L,[Na+]in=50 mmol/L[Cl?]in=52 mmol/L,ωp≈ 0.6 THz.Therefore,in the following calculation,the value of ωpis set to be around 0.6 THz.
When the plasmon is in an excited state,the electric neutrality is destroyed,and some net charges appear.The net charges can interact with the dipole in the tubulin dimmers,as shown in Fig.3.As shown in Appendix A,the local ion density fluctuation could excite ion density waves.There are different ion density waves,but the only one called plasma oscillation could be coupled with MTs,and the dispersion relation of plasma oscillation is
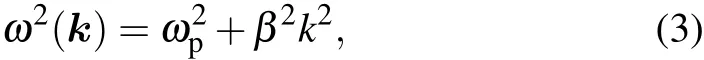
where β is the average value of ion thermal velocity,which has the same order of magnitude as the thermal velocity.
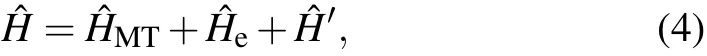
The total Hamiltonian of the MT-environmental systems can be derived as follows:whereis the Hamiltonian of the excited systems in the MTs,is the Hamiltonian of the plasmons in the cellular fluid environment,andrepresents the interaction between the MTs and cellular aqueous environment caused by the interactions between the dipole and net charges.is the reason for decoherence;if=0,the decoherence time is τ=∞.
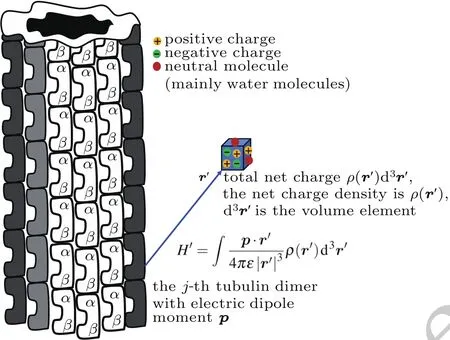
Fig.3.Schematic diagram of the coupling between tubulin dimers and the cellular fluid environment.
As shown in Fig.3,the interaction Hamiltonian between a single tubulin dimer with the electric dipole moment pand the cellular fluid environment can be shown as follows:
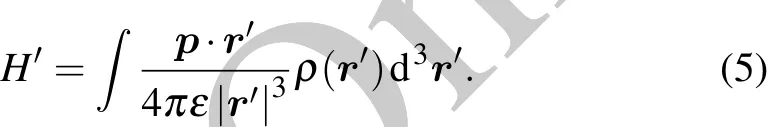
2.2.Computation method of decoherence timescale
Now,the total Hamiltonian equation(4)will be derived;some basic assumption or approximation is listed below,and will be discussed in Section 3 and appendix.
(i)Water is treated as an medium with a dielectric constant ε=80ε0,and detailed interaction of ion-water molecules and MT-water molecules is ignored.
(ii)Due to the Debye shielding,plasma oscillations could only be excited above the Debye length,that is to say,the wave numberk has an upper limit of k=kD=2π/λD;in our calculation,we consider k will decay rapidly as a small quantity for the short wavelength modes.
(iii)Random phase approximation(RPA)for many particles system,In equilibrium state or near equilibrium state,as the position of particles is random,∑iexp(ik ·ri)=0 unless k=0.
(iv)The tubulin dimers are seen as a mass point with electric dipole moment p.
As introduced in Subsection 2.1,the tubulin dimers have different conformational states,denoted by|ki,and let?c?k,?ckbe the creation operator and annihilation operator of the quantum state|ki,so the Hamiltonian of tubulin dimers can be expressed by

The detailed calculation ofwill be given in Appendix A and Appendix B,and the total Hamiltonian of the MTs and cellular environment can be expressed as follows:
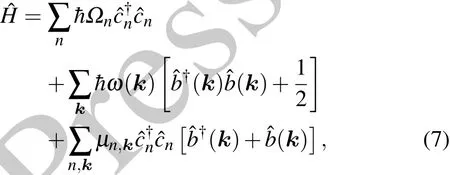
where ω(k)=is the dispersion relation of plasma oscillation,(k)and(k)are the creation operator and annihilation operator of plasma oscillations,respectively,and the coupling coefficient μn,kis given by
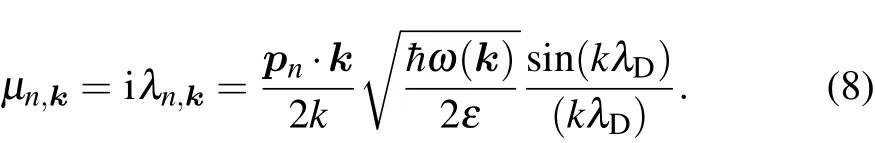
Equation(8)is given in Appendix C,and pnis the electric dipole moment in state|ni.
Next,Tolkunov’s model is used,[31,32]which describes the interaction between the spin system and Boson thermal reservoir.In 2-level approximation,the Hamiltonian equation(7)of our model is the same with that of Tolkunov’s in form,so the non-diagonal elements of density matrix will also change with time in the same way
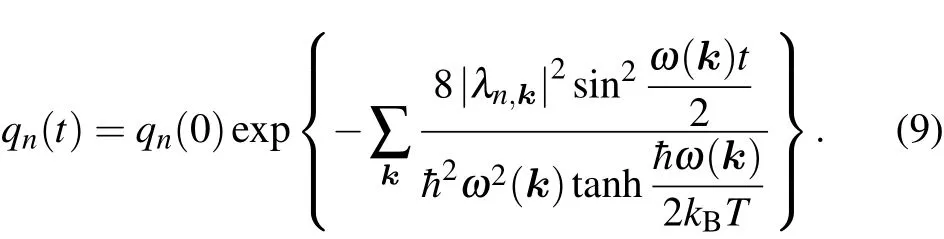
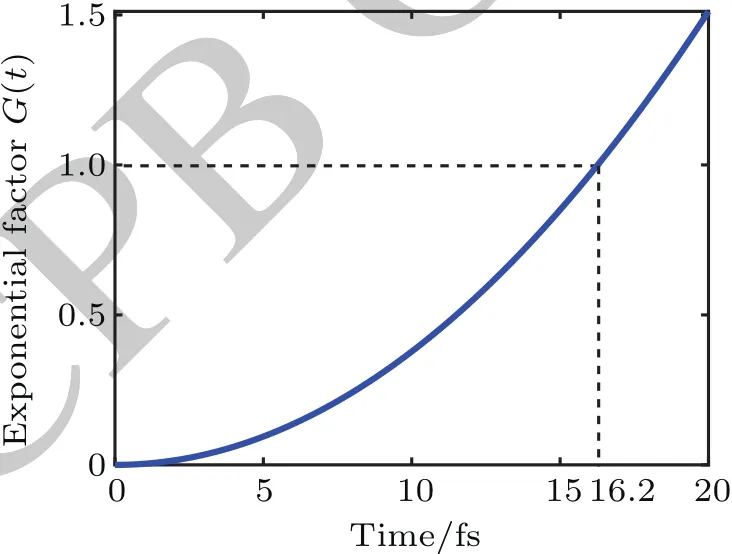
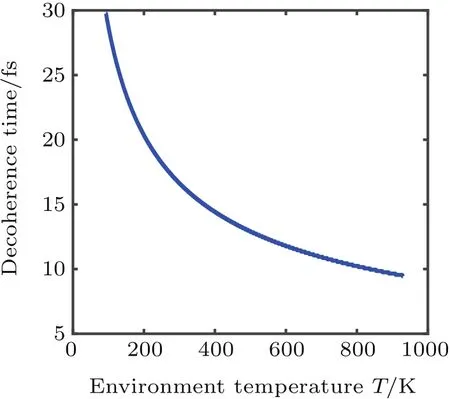
Here,and the integral region is 0 where Obviously,G(t)>0.In the quantum information theory,the decoherence process is reflected in the damping of the nondiagonal element of the density matrix,so we define decoherence timeτas the timescale when qn(t)decays into qn(0)/e,namely Equations(11)and(12)could be used to compute decoherence time. In this section, the typical value of decoherence time scale will be estimated by Eqs.(11)and(12).The parameters in Eq.(10)are chosen as follows: pn=3×10?28C·m is the electric dipole moment of tubulin dimer.[25] ε=80ε0is the dielectric constant of water.[29] λD~0.7 nm,ωp=0.6 THz;these two basic plasma parameters have been discussed in Subsection 2.1. T=310 K is the environment temperature. β=300 m/s since it has the same order of magnitude with the thermal velocity. kB=1.38×10?23J/K is the Boltzmann’s constant. =1.0546×10?34J·s is the Planck’s constant. The function G(t)can be computed in a numerical method(Fig.4).Set G(τ)=1 and the decoherence time could be easily obtained The decoherence timescale is about 10 fs. Fig.4.Schematic diagram of how to compute the decoherence time by the exponential factor G(t). Decoherence time may change with other parameters;how these parameters affect the decoherence time will be studied in this section.As discussed in Subsection 2.3,the typical time scale for decoherence is T0=10 fs.So set T0=10 fs as the time unit,six dimensionless physical quantities are shown below Then equations(11)and(12)become The typical values of these parameters are given in Subsection 2.3;in this section,their values are given in a wide range as follows: Here,some values may never be reached,such as T=900 K,ε=240ε0,and so on;but the purpose in this model is to analyze how the decoherence time changes with physical parameter,so the parameter distribution is in a very wide range. Case 1: Decoherence time changes with plasma frequency ωp As shown in Fig.5,decoherence remains almost unchanged when the plasma frequency changes. Fig.5.Decoherence time changes with plasma frequency ωpwhen other parameters are consistent with those in Subsection 2.3. Case 2:Decoherence time changes with average thermal velocity β As shown in Fig.6,decoherence remains almost unchanged when the average thermal velocity β changes,similar to Case 1. Fig.6.Decoherence time changes with average thermal velocity β when other parameters are consistent with those in Subsection 2.3. Case 3:Decoherence time changes with Debye length λD In Fig.7,the decoherence time increases with Debye length;since the plasma oscillation modes could only be excited when k<2π/λD,a larger Debye length means that fewer modes will be excited,so the number of the modes interacting with MTs will decrease,and the decoherence time will increase. Fig.7.Decoherence time changes with Debye length λDwhen other parameters are consistent with those in Subsection 2.3. Use τ=CλsDto fit the curve in Fig.7(or equivalently lnτ=slnλD+lnC),the power exponent s and linearly dependent coefficient for lnτ,lnλDare Doing the same work to other parameters and we find that τ=CλsDcould fit the relationship between τ,λD,so we can approximately consider that Case 4:Decoherence time changes with dielectric constant of water In Fig.8,the decoherence time increases with dielectric constant of water,and the reason is obvious.According to Eq.(5),a larger dielectric constant means the weaker interaction between MTs and environment. Fig.8.Decoherence time changes with dielectric constant of water when other parameters are consistent with those in Subsection 2.3. Doing the same work as Case 3 and we find that Case 5:Decoherence time changes with dipole moment of tubulin dimer pn In Fig.9,we show the decoherence time decreases as the dipole moment of tubulin dimer increases;according to Eq.(5),the increase of the dipole moment will enhance the interaction between MTs and environment,and then the decoherence time will decrease. Fig.9.Decoherence time changes with dipole moment of tubulin dimer pn when other parameters are consistent with those in Subsection 2.3. Doing the same work as Case 3 and we find that Case 6: Decoherence time changes with environment temperature T In Fig.10,the decoherence time decreases as the environment temperature increases,and it is also easy to understand.The higher temperature means that more oscillation modes will be excited,and this will have a greater impact on the MTs,so the decoherence time decreases. Fig.10.Decoherence time changes with environment temperature T when other parameters are consistent with those in Subsection 2.3. Doing the same work as Case 3 and we find that According to Eqs.(16)–(19),the decoherence time could be approximately expressed as Since the decoherence time relies less on ωp, β,then equation(20)will be changed into: In fact,equation(21)could be proved,since the plasma frequency THz,the decoherence time τ~10 fs–100 fs,and the temperature T ~ 100 K.Therefore, Under the condition of Eq.(22),equation(12)could be approximately expressed as Then the decoherence time satisfies Equation(24)could be used for calculating the decoherence time only under the condition of Eq.(22).However,equation(24)is useful for various actual parameters. If the Orch OR model can be verified both in theory and experiment,the influence will be inestimable;however,the conformational state is affected by the “warm and wet”cellular environment,and the decoherence time is a very important parameter. In this paper,the decoherence time scale is even smaller than 0.1 ps.This timescale is so short that quantum state will be destroyed by the cell solution environment soon.This model only considers the coupling between the tubulin dimers and ions in the cellular fluid system,treating the water as a medium and overlooking the interactions of MTs-water molecules;water molecules may shield some interactions of ion-MTs,and the interaction of water-ions and water-MTs may have influence on the decoherence process.[32,33]According to Eq.(24),if the interaction strength a√ttenuates to ε(0<ε<1),the decoherence will increase to 1/ε than before;an enough decoherence requires ε?1 and the strength of shielding by water molecules needs to be measured by experiment. Other mechanism for decoherence that is not considered is the coherent pumping of the system via the environment.[21]According to Fro¨hlich’s theory,if a system is strongly coupled to its environment via some degrees of freedom,and a coherent pumping source exists in environment,it might inhibit other degrees of freedom known as coherent oscillations.[35,36]Such oscillations might increase the decoherence time.Guanosine triphosphate(GTP)hydrolyzation in the cells might act as a pumping source.This mechanism was not considered in this paper. Decoherence is an important phenomenon in quantum information.Decoherence mainly comes from the interaction of quantum systems with the environment.In the range of molecule interactions,the main interaction between environment and tubulin dimers is the electromagnetic interaction;the electromagnetic field comes from ions and thermal radiation of the environment.However,in this model,the thermal radiation is ignored,and in the range of room temperature,the thermal frequency spectrum mainly concentrates in the range of THz band.The water molecules in the cell environment could strongly absorb the THz photon and the model only takes into account the electromagnetic field from ions.Besides,if the thermal radiation is considered,the decoherence time would be smaller than the result given before,and it will not change the conclusion. This model needs to be verified both experimentally and theoretically. This model may offer a helpful theoretical framework to compute the decoherence time in quantum biosystems,even though the environment of biological system is different.However,the electromagnetic interaction is essential in the scale of molecules,so this modelcould be used for reference when dealing with the interaction between the ions in cell environment and dipoles of bio-molecules.The direct experiment to verify this model is hard to be carried out at this time,but with the development of ultrafast biophysics,quantum information,quantum optics,and imaging technology,[37–41]the experiment could be carried out in the future. In Appendix A,the dispersion relation of ion density wave is derived by fluid theory.Note that ni,mi,vi,qirepresent the particle number density,ion mass,the macro velocity,and electric charge of the i-th ion. E is the space electric field,βiis used to represent the ion thermal velocity,and?mβ2i?niis the thermodynamic pressure of the i-th ion.Then according to fluid theory In order to deduce intrinsic oscillation mode and its dispersion relation,linearization is done for Eq.(A1).For arbitrary physical quantity A,it is divided into two parts Now,let us compute the eigenmode with intrinsic wavelength and frequency.Set?A=?A0exp[i(k·r?ωt)].Then the operator?/?t= ?iω,? =ik,and equation(A3)changes to According to Eq.(A4),the eigen-equation is Or equivalent in matrix form where ?l,k=(ω2?k2β2l)δkl?hnliqlqk/εml,and?=(?1,?2,...,?M)T.Set f(ω,k)=det?(ω,k),equation(A6)must have untrivial solution to ensure eigenmode exits,so the dispersion relation is determined by Set ql=(?1)υlZle,where Zlis the valence state of ions,e.g.,for Na+and Cl?,Zl=1,and for Ca2+,Zl=2,and υlrepresents the sign of ion charge,and In long-wavelength limit kβl/ω ?1,then whereis the plasma frequency,is the average thermal velocity of all ions,and cj(j=2,3,...,M)is the M?1 roots of the following equation So M kinds of waves are obtained,and their dispersion relation is The ion charged density is Use Eqs.(A11)and(A6),under the condition of longwavelength approximation,only when ω2=ω2p+β2k2,ρ 6=0;otherwise ρ =0.That is to say,ω2= ω2p+β2k2represents ion charged density wave,and can be coupled with MTs by dipole–charge interactions as shown in Fig.2.Other M ?1 kinds of waves could not couple with MTs under the condition of long-wavelength approximation. Finally,diagonalize matrix ? Set P(k)=P(0)+O(k2)and define another variable ρ=(ρ1,ρ2,...,ρM)T,which is determined by The transformation between n and ρ is Then Compare Eqs.(A16)and(A11),then So eρ1could also be used to represent net charge density of ions,and equations(A15)and(A17)will be used in Appendix B. In the coordinate representation,the Hamiltonian Heof cellular environment can be shown as follows: where rk,irepresents the position of the k-th kind of ions that have been numbered i,φ,A are scalar potential and vector potential,respectively,and pk,j=?k,jis the canonical momentum.The first term represents the kinetic energy of the ions,and the second term represents the field energy. The potentials φ,A are not unique.For two different potentials(φ,A),(φ0,A0),if they satisfy the two potentials will have the same field E, B as follows: We use an approach similar to the David Bohm’s electron gas model and define the Hamiltonian Eq.(B1)in another manner;[33]the second term is derived from the interactions between ions and the energy stored in the field.Therefore,equation(B1)can be written in an equivalent way as follows: First,set ξ =Rφdt so that φ0=0,then E = ??A/?t, B =?×A.ExpandAin Fourier series exp(ik·r) whereek=k/k is an unit vector parallel to the direction of the wave propagation,ekμ(μ =1,2)is another two-unit vector which is perpendicular to ek,and ek1⊥ek2.SoAkandA⊥represent longitudinal wave and transverse wave,respectively.Their electric field and magnetic field are where p(?k)=˙q(k),Pμ(?k)=˙Qμ(k).Aand Eare real and can be ensured as follows: Use Eqs.(B5)and(B6)as well as the commutative relation[^p,A]=?i??·A,the Hamiltonian equation(B4)will become where Now,use Eq.(B5),then we have where nlis the number of l-th kind of ions in a unit volume.The random phase approximation(RPA)makes the second term inconsiderably smaller than the first termtherefore Similarly, Use Eqs.(B6a)and(B6b),then we obtain means the kinetic energy,and it can be divide it into two parts The first term is the macroscopical translational energy,and the second term means the thermodynamic energy. The second term in Eq.(B14)can be changed into Now,use Eq.(A15)and ignore the cross term ρiρj(i6=j),then As discussed in Appendix A,eρ1represents net charge density of ions,so use Gauss’s theorem in k-space Use Eqs.(B8)–(B17),then the total Hamiltonian is expressed by where the first term means ion sound wave,the second term means interaction between ions and fields and it is neglected for the reason that each ion has a random phase(random phase approximation or RPA),?21(k)= ω2p+c2k2is the dispersion relation of electromagnetic wave in plasma,and ?22(k)=ω2p+β2k2is the dispersion relation of charged density wave or plasma oscillation. At last,using second quantization method,define(k),(k)as the creation operator and annihilation operator of electromagnetic wave,respectively,and(k)and ?a(k)as the creation operator and annihilation operator of the plasma oscillations,respectively,and we can obtain Andsatisfy the commutation relation Use Eqs.(B19)and(B20)and the random phase approximation,the Hamiltonian equation(B18)will become where In long-wavelength limit,β2k2/ω2p?1,so This is the dispersion relation of ion charged density wave as shown in Appendix A. In Eq.(B21),only the 3rd term could be coupled with MTs by dipole–charge interactions(as seen in Eq.(B17),ρ(k)is only related to p(k)instead of Pμ(k)),so this model only considers the 3rd term which is named namely,the coupling between MTs and cellular environment via interactions between plasma oscillations and dipoles.The interaction Hamiltonian for a single dipole with the cellular environment is determined by Eq.(5).Thus,after Fourier transformation,equation(5)becomes According to Eqs.(B17)and(B19b),then the MT’s dipole p can be written as follows: Here, pn=hn|? p|ni is the observed value of pin state|ni.In Eq.(B27),the the cross term pm,n?c?m?cnwas neglected,use Eqs.(B25)–(B27),then the coupling Hamiltonian can be written as follows: where The Hn,kmeans the interaction between MTs and cellular fluid environment mentioned later,and it is then used to compute decoherence time,and λn,kis the coupling coefficient.The method for computing the coupling coefficient λn,kwill be introduced in Appendix C. The coupling coefficient λn,kis expressed as follows: where pnis a constant vector;for a certaink,the z axis is set to be parallel tok.In the spherical coordinate frame,k·r =krcosθ,and the volume element dr =r2sinθdθd?;thus, pncan be expressed as follows: Thus, When the variable ? is integrated in the interval[0,2π],thenpzcosθ exp(ikrcosθ)sinθdrdθd? where Compute Eq.(C5),then A=0 and Here, pz= pn·k/k;generally,in the actual situation,plasma oscillations will be excited only when the wavelength is larger than the Debye length λD.Therefore,only k<2π/λDcould be used to refer to the excited state.The integral in Eq.(C1)in the space|r|> λDbecause a shielding layer charge appears on the surface of MTs with a thickness λD,as shown in Fig.2.The shielding layer charge is stable and cannot excite plasma oscillations;therefore,in Eq.(C6),rmin=λDand rmax=∞.Hence, Define b(k)= ?ia(k)as new creation operator and annihilation operator,then the total Hamiltonian is where and we have obtained Eqs.(7)and(8). [1]Turin L 1996 Chem.Senses 21 773 [2]Franco M I and Siddiqi O 2011 Proc.Natl.Acad.Sci.USA 108 3797 [3]Ritz T,Adem S and Schulten K 2000 Biophys.J.78 707 [4]Hiscock H G,Worster S,Kattnig D R,Steers C,Jin Y,Manolopoulos D E,Mouritsen H and Hore P J 2016 Proc.Natl.Acad.Sci.USA 113 201600341 [5]Gregory S E,Tessa R C,Elizabeth L R,Tae-Kyu A,Toma′s M,Yuan-Chung C,Robert E B and Graham R F 2007 Nature 446 782 [6]Romero E,Augulis R,Novoderezhkin V I,Ferretti M,Thieme J,Zigmantas D and Van Grondelle R 2014 Nat.Phys.10 676 [7]Levi F,Mostarda S,Rao F and Mintert F 2015 Rep.Prog.Phys.78 082001 [8]Novelli F,Nazir A,Richards G H,Roozbeh A,Wilk K E,Curmi P M and Davis J A 2015 J.Phys.Chem.Lett.6 4573 [9]Sarovar M,Ishizaki A,Fleming G and Whaley B 2010 Nat.Phys.3 462 [10]Marletto C,Coles D,Farrow T and Vedral V 2018 J.Phys.Commun.2 101001 [11]Mesquita M V,VasconcellosR,Luzzi R and Mascarenhas S 2005 Int.J.Quantum Chem.102 1116 [12]Jackendoff R 1987 Consciousness and the Computational Mind(Cambridge:The MIT Press)pp.275–280 [13]Tononi G,Boly M,Massimini M and Koch C 2016 Nat.Rev.Neurosci.17 450 [14]Crick F and Koch C 2003 Nat.Neurosci.6 119 [15]Edelman G M 2003 Proc.Natl.Acad.Sci.USA 100 5520 [16]Jahn R G and Dunne B J 2007 Found.Phys.3 306 [17]Mershin A,Sanabria H,Miller J H,Nawarathna D,Skoulakis E M,Mavromatos N E,Kolomenskii A A,Schuessler H A,Luduena R F and Nanopoulos D V 2006 The Emerging Physics of Consciousness(Berlin:Springer)pp.95–170 [18]Hameroff S and Penrose R 2014 Phys.Life Rev.11 39 [19]Hameroff S and Penrose R 2014 Phys.Life Rev.11 94 [20]Hameroff S R and Penrose R 2017 Biophysics of Consciousness:A Foundational Approach(Singapore:World Scientific)pp.517–599 [21]Craddock T J A and Tuszynski J A 2010 J.Biol.Phys.36 53 [22]Craddock T J,Priel A and Tuszynski J A 2014 J.Integr.Neurosci.13 293 [23]Fisher M 2015 Ann.Phys.61 593 [24]Hameroff S R 2007 Cogn.Sci.31 1035 [25]Mavromatos N E,Mershin A and Nanopoulos D V 2002 Int.J.Mod.Phys.B 16 3623 [26]Mavromatos N 1999 Bioelectrochemistry Bioenergetics 48 273 [27]Tegmark M 2000 Phys.Rev.E 61 4194 [28]Hagan S,Hameroff S R and Tuszy′nski J A 2002 Phys.Rev.E 65 061901 [29]Nelson P 2007 Biological Physics(New York:WH Freeman)p.416 [30]Priel A,Tuszynski J A and Woolf N J 2005 Eur.Biophys.J.Biophys.Lett.35 40 [31]Privman V and Tolkunov D 2005 Quantum Information and Computation III(Bellingham:The International Society for Optics and Photonics),pp.187–195 [32]Tolkunov D,Privman V and Aravind P K 2005 Phy.Rev.A 71 060308 [33]Craddock T J,Friesen D,Mane J,Hameroff S and Tuszynski J A 2014 J.R.Soc.Interface 11 20140677 [34]Chen Y,Okur H I,Gomopoulos N,Macias-Romero C,Cremer P S,Petersen P B,Tocci G,Wilkins D M,Liang C and Ceriotti M 2016 Sci.Adv.2 e1501891 [35]Fr?hlich H 1968 Int.J.Quantum Chem.2 641 [36]Wu T M and Austin S J 1981 J.Biol.Phys.9 97 [37]Bohm D and Pines D 1953 Phy.Rev.92 609 [38]Yin C C and Biophysics D O 2018 Chin.Phys.B 27 058703 [39]Zheng C J,Jia T Q,Zhao H,Xia Y J,Zhang S A and Sun Z R 2018 Chin.Phys.B 27 057802 [40]Wade C G,ˇSibali′c N,de Melo N R,Kondo J M,Adams C S and Weatherill K J 2017 Nat.Photon.11 40 [41]Trocha P,Karpov M,Ganin D,Pfeiffer M H,Kordts A,Wolf S,Krockenberger J,Marin-Palomo P,Weimann C and Randel S 2018 Science 359 887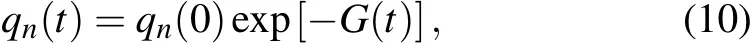
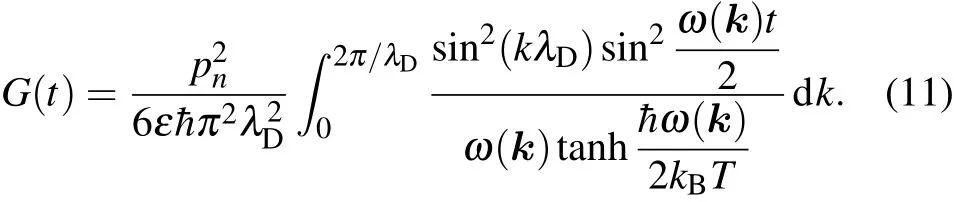

2.3.Typical order of magnitude of decoherence timescale

2.4.The dependence of decoherence time with other parameters
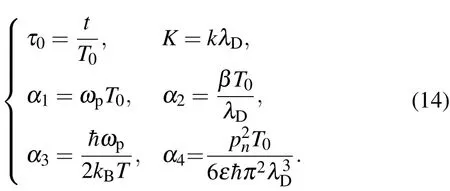
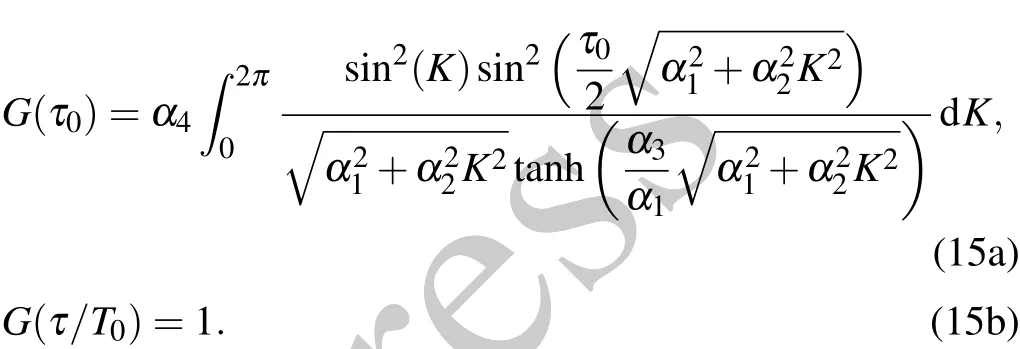

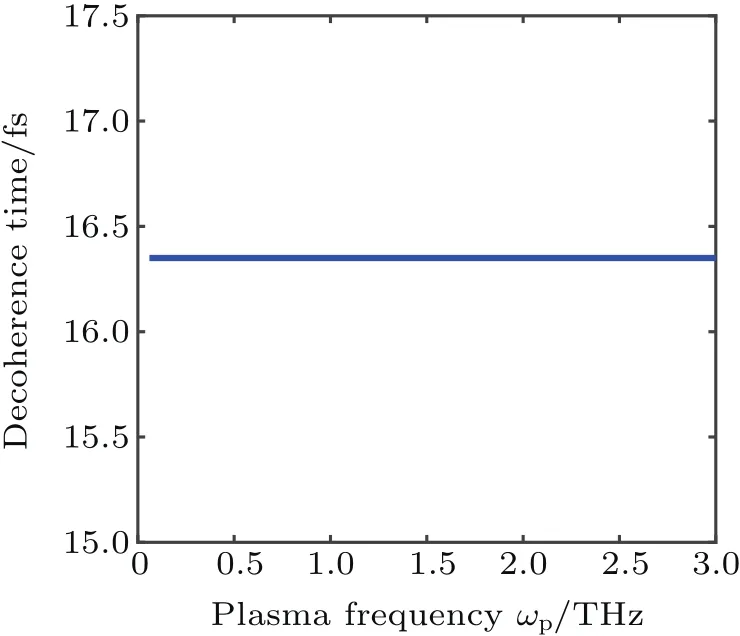
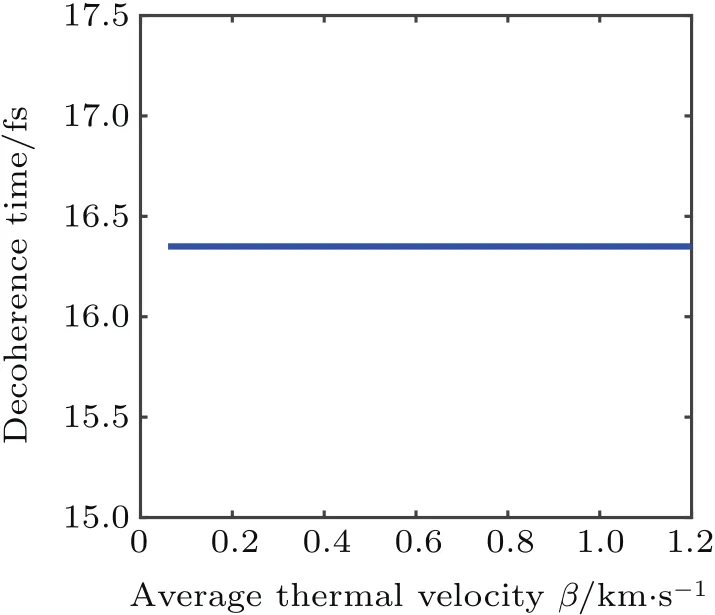
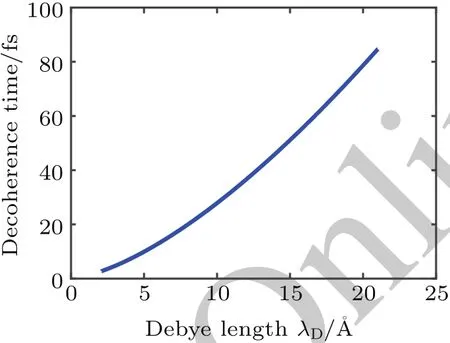
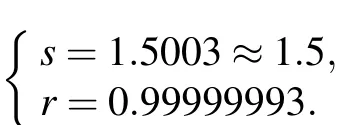
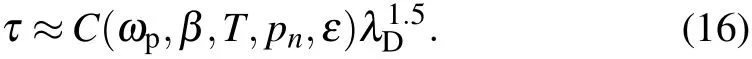
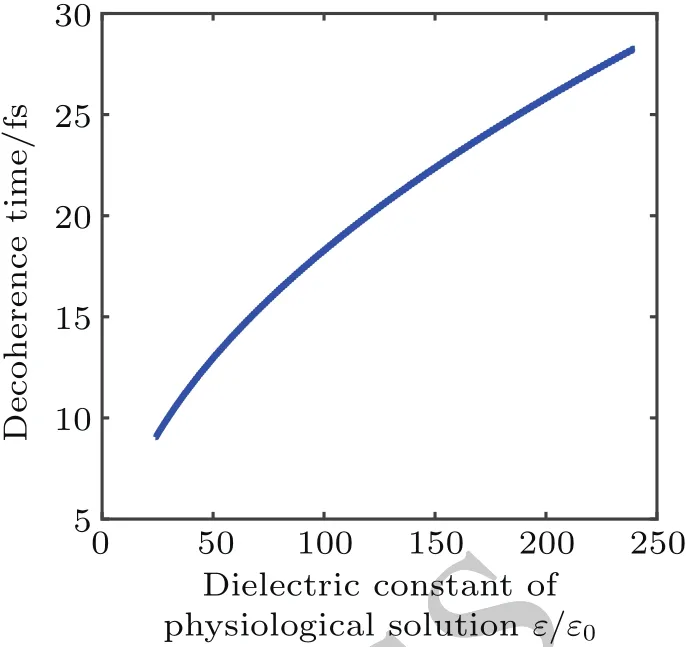
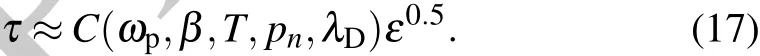
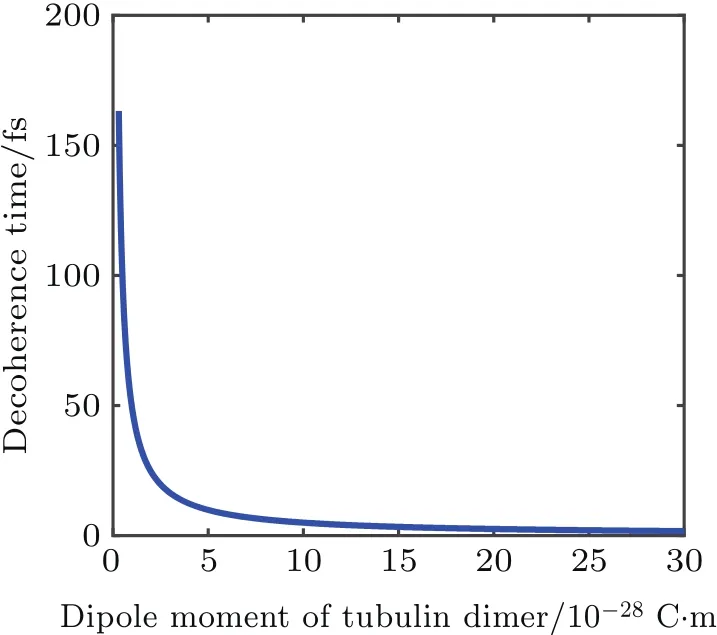
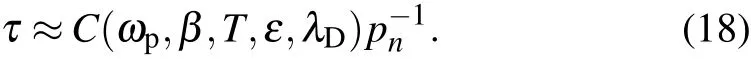
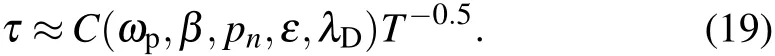
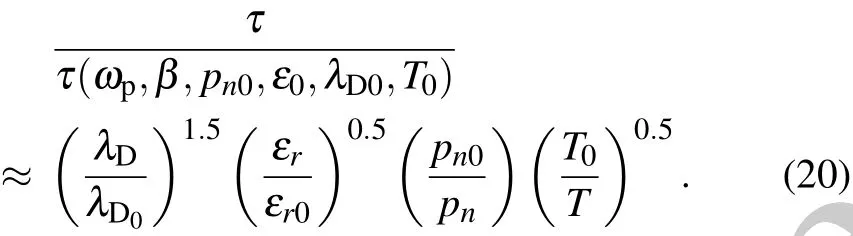
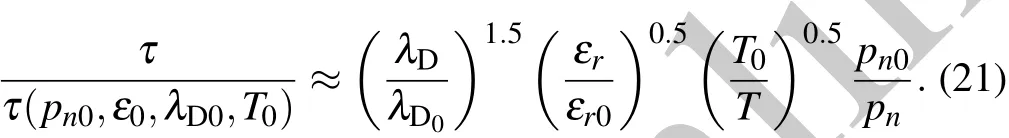
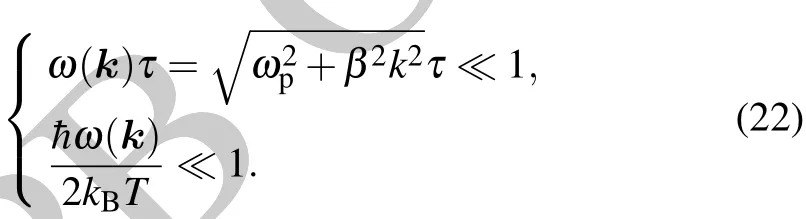
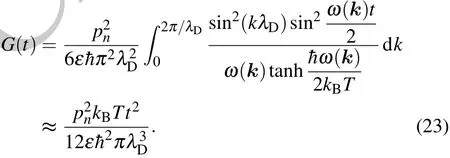
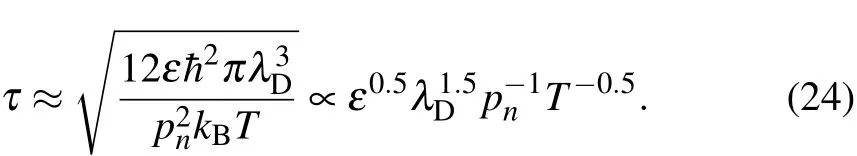
3.Conclusion and outlook
Appendix A:Dispersion relation of ion density wave


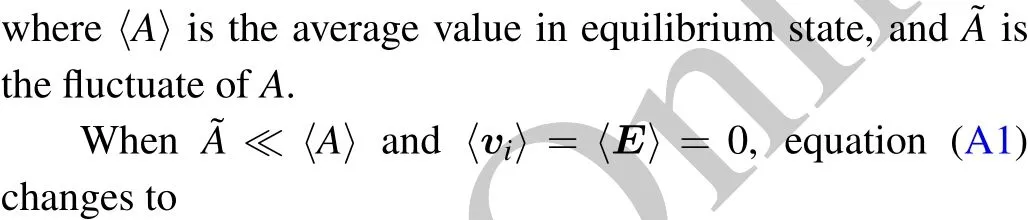
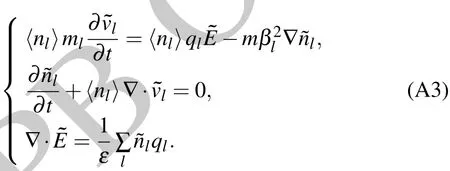
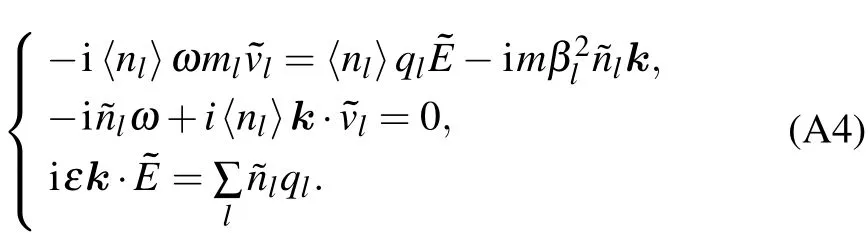
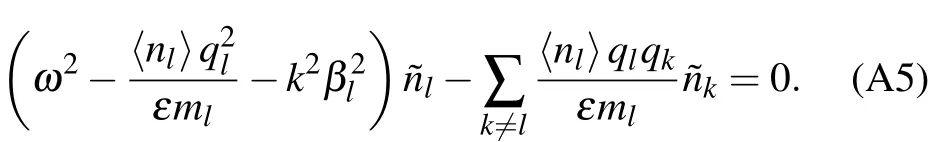


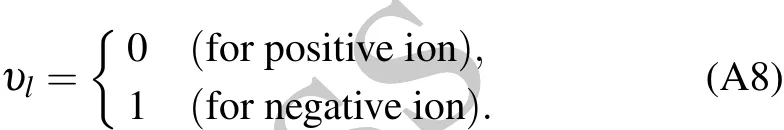
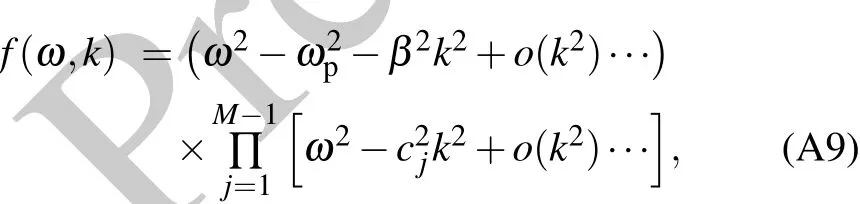
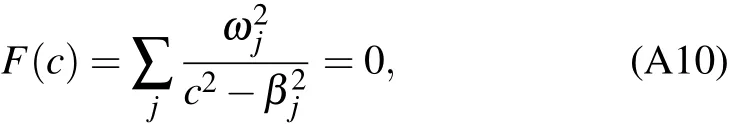
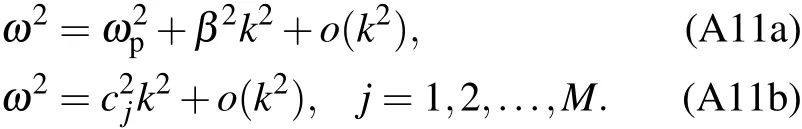
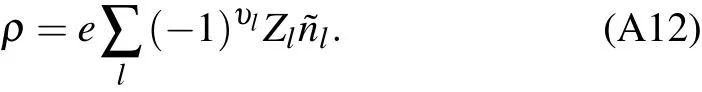
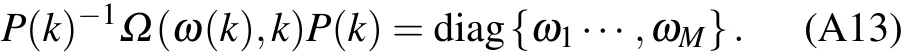
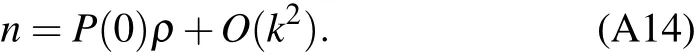
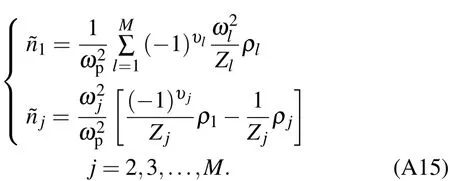
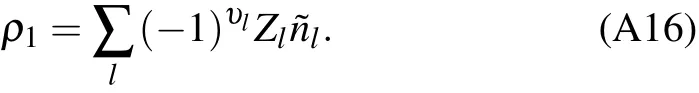

Appendix B:Second quantization of environment Hamiltonian Heand interaction Hamiltonian Hin
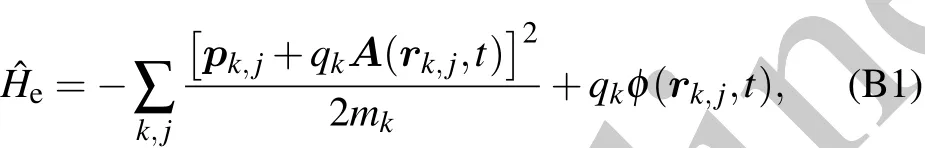
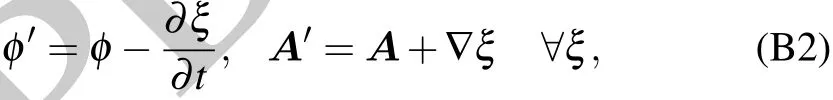
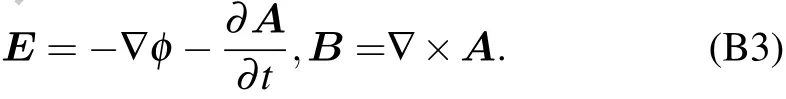
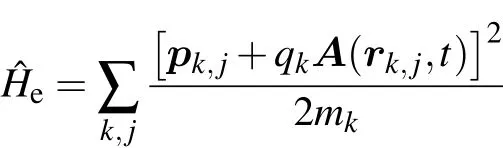
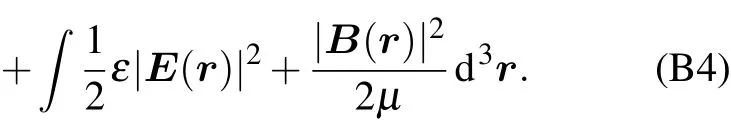
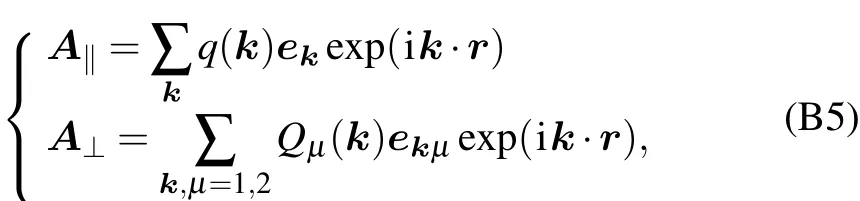
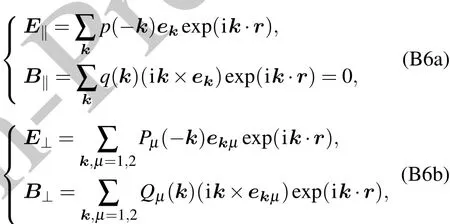
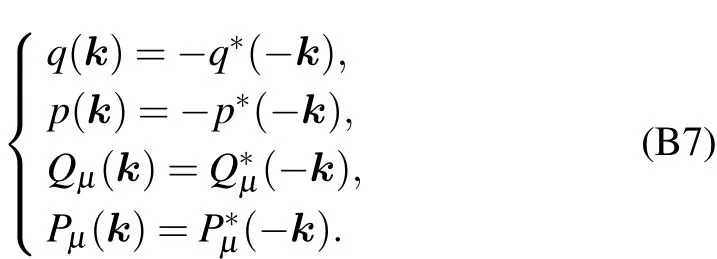
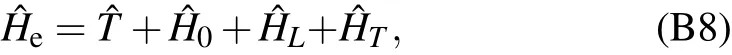
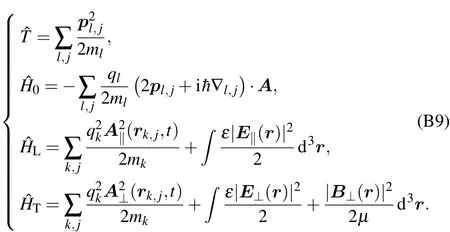
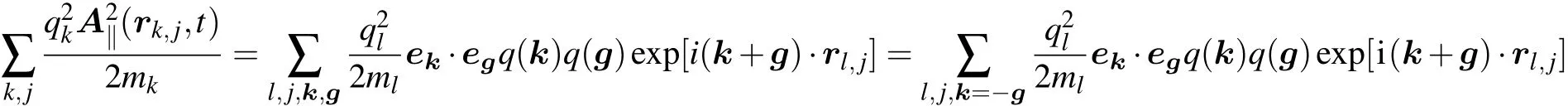
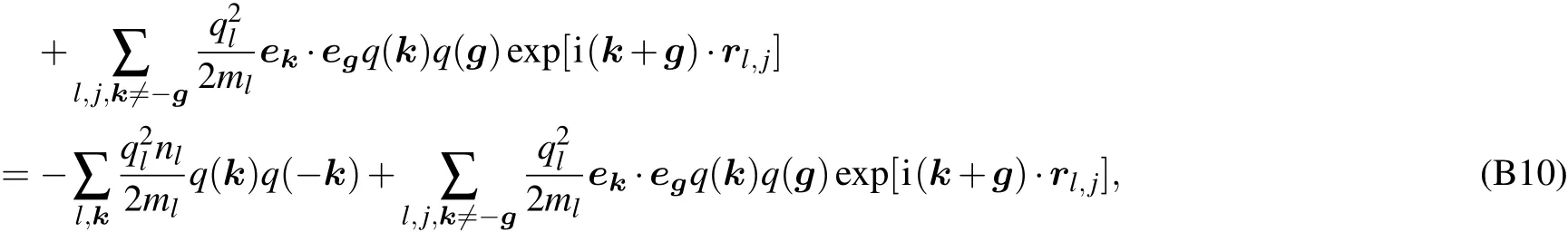
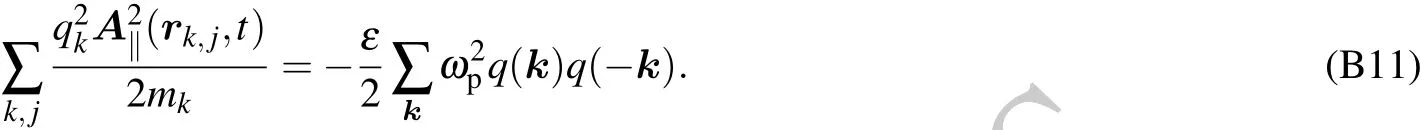
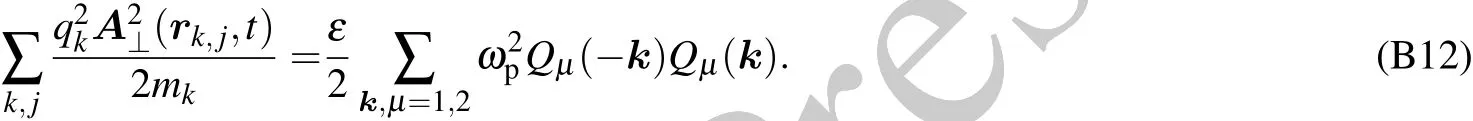
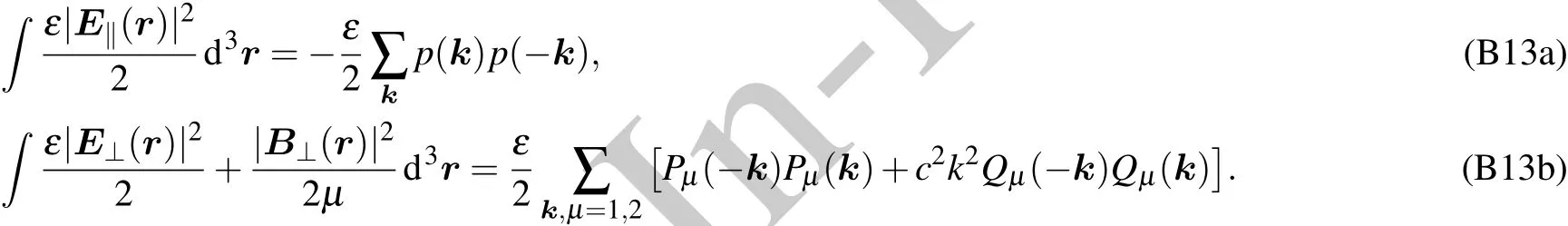
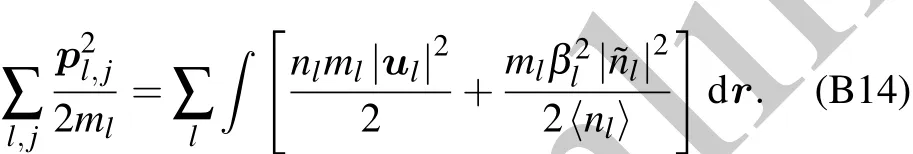
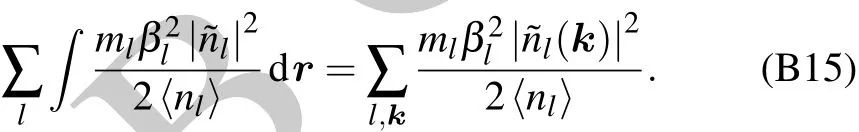
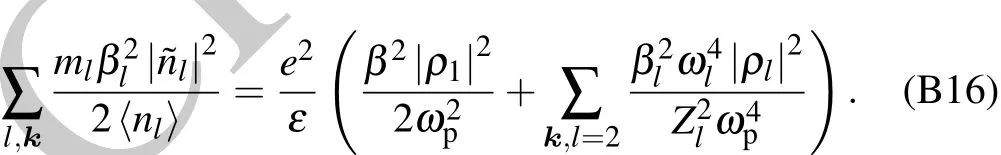

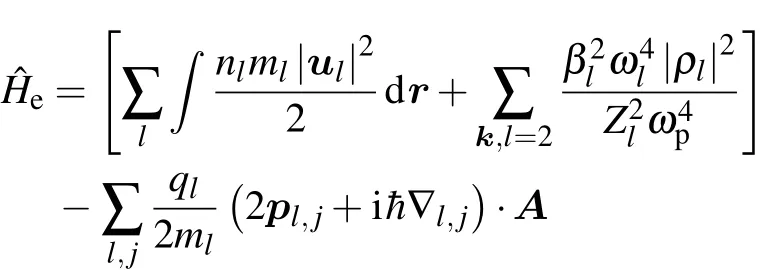
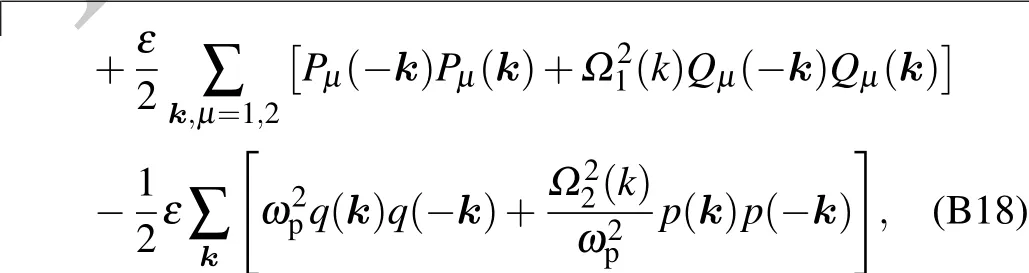
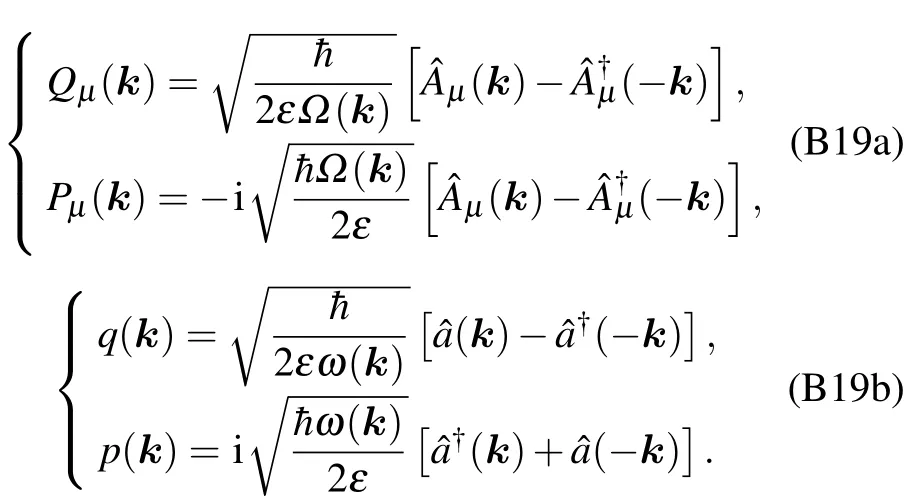

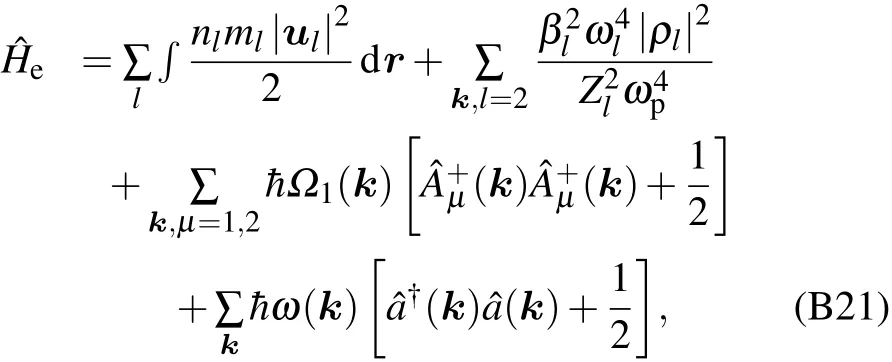
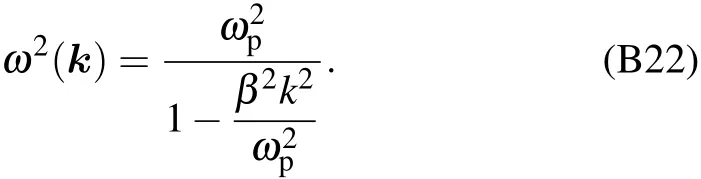
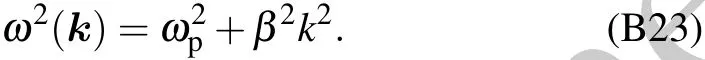
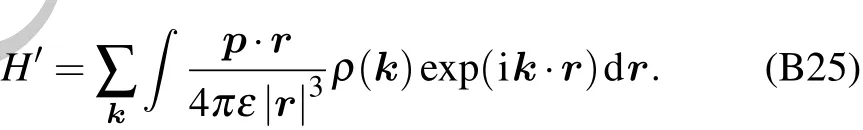
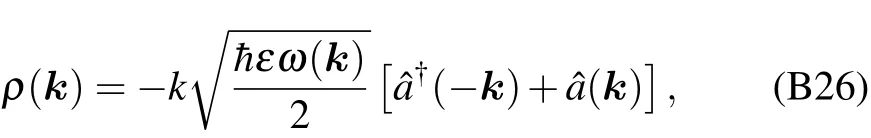


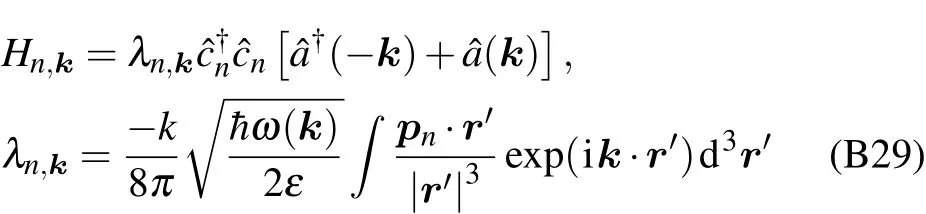
Appendix C:Computation of coupling coefficient λn,k
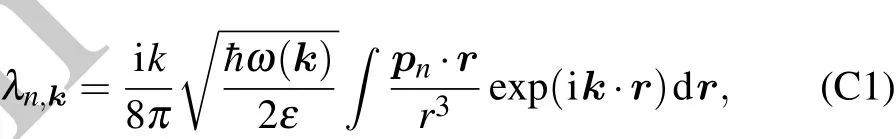
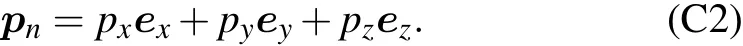
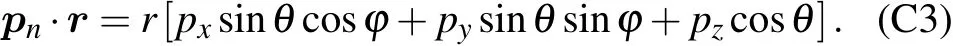
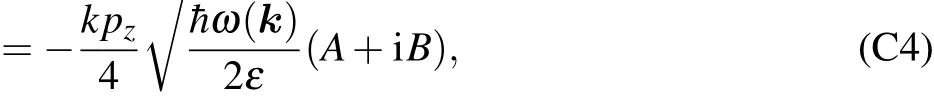
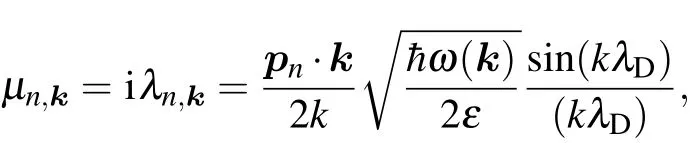
- Chinese Physics B的其它文章
- Effect of carrier mobility on performance of perovskite solar cells?
- Plasma electrolytic liquefaction of sawdust?
- Insight into band alignment of Zn(O,S)/CZTSe solar cell by simulation?
- Effect of terahertz pulse on gene expression in human eye cells?
- Ultraviolet photodetectors based on wide bandgap oxide semiconductor films?
- Effect of temperature on photoresponse properties of solar-blind Schottky barrier diode photodetector based on single crystal Ga2O3?

