Physics of quantum coherence in spin systems?

Maimaitiyiming Tusun(麥麥提依明·吐孫),Xing Rong(榮星),and Jiangfeng Du(杜江峰),?

1 CAS Key Laboratory of Microscale Magnetic Resonance and Department of Modern Physics,University of Science and Technology of China,Hefei 230026,China

2 Synergetic Innovation Center of Quantum Information and Quantum Physics,University of Science and Technology of China,Hefei 230026,China

3 School of Physics and Electronic Engineering,Xinjiang Normal University,Urumqi 830054,China

Keywords:coherence,decoherence,magnetic resonance techniques,uncertainty relation

1.Introduction

The coherent superposition of states combined with the quantification of observable represents one of the most fundamental features of quantum mechanics starting from the classical realm.Through the combination of energy quantization and tensor product structure of the state space,quantum interference,and multiple entanglement phenomena play an important role in the application of quantum physics and quantum information science.Here,we review recently remarkable progress of investigation and exploitation of quantum coherence and its protection based on spin systems,which employ the electron and nuclear spins as spin-qubits.

The present paper is organized as follows.In Section 2,we introduce the concepts of quantum coherence and decoherence.The decoherence we consider is caused by the coupling between the qubit and the environment.We formulate the decoherence as the entanglement between the electron spin and the nuclear spins,which is induced by nuclear spin bath evolution conditioned on the electron spin state.In Section 3,we focus on spin systems.One of the main barriers towards practical quantum computation is the decoherence effect.We utilize dynamical decoupling(DD)techniques to overcome this effect.The dynamical decoupling not only maintains the coherence of single spin qubit,but also preserves the entanglement of multiple qubits.Based on this progress,we demonstrate an anomalous decoherence effect(ADE)of a quantum bath on a spin higher than 1/2.We also discuss the application of quantum coherence in weak magnetic field detection and adiabatic quantum factorization algorithm in the system under study(here is the spin system).In Section 4,we introduce two different uncertainty relation and its experimental verification in the spin systems.The review concludes with Section 5.

2.Coherent spin dynamic

2.1.Coherence and decoherence

A quantum bit(qubit)is a two-level system that can be identified as a spin-1/2 with states|↑〉and|↓〉.The ability of the qubit in a coherent superposition of|↑〉and|↓〉,

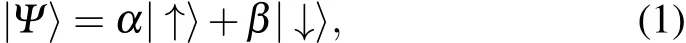
enables the parallel processing of many pieces of classical information.In order to keep this information,the qubit has to faithfully maintain its quantum state.The unavoidable coupling between the qubit and the environment spoils the quantum state by introducing uncontrolled evolution of the qubit.The qubit coherence is lost under the noisy environment.This decoherence problem is one of the obstacles in the road toward scalable quantum computation.

Let us consider the decoherence problem in the spin system.The system consists of an electron spin qubit and N nuclear spins as the spin bath.The total Hamiltonian can be written as

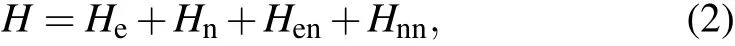
where He= ωeSzand Hn=are the Zeeman splitting in the applied magnetic field along the z axis,Henis the hyper fine interaction,and Hnnis the intrinsic nuclear-nuclear interaction.Suppose the initial state of the qubit-bath system has the form|Ψ(0)〉=|φ(0)〉?|J〉,which is the direct product of the qubit state|φ(0)〉=C+|↑〉+C-|↓〉and the bath state|J〉.After evolution under the Hamiltonian H,for time τ,the nuclear states associated with the two electron spin states diverge,yielding an entangled state of the form

When the nuclear spin degrees of freedom are traced out,the reduce density matrix becomes

The electron spin coherence is reduced from ρ+-(0)=to ρ+-(τ)=〈J(-)(τ)|J(+)(τ)〉.The decoherence is characterized by

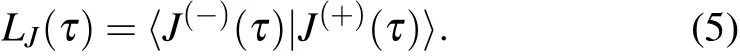
This formula simplifies the electron spin coherence to the overlap of the two nuclear states,each following the evolution conditioned on the state of the electron.Thus,the key is the many-body bath dynamics caused by the interaction within the bath.For example,a non-interacting nuclear spin bath would not evolve from an Overhauser field eigenstate(except for a trivial phase factor)and the qubit decoherence would be totally eliminated[1]by standard spin echo.[2]

2.2.Coherence protection

Since qubit decoherence results from uncontrolled evolution due to the coupling between the qubit and the bath,the coherence can be protected by dynamically eliminating the qubit-bath coupling during the evolution.The idea of dynamical decoupling originated in spin echo[2,3]in nuclear magnetic resonance,in which a single flip of nuclear spins by a radio frequency(RF)pulse at least partially cancels the noise.The standard periodic Carr-Purcell-Meiboom-Gill(CPMG)pulse sequences[3]can keep the spin coherence longer by decoupling a spin from its environment.[4]Iteratively concatenated sequences[5-8]can realize the dynamical decoupling to an arbitrarily high order of precision,but the number of pulses increases exponentially with the controlling order.A remarkable advance in dynamical decoupling theory is the discovery by Uhrig[9,10]of optimal sequences,which realizes the N th order of dynamical decoupling precision with the minimum number(N)of spin- flip pulses.For a pure dephasing model,the sequence of Uhrig dynamical decoupling(UDD)contains N π pulses applied at

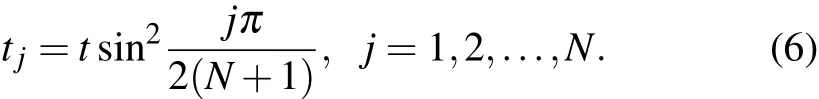
For comparison,the periodic multiple π pulses sequence called PDD[11]has timing tj=t(2 j-1)/(2N).The sequences of UDD and PDD are shown in Fig.1(a).The experimental preservation of electron spin coherence with dynamical decoupling has been investigated in γ-irradiated malonic acid single crystals.[12]The γ-irradiation may remove one hydrogen atom from a methylene group(-CH2)and create a radical(-CH),which provides an unpaired carbon valence electron.The coherence decay of the unpaired-electron spin is investigated both under UDD and PDD.Figure 1(b)shows the experimental results of the coherence decay under N-pulse UDD and PDD,with N=1,2,...,7.It is shown that UDD outperforms PDD in preserving the spin coherence.The coherence time is prolonged to about 30μs with UDD.It would otherwise be about 0.04μs without control or 6.2μs under onepulse control.

Dynamical decoupling can be utilized to preserve the pseudoentanglement.[13]The experiment was implemented on the system of phosphorus doped in silicon,which is an attractive candidate for spin-based quantum computing.Because the dephasing time of the electron spin(denoted byhereafter,=0.2μs)is much shorter than that of the nuclear spin(denoted byhereafter,=30μs),it is sufficient to only apply the DD sequence to the electron spin to preserve the pseudoentanglement on a much longer timescale.The degree of pseoduentanglement is quantified by the concurrence C.[14]Figure 2(b)shows the concurrence decay when PDD2 is applied to the electron spin.The decay rate is greatly suppressed compared to that without dynamical decoupling(Fig.2(a)).The concurrence decay with PDD2 can be well fitted by C=A2exp[-t/Tdecay1-(t/Tdecay2)3],where Tdecay1=27.673 μs,and Tdecay2=23.554 μs for|Φ〉=(|↑↓〉+|↓↑and Tdecay1=30.051μs,and Tdecay2=22.357μs for|Ψ〉=(|↑↑〉+|↓↓〉)/The cubic exponential term with Tdecay2is caused by the electron spin decoherence due to spin diffusion of the29Si spin bath.[15]The linear exponential term with Tdecay1is caused by both the nuclear spin dephasing and the electron spin decoherence[16].Since Tdecay1is comparable with the nuclear spin dephasing timebut smaller than the electron spin decoherence time T2e=60μs measured with the Hahn echo sequence,Tdecay1is mainly limited by the nuclear spin dephasing.To preserve the pseudoentangled states even longer,the suppression of the nuclear spin dephasing is also needed.In this experiment,although the DD sequence is applied only to the electron spin,the lifetime of the pseudoentangled states is extended and is about two orders of magnitude longer than that without dynamical decoupling.Besides,DD can also be used to protect quantum correlations including quantum discord.[17,18]

Fig.1.Experimental preservation of electron spin coherence with dynamical decoupling.(a)Pulse sequences of UDD and PDD when N=1,2,...,7.The N-pulse UDD and PDD are abbreviated as UDD N and PDD N,respectively.(b)Experimental results of the coherence decay under UDD(left panel)and PDD(right panel).The integer associated with each curve indicates the number N of π pulses.Insets:semi-logarithmic plots of the same data.Adapted from Ref.[12].Copyright 2009 by the Nature Publishing Group.

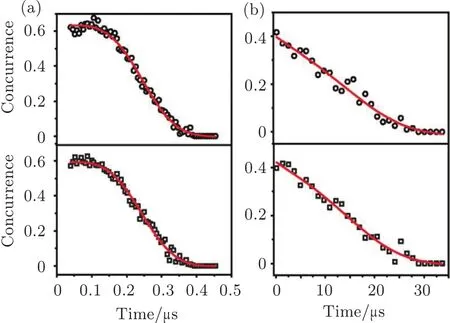
Fig.2.Experimental preservation of entanglement with PDD2.(a)Decay of concurrence without dynamical decoupling for initial state|Φ〉(upper panel)and|Ψ〉(lower panel).(b)Decay of concurrence with PDD2 for initial state|Φ〉(upper panel)and|Ψ〉(lower panel).Symbols are the experimental results and solid lines are the fitting results.Adapted from Ref.[13].Copyright 2011 by the American Physical Society.

The decoherence is caused by the coupling between a quantum object and its environment.Such coupling is usually understood in terms of classical noise,such as in the spectral diffusion theories that are widely used in,for example,magnetic resonance spectroscopy[19,20]and optical spectroscopy.[21,22]A recent theoretical study[23]predicted an anomalous decoherence effect of a quantum bath on a spin higher than 1/2.Considering a spin-1 under a unidirectional magnetic noise bzwith Hamiltonian bzSz,the spin,initially in a superposition of the Szeigenstates|Ψ(0)〉=a-|-〉+a0|0〉+a+|+〉,will evolve to|Ψ(t)〉=a-eiφ(t)|-〉+a0|0〉+a+eiφ(t)|+〉with an accumulated random phase φ(t)=b(τ)dτ.The coherence of the single-transitions|0〉?|±〉is determined by the average of the random phase factor as L0,±= 〈e±iφ(t)〉,whereas the double-transition has coherence L-,+= 〈e2iφ(t)〉.For Gaussian noise,as commonly encountered,andThis leads to the scaling relation

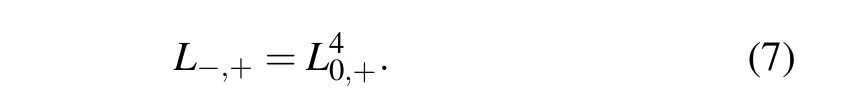
Decoherence of the double-transition behaves essentially the same as that of the single-transitions,but is faster as the double-transition suffers from noise that is twice as strong as that suffered by the single-transitions.Surprisingly,in a mesoscopic quantum bath made of nuclear spins,where the noise bzis the bath operator,the prediction is that the coherence time of the double-transition under dynamical decoupling,where the bath evolution is controlled through the flips of the central spin,can be increased above that of the single spin.[23]

The ADE has been experimentally observed using a nitrogen-vacancy(NV)center system at room temperature.[24]The system consists of center spin and the surrounding13C nuclear spin has a Hamiltonian H=HNV+HB+Hhf.The center spin Hamiltonian is HNV=-γeBSz,where Δ denotes the zero- field splitting and γe=1.76 × 1011s-1·T-1or 2.803 MHz/Gs(The unit 1 Gs=10-4T)is the electron gyromagnetic ratio.The bath Hamiltonian·Ijcontains the nuclear spin Zeeman splitting ω and the dipolar interaction between nuclear spins(with coefficients).The center spin couples to the nuclear spins through Hhf=Sz∑jAj·Ij≡,where Ajis the hyper fine coupling to the j-th nuclear spin Ij.Here,the transverse components of the hyper fine coupling have been dropped because they are too weak to cause the center spin flip(with Aj?Δ).

Under a weak magnetic field,the center spin decoherence is mainly induced by the single13C nuclear spin dynamics.[25-27]The dipolar interaction between nuclear spins can be neglected for the moment.Thus,the bath Hamiltonian HBonly contains the nuclear Zeeman energy(with γCB/2π～14.4 kHz, γC=6.73 × 107s-1·T-1being the gyromagnetic ratio of13C nuclei).The hyper fine field αAj(with Aj/2π～5 kHz for a nuclear spin Ijlocated 1.5 nm from the center)is comparable to the Zeeman frequency.Each nuclear spin precesses about different local fields=-γCB+αAj,conditioned on the center spin state|α〉.The center spin decoherence is expressed as[25-27]

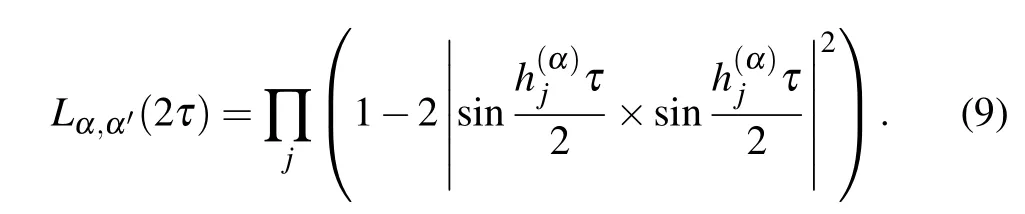
Figure 3 compares the single-and double-transition coherence under the periodic dynamical decoupling(PDD)control by equally spaced sequences of up to five pulses(applied at τ,3τ,5τ,...,called Carr-Purcell sequences for two or more pulses).[28-30]

In the Hahn echo(PDD-1),where the short time condition approximately holds,the single-transition coherence and the double-transition coherence approximately satisfy the scaling relation in Eq.(7).As the number of control pulses increases,the double-transition coherence time increases more than that of the single-transition.Surprisingly,under the fivepulse control,the double-transition has significantly longercoherence time than the single-transition.Such counter-intuitive phenomena unambiguously demonstrate the quantum nature of the nuclear spin bath.All the work indicates that the ADE is robust against the details of the decoherence mechanisms but it is a universal phenomenon due to the quantum nature of mesoscopic baths.

Fig.3.(a)Measured single-(black line with square symbols)and double-transition coherence(red line with circle symbols),under the one-to five-pulse PDD control(PDD-1 to PDD-5,from top to bottom).The scaled single-transition coherence(blue line with triangle symbols)is plotted for comparison.(b)The calculated data,plotted in the same format as in panel(a).(c)Comparison between the measured(symbols)and the calculated(solid lines)singletransition coherence.(d)The same as panel(c),but for the double-transition.Adapted from Ref.[24].○c 2011 by the Nature Publishing Group.

2.3.Applications of coherence in magnetometery

The detection of weak magnetic fields with high spatial resolution is an important problem in diverse areas ranging from fundamental physics and material science to data storage and biomedical science.An approach to the detection of weak magnetic fields has been developed that takes the advantage of techniques for the coherent control of solid-state electron spin qubits.[31]Specifically,we investigate a magnetic sensor based on nitrogen-vacancy centers in diamond at room temperature.The NV center is a point defect in the diamond lattice,consisting of a nearest-neighboring nitrogen atom substituted for a carbon atom,and a lattice vacancy as illustrated in Fig.4.The diamond lattice consists of covalently bonded carbon atoms.Each of the four valence electrons of the sp3-hybridized carbon participates in bonds to the neighboring atoms(distance 1.44?A).The diamond unit cell is in the F dˉ3m space group,which follows the face-centered cubic Bravais lattice(lattice constant 3.57?A).In the NV-center,six electrons occupy the dangling bonds of the vacancy complex,and he resultant defect has C3vpoint symmetry.[32,33]

Fig.4.Negatively charged NV center in diamond and the electronic energy level structure.Adapted from Ref.[34].c○2017 by the American Physical Society.

The NV system is described by the Hamiltonian as

Here,Δ is the crystal field splitting along[111]axis which is equal to 2.87 GHz,←→Ais the hyper fine coupling between the electron spin and the nearby nitrogen nuclear spin,and the strength of hyper fine coupling is about 2.2 MHz(14N)or 3.1 MHz(15N),and ΔN=4.95 MHz is quadrupolar coupling of14N and it equals 0 for15N.The external magnetic field leads to Zeeman splitting term in Eq.(10)of NV electron spin γeB ·S,and nitrogen nuclear spin γNB ·IN,where γeis the electron gyromagnetic ratio for the NV electron spin as given in Subsection 2.2,γN=0.30766 kHz/Gs for14N and γN=0.43156 kHz/Gs for15N.

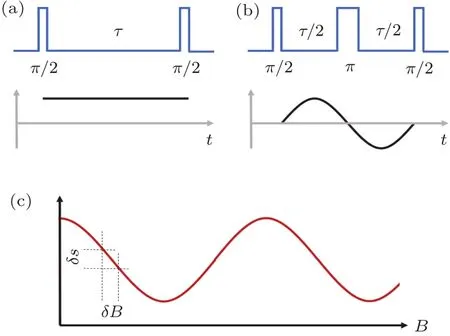
Fig.5.Protocols to measure DC and AC magnetic field.(a)Ramsey-type sequence applied to detect DC magnetic field.(b)Hahn-echo sequence applied to detect AC magnetic field.(c)Signal s versus magnetic field B.

A Ramsey-type sequence can be applied to detect a Zeeman shift caused by external magnetic field B,as shown in Fig.5(a).Aπ/2 pulse createsa quantum superposition state of|0〉and|1〉.The superposition statewill accumulate a phase φ=(gμB/hˉ)Bτ during the free evolution time τ(here,B is external magnetic field,g is Landé factor of spin,and μBis Bohr magneton).After the second π/2 pulse,the population left on|0〉state is s=(1+cos(2φ(B)))/2.In every measurement,deviationoccurs due to quantum projection noise and photon shot noise,where c is the contrast of Ramsey measurement and ηdis collection efficiency about 2%-3%.[35]

The minimum detectable magnetic field of NV magnetometer is δBmin=/d s(shown in Fig.5(c)),where=is the standard deviation of measurement after N times average,d s～gμBτ is the slope of the signal s versus magnetic field B and N=T/τ is the measurement times during the total measurement time T.Thus,the minimum detectable direct current(DC)magnetic field scales according to

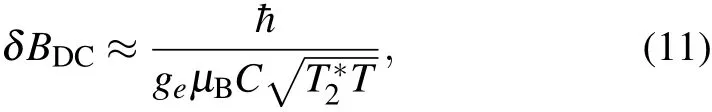
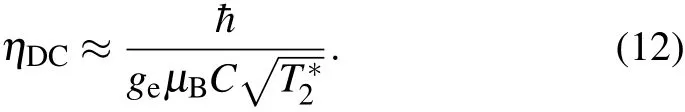
Furthermore,alternating current(AC)magnetic field BAC(t)=bACsin(νt)can be measured by matching the sequence π/2-τ/2- π - τ/2- π/2 with the AC oscillating frequency(Fig.5(b)).The Hahn echo sequence removes the slow environment noise at the same time.The phase accumulated during the free evolution time is

where during the second τ/2 free evolution time the spin flips.Sensitivity of AC magnetic field is[31]

The sensitivity of AC magnetic field can be improve furthermore by higher order dynamical decoupling sequence by extending the decoherence time.The magnetometer sensitivity achieved was 0.5±0.1μT·Hz-1/2in Ref.[36]and even 4 nT·Hz-1/2in Ref.[37].

NV-based nano-scale nuclear magnetic resonance(NMR)gives a unique opportunity to realize non-destructive and nolabeled structure characterization.In 2011,the theoreticalpossibility for atomic-scale NV magnetometry of nuclear spin clusters inside and outside diamond was proposed.[26]Later,distant single nuclear spins and several weakly coupled nuclear spins inside diamond were detected[38-41]by dynamical decoupling methods.And in 2013,another method to detect single nuclear spin was demonstrated[42]by continuous microwave(MW)Hartmann-Hahn method.Based on these two methods respectively,the authors in Refs.[43]and[44]proposed single molecule NMR schemes by NV magnetometry aimed in applications in single-molecule spectroscopy in chemistry and biology.Equipped with shallow NV created through ion implantation[45]and δ-doped chemical vapor deposition(CVD)technology,[46]NV magnetometry can be applied to external nuclear spins.The detection of1H,13C,or29Si nuclear spins in various liquid and solid samples has been shown in Refs.[47]-[51]on the diamond surface.This is a key milestone toward achieving nano-scale magnetic resonance imaging based on scanning NV centers.The technique additionally allows one to perform NMR on an arbitrary sample in the regime of ultra-weak and zero magnetic field,because it is based on statistical rather than thermal polarization of the nuclei.

The interactions between nuclear spins can also be investigated with NVcenterunderdynamicaldecoupling control.A nuclear-dimer induced modulation on the NV center spin coherence can be observed thus both the interactions within the dimer and between the dimer and the NV center electron spin can be characterized.[52]The Hamiltonian of the NV center electron spin and the13C nuclear spin dimer is[26,27]

In the strong magnetic field,the dimer dynamics can be described by a pseudo-spin model,where the two-spin states|↑↓〉and|↓↑〉of the dimer are mapped to the spin-up|?〉and spin-down|?〉states of the pseudo-spin σ.The dynamics of the pseudo-spin is governed by the Hamiltonian

where the component X is the nuclear spin flip- flop rate due to the inter-nuclear spin dipolar coupling D12and the component Z(ms)is due to the hyper fine couplings difference of the two nuclei induced by the nitrogen-vacancy center electron spin state|ms〉.Correspondingly,the pseudo-spin will precess with frequencies=X orWhen the nitrogen-vacancy center spin is prepared in a superposition statethe characteristic frequency of the noise induced by the pseudo-spin becomesIn our experiment,the pseudo-spin precession frequencywas measured by dynamical decoupling control[12,28,29]of the nitrogen-vacancy center spin(as shown in Fig.6).

Fig.6.Characterizing the interaction of a nuclear-spin dimer by fingerprint-matching between measurement and simulation.Nitrogen-vacancy spin coherence as a function of total evolution time under CPMG dynamical decoupling control with various numbers of pulses(N=8,10,12,14,16,and 18).The experimental data(symbols)are well reproduced by simulations(lines)based on a dimer with interaction[X,Z(m s)]=[0.685,14.6]kHz.Other nuclear-spin pairs do not produce dip features matching the experimental data.In these measurements,the magnetic field is B0=1770 Gs.The vertical axes show the probability in the|0〉state.Adapted from Ref.[52].c○2014 by the Nature Publishing Group.

Besides NV-based nano-scale nuclear magnetic resonance,NV-based single molecule electron spin resonance(ESR) finds broad application for studying basic molecular mechanisms in biology and chemistry.[53]Most proteins,however,are non-paramagnetic,and thus not accessible by the technique.Labeling biomolecules with a small spin-bearing moiety,such as nitroxide spin labels,enables electron spin resonance to acquire a broad range of structural and dynamical information.However,current methods require 1010uniform molecules to accumulate a sufficiently large signal-to-noise ratio.This substantially complicates compiling structural and dynamical information.New methods that have tried to push the sensitivity of magnetic resonance to the single spin level all require either a dedicated environment[54,55]or conducting surfaces and tips.[56]

The NV center’s triplet(S=1)ground state can be spinpolarized and read out optically.The magnetic dipole interaction between the NV spin and the dark electron spin is conveniently measured by simultaneously driving the probe(NV)and the dark electron spin.Single NV centers can be created roughly 5 nm below the surface of diamond by ion implantation.The dark spin sample can be deposited on diamond surface and characterized by atomic force microscopy(AFM).

Denoting the spins by SNV(NV sensor),Se(dark electron spin),and I(nuclear spin of dark electron spin),the combined system can be modelled by a coupling Hamiltonian

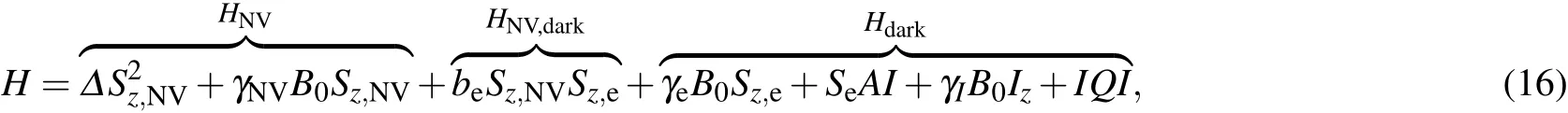
where dark denotes the dark electron spin,B0is the external static field(aligned along z),Δ is the zero- field splitting of the NV,Q is the nuclear quadrupole coupling constant,and γNV,γe,and γIare the gyromagnetic ratios of the NV,target electron,and nuclear spin,respectively.The coupling between the NV and the dark electron spin is approximated as a pure Sz,NV-Sz,einteraction with a coupling constant be,because it is much smaller than the Zeeman and zero- field splitting of the two spins.Within this approximation,the target spin generates an effective magnetic field Be=beSz,e/γNVat the NV center site,which depends on the quantum number Sz,e.

To reveal the coupling,two protocols of spin-echo detected the double electron-electron resonance(known as SEDOR or DEER[48,57-59]).In both schemes,the effective twolevel system|0〉=|Sz=0〉,|1〉=|Sz=-1〉of the NV spin S is addressed with a resonant microwave and performs a Hahnecho measurement on this system.In this measurement,an initial π/2 pulse prepares the spin in a coherent superpositionwith φ =0. φ evolves over time,and is refocused by the π pulse at t= τ and converted into population by the final π/2 pulse,so that the result of a subsequent measurement is|〈0|ψ〉|2=(1+C(τ)cos(φ(2τ))).

Here,

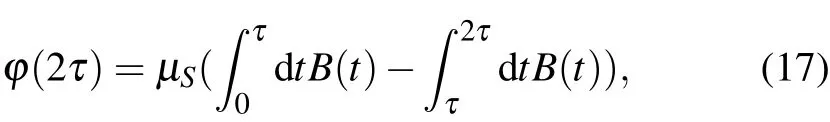
where the sign “-”accounts for the refocusing π pulse.C(τ)≤ 1 is a factor accounting for a possible loss of coherence.

A modified version of SEDOR can enhance sensitivity of single spin ESR protocols.The pulse sequence is shown in Fig.7(a).The phase φ evolves over time,is refocused by N π-pulses at t= τ0/2+nτ0,and is converted into a population by the final π/2 pulse at t=Nτ0.The key idea is to map the electron spin resonance signal of the spin label Seto a phase φ on the NV spin.The flip π pulses of NV electron spin and dark electron spin are synchronized with the dynamical decoupling period.The NV experiences an alternating field from the dark electron spin label and acquires a phase

where beffis the effective magnetic field generated by the spin label at the location of the NV spin.In this way,the dark electron spin ESR signal is mapped to the signal obtained from the NV sensor.

Fig.7.Experimental pulse sequence and electron spin resonance spectrum of dark spin.(a)Pulse sequence to measure the coupling of an NV sensor to the dark electron spin.The pulse sequences contain MW and RF channels,in which microwave and radio-frequency pulses are used to control the NV probe and synchronously flip the dark electron spin.(b)Single spin ESR spectra under ambient conditions.The spectrum disappears after removing the protein by acid cleaning.Adapted from Ref.[60].c○2015 by the American Association for the Advancement of Science.

Figure 7(b)shows the ESR spectrum of a single dark spin(a spin label on protein)under ambient environment.Upon cleaning the diamond surface,the signal disappears,demonstrating that it stems from the spin label on the protein.The spectra in Fig.7(b)are recorded at an external magnetic field B0=153.0 Gs.Three spectral peaks at 356.3 MHz,430.9 MHz,and 501.6 MHz,mark the hyper fine splitting between the spin label electron spin(S=1/2)and the nitrogen nuclear spin(I=1).The observation of hyper fine splitting proves that the detected spin is indeed the nitroxide spin on the protein and not,e.g.,that of a substitutional nitrogen impurity inside diamond.

3.Coherent spin control

3.1.Coherent spin control in single molecular magnets

Quantum computation requires not only quantum state with long coherent time but also precise coherent quantum control.Single molecular magnets(SMMs)are among the potential systems for quantum memory[61]and quantum information processing.[62]Quantum coherence and oscillation are critical for these applications. The ground-state quantum coherence and Rabi oscillations of the SMM V15have been observed at 2.4 K together with scrutinized validation.[64]The new signal of the Rabi oscillation of the ground state(S=1/2)is shown in Fig.8.Relaxation times are recorded to be T2=187.7±4.4 ns for S=3/2 and T2=149±10 ns for S=1/2 with echo decay curves shown in the inset of Fig.8.The observing of groundstate quantum oscillation is particularly important in further studies of quantum effect in SMMs.The coherence property of V15makes it potentially suitable for qubit implementation,where the coherence time can be improved by,for example,using deuterated surfactants and solvent or applying dynamic decoupling approaches.[12,13]

3.2.High fidelity coherent spin control

In order to achieve reliable quantum-information processing results,we need to protect quantum gates along with the qubits from decoherence.Among the various approaches to quantum coherence protection,dynamical decoupling[11]is a particularly promising strategy due to its integratability with quantum gates by elaborate designs.Protecting quantum logic tasks with pulsed DD has been reviewed in Section 2 for extending the coherence time of individual qubit and two-qubit entanglement.Despite the great success of pulsed DD in protecting the coherence,it becomes complicated to combine DD sequence with quantum gates when considering the commutation between the decoupling pulses and the control pulses.Continuous-wave dynamical decoupling(CWDD)approaches have been developed to retain the flexibility of carrying out quantum logic tasks while the qubits are protected.[65-69]The combination of CWDD and quantum gates has been presented in a solid-state NV center system in diamond.[70]

The lossofquantum coherence ofthe NVcenterismainly caused by the surrounding13C nuclear spin bath fluctuations.This can be described by an effective weak random magnetic field b.The linear dependence of the energies|±1〉on the magnetic field results in a sharp variation of the energy gap ω0,-1between the two states of the qubit(|0〉and|-1〉).This results in strong decoherence due to the random magnetic field b.An equally weighted superposition of|±1〉can result in states with eigenvalues insensitive to the random field b.This can be realized by applying two off-resonant continuous microwave driving fields to|0〉→ |±1〉at the same time by ω1and ω2.The Hamiltonian of the NV center driven by two microwaves of the same off-resonance δoand Rabi frequency Ω can be written in the interaction picture as follows:

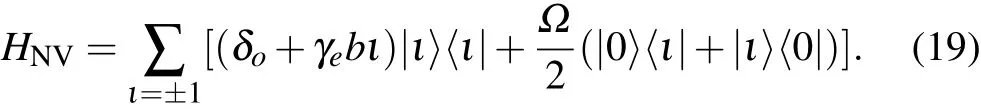
The diagonalization of HNVresults in three dressed states,|e〉,|d〉,and|g〉in the driven space.The two lower levels|d〉and|g〉of the gap wdgare used as a qubit.Owing to the symmetry of HNVand nonzero Ω,the energies of all the three states are only functions of b2,which are insensitive to b,in contrast to the linear dependence of δω0,-1on|b|.Hence,the dephasing between|d〉and|g〉will be strongly suppressed when the microwave Rabi frequency Ω is much larger than the weak effective random field.With the appropriate ratio of Ω/δo(=4),even the b2term in wdgis eliminated so that the lowest order is～b4,and a much greater coherence time can be achieved in the protected subspace spanned by|d〉and|g〉.[65]The gradual transfer from|0〉to|g〉when the microwave Rabi frequency Ω gradually increases allows adiabaticalpreparation and readout,and the manipulation of the dressed state can be realized by an RF pulse.

Figure 9(a)plots the Rabi oscillation in the Ms=0,-1 bases without the driven and|d〉,|g〉bases with CWDD.It clearly shows that the oscillation in|d〉,|g〉is well preserved almost without decay even after 25μs,while that in the Ms=0,-1 bases suffers considerable decay even in a fewμs.The performance of the CWDD-protected quantum gate is evaluated using the coherence of the state after successive NOT gate operations.It is shown in Fig.9(b)by plotting the indicator F defined to be|〈ψ|d〉|2for odd numbers of NOT gates and|〈ψ|g〉|2for even numbers of NOT gates.Compared to the decay time of 11μs in the undriven case,the coherence of the CWDD-driven case is maintained far beyond 50μs,clearly demonstrating the performance of the quantum gate protected with CWDD.

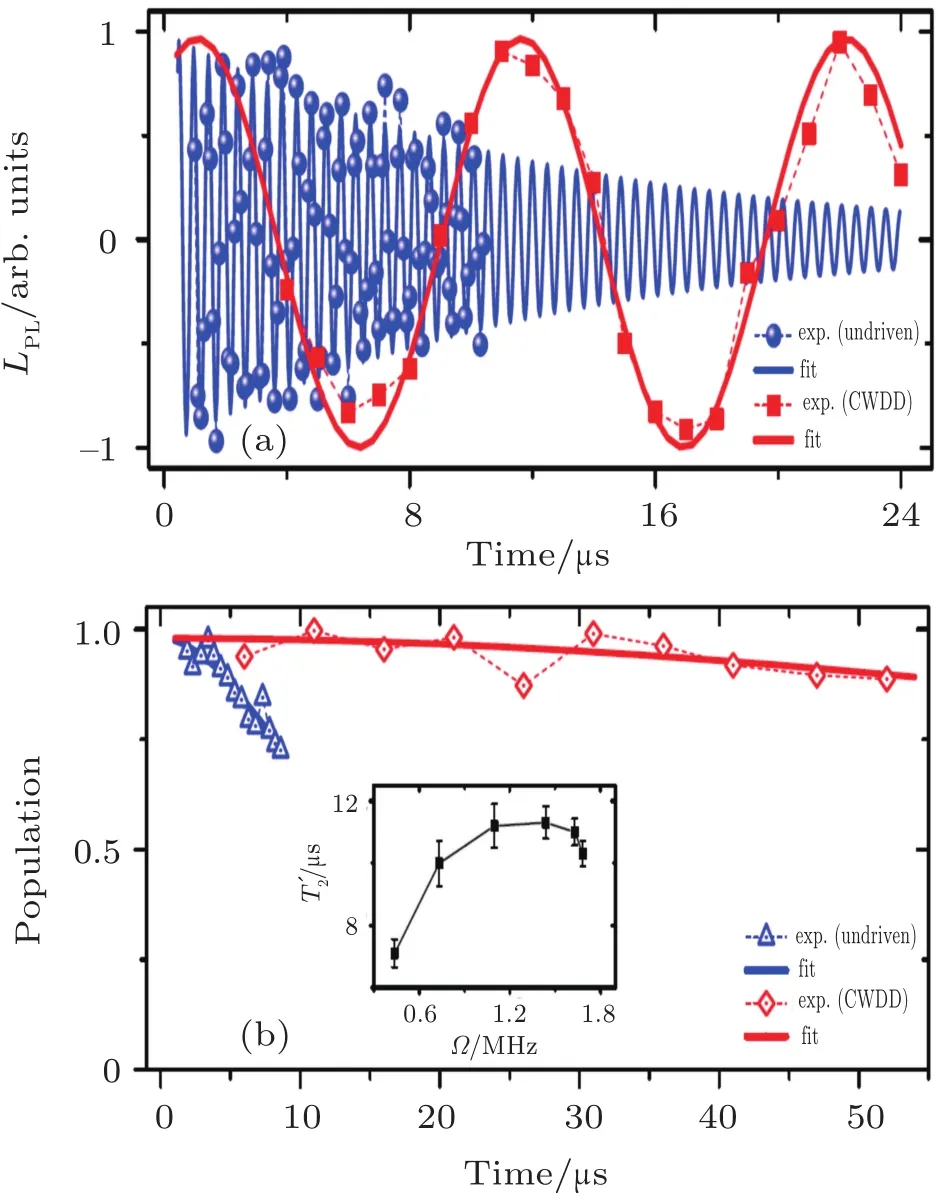
Fig.9.(a)Measured decay of Rabi oscillation both in the undriven space(spheres)and in the subspace protected by CWDD(squares);the curve is only for guiding the eyes.(b)The population of the designated state as a result of the successive NOT gate operation in undriven space with microwave π pulse(triangles),or in a CWDD-protected space with RF π pulse(diamonds).The curve is fitted to Gauss lineshape decays.The subset is the measured decay time as a function of the microwave field amplitude Ω.Adapted from Ref.[70].○c 2012 by the American Physical Society.

Except for the DD strategy for protecting quantum control discussed above,theoretical schemes termed dynamical corrected gates(DCGs)have been proposed.[71-75]To illustrate this,let us consider the case of realizing a target singlequbit gate Rφ(θ),which denotes the rotation of an angle θ around the axis in the equatorial plane with azimuth φ.For simplicity,we consider the on-resonance case(Ω=0)and set φ=0.Without considering the qubit-environment coupling,the target gate can be realized by appropriate duration of evolution under the Hamiltonian Hideal=2πω1Sx,where ω1is the strength of the control(microwave) field.Due to the inevitable qubit-environment coupling,the electron-spin qubit is subjected to the Hamiltonian Hprac=2π(δSz+ω1Sx),where δ is the random Overhauser field resulting from the interaction between the electron spin qubit and the nuclear spin bath.The error term δSzin the Hamiltonian renders the realized gate apart from the target.Due to the nuclear spin flip,the value of δ changes in every new trail of experiment,leading to different gates realized for different trails.When averaging over many trails to set up the statics,we will obtain a non-unitary process on average rather than the target unitary gate.

A type of DCG,named soft uniaxial positive control for orthogonal drift error(SUPCODE),[75]has been experimentally implemented to suppress decoherence during quantum gates to the limit set by T1ρ.[76]The SUPCODE is a class of pulse sequences which was originally proposed to suppress the fluctuations in the magnetic field gradient during quantum gates in the system of singlet-triplet spin qubit in a semiconductor double quantum dot.[75]It was soon experimentally demonstrated that SUPCODE can be utilized to suppress the fluctuation of the Overhauser field δ on the electron spin qubit.[76]The N-piece SUPCODE sequence contains N pieces of pulses. With each piece of pulse realizing an evolution operator containing δ,the total N pieces generate the target gate with the error δ suppressed to a certain order. Taking the five-piece SUPCODE as an example,the sequence for a target gate R0(θ)is τ1-R0(θ/2)- τ3-R0(θ/2)- τ1,where τ1=cscθ(1-and τ3=-2(τ1cos(θ/2)+sin(θ/2))are waiting times(in unit of 1/(2πω1))without the control pulse,θ ∈ (2π,3π).The sequence generates a gate of which the fidelity with the target gate only contains sixth and higher orders of δ/ω1.Note that the target gates R0(θ)when θ ∈ (0,π)can be realized with the five-piece SUPCODE sequence of R0(θ +2π),and R0(π)can be realized by repeating the five-piece SUPCODE sequence of R0(2.5π)twice.

The experiment was implemented on the single electron spin of an NV center in diamond.[77]The NV center consists of a substitutional nitrogen atom with an adjacent vacancy cite in the diamond crystal lattice.As an important candidate for quantum computation,[78]a single NV center provides a spin register composed of an electron spin,a host nitrogen nuclear spin,and several13C nuclear spins.In this experiment,the states|mS=0〉and|mS=1〉of the electron spin are encoded as a qubit.A magnetic field of 513 Gs is applied along the NV symmetry axis([111]crystal axis)to achieve effective polarization of the nitrogen nuclear spin.[79,80]The undesired couplings between the electron spin and the surrounding13C nuclear spins lead to the decoherence effect,which should be suppressed during quantum gates to achieve high fidelity.

The SUPCODE sequences are utilized to realize decoherence-protected quantum gates in the experiment.To minimize the in fluence of the instability of the control field,the control strength is set to ω1=1 MHz.In Fig.10(a),the quantum oscillation driven by five-piece SUPCODE and that driven by naive pulses are compared.The envelope decay of the oscillations presents loss of coherence during the state evolutions. It is clearly shown that the loss of coherence caused by decoherence effect is greatly suppressed when driving the qubit with five-piece SUPCODE compared to that with naive pulses.The decay time is derived to be TDCG=690(40)μs for the oscillation driven by five-piece SUPCODE,and=135(10)μs for that driven by naive pulses,from the fitting of the experimental data.As a reference, figure 10(c)shows the coherence time when N-pulse dynamical decoupling is applied.As N increases,the coherence time saturates at T1ρ=660(80)μs,which is determined by an independent spin-locking experiment.The decay times are summarized in Fig.10(d).It is noted that TDCGhas reached T1ρwithin the uncertainty.This indicates that the decoherence effect has been suppressed to the limit set by T1ρwhen realizing quantum gates with five-piece SUPCODE.To verify this,the five-piece SUPCODE sequence for R0(π/2)is successively applied and the fidelity[81]decay is recorded using quantum process tomography.As shown in Fig.10(b),the experimental fidelity decay matches the theoretical prediction in which only the T1ρprocess is taken into account.With this method,the fidelity of each five-piece SUPCODE π/2 gate is derived to be 0.9961(2).

Fig.10.Experimental suppression of decoherence effect during quantum gates via SUPCODE.(a)Comparison of the quantum oscillation driven by fivepiece SUPCODE pulses with that driven by naive pulses.Symbols are experimental results and solid lines are the fitting results.(b)Decay of the fidelity of successively applied gates by five-piece SUPCODE.Symbols are experimental results obtained via quantum process tomography,and the solid line is the theoretical prediction only considering the T1ρ process.The shaded region is calculated with the uncertainty of the measured T1ρ.(c)Extended coherence times via N-pulse dynamical decoupling.The coherence time saturates at T1ρ =660(80)μs for sufficiently large N.(d)Comparison of the decay times.Adapted from Ref.[76].c○2014 by the American Physical Society.

To further improve the gate fidelity,the instability of the control field[82]as well as the decoherence effect should be simultaneously suppressed during the quantum gates.The SUPCODE pulse can suppress the dephasing effect during the gate operations,but it is sensitive to the error due to the instability of the control field.That is why the control strength is set to ω1=1 MHz in the above experiment to demonstrate the suppression of decoherence to the T1ρlimit.[76]A pulse sequence which is insensitive to the instability of control field is named broadband number 1(BB1).[83]The BB1 sequence for a target gate R0(θ)is R0(θ/2)-Rφ(π)-R3φ(2π)-Rφ(π)-R0(θ/2),where φ =arccos(-θ/4π).To achieve simultaneous suppression of errors due to both decoherence effect and instability of the control field,the concept of concatenated composite[84]pulse may be adopted.A novel concatenated composite pulse named BB1inC has been designed and experimentally imple-mented on the electron spin of an NV center in diamond.[85]The BB1inC sequence for a target gate R0(θ)is R0(θ/2)-Rφ(π)-R3φ(2π)-Rφ(π)-R0(θ3)-Rπ(θ2)-R0(θ1),where φ =arccos(-θ/4π),θ1= θ/2-arcsin[sin(θ/2)/2],θ2=2π -2 arcsin[sin(θ/2)/2],and θ3=2π -arcsin[sin(θ/2)/2].The gate fidelity is experimentally quantified with the standard technique of randomized benchmarking.[86]The experimental resultsare shown in Fig.11(a),where the controlstrength isset to ω1=10 MHz.An average gate fidelity of Fa=0.999952(6)is achieved for the gates realized with BB1inC.

Fig.11.Experimental results of universal quantum gates with fault-tolerant fidelity on an NV center in diamond.(a)Experimental results of randomized benchmarking for quantifying the average gate fidelity F a of single-qubit gates on the electron spin qubit of the NV center.Symbols are experimental results and solid lines are the fitting results from which F a is derived.Inset:comparison of the error per gate(1-F a)of naive,SUPCODE,BB1,and BB1inC pulses.(b)Experimental results for measurement of the twoqubit CNOT gate fidelity.Symbols are experimental results and solid lines are the fitting results from which the CNOT gate fidelity is derived.Inset:the measurement sequence.Adapted from Ref.[85].○c 2014 by the Nature Publishing Group

Quantum computation requires a universal set of quantum gates,including not only universal single-qubit gates but also a non-trivial two-qubit gate(e.g.,the CNOT gate).The sequence of two-qubit CNOT gate with simultaneous suppression of the errors due to both decoherence effect and the instability of control field can be designed with the optimal control method,especially the technique of gradient ascent pulse engineering(GRAPE).[87]For the hybrid electron-nuclear spin system,since the electron spin qubit is more sensitive to noises than the nuclear spin,it is sufficient to take into account only the noise felt by the electron spin in the optimization process.The sequence for a CNOT gate on the electron and14N nuclear spins of an NV center has been designed with this method and experimentally implemented.[85]By repeatedly applying the CNOT gate and recording the dynamics of state evolution,the average fidelity of each CNOT gate can be derived.Figure 11(b)shows the experimental results of state population with repeated application of the CNOT gate;the population of state|01〉,P|01〉,exhibits oscillatory attenuation as the number of gates increases.The decay of P|01〉is mainly owing to the quasi-static fluctuation of δ and the instability of the control field,which are quantitatively characterized with additional experiments.The oscillation is due to the deviation of the practical Hamiltonian from the ideal one under which the evolution generates a CNOT gate.The parameters describing the practical Hamiltonian can be derived by fitting the experimental data.With the practical Hamiltonian as well as the errors due to δ and the instability of the control field characterized quantitatively,the practical evolution and its fidelity with the CNOT gate can be obtained.The gate fidelity is determined to be 0.9920(1).Together with the single-qubit gates realized with BB1inC,a universal set of quantum gates with fault-tolerant fidelity[88]has been demonstrated on the NV center in diamond.

3.3.Time-optimal control

Although high fidelity universal control has been reviewed above,the ultimate goal of quantum control is to achieve high- fidelity universal.The quantum brachistochrone equation(QBE)has been proposed to provide a general framework for finding time-optimal state evolutions or unitary operations.[89-95]The quantum system is considered to be driven by the Hamiltonian H(t),which is described by the Schr?dinger equation=-i H(t)U,with boundary conditions U(0)=I and U(T)=UF(we set=1).The path with the minimal time cost can be obtained by solving the QBE[90]togeth

er with Schr?dinger equation.The QBE is written as

where F= ?LC/?H and LC= ∑jλjfj(H),with λjbeing the Lagrange multiplier.One physically relevant constraint is the finite energy bandwidth described as f0(H)≡[Tr(H2)-E2]/2=0,where E is a constant.Reference[95]provides a method to obtain the accurate minimum-time protocol by solving the QBE equation.In realistic physical systems,part of the Hamiltonian H is usually time independent(e.g., fixed couplings between spin-qubits),and the reasonable constraint for the energy is actually for the time variable part(e.g.,the shaped microwave pulse with bounded power).The original QBE is not able to provide solution to this problem directly.The Hamiltonian can be rewritten as H(t)as H=H0+Hc(t),where the drift Hamiltonian H0stands for the time invariable part and Hc(t)stands for the control Hamiltonian.The drift Hamiltonian H0can be fixed spin couplings or nonzero constant external magnetic field.The control Hamiltonian Hc(t)can be a controllable external magnetic field or adjustable couplings between qubits.The constraint of finite energy bandwidth is modified to f0(Hc)=0.Then the time-optimal control(TOC)of multiple qubits,which is experimentally feasible,can be obtained by solving the QBE with the mentioned improvements.

The experimental realization of time-optimal universal control has been reported in a two-qubit system,which consists of an electron spin and a nuclear spin of a nitrogenvacancy center in diamond.[96]The electron(nuclear)spin states|mS=0〉and|mS=-1〉(|mI=1〉and|mI=0〉)are encoded as the electron(nuclear)spin qubit.Universal control of a single qubit requires the ability to realize rotations around two different axes of the Bloch sphere.The evolution operator is denoted as R(,θ),corresponding to a rotation of angle θ around the axis

The realization of a target unitary transformation R(,π)when δ=0 is taken as an example to compare the time cost between the derived TOC and a nonoptimized evolution path with Euler rotation:Figure 12(a)shows the state evolution during R(,π).The initial state is prepared toAs shown in Fig.12(a),the target evolution of R(?,π)is realized at 173.2 ns with TOC and at 200 ns with Euler rotation.The case when δ/=0 has also been experimentally implemented.Both R(,θ)and R(,θ)with various values of θ have been demonstrated.Furthermore,time-optimal universal single-qubit control with other constraints on Hcis also experimentally demonstrated.The preformance of the gates are characterized utilizing quantum process tomography.[97]All the gate fidelities are measured to be above 0.99.Except for the single qubit gates,a non-trivial two-qubit controlled-U gate

is also demonstrated.[96]The TOC Hamiltonian is obtained by numerically solving the QBE together with Schr?dinger equation.The time duration of the gate is 446 ns.The performance of the Ucgate is characterized by quantum process tomography as shown in Fig.12(b).The average gate fidelity of the two-qubit gate is 0.99(1),which reaches the threshold of fault-tolerant quantum computation.The time-optimal universal control of two-qubit system has been realized in diamond with high fidelity.

Fig.12.(a)State evolutions during R(?,π)with TOC and Euler rotation.The initial state is(|m=0〉+i|m=-1〉)/.The gate time of TOC is 26.8 nsss shorter than that of Euler rotation.(b)Quantum process tomography for the controlled-U gate by TOC.The left and right panels are the real and imaginary parts of the reconstructed process matrix χ.The error bar of each point is about 0.01 due to the statistics of photon counts.An average gate fidelity of 0.99(1)can be obtained from the process matrix.Adapted from Ref.[96].○c 2016 by the American Physical Society.

3.4.Adiabatic quantum factorization algorithm

After reviewing the quantum coherent optimal control technique,we discuss another different quantum computation,i.e.,the adiabatic quantum computing(AQC).It has been proposed by Farhi et al.[98]in 2000.The basic idea of this architecture is that the computational process can be realized by the adiabatic evolution of a system’s Hamiltonian and regarded as circuit model quantum computing.[99]As a universal and robust method of quantum computing,the AQC can solve the problem by adiabatically evolving the quantum processor from the ground state of a simple initial Hamiltonian to that of a final one,which encodes the solution of the problem.In quantum computing,a quantum algorithm is an algorithm that runs on a realistic model of quantum computing.One of the reason we are interested in quantum algorithms is that it can solve some problems faster than classical algorithms.For multiplying of large prime numbers,up to now,no efficient classical algorithm can factorize this large numbers.[100]A lot of experimental work on large number factorization has been done either based on Shor’s algorithm[101-107]or based on the AQC architecture with ensemble systems.[108,109]Adiabatic quantum factorization algorithm was developed by Burges et al.[110]for the first time.An improved version was realized by Xu et al.[108]Based on this version,the factorization of 35 on the adiabatic quantum processor with single spin has been reported at room temperature.[111]The main idea used here is to transform a factorization problem into an optimization problem and solve it under the AQC framework.

In the AQC framework,we first need to find a problem Hamiltonian Hpto solve a problem and the solution of the problem is encoded in the ground state of Hp.Letus getstarted from the ground state of H0,the Hamiltonian of the evolution progress can be written as

where T is the total evolution time,and the whole system is evolved under the Schr?dinger equation

Based on the adiabatic theorem,if the system evolves slowly enough,i.e.,T?1/,whereis the minimum spectral gap of H(t),it tends to stay on the ground state of H(t).When it is close to t=T,the system is on the ground state of H(T)and givesthe solution ofthe problem.According to the multiplication table(see Table 1),an equation set can be constructed.To solve these equations with fewer qubits,it can be simplified by using some logical constraints.

Table 1.Multiplication table for 5×7=35 in binary.The top row represents the significance of each bit.x and y are the multipliers.zij is the carry bit from the i-th bit to the j-th bit,and the row in the bottom is the number we want to factor,i.e.,35.This table is adapted from Ref.[111].c○2017 by the American Physical Society.

After the simplification(see Ref.[111]for more details),the result can be written as

and the simplification do not increase the complexity of the quantum algorithm.Based on the idea of Burges et al.,[110]the problem Hamiltonian is

where σ1,zand σ2,zare replaced with Szand Iz,i.e.,the electron and nuclear spin operators,respectively.Then one can drop the identity operator and scale it with a constant g1

The H0should be noncommutative with Hp,otherwise there will be energy level crossings.Generally,H0can be written as

The experiment was carried out in Type-IIa bulk diamond samples with nitrogen impurity concentration＜5 ppb and13C isotope of natural abundance(1.1%).With the direction of the external magnetic field aligned along the symmetry axis,the Hamiltonian of the NV center electron spin coupled with the14N nuclear spin is

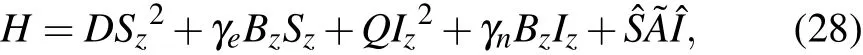
where Q=-4.95 MHz is the nuclear quadrupolar splitting andis the hyper fine interaction tensor between the electron spin and the nuclear spin.Here,one picked 4 out of 9 levels to perform the experiment and encoded them as two qubits.

In order to overcome the limitation of coherent time,the optimal control is used to replace the adiabatic evolution part,which is robust to noise and guarantees high fidelity.The adiabaticity of the whole process is reflected in the evolution with six measurements of the diagonal elements,as exhibited in Fig.13.The lines and dots show the results of theoretical calculations and experimental measurements,respectively.The deviation here comes from the imperfect initialization and control pulses.The population of the final state concentrates on|01〉and|10〉,which indicates that the solution of the factorization problem is{p=0,q=1}or{p=1,q=0},i.e.,the multipliers are{x=5,y=7}or{x=7,y=5}.The fidelity between the experimental and the ideal final stateis 0.81(6).It is worth mentioning that to achieve the optimal control of the hybrid spin system,not only did we use a shaping pulse,but also both the shaping pulses of electrons and nuclear spins were applied for the first time.[111]For experimentally factored 35 and the results with high fidelity,the optimal control technology has been used and it is also used on an electron-nuclear hybrid system,which is considered to be challenging due to the large mismatch of the electron and nuclear spin gyromagnetic ratio.[111]The arbitrary factorization of large numbers is related to the scalability of the method,which is very promising,but there are still several challenges.[111]The optimal control technique can also be extended to other single-spin systems because they[112-114]share a similar control method based on spin magnetic resonance.

Fig.13.The populations on computational basis of the system during the process of the adiabatic factorization.The lines are theoretical predictions with prefect initialization and control.The diamonds are the theoretical calculations taking imperfect initialization and control into consideration,and the dots are obtained from experimental data.Adapted from Ref.[111].c○2017 by the American Physical Society.

4.On experimentalimplementations and tests of the uncertainty principle

Based on the previous work,we study some fundamental problem such as Heisenberg’s uncertainty relation in spin system.The principle of uncertainty was first proposed by Heisenberg in his thought experiment,indicating that the measurement of the electron’s position inevitably interfered with the momentum.[115]In the following years,Kennard,[116]Robertson,[117]and Schr?dinger[118]mathematically derived tight relations,such as the famous Heisenberg-Robertson uncertainty relation[117]

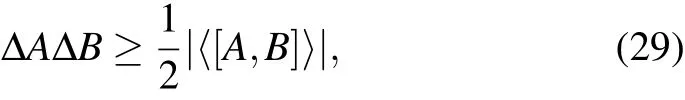
4.1.Uncertainty relation based on statistical distances

Recently,uncertainty relations dealing with the imprecisions in joint measurements approximating incompatible observables have been formulated by Busch,Lahti,and Werner(BLW).[120-122]Their results also apply to successive measurements,which are encompassed by joint measurement scenarios.The imprecisions or uncertainties,based on statistical distances between probability distributions of measurement outcomes are processed into state-independent and regarded as figures of merit of joint-measurementdevices.According to BLW’s theoretical framework,an improved relation for qubit measurement and experimental test has been reported[125]in a spin system using the NMR technique.

A and B are a pair of incompatible observables we consider.Incompatible means A and B cannot be jointly measured,i.e.,can not be measured simultaneously.For qubit measurements,A and B can be chosen as the two sharp observables with the spectral projections A±=(1±a·σ)/2 and B±=(1±b·σ)/2,where a and b are unit vectors.If a and b are non-collinear,the observables A and B are incompatible.A device composed of compatible observables C and D(each being used as an approximation of A and B)can be used to approximately measure A and B simultaneously.The observable C consists of positive operators C+=(c01+c·σ)/2,C-=1-C+,with|c|≤min{c0,2-c0}≤1 for the positivity.Similarly,the observable D consists of D+=(d01+d·σ)/2,D-=1-D+,with|d|≤min{d0,2-d0}≤1.Compatible or jointly measurable requires that there exists a positiveoperator valued measure(POVM)M of which C and D are the marginals,namely,Ci=and Dj=,with i,j=+or-(hereinafter the same)and Mij=(CiDj+DjCi)/2.When c0=d0=1,the criterion of compatibility has been simplified as[121,151,152]

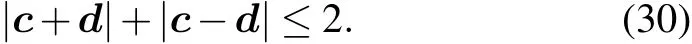
Compatibility permits C and D to be measured simultaneously,but imposes a strong limitation against C and D approaching A and B freely.The overall deviation of C and D from A and B,or the performance of the device,is rooted in probability distributions of measurement outcomes.

The operators O±(O=A,B,C,and D)are called effects and the probabilities of measurement outcomes are=Tr(ρO±),where ρ =(1+r·σ)/2 is the density operator of a qubit.Take outcomes of these measurements to be±1,then the observable O is given as a map±1→ O±.The statistical difference between the measurements of A and C,in other words the inaccuracy or uncertainty,can be quantified as=2|1-c0+r·(a-c)|.[121]In a similar way,the statistical difference between the measurements of B and D can be expressed as δρ(B,D):==2|1-d0+r·(b-d)|.Since the observables C and D are jointly measured,they face the same quantum state ρ and the combined difference Δρ(A,B;C,D):= δρ(A,C)+δρ(B,D)is the inaccuracy of the joint measurement for a specific state.The state-dependent quantity Δρ(A,B;C,D)has a vanishing lower bound for any given A,B,and ρ.In other words,Δρ(A,B;C,D)becomes zero when minimizing over all C and D for any given A,B,and ρ(see Section II.A in Ref.[125]).By maximizing Δρ(A,B;C,D)over all ρ ,one obtains Δ (A,B;C,D):=as the worst-case inaccuracy of the joint measurement.The state-independent quantity Δ(A,B;C,D)characterizes the integrated deviation of C and D from A and B and thus is a figure of merit of the measurement device.The inaccuracy trade-off relation can be written as

as shown in Fig.14(a).The lower bound Δlb(A,B)is the amount of violation of the inequality in Eq.(30),and is termed as the degree of incompatibility of A and B.[121]This lower bound is attained when C and D are the best approximations of A and B,and such C and D have c0=d0=1 and c,d depicted in Fig.14(c).

Compared with BLW’s original relation,the characteristic quantity Δ(A,B;C,D)possesses an explicit physical meaning as the worst-case inaccuracy and has a delicate lower bound without an additional coefficient(see Section II.B in Ref.[125]).Besides,as a modification of BLW’s basic framework,the improved approach also applies to any pair of incompatible observables like position and momentum,although the combined inaccuracy might not be in the additive form.Experimental demonstration of the relation in Eq.(31)has been implemented in the nuclear spin system,[125]operating on a 400 MHz liquid-state nuclear magnetic resonance spectrometer.In the experiment,the diethyl fluoromalonate was used as the sample dissolved in2H-labeled chloroform at 304 K.The19F,1H,and13C nuclear spins serve as the system,ancilla,and probe qubits,respectively.The device is simulated by joint measurement that measures two compatible observables at the same time.Several configurations of A,B and C,D with all the Bloch vectors in the xz plane have been chosen.Every pair of a and b is symmetric about the z axis,and is expressed as a=(-sin(θ/2),cos(θ/2)),b=(sin(θ/2),cos(θ/2)),where the former and latter components of a vector correspond to x and z,respectively(hereinafter the same).In the case where θ =90°,the vectors a and b are perpendicular to each other and the relevant observables A and B are maximally incompatible.Consider a series of compatible observables C and D with c=?-sinγcosγ,sin2γ?,d=?sinγcosγ,cos2γ?as illustrated in Fig.15(a).The inaccuracy Δ varies with γ and is bounded by≈0.83 as shown in Fig.15(b).When γ=45°,the corresponding C and D are the optimal approximations to A and B,and the inaccuracy Δ reaches its lower bound Δlb.The statistics of measurement outcomes for two instances where γ=15°and 45°are listed in Figs.15(c)and 15(d)which visually support the superiority of the optimal C and D.All the experimental results confirm the inaccuracy trade-off relation in Eq.(31).

Fig.14.Sketch of the theory.(a)Outline of the inaccuracy trade-off relation in Eq.(31).Here,compatible observables C and D are jointly measured to approximate incompatible observables A and B.(b)An example of Bloch vectors a,b,c,and d.The lengths of c and d are usually less than 1.(c)Bloch vectors c and d of the optimal compatible observables C and D that approximate A and B.The dashed lines are legs of an inscribed isosceles right triangle.The vectors a-c and b-d are orthogonal to these dashed lines,and the end points of c and d are the perpendicular feet.The whole pattern is coplanar and symmetric.Adapted from Ref.[125].c○2016 by the American Physical Society.

Fig.15.Experimental demonstration of the inaccuracy trade-off relation with maximally incompatible A and B.(a)Bloch vectors of observables.The whole configuration is coplanar.The vectors a and b are mutually perpendicular and incline symmetrically about the vertical direction,which is the z direction.The end points of vectors c and d are the diameter ends of the small circle which is internally tangent to the semicircle and passes through its center.The center of the semicircle is the origin and the tangent point is in the z axis.(b)The inaccuracy Δ as a function of the angle γ=arctan(|c|/|d|).The circles,solid curves,and dashed curves represent the measured,theoretical,and simulated values of Δ,respectively.The numerical simulation takes decoherence into account.The dashed straight line denotes the lower bound Δlb.(c)and(d)The statistics of measurement outcomes for γ=15° and 45°.Adapted from Ref.[125].c○2016 by the American Physical Society.

4.2.Uncertainty relations for the triple components of angular momentum

Recently,an uncertainty relation forthree pairwise canonical observables p,q,and r satisfying[p,q]=[q,r]=[r,p]=-iˉh with r=-p-q was derived by Kechrimparis and Weigert.[153]Here,p and q are the momentum and position,respectively.From the inequality in Eq.(29),one immediately obtains ΔpΔq≥ˉh/2,ΔqΔr≥ˉh/2,and ΔrΔp≥ˉh/2.By multiplying these inequalities and taking the square root,one gets ΔpΔqΔr≥(ˉh/2)3/2.However,this inequality is not tight.In other words,there is no state satisfying such lower bound.By introducing the triple constantthe tight triple uncertainty relation ΔpΔqΔr≥(τˉh/2)3/2is established.Compared with two observables p and q,the latecomer r looks artificial and should not exhibit a particular physical meaning.Yet the three components of angular momentum form a natural triple.[154]

The lower bound for spin-1/2 has been tightened by introducing the triple constant τ[34],i.e.,

where Sx,Sy,and Szare the angular momentum operators and satisfying commutation relations[Sx,Sy]=i Sz,[Sz,Sx]=i Sy,and[Sy,Sz]=i Sx.The equality in Eq.(32)holds when|rx|=.Here,rx,ry,and rzare the components of the Bloch vector r of a qubit state with the density matrix ρ =(1+r ·σ)/2.The lower bound is also tightened by introducing the triple constant τ,i.e.,

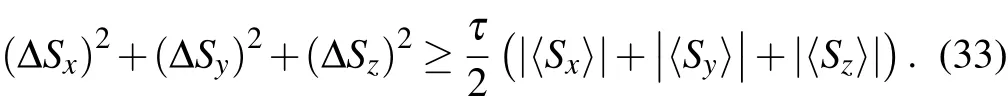
The equality in Eq.(33)is attained if and only if|rx|=for spin-1/2.The uncertainty relations in Eqs.(32)and(33)have state-dependent lower bounds.It is similar for uncertainty relations with state-independent lower bounds.The pairwise inequalities for spin-1/2,[121]namely,(ΔSx)2+(ΔSy)2≥ 1/4,(ΔSy)2+(ΔSz)2≥ 1/4,and(ΔSz)2+(ΔSx)2≥ 1/4,immediately yield the inequality(ΔSx)2+(ΔSy)2+(ΔSz)2≥3/8 which is not tight.A tight lower bound needs an additional factor τ2[148,155]written as

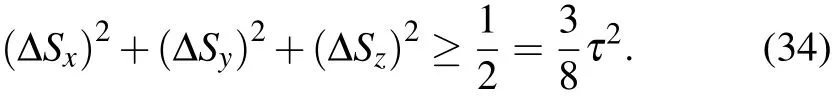
The equality is established only|r|=1,in other words,the qubit is in a pure state.

Fig.16.Experimental results.(a)Experimental demonstration for the uncertainty relation of the multiplicative form.The? solid orange,solid green,and dashed green curves,in turn,represent the theoretical values of Pro0,Pro1,and Pro2,where Pro0= ΔSxΔSyΔSz,Pro1=,and Pro2=.The orange and green scattered points represent the experimental value of Pro0 and Pro1,respectively.(b)Experimental demonstration forthe uncertainty relations of the additive form.The solid magenta,solid violet,and dashed violetcurves,in turn,represent the theoretical values of Sum0,Sum1,and Sum2,whereThe magenta and violet scattered points represent the experimental value of Sum0 and Sum1,respectively.Error bars represent±1 s.d.(c)Experimental demonstration for the uncertainty relation of the multiplicative form.(d)Experimental demonstration for the uncertainty relations of the additive form.Adapted from Ref.[34].○c 2017 by the American Physical Society.

Experimental verification of uncertainty relations in Eqs.(32)and(33)was reported[34]in an NV center in diamond(use a bulk sample with the13C nuclide at the natural abundance of about 1.1%and the nitrogen impurity less than 5 ppb).In this experiment,two series of pure states|ψ〉with Bloch vectorsandwere chosen;see Ref.[34]for more details about the expectations of Sx,Sy,and Sz.The verification of the multiplicative uncertainty relation in Eq.(32)is shown in Figs.16(a)and 16(c). The results demonstrate that for the product ΔSxΔSyΔSz,the lower bound with the triple constant τ,namely,outperforms the naive lower bound without the triple constant,namely,.The results for the sumare shown in Figs.16(b)and 16(d).The lower bound with the triple constant τ,namely,outperforms the naive one without the triple constant,namely,The same results also support the derivation[148,155]of the uncertainty relation in Eq.(34).Therefore,the triple uncertainty relations in Eqs.(32),(33),and(34)are confirmed by the experimental results.This work can consistently support the theoretical results and enrich the uncertainty relations of more than two observables.

5.Brief conclusions

Quantum coherence plays an important role in quantum information theory,quantum thermodynamics,and quantum biology,as well as physics more widely;therefore,it is interesting to study the coherence and its protection in various systems such as spin systems.In order to perform long coherence time quantum computations,a thorough understanding and suppression of decoherence are badly needed,together with quantum error correction and fault-tolerant quantum computation schemes.Isolated electron spin in the diamond nitrogenvacancy center has proven to be a unique and promising candidate for solid-state quantum computing.

In summary,this work presents a concise review on the field of quantum coherence and uncertainty relation in spin systems.The coherence can be preserved by several strategies such as reducing the nuclear spins in the environment,cooling the temperatures,and performing dynamical decoupling operations.In addition,the coherence can be applied to the weak magnetic fields detection with high spatial resolution.In recent years,research on various type uncertainty relations has been expanding with an increasing rate.In spite of the basic principle in quantum mechanics,uncertainty relation has demonstrated to be a fruitful concept both for fundamental studies and for designing novel experimental techniques.Potential applications of quantum coherence include such diverse topics as quantum computation,quantum communication,and quantum information processing.The experimental research of coherent spin developed here will provide insights and a useful guide for further applications of coherence.