Waves propagating over a two-layer porous barrier on a seabed ＊

Qiang Lin (林強), Qing-rui Meng (孟慶瑞), Dong-qiang Lu (盧東強)

1. China Ship Scientific Research Center, Wuxi 214082, China

2. Shanghai Oriental Maritime Engineering Technology Company Limited, Shanghai 200011, China

3. Shanghai Institute of Applied Mathematics and Mechanics, Shanghai University, Shanghai 200072, China

4. Shanghai Key Laboratory of Mechanics in Energy Engineering, Shanghai 200072, China

Introduction

The interactions between waves and porous regions have given rise to extensive attention among costal engineering designers. The porous media are probably rocks and breakwaters, which may reflect the energy by adopting the proper porosity and dissipate the energy by friction. The study on the interactions between waves and porous regions is useful to analyze the wave motion and wave loads on the marine structures. For instance, the bottoms of permeable breakwaters are stuck on the seabed, while their tops are below or pierce the water. The porous breakwaters may play a significant role in reducing the total load on the structures.

When the waves encounter the porous structures,some energy is reflected into the open water; some is transmitted into the porous region, the others dissipated. The specific amount of each part depends on the parameters of the porous media. Sollitt and Cross[1]proposed a theory to predict the reflected and transmitted energy of a rectangular breakwater with the matching conditions at the windward and leeward faces. With a similar model, Chwang[2]developed a porous-wavemaker theory to analyze the small amplitude surface waves generated by the horizontal oscillations of a porous vertical plate. The effects of two important parameters, namely the wave-effect and the porous-effect parameters, on the surface waves and hydrodynamic pressures were analyzed in detail.Sahoo et al.[3]extended this work to four different configurations: a bottom-standing barrier, a surfacepiercing barrier, a barrier with a gap, and a submerged barrier, in the case of obliquely incident surface waves.A new model of a vertical porous structure placed near and away from a rigid vertical wall was studied by Das and Bora[4]within the framework of linear water wave theory. Zhao et al.[5]considered the wave interaction with a vertical wall protected by a submerged porous bar and claimed that the wave run-up and wave force were effectively reduced by the porous bar.In order to verify the theoretical method, some experiments were carried out by Zhang et al.[6]and Zhai et al.[7]in wave flumes to measure the pore pressure.

For an impermeable seabed, free surface waves consist of the propagating and evanescent waves. As for the waves in the porous region, the wave numbers become complex ones, which was detailedly analyzed by Jeng[8]. The real part is related to the wavelength,while the imaginary part is the damping of the water waves. Metallinos et al.[9]investigated the submerged porous breakwaters of mild to steep slopes with theoretical and experimental methods. Mohapatra[10]presented an expression of Green’s function suitable for the scattering problem with obliquely incident waves propagating over a region, in which the upper surface was covered by an infinitely extended thin elastic plate and the lower surface was a porous bottom with a small deformation. The influences of poroelastic bed on flexural-gravity waves in both cases of single-layer and two-layer fluids were studied by Das et al.[11]which revealed that the phase speed for the flexural-gravity mode in the two-layer fluid reaches the maximum value for large porosities when the interface is close to the poroelastic bed. With a numerical model, Shoushtari and Cartwright[12]analyzed the effects of porous medium deformation on the dispersion of water-table waves.

In real circumstances, ocean waves are usually simultaneously accompanied by currents. Based on Biot’s poroelastic dynamic theory, Ye and Jeng[13]investigated the model of seabed response with waves and currents. Furthermore, Zhang et al.[14]had a parametric study for the influence of the currents and non-linear waves on the seabed responses. A numerical calculation model was proposed by Zhang et al.[15]to analyze the stability of seabed under wave and current loadings. It has shown that the excess pore pressure increases with increasing flow velocity.

A porous model of different parameters is more appropriate when the seabed consists of multiple-layer breakwater and rocks. Seymour et al.[16]proposed a new method for the wave-induced response in a soil matrix, with the permeability as a function of depth.Jeng and Seymour[17]verified an analytical solution of soil response with variable permeability by a comparison with the conventional solution for uniform permeability. A stochastic finite element model was put forward to study the wave-induced seabed response in a spatially random porous seabed by Zhang et al.[18].

1. Mathematical formulation

The Cartesian coordinates are chosen in such a way thatz= 0 coincides with the undisturbed upper surface. Thexaxis points horizontally rightwards and thezaxis points vertically upwards, withz=-Has the flat bottom, as shown in Fig. 1. With the assumptions that the fluids are inviscid and incompressible and that the motion is irrotational, the problem can be described by the potential flow theory.The whole flow domain is mathematically divided into three parts, an open water region Ω1(-∞＜x＜-b), a porous water region Ω2(-b＜x＜b) with a two-layer porous barrier mounted on seabed, and an open water region Ω3(b＜x＜ ∞). In the porous water region Ω2,h0,h1andh2are the depths of the pure water region, and the first-layer and the second-layer porous water, respectively, whereh0+h1+h2=H.

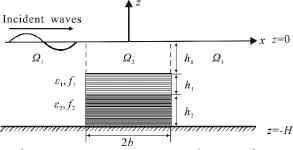
Fig. 1 Schematic diagram for waves propagation over a twolayer porous barrier on a seabed

Assuming that the incident waves are simply time-harmonic with a given angular frequency ω, we have, via separating the time factor, the velocity potential, the surface elevationare the spatial elevations on the surfacez= 0 andtis the time variable. The spatial velocity potential Φ(x,z) satisfies the Laplace equation

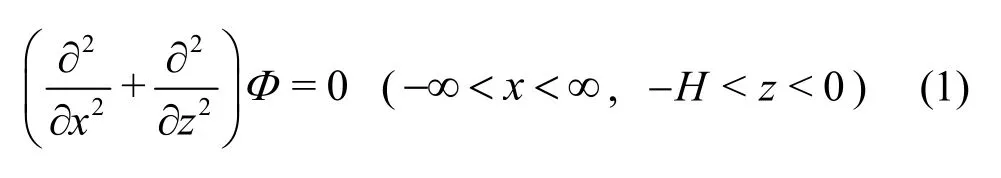
The boundary conditions on the free surface, in combination of the kinematic and dynamic conditions,can be formulated as

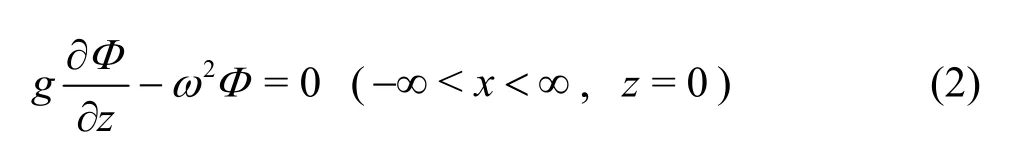
wheregis the gravitational acceleration.

The bottom boundary condition of the flat rigid seabed reads

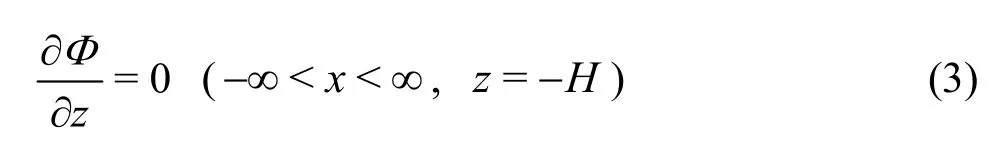
The velocity and pressure must be continuous at the interface between media for different layers,respectively. Three dimensionless physical parameters of the porous media, i.e., the porosity ε, the linear friction factorfand the inertial terms, are introduced by Sollitt and Cross[1]. The continuous conditions at the interface are written as, for -b＜x＜b,

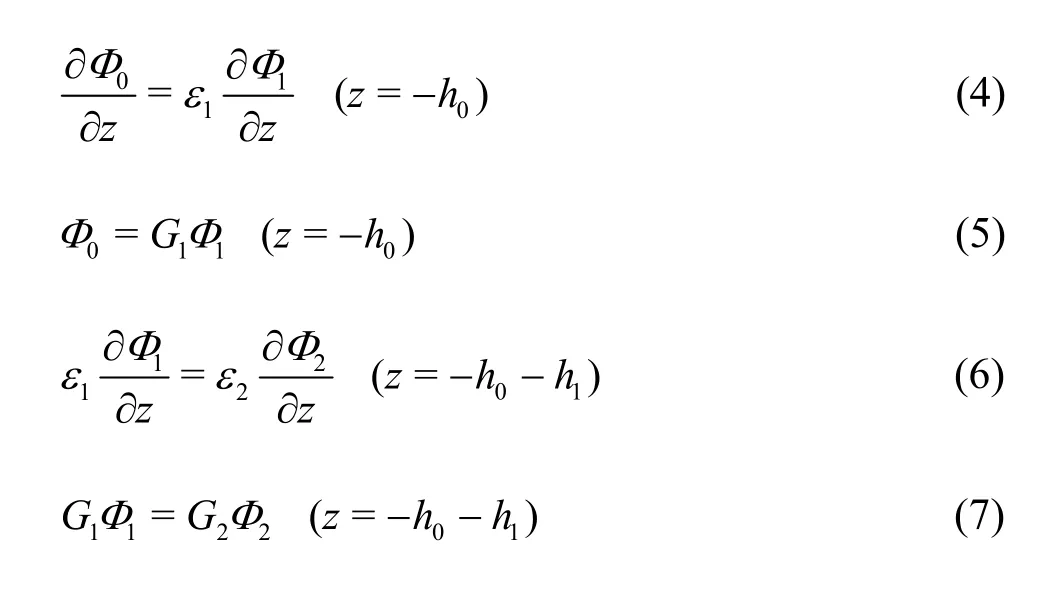
where Φm(x,z) withm= 0,1,2 are the spatial velocity potentials of the pure water (m= 0), the first layer porous region (m= 1) and the second layer porous region (m=2) in Ω2, εmwithm=0,1,2 are the porosity of the pure water (m= 0), the first layer porous region (m= 1) and the second layer porous region (m= 2),Gmwithm= 0,1,2 is calculated fromsm+ifm,smandfmare the inertial term and the linear friction factor of the first layer porous region (m= 1) and the second layer porous region (m= 2) whiles0=1 andf0=1 represent those for the pure water.

The matching relations of the pressure and the velocity on the interfacex=±bbetween the open water region （Ω1, Ω3) and the porous water region Ω2are presented via the following equations:

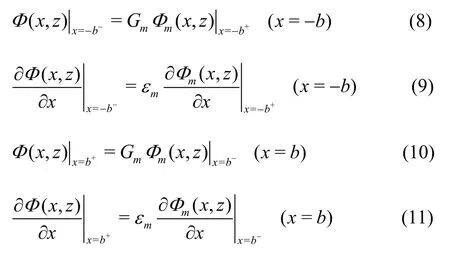
2. Method of solution

2.1 Dispersion relations

It is well known that the dispersion relation for the pure water in the regions1Ω and3Ω can be easily obtained as follows

wherekis the wave number. For a given frequency ω, the dispersion relation Eq. (12) for the open water region yields one positive real rootk0, and has an infinite number of imaginary roots iki(i= 1,2,…),wherekiis positive and real. The real root corresponds to the propagating wave modes in the open water region and the imaginary roots ikicorrespond to the evanescent modes in the open water region.

With the help of the general solutions of Eq. (1)consisting of eik~x+k~z, wherek~is the wave number of the porous region, the dispersion relation for the porous region can be derived by solving simultaneously Eqs. (2)-(7), which is formulated as

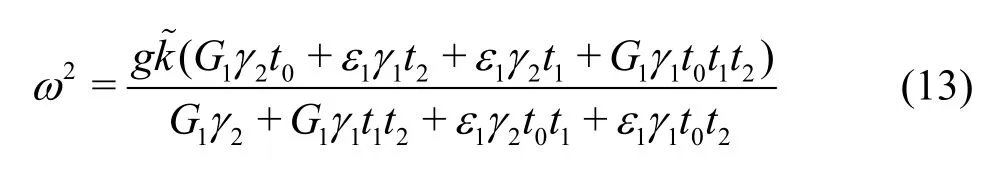
whereγ1=G1/G2and γ2= ε1/ε2. In accordance with the expressions, γ1is a complex number while γ2is a positive real number. Only whens1/s2=f1/f2, γ1reduces to a positive one.

As the value of the depthh2tends to zero,t2tends to zero and γ1and γ2tend to 1.

The equation then reduces to the expression

which is the same as the equation derived by Meng and Lu[19]. When1htends to zero and1ttends to zero, the above equation reduces to the expression

which is similar to Eq. (12).

From Eq. (13), we can obtain, for a given ω andf= 0, one positive real roots and an infinite number of imaginary roots. For a non-zero linear friction factorf, the equation will have an infinite number of complex roots=+i, where α~jand β~jwith (j= 0,1,2,3…) are real numbers,which are associated with the decaying propagating wave modes in the porous region. Amongj=0,1,2,3…), the waves corresponding tohave the smallest wavelength and decaying rate.

2.2 Expression for the spatial velocity potential

The plane incident waves from the negative infinity in the Cartesian coordinates are denoted by ζ0eikx, whereζ0is the wave amplitude. The velocity potentials referring to the open water region Ω1(-∞ ＜x＜ -b), the porous water region Ω2(-b＜x＜b) and the open water region Ω3(b＜x＜ ∞)are marked with ΦΩ1, ΦΩ2and ΦΩ3, respectively.With the method of separation of variables, the velocity potentials ΦΩ1, ΦΩ2and ΦΩ3can be formulated by

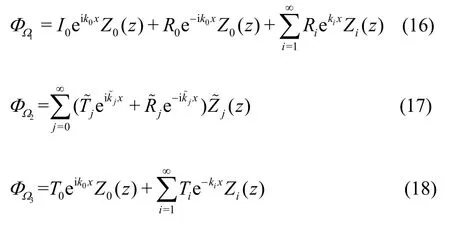
where

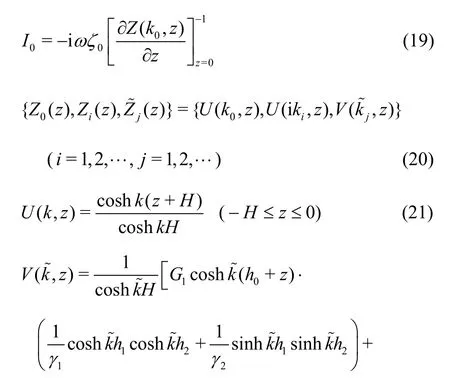
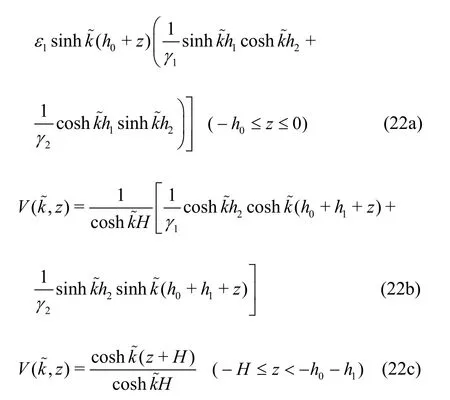
whereU(k,z) andV(z) are the vertical eigenfunctions of the open water region and porous regions,respectively, the reflection coefficientsR0andRi,the transmission coefficientsT0andTi, and the intermediate variablesandare complex numbers to be determined, wherei= 1,2,… andare the summation symbols corresponding toi= 1,2,… andj= 0,1,2,…,respectively.

2.3 Solutions for the reection and transmission coefficients

The core process is to solve unknown expansion coefficients from the series equations. Substituting ΦΩ1, ΦΩ2and ΦΩ3in Eqs. (16)-(18) into the matching conditions Eqs. (8)-(11) for the interface atx=±b, we obtain, form= 0,1,2,

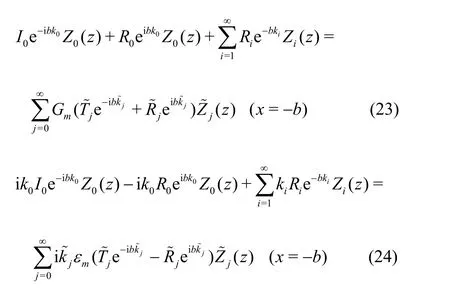
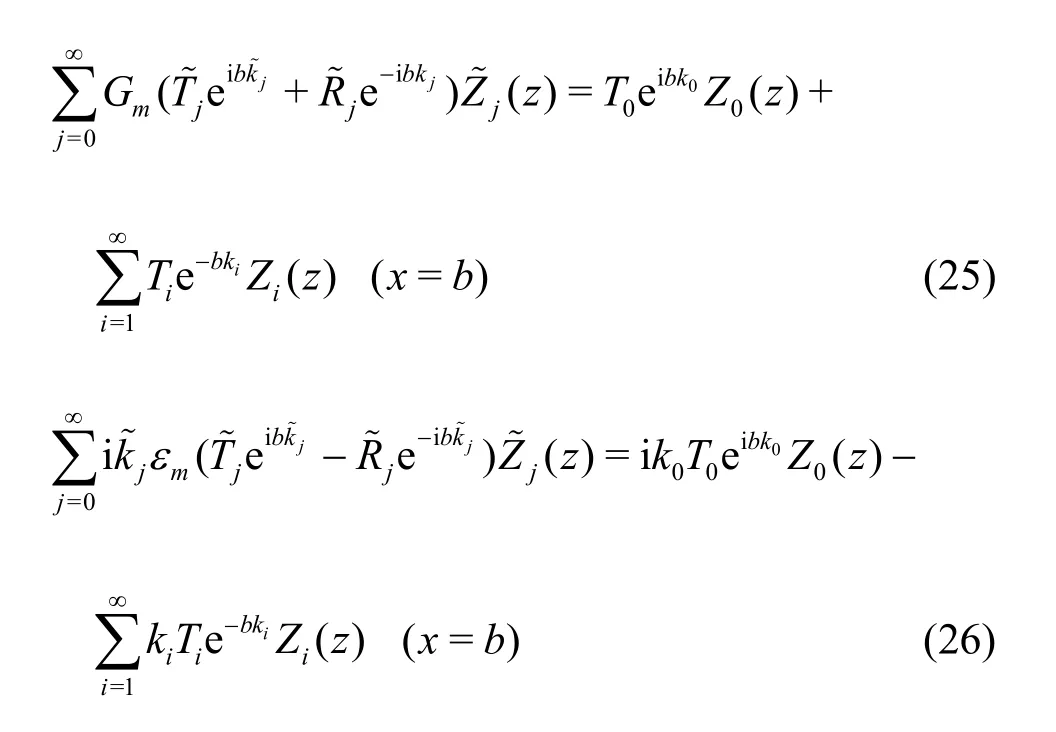
From Eqs. (23)-(26), we notice that the left- and right-hand sides of the equations are functions of the vertical coordinatez. In order to obtain the unknown expansion coefficients, we use the orthogonality of the vertical eigenfunctions for the two-layer porous region and define an inner product as follows

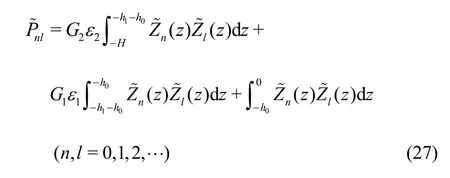
In the case ofn≠l, we have=0.

Employing the inner product on both sides of Eqs.(23)-(26) with different vertical eigenfunctions(z)(n= 0,1,2,…) in the porous region, we eliminate the intermediate variablesandand derive

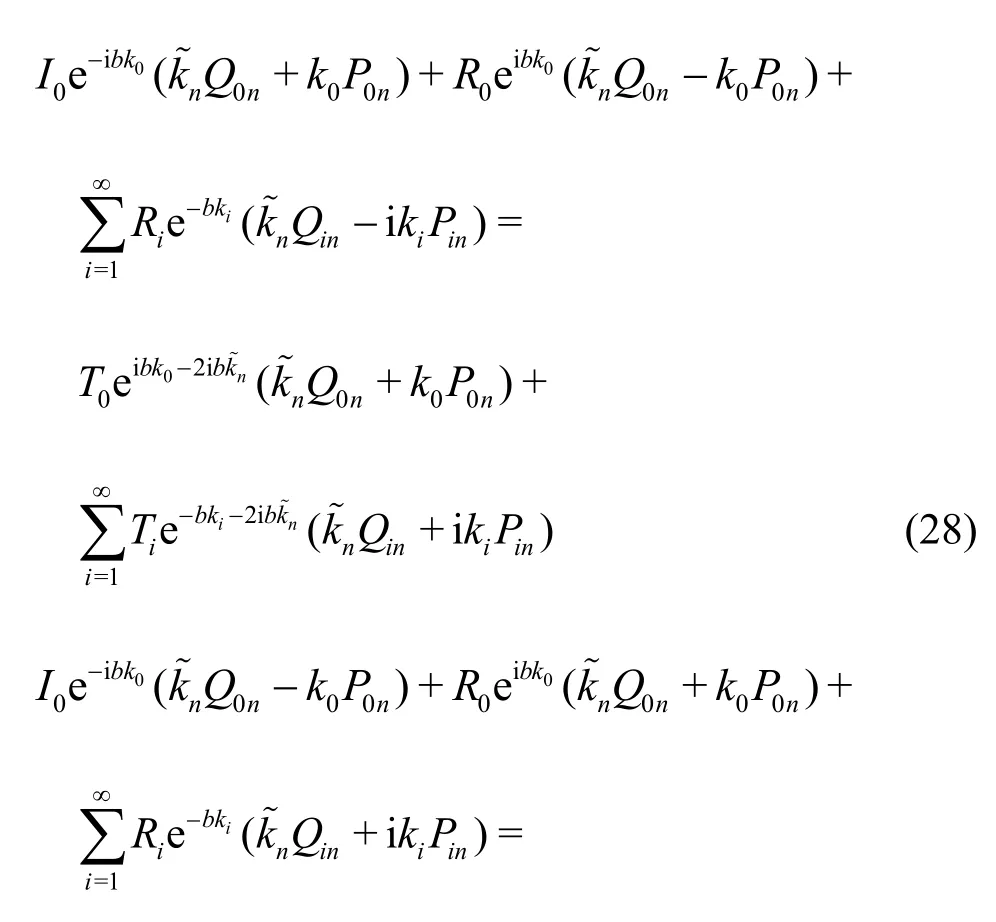
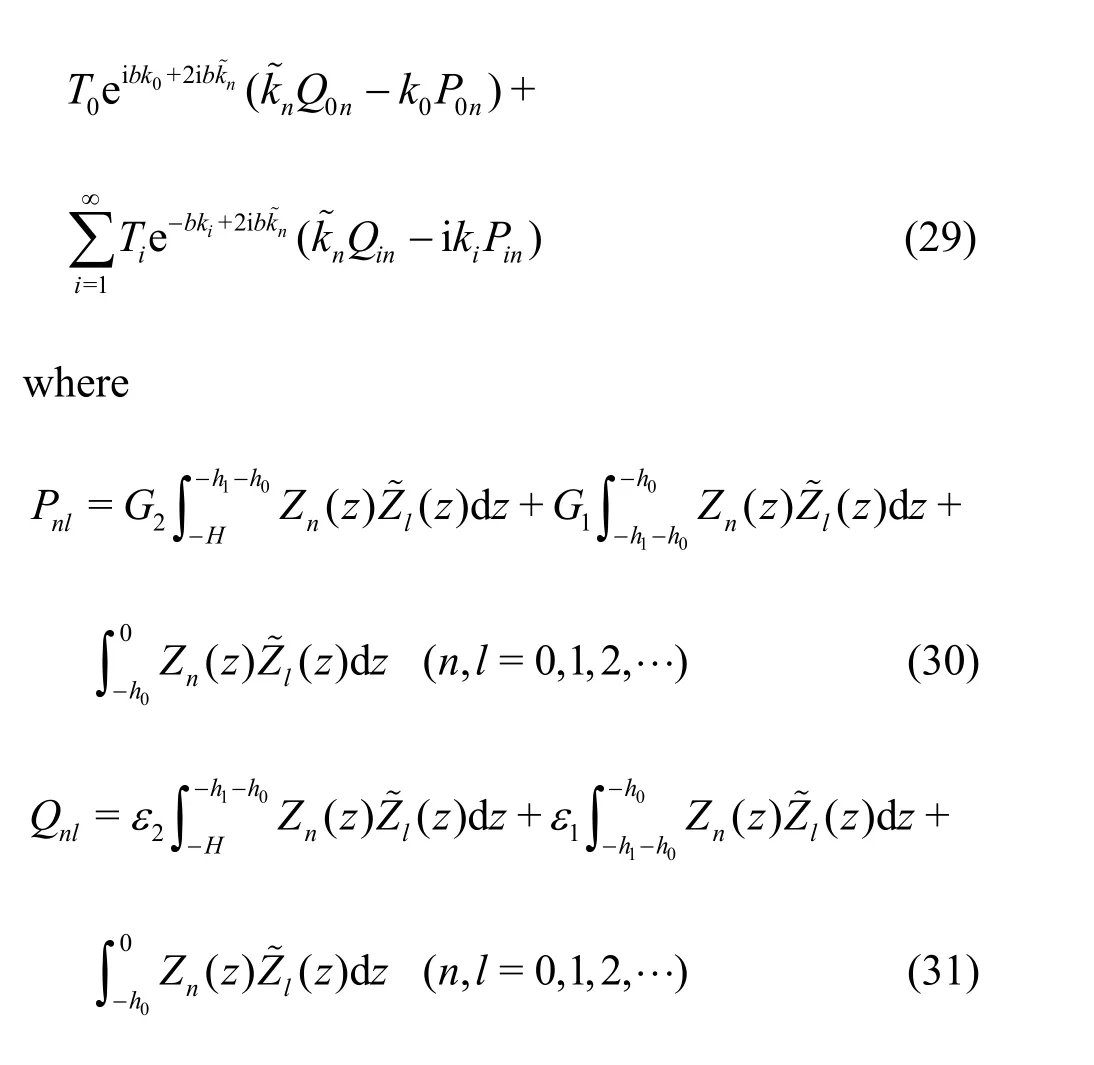
When we seti=Mfrom the infinite summationa combination of Eqs. (28) and (29) yields a system of 2M+ 2 simultaneous equations for 2M+ 2 unknown expansion coefficients,R0,Ri,T0,Tiwithi=1,2,…M, which can readily be solved numerically.

3. Numerical results and discussion

For clarity, selecting two independent fundamental dimensions, the total depth of the fluidHand the gravitational accelerationgas a unit system allows us to nondimensionalize all the quantities:

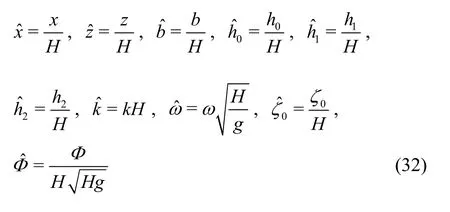
The nondimensional variables, throughout the rest of the paper, will be written without overhead hat symbols for convenience.

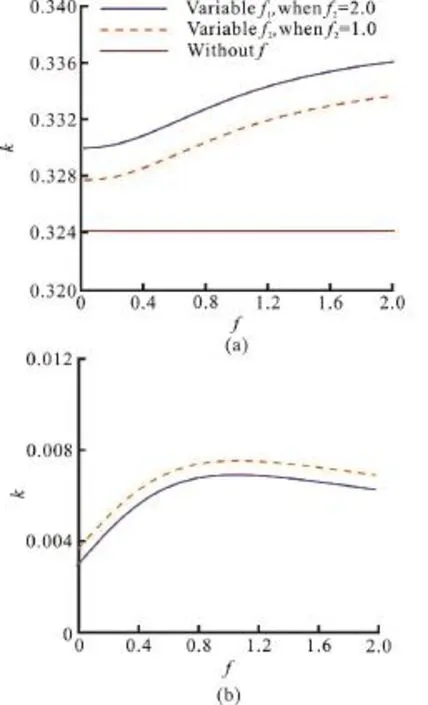
Fig. 3 (Color online) The effects of f1 and f2 on the wave numbers, where h0 :h 1 : h 2 =8:1:1, ε1 = ε 2 = 0.4 and ω=0.3

To begin with, Figs. 2-4 illustrate the effects of the parameters, which include the porosity and friction of media and the depth of the porous region, on the wave numbers (k0of the pure water region,of the porous region andof the porous region). In Fig. 2, the effects of ε1and ε2on the wave numbers is shown by different lines, whereh0:h1:h2=8:1:1,f1=1.0,f2=1.3 and ω=0.3. α~0decreases linearly andincreases nearly linearly no matter whether ε1or ε2decreases. Whenf=0,=0, which reveals that the amplitudes of the waves remain stable and there is no energy loss.Larger porosities result in larger wavelength and decaying rate of the waves.

Figure 3 describes the effects off1andf2on the wave numbers, whereh0:h1:h2=8:1:1, ε1=ε2=0.4 and ω=0.3. As can be seen from the figure, the values ofincrease gradually with the increment of the friction, but the increasing relationship is nonlinear.reaches the peak aroundf1=1 orf2=1 and then declines slowly.

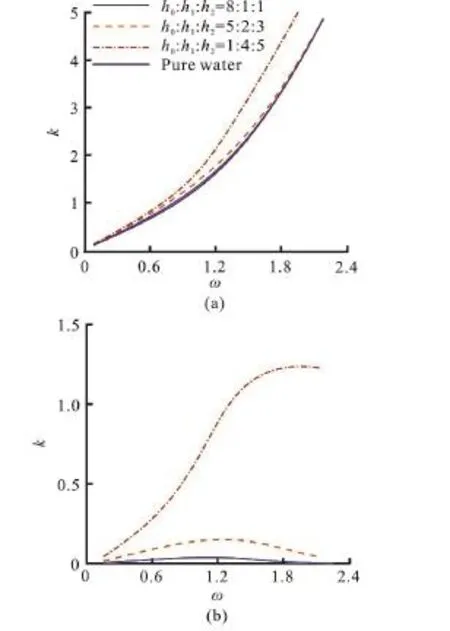
Fig. 4 (Color online) The effects of the depth rates on the wave numbers, where ε1=0.9,ε2=0.8 and f1 =f2=1.1

The effects of the depth rates on the wave numbers are displayed in Fig. 4, where ε1=0.9,ε2= 0.8,f1=f2=1.1 and ω=0.3. The porous media occupying more region cause the curves of the dispersion relation to move upwards. As for, there exists a maximum point and the values of the peak become larger as the depth of the porous region increases.

Forf1=f2=0, we can calculateE= (R/I0)2+(T/I)2=1, which indicates the conservation of the

0 energy; while forf1≠ 0 orf2≠ 0, the energy is dissipated due to the friction effect andE=represent the relative loss of the energy, whereECis the total energy of the reflected and transmitted waves when the computation is converged. Here we considerh0=0.5,h1=0.3,h2=0.2, ζ0= 0.01,b= 0.4,ω=2.0, ε1=0.9, ε2=0.8,f1=1.0,f2=1.1 ands1=s2=1. Table 1 is shown to examine the convergence of the result for differentM, whereMis the number of evanescent modes. AsMincreases,the corresponding reflectionand transmissioncoefficients converge. WhenM≥ 1 6, the numerical result for the energy is approximately conserved. The following figures are plotted withM= 16,h0=0.1,h1=0.4,h2=0.5, ζ0= 0.01 ands1=s2=1 for illustration.

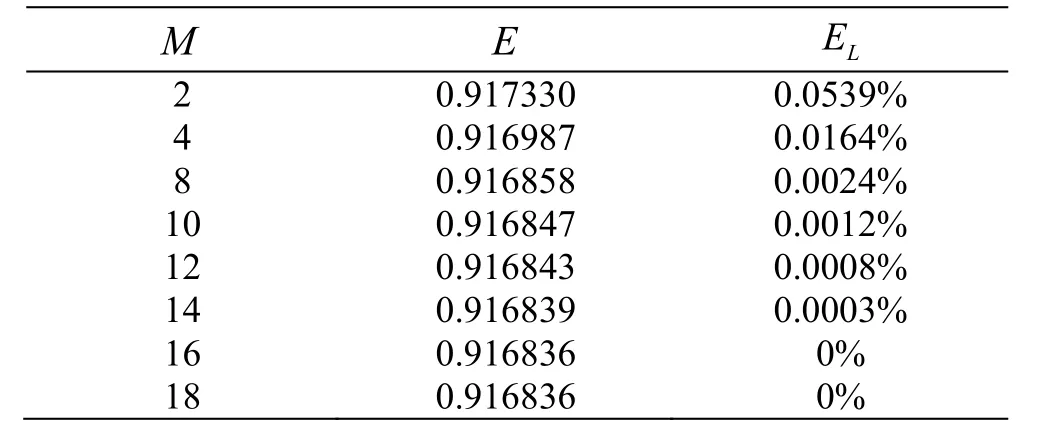
Table 1 The values of E and LE for different M

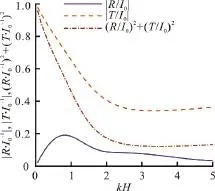
Fig. 5 (Color online) The effects of kH on the coefficients, and ( R /I 0 )2+(T/I 0)2, where b =0.4, ε1=0.9, ε2=0.8, f1=1.0 and f2=1.1

Figure 5 shows the effects of the non-dimensional water depthkHon the coefficientswhereb= 0.4,ε1=0.9, ε2=0.8,f1=1.0 andf2=1.1. As the increment ofkH, the reflection coefficientspresent a fluctuant profile and reaches the first peak atkH≈ 0 .75, while the transmission coefficientfirstly decreases and reaches the minimum atkH≈3.5.

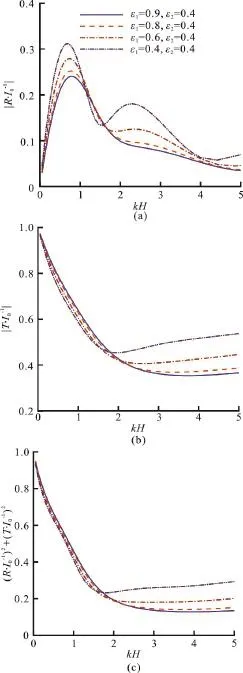
Fig. 6 (Color online) The effects of kH on the coefficients, and ( R /I )2+(T/I )2in the case of00 different ε1, where b=0.4, ε2=0.4 and f1=f2=1

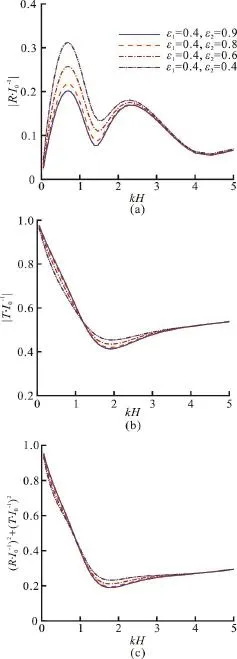
Fig. 7 (Color online) The effects of kH on the coefficients, and ( R /I )2+(T/I )2in the case of00 different ε2, where b=0.4, ε1=0.4 and f1=f2=1

It is shown, in Figs. 6, 7, that the different porosities have remarkable influence on the reflection coefficientsand the transmission coefficientwhereb= 0.4,f1=f2=1. When ε2is fixed at about 0.4, the maximum ofincreases and the second peak becomes obvious as the decrease of ε1, while the value of the transmission coefficientis becoming larger for largerkH. From Fig.7, it can be seen thatis also insensitive to the changes of ε2, butis not. For ε1=0.4, the smaller ε2, the larger the peak values ofThe values ofhowever, remain unchanged for largerkH.

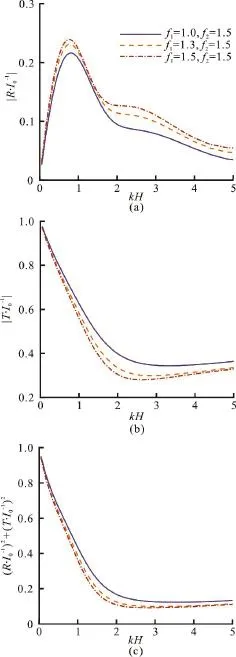
Fig. 8 (Color online) The effects of kH on the coefficients, and ( R /I0 )2+(T/I 0)2in the case of different f1, where b=0.4, ε1=0.9 and ε2=0.8

Figures 8, 9 respectively showand (R/I0)2+(T/I0)2for different friction factorsf1andf2of the porous region, whereb= 0.4,ε1=0.9 and ε2=0.8. The large friction factors enlarge the reflection coefficientand weaken the transmission coefficien tdue to the resistance and dissipation effects in the porous region.

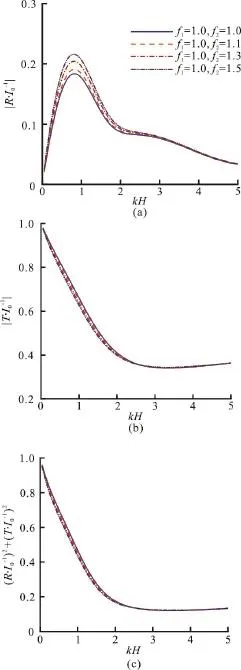
Fig. 9 (Color online) The effects of kH on the coefficients, and ( R /I0 )2+(T/I0 )2in the case of0 different f2, where b=0.4, ε1=0.9 and ε2=0.8

The effects of the width of the porous region on the coefficientsand (R/I0)2+(T/I0)2for different ε1and ε2are illustrated in Fig. 10, whereω=1.0,f1=1.0 andf2=1.1. It is obvious that the loss of the energy increases with increasing value ofb/H. The reflection coefficientsexhibit fluctuant behavior with the increment ofb/Hand finally remain steady forb/H≥ 2 .And the values ofdecline all the way back to the near-zero. Furthermore, we consider the impact of the porosity on the coefficients. The decrease of ε1and ε2will cause more reflected waves and the increase of the peak values ofThe curves with small ε1and ε2have a fast descent rate.

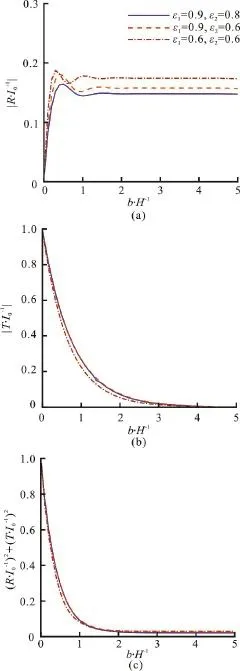
Fig. 10 (Color online) The effects of the width of b/ H on the coefficients , and ( R /I )2+(T/I )200 in the case of different ε1 and ε2, where ω=1.0,f1 =1.0 and f2=1.1

4. Conclusions

This paper herein has presented an semianalytical method for the problem that the simple time-harmonic incident waves with a given angular frequent propagate over a two-layer porous barrier.With the framework of the linear potential flow theory,we adopt the method of matched eigenfunction expansions and define a new form of the inner product for the two-layer porous barrier to simplify the series in the simultaneous equations. A suitable truncation number of the series will save much calculating time without sacrificing the accuracy of the solution.

We have discussed the influence of the characteristics of the porous media on the dispersion relation,reflected and transmitted energy. The relationships between the wave numberand the porosity (ε1or ε2) are linear, but the relationships betweenand the friction (f1orf2) are nonlinear. The small porosities and large friction cause the wavelength to become short. The reflection coefficients have a fluctuant profile with the increase ofkH. With the decrease of the porosity ε1and ε2, the reflection coefficientscrease and the profiles exhibit fluctuant obviously, while for largerkH, the transmission coefficientsincrease to some extent.The large friction will enhance the reflection waves and reduce the transmission ones. Moreover, when the width of the porous region reaches a certain value, the reflection coefficient will remain constant, but the transmission waves will disappear.

Acknowledgements

The authors would like to thank Professor S. Q.Dai of Shanghai University for his helpful suggestions and thank the anonymous reviewers for their constructive comments.

[1] Sollitt C. K., Cross R. H. Wave transmission through permeable breakwaters [J].Coastal Engineering Proceedings, 1972, 1(13): 1827-1846.

[2] Chwang A. T. A porous-wavemaker theory [J].Journal of Fluid Mechanics, 1983, 132: 395-406.

[3] Sahoo T., Chan A. T., Chwang A. T. Scattering of oblique surface waves by permeable barriers [J].Journal of Waterway, Port, Coastal, and Ocean Engineering, 2000,126(4): 196-205.

[4] Das S., Bora S. N. Wave damping by a vertical porous structure placed near and away from a rigid vertical wall[J].Geophysical and Astrophysical Fluid Dynamics, 2014,108(2): 147-167.

[5] Zhao Y., Liu Y., Li H. J. Wave interaction with a partially reflecting vertical wall protected by a submerged porous bar [J].Journal of Ocean University of China, 2016, 15(4):619-626.

[6] Zhang J., Li Q., Ding C. et al. Experimental investigation of wave-driven pore-water pressure and wave attenuation in a sandy seabed [J].Advances in Mechanical Engineering, 2016, 8(6): 1-10.

[7] Zhai Y., Zhang J., Jiang L. et al. Experimental study of wave motion and pore pressure around a submerged impermeable breakwater in a sandy seabed [J].International Journal of Offshore and Polar Engineering, 2016, 28(1):87-95.

[8] Jeng D. S. Wave dispersion equation in a porous seabed[J].Ocean Engineering, 2001, 28(12): 1585-1599.

[9] Metallinos A. S., Repousis E. G., Memos C. D. Wave propagation over a submerged porous breakwater with steep slopes [J].Ocean Engineering, 2016, 111: 424-438.

[10] Mohapatra S. The interaction of oblique flexural gravity incident waves with a small bottom deformation on a porous ocean-bed: Green’s function approach [J].Journal of Marine Science and Application, 2016, 15(2): 112-122.

[11] Das S., Behera H., Sahoo T. Flexural gravity wave motion over poroelastic bed [J].Wave Motion, 2016, 63: 135-148.[12] Shoushtari S. M. H. J., Cartwright N. Modelling the effects of porous media deformation on the propagation of water-table waves in a sandy unconfined aquifer [J].Hydrogeology Journal, 2017, 25(2): 287-295.

[13] Ye J. H., Jeng D. S. Response of porous seabed to nature loadings: Waves and currents [J].Journal of Engineering Mechanics, 2011, 138(6): 601-613.

[14] Zhang Y., Jeng D. S., Gao F. P. et al. An analytical solution for response of a porous seabed to combined wave and current loading [J].Ocean Engineering, 2013, 57:240-247.

[15] Zhang X., Zhang G., Xu C. Stability analysis on a porous seabed under wave and current loading [J].Marine Georesources and Geotechnology, 2017, 35(5): 710-718.

[16] Seymour B. R., Jeng D. S., Hsu J. R. C. Transient soil response in a porous seabed with variable permeability [J].Ocean Engineering, 1996, 23(1): 27-46.

[17] Jeng D. S., Seymour B. R. Response in seabed of finite depth with variable permeability [J].Journal of Geotechnical and Geoenvironmental Engineering, 1997,123(10): 902-911.

[18] Zhang L. L., Cheng Y., Li J. H. et al. Wave-induced oscillatory response in a randomly heterogeneous porous seabed [J].Ocean Engineering, 2016, 111: 116-127.

[19] Meng Q. R., Lu D. Q. Scattering of gravity waves by a porous rectangular barrier on a seabed [J].Journal of Hydrodynamics, 2016, 28(3): 519-522.