Spectral/hp elementmethods:Recent developments,applications, and perspectives *

Hui Xu, Chris D. Cantwell,Carlos Monteserin,Claes Eskilsson,Allan P. Engsig-Karup, 3,Spencer J. Sherwin

?

Spectral/elementmethods:Recent developments,applications, and perspectives*

Hui Xu1, Chris D. Cantwell1,Carlos Monteserin2,Claes Eskilsson4, 5,Allan P. Engsig-Karup2, 3,Spencer J. Sherwin1

1.2.3.4.5.

High-precision spectral/elements, continuous Galerkin method, discontinuous Galerkin method, implicit large eddy simulation

Project Leader

Spencer Sherwin is Professor of Computational Fluid Mechanics and the Head of Aerodynamics Section in the Department of Aeronautics at Imperial College London. He received his MSE and Ph. D. from the Department of Mechanical and Aerospace Engineering Department at Princeton University in 1995. Prior to this he received his BEng from the Department of Aeronautics at Imperial College London in 1990. In 1995, he joined the Department of Aeronautics at Imperial College as a lecturer and subsequently became a full professor in 2005. Over the past 27 years he has specialised in the develop- ment and application of advanced parallel spectral/element methods for flow around complex geometries with a particular emphasis on vortical and bluff body flows, biomedical modelling of the cardiovascular system and more recently in industrial practice through the partnerships with McLaren Racing and Rolls Royce. Professor Sherwin’s research group also develops and distributes the open-source spectral/element package++ (www.nektar.info) which has been applied to direct numerical simulation, large eddy simulation and stability analysis to a range of applications including vortex flows of relevance to offshore engineering and vehicle aerodynamics as well as biomedical flows associated with arterial atherosclerosis. He has published numerous peer- reviewed papers in international journals covering topics from numerical analysis to applied and funda- mental fluid mechanics and co-authored a highly cited book on the spectral/element method.Since 2014 Prof. Sherwin has served as an associate editor of the Journal of Fluid Mechanics. He is a Fellow of the Royal Aeronautical Society, a Fellow of the American Physical Society and in 2017 he was elected a Fellow of the Royal Academy of Engineering.

Introduction

Over the past few decades, computational fluid dynamics (CFD) has become increasingly powerful and has therefore been seen as the natural starting point to investigate a variety of mathematical and physicalproblemsinscienceandengineering. Traditio- nally, “l(fā)ow-order methods” with up to second-order spatial accuracy have been widely adopted as the default implementation for the simulation of fluid flows, often based around the Reynolds averaged Navier-Stokes (RANS) equations. This approach has achieved a great deal of success in many applications due to its well-established robustness and efficiency. However, as the demands on the accuracy of CFD outputs have increased, such as requiring the solution of the unsteady flow equations in complex geometries, low-order methods are less able to provide the neces- sary level of precision in capturing transient dynamics, as compared to higher accuracy schemes for a given computational cost. Therefore, there is currently a great interest in the development and application of high-order methods such as the spectral/element discretisation.

Finite element methods are widely used across a broad range of engineering and scientific disciplines. They can be categorised into three clazzzsses[1, 2]: (1) the classical-version finite element method, (2) the spectral element method, or-version finite element method, (3) the-version finite element method, called the spectral/element method. Once the com- putational domain is partitioned into a non-overlap- ping element set, the spectral/element method employs a “spectral-like” approach in each element, representing the solution through a basis of poly- nomials. Therefore, the spectral/element method combines the advantages of the spectral element method, in terms of the properties of accuracy and rapid convergence, with those of the classical-version finite element method, that allows complex geometries to be effectively captured. Compared with traditional low-order finite element schemes, the spectral/element method can provide an arbitrary order of spatial-approximation accuracy under the assumption of sufficient smoothness of the solution. It therefore combines the advantages of the low-order finite element method family, whilst also providing an additional attractive higher-precision, approximation for solving partial differential equations[3, 4]. Recent studies also indicate that the compact nature of the spectral/element method is well-placed to take advantage of modern multi-core and many-core computing hardware[5, 6]. All of the above properties have positioned the spectral/element method as an attractive numerical strategy for obtaining high- precision solutions with a relatively low computa- tional cost.

The spectral/element method is gaining increasing traction in the field of CFD[3], and it has achieved great success in both direct and large eddy simulation (LES) of complex flows[7-11]. It has also been successfully applied to a broad range of other applications in various research fields, for instance, cardiac electro-physiology[12], solid mechanics[13, 14], porous media[15]and oceanographic modelling[16].

One of the challenges of these methods is that they are more challenging to implement than low- order methods. There are now, however, now a number of open-source packageswhich encapsulate the complexities of the method. One such package that the authors have been developing is++, a cross-platform spectral/element framework (http:// www.nektar.info) which has made high-order finite element methods more accessible to the broader com- munity and can be used to solve a range of the emerging challenges in high-fidelity scientific compu- tations[4]. It enables the construction of high-order dis- cretisations for solving a wide range of partial diffe- rential equations, supporting hybrid meshes, for example triangles and quadrilaterals or tetrahedra, prisms, pyramids and hexahedra. The current software package includes a number of pre-written scalable solvers, including for incompressible flow, compressi- ble flow, shallow water equations, acoustic perturba- tion equations and others.

In this paper, we present a review of the state-of- the-art of the spectral/element method, and its applications. In Section 1, we briefly describe the spectral/element method and discuss the numerical advantages and robustness of the method in solving partial differential equations. In Section 2, we high light some of the implementation challenges of the method in order to achieve computational efficiency and discuss potential solutions through our efforts with++. In Section 3, we then provide a survey of the applications in transitional flows and waves (wave propagation and wave-body interaction) in ocean engineering to which the spectral/element method has been applied. Finally, in Section 4, we conclude with further discussions and some perspec- tives on future directions.

1. Spectral/hp element method

In this section, we provide an overview of the mathematical foundations of the spectral/element method. A more detailed derivation of the mathema- tical theory can be found in Ref. [3] but is beyond the scope of this paper.

1.1 Overview of method

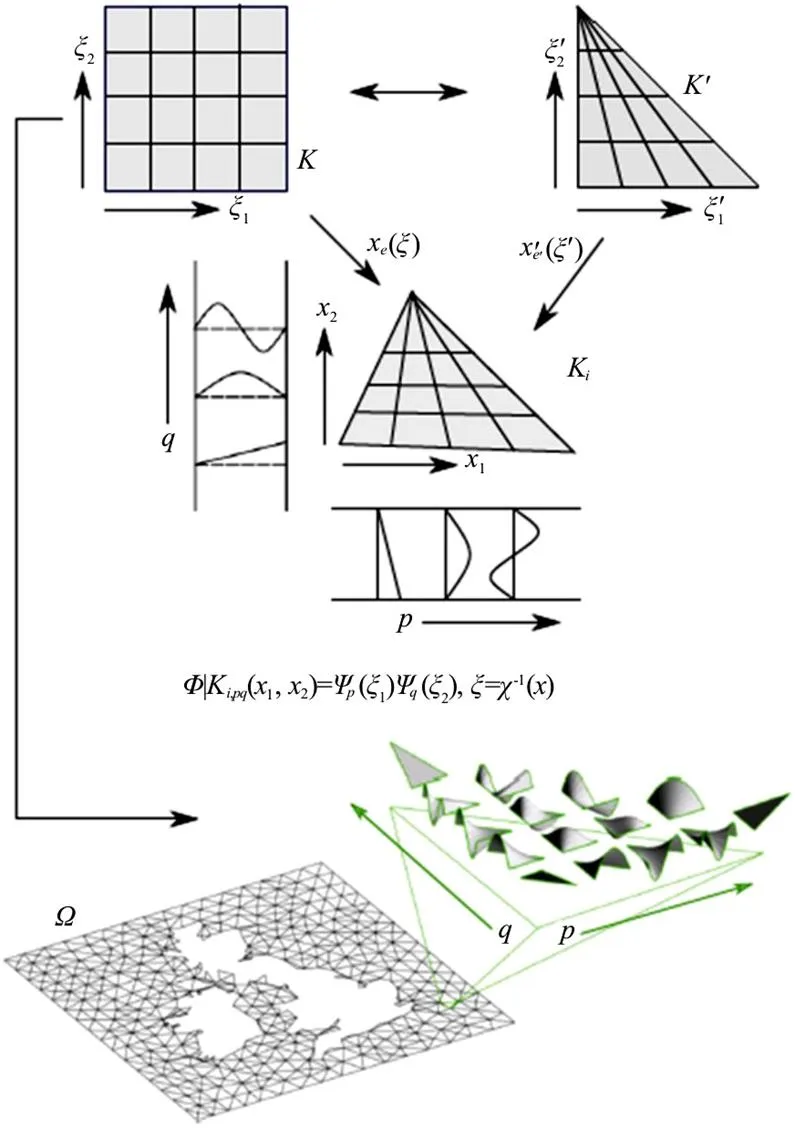
1.2 Outline of mathematical formulation

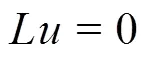
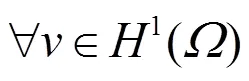
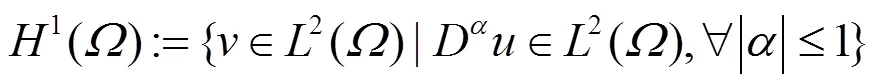
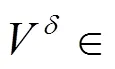
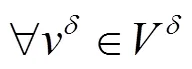
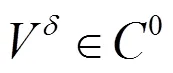
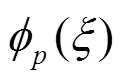
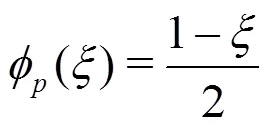
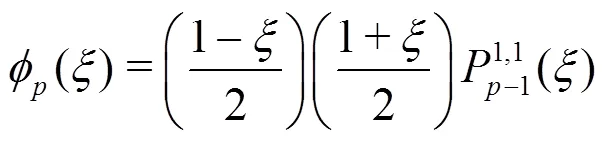
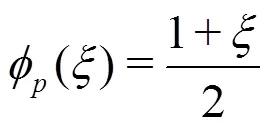
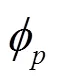
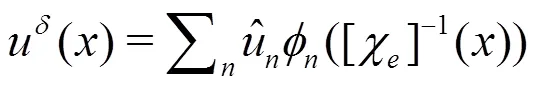
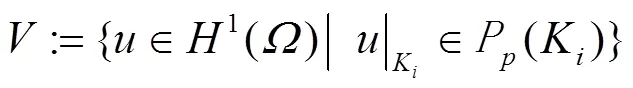
Fig. 2 Propagation of a cone initial condition using a DG formulation of the advection equation. After one rotation, we see the solution using a , and order approximations

1.3What are the beneficial properties of using a spectral/hp element method?

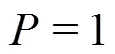
Recently, a comparison between high-order flux reconstruction and the industrial-standard solver STAR-CCM+, was made, in which the accuracy and computational cost of flux reconstruction (FR) me- thods in PyFR and STAR-CCM+, for a range of test cases including scale-resolving simulations of turbu- lent flow were investigated[21]. The results from both PyFR and STAR-CCM+ show that third-order sche- mes can be more accurate than second-order schemes for a given cost. Moreover, advancing to higher-order schemes on GPUs with PyFR was found to offer even further accuracy vs cost benefits relative to industry- standard tools. These demonstrate the potential utility of high-order methods on GPUs for scale-resolving simulations of unsteady turbulent flows.

1.4Using the spectral/hp element method in margi- nally resolved problems

In the previous sections, we outlined the underl- ying formulation of the spectral/element method- ology and we now describe some of the state-of-the- art developments necessary for simulating problems which are only marginally resolved. These tend to arise at higher Reynolds numbers, which generally promote greater levels of turbulence that cannot realistically be captured, even on the latest parallel computers. This leads to the build-up of energy in the larger resolved scales, due to the inability of the discretisation to fully capture the smaller scales of the flow. This is addressed with two techniques. The first involves performing the numerical integration of non- linear terms consistently. Even with this, non-linear interactions may still lead to an artificial build-up of energy in the smaller resolved scales. A second technique is then to apply a spectral filtering, known as spectral vanishing viscosity, to dampen such energies.

1.4.1 Dealiasing

Dealiasing strategies have been observed to be effective in enhancing the numerical stability when solving problems using the spectral/element method[22-26]. The errors are typically caused byquadrature employed in the Galerkin discre- tisation of nonlinear terms[3]. When the simulation is not sufficiently well- resolved, this leads to energy in the shorter length scales to be transferred back into the longer length scales. When simulations are well- resolved, the numerical errors created by insufficient quadrature are negligible[23, 24]. However, in margi- nally resolved or under-resolved simulations, aliasing errors may significantly pollute the solution[23]. As discussed in Ref. [26], there are three kinds of aliasing sources:

(1) PDE aliasing, which relates to quasi-linear and non-linear terms[23].

(2) Geometrical aliasing, which arises due to deformed/curved elements.

(3) Interface-flux aliasing, in the case of discon- tinuous methods[26].

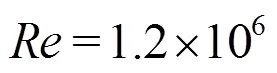
Fig.3Helicity for an incompressible viscous flow over a NACA 0012 wing[26]

We can categorise dealiasing techniques into two strategies:

(1): PDE-dealiasing through consistent integration of the nonlinear terms only[23, 26].

(2): PDE- and geometrical- dealiasing through consistent integration of all the terms of the discretisation[26].

The phraserefers to poly- nomial nonlinearities, where it is effectively possible to know a priori the number of quadrature points necessary for the integration to be exact[23, 27]. There- fore, the non-linearities can be consistently integrated. For non-polynomial functions, as typically arise in the Euler equations, the concept of consistent integration is not well defined since it is impossible to fully control the quadrature error. We refer to the reader to Ref. [26] for a more complete discussion of these strategies as well as a discussion of interface aliasing.

1.4.2 Spectral vanishing viscosity

As previously discussed, it is well known that spectral/element discretisations generally lead to approximations that have low dissipation and low dispersion[3]per degree of freedom when compared to lower-order methods. In solving advection-diffusion equations and nonlinear partial differential equations such as advection-dominated flows, at marginal reso- lutions, oscillations appear that may render the com- putation unstable[3]. Artificial viscosity has been used in may discretisation methods to suppress wiggles associated with high wavenumbers, for example hyperviscosity has been broadly and effectively used in simulations using the Fourier method. A related concept is the so-called(SVV), which was originally proposed based on a second-order diffusion (convolution) operator for spectral Fourier methods[28]. The SVV concept was originally motivated through the inviscid Burgers equation where an additional diffusion term was added, i.e.

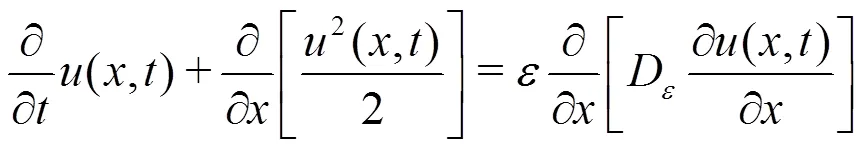
To provide some intuition about the influence of SVV, we show in Fig. 5 an example from Ref. [30] of applying SVV to the parabolic equation

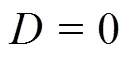
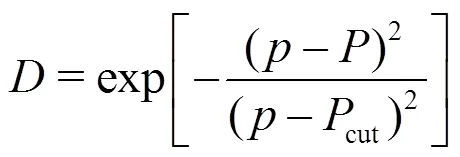
where is the total number of modes employed and is the cutoff polynomial order. SVV with the kernel function can be regarded as a low-pass filter. We see that the SVV dissipation added to the high mode numbers with respect to the spectral element discretisation does indeed yield dissipation at the global high wavenumber scales of the solution in Fig. 5.

In applications, Karamanos and Karniadakis applied SVV to high Reynolds number turbulent flows and the method was viewed as anLES approach[29]. Kirby and Karniadakis computed the artificial viscosity by incorporating the local strain and the Panton function and the methodology was called SVV-LES[33]. The SVV approach has been reasonably widely used to simulate turbulent flow and vortical flows[7, 30-36]. SVV has been explicitly regarded as a turbulent model of implementing implicit large eddy simulation (iLES) under the assumption “”[37], even though SVV is not explicitly designed as a subgrid-scale model.

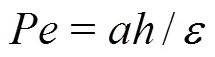
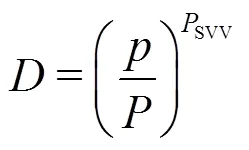
In turbulence simulations using DG methods, there were early discussions[40, 41], highlighting that the scheme successfully predicted low-order statistics with fewer degrees of freedom (DoFs) than traditional numerical methods. More extensive assessments[42, 43]indicated that DG can predict high-order statistics with accuracy comparable to that of spectral methods for an equivalent number of DoFs. However, there is still little understanding ofandone can use the spectral/hp element method for under-resolved turbulence simulations when either spectral vanishing viscosity (as sometime employed in CG methods) or upwind fluxes (as naturally arise in DG methods) are used to provide dissipation at under-resolved scales. Recently, exploratory studies, focusing on the DG formulation,wereundertakentoaddresshow numerical dissipation affects the under-resolved scales[44, 90]. By exploring DG’s propagation characteristics directly from the dispersion-diffusion curves of a linear advection problem, a simple criterion (named “the 1% rule”) was proposed to estimate the effective resolu- tion of the DG scheme for a givenapproximation space.

2. Implementation of spectral/hp element method

One of the challenges of enabling the spectral/element method to become more pervasive for indu- strial and environmental problems is the implementa- tional complexity of the methods. One of the overarc- hing aims of the++ project is to provide an efficient framework upon which a broad range of physical processes can be modelled using these appro- aches. With this in mind, we outline some of effi- ciency challenges associated with implementing these methods for practical use and detail some suitable solutions in the context of++.

2.1 Nektar++ overview

The design of++ is intended to mirror the mathematical formulation of the spectral/element method,from one-dimensional basis functions up to multi-dimensional, multi-element discretisationsofcomplexgeometries. Thepackageconsists of a tiered collection of libraries which implement different aspects of the formulation, as illustrated in Fig. 6. On top of this, domain-specific application solvers can be readily developed which specify the physical pro- cesses to be modelled, while leveraging the imple- mentation of the discretisation provided by the libra- ries in a relatively transparent manner.

At the lowest level theimplements 1-D bases of orthogonal polynomials which are used to construct the expansion bases on individual elements. Their analytical derivatives and the distributions of points used for performing Gaussian quadraturearealsocaptured.Ontopofthis,the reference elements are defined for tessellating 1-D, 2-D and 3-D domains in thelibrary.++ supports a range of elemental regions to enable maximum flexibility in defining meshes which can effectively capture complex geometries, including segments in 1-D, quadrilaterals and triangles in 2-D, and hexahedra, prisms, pyramids and tetrahedra in 3-D. For multi-dimensional regions expansion bases may be defined using natively 2-D bases (e.g., Lagrange polynomials at Fekete points), or though a tensor-product construction of 1-D polynomials. For each of these regions, core finite element operators, including backward transform, inner product and derivative operators are defined.

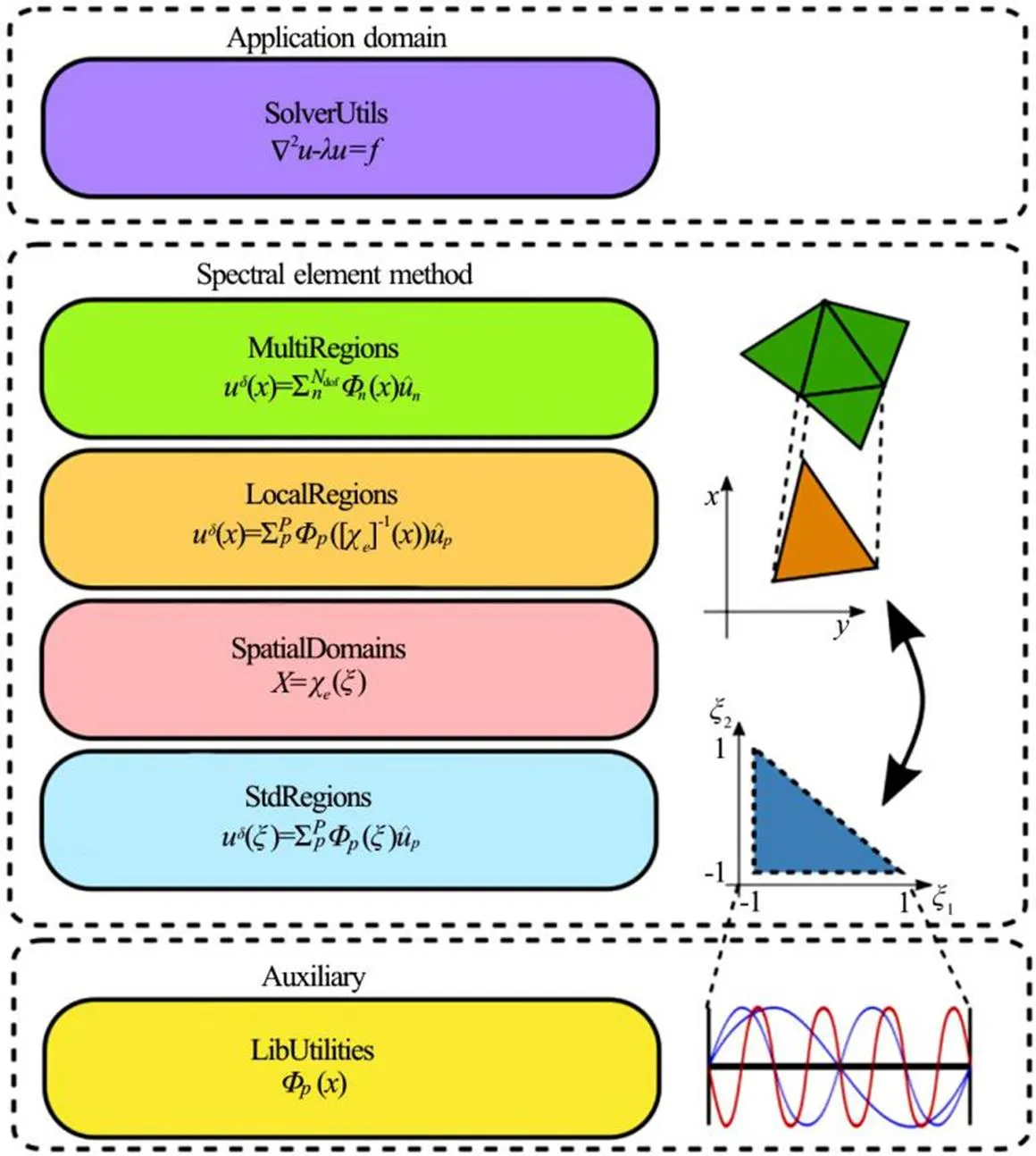
Fig.6Diagrammatic representation of the libraries in++[4]

Constituent elements of the computational mesh arerepresentedinthelibrarythrougha mapping from the reference region to the physical coordinates of the element. These mappings are cap- tured in thelibrary and can capture high-order geometric curvature in the element. These geometric factors are used to extend the finite element operators defined for the standard reference regions to the physical elements. Thelibraryencapsulates the construction of multi-element global expansions through the construction of assembly operators which identify corresponding degrees of freedom in the local and global representations. Through this mapping, global finite element operators areconstructed.Globallinearsystemscanthenbe solved using a number of direct and iterative linear algebra techniques. Iterative approaches, such as the preconditioned conjugate gradient method, solve a system through the repeated action of the operator, providing scope for a range of performance optimisa- tions, discussed in Section 2.3.

While the central concept captured in++ are high-order spectral/element spatial discretisa- tions, high-order time integration algorithms are also implemented to allow for highly accurate transient simulations. These include fully explicit, implicit and mixed implicit-explicit (IMEX) schemes.

2.2 Combined spectral/hp-Fourier discretisation

While the spectral/hp element method exhibits some of the numerical characteristics of a pure spectral method, the use of the latter is still preferred in the case of regular geometries such as rectangles and cuboidal domains. This situation occurs widely in many, particularly fundamental, hydrodynamics pro- blems. In++, we leverage this by allowing for a mixed spectral/-Fourier discretisation. In this confi- guration, geometrically homogeneous coordinate di- rections are represented with a truncated Fourier expansion, while coordinate directions with geometric complexity use the spectral/element discretisation. This has the effect of decoupling the individual Fourier modes, allowing the spectral/operator to be applied independently within each component of each Fourier mode.

The Fourier decomposition also enables parallel decomposition of the modes to different processes[45]. Combined with the parallelisation of the spectral/element discretisation this leads to a hybrid paralle- lism. An open challenge here is identifying the optimal parallelisation of such mixed-discretisation domains to achieve optimal performance.

Thelibrary further extends this discretisation strategy by supporting geometries in which a coordinate direction can be transformed to a homogeneous representation by an analytical function. This enables more complex geometries to be discre- tised using this efficient formulation.

2.3 From to efficiently

One of the challenges in implementing the spectral/method is achieving computational perfor- mance across a broad range of polynomial orders. The classic approach to implementing linear finite element operators is to assemble the global form of the operator and act directly on the global degrees of freedom. This is performant since each mesh vertex has a high valency and the assembly operation dramatically reduces the size of the global linear system used within the iterative solver. With increa- sing polynomial order, this reduction is less and the memory indirection associated with the global operator leads to reduced through-put and degraded performance.

Recalling the construction of the local elemental operators as the reference region operator, transfor- med under a geometric mapping, one can exploit the decomposition of the elemental operators into these constituent parts. Thelibrary in++ exploits this decomposition on groups of similar elements (same shape and expansion basis) by applying first the geometric factors associated with the operator, before acting with the reference region operator on all of the elements in the group simul- taneously[50]. This effectively replaces a sequence of matrix-vector operations with a single matrix-matrix operation, reducing data movement and improving floating-point performance. This decomposition can be applied both to the local elemental matrix repre- sentation as well as the sum-factorisation approach.

2.4 High-order mesh generation

For complex 3-D geometries, the generation of high-order curved meshes along solid surfaces is a challenging topic[51-55]. Approaches for generating unstructured high-order meshes, extending coarse lineargridstoincorporatehigh-ordercurvature,area relatively new development[52, 56, 57]. The main chal- lenge is robustness, since near-wall curvature must be introduced in such a way as to prevent the generation of self-intersecting elements[51]. Recently, several methods have been proposed to cope with high-order curvilinear boundary layer meshing, namely (1) the isoparametric approach[51], (2) the variational ap- proach[53], and (3) the thermo-elastic analogy[54]. In the isoparametric approach, a reference element is mapped to a physical element with the supplied curvature information. The generation of a boundary layer mesh is achieved by splitting the reference element along the wall normal coordinate and then applying the mapping from a reference element to a physical element yielding the desired boundary layer mesh as illustrated in Fig. 7. In Fig. 8, a mesh for the NACA0012 aerofoil profile is shown which is generated by the isoparametric approach[51]. In the variational approach, a functional which defines a measure of energy over mesh and takes the mesh displacement and its derivatives as its arguments, is minimised using a nonlinear optimisation strategy[53]. It is demonstrated that the variational framework is efficient for both mesh quality optimisation and untangling of invalid meshes. In order to circumvent the drawback of elastic-model based methods which are used to tackle element self-intersection, a thermo- elastic analogy, as an extension of the elastic formu- lation, is proposed to “heat” or “cool” elements. The thermo-elastic formulation leads to an additional degree of robustness, which shows the potential to significantly improve meshing[54]., which is a mesh generation and manipulation utility bundled with++, supports these strategies for high- order mesh generation.

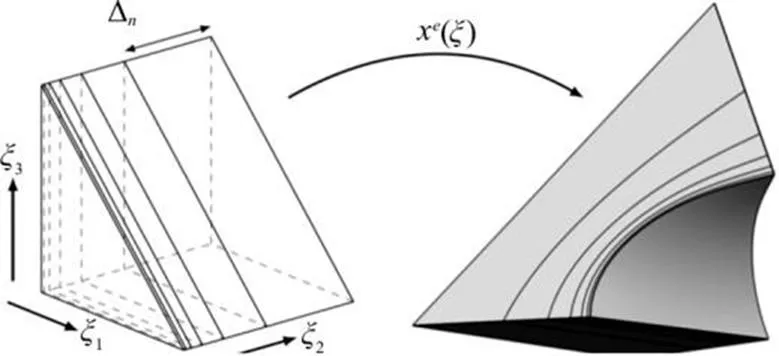
Fig.7Splitting a reference prismatic element and applying the mapping to obtain a high-order layer of prisms from the macro-element[51]

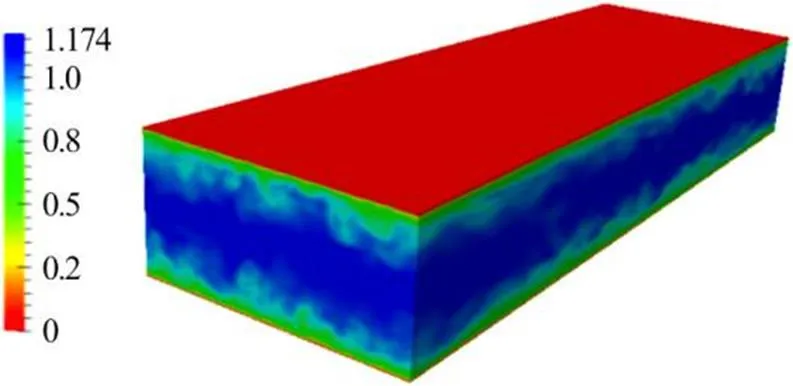
Fig.9(a)Turbulent channel flow

Fig.9(b)Turbulent pipe flow

3. Applications

In this section, we illustrate some typical appli- cations of spectral/element methods in fluid me- chanics, typically in hydrodynamics. Some examples will be given through use of the pre-written solvers in++.

3.1 The incompressible Navier-Stokes equations

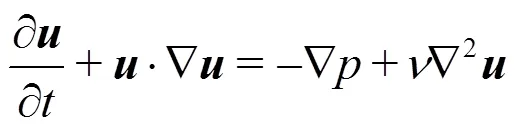
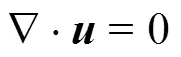
with appropriate boundary conditions. In++, a velocity correction scheme is employed, which uses a splitting/projection method where the velocity and the pressure are decoupled[58]. In the original approach, a stiffly stable time integration scheme was proposed. Briefly, high-order splitting schemes comprise of three steps involving explicit evaluation of the non-linear terms, followed by the implicit solution of the pressure Poisson system and finally solving a series of Helmholtz problems to enforce the viscous terms and velocity boundary conditions. Time integra- tion is handled using a generic time-stepping frame- work, utilising one of a number of implicit-explicit (IMEX) time-integration schemes, the details of which can be found in Ref. [59].

3.2 Transitional flows

In the past few decades, the spectral/element method has been applied to laminar and transitional flows[58, 60-64]. As discussed earlier, the advantages of the spectral/element method are its low numerical dissipation and dispersion errors, which allow indivi- dual flow structures to be accurately captured over long time periods. Combined with the development of effective stabilisation techniques (e.g., SVV or filter- based stabilisation[65]), the spectral/element method has in most recent years proved effective in modelling turbulent flow[33, 66-70].

Transitional problems are those in which turbu- lence dominates the flow domain, or in which the transition to turbulence is a fundamental aspect of the simulation. Here we provide a survey of the range of studies undertaken using the spectral/element method in relation to transitional flows, focusing on (1) turbulence, (2) separated flows, (3) hydrodynamic stability, and (4) vortical flows and high Reynolds number wingtip vortices.

3.2.1 Turbulent flows

As noted in Ref. [4], highly resolved turbulent simulations were traditionally undertaken using spec- tral methods, imposing strong geometrical restrictions. Spectral/element methods alleviate this constraint although, as discussed in Section 2, when the domain of interest has a geometrically homogeneous direction, a combination of the spectral/element method and the traditional spectral method is still particularly advantageous[45, 71].

Recently, a global mapping technique has been developed which allows the simulation of fluid flows with geometrically periodic variation along homoge- neous directions[8, 11]. A typical example is to simulate turbulent flows induced by a localised surface defor- mation in the boundary layer[11]. The computational domain is illustrated in Fig. 10(a) and the turbulent flow which forms downstream of the surface deformation is shown in Fig. 10(b). The freestream unit Reynolds number is 1.2′106and the reference free-stream velocity is 18m/s. The laminar-turbulent transition is initialised by the nonlinear process of upstream Tollmien-Schlichting (TS) disturbance breakdown to turbulence downstream of the surface indentation. The disturbance is generated by a disturbance strip as illustrated in Fig. 10(a), which has a vibration frequency of 172 Hz and is used to mimic the TS disturbance by the receptivity mechanism. The numerical calculations of this case are validated with an experimental study for which excellent agreement is obtained.

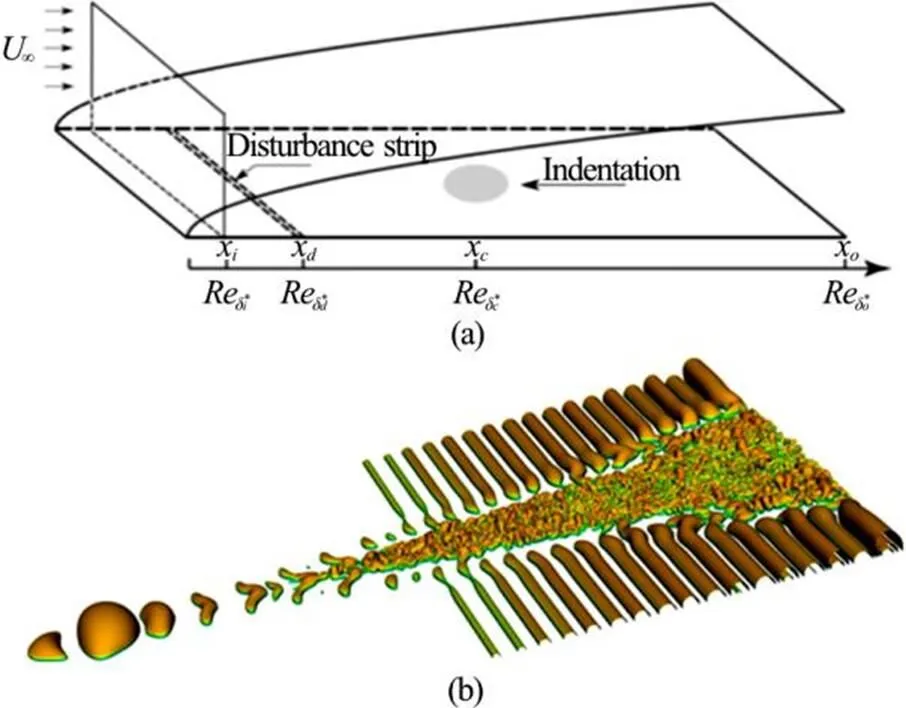
Fig.10 An illustration of the computational domain for the turbulent simulation in a boundary layer (a) and laminar-turbulent transition triggered by TS instability in a boundary layer. The iso-surfaces indicate the different pressure levels[11]

3.2.2 Separated flows

Flow separation can be one of the most important topics in fluid mechanics, due to its relevance to aerodynamic performance in many engineering appli- cations. There are typically two kinds of separations: geometrical, where the flow separates from a sharp obstacle in the flow, and pressure-induced, depending on the pressure gradient over a smooth surface. For both kinds of separation, the spectral/element method has been used to accurately capture detach- ment and reattachment points, e.g., laminar flow in a channel expansion[72], turbulent separation in a 3-D diffuser[25], the flow around a wall-mounted square cylinder[73], flows over periodic hills[74], small separa- tion bubbles induced by localised imperfections[11, 75]. Practically, the studies of separated flows are always accompanied by turbulent flows due to the occurrence of sensitive instabilities induced by the geometrical discontinuity.

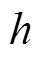
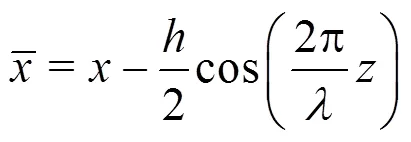
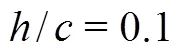
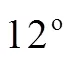
3.2.3 Hydrodynamic stability

In addition to solving the fully non-linear in- compressible Navier-Stokes equations in++, the solution of the linearised incompressible Navier- Stokes equations is also supported to enable global flow stability analyses to be performedwith respect to a steady or a time-periodic base flow. This process identifies whether such flows are susceptible to a fundamental change of state when an infinitesimal disturbance is introduction. The linearised incompres- sibleNavier-Stokes equations take the following form

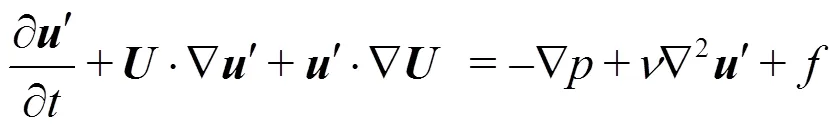
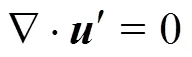
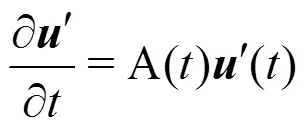
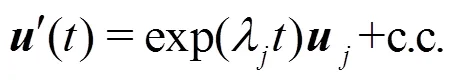
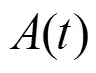
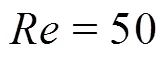
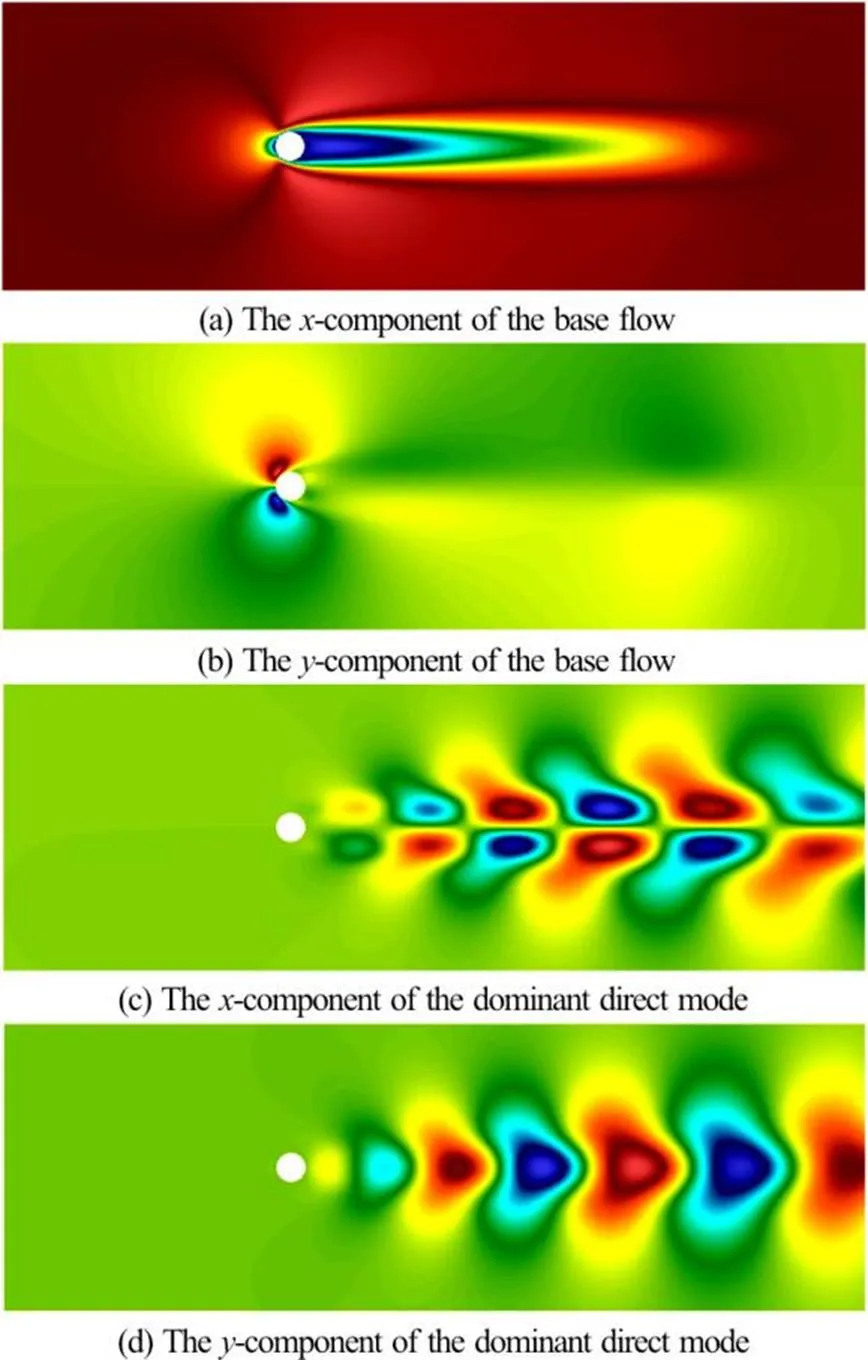
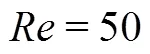
Fig. 14Tip vortex of an elliptic hydrofoil

3.2.4 Vortical flows and wingtip vortex

Simulating and understanding vortical flows are vital in hydrodynamics and aerodynamics. In many applications, manipulation of vortices in the vicinity of flow boundaries is crucial for improving perfor- mance in engineering practice[7, 85-89]. Developing a better understanding of the near wake of the vortex, lying within one chord length of the trailing edge, is essential in understanding the complex flow structure interactions[7], which is also crucial in understanding cavitation in vortical structures generated by hydro propellers[86]. Computationally, in high Reynolds number flows, accurate numerical simulations of these kinds of vortical structures are challenging for the traditional numerical methods due to numerical dissipation. A recent study in which wingtip vortices were simulated demonstrated that the adjustable and controllable low-dissipation properties of the spectral/element method were beneficial for modelling and simulating vortical flows[7, 44, 90].

To illustrate the ability of the spectral/element method to accurately capture vortical flows at a Reynolds number 1.2′106, a rectangular wing with a NACA0012 profile, is investigated with a rounded wing cap (consequently, a longer semispan where the wing is thickest) and a blunt trailing edge[7]. The results showed better correlation with experimental results than previous numerical results, both in terms of the static pressure distribution, prediction of the jetting velocity, vortex spanwise location, and the ability to resolve the secondary vortex interaction with the main wingtip vortex. The iLES method based on SVV has been shown to be a compelling alternative for computing complex vortex-dominated flows, such as the wingtip vortex, motivating its use for complex industrially relevant cases where high-fidelity compu- tational fluid dynamics can become an enabling tech- nology.

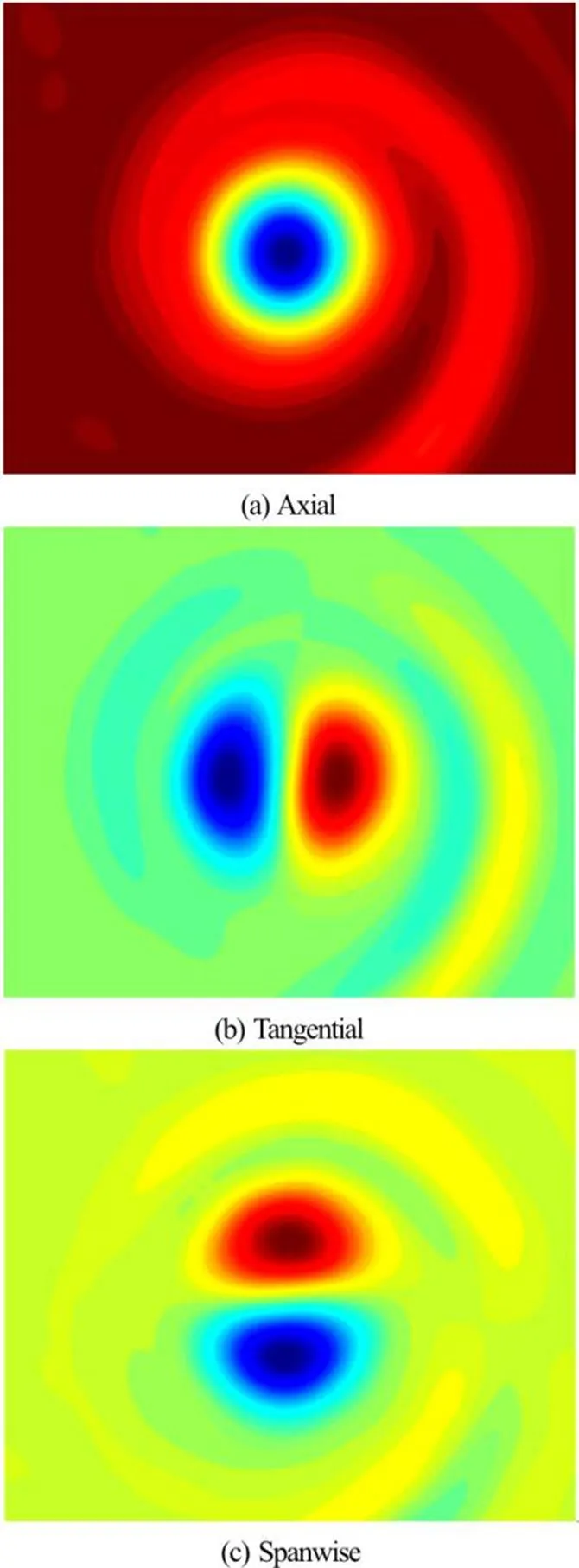
Fig. 15Vorticity components , and directions at the section

3.3 Waves in ocean engineering

This section is devoted to outlining recent progress in spectral/element modelling of wave propagation and wave-body interaction. For water waves propagation, the fully nonlinear potential flow (FNPF) equations is the fundamental governing equation and can be derived from the Navier-Stokes equations by assuming inviscid and irrotational flow. One of the main challenges in the last decade have focused on use of spectral/element methods for coastal engineering[91], and the development of robust and efficient solvers with support for unstructured meshes to capture realistic shore lines, geometric features, and adapt meshes to relevant features of the solution[92].

3.3.1 Fully nonlinear potential flow

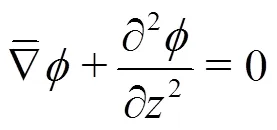
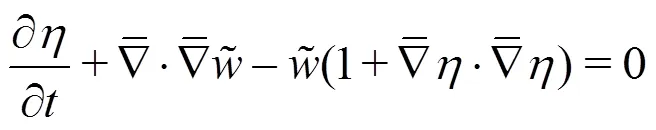
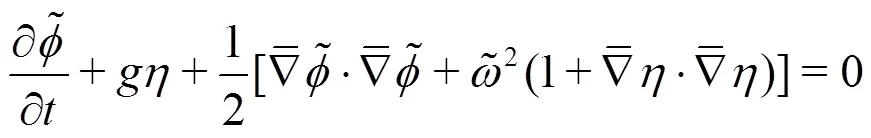
Fig. 16Snap shot of free surface elevation in the Port of Visby using fifth order method

Fig. 17Wave scattering of regular waves by a cylinder. Wave propagating from (a) to (b)

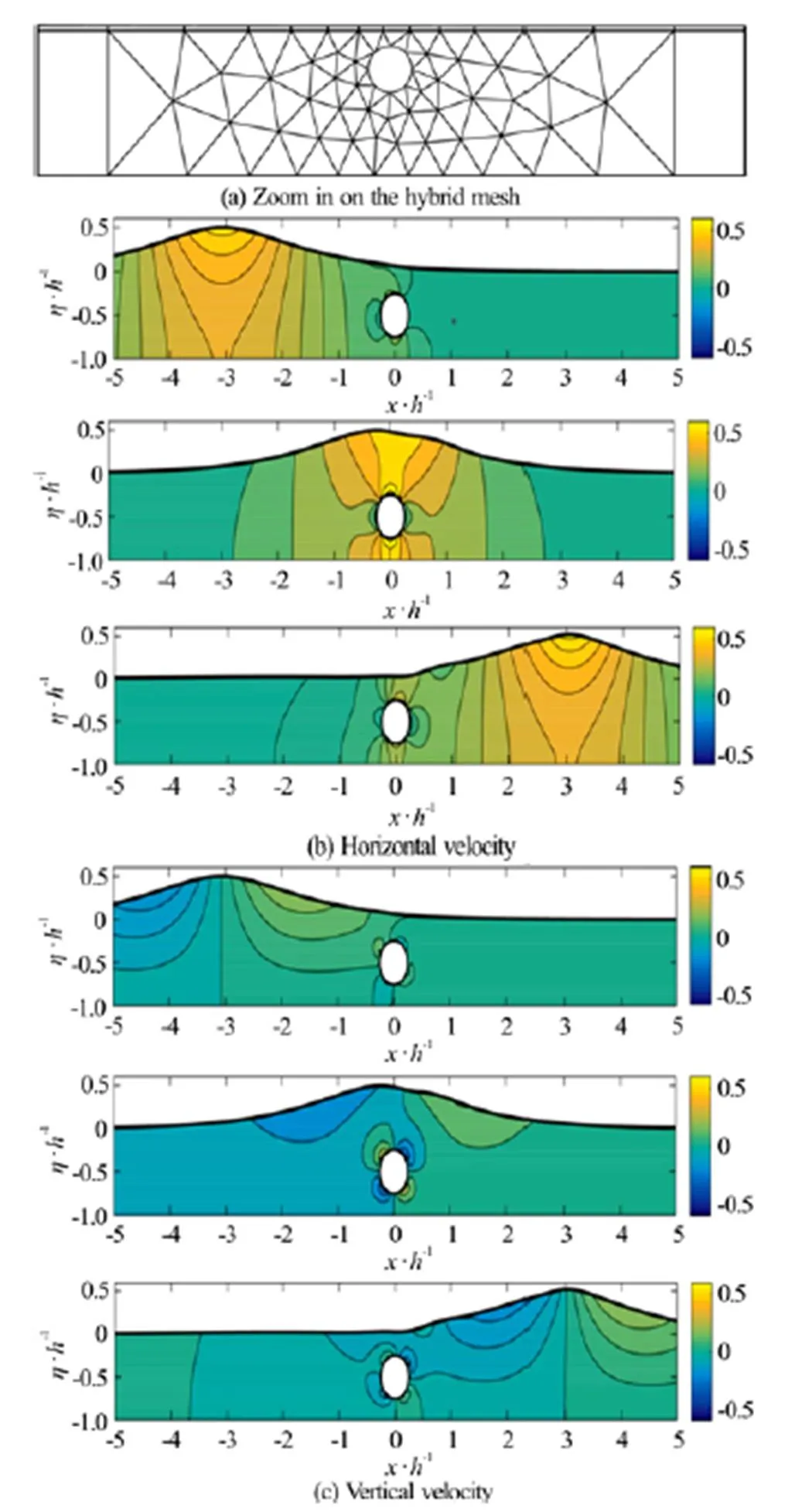
Fig.18Solitary wave passing a submerged horizontal cylinder[102]

3.3.2 Shallow water wave equations

While the application of spectral/element method for FNPF equations is emerging, in the field of depth-integrated shallow water long wave equa- tions there is a wider use of spectral/elements methods. These equations can be derived from the FNPF equations by expanding the velocity potential in terms of the vertical coordinate and integrating the Laplace problem over the fluid depth. This removes the vertical dependence of the problem. Non-hydro- static wave equations (such as Boussinesq-, Serre- or Green-Naghdi-type equations) are used for wave pro- pagation and transformation in nearshore regions. The dispersive effects are included in the equations through higher-order mixed and spatial derivatives. Eskilsson and Sherwin presented the first spectral/model for 1-D Boussinesq-type equa- tions[103], and later in 2-D[104]. In the latter study was illustrated that the use of high-order schemes is computationally efficient compared to low-order methods for long- time integration. This is general knowledge, mathema- tically proven in Ref. [105], but the importance is accenturated in wave equation where the numerical dispersion error must be kept small compared to the physical dispersion terms. Additional spectral/studies of weakly dispersive Boussinesq equations are Refs. [106, 107]. Engsig-Karup et al.[108-110]solved a set highly dispersive and nonlinear Boussinesq-type equations. More recently the interest has turned toward Green-Naghdi type equations due to their description of nonlinearity and a number of spectral/element methods have been put for- ward[111-113]. We note that all the above models are based on high-order DG methods.

The classical Boussinesq equations due to Pere- grine[114]read

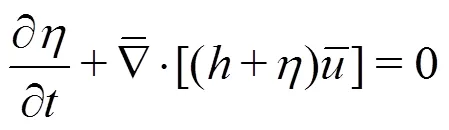
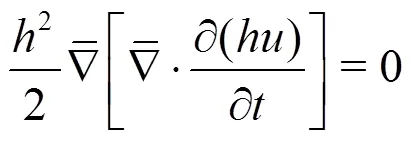
With regard to non-dispersive, hydrostatic wave equations the shallow water equations (SWE) are typically used in marine applications to predict tidal forcing but can also be used for other long wave phenomena such as tsunami and storm-surge predic- tions. For tsunami modelling-adaptive DG models have been presented in order to resolve the shock wave propagation in detail[116-118]. However, the main bulk of work on spectral/element methods for the SWE are linked to numerical weather prediction or ocean circulation where the SWE is used as a stepping stone towards solving the 3-D primitive equa- tions[119-125].

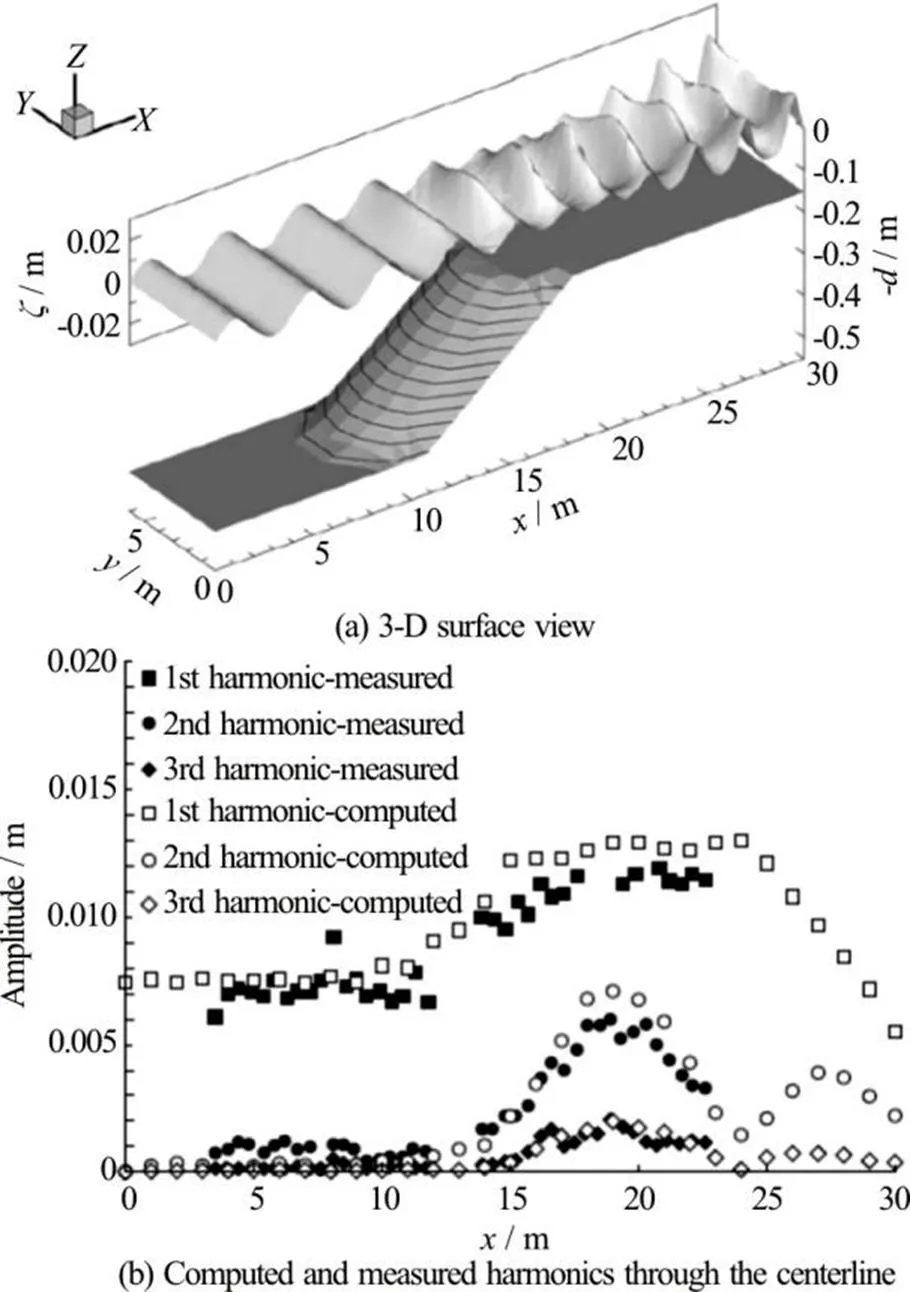
Fig.19 Higher harmonics generation on a semi-circular shoal[115]

The SWE is solved in++ as a sub-model for the dispersive Boussinesq solver simply by ignoring the dispersive step. Recently a version of the SWE model capable of solving the flow on curved surfaces using++ was presented in Ref. [126]. The model uses the so-called method of moving frames[127]to express the SWE on curved and rotating geometries. The model was shown to exhibit exponen- tial convergence and handled the standard test cases for spherical SWE, see Fig. 20 for the flow around an isolated mountain.

4. Future directions and perspectives

Significant progress has been made in theoretical and applied aspects of the spectral/element method over the past two decades which have enabled its application to a wide range of challenging hydrody- namicsandbroaderindustrialproblems.However, there still remain a number of challenges[55]. In order to enable the spectral/element method to be used to address difficult, large-scale, high Reynolds number flow problems in complex geometries, we see a number of areas which still require improvement:

(1) High-order meshgeneration:Robustlygene-rating high-order meshes with CAD conforming rep- resentation of the underlying geometry remains one of the key challenges to industrial application.

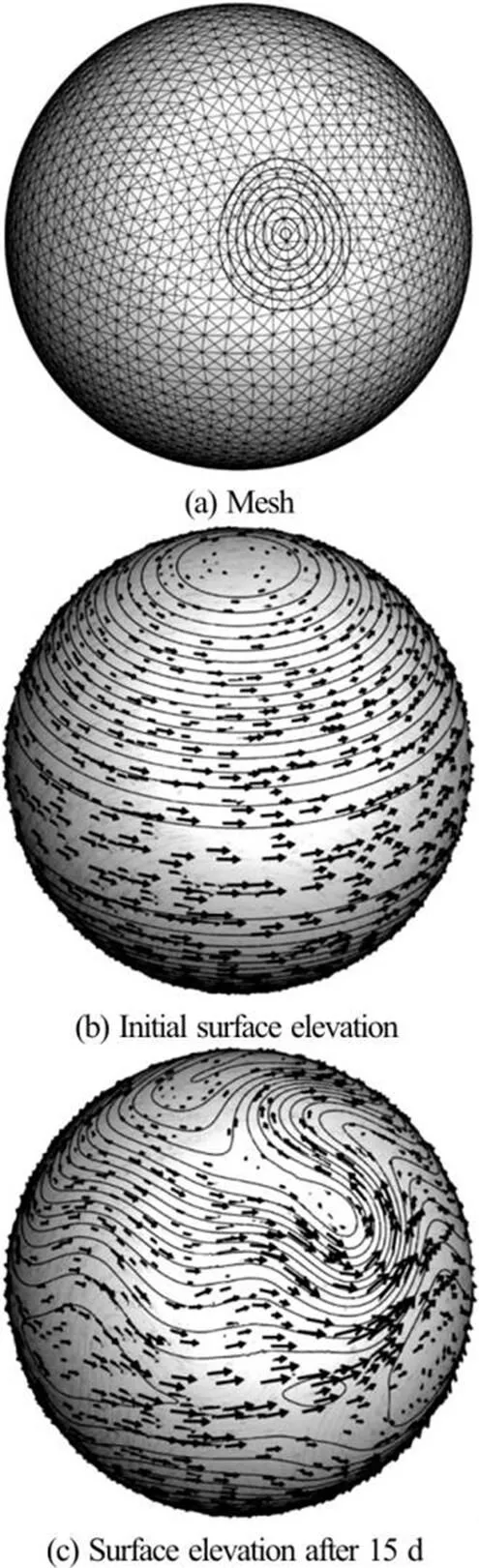
Fig. 20Spherical shallow water flow over an isolated moun- tain[126]

(3) The stabilisation techniques discussed in Section 1, such as SVV and projection-based filtering techniques, require further improvement through further calibration for marginal/under-resolved com- putations. As mentioned by Sagaut[37], “”. In terms of the similarity between artificial dissipation and the direct energy cascade model, some numerical stabilisation techniques can be used to perform “no-model” large eddy simulations (iLES). However, Sagaut stated that “[130]”. The proposed “DGKernel”, which emu- lates the upwind properties of a DG scheme, still requires more detailed calibration for a range of high-Reynolds fluid flows.

(4) Verification and Validation of spectral/element simulations for under-resolved computations: The use of stabilisation techniques, such as SVV, allows us to interpret the under-resolved numerical calculations as implicit large eddy simulation. How- ever, we need to continue to investigate how the stabilisation methods and numerical properties interact to ensure the benefits of high-precision are not destroyed through artificial/ numerical pollution.

In the context of hydrodynamics applications, there is substantial opportunity for gaining an impro- ved understanding of a wide range of physical mecha- nisms through the use of the spectral/element method. In particular:

(1) Tip vortex modelling: As indicated in Ref. [7], without the accurate modelling of the 3-D boundary layer, the developing vortex remained challenging to compute accurately, even for the advanced RANS models correcting for the high degree of curvature in the flow. In addition, accurately capturing the low- pressure region within the vortex core and sustaining this low pressure even just one chord length down- stream of the trailing edge is particularly challenging. As demonstrated[7], the SVV-based iLES method has been shown to be potential alternative for computing complex unsteady vortex dominated flows. Simulating vortical flows using the spectral/element method with the concept of the SVV-based iLES can be regarded as an interesting alternative method in hydrodynamics.

(2) Implicit large eddy simulation: A notable effort has been made to refinethe SVV-based strategy for implementing under-resolved simulations of high Reynolds fluid flows[38, 44]. This strategy has a great potential to provide high fidelity iLEScomputations for a broad range of applications in hydrodynamics.

(3) Fluid-structure interaction: As indicated in Refs. [131-135], spectral elements offer superior wave propagation capabilities, which has been used for simulations of fluid-structure interaction[133, 134, 136]. Interaction subject to surface waves can be attractive.

(4) Cavitating flow: Recently, discontinuous spectral/element method has been implemented for the efficient and accurate simulation of multiphase flows[137]. The compressible Navier-Stokes equations, coupled with a highly realistic equation of state, are solved by a DG spectral element method for flows with cavitation. In++, the DG method and the flux reconstruction approach have been used to solve the compressible Navier-Stokes equations. This therefore provides a basis to apply the spectral/element method in applications of cavitating flows.

(5) Free surface flows: As is well known free surface flows can be modelled as a depth average “shallow-water” approach or using ALE moving mesh techniques. Spectral/element method has been used to treat these two kinds of free surface flows[97, 138-141]. For the second free surface problem, discontinuous spectral/element methods hava great potential in applications[139-141, 143, 144], especially when/-adap- tivity is employed.

Acknowledgments

The authors kindly thank the Executive Editor- in-Chief Prof. Lian-di Zhou for the invitation to contribute this review article and Dr. Wei Zhang for his contribution to conducting the tip-vortex simula- tion. H.X. and S.J.S would like to acknowledge support under EPSRC (Grant No. EP/L000407/1).

This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.

[1] Babu?ka I., Suri M. The- and-versions of the finite element method, an overview [J]., 1990, 80(1): 5-26.

[2] Babu?ka I., Suri M. The p and h-p versions of the finite element method, basic principles and properties [J]., 1994, 36(4): 578-632.

[3] Karniadakis G., Sherwin S. Spectral/element methods for computational fluid dynamics [M]. Second Edition, New York, USA, Oxford University Press, 2005.

[4] Cantwell C. D., Moxey D., Comerford A. et al. Nektar++: An open-source spectral/hp element framework [J]., 2015, 192: 205-219.

[5] Yakovlev S., Moxey D., Kirby R. M. et al. To CG or to HDG: A comparative study in 3D [J]., 2016, 67(1): 192-220.

[6] King J., Yakovlev S., Fu Z. S. et al. Exploiting batch processing on streaming architectures to solve 2D elliptic finite element problems: A hybridized discontinuous Galerkin (HDG) case study [J]., 2014, 60(2): 457-482.

[7] Lombard J. E. W., Moxey D., Sherwin S. J. et al. Implicit large-eddy simulation of a wingtip vortex [J]., 2016, 54(2): 506-518.

[8] Serson D., Meneghini J. R., Sherwin S. J. Velocity-correc- tion schemes for the incompressible navier-stokes equa- tions in general coordinate systems [J]., 2016, 316: 243-254.

[9] Serson D., Meneghini J. R., Sherwin S. J. Direct numeri- cal simulations of the flow around wings with spanwise waviness at a very low Reynolds number [J]., 2017, 146: 117-124.

[10] Xu H., Lombard J.-E. W., Sherwin S. J. Influence of loca- lised smooth steps on the instability of a boundary layer [J]., 2017, 817: 138-170.

[11] Xu H., Mughal S. M., Gowree E. R. et al. Destabilisation and modification of Tollmien-Schlichting disturbances by a three-dimensional surface indentation [J]., 2017, 819: 592-620.

[12]Cantwell C. D., Yakovlev S., Kirby R. M. et al. High- order spectral/element discretisation for reaction- diffusion problems on surfaces: Application to cardiac electrophysiology [J]., 2017, 257: 813-829.

[13]Szabó B., Babuka I. Finite element analysis [M]. New York, USA: John Wiley and Sons, Inc., 1991.

[14]Moxey D., Ekelschot D., Keskin ü. et al. A thermo-elastic analogy for high-order curvilinear meshing with control of mesh validity and quality [C]., London, UK, 2014, 82: 127-135.

[15] Comerford A., Chooi K. Y., Nowak M. et al. A combined numerical and experimental framework for determining permeability properties of the arterial media [J]., 2015, 14(2): 297-313.

[16]Eskilsson C., Sherwin S. J. Spectral/discontinuous Galerkin methods for modelling 2D Boussinesq equations [J]., 2016, 212(2): 566-589.

[17]Duffy M. G. Quadrature over a pyramid or cube of integrands with a singularity at a vertex [J]., 1982, 19(6): 1260-1262.

[18]HesthavenJ. S., Warburton T. Nodal discontinuous Galerkin methods [M]. New York, USA: Springer-Verlag, 2008.

[19] Reed W. H., Hill T. R. Triangular mesh methods for the neutron transport equation [R]. Technical report, Los Alamos National Laboratory, 1973, lA-UR-73-479.

[20]Adams R. A. Sobolev spaces [M]. New York, USA: Aca- demic Press, 1975.

[21] Vermeire B., Witherden F., Vincent P. On the utility of GPU accelerated high-order methods for unsteady flow simulations: A comparison with industry-standard tools [J]., 2017, 334: 497-521.

[22]Gottlieb D., Orszag S. A. Numerical analysis of spectral methods: Theory and applications [M]. Philadelphia, USA: Society for Industrial and Applied Mathematics, 1977.

[23]Kirby R. M., Karniadakis G. E. De-aliasing on non-uni- form grids: Algorithms and applications [J]., 2003, 191(1): 249-264.

[24] Kirby R. M., Sherwin S. J. Aliasing errors due to quadratic nonlinearities on triangular spectral/element discretisa- tions [J]., 2006, 56(3): 273-288.

[25] Malm J., Schlatter P., Henningson D. S. Coherent struc- tures and dominant frequencies in a turbulent three- dimensional diffuser [J]., 2012, 699: 320-351.

[26] Mengaldo G., Grazia D. D., Moxey D. et al. Dealiasing techniques for high-order spectral element methods on regular and irregular grids [J]., 2015, 299: 56-81.

[27] Cockburn B., Hou S. C., Shu C. W. The Runge-Kutta local projection discontinuous Galerkin finite element method for conservation laws. IV. The multidimensional case [J]., 1990, 54(190): 545-581.

[28] Tadmor E. Convergence of spectral methods for nonlinear conservation laws [J]., 1989, 26(1): 30-44.

[29] Karamanos G. S., Karniadakis G. E. A spectral vanishing viscosity method for large-eddy simulations [J]., 2000, 163(1): 22-50.

[30]Kirby R. M., Sherwin S. J. Stabilisation of spectral/hp element methods through spectral vanishing viscosity: Application to fluid mechanics modelling [J]., 2006, 195(23): 3128-3144.

[31] Pasquetti R. Spectral vanishing viscosity method for LES: sensitivity to the SVV control parameters [J]., 2005, 6(12): 1-14.

[32] Pasquetti R. Spectral vanishing viscosity method for large- eddy simulation of turbulent flows [J],, 2006, 27(1): 365-375.

[33] Kirby R. M., Karniadakis G. E. Coarse resolution turbu- lence simulations with spectral vanishing viscosity-large- eddy simulations (SVV-LES) [J]., 2002, 124(4): 886-891.

[34] Xu C. Stabilization methods for spectral element computa- tions of incompressible flows [J]., 2006, 27(1): 495-505.

[35] Severac E., Serre E. A spectral vanishing viscosity for the LES of turbulent flows within rotating cavities [J]., 2007, 226(2): 1234-1255.

[36]Koal K., Stiller J., Blackburn H. Adapting the spectral vanishing viscosity method for large-eddy simulations in cylindrical configurations [J]., 2012, 231(8): 3389-3405.

[37] Sagaut P. Large eddy simulation for incompressible flows [M]. Berlin, Heidelberg, Germany: Springer-Verlag, 2001.

[38] Moura R. C., Sherwin S. J., Peiró J. Eigensolution analysis of spectral/continuous Galerkin approximations to advection-diffusion problems: Insights into spectral vani- shing viscosity [J]., 2016, 307: 401-422.

[39] Maday Y., Kaber S. M. O., Tadmor E. Legendre pseudo- spectral viscosity method for nonlinear conservation laws [J]., 1993, 30(2): 321-342.

[40] Collis S. Discontinuous Galerkin methods for turbulence simulation [C]., San Francisco, USA, 2002, 155-167.

[41] Collis S., Ghayour K. Discontinuous Galerkin methods for compressible DNS [C]., Honolulu, USA, 2003, 1777-1786.

[42] Wei L., Pollard A. Direct numerical simulation of com- pressible turbulent channel flows using the discontinuous Galerkin method [J]., 2011, 47(1): 85-100.

[43]Chapelier J. B., de la Llave Plata M., Renac F. et al. Evaluation of a high-order discontinuous Galerkin method for the DNS of turbulent flows [J]., 2014, 95(3): 210-226.

[44]Moura R. C., Sherwin S. J., Peiró J. Linear dispersion- diffusion analysis and its application to under-resolved turbulence simulations using discontinuous Galerkin spectral/methods [J]., 2015, 298: 695-710.

[45]Bolis A., Cantwell C. D., Moxey D. et al. An adaptable parallel algorithm for the direct numerical simulation of incompressible turbulent flows using a Fourier spectral/element method and MPI virtual topologies [J]., 2016, 206: 17-25.

[46] Vos P. E., Sherwin S. J., Kirby R. M. Fromtoeffi- ciently: Implementing finite and spectral/element methods to achieve optimal performance for low- and high-order discretisations [J]., 2010, 229(13): 5161-5181.

[47] Cantwell C. D., Sherwin S. J., Kirby R. M. et al. Fromtoefficiently: Strategy selection for operator evaluation on hexahedral and tetrahedral elements [J]., 2011, 43(1): 23-28.

[48] Cantwell C. D., Sherwin S. J., Kirby R. M. et al. Fromtoefficiently: Selecting the optimal spectral/discretisa- tion in three dimensions [J]., 2011, 6(3): 84-96.

[49] Bolis A., Cantwell C. D., Kirby R. M. et al. Fromtoefficiently: Optimal implementation strategies for explicit time-dependent problems using the spectral/element method [J]., 2014, 75(8): 591-607.

[50] Moxey D., Cantwell C. D., Kirby R. M. et al. Optimising the performance of the spectral/element method with collective linear algebra operations [J]., 2016, 310: 628-645.

[51] Moxey D., Green M. D., Sherwin S. J. et al. An isopara- metric approach to high-order curvilinear boundary-layer meshing [J]., 2015, 283: 636-650.

[52]Sherwin S. J., Peiró J. Mesh generation in curvilinear domains using high-order elements [J]., 2002, 53(1): 207-223.

[53]Turner M., Peiró J., Moxey D. A variational framework for high-order mesh generation [C]., Washington DC, USA, 2016, 163: 340-352.

[54]MoxeyD., EkelschotD., Keskinü.et al. High-order curvi- linear meshing using a thermo-elastic analogy [C]., London, UK, 2016, 72: 130-139.

[55]Wang Z., Fidkowski K., Abgrall R. et al. High-order CFD methods: Current status and perspective [J]., 2013, 72(8): 811-845.

[56]Dey S., O’Bara R. M., Shephard M. S. Curvilinear mesh generation in 3D [C]., Lake Tahoe, California, USA, 1999.

[57]Geuzaine C., Remacle J. F. Gmsh: A 3-D finite element mesh generator with built-in pre- and post-processing facilities [J]., 2009, 79(11): 1309-1331.

[58]Karniadakis G. E., Israeli M., Orszag S. A. High-order splitting methods for the incompressible Navier-Stokes equations [J]., 1991, 97(2): 414-443.

[59]Vos P. E., Eskilsson C., Bolis A. et al. A generic frame- work for time-stepping partial differential equations (PDEs): General linear methods, object-oriented imple- mentation and application to fluid problems [J]., 2011, 25(3): 107-125.

[60]Fischer P. F., R?nquist E. M. Spectral element methods for large scale parallel Navier-Stokes calculations [J]., 1994, 116(1): 69-76.

[61]Sherwin S. J., Karniadakis G. E. A triangular spectral element method, applications to the incompressible Navier-Stokes equations [J]., 1995, 123(1): 189-229.

[62]Sherwin S. J., Karniadakis G. E. Tetrahedralfinite elements: Algorithms and flow simulations [J]., 1996, 124(1): 14-45.

[63] Fischer P. F. An overlapping Schwarz method for spectral element solution of the incompressible Navier-Stokes equations [J]., 1997, 133(1): 84-101.

[64] Tomboulides A. G., Orszag S. A. Numerical investigation of transitional and weak turbulent flow past a sphere [J]., 2000, 416: 45-73.

[65] Fischer P., Mullen J. Filter-based stabilization of spectral element methods [J]., 2001, 332(3): 265-270.

[66] Wasberg C. E., Gjesdal T., Reif B. A. P. et al. Variational multiscale turbulence modelling in a high order spectral element method [J]., 2009, 228(19): 7333-7356.

[67] Blackburn H., Schmidt S. Spectral element filtering tech- niques for large eddy simulation with dynamic estimation [J]., 2003, 186(2): 610-629.

[68] Iliescu T., Fischer P. F. Large eddy simulation of turbulent channel flows by the rational large eddy simulation model [J]., 2003, 15(10): 3036-3047.

[69] Ohlsson J., Schlatter P., Fischer P. F. et al. Stabilization of the spectral-element method in turbulent flow simulations [M]. Berlin Heidelberg, Germany: Springer-Verlag, 2011, 449-458.

[70] Beck A. D., Bolemann T., Flad D. et al. High-order dis- continuous Galerkin spectral element methods for transitional and turbulent flow simulations [J]., 2014, 76(8): 522-548.

[71] Blackburn H. M., Sherwin S. J. Formulation of a Galerkin spectral element-Fourier method for three-dimensional incompressible flows in cylindrical geometries [J]., 2004, 197(2): 759-778.

[72] Patera A. T. A spectral element method for fluid dynamics: Laminar flow in a channel expansion [J]., 1984, 54(3): 468-488.

[73]Vinuesa R., Schlatter P., Malm J. et al. Direct numerical simulation of the flow around a wall-mounted square cylinder under various inflow conditions [J]., 2015, 16(6): 555-587.

[74] Diosady L. T., Murman S. M. DNS of flows over periodic hills using a discontinuous Galerkin spectral-element method [C]., Atlanta, GA, USA, 2014.

[75]Xu H., Sherwin S. J., Hall P. et al. The behaviour of Tollmien-Schlichting waves undergoing small-scale loca- lised distortions [J]., 2016, 792: 499-525.

[76] Serson D., Meneghini J. R., Sherwin S. J. Direct numerical simulations of the flow around wings with spanwise waviness [J]., 2017, 826: 714-731.

[77] Barkley D., Blackburn H. M., Sherwin S. J. Direct optimal growth analysis for timesteppers [J]., 2008, 57(9): 1435-1458.

[78] Blackburn H., Barkley D., Sherwin S. J. Convective insta- bility and transient growth in flow over a backward-facing step [J]., 2008, 603: 271-304.

[79] Blackburn H., Sherwin S. J., Barkley D. Convective insta- bility and transient growth in steady and pulsatile stenotic flows [J]., 2008, 607: 267-277.

[80]Cantwell C. D., Barkley D., Blackburn H. M. Transient growth analysis of flow through a sudden expansion in a circular pipe [J]., 2010, 22(3): 034101.

[81] Cantwell C. D., Barkley D. Computational study of subcri- tical response in flow past a circular cylinder [J]., 2010, 82(2): 026315.

[82]Broadhurst M. S., Theofilis V., Sherwin S. J. Spectral element stability analysis of vortical flows [C]., Bangalore, India, 2006, 153-158.

[83] Rocco G. Advanced instability methods using spectral/discretisations and their applications to complex geome- tries [D]. Doctoral Thesis, London, UK: Imperial College London, 2014.

[84] Jordi B. Steady-state solvers for stability analysis of vortex dominated flows [D]. Doctoral Thesis, London, UK: Imperial College London (2015).

[85] Devenport W. J., Rife M. C., Liapis S. I. et al. The struc- ture and development of a wing-tip vortex [J]., 1996, 312: 67-106.

[86] Arndt R. E. Cavitation in vortical flows [J]., 2002, 34(1): 143-175.

[87]Ford C. W. P., Babinsky H. Lift and the leading-edge vortex [J]., 2013, 720: 280-313.

[88] Leweke T., Dizès S. L., Williamson C. H. Dynamics and instabilities of vortex pairs [J]., 2016, 48(1): 507-541.

[89] Feys J., Maslowe S. A. Elliptical instability of the moore- saffman model for a trailing wingtip vortex [J]., 2016, 803: 556-590.

[90] Moura R. C., Mengaldo G., Peiró J. et al. On the eddy- resolving capability of high-order discontinuous galerkin approaches to implicit LES / under-resolved DNS of Euler turbulence [J]., 2017, 330: 615-623.

[91] Eskilsson C., Engsig-Karup A. P., Sherwin S. J. et al. The next step in coastal numerical models: spectral/hp element methods? [C]., Madrid, Spain, 2005.

[92] Brocchini M., A reasoned overview on Boussinesq-type models: The interplay between physics, mathematics and numerics [J]., 2013, 469(2160): 1-27.

[93] Wu G. X., Taylor R. E. Finite element analysis of two- dimensional non-linear transient water waves [J]., 1994, 16(6): 363-372.

[94] Cai X., Langtangen H. P., Nielsen B. F. et al. A finite element method for fully nonlinear water waves [J]., 1998, 143(2): 544-568.

[95] Ma Q. W.,Wu G. X., Taylor R. E. Finite element simu- lation of fully non-linear interaction between vertical cylinders and steep waves. Part 1: Methodology and numerical procedure [J]., 2001, 36(3): 265-285.

[96] Ma Q. W., Yan S. Quasi ALE finite element method for nonlinear water waves [J]., 2006, 212(1): 52 -72.

[97] Robertson I., Sherwin S. J. Free-surface flow simulation using/spectral elements [J]., 1999, 155(1): 26-53.

[98]Engsig-Karup A. P., Eskilsson C., Bigoni D. A stabilised nodal spectral element method for fully nonlinear water waves [J]., 2016, 318(2): 1-21.

[99] Engsig-Karup A. P., Eskilsson C., Bigoni D. Unstructured spectral element model for dispersive and nonlinear wave propagation [C]., Rhodes, Greece, 2016, 3: 661-669.

[100]Zakharov V. E. Stability of periodic waves of finite am- plitude on the surface of a deep fluid [J]., 1968, 9(2): 190-194.

[101]Mieritz A., Engsig-Karup A., Eskilsson C. et al. Large- scale water wave simulations using a spectral/element fully nonlinear potential flow model [J]. (in preparation).

[102]Engsig-Karup A. P., Eskilsson C., Bigoni D. A stabilised nodal spectral element method for fully nonlinear water waves [J]., 2016, 318(2): 1-21.

[103]Eskilsson C., Sherwin S. J. A discontinuous spectral element model for Boussinesq-type equations [J]., 2002, 17(1-4): 143-152.

[104]EskilssonC.,SherwinS. J.Discontinuous Galerkin spectral/hp element modelling of dispersive shallow water systems [J]., 2005, 22-23(1): 269-288.

[105]Kreiss H. O., Oliger J. Comparison of accurate methods for the integration of hyperbolic equations [J]., 1972, 24: 199-215.

[106]Eskilsson C., Sherwin S. J., Bergdahl L. An unstructured spectral/hp element model for enhanced Boussinesq-type equations [J]., 2006, 53(11): 947-963.

[107]Dumbser M., Facchini M. A space-time discontinuous Galerkin method for Boussinesq-type equations [J]., 2016, 272: 336-346.

[108]Engsig-Karup A. P. Unstructured nodal DG-FEM solu- tion of high-order Boussinesq-type equations [D]. Doctoral Thesis, Copenhagen, Denmark: Technical University of Denmark, 2006.

[109]Engsig-Karup A. P., Hesthaven J. S., Bingham H. B. et al. Nodal DG-FEM solutions of high-order Boussinesq-type equations [J]., 2006, 56(3): 351-370.

[110]Engsig-Karup A. P., Hesthaven J. S., Bingham H. B. et al. DG-FEM solution for nonlinear wave-structure interaction using Boussinesq-type equations [J]., 2008, 55(3): 197-208.

[111]Panda N., Dawson C., Zhang Y. et al. Discontinuous Galerkin methods for solving Boussinesq-Green-Naghdi equations in resolving non-linear and dispersive surface water waves [J]., 2014, 273: 572-588.

[112]Duran A., Marche F. Discontinuous-Galerkin discretiza- tion of a new class of Green-Naghdi equations [J]., 2015, 17(3): 721-760.

[113]Samii A., Dawson C. An explicit hybridized disconti- nuous Galerkin method for Serre-Green-Naghdi wave model [J]., 2018, 330: 447-470.

[114]Peregrine D. Long waves on a beach [J]., 1976, 27: 815-827.

[115]Eskilsson C., Sherwin S. J. Spectral/discontinuous Galerkin methods for modelling 2D Boussinesq equations [J]., 2006, 212(2): 566-589.

[116]BlaiseS., St-CyrA. A dynamic hp-adaptive discontinuous Galerkin method for shallow-water flows on the sphere with application to a global tsunami simulation [J]., 2012, 140(3): 978-996.

[117]Blaise S., St-Cyr A., Mavriplis D. et al. Discontinuous Galerkin unsteady discrete adjoint method for real-time efficient tsunami simulations [J]., 2013, 232(1): 416-430.

[118]Bonev B., Hesthaven J., Giraldo F. et al. Discontinuous Galerkin scheme for the spherical shallow water equations with applications to tsunami modelling and prediction [J]. Submitted to:, 2017.

[119]Ma H. A spectral element basin model for the shallow water equations [J]., 1993, 109(1): 133-149.

[120]Iskandarani M., Haidvogel D., Boyd J. A staggered spec- tral element model with application to the oceanic shallow water equations [J]., 1995, 20(5): 393-414.

[121]Taylor M., Tribbia J., Iskandarani M. The spectral element method for the shallow water equations on the sphere [J]., 1997, 130(1): 92-108.

[122]Giraldo F. X., Hesthaven J. S., Warburton T. Nodal high-order discontinuous Galerkin methods for the sphe- rical shallow water equations [J]., 2002, 181(2): 499-525.

[123]Nair R., Thomas S., Loft R. A discontinuous Galerkin global shallow water model [J]., 2005, 133(4): 876-888.

[124]Lauter M., Giraldo F., Handorf D. et al. A discontinuous Galerkin method for the shallow water equations in spherical triangular coordinates [J]., 2008, 227(24): 10226-10242.

[125]Bao L., Nair R., Tufo H. A mass and momentum flux- form high-order discontinuous Galerkin shallow water model on the cubed-sphere [J]., 2014, 271: 224-243.

[126]Chun S., Eskilsson C. Method of moving frames to solve the shallow water equations on arbitrary rotating curved surfaces [J]., 2017, 333: 1-23

[127]Chun S. Method of moving frames to solve conservation laws on curved surfaces [J]., 2012, 53(2): 268-294.

[128]Moxey D., Cantwell C. D., Mengaldo G. et al. Towards p-adaptive spectral/hp element methods for modelling industrial flows [C]., Rio de Janeiro, Brazil, 2016.

[129]Ekelschot D., Moxey D., Sherwin S. J. et al. A p-adapta- tion method for compressible flow problems using a goal-based error indicator [J]., 2017, 181: 55-69.

[130]Tafti D. Comparison of some upwind-biased high-order formulations with a second-order central-difference sche- me for time integration of the incompressible Navier- Stokes equations [J]., 1996, 25(7): 647-665.

[131]Priolo E., Carcione J. M., Seriani G. Numerical simula- tion of interface waves by high-order spectral modelling techniques [J]., 1994, 95(2): 681-693.

[132]Sprague M. A., Geers T. L. A spectral-element method for modelling cavitation in transient fluid-structure inter- action [J]., 2004, 60(15): 2467-2499.

[133]Bodard N., Deville M. O. Fluid-structure interaction by the spectral element method [J]., 2006, 27(1): 123-136.

[134]Sprague M. A., Geers T. L. A spectral-element/finite- element analysis of a ship-like structure subjected to an underwater explosion [J]., 2006, 195(17): 2149-2167.

[135]Sprague M. A., Geers T. L. Spectral elements and field separation for an acoustic fluid subject to cavitation [J]., 2003, 184(1): 149-162.

[136]Van Loon R., Anderson P. D., Van de Vosse F. N. et al. Comparison of various fluid-structure interaction methods for deformable bodies [J]., 2007, 85(11): 833-843.

[137]Hoffmann M., Boblest S., Offenh?user P. et al. A robust high-order discontinuous Galerkin solver for fluid flow with cavitation [C]., Istanbul, Turkey, 2016.

[138]Lee-Wing H., Patera A. T. A legendre spectral element method for simulation of unsteady incompressible viscous free-surface flows [J]., 1990, 80(1): 355-366.

[139]Sussman M., Hussaini M. Y. A discontinuous spectral element method for the level set equation [J]., 2003, 19(1): 479-500.

[140]Lin C. L., Lee H., Lee T. et al. A level set characteristic Galerkin finite element method for free surface flows [J]., 2005, 49(5): 521-547.

[141]Bouffanais R., Deville M. O. Mesh update techniques for free-surface flow solvers using spectral element method [J]., 2006, 27(1): 137-149.

[142]Grooss J., Hesthaven J. A level set discontinuous Galerkin method for free surface flows [J]., 2006, 195(25): 3406-3429.

[143]Marchandise E., Remacle J. F. A stabilized finite element method using a discontinuous level set approach for solving two phase incompressible flows [J]., 2006, 219(2): 780-800.

[144]Nguyen V. T., Peraire J., Khoo B. C. et al. A disconti- nuous Galerkin front tracking method for two-phase flows with surface tension [J]., 2010, 39(1): 1-14.

Hui Xu (1981-), Male, Ph. D.

(December 22, 2017, Accepted December 28, 2017)

? The Authors [2018] This article is published with open access at link.springer.com

Hui Xu,

E-mail:hui.xu@imperial.ac.uk