Highly accurate symplectic element based on two variational principles

Guanghui Qing·Jia Tian

1 Introduction

Classical mixed methods for various physical problems indicate a wide range of possibilities,many with potentially higher accuracy and robustness than those offered by displacement methods or hybrid stress methods.The behaviour of classical mixed methods can frequently reveal weaknesses or lack of robustness in displacement methods which other wise would be difficult to determine.The mixed approximation,if properly understood,expands the potential of the finite element method and presents almost limitless possibilities of detailed improvement.We refer readers to Refs.[1–3]for surveys on the detailed analyses of the classical mixed methods.

It should mentioned that the discretization of linear elliptic boundary value problems by classical mixed methods typically leads to indefinite linear systems.Thus,some of the solutions or the stable mixed schemes are unavoidable.Consequently,the theoretical process of the classical mixed methods is relatively complex.In other words,the mathematical theory of the classical mixed methods is more involved(and more interesting)than for displacement methods,and the design of stable and effective mixed methods requires more expertise than for displacement methods used widely[3].

In general,we are accustomed to develop a finite element method by one of various variational principles except domain decomposition methods.However,without any nonconventional stable mixed schemes,compatible and noncompatible generalized mixed elements[1]with eight nodes for 3-D linear elasticity problems were derived by combining the minimum potential energy principle and the Hellinger-Reissner(H-R)mixed variational principle.Of course,based on the generalized H-R mixed variational principle alone,different noncompatible generalized mixed elements[4]can also be directionally constructed.Such as Refs.[1,4]indicate that the development of generalized mixed elements is simple and straightforward.One of the most prominent advantages of generalized mixed methods is that the coefficient matrix of a linear system of equations is not only symmetric,but also invertible(i.e.,there are no zeros on the diagonal).Thus,the stability of a linear system is guaranteed.On the other hand,the generalized mixed methods are also preferable for the introduction of displacement and tractions boundary conditions simultaneously.The convergence rate of both stress and displacement variables of noncompatible generalized mixed method can be close to the exact solutions.Such generalized mixed methods can be easily extended for various linear elasticity problems.

In modern numerical analysis,the development of numerical schemes that incorporate additional structure enjoyed by the problem being an approximation has become quite popular.The classical instances of such schemes are the symplectic integrators arising in Hamiltonian mechanics and the related energy conserving methods since the Legendre transform gives rise to a natural class of Hamiltonian systems on the cotangent bundle of the configuration space.Compared with other nonsymplectic schemes,the symplectic algorithm[5,6]and multi symplectic algorithm[7,8]are very powerful and successful for the finite and infinite dimensional Hamiltonian systems,respectively.

In the last more than 20 years,some symplectic finite element methods were developed.For example,semi-analytical partial mixed solutions[9–15].It should be mentioned first that when the governing equations for 2-D or 3-D problems in the state space form being deduced from the constitutive relations and equilibrium equations in linear elasticity,they are oftentimes called the state-vector equations(SVEs).While,if the governing equations are being derived directly from a modified H-R mixed variational principle,they are called as the Hamilton canonical equations(HCEs).SVEs or HCEs for 3-D problems allow introducing the out-plane stresses as primary unknowns owing to a Legendre transformation.Thus,both analytical[16–27]and semi-analytical partial mixed solutions[9–15]of Hamilton HCEs or SVEs fall naturally into the methodologies of a sympectic system.

Semi-analytical partial-mixed solutions have been proposed first for the analysis of elastic composite structures since the early nineties.They differ by the numerical approximation along the laminate thickness direction or plane and the evaluation method of state matrix exponential.Hence,an in-plane partial mixed approximation and a power series expansion were used,while a mixed finite element and precise time(substituted by the thickness)step integration method were retained.However,the matrix exponent eAz(Ais a coefficient matrix of an ordinary differential equation and variablezrefers to the thickness)requires large computational efforts and is time consuming.Such a solution cannot be suitable for large-scale finite element problems.

There are some disadvantages in the conventional displacement finite element methods for solving the fracture problem.Hence,many variants of the finite element method(FEM)for evaluating the stress intensity factors(SIFs)have been developed.Such as hybrid singular element[28],extended finite element method[29],classical mixed method combining enriched element[30],recent finite element discretized symplectic method(FEDSM)[31],and so on.FEDSM has three advantages.First,the number of unknown variables is reduced to a very low level.Second,no special finite elements and post-processing are needed to determine SIFs,and the exact solutions in the near fields are obtained at the same time.Third,as the analytical solution is embodied in the transformation,the accuracy of the predicted SIFs and their derivatives is high[31].

Much of the existing literature shows that if a physical problem is designed to conserve symplectic structure,the corresponding symplectic integratorcan conserve the energy quite well.On the other hand,if the coefficient matrix of displacement element formulations based on various varitional principles is symmetric,the symlectic structure of an element can be deduced[32].This is a key feature that the finite element method conserve the energy on nodes and has high reliability.As a general property,the symplectic integrator or numerical algorithms in terms of the symplectic structure can effectively improve the accuracy of numerical results[19,32–34].

According to the seminal idea constructing generalized mixed elements,the objective of this work is to develop as imple and straightforward noncompatible symplectic element.We hope such an element is suitable for various complex 3-D linear elasticity problems and it can improve the quality of solutions.

2 Basic theory

2.1 Known variational principles for linear elasticity

Considera solid continuumVwith boundaryS.S=Su∪Sσ,whereSuandSσare the segments ofSwhere displacements and surface tractions are prescribed,respectively.Let?be the gradient operator in the undeformed body which,under the assumption of infinitesimal deformation,is indistinguishable from the deformed body.

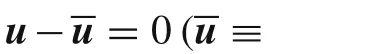
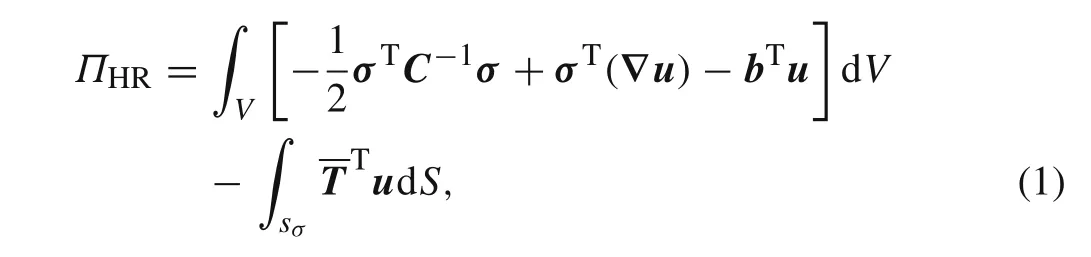
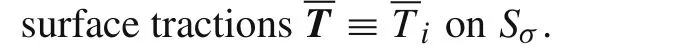
It is well known that,using the constitutive relations,the H-R mixed variational principle reduces to the minimum potential energy principle

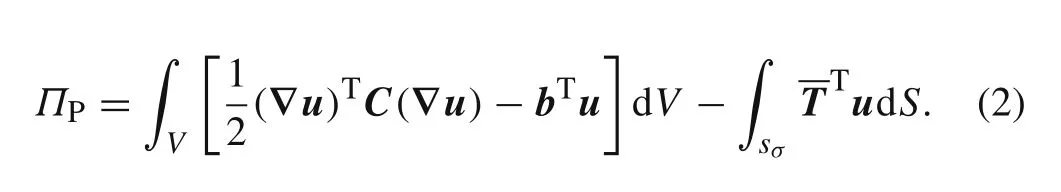
In the following,suppose that the out-plane stress vector is

and the in-plane stress vector is

Based on Refs.[17,34],the modified H-R mixed variational principle can be stated as

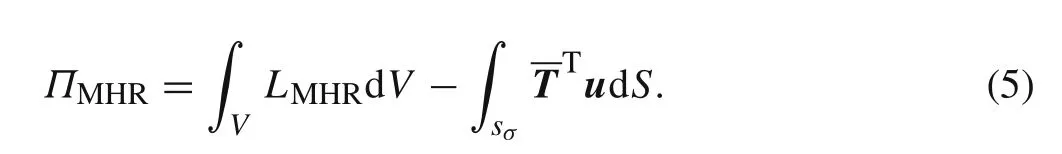
The modified energy densityLMHRin Eq.(9)is given by

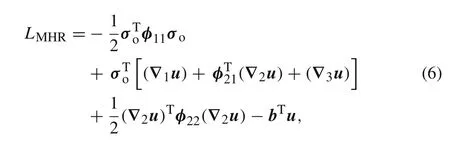
where,φ11,φ21,andφ22are submatrices of a material stiffness coefficients:

?1,?2,and?3refer to differential operator matrices

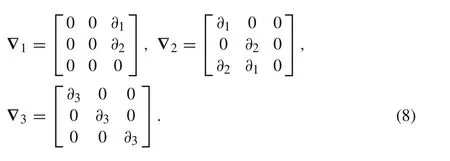
The in-plane stress vectorσican be expressed by both out-plane stress vectorσoand displacement vectoru.

2.2 Partial-mixed elements

2.2.1 Shape functions of displacement and out-plane stress

For an 8-node noncompatible element[35,36]weak discontinuity,the displacement field can be expressed as a sum of the compatible partN qeand the noncompatible partNrre.

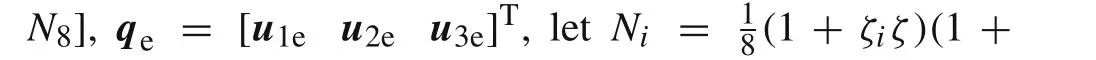
Nrin Eq.(10)may be stated in the following matrix form[36]

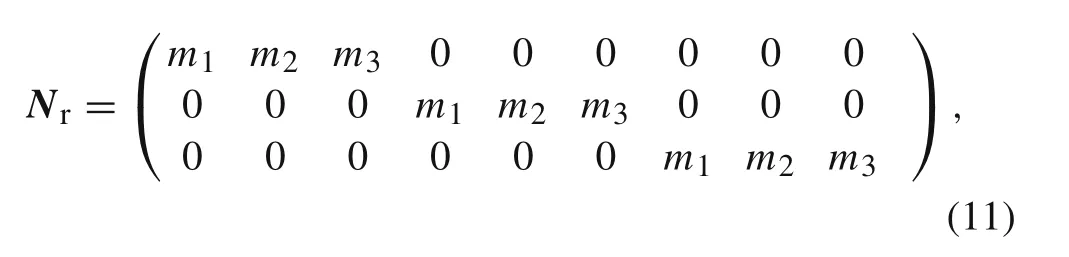
The same shape functions matrixNis also employed to express the out-plane stress vectorσoin this work.

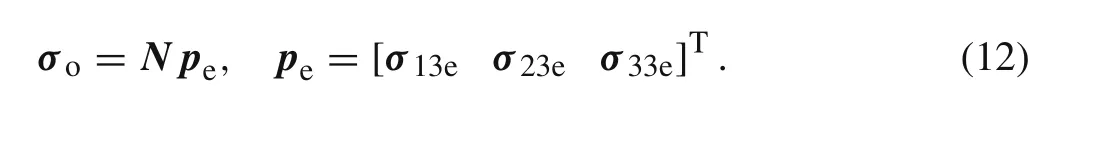
2.2.2 Compatible partial-mixed element

Introducing Eqs.(12)and(10)without the noncompatible partNrreinto Eq.(5),yields the following partial-mixed element

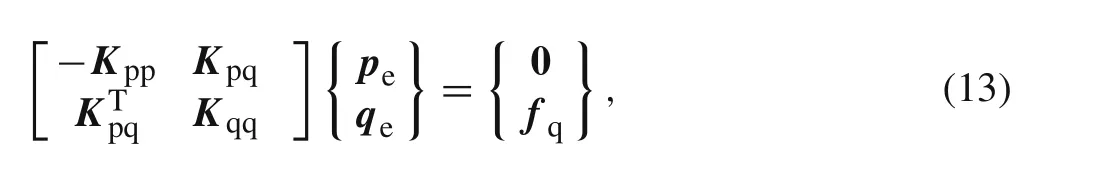
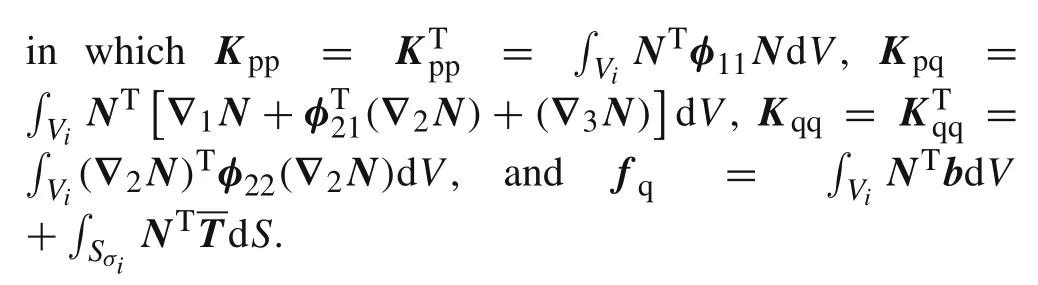
In Eq.(13),Kppis asymmetric and positive definite matrix andKqqpossesses zeros on the diagonal since?2is a differential operator matrix with rank deficiency.Hence,the above partial-mixed element is subject to possible instabilities.Such a feature is the same as the classical mixed elements without employing the nonconventional stable mixed scheme[1–3].

Therefore,if the out-plane stresses and displacements share the same finite space or any stable mixed element schemes used in classical mixed methods are not employed,we cannot obtain a stable generalized partial mixed element in a compatible displacement mode.

Substituting Eqs.(12)and(10)into Eq.(5),yields

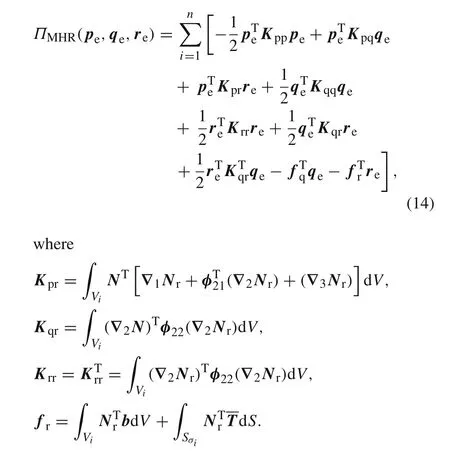
We have observed that it is impossible to condense the vectorrein Eq.(14)by a certain Euler–Lagrange(EL)equation ofδΠMHR(pe,qe,re)=0 sinceKrrhere is not a matrix sufficient rank and,of course,it is not invertible.

Asisknown to all,on substitution ofEq.(10)into the minimum potential energy principle in Eq.(2),the finite element functional∏P(qe,re)can be written as follows

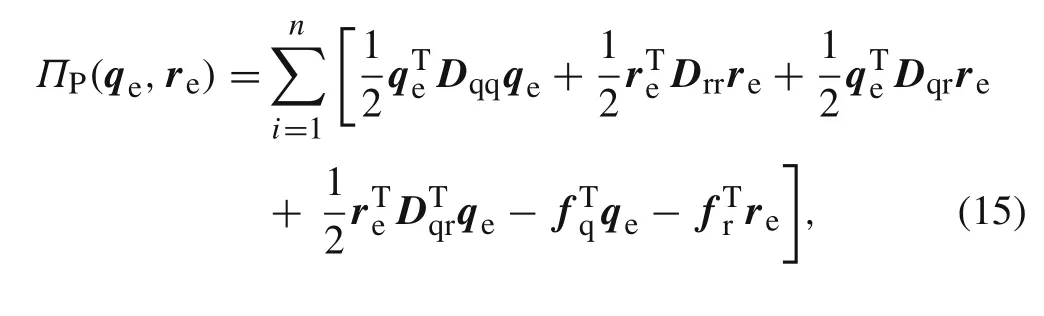
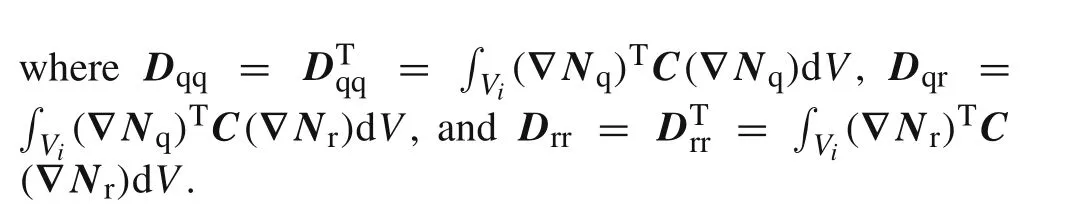
Fromδ∏P(re)=0,the following expression can be obtained

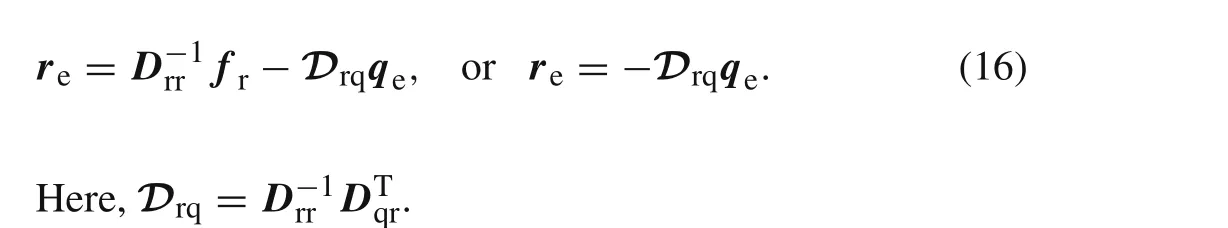
Notethat,ifno body force,fTrrein Eq.(16)can beomitted[35–37].

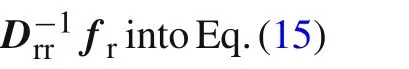
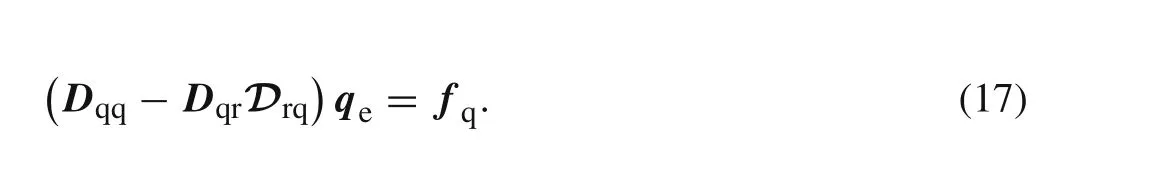
We have pointed out above that the termfTrrecan be neglected in the noncompatible displacement methods.For the same reason,fTrrein Eq.(15)is also neglected.

It is of interest to be observed that we can eliminate the vectorrein Eq.(14)by Eq.(16).Thus,the new functionalΠMHR(pe,qe)has the form

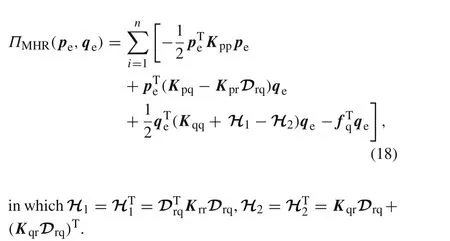
Finding the extremum values of the above equation with respect topeandqe,the following noncompatible partial mixed element with eight nodes can be obtained

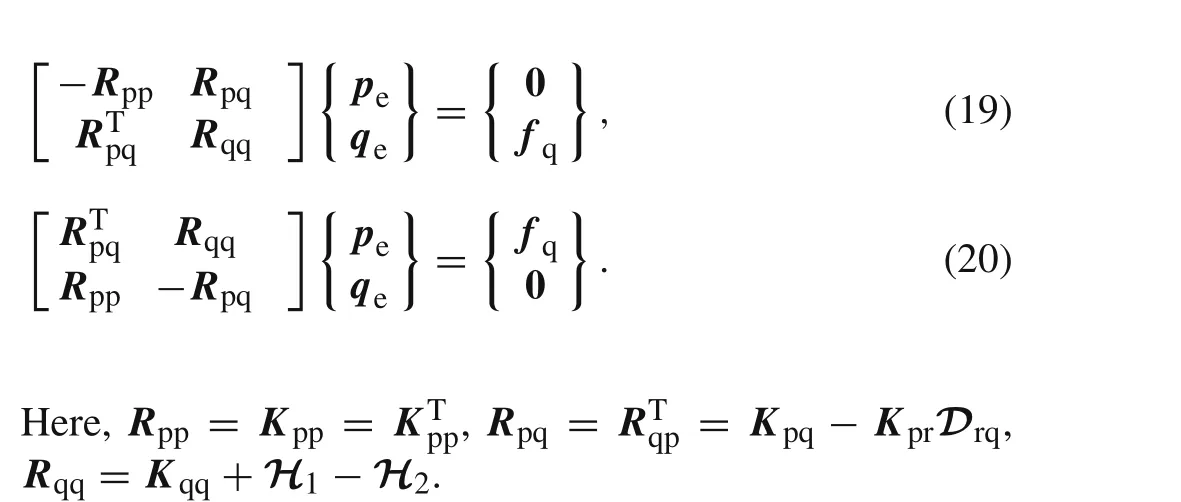
Generally,the submatrixRqqin the above equation is symmetric and there does not exit zeros on the leading diagonal.

2.3 Symplectic structure of partial-mixed element

In what follows,Hrefers to the coefficient matrix of Eq.(20)

In order to prove the symplectic feature of Eq.(21),the identity symplectic matrixJis introduced first

Suppose that the dimensions ofHis 2m×2m,I mis anm×midentity matrix.Herem=24.Based on the symmetric definition of the matrix in symplectic algebra,the following two expressions are obvious

Equation(23a)or(23b)shows thatHhas the symplectic structure,so Eq.(20)can be called as thesymplectic element.

As mentioned in Sect.1,thesymplectic structurewill play a very important role in the finite element analysis(i.e.,it implies the numerical results of finite element analysis are highly stable and reliable[19,32–34]).

3 Symplectic finite element model and solutions

3.1 Symplectic finite element model

The finite element models corresponding to Eqs.(19)and(20)can be written as follows,respectively,

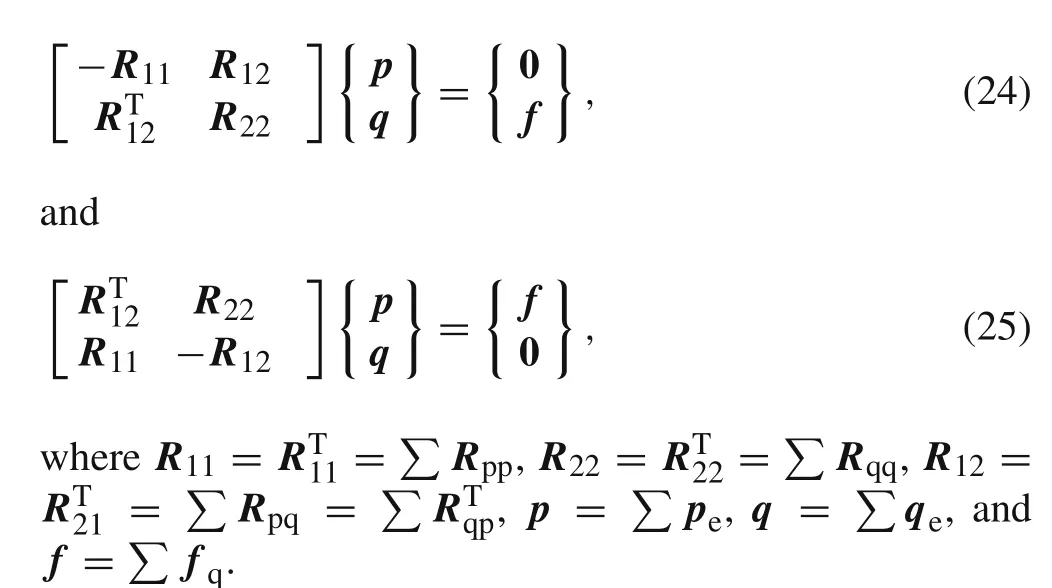
In general,on the system level the coefficient matrix has a structure equivalent to that of an element.Hence,Eq.(24)or(25)can be termed thesymplectic finite element modelin noncompatible displacement mode.

3.2 Solution for displacements and out-plane stresses

Exchanging rows and columns of Eq.(25),and then it can be rewritten as the following form

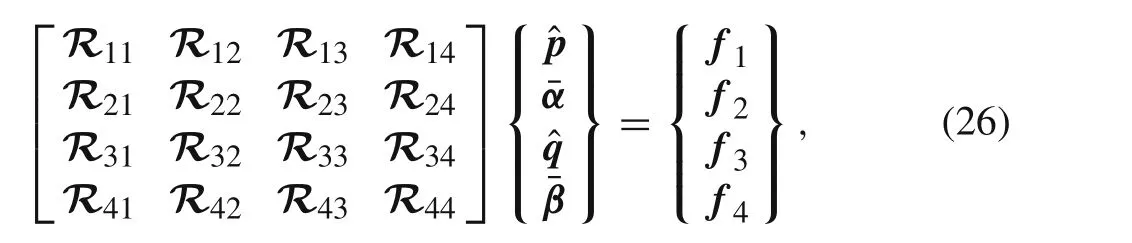
Therefore,

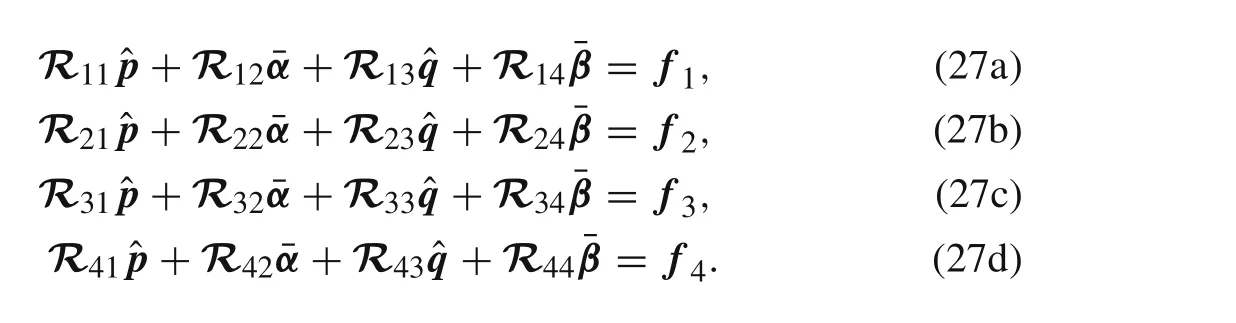
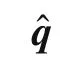
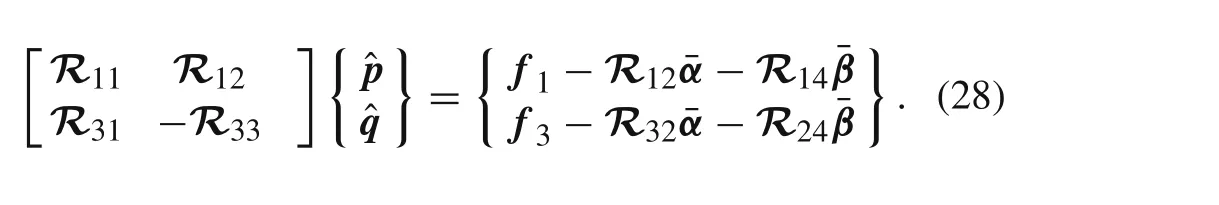
3.3 Simultaneous equations approach for in-plane stresses

The following simultaneous equation approach for the in plane stresses can avoid the discontinuity of in-plane stresses at a node connecting neighbouring elements,and it can also ensure the accuracy of in-plane stress results.

Substituting Eqs.(10)and(12)together with Eq.(16)into Eq.(9),the in-plane stress vector of an element

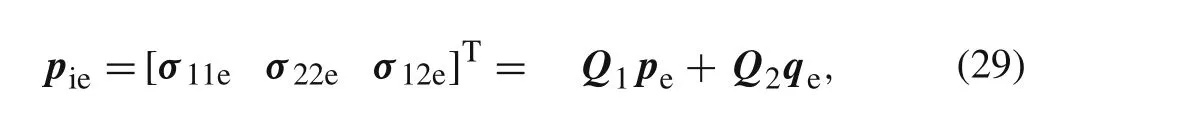
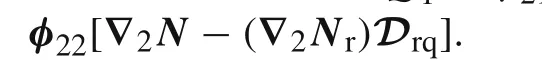
Assembling Eq.(29)for all elements(i.e.,the standard finite element assemblage process is employed here),yields a set of simultaneous equations,which is similar to the linear system of equations for finite element analysis

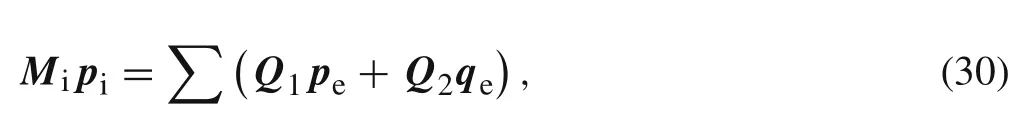
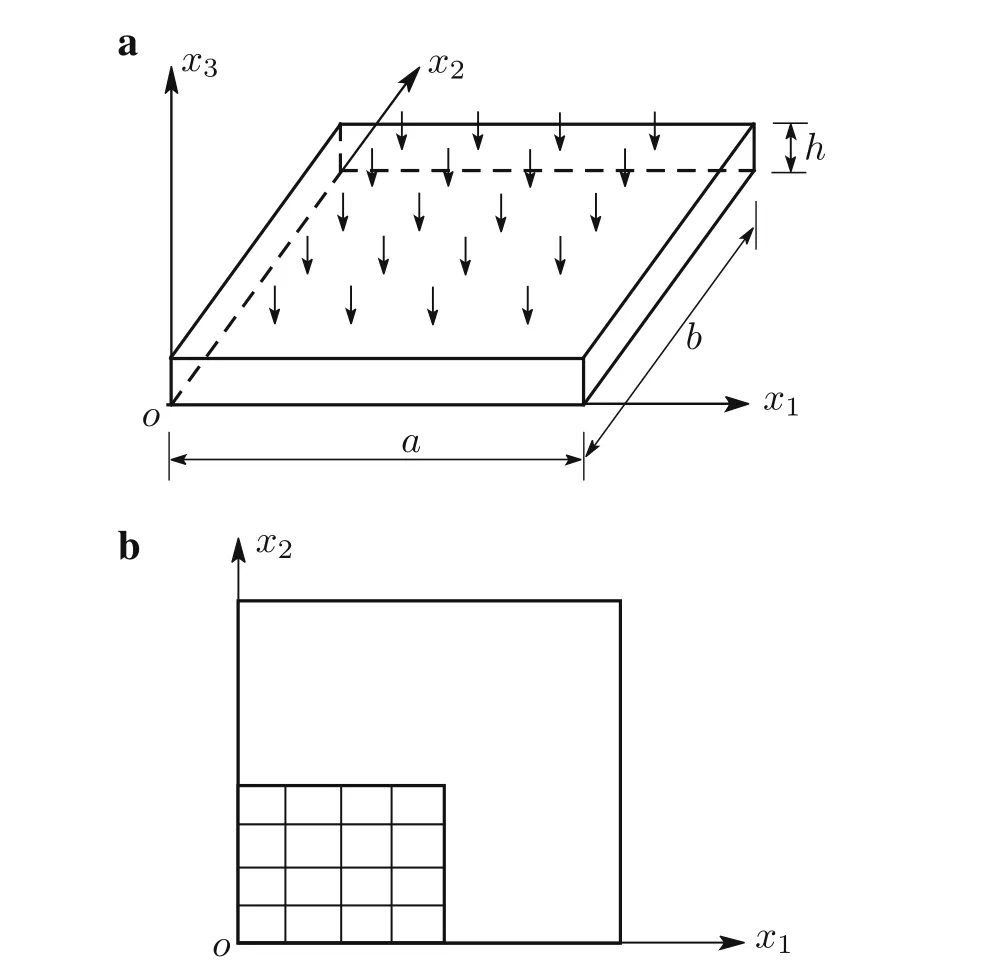
Fig.1 Coordinates and dimensions

4 Numerical examples and analysis

4.1 A thick rectangular plate with simply supported edges

Consider a thick rectangular plate with in-plane dimensions(as shown in Fig.1a)a=b=1.0 and thicknessh=0.10.Compressiblematerial properties:E=210,ν=0.3.Nearly incompressible material properties:E=240,ν=0.49995.Boundary conditions:σ11=u2=u3=0 onx1=0,x1=a;σ22=u1=u3=0 onx2=0,x2=b.The uniform normal load 1.0 is on the upper surface of plate.

Using the symmetry about thex1andx2-axes,only one quarter of the plate(Fig.1b)is analyzed with uniformmeshes.The notationl×m×nmesh denoteslsubdivisions along thex1-axis andmsubdivisions along thex2-axis with the same type of elements,whilendenotes the element number in thex3direction.

The convergence rate and accuracy of displacements and stresses at specific locations are depicted in Figs.2–13.Table 1 gives the map of numbers of horizontal axis and mesh models,8 subdivisions in thex3direction for all models.

On the basis of the results of 14×14×8 mesh,the percentage errors which are illustrated in the legends of Figs.

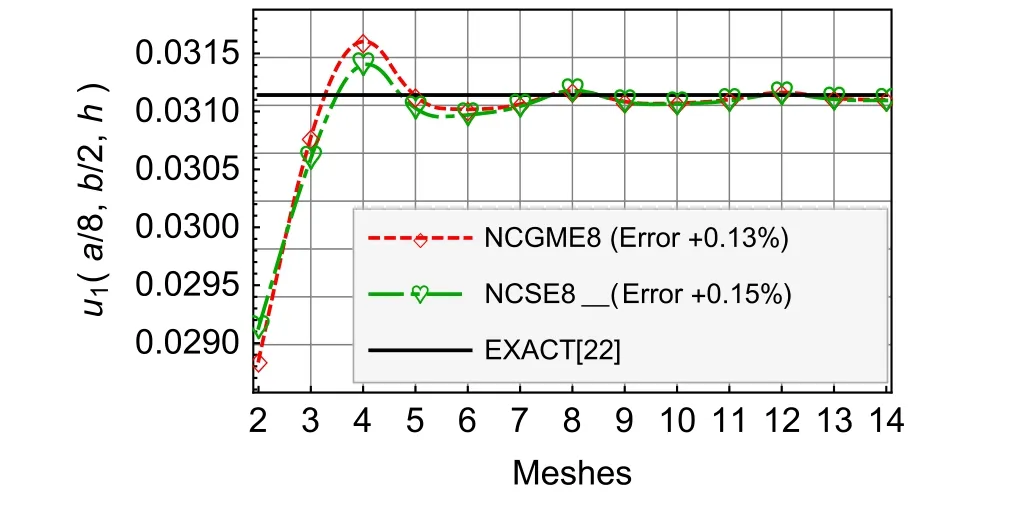
Fig.2 Compressible material u1

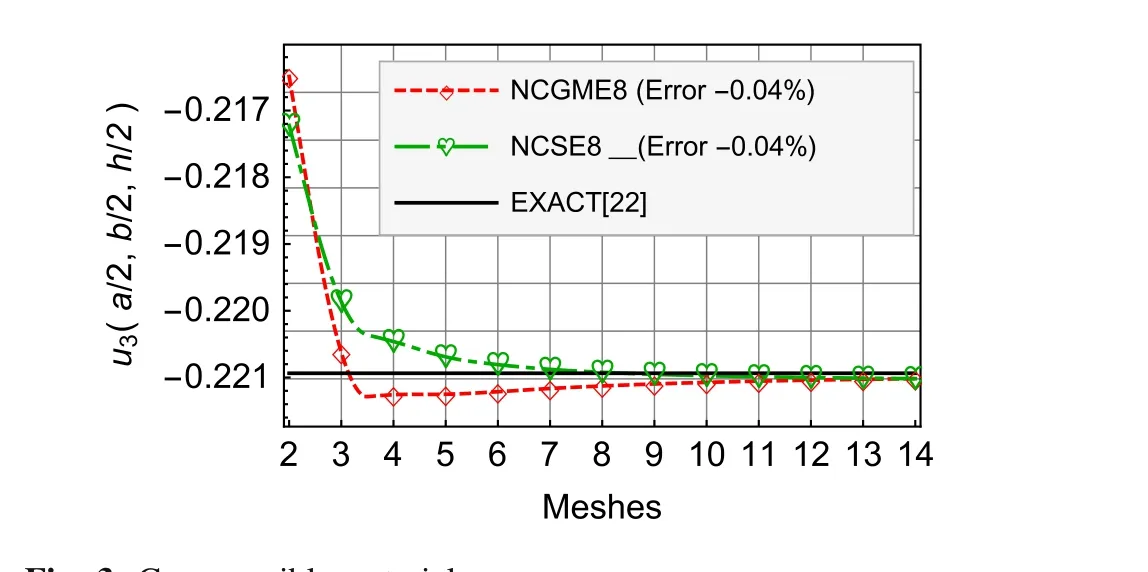
Fig.3 Compressible material u3

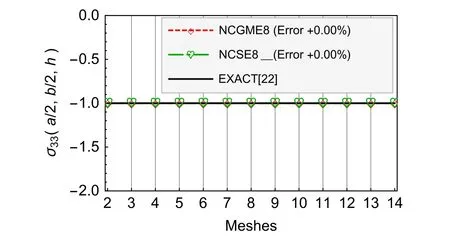
Fig.5 Compressible material σ33

Fig.4Compressible materialσ13are computed by the following formulationin which,Exact denotes the exact solution which is obtained by the method in reference[22]Element denotes the solutions of NCGME8[1]or NCSE8.

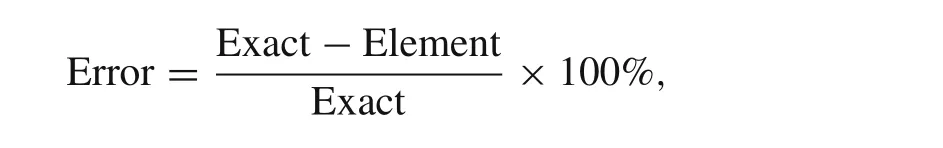
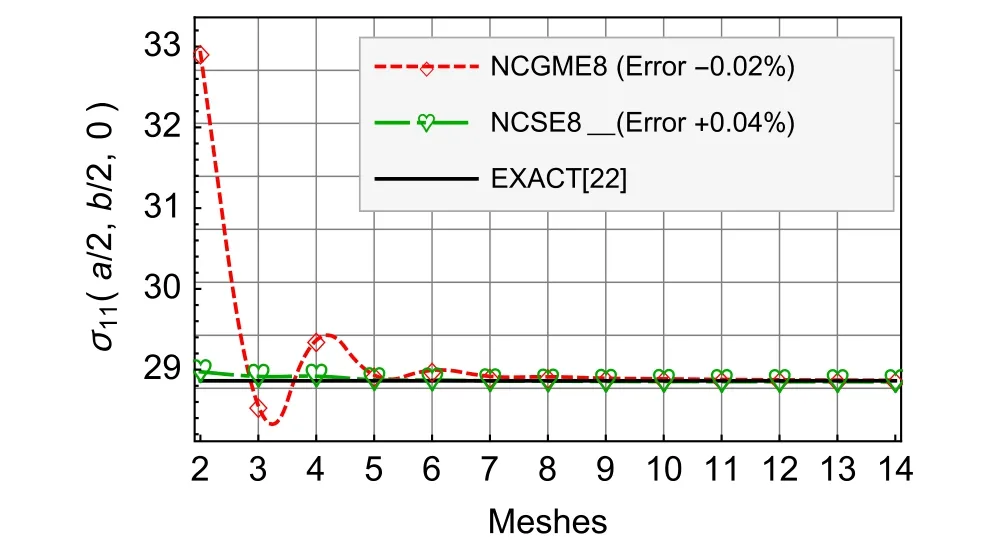
Fig.6 Compressible material σ11

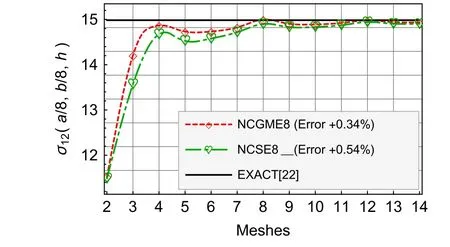
Fig.7 Compressible material σ12

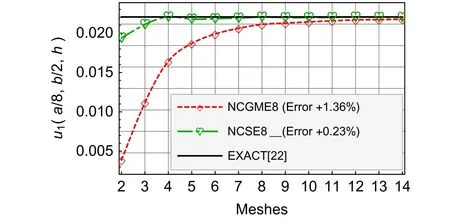
Fig.8 Nearly incompressible material u1

For the results ofu1,u3,σ33,andσ12,Figs.4–9 show that there is no obvious distinction between NCGME8 and NCSE8.But the accuracy of transverseσ13of NCSE8 is superior to NCGME8 and the stressσ11of NCSE8 is characterised by rapid convergence.

Certainly,like the classical mixed methods,a drawback of NCSE8 is the added number of stress variables means that generally larger size algebraic problems have to be handled.Generally,to obtain conveniently the stable and highly accurate numerical results is the first priority for the design of engineering structures.It can also be realized easily by NCSE8.

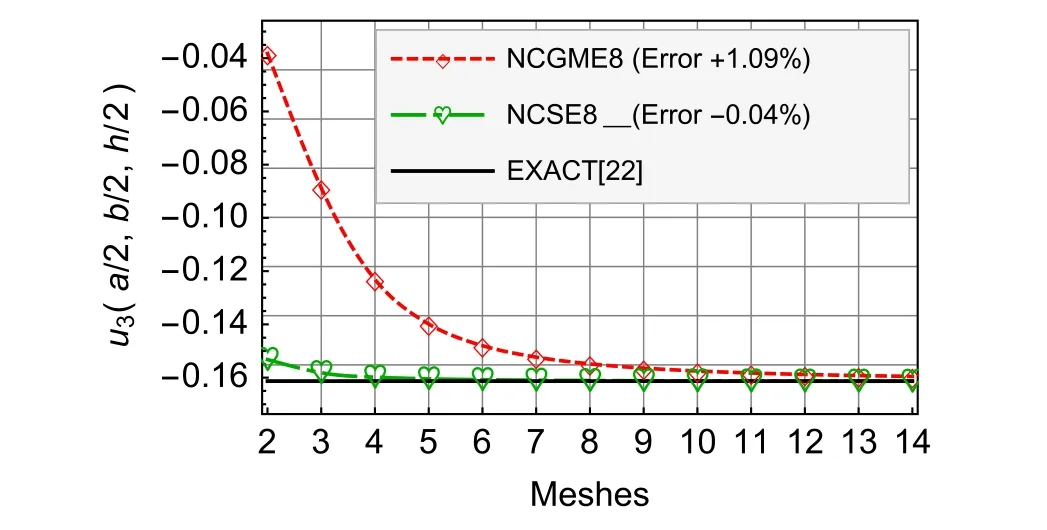
Fig.9 Nearly incompressible material u3

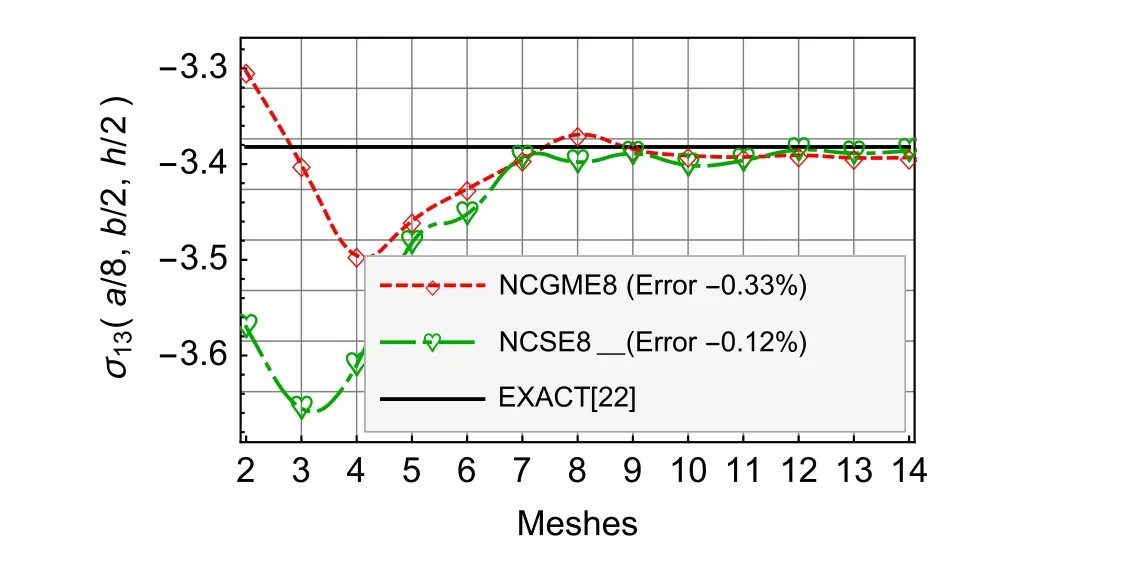
Fig.10 Nearly incompressible material σ13

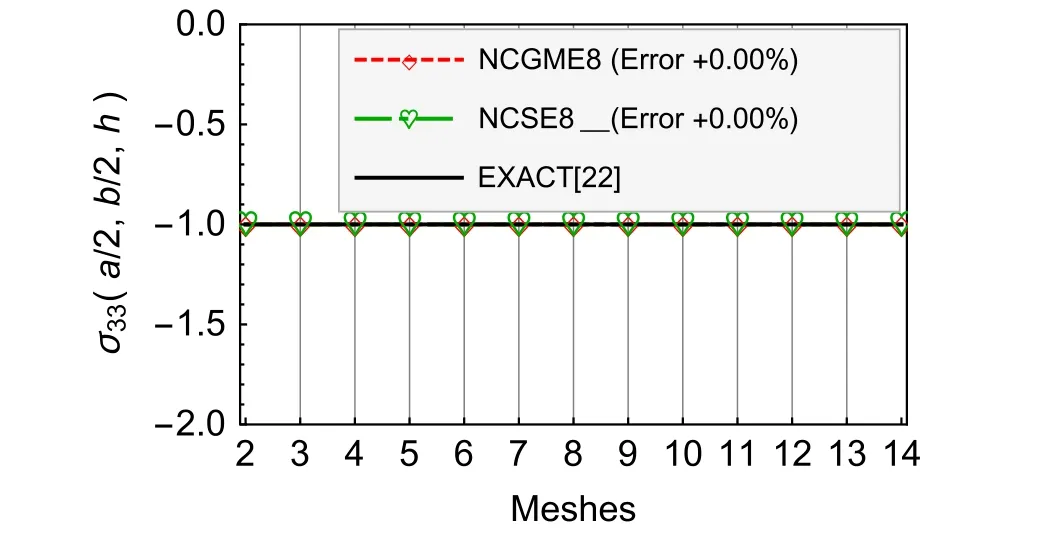
Fig.11 Nearly incompressible material σ33

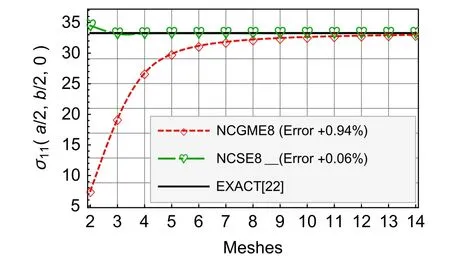
Fig.12 Nearly incompressible material σ11

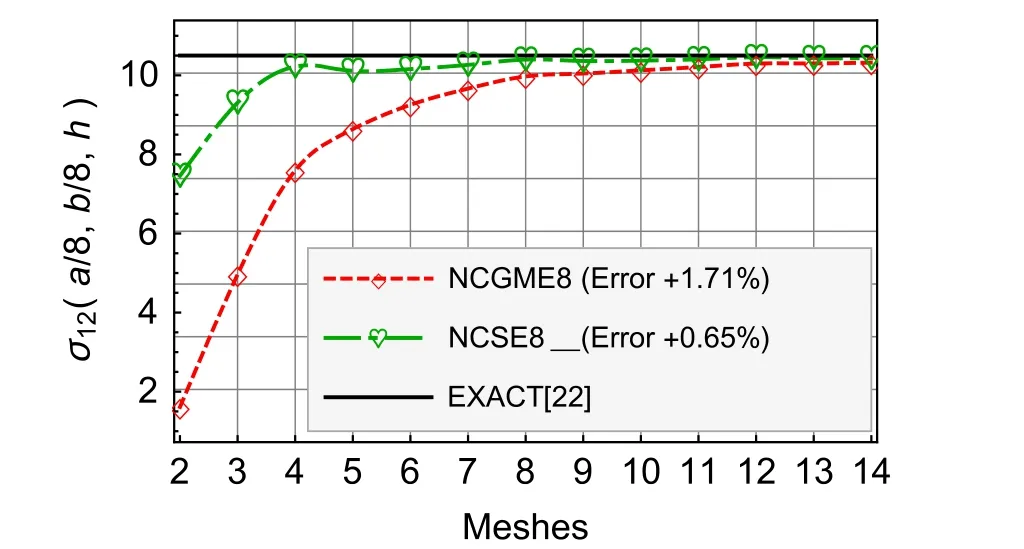
Fig.13 Nearly incompressible material σ12

Table 1 Map of numbers of horizontal axis and models

Table 2 Comparison of time requirement of NCGME8[1]and NCSE8

Table 3 Comparison of NCGME8 and NCSE8

For ourprogram in MATHEMATICA?,the time requirements of NCGME8 and NCSE8 are listed in Table 2.For NCSE8,the in-plane stress has to be computed separately by both displacements and out-plane stresses.Thus,the calculating speed of NCSE8 is slightly slow.

For the nearly incompressible material,NCSE8 yields the reliable and highly accurate results(see Figs.8–13).The accuracy of displacement and stress results of NCSE8 is superior to NCGME8[1]except the stressσ33.On the other hand,whether the displacements or not the stresses of NCSE8,their accuracy are nearly the same.

Based on the theory in Sect.3 and above numerical experimentation,Table 3 gives a summary of NCGME8[1]and present NCSE8.

4.2 A square plate with a circular hole at centre

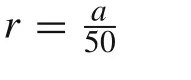
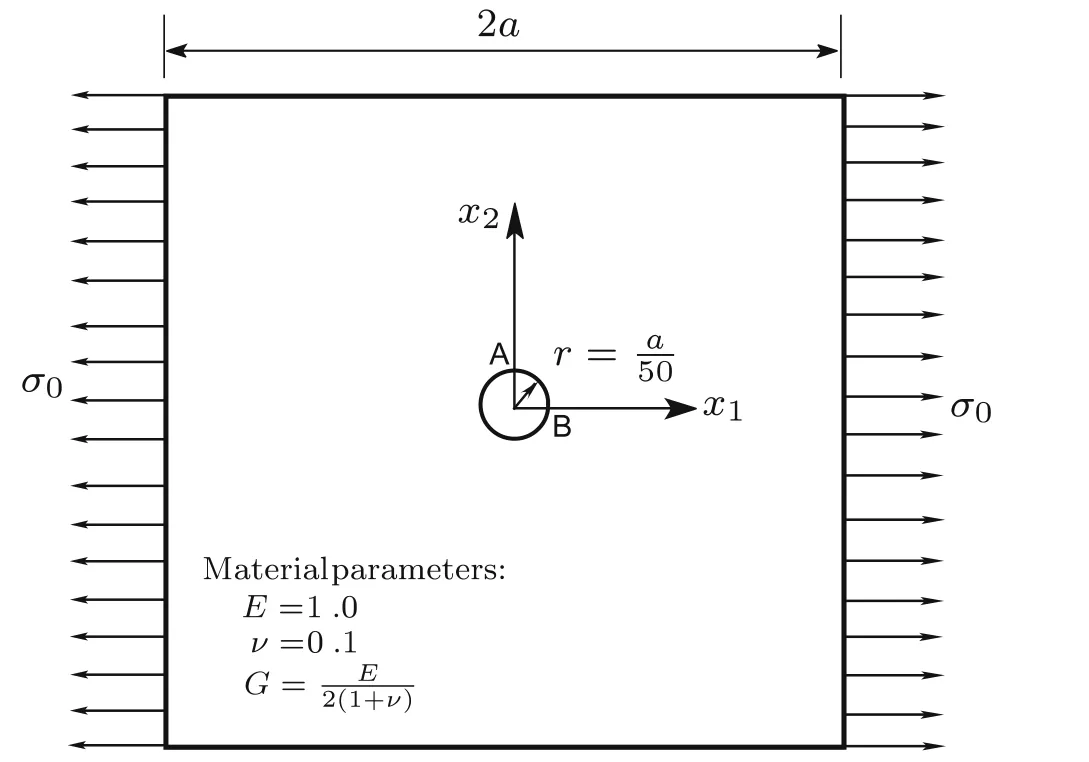
Fig.14 A square plate with a circular hole at centre

Fig.15 One quarter of mesh

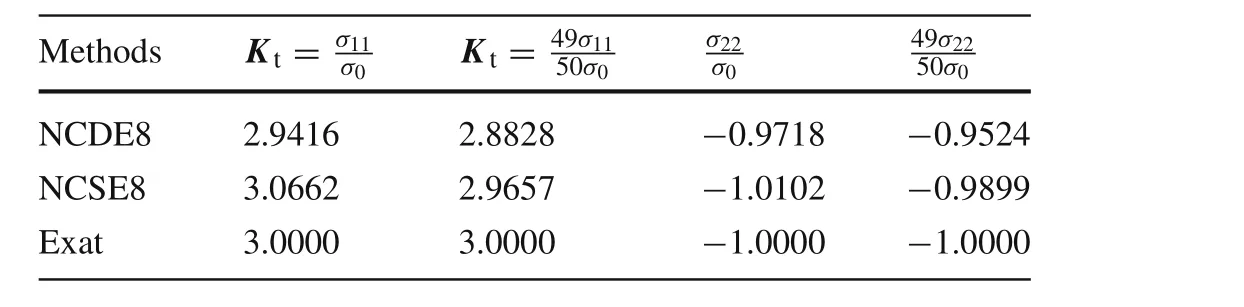
Table 4 Stress at edges of hole in square plate under uniaxial tension

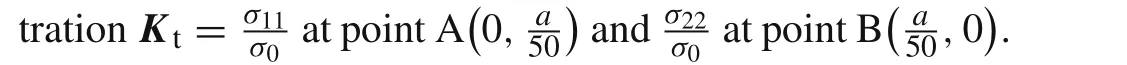
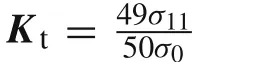
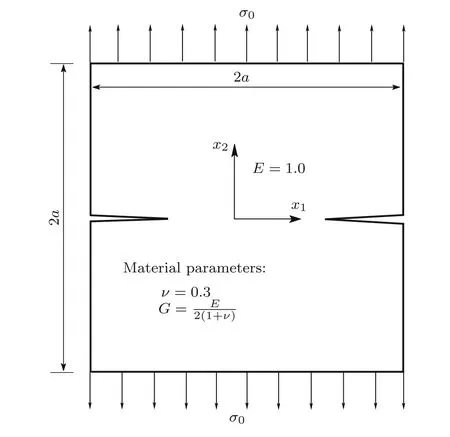
Fig.16 A square plate with edge cracks under uniaxial tension

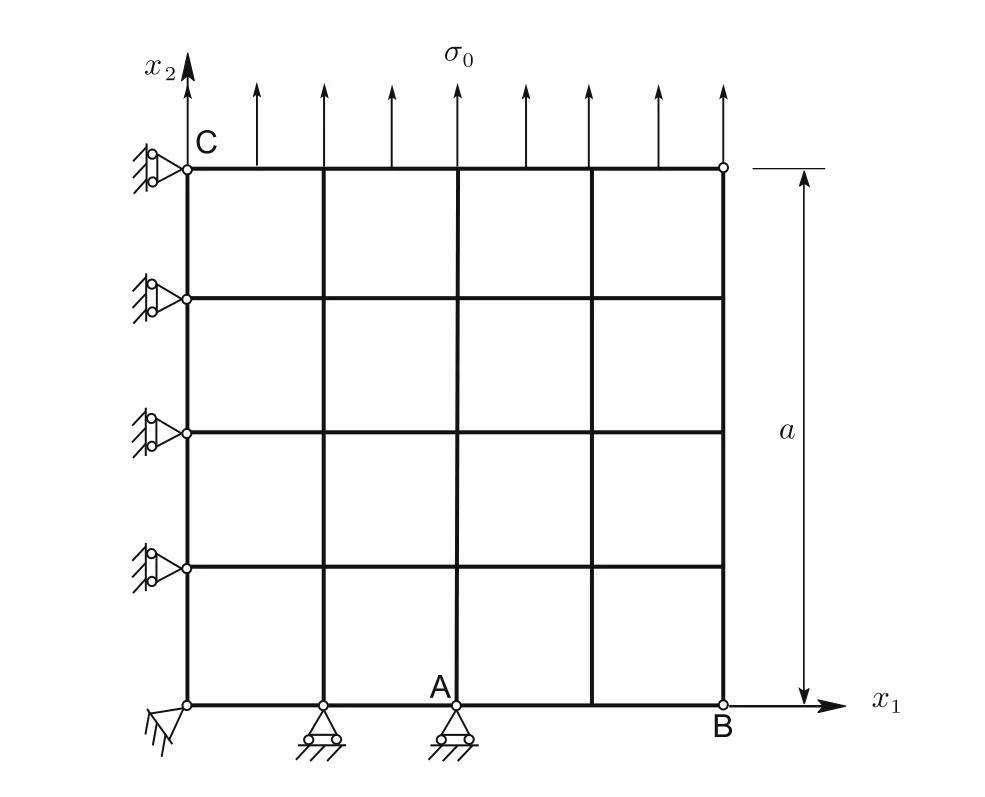
Fig.17 Finite element idealization of quarter plate along with boundary conditions(N=4)

4.3 Convergence in strain energy of a square plate with edge cracks uniaxial tension

The problem of a square plate with symmetric edge cracks(mode I)is considered next.Figure 16 shows the problem description and Fig.17 illustrates the finite element idealization of a quarter of the plate considered using the symmetry.

Figure 18 shows a comparison with the solutions obtained using various other elements.Present NCSE8 definitely shows a faster strain energy convergence than the constant stress triangles,the linear stress triangles,and the hybrid stress rectangles with cubic stress distribution within the element and quadratic displacements along the boundaries.

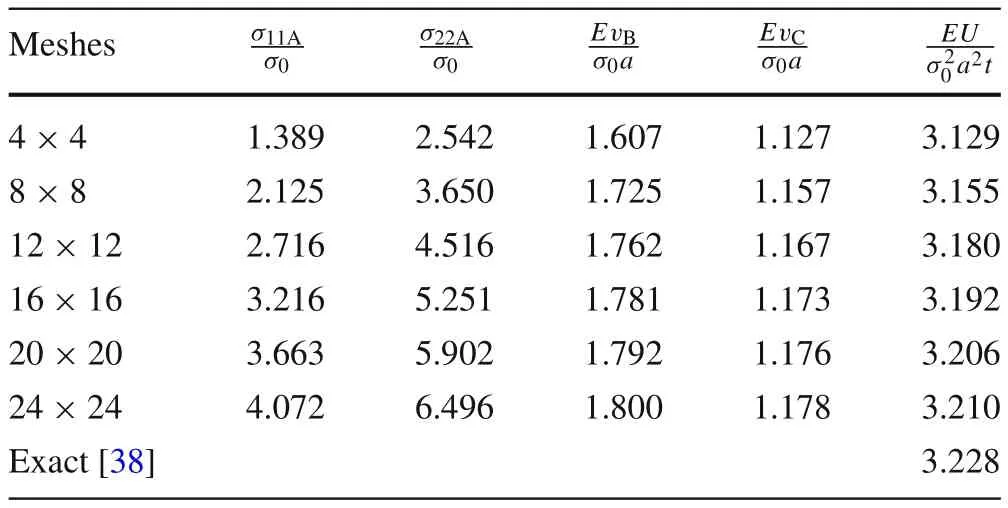
Table5 Numerical results for square plate with symmetric edge cracks

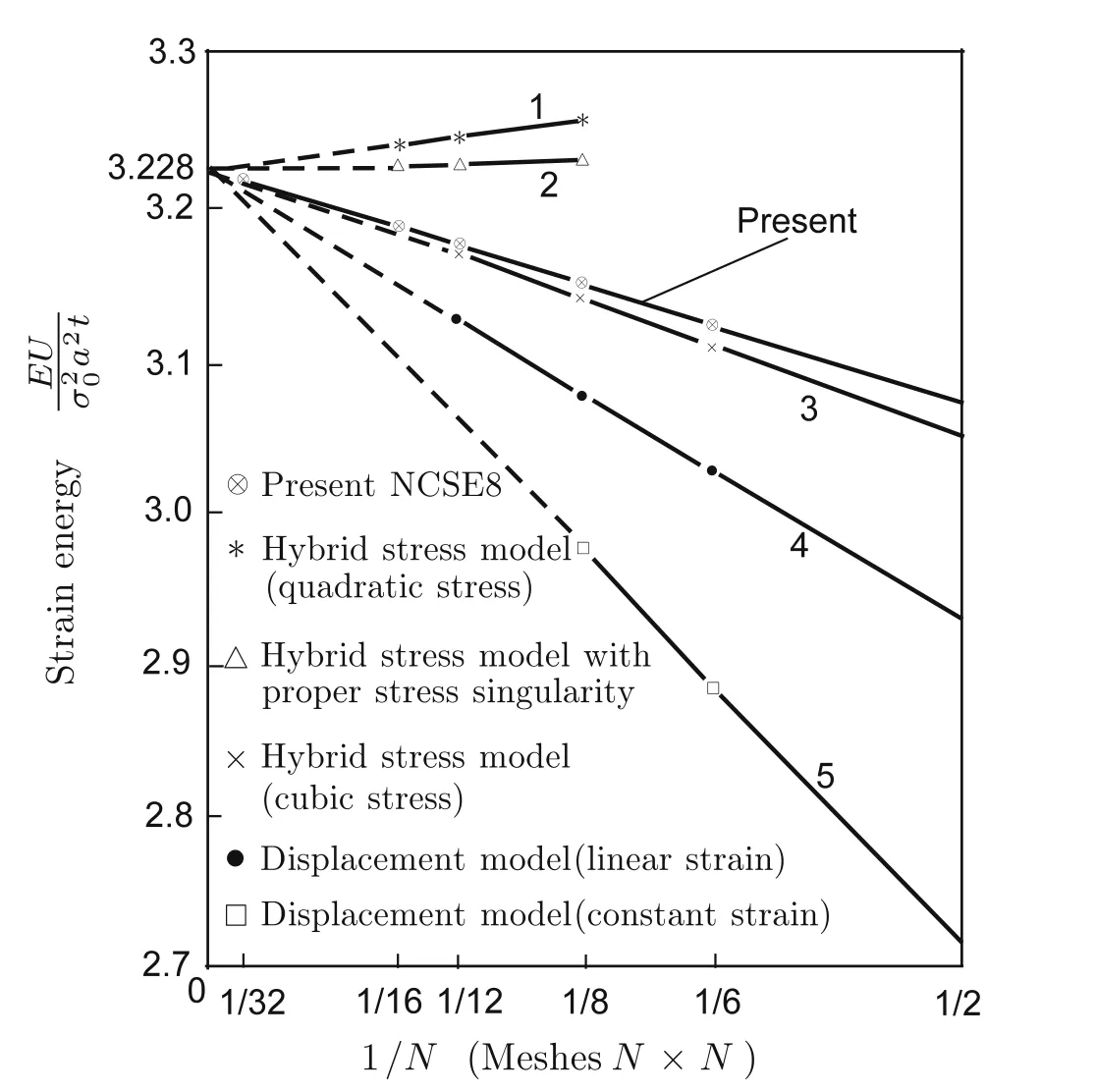
Fig.18 Convergence in strain energy.Data lines 1–5 come from Ref.[38]

5 Conclusions

In this paper,attention was focused on the symplectic element in noncompatible displacement mode.A systematic mathematical derivation for such an element was presented.The elimination of displacement vector corresponding to points within the element by the formulation derived from the minimum potential energy principle is crucial technology.Just because of the noncompatible displacement mode,there are no zeros on the leading diagonal of a present symplectic element.The simultaneous equation approach for the inplane stresses was also suggested.The simultaneous equation approach can improve the accuracy of in-plane stress results on nodes.

The symplectic finite element model in terms of NCSE8 seems to give the simplest and most flexible system of equations,since nonconventional solutions or the stable mixed schemes used in classical mixed models is unnecessary.The nodal out-plane stress results are automatically continuous.NCSE8 has advantages of clear concept,easy calculation by a finite element computer program, higher precision and wide applicability for linear elasticity problems.

Generally,the displacement methods or the hybrid methods can be extended for analyzing the fracture problems.Unlike displacement elements,the present NCSE8 is a mixed one.However,by an enriched mixed element scheme[30]or the idea of FEDSM[31],it is also possible that NCSE8 orthe generalized mixed elements for 2-D problems are extended for evaluating SIFs.This work will be discussed in the next paper.

If we begin with the modified H-R mixed variational principles for the magneto-piezoelastic anisotropic materials[26],the corresponding symplectic element can also be constructed.

AcknowledgementsThis work was supported by the National Natural Science Foundations of China(Grant 11502286).

1.Qing,G.,Mao,J.,Liu,Y.:Generalized mixed finite element method for 3D elasticity problems,Acta Mech.Sin.(2017).(online)http://rdcu.be/tLYj,https://doi.org/10.1007/s10409-017-0690-7

2.Zienkiewicz,O.C.,Taylor,R.L.,Zhu,J.:The Finite Element Method:Its Basis and Fundamentals.Butterworth-Heinemann,Oxford(2005)

3.Arnold,D.N.:Mixed finite element methods for elliptic problems.Comput.Methods Appl.Mech.Eng.82,281–300(1990)

4.Qing,G.,Mao,J.,Liu,Y.:Highly accurate noncompatible generalized mixed finite element method for 3D elasticity problems.J.Mech.Mater.Struct.12,505–519(2017)

5.Qing,M.,Feng,K.:Collected Works of Feng Kang.Volume I,II.National Defence Industry Press,Beijing(1995).(in Chinese)

6.Fu,M.H.,Lu,K.L.L.,Lan,H.:High order symplectic conservative perturbation method for time-varying hamiltonian system.Acta Mech.Sin.28,885–890(2012)

7.Bridges,T.J.,Hydon,P.E.,Lawson,J.K.:Multisymplectic structures and the variational bicomplex.Math.Proc.Camb.Philos.Soc.148,159–178(2010)

8.Hu,W.-P.,Qin,Y.-Y.,Zhang,W.-R.:Multi-symplecti cmethod for the generalized(2+1)—dimensional KDV–MKDV equation.Acta Mech.Sin.28,793–800(2012)

9.Zou,G.,Tang,L.:A semi-analytical solution for laminated composite platesin hamiltonian system.Comput.Methods Appl.Mech.Eng.128,395–404(1995)

10.Sheng,H.,Ye,J.:A three-dimensional state space finite element solution for laminated composite cylindrical shells.Comput.Methods Appl.Mech.Eng.192,2441–2459(2003)

11.Qing,G.,Qiu,J.,Liu,Y.:A semi-analytical solution for static and dynamic analysis of plates with piezoelectric patches.Int.J.Solids Struct.43,1388–1403(2006)

12.Qing,G.,Qiu,J.,Liu,Y.:Free vibration analysis of stiffened laminated plates.Int.J.Solids Struct.43,1357–1371(2006)

13.Qing,G.,Wang,F.,Liu,Y.:State space approach for energy release rate analysis of delaminated laminates with stiffeners.Aiaa J.49,2123–2129(2011)

14.Andrianarison,O.,Benjeddou,A.:Hamiltonian partial mixed finite element-state space symplectic semi-analytical approach for the piezoelectric smart composites and FGManalysis.Acta Mech.223,1597–1610(2012)

15.Li,D.,Qing,G.:Free vibration analysis of composite laminates with delamination based on state space theory.Mech.Adv.Mater.Struct.21,402–411(2014)

16.Fan,J.,Ye,J.:An exact solution for the statics and dynamics of laminated thick plates with orthotropic layers.Int.J.Solids Struct.26,655–662(1990)

17.Steele,Y.Y.,Kim,C.R.:Modified mixed variational principle and the state-vector equation for elastic bodies and shells of revolution.J.Appl.Mech.59,587–595(1992)

18.Tang,L.,Zhou,G.P.:Mixed formulation and Hamilton canonical equations of theory of elasticity.Comput.Struct.Mech.Appl.8,343–349(1991).(in Chinese)

19.Zhong,W.:New Solution System of Elasticity.Dalian University of Technology Press,Dalian(1995).(in Chinese)

20.Heyliger,P.,Saravanos,D.:Exact free-vibration analysis of laminated plates with embedded piezo-electric layers.J.Acoust.Soc.Am.98,1547–1557(1995)

21.Lee,J.S.,Jiang,L.Z.:Exact electrostatic analysis of piezoelectric laminae via state space approach.Int.J.Solids Struct.33,977–990(1996)

22.Fan,J.:Exact Theory of Laminated Thick Plates and Shells.Science Press,Beijing(1996).(in Chinese)

23.Chen,W.,Lee,K.Y.,Ding,H.:On free vibration of non-homogeneous transversely isotropic magneto-electro-elastic plates.J.Sound Vib.279,237–251(2005)

24.Cheng,Z.,Batra,R.:Three-dimensional asymptotic analysis of multiple-electroded piezoelectric laminates.AIAA J.38,317–324(2000)

25.Pan,E.:Exact solution for functionally graded anisotropic elastic composite laminates.J.Compos.Mater.37,1903–1920(2003)

26.Qing,G.,Qiu,J.,Liu,Y.:Modified H-R mixed variational principle for magneto electroelastic bodies and state-vector equation.Appl.Math.Mech.26,722–728(2005)

27.Li,R.,Zhong,Y.,Tian,B.:On new symplectic superposition method for exact bending solutions of rectangular cantilever thin plates.Mech.Res.Commun.38,111–116(2011)

28.Tong,P.,Pian,T.H.H.,Lasry,S.J.:A hybrid element approach to crack problems in plane elasticity.Int.J.Numer.Methods Eng.7,297–308(1973)

29.Belytschko,B.T.:Elastic crack growth in finite elements with minimal remeshing.Int.J.Numer.Methods Eng.45,601–620(1999)

30.Heyliger,P.R.,Kriz,R.D.:Stress intensity factors by enriched mixed finite elements.Int.J.Numer.Methods Eng.28,1461–1473(1989)

31.Leung,A.Y.T.,Zhou,Z.,Xu,X.:Determination of stress intensity factors by the finite element discretized symplectic method.Int.J.Solids Struct.51,1115–1122(2014)

32.Zhong,W.,Gao,Q.:Break the Laminations of Symplecticity.Dalian University of Technology Press,Dalian(2011).(in Chinese)

33.Yao,W.,Zhong,W.:Symplectic Elasticity.High Education Press,Beijing(2002).(in Chinese)

34.Zhong,W.:Symplectic System of Applied Mechanics.Science Press,Beijing(2003).(in Chinese)

35.Taylor,R.L.,Beresford,P.J.,Wilson,E.L.:A non-conforming element for stress analysis.Int.J.Numer.Methods Eng.10,1211–1219(1976)

36.Chen,W.:A high precision eight-node hexahedron element.Chin.J.Theor.Appl.Mech.18,262–271(1982).(in Chinese)

37.Tian,S.,Pian,T.H.H.:Variational Principles with Multivariables and Finite Elements with Multivariables.Science Press,Beijing(2011).(in Chinese)

38.Tong,P.,Pian,T.H.H.:On the convergence of the finite element method for problems with singularity.Int.J.Solids Struct.9,313–321(1973)