The rough representation and measurement of quotient structure in algebraic quotient space model①
Chen Linshu (陳林書), Wang Jiayang
(*School of Computer Science and Technology, Hunan University of Science and Technology, Xiangtan 411201, P.R. China)(**School of Information Science and Engineering, Central South University, Changsha 410083, P.R. China)
The rough representation and measurement of quotient structure in algebraic quotient space model①
Chen Linshu (陳林書)②*, Wang Jiayang**
(*School of Computer Science and Technology, Hunan University of Science and Technology, Xiangtan 411201, P.R. China)
(**School of Information Science and Engineering, Central South University, Changsha 410083, P.R. China)
Granular computing is a very hot research field in recent years. In our previous work an algebraic quotient space model was proposed, where the quotient structure could not be deduced if the granulation was based on an equivalence relation. In this paper, definitions were given and formulas of the lower quotient congruence and upper quotient congruence were calculated to roughly represent the quotient structure. Then the accuracy and roughness were defined to measure the quotient structure in quantification. Finally, a numerical example was given to demonstrate that the rough representation and measuring methods are efficient and applicable. The work has greatly enriched the algebraic quotient space model and granular computing theory.
granular computing, algebraic quotient space model, quotient structure, upper ( lower) congruence relation
0 Introduction
Granular computing, which was first introduced in 1997 by Lin[1,2], is an emerging computing paradigm of information processing, and is now viewed as a superset of models including rough set, topology quotient space[3], fuzzy set[4], word theory, etc. Granular computing has been widely applied in image processing, data mining, complex problem solving, pattern recognition, intelligent control, artificial neural network, knowledge acquisition, and so on[5-8].
Being a widely applied structure in data coding, formal language and electronic circuit design, algebra is used broadly to describe the granule structure[9-10]. Based on the topology quotient space model (U,F,T) proposed in Ref. [11], and supposing the granule structure T as an algebraic operator °, in Refs [12,13] of our previous work, algebraic quotient space model (U,F,°) was proposed.
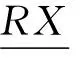
In the algebraic quotient space theory, given equivalence relation R on granularity (U,F,°), one can only get the quotient universe [U] and quotient attribute [F] according to Refs [3,11], but can not get the quotient structure [°] by the conclusion of Refs [12,13]. Thus, is there a method of roughly representing the quotient structure? If yes, how to measure the new method?
In this paper, an equivalence relation R is given as a granulation rule in the algebraic quotient space model. Inspired by the lower approximation and upper approximation to approximately represent a rough set, a rough representation method of quotient structure is shown in algebraic quotient space model. Rough set theory and algebraic quotient space model in Refs [12,13] are simply introduced in Section 1.in Section 2, the lower quotient structure and upper quotient structure are defined to roughly represent the quotient structure. Section 3 gives the measurement of the above rough representation method. Section 4 presents a numeral example which shows that the rough representation and measuring methods are feasible and applicable.
1 Research basis
In this section, simple introductions are given to the rough set theory and the algebraic quotient space model in our previous work in Refs[12,13].
The rough set theory, first proposed by Polish scientist Pawlak[14,15]in 1982, is an effective mathematical tool for the characterization of incomplete and uncertain problems. The rough set is defined as follows.
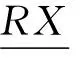
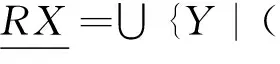
(1)
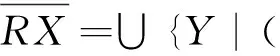
(2)
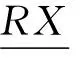
The algebraic quotient space model (U,F,°) in Refs [12,13] was proposed as follows.
Definition 2[12,13]Given congruence relation R on granularity (U,F,°), where U is the universe, F:U→Y is the attribute function, and ° is the granule structure on U. It defines: the quotient universe [U] as p:U→U/R, the quotient attribute [F] as [F]:[U]→2Y, where
?x∈[U],[F](x)=F(p-1(x)) ={F(y)|y∈p-1(x)}
(3)
the quotient structure [°] as
?x,y∈U,p(x°y)=p(x)[°]p(y)
(4)
then ([U],[F],[°]) is defined as an algebraic quotient space of (U,F,°).
In Definition 2, it gives the mapping functions of the quotient universe [U], the quotient attribute [F] and the quotient structure [°]. The quotient universe is a natural mapping, and the quotient attribute provides a general solution, because [F]:[U]→2Ymust satisfy some optimization principle specified as a certain value such as a statistic number, the average, the maximum, the sum, the intersection or the union, etc.[13]. The quotient structure is a homomorphic mapping between the original structure and quotient structure.
In Definition 2, the sufficient condition of having the algebraic quotient space ([U],[F],[°]) is that R is a congruence relation, which is proved in theorem in Refs [12,13]. From the view point of the algebraic theory, in order to keep the original structure ° and quotient structure [°] being homomorphic, the granulation rule must be a congruence relation, i.e., only if congruence relation R is given on granularity (U,F,°), one can get the quotient space [°].
2 Rough representation of quotient structure
Given equivalence relation R on granularity (U,F,°), by Definition 2 the quotient structure [°] does not exist, and the key of getting an approximate quotient structure is to find an approximate congruence relation. Hence, the properties of congruence relation and equivalence relation are first discussed.
On universe U, by Refs [3,11] all the equivalence relations form a complete semi-order lattice, and by Refs [12,13] all the congruence relations form a complete semi-order lattice. Meanwhile, it is known that the congruence relation is a special case of the equivalence relation, i.e., a congruence relation must be an equivalence relation, but an equivalence relation may not be a congruence relation.
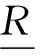
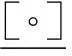
On granularity (U,F,°), let R be all the equivalence relations, Ω be all the congruence relations, and R∈R. Then, under the containment order of equivalence relation, (R,?) is a complete semi-order lattice, and (Ω,?) is a complete semi-order lattice. The lattice Hasse graphic is shown in Fig.1, where the hollow point is an equivalence relation, and the solid point is a congruence relation.
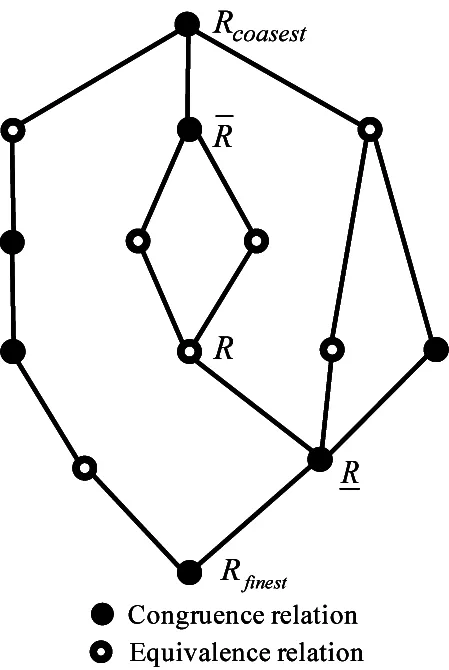
Fig. 1 The lattice Hasse graph of R and Ω
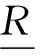
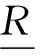
(5)
(6)
Firstly, ?(x,y)∈∩Rα∈Ω,Rα?RRα, so ?R0∈{Rα|Rα∈Ω,Rα?R}α, (x,y)∈R0, thus, ?z∈U, (x°z,y°z),(z°x,z°y)∈R0∈∩Rα∈Ω,Rα?RRα, therefore, ∩Rα∈Ω,Rα?RRαis a congruence relation.
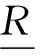
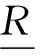

Firstly, it is proved that t(∪R?Rβ∈ΩRβ) is a congruence relation. For ?(x,y)∈t(∪R?Rβ∈ΩRβ), it has two cases: On the one hand,(x,y)∈∪R?Rβ∈ΩRβ. Then ?R0∈{Rβ|R?Rβ∈Ω}, where (x,y)∈R0, so ?z∈U,(x°z,y°z),(z°x,z°y)∈R0?∪R?Rβ∈ΩRβ. On the other hand, (x,y)?∪R?Rβ∈ΩRβ, then, ?(x=p1),p2,…,(pm=y), where (pi,pi+1)∈R0∈{Rβ|R?Rβ∈Ω}, so ?z∈U, (pi°z,pi+1°z),(z°pi,z°pi+1)∈R0?t(∪R?Rβ∈ΩRβ). Therefore, t(∪R?Rβ∈ΩRβ) is a congruence relation.
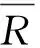
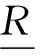
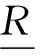
Thus, the lower quotient structure or upper quotient structure can be used to roughly represent the quotient structure which are not actually exist.
3 Rough measurement of quotient structure
In the front section, just the rough representing method of quotient structure is discussed,i.e., the concepts of lower congruence relation and upper congruence relation are defined and their calculating formulas are given. In the following, the rough measuring method of quotient structure is discussed in detail by defining the accuracy and roughness of quotient structure.
In order to describe the quotient structure in quantification more exactly, accuracy αR[°] and roughness ρR[°] are defined as follows from the reverse side.
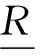
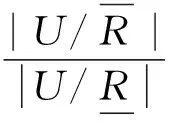
(7)
ρR[°]=1-αR[°]
(8)
Clearly, accuracy 0<αR[°]≤1, and the larger the accuracy αR[°] is, the smaller the roughness ρR[°] is.
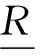
4 Numerical example
In this section, a numerical example is demonstrated which shows that the rough representation and measuring methods above are feasible and applicable.
Supposing R is an equivalence relation on granularity (U,F,°), where X={0,1,2,3,4,5,6,7}, X/R={{0,2},{1,5},{3,7},{4,6}} and the algebraic operation ° is shown in Table 1.
Seeing from Table 1, the binary algebraic operation x°y means (x×y) mod8. It can be proved that R is only an equivalence relation but not a congruence relation, then by Definition 2 there does not exist the quotient structure.
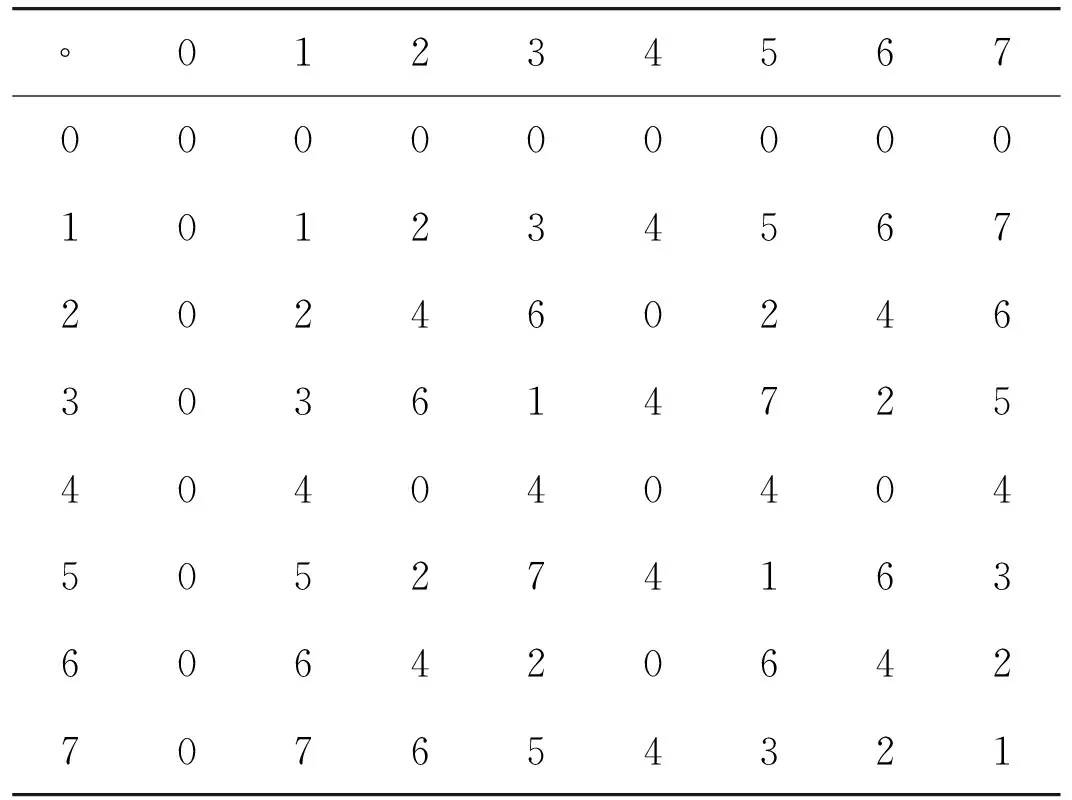
Table 1 Algebraic operation ° on U
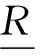
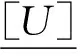
Table 3 On after isomorphic mapping
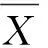
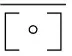
Table 4 Algebraic operation on

Table 5 on after isomorphic mapping
According to Eq. (7) of Definition 4, the accuracy αR[°] of quotient structure is
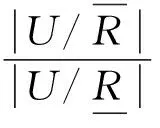
ρR[°]=1-αR[°]=1-50%=50%.
5 Conclusion
In Refs [12,13] of the previous work, it is granulated by a congruence relation in the algebraic quotient space model. In this paper, granulated by an equivalence relation, one can only get the quotient universe and quotient attribute but can’t get the quotient structure according to Refs [3,11] in the algebraic quotient space model.
Inspired by the definitions of lower approximation and upper approximation in the rough set theory, this paper gives the definitions and calculating formulas of the lower quotient congruence relation and upper quotient congruence relation, based on which one can easily get the lower quotient structure and upper quotient structure, which can be used to roughly represent the quotient structure.
Then the accuracy and roughness are defined to measure the quotient structure in quantification. Finally, a numerical example is given to demonstrate that the rough representation and measuring methods are efficient and applicable.
This work enriches the algebraic quotient space model and granular computing models greatly.
[ 1] Lin T Y. Granular computing: structures, representations, and applications. In: Proceedings of the 9th International Conference on Rough Sets, Fuzzy Sets, Data Mining and Granular Computing, Chongqing, China, 2003. 16-24
[ 2] Lin T Y. Granular computing: a problem solving paradigm. In: Proceedings of the IEEE International Conference on Fuzzy Systems, Reno, USA , 2005. 132-137
[ 3] Zhang L, Zhang B. The Quotient space theory of problem solving. Fundamenta Informaticae, 2004, 59(2):11-15
[ 4] Zadeh L A. Towards a theory of fuzzy information granulation and its centrality in human reasoning and fuzzy logic. Fuzzy Sets and Systems, 1997, 90(90): 111-127
[ 5] Zhao L, Xue Z. Generalized dominance-based set approach to security evaluation with imprecise information. High Technology Letters, 2010, 16(3): 254-262
[ 6] Zeng Y, Liang X W, Li Y. A distributed routing algorithm based-on simplified topology in LEO satellite networks. High Technology Letters, 2010, 16(2): 117-123
[ 7] Ren B, Zhang S Y, Shi Y D. The partition and regeneration of multi-granularity transplantable structures for structural variant design. Chinese High Technology Letters, 2012, 22(1): 100-105 (In Chinese)
[ 8] Meng Z Q, Shi Z Z. Self-adaptive image semantic classification based on tolerance granular space model. Chinese High Technology Letters, 2012, 22(7): 697-705 (In Chinese)
[ 9] Wang Y X, Zadeh L A, Yao Y. On the system algebra foundations for granular computing. International Journal of Software Science and Computational Intelligence, 2009, 1(1) : 64-86
[10] Wang Y X. Granular algebra for modeling granular systems and granular computing. In: Proceedings of IEEE International Conference on Cognitive Informatics, Hong Kong, China, 2009. 145-154
[11] Zhang L, Zhang B. Theory and Applications of Problem Solving. 2ndEdition. Beijing: Tsinghua University Press, 2007. (In Chinese)
[12] Chen L S, Wang J Y, Li L, et al. Quotient space model based on algebraic structure. High Technology Letters, 2016, 22(2): 160-169
[13] Chen L S, Wang J Y, Li L. The models of granular system and algebraic quotient space in granular computing. Chinese Journal of Electronics, 2016, 25(6): 1109-1113
[14] Pawlak Z. Rough sets. International Journal of Computer and Information Sciences, 1982, 11: 341-356
[15] Pawlak Z. Granularity of knowledge, indiscernibility and rough sets. In: Proceedings of IEEE International Conference on Fuzzy Systems, San Antonio, USA, 1998. 106-110
his Ph.D and M.E. degrees in School of Information Science and Engineering, Central South University. His research interest is granular computing and intelligent information processing.
10.3772/j.issn.1006-6748.2017.03.010
Supported by the National Natural Science Foundation of China (No. 61772031) and the Special Energy Saving Foundation of Changsha, Hunan Province in 2017.
To whom correspondence should be addressed. E-mail: chen-lin-shu@163.com
on July 7, 2016
 High Technology Letters2017年3期
High Technology Letters2017年3期
- High Technology Letters的其它文章
- A leveling mechanism for the platform based on booms-constraint control of aerial vehicle①
- Characterizing big data analytics workloads on POWER8 SMT processors①
- Quantitative analysis of the performance of vector tracking algorithms①
- ZnO whiskers growth on the surface of Sn9Zn/Cu solder joints in concentrator silicon solar cells solder layer①
- Structure design of gradient hard coatings on YG8 and their residual stress analysis by ANSYS①
- Application of linear active disturbance rejection control for photoelectric tracking system①
