A numerical study of violent sloshing problems with modified MPS method*

Debadatta Jena, Kishore Chandra Biswal

1.Department of Civil Engineering, National Institute of Technology, Rourkela, India, E-mail: deba_datta10@rediffmail.com

2.Department of Civil Engineering, National Institute of Technology, Rourkela, India

A numerical study of violent sloshing problems with modified MPS method*

Debadatta Jena1, Kishore Chandra Biswal2

1.Department of Civil Engineering, National Institute of Technology, Rourkela, India, E-mail: deba_datta10@rediffmail.com

2.Department of Civil Engineering, National Institute of Technology, Rourkela, India

A numerical study on violent liquid sloshing phenomenon in a partially filled rectangular container is carried out by using moving particle semi-implicit (MPS) method. The present study deals with the implementation of five modifications all together over the original MPS method. The modifications include improved source terms for pressure Poisson equation, special approximation technique for the representation of gradient differential operator, collective action of mixed free surface particle identification boundary conditions, effecting Neumann boundary condition on solving the PPE and fixing judiciously the parting distance among particles to prevent collision. The suitability of the kernel function used in the original MPS method along with these five modifications is investigated for violent sloshing problems. The present model ensures a good agreement between numerical results with the existing experimental observations. The model is successfully applied to a partially filled tank undergoing horizontal sinusoidal excitation to compute the sloshing wave amplitudes and pressure on tank walls. The assessment of dynamic behaviour manifested in terms of base shear, overturning moment and impact pressure load exerted on tank ceiling induced by violent sloshing motion using MPS method is not reported in the open literature and has been efficiently carried out in the present study.

Sloshing, particle method, impact pressure, base shear, overturning moment

Introduction

The sloshing event refers to the movement of liquid with a free surface inside a partially filled container due to external excitations. It comprises a significant class of problems in many engineering fields such as aerospace, civil, marine and nuclear and so on. There is a considerable need for understanding of the sloshing behaviour with regard to safety of water retaining structures and several transportation means, such as surface haulage of oil tankers, ocean going ships with liquid cargo and liquid propellant tanks used in satellites and spacecraft vehicles. In this context, the principal concern is to predict the interesting effects arising from the motion of the liquid-free surface, due to sloshing, in a partially filled container.

The study of sloshing phenomenon has long since drawn the attention of researchers[1]. The analytical models have been used to evaluate the sloshingeffects successfully where the motions of the liquid as well as container are assumed to be small. The performance of the analytical study is limited to waves of low height, simple tank geometry and uncomplicated boundary conditions[2]. The analytical solution is also observed to be unsound for studying sloshing in resonance frequency and in case of extensive fluid-structure interaction with complex geometry. A good number of experimental works have been carried out to understand the complex sloshing behaviour in tanks of different shapes under varieties of external excitations[3]. Generally the experimental studies furnish accurate results regardless of type of motion and boundary conditions. The constraint of the experimental works is a subject of huge expense with a prolonged effort. The numerical methods such as finite difference method (FDM)[4], boundary element method (BEM)[5], and finite element method (FEM)[6]are in prevalence for the study of sloshing motions. However, it is difficult to model the violent sloshing phenomenon with changing and breaking of free surface with these grid based methods.

To overcome these difficulties, a distinctive classof meshless method called particle method is adopted in recent time. The basic idea of the meshless method is to solve the flow field based on a set of Lagrangian particles. The particle methods are the Lagrangian messless methods where particles are free to move in a specified domain. So these methods have the ability to model highly deformed free surface flow, especially the problem involving complicated boundary and interface. The smoothed particle hydrodynamics (SPH) and moving particle semi-implicit (MPS) methods are two of the more powerful approaches. One of the earliest and most often used particle methods is the SPH method. It was primarily developed for astrophysical problems and later extended to model a wide range of hydrodynamics problems[7]. Shao et al.[8]presented an improved SPH method for modelling viscous incompressible liquid sloshing dynamics. They studied the effect of middle baffle with different heights on the wave elevation in a partially filled rectangular tank. Shao et al.[9]used SPH simulation to investigate the effect of different baffles such as I-shaped baffle, T-shaped baffle and porous baffle on liquid sloshing in a rectangular tank due to a horizontal excitation. They concluded that the I-shaped and T-shaped baffles can be good choices to mitigate sloshing effects. The MPS method is another class of particle methods. It was originally proposed for simulation of incompressible free-surface fluid flows.

In the MPS method, fluids are represented by particles. Each particle is followed in a Lagrangian manner. The Lagrangian approach in hydraulic flow simulation is advantageous as convection is directly calculated by the motion of particles without any numerical diffusion. The motion of each particle is calculated through the interaction of its neighbouring particles by means of a kernel (or weight) function and according to the governing equations of fluid motion. Deterministic particle interaction models are used to approximate the differentials like gradient, Laplacian and divergence. Constant particle number density criterion is followed to express the incompressibility of fluid. The Poisson equation of pressure is solved implicitly to calculate pressure while other terms are calculated explicitly.

Examples of implementation of MPS method for flow problems belonging to different classes of engineering and science have been reported in the literature. Dam break flow simulation is adopted as a test problem by a number of researchers to discuss the performance of the developed method. Kondo and Koshizuka[10]have employed a modified PPE containing three source terms to suppress the unphysical pressure oscillation which is a very common feature in the studies with original MPS method. Tanaka and Masunaga[11]have made some modifications to the original MPS method. However, their studies are limited to the simulation of dam breaking flow problems. Khayyer and Gotoh[12]used a modified MPS for the prediction of wave impact pressure and compared the numerical results with the experimental data. Zhang et al.[13]have simulated the heat transfer problem with the use of MPS method. Khayyer and Gotoh[14]have used a modified MPS method to simulate liquid sloshing in a 2-D container under harmonic excitation. The study contains only the time history of pressure at a specified location of the tank wall and a validation test. Lee et al.[15]have used MPS method with a kernel function of higher order than that of original one to simulate sloshing flow in a 2-D liquid tank.

The assessment of pressure, base shear, overturning moment and impact pressure on tank ceiling under violent sloshing motion is very important for the safe design of ground supported liquid retaining container. Again the liquid tanks are also employed in tall structures to act as dampers to attenuate the unwanted vibrations due to wind or earthquake. The computation of developed base shear in case of sloshing motion helps in assessing the effectiveness of these kinds of dampers. The local effects such as broken free surface and turbulence have importance in some cases, but the simulation of global flow plays a more critical role in many sloshing problems[16]. Lee et al.[17]stated in their study that the effect of liquid turbulence on the impact pressure appeared to be negligible.

In the present study, the suitability of the kernel function used in the original MPS method along with five modifications is investigated for violent sloshing problems. As the study focuses on global violent liquid motion, the local effect such as turbulence is not considered. However, the modified MPS method used in this study can competently capture the flow dynamics with distorted and broken free surface. The assessment of dynamic features such as hydrodynamic pressure, sloshing wave elevation, base shear, overturning moment and impact pressure load on tank ceiling evolved during a violent sloshing motion is carried out which is not reported by earlier studies available in the open literature.

1. Original MPS method

1.1 Governing equations

The governing equations for incompressible viscous flows are the continuity and Navier-Stokes equation as follows:

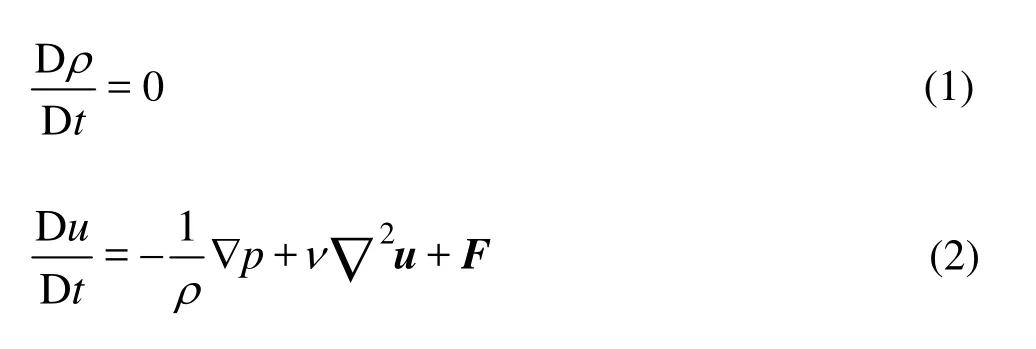
whereρis the constant density,tis time,uis a velocity vector, ? is the gradient,pis pressure,νis kinematic viscosity andFis external force. The continuity equation Eq.(1) is written with respect to the density. The left hand side of Navier-Stokes equation Eq.(2) denotes Lagrangian differentiation including convection terms. This is directly calculated by moving particles in a Lagrangian manner. The right hand side consists of pressure gradient, viscous, and external force term.

1.2 Kernel function

All terms expressed by differential operators in the governing equations are replaced by the particle interaction models of the MPS method for the simulation of incompressible flows. Particle interactions are evaluated using a weight function. The weight function adopted is as follows:

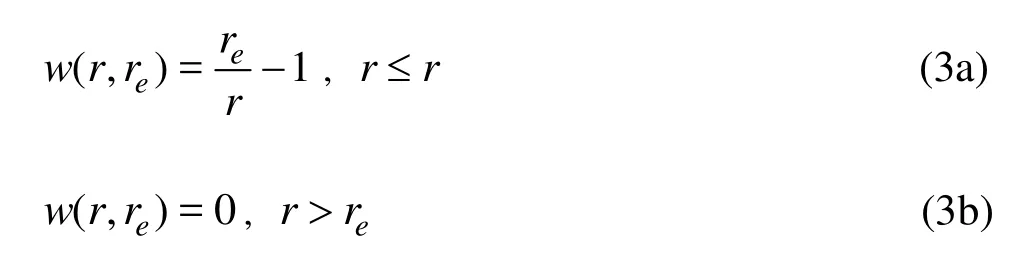
whereris the distance between particles andreis the effect radius. The particle number density is evaluated by using the following equation.

wherewijis the weight function between particleiandj. It is calculated as follows

whererijis the distance between particleiandj.

The particle number density in an incompressible state is called the particle number density criterion0n. The time step is controlled in the computation to satisfy the following Courant condition

where Δlis the initial distance between two particles, andumaxis the maximum velocity among all particles.

In this study, a relative vector between particleiandjis represented as

The differential operators of gradient, Laplacian and divergence are formulated as

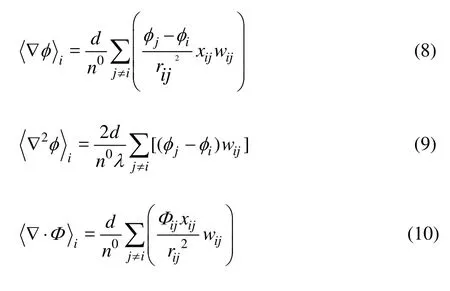
whereφis an arbitrary scalar,Φis an arbitrary vector,dis the number of dimensions,xis the coordinate of a particle. The coefficientλin Laplacian model is defined as

1.3 Pressure Poisson equation

Pressure is computed by solution of pressure Poisson equation which includes particle number density in the source term.

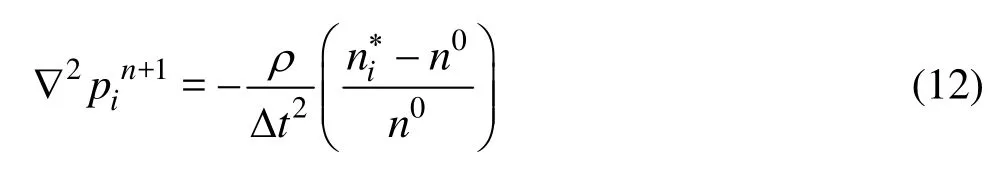
1.4 Free surface boundary condition

Both the kinematic and dynamic boundary conditions are imposed as the free surface boundary conditions on surface particles. The kinematic condition is directly satisfied as a result of the fully Lagrangian treatment of particles. The continuity of normal and tangential stress components which is referred to as dynamic boundary conditions must be satisfied on the free surface. As the viscous effects on the free surface are not considered, the continuity of tangential stress components is satisfied automatically. The effect of surface tension is negligible[18]and not considered in this study. The surface pressure effects are neglected on the free surface. Hence, the normal stress boundary condition becomes

The particle number density is reduced near the free surface than that in the inner field due to truncation of interaction domain in the free surface. Theparticle satisfying the following simple condition is considered as free surface particle.

whereβis a free surface parameter chosen between 0.80 and 0.99.

2. Modifications to original MPS

2.1 Modified PPE with higher source terms

Zhang et al.[13]have used the modified PPE given by Eq.(15) for simulation of convective heat transfer problem.

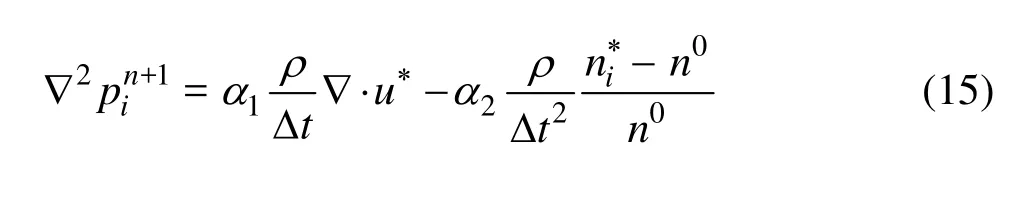
The values forα1andα2are taken as 0.8 and 0.2, respectively. Tanaka and Masunaga[11]have used the above equation by replacing the temporary particle number density (n*) with particle number density (nn) at time stepn. The coefficientsα1andα2are taken as 1.0 and a very small value in the order of 1.0×10-3, respectively. Lee et al.[15]have also replacedwithnn. The coefficientα2is taken to be less than 1.0 and the summation of both the coefficients is considered as unity. The present study uses the above expression for PPE by replacingwithand the coefficientα2is less than 1.0 and

2.2 Additional condition for identification of free surface particles

The original MPS method uses Eq.(14) for the detection of free surface particles. The non-uniformity in the spatial distribution of the particle number density results in wrong detection of free surface particles leading to spatial fluctuation of pressure field. The additional condition uses the number of neighbouring particles in identifying free surface particles. Free surface particles are recognized by the combined use of both the conditions. The additional condition is used for violent sloshing flow phenomenon as proposed by Tanaka and Masunaga[11]for the dam breaking flow simulation.

It is given in the following equation.

whereNiis the number of neighbouring particles within effective range of particle interactionreandN0is the maximum number of neighbouring particles for fully submerged particles in the initial distribution.β′ is a free surface parameter.

2.3 Wall boundary condidate

Lee et al.[19]have simulated the dam-break flow, 2-D lid-driven cavity flow, flow around a bluff body using smooth particle hydrodynamics (SPH) method. The Neumann boundary condition for pressure is implemented through the use of four layers of dummy particles. In the simulation of liquid sloshing problem using SPH formulation, Shao et al.[8]have used virtual particles, repulsive particles and ghost particles for the representation of the solid boundary and implementation of the wall boundary conditions.

In the present MPS model, one layer of wall particles and two layers of dummy particles are used to represent the solid boundary as shown in Fig.1. The wall particles are directly in contact with both the fluid and dummy particles. They are involved in the pressure correction calculation and prevent the concentration of particles near the wall. They have zero velocities throughout the whole simulation and are treated as no-slip on wall. Dummy particles do not move but carry an identical pressure to edge particles normal to the wall which satisfies the Neumann boundary condition of pressure.

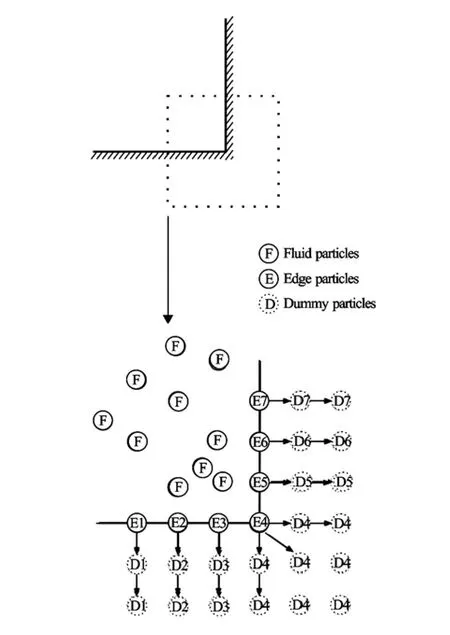
Fig.1 Outside of tank wall with dummy particles

2.4 Prevention of collision of particles

In the original MPS method, Eq.(8) is used to calculate the gradient of any physical variable. The conservation of momentum is not fully satisfied by using Eq.(8). Additionally it results in numerical instability in the calculation process. The modified gradient operator is used to move off the simulation process with greater stability and accuracy.

2.5 Improved gradient operator

In the original MPS method, Eq.(8) is used to calculate the gradient of any physical variable. The conservation of momentum is not fully satisfied by using Eq.(8). Additionally it results in numerical instability in the calculation process. The modified gradient operator is used to move off the simulation process with greater stability and accuracy.

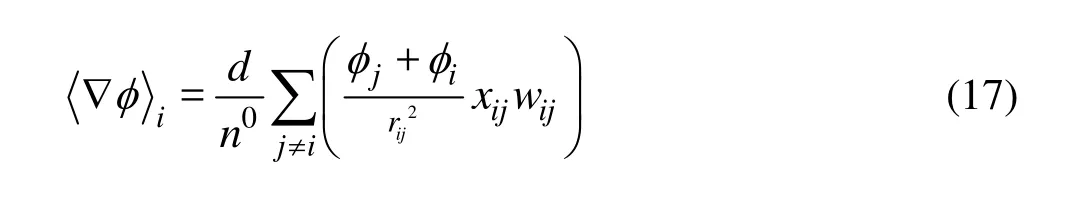
The value of the weight function used in the present study varies inversely proportional to the distance (r) between the candidate particle and its neighbouring particle in the support domain of radius reand takes an infinite or a large value whenrbecomes zero or small. This incidence leads to numerical instability of the simulation. In order to avoid this, the closely spaced particles are separated by a distance parameter and the weight function is computed accordingly.

3. Numerical results and discussion

3.1 Validation

The experimental investigation by Kishev et al.[20]is considered here to validate the modified MPS model. The length of the tank and liquid depth are 600 mm and 120 mm, respectively. The experimental results are presented by Lee et al.[15]along with the results obtained using the original MPS method. Those results have been reproduced in Fig.2. The numerical findings using the present modified MPS method is also presented in Fig.2. It is found from the figure that numerical results agree fairly well with that of experimental observation. It is also observed that the frequency of impact pressure on the test location is very close to the frequency of the external excitation.

3.2 Violent sloshing

A 2-D partially filled rectangular container is considered to study the sloshing phenomenon under horizontal sinusoidal excitation. The tank geometry is shown in Fig.3. The dimensions of the tank are 600 mm long and 200 mm high. The depth of water is 100 mm and a freeboard of equal magnitude is provided. The density of water,ρ=1 000 kg/m3and the coefficient of kinematic viscosity,ν=1.0× 10-6m2/sare considered in this study.

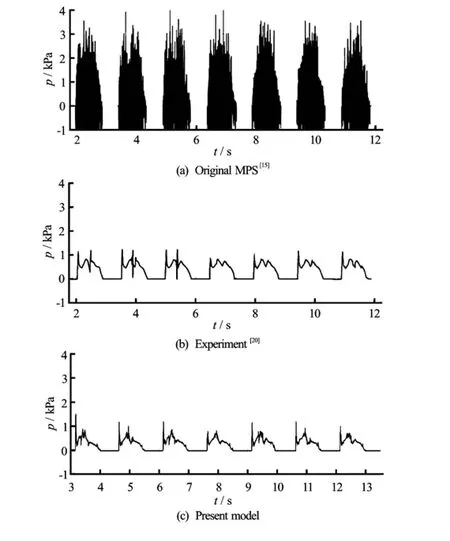
Fig.2 Time history of the pressure at a point on the right wall, 100 mm above the bottom of the tank

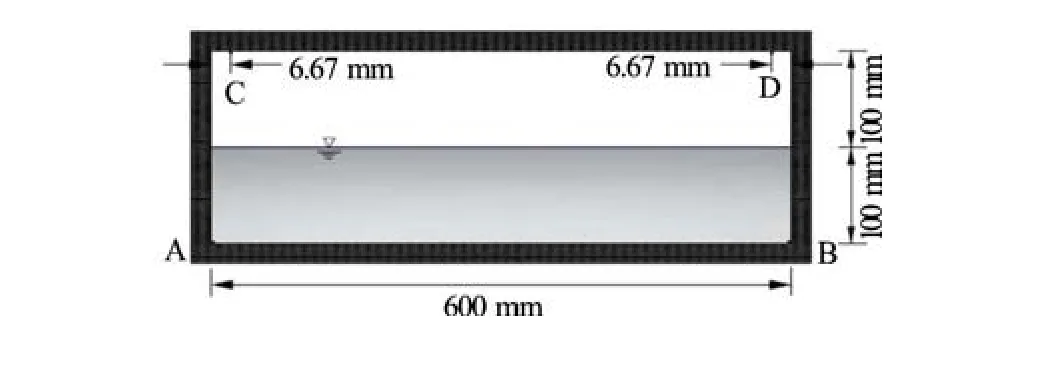
Fig.3 Geometry of the 2-D rectangular tank

The motion of the tank is defined as follows

wherex0andωare taken as 0.05 m and 4.468 rad/s respectively. The duration of the external excitation applied to the tank is 40 s. The time step selected for the present study is 0.5×10-3s.

3.3 Convergence study

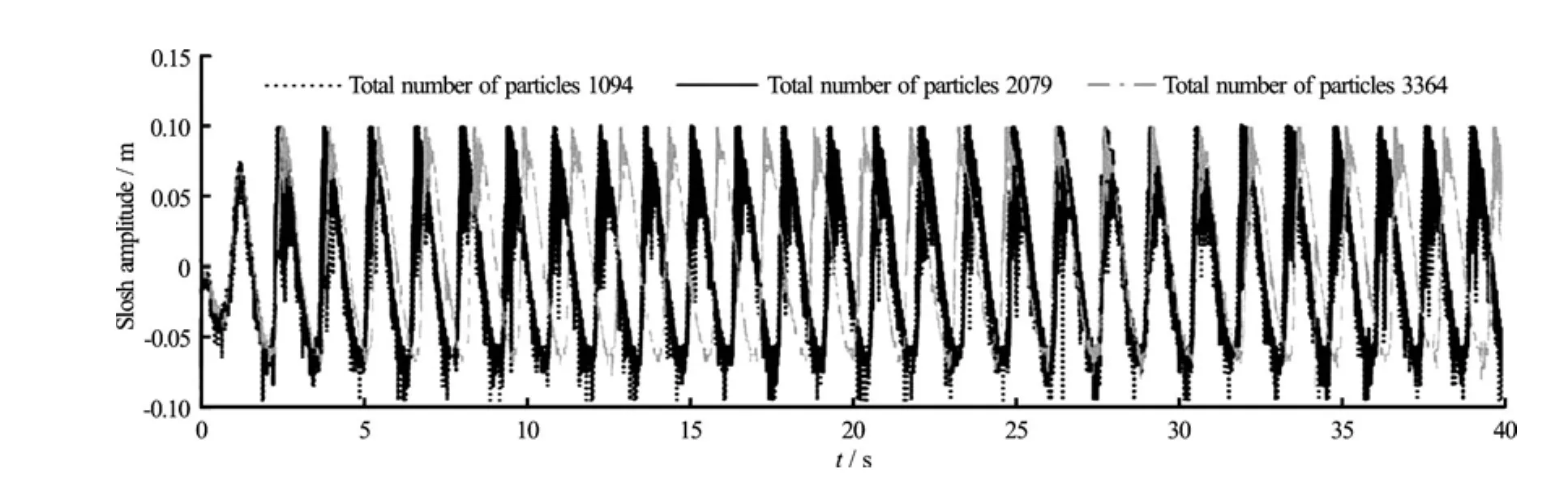
Fig.4 Slosh amplitude at the left tank wall for three sets of particle numbers

A convergence study is carried out with the model employing all the five modifications simultaneously. The slosh amplitude at left wall is computed for a duration of 40 s by varying the total number particles. Three cases mentioned below are considered by changing the number of fluid particles. Hence, the number of solid particles are changed for each case.

(1) Case 1 total no of particles 1 094 including 590 number of fluid particles.

(2) Case 2 total no of particles 2 079 including 1 335 number of fluid particles.

(3)Case 3 total no of particles 3 364 including 2 380 number of fluid particles.

The time histories of slosh amplitude at the tank left wall for varying particle numbers are depicted in Fig.4. The slosh amplitude for the Case 1 is higher than the other cases. However, the Case 2 and Case 3 exhibit similar results. Hence, the number of particles as mentioned in Case 2 are considered for the study of dynamic behaviour of sloshing liquid in the tank presented in Fig.3.

3.4 Computation of various dynamic parameters during violent sloshing

3.4.1 Evolution of velocity vectors and tracking of free surface profile

The fluid flow patterns are captured during the simulation and the evolution of velocity vectors for sloshing liquid are drawn for two successive cycles of excitation starting from 30 s and presented in Fig.5. It is observed from the figure that at the instant of 30 s, the liquid starts moving towards the left wall after striking the right wall and tank ceiling. At time (30+T/4)s, the liquid is seen moving towards the left wall. At time (30+T/2)s, liquid starts moving towards the right wall after striking the left wall and tank ceiling. At (30+3T/4)s, the liquid is seen moving towards the right wall. At (30+T)s, the free surface configuration and fluid flow pattern are identical with those obtained at 30 s. This completes one cycle of excitation. Similar flow patterns are observed for the next cycle. The free surface profile represents the positions of free surface particles during the sloshing phenomenon. The free surface particlesare identified as per the mixed action of two free surface particle tracking boundary conditions proposed in the model. The capability of the model in recognizing the free surface particles is evident from the figures. The misjudgement of inside particles as free surface particle is completely eliminated by implementing the suggested modification. The free surface profile figures at respective instants are placed adjacent to the corresponding velocity vector plots.

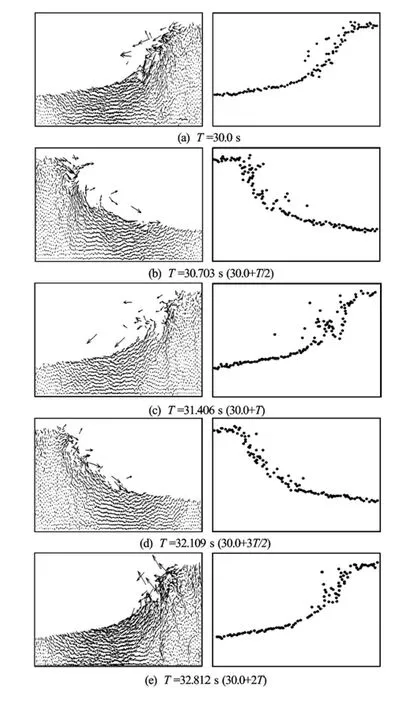
Fig.5 The evolution of velocity vectors of sloshing motion and free surface profile

3.4.2 Pressure contour of sloshing motion

The pressure contours in the fluid flow domain for one cycle of sloshing motion starting from 30 s are presented in Fig.6. The results obtained in this part of the study demonstrate the pressure variation in the entire flow field. The time instants selected for capturing the pressure contour are the same instants of time chosen for plotting the velocity vectors of fluid particles during the sloshing motion. It is observed from Fig.6 that at instant of 30 s the sloshing liquid moves towards the left after striking the right wall. At this moment, the pressure developed on the right wall is higher than that of left wall. Again the pressure at the right bottom is maximum and decreases towards the free surface. The pressure variation at the left wall at (30+T/2)s is similar to that of right wall of the tank at 30 s. However, similar trend is observed at (30+T)s compared to the time instant of 30 s.

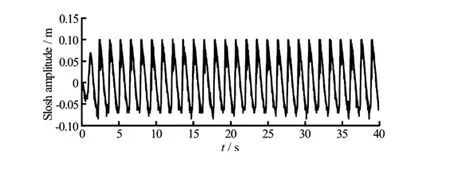
Fig.7 Time history of slosh amplitude produced at the left side wall of the tank

Fig.8 Time history of slosh amplitude produced at the right side wall of the tank

3.4.3 Time history of sloshing amplitude

The sloshing wave amplitude at the left and right walls is computed for a time duration of 40 s and presented in Fig.7 and Fig.8, respectively. It is observed that both the plots exhibit similar pattern but opposite in phase state. The maximum sloshing elevation is restricted to 0.1 m which remains equal to the dimension of available free board. The time interval between successive peaks as obtained from Fig.7 and Fig.8 is 1.40 s, which stays apparently close to the time period (1.406 s) of the external excitation.

3.4.4 Time history of liquid pressure on tanks walls

The pressure at A and B as located in Fig.3 are computed for a time duration of 40 s. The locations A and B represent the left and right bottom of the tank base. The time histories of pressure at point A and B are shown in Fig.9 and Fig.10, respectively. It is observed that at the begining of simulation, the pressure predicted at A and B are identical and very close tothe hydrostatic pressure. As the excitation progresses, the dynamic effect comes into play and the pressure values rise and fall periodically. The time histories of pressure at point A and B are similar in pattern but the phase is opposite. The impact pressure is observed to be maximum at A when the sloshing liquid strikes the left wall and at that instant the pressure at B records minimum value for one cycle of motion.

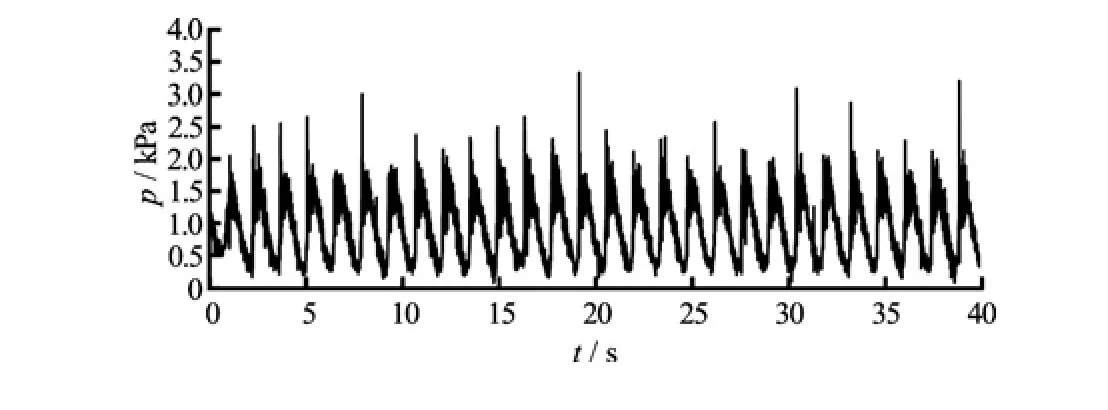
Fig.9 Time history of pressure produced at the left side corner bottom (Position A) of the tank

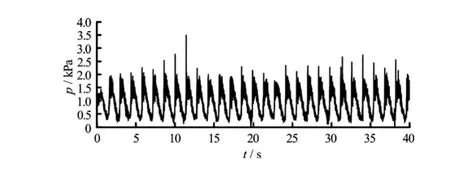
Fig.10 Time history of pressure produced at the right side corner bottom (Position B) of the tank

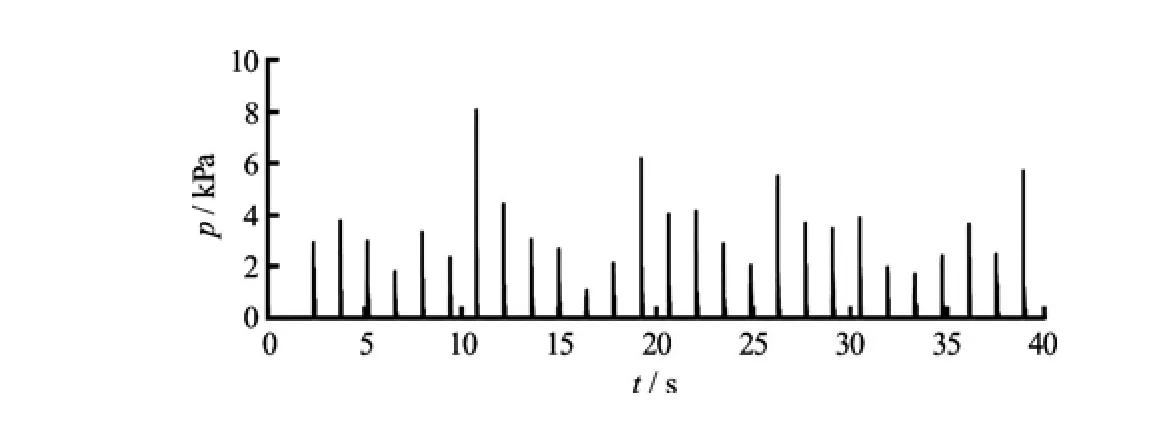
Fig.11 Time history of pressure produced at left side tank ceiling (Position C) of the tank

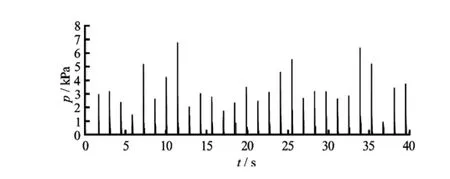
Fig.12 Time history of pressure produced at right side tank ceiling (Position D) of the tank

3.4.5 Time history of impact load pressure on tank ceiling

The pressure at locations C and D as shown in Fig.3 are computed for a time duration of 40 s. C and D represent the locations at the left and right tank ceiling. The impact load pressure exerted on the tank ceiling at location C which is 6.67 mm from the left top of the wall and location D which is 6.67 mm from the right top of the wall is computed for duration of 40 s and presented in the Fig.11 and Fig.12, respectively. It is observed from the figures that the first impact on the right side tank ceiling occurs at 1.717 s and on the left side tank ceiling at 2.359 s. Afterwards, impact phenomenon of sloshing fluid takes place on regular interval. This impact on left or right side of the tank ceiling occurs at a regular interval of 1.38 s, which remains close to the time period of the external excitation (1.406 s) applied to the liquid tank.

3.4.6 Time history of base shear

The computation of base shear is of great importance in order to check the stability of water tank subjected to dynamic loading. When the water tanks are used as slosh dampers in high rise structures, the base shear developed during the sloshing motion will play a vital role in suppressing the structural vibration. Keeping those aspects in mind, the base shear under the violent sloshing motion is computed in the present study.

The base shear is computed from the forces acting on the right and left walls of the tank. These forces are due to pressure and viscous stresses. The viscous stresses act parallel to tank walls and do not contribute to the base shear developed in the tank. The hydrodynamic pressure forces acting on the walls are considered for the computation of base shear. The time history of base shear is shown in Fig.13. It represents a similar pattern to that of pressure profile as it is computed from the pressure load generated on the left and right walls.

Fig.13 Time history of base shear due to hydrodynamic pressure

3.4.7 Time history of overturning moment at the base

The overturning moment at the base of a liquid retaining structure during a dynamic event needs to be evaluated precisely to check the stability of the liquid retaining structures. In the present study it is estimated by taking moments of dynamic pressure forces acting on the tank bottom, both walls and ceiling. The timehistory of overturning moment at the base is shown in Fig.14. It is observed from the figure that there is a periodic rise and fall of moment values as the excitation time advances.

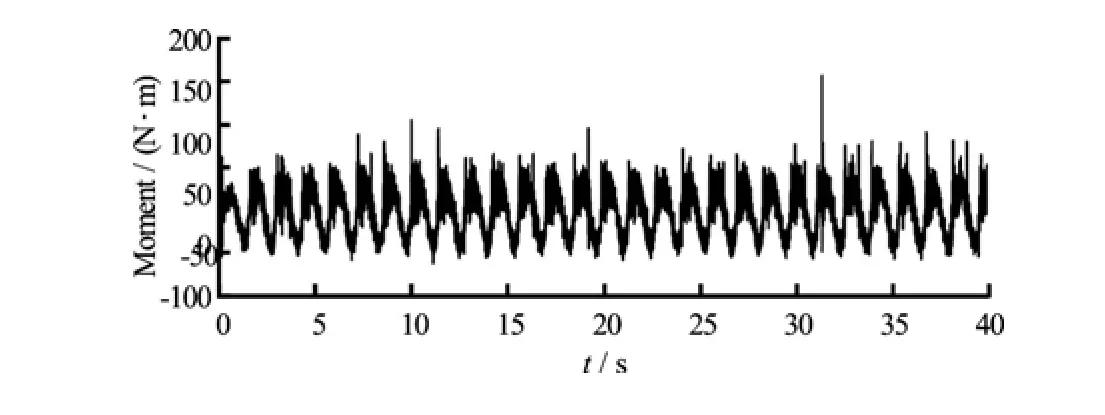
Fig.14 Time history of overturning moment at the base due to hydrodynamic pressure

4. Conclusion

In the present study, a modified MPS model has been used to simulate the violent sloshing motion in a partially filled liquid tank undergoing a horizontal sinusoidal motion. The model includes five modifications over original MPS method. The suggested modifications are multiple source terms for pressure Poisson equation, special approximation technique for the representation of gradient differential operator, collective action of mixed free surface particle identification boundary conditions, effecting Neumann boundary condition on solving the PPE and fixing judiciously the parting distance among particles to prevent collision. The present model is validated through a comparison between numerical results and experimental observations. The fluid flow pattern and free surface profile are well captured during a violent sloshing motion with varying and breaking free surface. The dynamic parameters required for a safe design of a liquid filled container such as sloshing wave amplitude, pressure on the tank walls, impact pressure load exerted on the tank ceiling, base shear and over turning moment are fully assessed.

Acknowledgements

This study is part of a project SR/S3/MERC-0078/2010 funded by Department of Science and Technology, Government of India under its R & D scheme. The authors would like to express their deepest gratitude for the intense support of DST, New Delhi.

[1] Silverman S., Abramson H. N. Lateral sloshing in moving containers [R]. NASA SP-106, 1966, 13-78.

[2] Taniguchi T. Rocking behavior of unanchored flat-bottom cylindrical shell tanks under action of horizontal base excitation [J].Journal of Engineering Structures, 2004, 26(4): 415-426.

[3] Akyildiz H., UNAL E. Experimental investigation of pressure distribution on a rectangular tank due to the liquid sloshing [J].Ocean Engineering, 2005, 32(11-12): 1503-1516.

[4] Frandsen J. B. Sloshing motion in excited tanks [J].Journal of Computational Physics, 2004, 196(1): 53-87.

[5] Faltinsen O. M., Timokha A. N. A multimodal method for liquid sloshing in a two dimensional circular tank [J].Journal of Fluid Mechanics, 2010, 665: 457-479.

[6] Biswal K. C., Bhattacharya S. K. and Sinha P. K. Non linear sloshing in partially liquid filled containers with baffles [J].International Journal for Numerical Methods in Engineering, 2006, 68(3): 317-337.

[7] Monaghan J. J. Simulating free surface flows with SPH [J].Journal of Computational Physics, 1994, 110(2): 399-406.

[8] Shao J. R., Li H. Q., LIU G. R. et al. An improved SPH method for modeling liquid sloshing dynamics [J].Computers and Structures, 2012, 100-101(6): 18-26.

[9] Shao J., LI S., LI Z. et al. A comparative study of different baffles on mitigating liquid sloshing in a rectangular tank due to a horizontal excitation [J].Engineering Computations, 2015, 13(4): 1172-1190.

[10] Kondo M., Koshizuka S. Improvement of stability in moving particle semi implicit method [J].International Journal for Numerical Methods in Fluids, 2011, 65(6): 638-654.

[11] Tanaka M., Masunaga T. Stabilization and smoothing of pressure on MPS by quasi-compressibility [J].Journal of Computational Physics, 2010, 229(11): 4279-4290.

[12] Khayar A., Gotoh H. Modified moving particle semiimplicit methods for the prediction of 2D wave impact pressure [J].Coastal Engineering, 2009, 56(4): 419-440.

[13] Zhang S., Morita K., Fukuda K. et al. An improved MPS method for numerical simulation of convective heat transfer problems [J].International Journal for Numerical Methods in Fluids, 2006, 51(1): 31-47.

[14] Khayar A, Gotoh H. Enhancement of stability and accuracy of the moving-particle-semi-implicit method [J].Journal of Computational Physics, 2011, 230(8): 3093-3118.

[15] Lee B. H., Park J. C., Kim M. H. et al. Step by step improvement of MPS method in simulating violent free surface motions and impact loads [J].Computer Methods in Applied Mechanics and Engineering, 2011, 200(9): 1113-1125.

[16] Akyildiz H. A numerical study of the effects of the vertical baffle on liquid sloshing in two-dimensional rectangular tank [J].Journal of Sound and Vibration, 2012, 331(1): 41-52.

[17] Lee D. H., Kim M. H., Kwon S. H. et al. A parametric sensitivity study on LNG tank sloshing loads by numerical simulations [J].Ocean Engineering, 2007, 34(1): 3-9.

[18] Chen B. F. Viscous free surface effect on coastal embankment hydrodynamics [J].Ocean Engineering, 1999, 26(1): 47-65.

[19] Lee E. S., Moulinec C., Xu R. et al. Comparisons of weakly compressible and truly incompressible algorithms for the SPH mesh free particle method [J].Journal of Computational Physics, 2008, 227(18): 8417-8436.

[20] Kishev Z. R., Hu C. and Kashiwagi M. Numerical simulation of violent sloshing by a CIP-based method [J].Journal of Marine Science and Technology,2006, 11(2): 111-122.

(Received November 29, 2015, Revised March 27, 2016)

*Biography:Debadatta Jena (1972-), Male, Master,

Research Scholar