Numerical investigation of entropy generation and heat transfer of pulsating flow in a horizontal channel with an open cavity*

Fatma Zamzari, Zouhaier Mehrez, Afif El Cafsi, Ali Belghith, Patrick Le Quéré

1.Faculty of Sciences of Tunis, Laboratory of Energy, Heat and Mass Transfer (LETTM), Department of Physics, El Manar University, El Manar 2092, Tunisia, E-mail: fatmazamzari@live.fr

2.Computer Science Laboratory for Mechanics and Engineering Sciences (LIMSI), CNRS Bat 508, BP 133, 91403 Orsay Cedex, France

Numerical investigation of entropy generation and heat transfer of pulsating flow in a horizontal channel with an open cavity*

Fatma Zamzari1, Zouhaier Mehrez1, Afif El Cafsi1, Ali Belghith1, Patrick Le Quéré2

1.Faculty of Sciences of Tunis, Laboratory of Energy, Heat and Mass Transfer (LETTM), Department of Physics, El Manar University, El Manar 2092, Tunisia, E-mail: fatmazamzari@live.fr

2.Computer Science Laboratory for Mechanics and Engineering Sciences (LIMSI), CNRS Bat 508, BP 133, 91403 Orsay Cedex, France

In this study, the entropy generation and the heat transfer of pulsating air flow in a horizontal channel with an open cavity heated from below with uniform temperature distribution are numerically investigated. A numerical method based on finite volume method is used to discretize the governing equations. At the inlet of the channel, pulsating velocity is imposed for a range of Strouhal numbersStpfrom 0 to 1 and amplitudeApfrom 0 to 0.5. The effects of the governing parameters, such as frequency and amplitude of the pulsation, Richardson number, Ri, and aspect ratio of the cavity,L/H, on the flow field, temperature distribution, average Nusselt number and average entropy generation, are numerically analyzed. The results indicate that the heat transfer and entropy generation are strongly affected by the frequency and amplitude of the pulsation and this depends on the Richardson number and aspect ratio of the cavity. The pulsation is more effective with the aspect ratio of the cavityin terms of heat transfer enhancement and entropy generation minimization.

Pulsating flow, entropy generation, mixed convection heat transfer, open cavity

Introduction

Heat transfer in open cavities has received considerable attention, due to its presence in various engineering applications such as cooling of electronic devices, electronic chips and solar receivers. Thus, the knowledge of this flow type is crucial from an economic viewpoint or in terms of environmental acceptability. For this reason, a large number of papers have been recently published on this specific subject. In this context, Manca et al.[1]studied numerically the mixed convection in an open cavity heated from different sides with constant flux. They found that the opposing forced flow configuration has the highest thermal performance in terms of heat transfer rate. In Ref.[2], the same authors carried out an experimental investigationon mixed convection in an open cavity heated from the left wall. They showed that the maximum dimensional temperature rise values decrease as the Reynolds and Richardson numbers decrease. Leong et al.[3]analyzed the mixed convection in an open cavity in a horizontal channel. They found that the heat transfer rate was reduced and the flow becomes unstable in the mixed convection regime. Aminossadati and Ghasemi[4]presented a numerical study of mixed convection in a horizontal channel with a discrete heat source in an open cavity. They showed that the best cooling performance is given when the heat source is located on the right wall. Rahman et al.[5]studied the conjugated effect of joule heating and magneto-hydrodynamic on double-diffusive mixed convection in a horizontal channel with an open cavity. They showed that the flow behavior, heat and mass transfers are affected by applying external magnetic field. Mehrez et al.[6]performed a numerical investigation for the effect of non-isothermal heater on nanofluid flow in an open cavity. They showed thatthe flow behavior, heat transfer and entropy generation are strongly affected by the heater position. Abdelmassih et al.[7]conducted a three-dimensional numerical simulation for mixed convection flow inside a cubic open cavity. They showed that the flow becomes unstable and complicated for a higher Reynolds and Richardson numbers. Stiriba et al.[8]investigated heat transfer and fluid flow characteristics of laminar flow past a three-dimensional open cavity heated from below. They showed that the flow becomes steady and the heat diffusion is predominant at low Reynolds and Richardson numbers.

To improve heat transfer, several techniques have been introduced which can be classified into two methods: active method (which requires external power source) and passive method (requires no external power source). Recently, the pulsating flow (active technique of control) received a great deal of research interest because it is frequently encountered in large application areas: biological systems (arterial flows in the human body), engineering systems (pulsed heat exchanger, cooling system of nuclear reactor, electronic cooling, pulse combustor for both civil and military uses, etc.). A numerical study of mixed convection of pulsating flow and heat transfer characteristics over a backward-facing step under laminar regime was numerically investigated by Khanafer et al.[9]. They showed that the average Nusselt number increases by increasing the pulsation frequency. Khanafer et al.[10]performed a numerical simulation of unsteady mixed convection in a driven cavity using an externally exited sliding lid. They showed that the average Nusselt number increases by increasing the lid frequency. Velazquez et al.[11]investigated a two-dimensional laminar pulsating flow in a heated rectangular cavity with different aspect ratios. They showed that the pulsation enhances heat transfer in the cavity. Sourtiji et al.[12]have numerically investigated the oscillating fluid flow and heat transfer characteristics in a square cavity with inlet and outlet ports. They showed that the heat transfer is enhanced for all the investigated Strouhal numbers in comparison to its steady state case. Selimefendigil and Oztop[13]have numerically investigated the forced convection in pulsating nanofluid flow over a backward facing step with a stationary circular cylin- der. They showed that the heat transfer is enhanced by increasing the frequency of the oscillation. Unal at al.[14]performed a numerical study of heat transfer characteristics and nanofluid flow in a wavy minichannel under pulsating inlet flow conditions. They showed that the heat transfer performance is enhanced at high nanoparticle volume fraction and at low pulsating frequency. In the case of open cavity geometry, Selimefendigil and Yurddas[15]performed a numerical study of pulsating flow in a channel with a cavity heated from below and a left vertical side. They showed that the heat transfer enhancement is affected by the pulsation and this depends on the Reynolds and Richardson numbers.

The second law of thermodynamics is considerably important because it presents the basis of assessing the irreversibility (entropy generation). The minimization of entropy generation has been considered as an effective tool to improve the performance of heat transfer process and consequently enhances the efficiency of energy utilization. Entropy generation has recently been the topic of great interest in fields such as heat exchangers, turbo machinery, electronic cooling, porous media and combustion. The entropy generation in the convective flows is caused by the variations of irreversibilities due to the heat transfer (due to the conduction) and friction (due to the viscosity). Many studies have been published on entropy generation. Abu-Nada[16]investigated the entropy generation of laminar flow over a backward facing step. He showed that the entropy generation varies by variation of Reynolds number, Brinkman number and dimensionless temperature parameter. In the same context, Abu-Nada[17]showed that the entropy generation depends on the expansion ratio. Khorasanizadeh et al.[18]investigated the mixed convection and entropy generation of Cu-water nanofluid and pure water in a lid-driven square cavity. They showed that it is possible to obtain a configuration giving maximum heat transfer against minimum entropy production. Nayak et al.[19]have numerically studied the mixed convection of copper-water nanofluid inside a differentially heated skew enclosure. They showed that the average rate of heat transfer and entropy generation is sensitive to the skew angle and the nanoparticle volume fraction. Recently, a critical review of contributions to the theory and application of entropy generation analysis to different types of engineering systems is performed by Sciacovelli et al.[20].

In the case of open cavity geometry, Mehrez et al.[21]numerically studied the heat transfer and entropy generation of nanofluid flow in an open cavity for various types of nanoparticles (Cu, CuO, Al2O3, TiO2). They showed that the heat transfer and the entropy generation rates are affected by varying the volume fraction and type of nanoparticles, Reynolds and Richardson numbers and aspect ratio of the cavity. For the same configuration, Mehrez et al.[22]analyzed the MHD effects on the flow structure, heat transfer and entropy generation of Cu-water nanofluid flow. They showed that the entropy generation and the heat transfer are strongly affected by the presence of external magnetic field. Recentely in Ref.[23], Mehrez et al. studied the effect of inclination angle of the channel on nanofluid flow. They showed that the heat transfer phenomenon and irreversibility mechanism depend mainly on the inclination angle. Zamzari etal.[24]studied the entropy generation and the heat transfer of air-flow in a horizontal channel with an open cavity, they showed that, with an appropriate choice of pertinent parameters of the flow and aspect ratio, it can obtain minimum entropy generation with high heat transfer.

To our knowledge, the effect of pulsation on the flow behavior, heat transfer and entropy generation in an open cavity is not yet studied; this motivated us to study this problem. Therefore, the main objective of the current investigation is to understand how heat transfer and entropy generation are influenced by the presence of pulsation at the inlet. The results are graphically presented by streamlines, isotherms, spatial and spatial-temporal averaged Nusselt numbers, entropy generation and Bejan numbers for different Richardson numbers, aspect ratios of the cavity and various frequencies, phases and amplitudes of the pulsation.

1. Physical problem

A schematic description of the physical problem is shown in Fig.1. It consists of a two-dimensional horizontal channel including an open cavity.LandHare the length and height of the cavity respectively. The channel lengthlis set to 7H. The bottom wall of the cavity is heated by a uniform temperature distribution while the other walls are insulated. The Richardson number is varied in the range of 0.25≤Ri≤1. Three aspect ratios of the cavity,L/H=1, 1.5 and 2 are considered in this study. At the inlet the cold fluid is maintained at a uniform temperatureTc. The bottom wall of the cavity is heated with a constant temperatureTH. A sinusoidal velocity is imposed in the entrance of the cavity:wherefpandApare the frequency and the amplitude of the pulsation respectively.

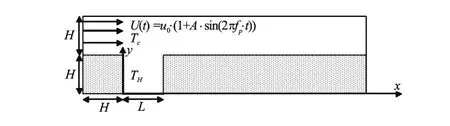
Fig.1 Geometric configuration

2. Governing equations

A two-dimensional, incompressible and laminar flow is considered. The fluid properties are assumed to be constant. The dimensional form equations, continuity (1), momentum (2), (3) and energy (4), describing the flow under Boussinesq approximation are as follows:

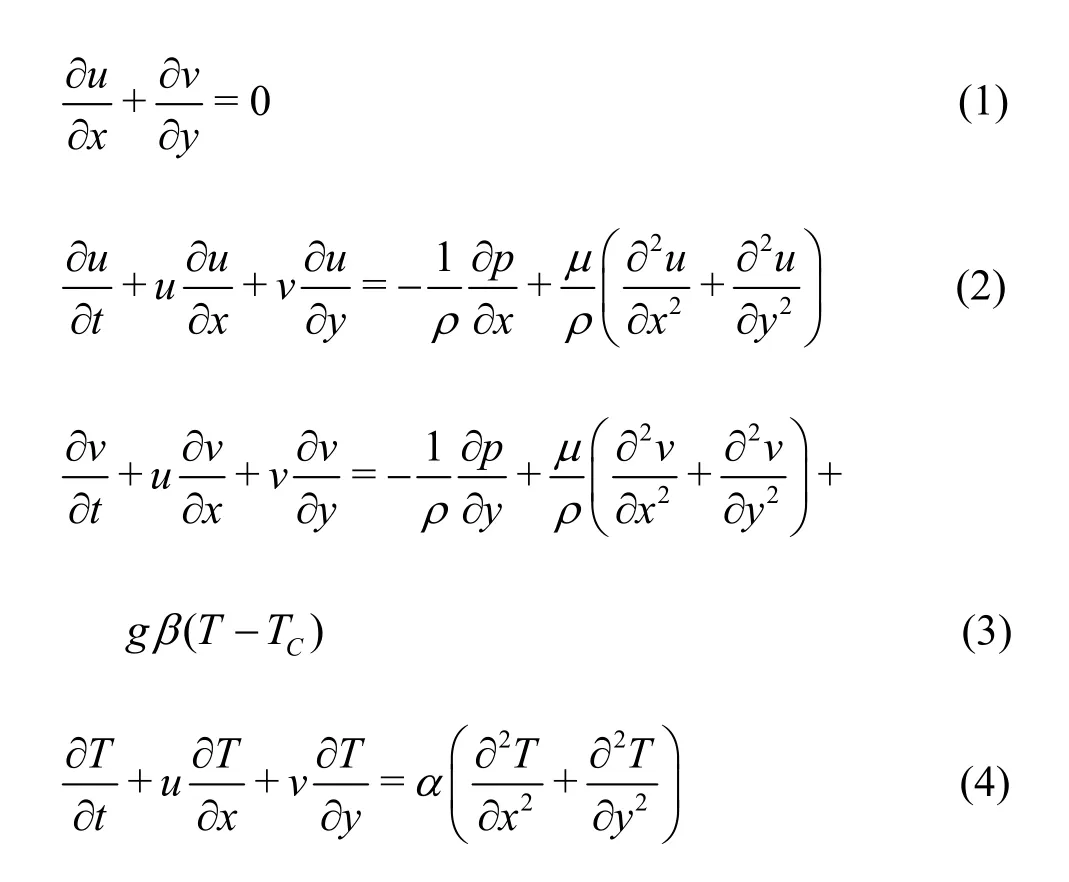
These equations are used in previous published works[3,4,7].

The following dimensionless parameters are used to obtain the dimensionless form of the above equations:

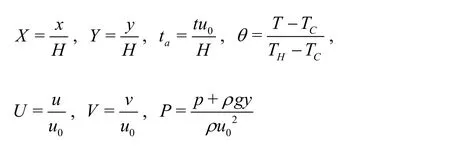
The governing equations, in dimensionless form, are expressed as follows:

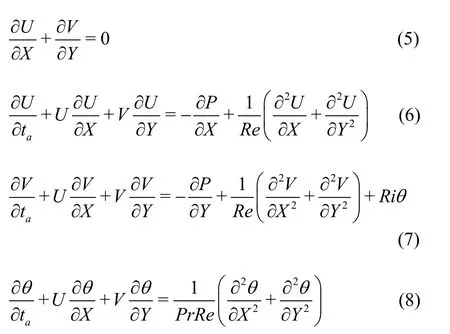
The relevant physical parameters are:

Richardson number

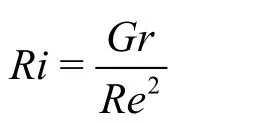
whereGris the Grashof number,

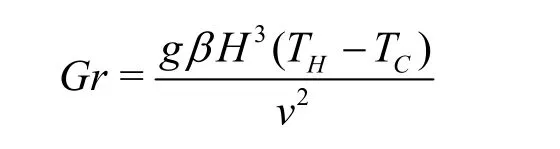
Reynolds number

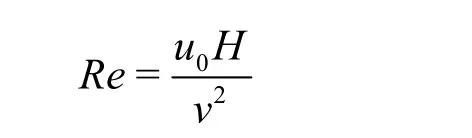
This expression ofRe, based on the cavity height and velocity at the inlet, is already used by previous works: Manca et al.[1], Abu-Nada et al.[16,17]and Mehrez et al.[21].

Prandtl number

in all the work has a fixed value of 0.71 correspond to the air.

The boundary condition in dimensionless form can be expressed as:

At the channel inlet: A velocity with a sinusoidal time dependent part is imposedU=[1+Asin(2πStp·ta)], whereAis the non-dimensional amplitude,

is the Strouhal number based on the pulsation frequency

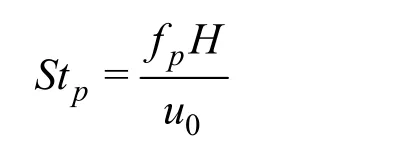
On the bottom wall of the cavity, temperature is constantθ=1 and the remaining walls are insulated. (10)

On the solid surfaces, a No-slip conditions are prescribed:U=V=0 (11)

At the exit, convective boundary conditions are applied

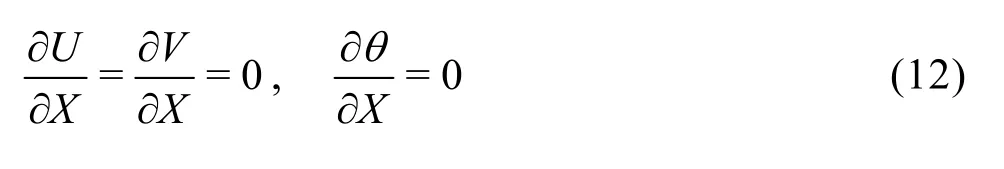
Heat exchanges for fluid flow within the cavity between the hot wall and the fluid are characterized by local Nusselt number given by the relation

The spatial average Nusselt number,Nus, is obtained by integrating the above local Nusselt number

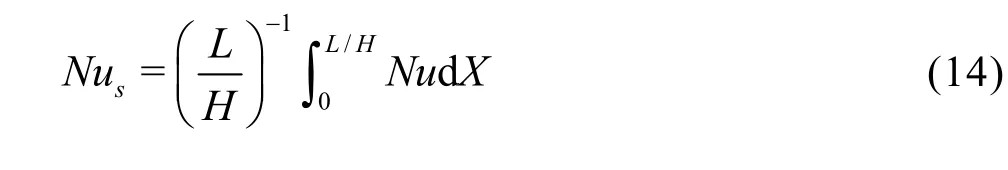
The spatial and temporal average Nusselt number,Num, is obtained by integratingNusfor one period of the pulsation,τ, and is given by

The normalized Nusselt numberis defined as

whereis the non pulsating case.gives the rate of heat transfer variation by applying pulsation.

Entropygeneration rate for a two-dimensional flow in Cartesian coordinates is given by Bejan[25]

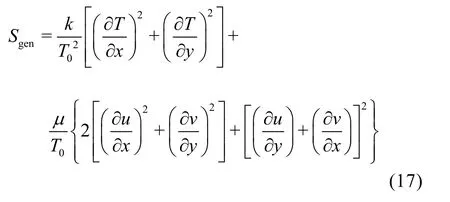
While dividingSgenby

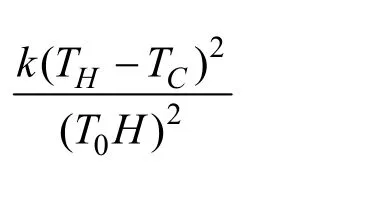
and by using the same dimensionless parameters given above, the dimensionless entropy generation is given as follows:

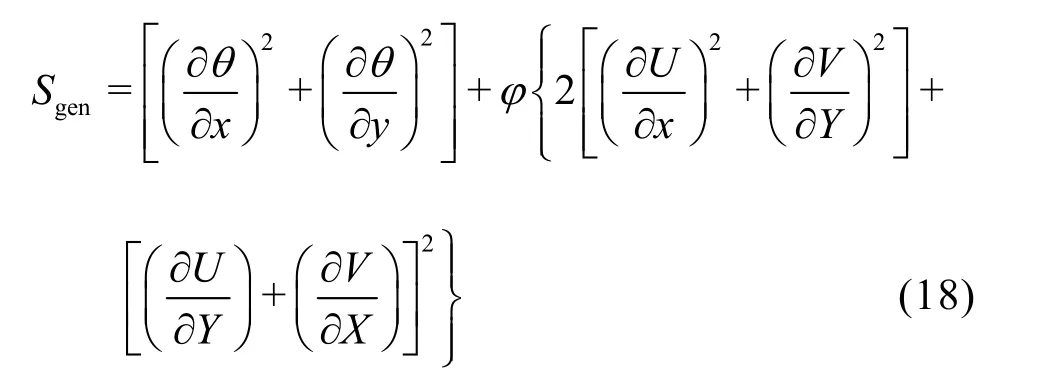
where the irreversibility factorφis given as

φcan be expressed as a function of non-dimensional numbers as follows

whereis the Eckert number,is the Prandtl number,is the dimensionless temperature difference and

The first term on the right-hand side of Eq.(19) corresponds to the heat transfer irreversibility (Sgen,c) whereas the second term corresponds to the irreversibility due to viscous dissipation (Sgen,v).

The spatial average entropy generation over the entire flow domain is calculated by using the following equation

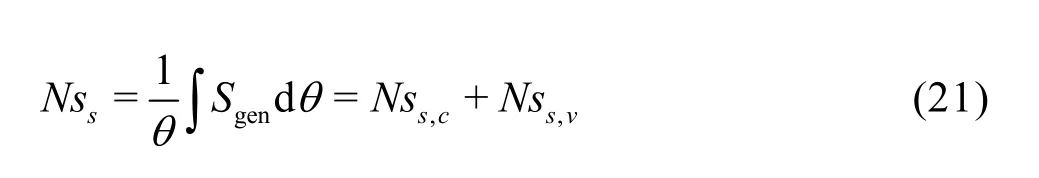
where

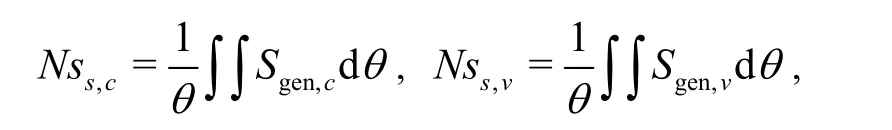
andθis the volume of computational domain.

The spatial-temporal average entropy generation is obtained by integratingNssduring one period of pulsation

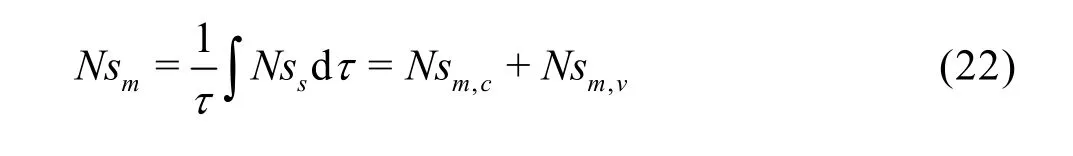
The normalized entropy generationis defined as

whereSt=0is the non pulsating case.gives the rate of entropy generation variation.

The Bejan number,Be, defined as the ratio between the entropy generation due to heat transfer by the total entropy generation, is expressed as

It is known that whenBe?0.5 the irreversibility due to heat transfer dominates. WhenBe?0.5 the irreversibility due to the viscous effects dominates the processes and ifBe=0.5 the entropy generation due to the viscous effects and the heat transfer effects are equal.

3. Numerical procedure

3.1 Numerical method

The unsteady Navier-Stokes equations are discretized in space by the finite volume method. The time integration is performed using a time-splitting algorithm, also known as a prediction projection algorithm, which allows one to decouple pressure from velocity[26,27]. Assuming all quantities known at timenΔT, the solution at time (n+1)ΔTis obtained as follows:

An intermediate velocity fieldV*is first computed using a second-order time scheme. This time stepping combines a second order backward Euler scheme for the diffusion terms, with an explicit second-order Adams-Bashforth extrapolation for the non-linear terms, taking into account known pressure field. This step reads

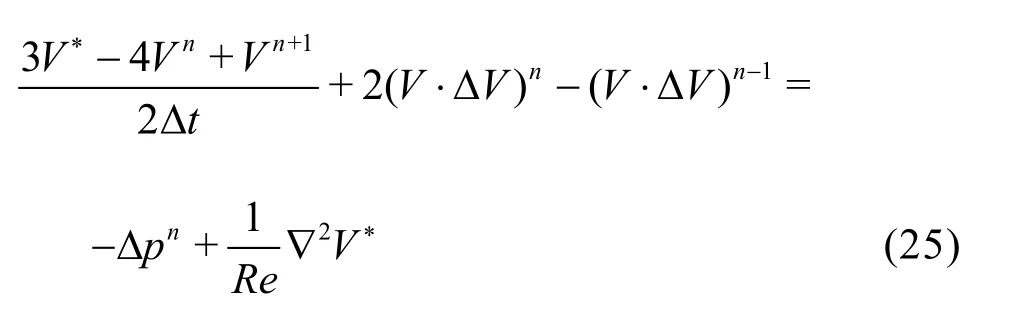
In the second step, this intermediate velocity field is projected on to the subspace of divergence free vector field using the Helmholtz decomposition theorem. This step reads

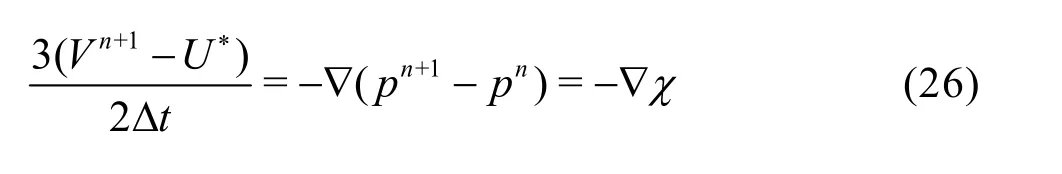
where

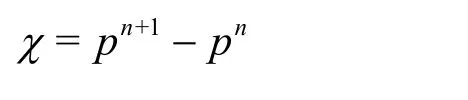
It is accomplished by taking the divergence of equation giving rise to a Poisson’s type equation for the incremental pressure

This equation is solved with a multigrid algorithm, in which the presence of internal blockings is automatically taken into account.

Once the pressure field is obtained, the newquantities atn+1 are given by

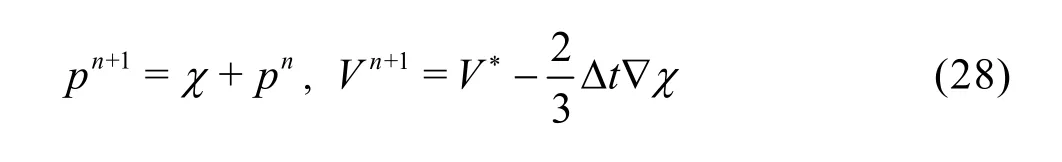
A second order upwind finite difference method by means of a QUICK scheme, proposed by Leonard[28]is used for the convective terms and a centered scheme for the diffusive ones.

The computations are carried out by using a FORTRAN house code developed in collaboration between LIMSI (France) and LETTM (Tunisia). This code has been successfully used for different types of problems[26,27,29,30].

3.2 Grid testing

The effect of grid size is examined by running different combinations ofRi,L/H,ApandStpon different uniform grids. (Figs.2, 3) represent a sample of results giving the effect of grid refinement on the time and space averaged Nusselt and entropy generation, numbers forRe=200,Ri=1,L/H=1,Ap=0.1 andStp=0.4 (Fig.2) and local Nusselt numberNuforRe=200,Ri=1,L/H=1 andAp=0 (Fig.3). The grid of 132×124 is chosen for the present investigation because it makes a good compromise between the accuracy of the solution and the cost of computation time. It is noted that in the present wok, the aspect ratio of the cavityL/His varied by varying the length of the cavityLwhile fixing the heightH. For higher aspect ratios of the cavity, the number of grid points in theXdirection is increased accordingly.

3.3 Solution verification

It is known that the main source of numerical errors is the discretization due to limited number of grid points. To evaluate the numerical errors and associated uncertainties, the solution verification is performed following the method of safety factor proposed by Xing et al.[31-33]with three different grids: fine (132×124), medium (110×103) and coarse (92×86) forRe=200,Ri=1,L/H=1,Ap=0.1 andStp=0.4 using two parameters: time and space averaged Nusselt numberNumand time and space averaged entropy generation numberNsm(Table 1).The three chosen grids are generated using a constant grid refinement ratior=1.2 in the two spatial directions (XandY). If 3, 2, and 1 represent the coarse, medium, and fine grids with spacing Δx3, Δx2and Δx1,ris given as follows

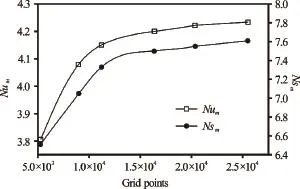
Fig.2 Variation of time- spatial averaged Nusselt and entropy generation numbers with the grid size

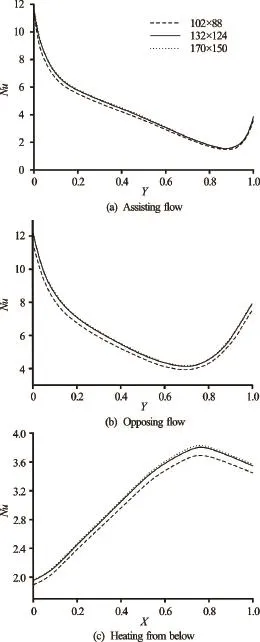
Fig.3 Local Nusselt number profiles for various grid sizes

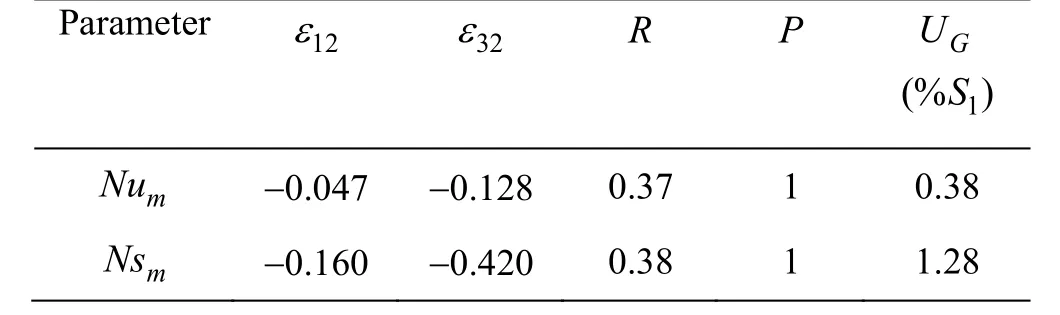
Table 1 Solution verification for time and space averaged Nusselt and entropy generation numbers

If the solutions for the fine, medium and coarse grids areS1,S2andS3, respectively, solution changesεfor medium-fine and coarse-medium solutions and the convergence ratioRare defined by:

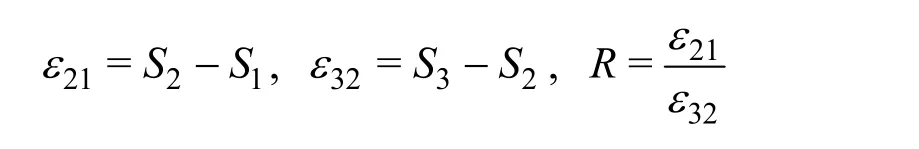
The monotonic convergence is achieved when 0＜R＜1. Then the three grid solutions can be used to compute the estimated order of accuracypRE, error

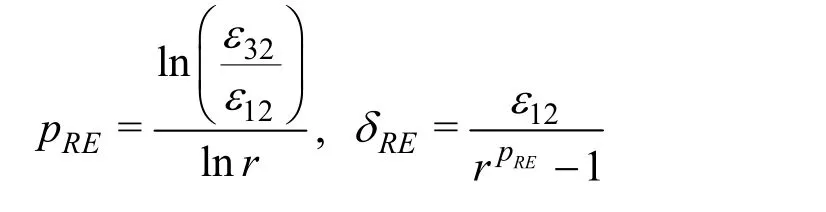
When solutions are in the asymptotic range, i.e.,however, in many circumstances, especially for industrial applications, solutions are far from the asymptotic range such thatpREis greater or smaller thanpth[34]. In this work all the solutions are calculated in the asymptotic range. The ratio ofpREtopthis used as the distance metric

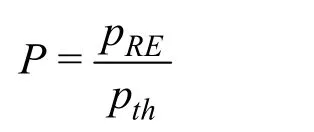
The grid uncertainty is estimated by:

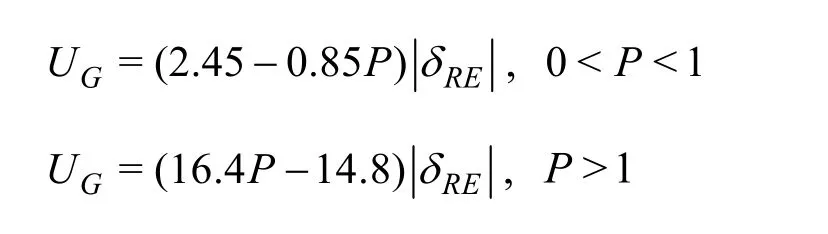
As shown in Table 1, monotonic convergence is achieved with a low grid uncertainty of 0.38%S1forNumand 1.28%S1forNsm. This shows that the current fine grid resolution is sufficient for the present problem. It is used for all simulations.

3.4 Code validation

In order to testing the performance of the present numerical code, the steady-state solution represented by maximum temperatureθmaxand dimensionless minimum stream functionΨmin, which is obtained in a two-dimensional channel with a cavity heated from different sides with uniform heat flux atRe=100,Pr=0.71, is compared with the results of Manca et al.[1](see Table 2). Also, Fig.4 compares the temperature profile at midsection of the enclosure for assisting forced flow case given by our code and that of Manca et al.[1], =100ReandRi=0.1. In Table 2 and Fig.4 a good agreement between the present results and those of Ref.[1] is observed.

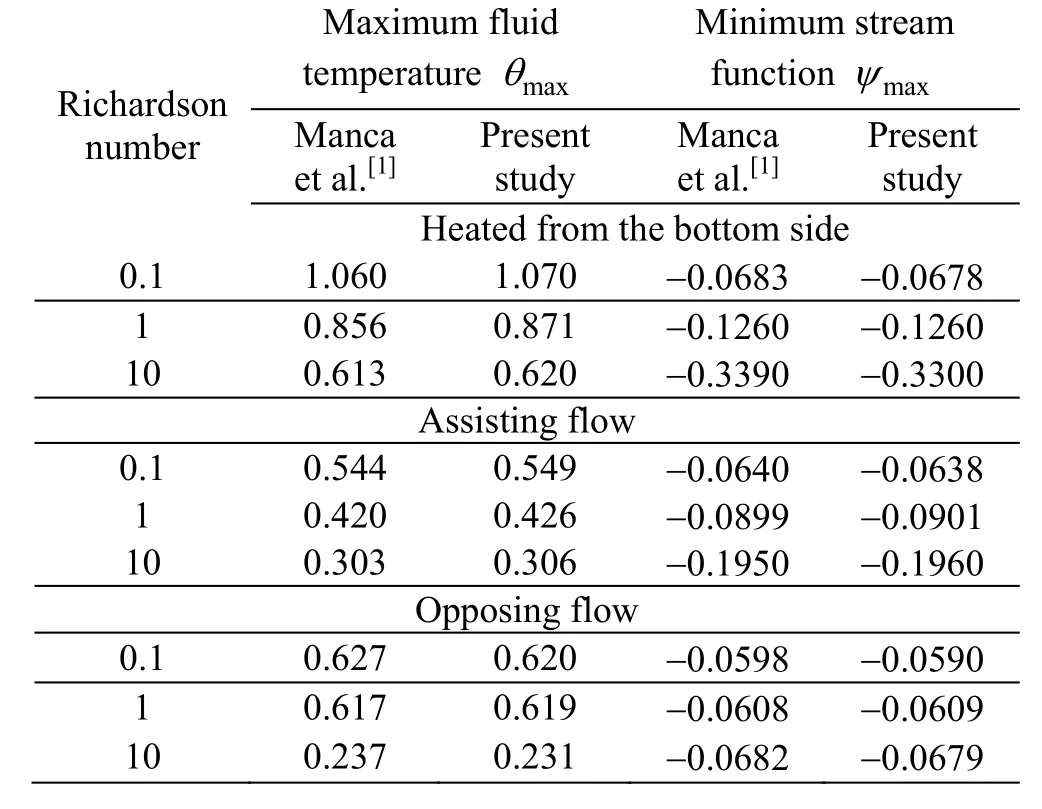
Table 2 A comparison between the present study and Manca et al.[1]

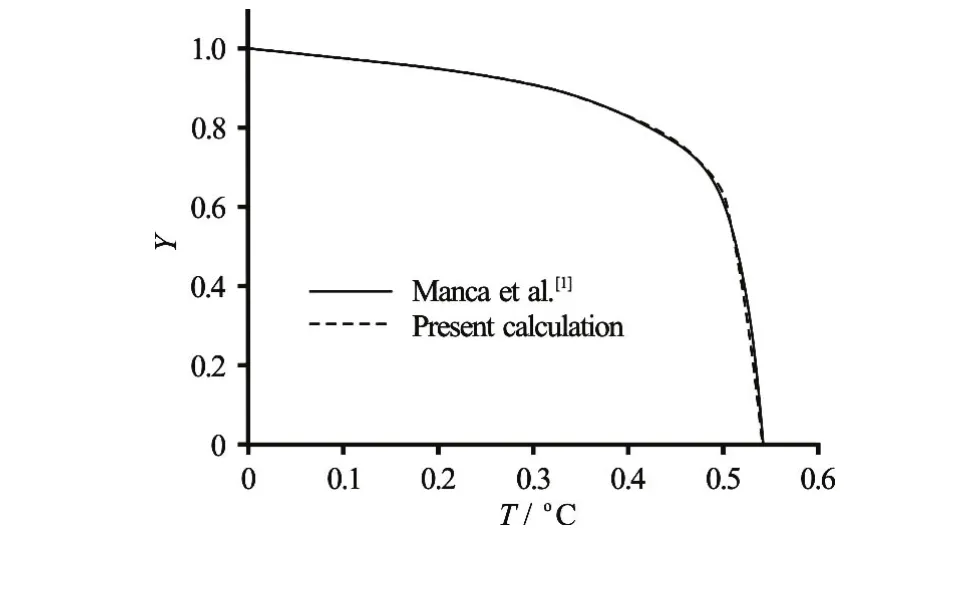
Fig.4 Comparison of temperature profile at midsection between the present study and Manca et al.[1]

4. Results and discussion

In the present work, investigations were performed within the range of Strouhal number:, amplitude of pulsation:Richardson number 0.25≤Ri≤1 and aspect ratio of the cavity 1≤L/H≤2 and for Reynolds numberRe=200, the Prandtl number is kept constant at 0.71 to guarantee constant fluid physical properties for mo-derate and small values of temperature difference. The irreversibility factorφis set equal to 0.01. To analyze the flow behavior and the effect of the mixed convection, the streamlines and the isotherms during a periodic-steady cycle for three values of aspect ratios:L/H=1,L/H=1.5 andL/H=2 are illustrated in Fig.5 forAp=0.1,Stp=0.3,Ri=0.5.

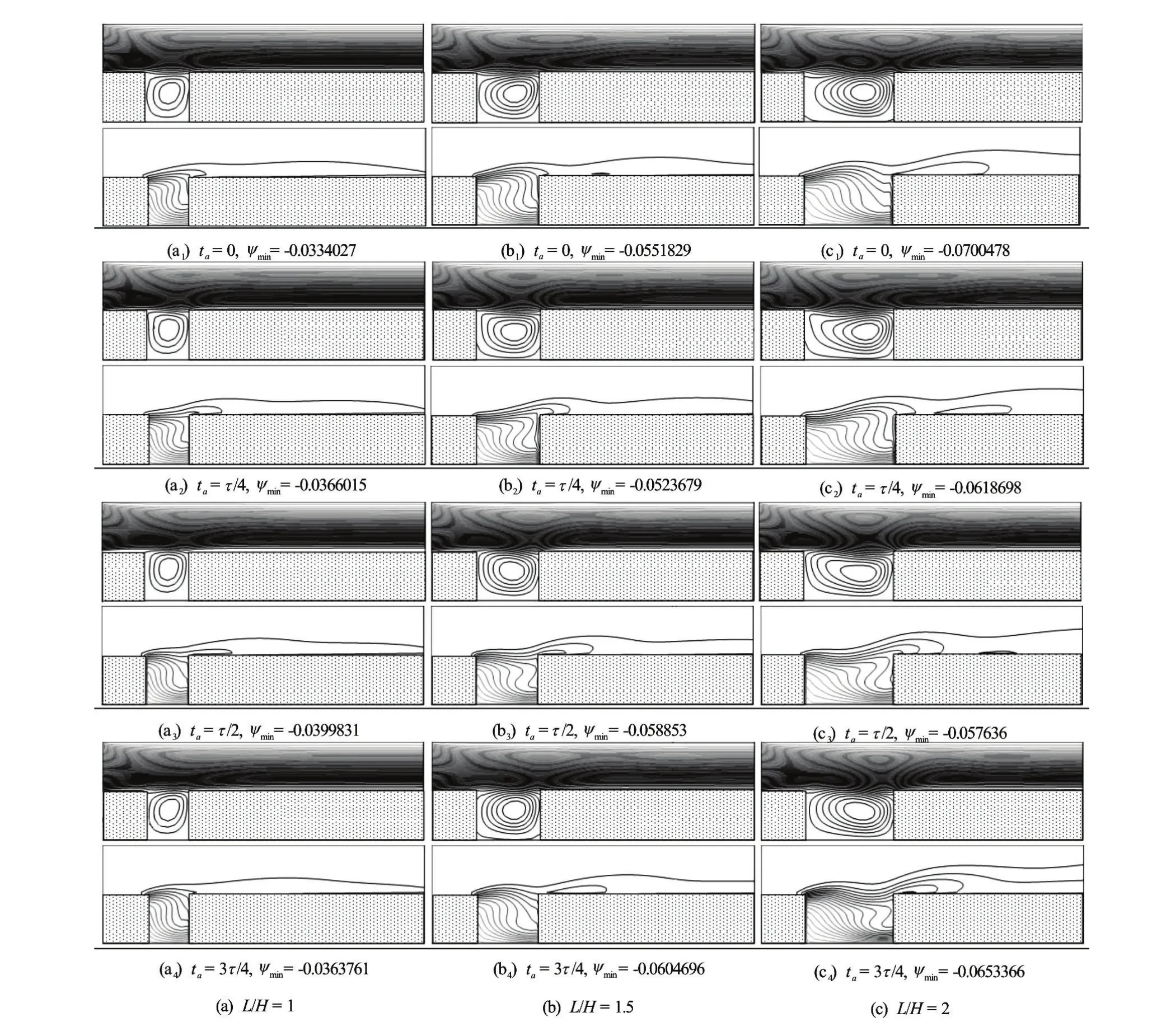
Fig.5 On the top: Streamlines, on the bottom: Isotherms at different pulsation phase and variousL/H,Ap=0.1,Stp=0.3 and

It is noted that, for all the consideredL/H, the presence of a large recirculation cell which fills the entire cavity. The intensity of this eddy varies during a pulsation period due to the temporal variation of the velocity on the entrance. It is also noted that the intensification of the flow field by increasingL/Hduring the whole period except tota=τ/2 when the flow forL/H=1.5 is slightly more intense thanL/H=2.

Isotherm plots show the formation of thermal flow forL/H=1.5 is slightly more intense than layer near the heated surface (thermal stratification), where the temperature gradually varied from the heated wall to the cold part indicating the domination of heat transfer conduction mechanism. It is clearly seen that the thickness of the thermal layer near the heated surface and the clustering of the isotherms are changed during a period. It is noted also that, by increasingL/Hthe isotherms become closer near the hot wall showing the increase of temperature gradients.

Fig.6 Variations of spatial-averaged Nusselt number versus time for different amplitudes of pulsation atRi=0.5

Temporal variations of spatial-averaged Nusselt numberNus(Eq.(14)) for different pulsation amplitudesAp, different Strouhal numbersStpand various aspect ratiosL/Hare depicted in Fig.6. As can be seen in this Figure a sinusoidal shape of theNuswith time can be observed. The oscillation ofNusaround a mean value is obtained with a time period equal to that of the pulsation. The maximum value ofNusincreases with increasing the pulsation amplitude. The shape of the oscillation is preserved for low frequency, but by increasingStpthere appears distortion of the pure sinusoids.

In order to evaluate the effects of the pulsation flow on the heat transfer enhancement, Fig.7 displays the time-spatial averaged Nusselt numberNum(Eq.(15)) versus Strouhal number, for different Richardson numbers (Ri=0.25,Ri=0.5 andRi= 1), for various aspect ratios of the cavity atAp=0.1. It is clearly seen that the all curves have the same increase-decrease profile with a peak at a certainStp.

This phenomenon clearly illustrates the existence of an optimum frequency for the maximum heat transfer enhancement ratio. Starting fromStp=0 (steady flow)Numincreases by increasing Strouhal number until an optimalStpheat transfer rate is reached, and then decreases afterward. This enhancement of heat transfer rate is more effective by increasingRi. Thus, the heat transfer into the cavity is enhanced by increasing the buoyancy effects. It isnoted also that the location of the maximum heat transfer shifts towards the right (low value ofStp) by increasing the aspect ratio of the cavity. The maximum enhancement of heat transfer is obtained atStp=0.4 forL/H=1, atStp=0.4 forL/H=1.5 and forStpbetween 0.2 and 0.3 forL/H=2. This figure shows also that the flow with the aspect ratio of the cavityL/H=1.5 gives higher values ofNumcompared with the other cases.

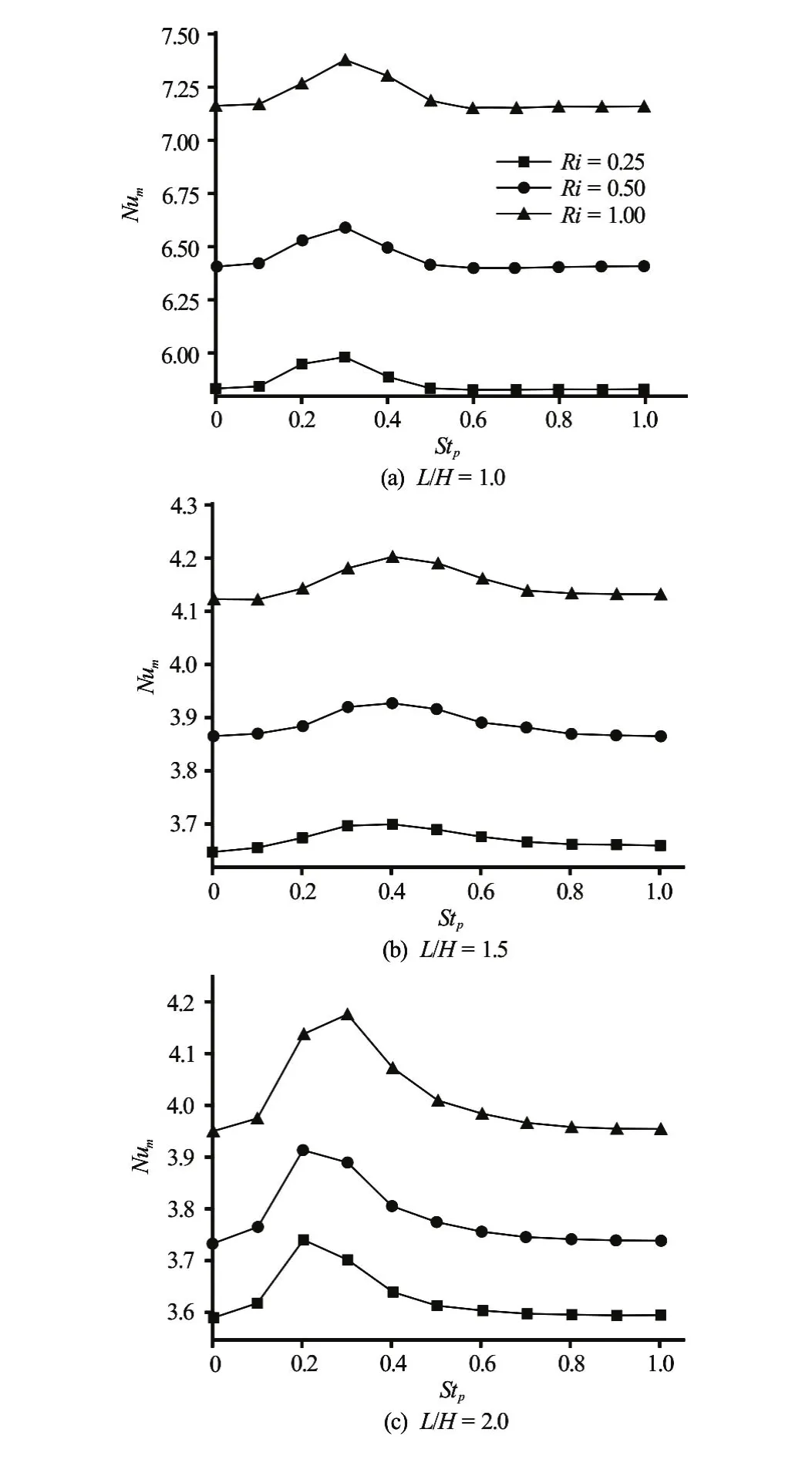
Fig.7 Time- spatial averaged Nusselt number against pulsation frequency for various Richardson numbers forAp=0.1

The time-spatial averaged Nusselt numberNumagainst pulsation amplitudeApis plotted in Fig.8 for various Richardson numbers, and various aspect ratios (Stp=0.3). This figure shows the effect of increasing Richardson number on improvement of heat transfer for allApandL/Hvalues, and this is due to the intensification of buoyancy effect.

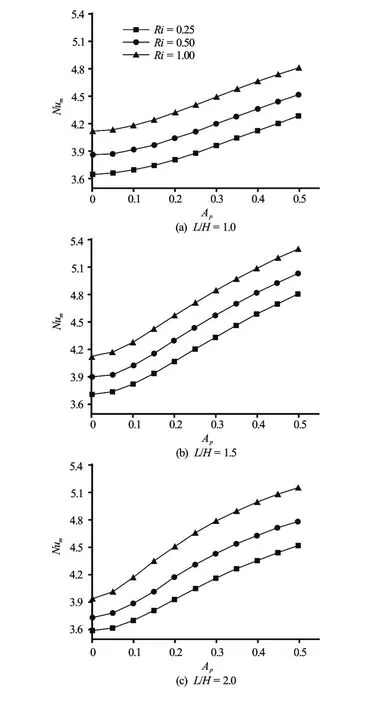
Fig.8 Time-spatial averaged Nusselt number against pulsation amplitude for various Richardson numbers forStp=0.3

Furthermore it is observed that, for all Richardson numbers, the time-spatial averaged Nusselt number increases sharply with the velocity amplitudes and this can be explained by the increase of the temperature gradient due to the increase ofAp. This shows the importance of the pulsation to improve heat transfer. It is noted also that the highest heat trans-fer is obtained withL/H=1.5.

Fig.9 Variations of spatial-averaged entropy generation versus time for different amplitudes of pulsation atRi=0.5

Temporal variations of spatial-averaged entropy generationNss(Eq.(21)) for different velocity amplitudes, different Strouhal numbers and various aspect ratios are depicted in Fig.9.Nssoscillates periodically around a mean value with a time period equal to that of pulsation. The sinusoidal aspect ofNssappears by increasing the Strouhal number. In all cases, the peak of the entropy generation increases generally with increasing the amplitude of the pulsation periodically around a mean value with a time period equal to that of pulsation. The sinusoidal aspect ofNssis more visible for low value ofStpand a distortion appears by increasing the Strouhal numfor various Richardson numbers atis displayed in Fig.10. Obviously, the figure shows a resonant type behavior similar to Fig.11.Nsmincreases by increasing pulsation frequency, attains a maximum and then decreases. This diagram not only verifies the effect ofStpon average entropy generation but also shows that by increasing Richardson numberNsmincreases due to augmentation of the ber. In all cases, the peak of the entropy generation increases generally with increasing the amplitude of the pulsation.

To testing the influence of the pulsation on entropy generation, the time-spatial averaged entropy generationNsm(Eq.(23)) versus Strouhal numberbuoyancy effect. This increases the velocity and temperature gradients and therefore leads to an increase in viscous and conduction contribution to the entropy generation.

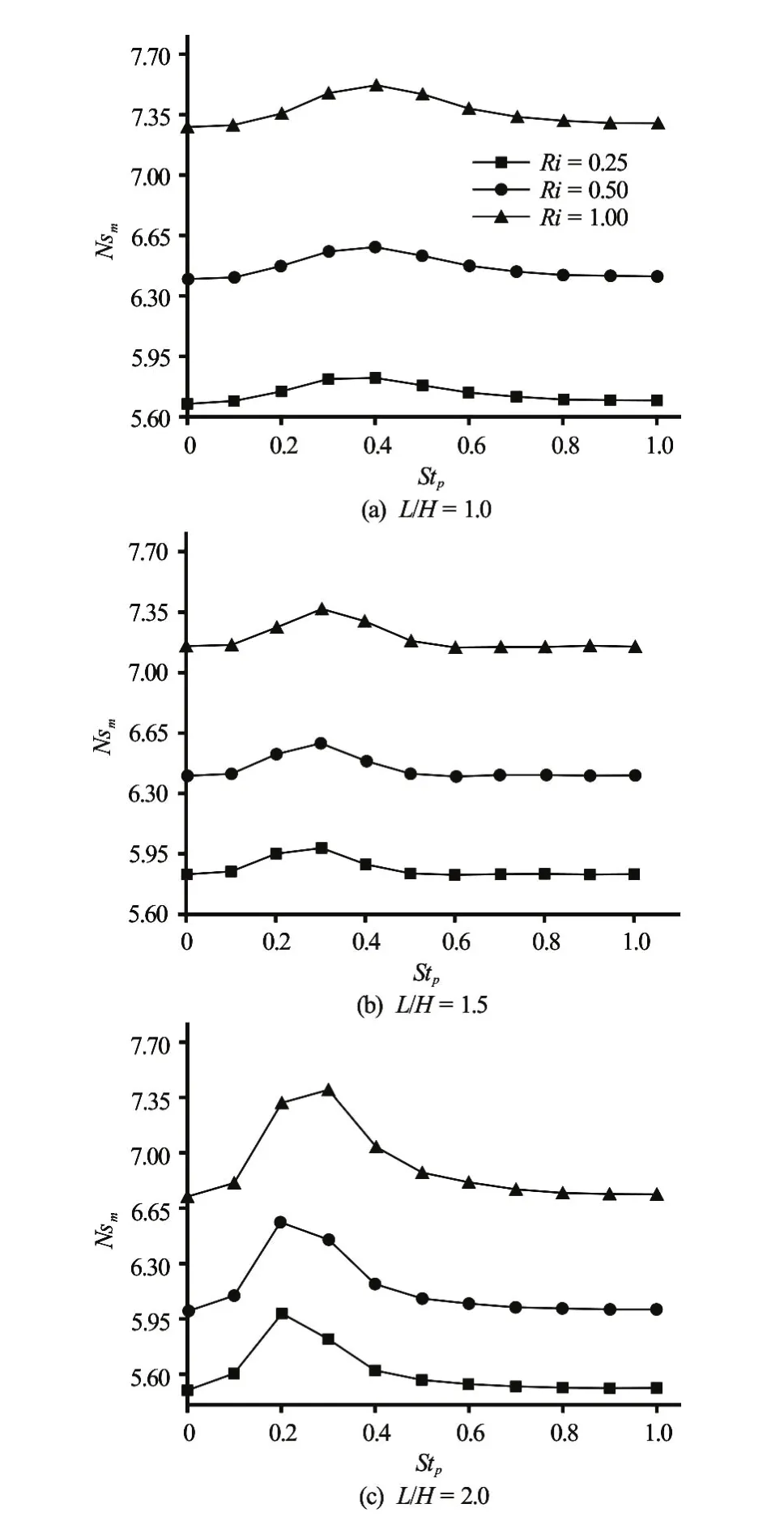
Fig.10 Time- spatial averaged entropy generation against pulsation frequency for various Richardson number for

These effects are more pronounced atL/H= 1.5 forRi=0.25 andRi=0.5 which gives a maximum entropy generation, but forRi=1 entropy generation becomes minimal. It is noted also that the maximum ofNsmis shifted toward the right by increasing the aspect ratio of the cavity. Thus this maximum is obtained atStp=0.4 forL/H=1,Stp=0.4 forL/H=1.5 andStpbetween 0.2 and 0.3 forL/H=2.

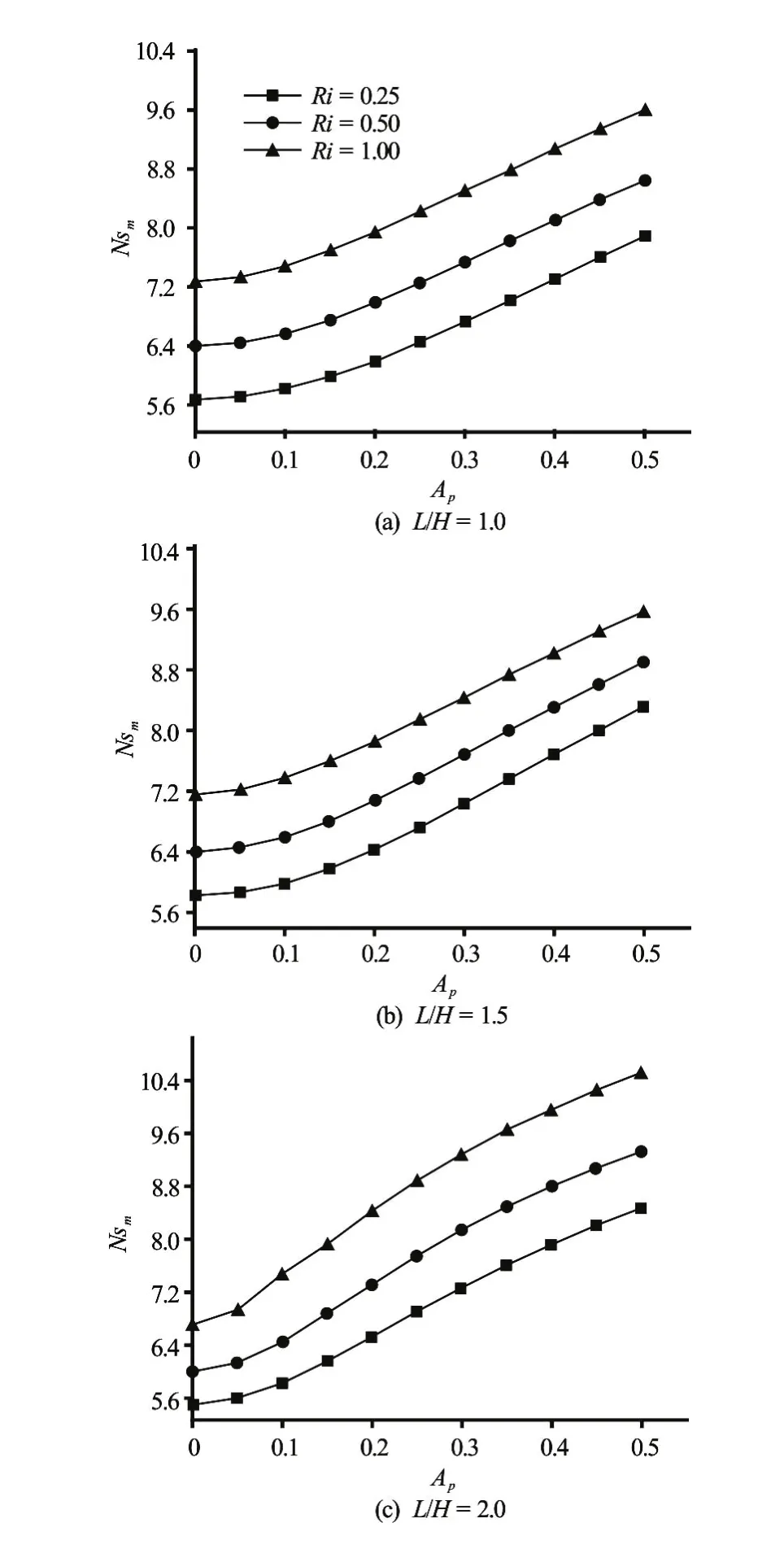
Fig.11 Time- spatial averaged entropy generation against pulsation amplitude for various Richardson numbers for

Figure 12 illustrates the variations of Bejan numberBe(Eq.(25)) versus Strouhal number for various aspect ratios atAp=0.1. It is seen that, by comparing the curves of different cases, the Bejan number increases by increasing aspect ratio of the cavity and this can be explained by the intensification of heat transfer irreversibility relative to the friction one. Results show also that the increase ofStpreducesBecompared with non-pulsed case. This is due to the intensification of viscous irreversibility compared with that of conduction.

The Bejan number against pulsating amplitude for various aspect ratios, various Richardson numbersatStp=0.3 is plotted in Fig.13. It is observed, for all the cases, that the Bejan number decreases with the increment of the pulsation amplitudeAp, except atL/H=1.5 forRi=0.25 andRi=0.5 where Bejan number increases slightly with increasingApand then decreases. It can be observed from this figure that for low value ofAp,Beincreases by increasingL/H, but from a certain value of pulsation amplitude (Ap=0.25forRi=0.25,Ap=0.35 forRi=0.5 andAp=0.5 forRi=1), the values ofBeforL/H=1.5 are greater than those forL/H=2.

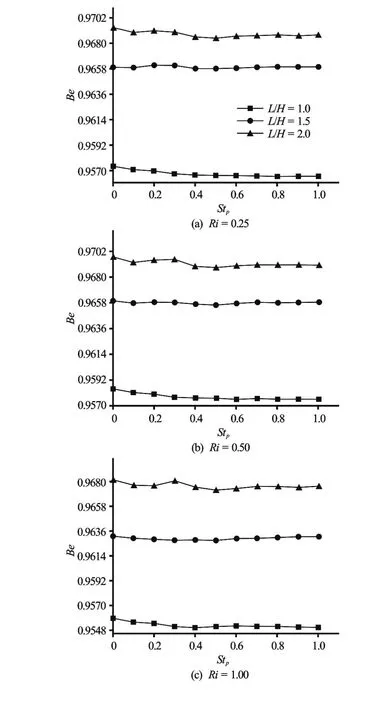
Fig.12 Bejan number against Strouhal number for various aspect ratios atAp=0.1

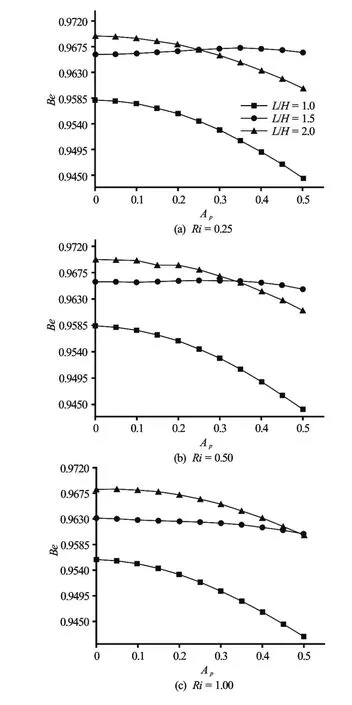
Fig.13 Bejan number against pulsation amplitude for various aspect ratios atStp=0.3

It is noted that the values of Bejan number are high (close to 0.9). This proves that entropy generation contributed by conduction,Nsm,c, is dominant relative to that contributed by viscous irreversibility,Nsm,yin the entropy generation.

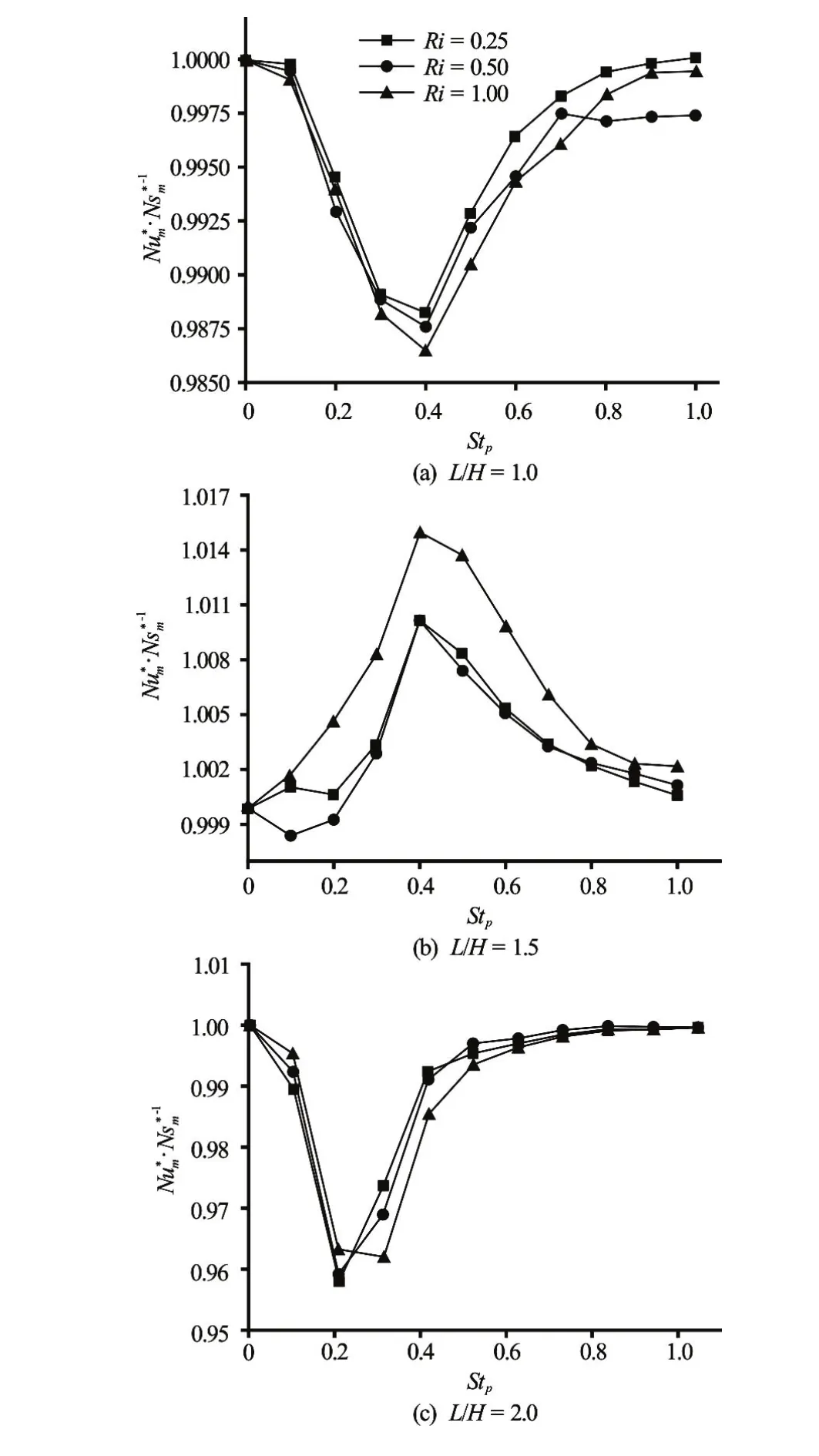
Fig.14against Strouhal number for various Richardson numbers at

To complete our investigation it is very important to see the effectiveness of the pulsation. So we choose to study the variations of the quotient between the normalized Nusselt number(Eq.(16)) and the normalized entropy generation(Eq.(24)) versus Strouhal number for various Richardson number atAp=1 (Fig.14). As shown in this figure, the quotientdecreases as a function ofStpattains a minimum and then increases and this for a value of aspect ratioL/H=1 andL/H=2. However forL/H=1.5, the reverse trend was observed,increases as a function ofStpattains a maximum forStp=0.4 and then decreases. In this case, the maximum of this quotient becomes more apparent by increasingRi. By comparing the quotient with the unit, it can be concluded that for configurations withL/H=1 andwhich means that the rate of entropy generation is more important than the rate of heat transfer enhancement. But for the case ofL/H=1.5, this ratio is greater than 1. This shows that the rate of heat transfer enhancement is greater than the rate of entropy generation. It should be noted that the mentioned variations ofare generally small, since the maximum variation is about 4 %.

Finally, it can be concluded that, for all cases studied the pulsation is relatively more effective forL/H=1.5,Ri=1 and for a pulsation frequencySt=0.4 with a pulsation amplitudeAp=0.1.

5. Conclusions

In this paper, heat transfer and entropy generation of pulsating flow in an open cavity heated from the bottom wall are numerically studied. The effects of the pulsation parameters such as phase, frequency and amplitude as well as pertinent parameters such as Richardson number and the aspect ratio of the cavity are studied. The main conclusions obtained are summarized as follows:

(1) The flow behavior and the temperature distribution are strongly affected by the pulsation.

(2) The space-averaged Nusselt and entropy generation numbers oscillate periodically versus the time with a period equal to that of pulsation.

(3) The pulsation increases heat transfer and entropy generation. The maximum heat transfer rate is observed for an optimum Strouhal number which depends on Richardson number and aspect ratio of the cavity.

(4) The heat transfer and the entropy generation rates during a pulsation cycle increase considerably by increasing the pulsation amplitude.

(5) The contribution rate of each irreversibility type in the entropy generation varies by varying the frequency and the amplitude of the pulsation. It depends on Richardson number and aspect ratio of the cavity.

(6) The configuration with aspect ratio of the cavityL/H=1.5 is more effective because it gives, by applying a pulsation at the inlet, an enhancement rate of heat transfer greater than the increase rate of the entropy generation.

[1] Manca O., Nardini S., Khanafer K. Effect of heatedwall position on mixed convection in a channel with an open cavity [J].Numerical Heat Transfer, 2003, 43(3): 259-282.

[2] Manca O., Nardini S., VafaI K. Experimental investigation of mixed convection in a channel with an open cavity [J].Experimental Heat Transfer, 2006, 19(1): 53-68.

[3] Leong J. C., Brown N. M., Lai F. C. Mixed convection from an open cavity in a horizontal channel [J].Inter-national Communications Heat Mass Transfer, 2005, 32(5): 583-592.

[4] Aminossadati S. M., Ghasemi B. A numerical study of mixed convection in a horizontal channel with a discrete heat source in an open cavity [J].European Journal of Mechanics B/Fluids, 2009, 28(4): 590-598.

[5] Rahman M. M., Saidur R., Rahimn A. Conjugated effect of joule heating and magneto-hydrodynamic on doublediffusive mixed convection in a horizontal channel with an open cavity [J].International Journal of Heat and Mass Transfer, 2011, 54(15): 3201-3213.

[6] Mehrez Z., Cafsi A. E., Belghith A. et al. Effect of heated wall position on heat transfer and entropy generation of Cu water nanofluid flow in an open cavity [J].Canadian Journal of Physics, 2015, 93(12): 1615-1629.

[7] Abdelmassih G., Vernet A., Pallares J. Numerical simulation of incompressible laminar flow in a three-dimensional channel with a cubical open cavity with a bottom wall heated [J].Journal of Physics: Conference series, 2012, 395(1): 012099

[8] Stiriba Y., Ferré J. A., Grau F. X. Heat transfer and fluid flow characteristics of laminar flow past an opencavity with heating from below [J].International Communications in Heat and Mass Transfer, 2013, 43(4): 8-15.

[9] Khanafer K., Al-Azmi B., Al-Shammar A. et al. Mixed convection analysis of laminar pulsating flow and heat transfer over a backward-facing step [J].International Journal of Heat and Mass Transfer, 2008, 51(25): 5785-5793

[10] Khanafer K. M., Al-Amiri A. M., Pop I. Numerical simulation of unsteady convection in a driven cavity using an externally exited sliding lid [J].European Journal of Mechanics B/Fluids, 2007, 26(5): 669-687.

[11] Velazquez A., Arias J., Montanes J. Pulsating flow and convective heat transfer in a cavity with inlet and outlet sections [J]International Journal of Heat and Mass Transfer, 2009, 52(3-4): 647-654.

[12] Sourtiji E., Hosseinizadeh S. F., Gorji-Bandpy M. et al. Heat transfer enhancement of mixed convection in a square cavity with inlet and outlet ports due to oscillation of incoming flow [J].International Communications in Heat and Mass Transfer, 2011, 38(6): 806-814.

[13] Selimefendigil F., Oztop H. Identification of forced convection in pulsating flow at a backward facing step with a stationary cylinder subjected to nanofluid [J].International Communications in Heat and Mass Transfer, 2013, 45(7): 111-121.

[14] Unal A., Selma A., Dogan D. Heat transfer enhancement with laminar pulsating nanofluid flow in a wavy channel [J].International Communications in Heat and Mass Transfer, 2014, 59: 17-23

[15] Selimefendigil F., Yurddas A. Numerical analysis of mixed convection heat transfer in pulsating flow for a horizontal channel with a cavity heated from vertical side and below [J].Heat Transfer Research, 2012, 43(6): 509-525.

[16] Abu-Nada E. Numerical prediction of entropy generation in separated flows [J].Entropy, 2005, 7(4): 234-252.

[17] Abu-Nada E. Entropy generation due to heat and fluid flow in backward facing step flow with various expansion ratios [J].International Journal of Exergy, 2006, 3(4): 419-435.

[18] Khorasanizadeh H., Nikfar M., Amani J. Entropy generation of Cu-water nanofluid mixed convection in a cavity [J].European Journal of Mechanics, 2013, 37(28): 143-152.

[19] Nayak R. K., Bhattacharyya S., Pop I. Numerical study on mixed convection and entropy generation of Cu-water nanofluid in a differentially heated skewed enclosure [J].International Journal of Heat and Mass Transfer, 2015, 85(6): 620-634.

[20] Sciacovelli A., Verda V., Sciubba E. Entropy generation analysis as a design tool-A review [J].Renewable and Sustainable Energy Reviews, 2015, 43: 1167-1181.

[21] Mehrez Z., Bouterra M., Cafsi A. E. et al. Heat transfer and entropy generation analysis of nanofluids flow in an open cavity [J].Computers and Fluids, 2013, 88(4): 363-373

[22] Mehrez Z., Cafsi A. E., Belghith A. et al. MHD effects on heat transfer and entropy generation of nanofluidflow in an open cavity [J].Magnetism and Magnetic Materials, 2015, 374: 214-224.

[23] Mehrez Z., Cafsi A. E., BELGHITH A. et al. The entropy generation analysis in the mixed convective assisting flow of Cu-water nanofluid in an inclined open cavity [J].Advanced Powder Technology, 2015, 26(5): 1442-1451.

[24] Zamzari F., Mehrez Z., Cafsi A. E. et al. Entropy generation and mixed convection in a horizontal channel with an open cavity [J].International Journal of Exergy, 2015, 17(2): 219-239.

[25] Bejan A. A study of entropy generation in fundamental convective heat transfer [J].Journal of Heat Transfer, 1979, 101: 718-725.

[26] Mehrez Z., Bouterra M., Cafsi A. E. et al. Mass transfer control of a backward-facing step flow by local forcingeffect of Reynolds number [J].Thermal Science, 2011, 15(2): 367-378.

[27] Nasri Z., Laatar A. H., Balti J. Natural convection enhancement in an asymmetrically heated channelchimney system [J].International Journal of Thermal Sciences, 2015, 90: 122-134.

[28] LEONARD B. P. Simple high accuracy resolution program for convection modeling of discontinuities [J].International Journal for Numerical Methods in Fluids, 1988, 8(10): 1291-1318.

[29] Mehrez Z., Bouterra M., Cafsi A. E. et al. The influence of the periodic disturbance on the local heat transfer in separated and reattached flow [J].Heat Mass Transfer, 2009, 46(1): 107-112.

[30] Taieb S., Laatar A. H., Balti J. Natural convection in an asymmetrically heated vertical channel with an adiabatic auxiliary plate [J].International Journal of Thermal Sciences, 2013, 74(6): 24-36.

[31] Xing T., Stern F. Factors of safety for Richardson extrapolation [J].Journal of Fluids Engineering, 2010, 132(6): 061403.

[32] Xing T., Stern F. Closure to “Discussion of “Factors of Safety for Richardson Extrapolation” 2011, J. Fluids Eng., 133, 11550 [J].Journal of Fluids Engineering, 2011, 133(11): 115502.

[33] Xing T. Direct numerical simulation of Open Von Kármán Swirling Flow [J].Journal of Hydrodynamics, 2014, 26(2): 165-177.

[34] Xing T., Carrica P., Stern F. Computational towing tank procedures for single run curves of resistance and propulsion [J].Journal of Fluids Engineering, 2008, 130(10): 101102.

(Received May 2, 2016, Revised May 23, 2017)

*Biography:Fatma Zamzari (1986-), Female, Ph. D., Researcher

Zouhaier Mehrez,

E-mail: zouhaier.mehrez@yahoo.fr