Peaked Periodic Wave Solutions to the Broer–Kaup Equation?
Bo Jiang(江波) and Qin-Sheng Bi(畢勤勝)Department of Applied Mathematics,Jiangsu University of Technology,Changzhou 3001,China
2Faculty of Civil Engineering and Mechanics,Jiangsu University,Zhenjiang 212013,China
1 Introduction
In recent years,nonlinear wave equations with peaked wave solutions attracted much attention(see Refs.[1–9]and the references cited in).It is known that the wave type of peaked wave solutions may be solitary or periodic as in the case of Camassa–Holm equation.Peaked solitary wave,also called peakon,has a unique peak at crest or trough.Peaked periodic wave,however,is a type of periodic traveling wave with a peak at each crest or trough,which was also called periodic peakon by Lenells,[2?3]coshoidal wave by Boyd[4]and periodic cusp wave by Li and Liu.[5]Usually,we say a continuous function has a peak at some point if at this point its left and right derivatives are fi nite and have different sign,and naturally its wave pro fi le is called a peaked wave solution.
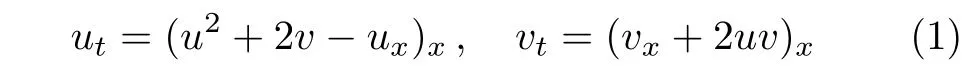
The following nonlinear wave equation was proposed by Broer and Kaup(BK)as a model describing the bi-directional propagation of long waves in shallow water,where u(x,t)is related to the horizontal velocity,and v(x,t)represents the height of the water surface above a horizontal bottom.[10?11]It turns out that this equation was also derived from the Kadomtsev–Petviashvili equation.[12]Various aspects of BK equation(1)have been studied.[13?19]It was shown in Ref.[13]that Eq.(1)is integrable and possesses tri-Hamiltonian structure and an in fi nite number of conservation laws.The geometric properties of non-Noether symmetries as well as their applications were discussed in Ref.[14].A Darboux transformation and some exact solutions were presented in Ref.[15].Satsuma etal.obtained the soliton solutions and revealed fi ssion and fusion phenomena.[16]The author of Ref.[17]gave a family of traveling wave solution and its higher version.The interaction solutions between the solitons and other different types of nonlinear waves were given using a consistent tanh expansion method in Ref.[18].Very recently,by the bifurcation method of dynamical system,Meng etal.[19]constructed some smooth and peaked solitary wave solutions.However whether there are the peaked periodic waves to Eq.(1)remains unknown.
In the present paper,we employ the qualitative analysis method for differential equations,which was first introduced by Lenells,[2?3]to prove the existence of peaked periodic waves to Eq.(1)and obtain some exact expressions of peaked periodic wave solutions.To the best of our knowledge,those obtained solutions have not been reported in the literature.
2 Existence of Peaked Periodic Waves of Eq.(1)
In this section we first introduce some notations.Cn(X)denotes the set of all n times continuously differentiable functions on the open set X.represents the space of smooth functions with compact support.refers to the set of all functions whose restriction on any compact subset is Lpintegrable.stands for
Substituting u(x,t)=u(ξ)and v(x,t)=v(ξ)with ξ=x?ct into Eq.(1)leads to

It can be observed that Eq.(2)is valid in the sense of distributions if u,v∈Therefore the following Definition is natural.
Definition 1A pair of functions(u,v)where u,v∈is called a traveling wave solution of Eq.(1)if u and v satisfy Eq.(2)in the sense of distributions.
Since every distribution has a primitive which is a distribution,we may integrate Eq.(2)to get
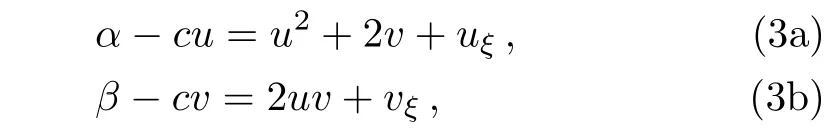
with two integration constants α and β.By Eq.(3b),u can be solved as

for v≠0.Substituting Eq.(4)into Eq.(3a)we can obtain an equation for the unknown v only
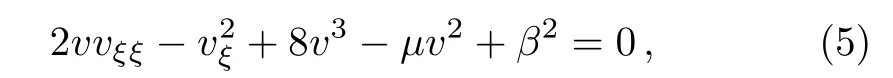
whereμ =c2+4α.
To deal with the regularity of the traveling wave solutions,we give the following lemma,which is inspired by the study of traveling waves of Camassa–Holm equation.[2]
Lemma 1Let(u,v)be a traveling wave solution of Eq.(1).Then we have

Therefore

Proof Denote p(v)= ?8v3+μv2?β2.Thus p(v)is a polynomial in v and then Eq.(5)can be written as Since v∈
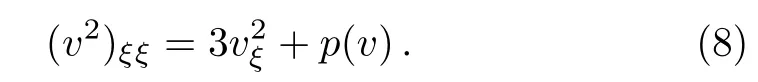
Therefore(v2)ξis absolutely continuous and v2∈C1(R).Eq.(8)implies that(v2)ξξNote that v∈(R)?C(R).Moreover,
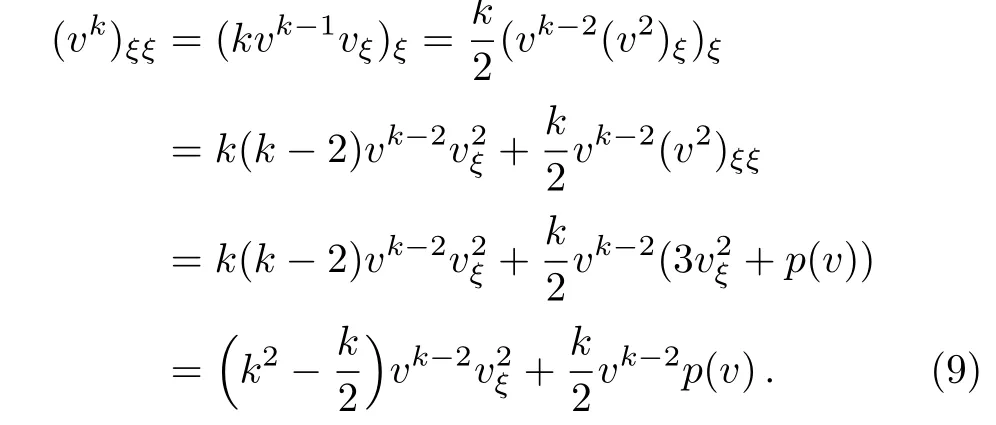
For k≥3 the right-hand side of(9)is in(R).Therefore
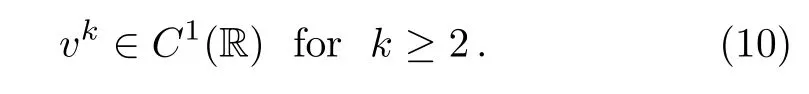
Thus Eq.(6)holds for j=1.Next,we assume that
vk∈ Cj?1(R)for k ≥ 2j?1and j≥ 2.
Then for k≥2jwe have

Also we have vk?2p(v) ∈ Cj?1(R).Therefore the righthand side of Eq.(9)is in Cj?2(R).Hence,by induction on j,we know Eq.(6)holds.
Furthermore,it follows from Eq.(10)that

which implies that vξ∈ C(Rv?1(0)).Therefore,v ∈C1(Rv?1(0)).Now,we assume that v∈ Cj(Rv?1(0))for j≥1.Then for k≥2j+1,we have vk∈Cj+1(R).Thus

which shows that vξ∈ Cj(Rv?1(0)).Hence,v ∈Cj+1(Rv?1(0)).Thus,by induction on j,we know Eq.(7)holds.
Remark 1 In view of Eq.(4),it follows from Lemma 1 that u∈C∞(Rv?1(0)).From this fact and Eq.(7),we know that the traveling wave solutions(u,v)of Eq.(1)are smooth except at points where v=0.
Since v is continuous on R,then v?1(0)is a closed set.This implies that Rv?1(0)is an open set.Since every open set is a countable union of disjoint open intervals,then there are disjoint open intervals(ai,bi),i≥1,such that Rv?1(0)=(ai,bi).Then it follows from Lemma 1 that v is smooth on every interval(ai,bi)and hence Eq.(5)holds pointwise on(ai,bi).Therefore,we may multiply both sides of Eq.(5)by v?2vξand integrate on(ai,bi)to get
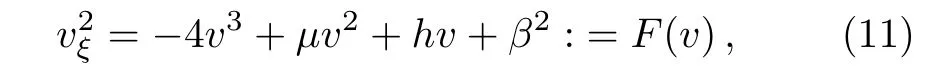
with a new integration constant h.
Remark 2Notice that F(v)≥0 if v is a solution of Eq.(11).Moreover,from the continuity of v on R,we know that v→0 at the fi nite endpoints of(ai,bi).
To establish the existence of periodic peaked wave solutions of Eq.(1),we need the following lemma.
Lemma 2The solution of Eq.(11)has the following asymptotic properties:
(i)If v approaches 0,then we have
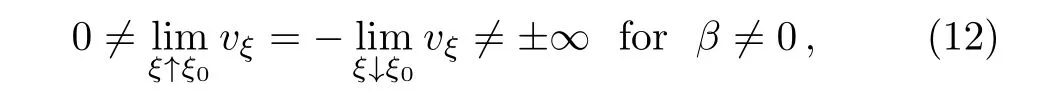
where v(ξ0)=0.
(ii)If v approaches a simple zero m of F(v),then we have

where v(ξ0)=m and f(ξ)=O(g(ξ))as ξ→ a means that|f(ξ)/g(ξ)|is bounded in some neighborhood of a.
ProofSince the proof of(ii)can be found in Ref.[2],here we only consider the proof of(i).In a small neighbourhood of v=0,Eq.(11)can be expanded as

where F(0)= β2>0.For ξ close enough to ξ0,integration of Eq.(14)yields

which implies O(|ξ? ξ0|2)=O(v2).Thus we have

From Eq.(17)we obtain Eq.(12).
Remark 3If the solution v of Eq.(11)approaches a double zero or a triple zero m of F(v),by similar analysis to the proof of Lemma 2,we can prove that v(ξ)→ m as ξ→±∞.
Using Lemma 2,we can obtain the following result which gives a sufficient condition for the existence of peaked periodic wave solutions of Eq.(1).
Theorem 1 If β/=0 and F(v)has a simply zero at vssuch that vs>0(or vs<0)and F(v)>0 for v∈(0,vs)(or v∈(vs,0)),then there exists a periodic peaked wave solution v(ξ)of Eq.(1)satisfying minξ∈Rv(ξ)=0 and maxξ∈Rv(ξ)=vs(or minξ∈Rv(ξ)=vsand maxξ∈Rv(ξ)=0).
Proof Here we only consider the case vs>0 since similar analysis can be employed for the case vs<0.It follows from Eq.(11)that
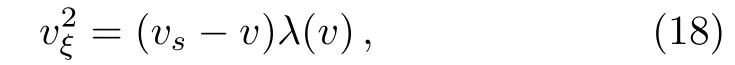
where λ(v)is a second-order factor of F(v)such that λ(v)>0 for v∈ (0,vs).Assume that v is the solution in this interval.If v increases and approaches vs,by Eq.(13),we get that v is symmetric with respect to ξ1,where v(ξ1)=vs,i.e.v(ξ)=v(ξ1? (ξ? ξ1)),which means that v will reach vsand immediately turn back down.From Lemma 1,we know that v will not stop or turn back anywhere because that would yield a singularity of v at a point where v≠0.When v decreases and approaches the point v=0,according to Eq.(12),v will suddenly change its direction at ξ0=0,where v(ξ0)=0,i.e.vξ7→ ?vξ,so that v will yield a peak at v=0.Hence,we deduce that there exists a peaked periodic wave solution of Eq.(1)with minξ∈Rv(ξ)=0,maxξ∈Rv(ξ)=vs.Remark 4 For a solution v(ξ)of Eq.(11),if there exists a double zero or a triple zero vs≠0 of F(v)such that F(v)>0 for v∈(0,vs)(or v∈(vs,0)),in view of(i)of Lemma 2 and Remark 3,employing a similar analysis to the proof of Theorem 1,we can infer that v(ξ)gives a peaked solitary wave solution of Eq.(1)with a single peak at ξ0such that v(ξ0)=0,which satis fi es minξ∈Rv(ξ)=0(or maxξ∈Rv(ξ)=0)and lim|ξ|→∞=vs.
3 Exact Peaked Periodic Wave Solutions of Eq.(1)
To determine the peaked periodic wave solutions of Eq.(1)in speci fi ed parameter region of parameter space,we need to discuss the distribution of zero points of F(v)for β/=0.differentiating F(v)with respect to v yields F′(v)= ?12v2+2μv+h.(19)Let? = μ2+12h.If? <0,then F′(v)<0 holds for v∈R and thus F(v)is strictly monotonically decreasing on R.Moreover,in view of the fact that F(0)=β2>0,we can deduce that there exists a unique simple zero v(1)afor F(v)such that v(1)a>0.If?=0,solving the equation F′(v)=0 gives v=v?= μ/12 such that F(v?)=F′(v?)=F′′(v?)=0 and F′′′(v?)= ?24/=0,which means that v?is a triple zero of F(v).Moreover,due to the fact that F(0)>0 and F′(v)<0 for v ∈ R{v?},we can infer that v?>0.If? >0,setting F′(v)to zero leads to

withFrom Eqs.(19)and(20),it follows that
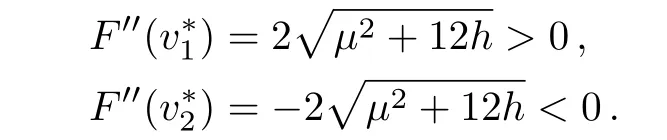
This shows that F(v)has a minimum atand has a maximum atFurther,we can check that
Based on the above analysis,it can be checked that there exist in total nine qualitatively cases for F(v)when β≠0(see Fig.1).
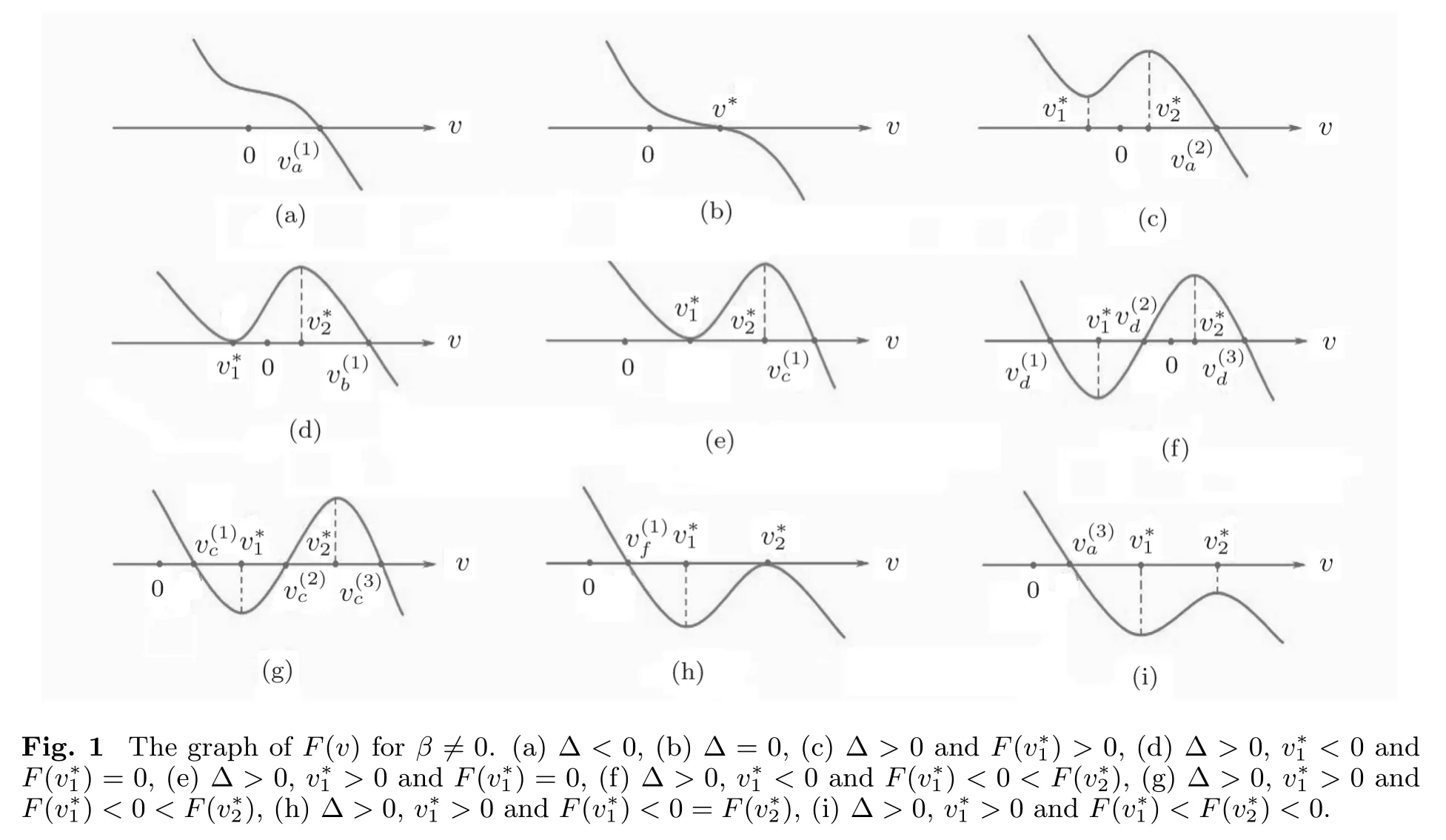
According to Theorem 1 and Fig.1,exact peaked periodic wave solutions of Eq.(1)in different parameter regions of parameter space can be presented.We will use some symbols on the elliptic functions and elliptic integrals(see Ref.[20]).sn(u,k)and cn(u,k)are Jacobian elliptic functions with the modulus k.sn?1(u,k)and cn?1(u,k)are the inverse functions of sn(u,k)and cn(u,k),respectively.
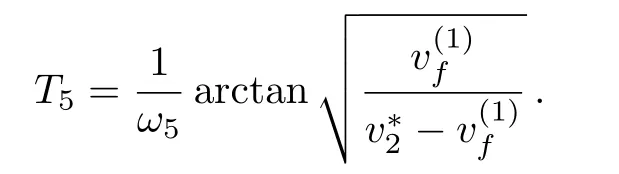
Proposition 1(The expression of peaked periodic wave pointing upwards)If?><0 whereandsatisfyingare three distinct simple zeros of F(v)(see Fig.1(f)), Proof It can be observed from Fig.1(f)that F(v)>0 for v∈I=where<0 is a simple zero of F(v).By Theorem 1,we know that there exists a peaked periodic wave solution with minξ∈Rv(ξ)=and maxξ∈Rv(ξ)=0.For the solution v1(ξ)in the interval I,it follows from Eq.(11)that Integration of Eq.(22)leads to In view of Eq.(4),completing the integrals in Eqs.(23)and(24)gives Eq.(21). Employing a similar analysis as above,we have the following results. Proposition 2(The expressions of peaked periodic waves pointing downwards)(i)Under the same assumptions as in Proposition 1,Eq.(1)has a peaked periodic wave solution pointing downwards with period 2T2,which on the interval(?T2,T2)has the explicit expression whereandare the same as described in Proposition 1,ω2= ω1,k2=k1and wheresatisfyingare a double zero and a simple zero of F(v)(see Fig.1(d)), (iii)If?>0,for β≠0,Eq.(1)has a peaked periodic wave solution pointing downwards with period 2T4,which on the interval(?T4,T4)has the explicit expression wheresatisfying 0 (iv)If?>0,for β≠0,Eq.(1)has a peaked periodic wave solution pointing downwards with period 2T5,which on the interval(?T5,T5)has the explicit expression whereandsatisfyingare a simple zero and a double zero of F(v)(see Fig.1(h)),and (v)Under one of the parameter conditions:(c1)?<0,(c2)?>0 and>0,(c3)?>0,and<0,Eq.(1)has a peaked periodic wave solution pointing downwards with period 2T6,which on the interval(?T6,T6)has the explicit expression where>0 and mj±nji(mj,nj∈ R),are a unique real root and a pair of conjugate complex roots of F(v)=_0(see Figs.1(a),1(c),1(i)),A= To show the correctness of our results,we select the peaked periodic wave solutions for v given by Eqs.(21)and(25)as two examples and plot their planar graphs in Fig.2.In such two cases we take c=2,α= ?6 and β=4,so that the parameter conditions of Proposition 1 are satis fi ed. References [1]R.Camassa and D.D.Holm,Phys.Rev.Lett.71(1993)1661. [2]J.Lenells,J.Di ff.Equ.217(2005)393. [3]J.Lenells,J.Math.Anal.Appl.306(2005)72. [4]J.P.Boyd,Appl.Math.Comput.81(1997)173. [5]J.B.Li and Z.R.Liu,Appl.Math.Model.25(2000)41. [6]Z.R.Liu and R.Wang,Chaos,Solitons and Fractals 19(2004)77. [7]J.B.Zhou and L.X.Tian,Nonlinear Anal-Real 11(2010)356. [8]B.Jiang,Y.Lu,J.H.Zhang,and Q.S.Bi,Appl.Math.Comput.228(2014)220. [9]L.J.Qiao,S.Q.Tang,and H.X.Zhao,Commun.Theor.Phys.63(2015)731. [10]L.J.F.Broer,Appl.Sci.Res.31(1975)377. [11]D.J.Kaup,Prog.Theor.Phys.54(1975)396. [12]S.Y.Lou and X.B.Hu,J.Math.Phys.38(1997)6401. [13]B.A.Kupershmidt,Cormrmn.Math.Phys.99(1985)51. [14]G.Chavchanidze,Mem.differential Equations Math.Phys.36(2005)81. [15]Z.J.Zhou and Z.B.Li,Acta Phys.Sin.52(2003)262. [16]J.Satuma,K.Kajiwara,J.Matsukidaira,and J.Hietarinta,J.Phys.Soc.Jpn.61(1992)3096. [17]A.K.Svinin,Inverse Problems 17(2001)1061. [18]C.L.Bai and S.Y.Lou,Chin.Phys.Lett.30(2013)110202. [19]Q.Meng,W.Li,and B.He,Commun.Theor.Phys.62(2014)308. [20]P.F.Byrd and M.D.Friedman,Handbook of Elliptic Integrals for Engineers and Scientists,Springer,New York(1971).
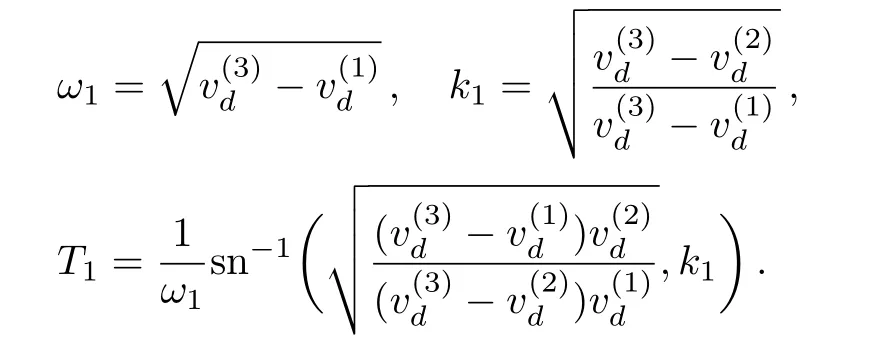

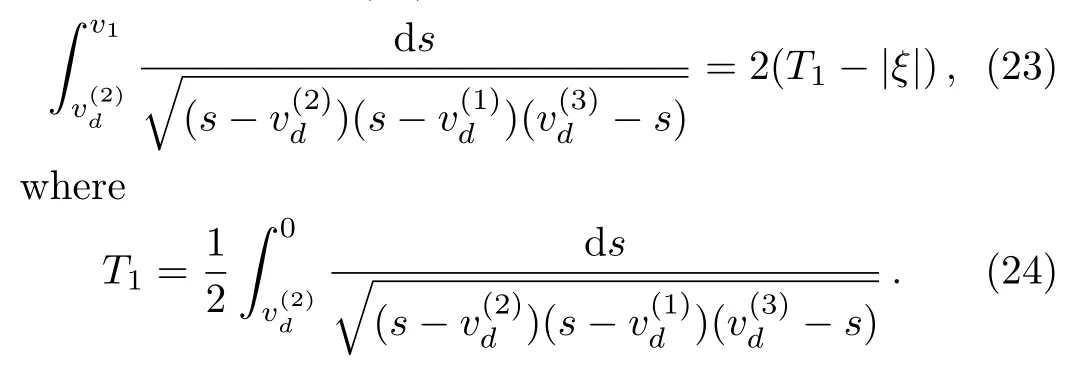
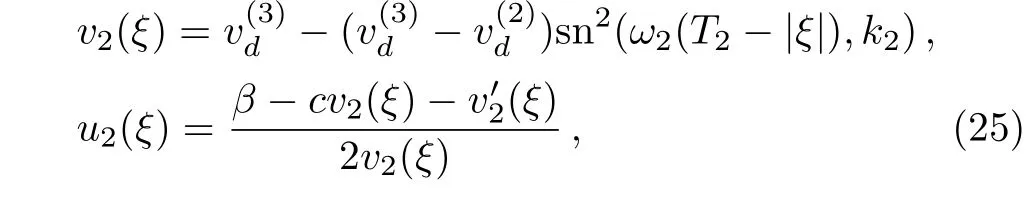


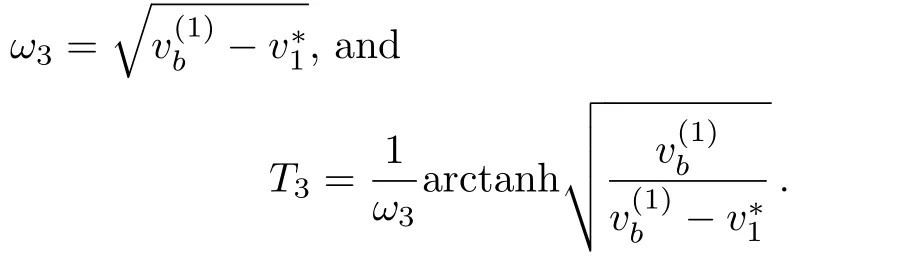






 Communications in Theoretical Physics2017年1期
Communications in Theoretical Physics2017年1期
