Quantum Coherence Quantifiers Based on R′enyi α-Relative Entropy?
Lian-He Shao(邵連合),Yong-Ming Li(李永明), Yu Luo(羅宇),and Zheng-Jun Xi(席政軍)
College of Computer Science,Shaanxi Normal University,Xi’an 710062,China
1 Introduction
Coherence arising from quantum superposition rule,is an important resources in quantum information theory.Coherence is discussed in the interference phenomena and it is know due to the role of phase coherence in optical phenomena.[1]A rigorous framework for quantifying coherence was proposed by Baumgratz et al.and they proposed several measures of coherence,which are based on information distance measures including relative entropy andl1norm.[2]The quantification framework of quantum coherence stimulated many further considerations,which include other coherence measures,[3?5]the operational interpretations of quantum coherence,[6?8]the relationship among quantum entanglement,quantum discord and quantum deficit,[9?13]quantification of coherence in in finite dimensional system,[14?15]the other properties are similar to quantum entanglement theory.[16?29]
From the view point of the definition,one can straightforwardly quantify the coherence in a given basis by measuring the distance between the quantum stateρand its nearest incoherent state.Baumgratz et al.gave four necessary criteria,[2]which any quantity should fulfill them.Given a finite-dimensional Hilbert space H withd=dim(H).We note that I is the set of quantum states,which is called incoherent state that are diagonal in a fixed basis{Kn}is a set of Kraus operators,and sat-?I.Then any proper measure of the coherenceCmust satisfy the following conditions:
(C1)C(ρ)≥ 0 for all quantum statesρ,andC(ρ)=0 if and only ifρ∈I.
(C2a) Monotonicity under all the incoherent completely positive and trace preserving(ICPTP)maps Φ:C(ρ)≥C(Φ(ρ)),where Φ(ρ)= ∑nKnρ.
(C2b)Monotonicity for average coherence under subselection based on measurements outcomes:

The R′enyi entropy is important in quantum information theory. It can be used as a measure of entanglement.[30]In Ref.[31],Mosonyi and Hiai defined the R′enyiα-relative entropy,which can act as an information distance measure.In Ref.[32],Chitambar et al.proposed that the R′enyiα-relative entropy of coherence fulfills condition C1 and C2a forα∈ [0,2],then we call the R′enyiαrelative entropy of coherence is a coherence monotone.[34]As we know,the condition C2b is important as it allows for sub-selection based on measurement outcomes,a process available in well controlled quantum experiments and it is also difficult to verify.[2]A natural question arises immediately,is the condition C2b satisfied for the R′enyiα-relative entropy of coherence?
In this paper,we will resolve the above question.In Sec.2,we review basic points for the R′enyiα-relative entropy of coherence.In Sec.3,we prove that the R′enyiα-relative entropy of coherence does’t fulfill the condition C2b and it also does not ful fill the extension condition C2b presented in Ref.[35].We give the trade offrelation between the R′enyiα-relative entropy of coherence and mixedness in Sec.4.The case of the R′enyiα-relative entropy of coherence for a single qubit is discussed in Sec.5.In Sec.6 we give the summary of results.
2 The R′enyiα-Relative Entropy of Coherence
In this section,we recall basic points of the R′enyiαrelative entropy of coherence present in Ref.[32].Forα∈ [0,∞]the R′enyiα-relative entropy of the statesρbyδis defined by[31]

This quantity is contractive for allα∈[0,2]. Since the R′enyiα-relative entropy can act as an information distance measure.[31]Then,we can define the R′enyiαrelative entropy of coherence as:

Note that in the limitα→ 1,Sα→1(ρ‖δ)gives the relative entropyS(ρ‖δ)= tr(ρlogρ) ? tr(ρlogδ). Letδ=∑
iqi|i〉〈i|be some incoherent states,then the analytical expression ofCα(ρ)can be obtained as[32]

Equation(3)can be further simplified as[32]

In this paper,we do not consider the cases forα=0 and the limitα→ 1.Forα=0,the R′enyi relative entropy of coherence is always equal to 0.For the limitα→ 1,a detailed study for the standard relative entropy of coherence is presented in Ref.[2].
3 The Monotoncity Property
First we show thatCα(ρ)ful fills the condition C3 forα∈ [0,1).In Ref.[31],it is shown thatSα(ρ||δ)is convexity forα∈ [0,1).For any ensemble{pi,ρi},we assume the incoherent statesare closet with respect toρi,then we have

where the second inequality using the convexity ofSα(ρ||δ).We conclude that forα∈ [0,1),Cα(ρ)cannot increase under mixing of quantum states,thenCα(ρ)ful fills the condition C3 forα∈ [0,1).Sα(ρ||δ)is not convexity anymore forα∈(1,2],[31]there may exist some cases,The condition C3 combined with C2b,implies C2a.In Ref.[32],Chitambar et al.studied the R′enyiα-relative entropy of coherence ful fills C2a for different kinds of incoherent operations.They do not consider whether the R′enyiα-relative entropy of coherence ful fills the condition C2b.This motivates us to study whether C2b is satis fied forCα(ρ).
Now we use the example,which presented in Ref.[2]to show that condition C2b is violated.We choose

are the prescribed orthonormal basis.The two Kraus operators are written as

where the complex numbersaandbobey|a|2+|b|2=1.This condition guarantees that∑nKn=I.The density matrix is presented as

After applying this channel to the density matrixρ,we obtain the output states:

With the probabilities:
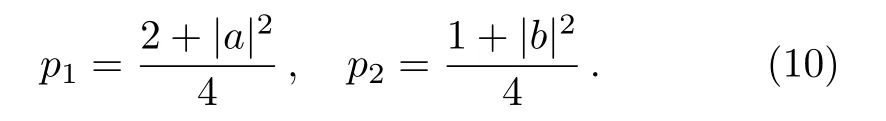
By using Eq.(4),we obtain the R′enyiα-relative entropy of coherence forρas
Note that the operatorK1makesCα(ρ1)=0,we only need to calculateCα(ρ2).
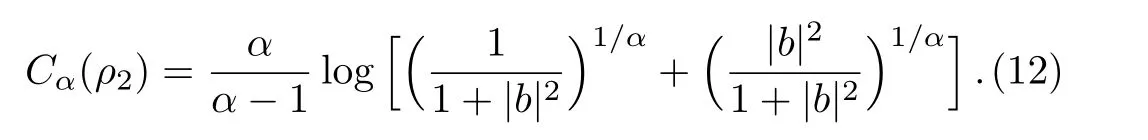
We chooseb=1,substituting it into Eqs.(9)and(10),we then get

The equality holding if and only ifα=1.Thus,forα∈(0,1)


Fig.1 (Color online)Comparison between Cα(ρ)and p2Cα(ρ2)for b=1/2.The black line shows p2Cα(ρ2).The red line shows Cα(ρ).
Recently,Yu et al.proposed an alternative framework for quantifying coherence,which is more flexible and convenient for applications than the original one.[33]Their framework can be expressed as follows.Any proper measure of the coherenceCmust satisfy the following three conditions:
(B1)Nonnegativity:C(ρ)≥ 0 for all quantum statesρ,andC(ρ)=0 if and only ifρ∈ I.
(B2)Monotonicity:C(ρ) ≥C(Φ(ρ)),where Φ(ρ)=is an incoherent operation.
(B3) Additivity of coherence for subspace-independent states:C(p1ρ1⊕p2ρ2)=p1C(ρ1)+p2C(ρ2)for blockdiagonal statesρin the incoherent basis,where density operatorsρ1andρ2are defined on the two independent subspaces,p1andp2are two possibility coefficients withp1+p2=1 and

The above three conditions(B1,B2,B3)are fulfilled by all the coherence measures based on the original four conditions(C1,C2a,C2b,C3). Thus,this framework provides us an alternative method to illustrate that the measure of coherence induced by R′enyiαrelative entropy must violate C2b.We consider a stateρ=p1ρ1⊕p2ρ2,withρ1=(1/2)(|0〉+|1〉)(〈0|+ 〈1|)andρ2=(1/3)(|2〉+|3〉+|4〉)(〈2|+ 〈3|+ 〈4|).[33]We choose the computational basis|i〉4i=0as the reference basis,then we have
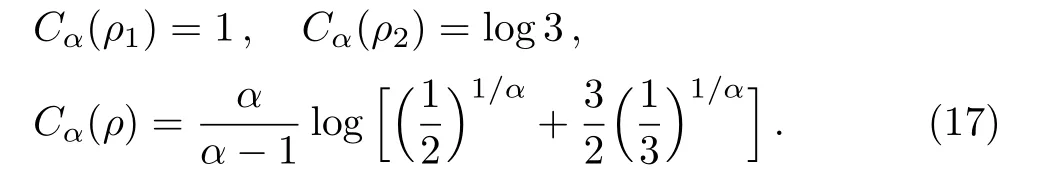
We plotCα(ρ)and(1/2)C(ρ1)+(1/2)C(ρ2)in Fig.2.It is shown that
Cα(ρ)=Cα(p1ρ1⊕p2ρ2)/=p1Cα(ρ1)+p2Cα(ρ2).(18)We note that for the limitα→ 1,the R′enyiαrelative entropy of coherence will become the standard relative entropy of coherence,thus we haveCα→1(ρ)=p1Cα→1(ρ1)+p2Cα→1(ρ2). Therefore,the R′enyiαrelative entropy of coherence must violate C2b in general.

Fig.2 (Color online)Comparison between Cα(ρ)and(1/2)C(ρ1)+(1/2)C(ρ2). The black solid line shows p2Cα(ρ2). The red dotted line shows(1/2)C(ρ1)+(1/2)C(ρ2).
From the above examples,we then conclude that condition C2b,i.e.,Cα(ρ) ≥ ∑npnCα(ρn)is not generally true for the measure of coherence induced by R′enyiαrelative entropy.
In Ref.[35],Rastegin studied the Tsallis relativeαentropies of coherence

and give an extension of condition C2b.The extension of condition C2b can be represented as

violates condition C2b.[5]Another related quantity is geometric coherenceCg(ρ)=1 ? maxδ∈IF(ρ,δ),ful fills conditions C1,C2a,C2b,and C3.[4]AlthoughCF(ρ)andCg(ρ)are different with the square root function,butCg(ρ)ful fills the conditions C2b andCF(ρ)does not fulfill condition C2b.Another question arises immediately,is the extension of condition C2b satis fied for the R′enyiα-relative entropy of coherenceCα(ρ)?
We also use the above example to solve this problem.According to Ref.[32],when we use the R′enyiαrelative entropy to quantify coherence,the optimal incoherent state forρis

With the corresponding probabilities:

Compare Eq.(13)with Eq.(22),after some simple algebraic operation,we obtain

The equality holding if and only ifα=1.Thus,forα∈(0,1)

From the above example,we then conclude that the extension of condition C2b,i.e.,

is not generally true for the measure of coherence induced by R′enyiα-relative entropy.
4 The R′enyiα-Relative Entropy of Coherence and Mixedness
In order to be a meaningful resource quantum quantifier for coherence,the minimal requirements are the conditions C1 and C2a for any quantityC.[34]We have proved that the R′enyiα-relative entropy of coherence does not fulfill the condition C2b and the extension of condition C2b,but the R′enyiα-relative entropy of coherence is satisfied the minimal requirements to be a coherence quantifier forα∈ [0,2],thus the R′enyiα-relative entropy of coherence can act as a coherence monotone quantifier,[34]An important problem for quantifying coherence is the relationship between quantum coherence quantities and mixedness.The trade-off between some quantities and mixedness have been discussed in Refs.[37–38].Here we focus on the trade-off between the R′enyiα-relative entropy of coherence and mixedness.
Theorem 1For 0<α≤2 andα/=1,the upper bound of the R′enyiα-relative entropy of coherence is given by

and the trade-off betweenCα(ρ)and mixedness can be expressed as

whereM(ρ):=[d/(d?1)][1? tr(ρ2)].
ProofWe only prove the case ofα∈ (0,1),α∈ (1,2]is completely analogous.Forα∈ (0,2]andα/=1,we chooseδis the completely mixed stateδ= ∑i(1/d)|i〉〈i|,then we can obtain

T∑he inequation holding is that the completely mixed state(1/d)|i〉〈i|may not be the optimal incoherent state forAccording to Ref.[35],forα∈ (0,2]andα/=1,the functionε→εα?1/(α? 1)is concave,applying Jensen’s inequality,we then have

Hereλiare the eigenvalues ofρand obey the normalization condition.Forα∈(0,1),α?1<0,then


CombineM(ρ):=[d/(d?1)][1 ? tr(ρ2)]and the above inequation,we get

Equation(25)provides an upper bound on R′enyiαrelative entropy of coherence in terms of the purity tr(ρ2).Equation(26)shows that when mixedness increases,an upper bound on R′enyiα-relative entropy of coherence decreases.
5 The R′enyiα-Relative Entropy of Coherence for a Single Qubit
Due to the analytical expression ofCα(ρ)for qubit is complicated,so we consider a simple case that we chooseα=2 for the coherence quantity.The qubit states can write as



Fig.3 The values of ln2C(ρ)+M(ρ)and 22 as functions of a.
6 Summary
In this paper,we show that the R′enyiα-relative entropy of coherence does not satisfy condition C2b and extension of C2b forα∈(0,1)by presenting examples.Thus the measure of coherence induced by the R′enyiα-relative entropy can not be called coherence measure.[34]Due to the R′enyiα-relative entropy of coherence fulfill the condition C1 and C2a,so the R′enyiα-relative entropy of coherence can be called as a coherence monotone quantifier.The R′enyiα-relative entropy of coherence fulfills the minimal requirements to be a meaningful resource quantum quantifier for coherence,[34]then we examine the trade-offrelations between coherence and mixedness.Some properties are further exemplified with a single qubit forα=2.Our findings complement the results present in Ref.[32].
References
[1]L.Mandel and E.Wolf,Optical Coherence and Quantum Optics,Cambridge University Press,Cambridge,UK(1995).
[2]T.Baumgratz,M.Cramer,and M.B.Plenio,Phys.Rev.Lett.113(2014)140401.
[3]S.Rana,P.Parashar,and M.Lewenstein,Phys.Rev.A 93(2016)012110.
[4]A.Streltsov,U.Singh,H.S.Dhar,M.N.Bera,and G.Adesso,Phys.Rev.Lett.115(2015)020403.
[5]L.H.Shao,Z.Xi,H.Fan,and Y.Li,Phys.Rev.A 91(2015)042120.
[6]C.Napoli,T.R.Bromley,M.Cianciaruso,M.Piani,N.Johnston,and G.Adesso,Phys.Rev.Lett.116(2016)150502.
[7]U.Singh,M.N.Bera,A.Misra,and A.K.Pati,Erasing Quantum Coherence:An Operational Approach,arXiv:1506.08186[quant-ph](2015).
[8]A.Winter and D.Yang,Phys.Rev.Lett.116(2016)120404.
[9]Y.Peng,Y.R.Zhang,Z.Y.Fan,S.Liu,and H.Fan,Complementary Relation of Quantum Coherence and Quantum Correlations in Multiple Measurements,arXiv:1608.07950[quant-ph](2016).
[10]Z.Xi,Y.Li,and H.Fan,Sci.Rep.5(2015)10922.
[11]E.Chitambar and Min-Hsiu Hsieh,Phys.Rev.Lett.117(2016)020402.
[12]Y.Yao,X.Xiao,L.Ge,and C.P.Sun,Phys.Rev.A 92(2015)022112.
[13]J.Ma,B.Yadin,D.Girolami,V.Vedral,and M.Gu,Phys.Rev.Lett.116(2016)160407.
[14]Y.R.Zhang,L.H.Shao,Y.Li,and H.Fan,Phys.Rev.A 93(2016)012334.
[15]J.Xu,Phys.Rev.A 93(2016)032111.
[16]C.L.Liu,X.D.Yu,G.F.Xu,and D.M.Tong,Quantum Inf.Process.15(2016)4189.
[17]F.G.Zhang,L.H.Shao,Y.Luo,and Y.Li,Quantum Inf.Process.16(2017)31.
[18]J.J.Chen,J.Cui,Y.R.Zhang,and H.Fan,Phys.Rev.A 94(2016)022112.
[19]E.Chitambar,A.Streltsov,S.Rana,M.N.Bera,G.Adesso,and M.Lewenstein,Phys.Rev.Lett.116(2016)070402.
[20]C.Radhakrishnan,M.Parthasarathy,S.Jambulingam,and T.Byrnes,Phys.Rev.Lett.116(2016)150504.
[21]A.Mani and V.Karimipour,Phys.Rev.A 92(2015)032331.
[22]Y.Peng,Y.Jiang,and H.Fan,Phys.Rev.A 93(2016)032326.
[23]H.J.Zhang,B.Chen,M.Li,S.M.Fei,and G.L.Long,Commun.Theor.Phys.67(2017)166.
[24]X.D.Yu,D.J.Zhang,C.L.Liu,and D.M.Tong,Phys.Rev.A 93(2016)060303.
[25]K.Bu,U.Singh,and J.Wu,Phys.Rev.A 93(2016)042326.
[26]J.Wang,Z.Tian,J.Jing,and H.Fan,Phys.Rev.A 93(2016)062105.
[27]M.Piani,M.Cianciaruso,T.R.Bromley,C.Napoli,N.Johnston,and G.Adesso,Phys.Rev.A 93(2016)042107.
[28]T.R.Bromley,M.Cianciaruso,and G.Adesso,Phys.Rev.Lett.114(2015)210401.
[29]S.Du,Z.Bai,and Y.Guo,Phys.Rev.A 91(2015)052120.
[30]Y.X.Wang,L.Z.Mu,V.Vedral,and H.Fan,Phys.Rev.A 93(2016)022324.
[31]M.Mosonyi and F.Hiai,IEEE Trans.Inf.Theory 57(2011)2474.
[32]E.Chitambar and G.Gour,Phys.Rev.A 94(2016)052336.
[33]X.D.Yu,D.J.Zhang,G.F.Xu,and D.M.Tong,Phys.Rev.A 94(2016)060302.
[34]A.Streltsov,G.Adesso,and M.B.Plenio,Quantum Coherence as a Resource,arXiv:1609.02439[quant-ph](2016).
[35]A.E.Rastegin,Phys.Rev.A 93(2016)032136.
[36]F.Hiai,M.Mosonyi,D.Petz,and C.Beny,Rev.Math.Phys.23(2011)691.
[37]U.Singh,M.N.Bera,H.S.Dhar,and A.K.Pati,Phys.Rev.A 91(2015)052115.
[38]S.Cheng and M.J.W.Hall,Phys.Rev.A 92(2015)042101.
 Communications in Theoretical Physics2017年6期
Communications in Theoretical Physics2017年6期
- Communications in Theoretical Physics的其它文章
- A New Quantum Watermarking Based on Quantum Wavelet Transforms?
- Effects of Variable Thermal Conductivity and Non-linear Thermal Radiation Past an Eyring Powell Nano fluid Flow with Chemical Reaction?
- Analysis of Energy Eigenvalue in Complex Ginzburg–Landau Equation?
- Role of Inclined Magnetic Field and Copper Nanoparticles on Peristaltic Flow of Nano fluid through Inclined Annulus:Application of the Clot Model
- MHD Flow and Heat Transfer of a Generalized Burgers’Fluid Due to an Exponential Accelerating Plate with Effects of the Second Order Slip and Viscous Dissipation?
- MHD Stagnation Point Flow of Williamson Fluid over a Stretching Cylinder with Variable Thermal Conductivity and Homogeneous/Heterogeneous Reaction
