Mass transport in a thin layer of power-law fluid in an Eulerian coordinate system*

Jie LIU (劉潔), Yu-chuan BAI (白玉川)

?

Mass transport in a thin layer of power-law fluid in an Eulerian coordinate system*

Jie LIU (劉潔), Yu-chuan BAI (白玉川)

State Key Laboratory of Hydraulic Engineering Simulation and Safety, Tianjin University, Tianjin 300072, China, E-mail: from_mars@126.com (Received July 6, 2014, Revised June 18, 2015)

The mass transport velocity in a thin layer of muddy fluid is studied theoretically. The mud motion is driven by a periodic pressure load on the free surface, and the mud is described by a power-law model. Based on the key assumptions of the shallowness and the small deformation, a perturbation analysis is conducted up to the second order to find the mean Eulerian velocity in an Eulerian coordinate system. The numerical iteration method is adopted to solve these non-linear equations of the leading order. From the numerical results, both the first-order flow fields and the second-order mass transport velocities are examined. The verifications are made by comparing the numerical results with experimental results in the literature, and a good agreement is confirmed.

mass transport velocity, power-law model, periodic pressure load, Eulerian coordinates system

Introduction

The muddy estuarine coast is widely encountered around the world. The interaction between waves and soft mud is one of the key mechanisms controlling the transport of cohesive sediments in coastal and estuari- ne waters, and the mass transport generated by the wave motion is with a steady second-order drift velo- city. Although its velocity is small in magnitude, the mass transport is one of the notable phenomena for the soft mud, because it plays an important role in dete- rmining the migration of nutrients and pollutants[1,2]. Moreover, it could also be used to predict the bed evo- lution in the long term.

Various models were proposed to describe the re- lationship between the stress and the shear rate for the soft mud. In most cases, the muddy bed is assumed as a linear medium, Liu and Chan[3], Hu et al.[4],Yang and Chen[5]and Ng[6]used a viscous fluid model to describe the deformable muddy bed, Lee et al.[7]used a poro-elastic model. Another linear model which combines the features of these two models was widely used, known as the visco-elastic solid model. The typical examples of this model include the Voigt model by Ng et al.[8]and the Jeffreys model by Niu and Yu[9]. Instead of the linear assumption, nonlinear models such as visco-plastic solid models were deve- loped: Becker and Bercovici[10]and Zhang and Ng[11]adopted the Bingham plastic model, whereas Xia and zhu[12,13]used the Maxwell model to study the wave- mud interaction. Moreover, a visco-elasto-plastic model was adopted by Niu and Yu[14].

The studies mentioned above mainly focus on the wave damping up to the first-order. The mass transpo- rt velocity, which can be determined only when the second-order wave motion is considered, has received a great deal of attention in some theoretical and exper- mental studies. A general theory of the mass transport in water was developed by Longuet-Higgins[15]. Sakakiyama and Bijker[16]measured the mass transpo- rt velocity in the soft mud layer, with a progressive wave over a Bingham mud layer. The experimental re- sults were compared with their theoretical results app- licable only to a Newtonian fluid. Ng[17]developed an asymptotic theory in a thin bi-viscous mud layer, with the assumption that the mud layer thickness is compa- rable to the Stokes boundary layer thickness. Zhang and Ng[11]also deduced an analytical expression of the mass transport velocity in the mud layer, described by the viscoelastic Voigt model.

On the other hand, the Bingham model, with the mud being assumed as a rigid body at a low stress level and a fluid with a constant viscosity coefficient when the stress exceeds the yield stress, is widely used to describe the non-linear rheological properties of the soft mud. With this model, it is often difficult to determine the position of the yield surface in the tran- sient theory, where the shear stress is equal to the yield stress, and the yield surface cannot be predefined and has to be resolved as a part of the problem. There- fore, a more convenient model which is known as the power-law model is preferred, it could describe the shear thinning phenomenon, especially at a low shear ratio. The power-law model could also well represent the non-linear rheological properties of the estuarine mud. This is verified by the experimental results of Ng et al.[8]and Tian[18]who studied the mud in the Haihe Estuary in China, similar results were obtained by Pang[19]who studied the mud in the Lianyun Harbor in China. Thus, the power-law model is used in this paper.

Under the action of a progressive wave, the pre- ssure is transmitted from the water body to the mud layer, to produce the shear stress on the mud surface. Under the shear stress, the mud bed moves to form a muddy fluid with a high concentration. In this paper, a theory is developed to calculate the mass transport ve- locity in the layer of the non-Newtonian mud which behaves like a power-law fluid. To simplify the ma- thematical problem, unlike the traditional double-layer or multi-layer model, it is assumed that only a thin mud layer exists, a pressure load described as a perio- dic function of time and space is applied directly on the mud free surface, and it can reflect the wave action on the water-mud interface to a certain extent, and the similar assumption was adopted in the two-layer model by Bercovici and Becker[20]. In fact, the water viscosity is much smaller than the mud viscosity, the shearing action that the water imposes on the mud sur- face is not remarkable, so the shear stress on the free surface will be assumed to be equal to zero in this paper.

In a Lagrangian coordinate system, Ng[2]studied the mass transport in a thin layer of muddy fluid, and a straightforward expression of the mass transport ve- locity was induced. However, the derived equations were very complex and non-intuitive. Thus, the theory in this paper will be based on an Eulerian coordinate system. Different from the approach of Sakakiyama and Bijker[16], the mass transport velocity investigated by Longuet-Higgins[15]is adopted in this paper so that the mechanism of the mud mass transport could be fully described.

1. Analytical model and method

1.1

Consider a single uniform mud layer lying on the horizontal rigid bed with an undisturbed depth, the mud’s behavior is described by a power-law model with a high concentration. The mud layer is homoge- neous and incompressible with a constant density, and the size of the mud layer is assumed to be infinite in the longitudinal direction., an external periodic pre- ssure load is applied directly on the mud surface to drive the wave motion, and it is a periodic function of time and space with a form like the periodic progressi- ve wave:,is the amplitude,is the wave number, andis the angular freque- ncy. The mud wave propagates along thedirection, the bottom of the mud layer is fixed at, and the elevation of the free surfaceis denoted by. The sketch of the problem geometry is shown in Fig.1.

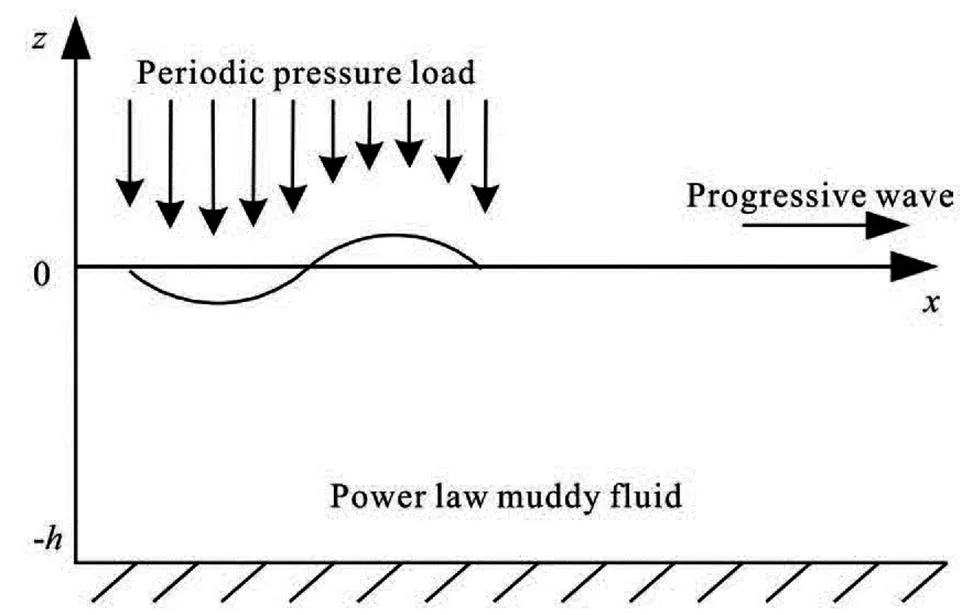
Fig.1 Sketch of the problem geometry

The motion equations, which include the conti- nuity equation for an incompressible fluid and the mo- mentum equations in horizontal and vertical planes, are as follows:

As mentioned in the Introduction, the rheological characteristics of the estuarine mud can be well de- scribed by the power-law model, especially in the case of a low shearing rate (5 s?150 s?1). In the power-law model, the shear stressis related to the shear rateas

so the stress components in the power-law model could be described as

To solve the equations, it is necessary to consider the boundary conditions. First, the tangential stressand the normal stresson a material surface are:

and the kinematics condition on the free surface is

1.2

The key assumption in this paper is that the mud layer thicknessis much smaller compared to the wavelength, namely, so there is a sharp contrast between the horizontal and the vertical len- gth-scales, the ratio of the mud thicknessto the wa- velengthis a very small parameter. Thus, the wave steepnesswill be used as an ordering pa- rameter in the present analysis. According to the work of Sakakiyama and Bijker[16]and Ng[17], the following normalized variables are introduced:

Substituting Eq.(18) into Eqs.(1) through (17), the non-dimensional formulations are obtained.

The dimensionless motion equations are

The dimensionless viscous stress components are as follows:

The boundary conditions along the free surfacebecome

1.3

On the basis of the work of Ng[2]and Bercovici and Beck[20], a perturbation is made and the variables,andare expanded into powers of

2. First-order problem

Only the shear stress componentappears in the first order terms, and it is

The boundary conditions require that the shear st- ress vanishes on the surface

and the normal stress is equal to the external pressure load

No displacement occurs at the bottom

The displacement of the mud surface of the leadi- ng order is

In order to solve these non-linear equations, it is assumed that,,andare separable and periodic inand, which could be written as,, so the variables become

Substituting Eqs.(37) and (43) into Eq.(35), the governing equation of motion with independent varia- blesandof the leading order are obtained as

However, Eq.(45) is a non-linear differential equation, the analytical solutions could be found only when the flow index[2]. Therefore, the problem has to be solved numerically, the details of the nume- rical solution are explained in Section 4.

3. Second order problem

and the horizontal and vertical momentum equations are

and the second shear stress componentis

With Eq.(44), substituting Eqs.(50) and (52) into Eq.(48), the governing equation of motion of the seco- nd-order steady currents is obtained as

where the overbar donates the mean value with respe- ct toover a complete period, the subscriptmeans the Lagrangian coordinates. The first term on the right-hand side of Eq.(56)is the mean Eulerian velocity which is related to the fluid viscosity, and the second termis the Stoke’s drift.

The physical explanation of the Stoke’s drift is as follow: A fluid particle makes an orbital path during a wave period, and the orbital path is not closed over a wave period, for the velocity of fluid on the top is di- fferent from that at the bottom, although the difference is small. As a result, the fluid particle moves along the propagating direction.

According to the mass transport velocity, the net discharge rate of mud per unit crest length of wave is given by

4. Numerical solutions and discussions

As mentioned above, Eq.(45) is a non-linear di- fferential equation, which has to be solved numerica- lly. A pseudo transient iterative method is used in this paper, and the pseudo-time stepis introduced to adjust the iteration progression and to improve the quality of the convergence and the calculation. So the following diffusion equation is obtained

The analytical solutions for the caseprovi- de an initial guess to start the iteration of solutions, when the maximum relative change between the two iterations falls below 10-4, the calculation will be sto- pped. The accuracy of the codes has been examined by comparing the numerical results with the analytical solutions for the Newtonian case.

The numerical results for the first order problem will be used to solve the second order problem, and because Eq.(55) is a linear differential equation, an improved chasing method for the five-diagonal sparse matrix is developed.

Figure 2 shows the flow field of the leading order over a period for, where. It indicates that in the Newtonian case, the motion is a harmonic function of the phase variable. With a forced change of the pressure gradient, both the verti- cal and horizontal velocities are harmonic. Specifica- lly, the vertical velocity reaches the positive and nega- tive maximum values nearand, respe- ctively, and is equal to zero nearand.

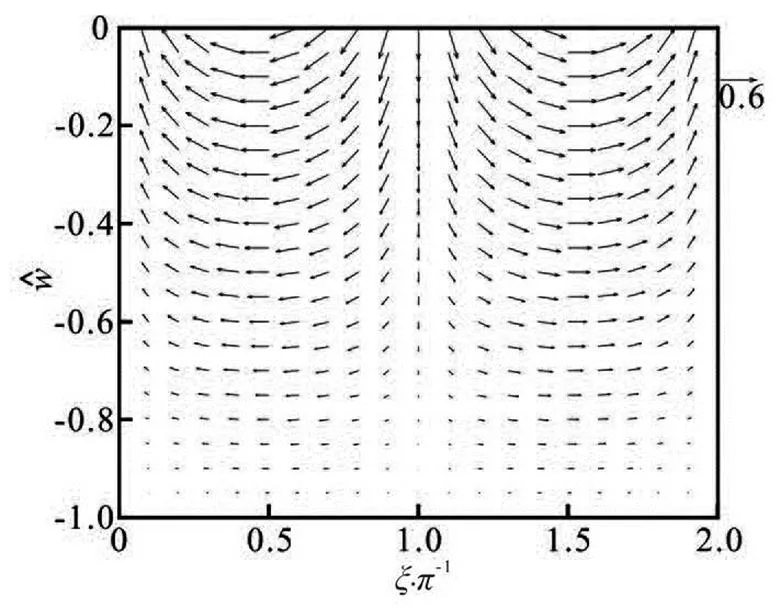
Fig.2 Two-dimensional plot of the flow field for with

Figure 3 is obviously different from Fig.2, al- though, in Fig.3, a periodic nature can still be obse- rved. With the effect of non-Newtonian behavior, the fluid particles are no longer in a simple harmonic mo- tion, the maximum velocity value foris app- roximately half of that for the Newtonian fluid. The muddy fluid is motionless at the phases ofand, where the horizontal velocity is equal to zero in magnitude. This phenomenon could be explained by the fluid shear-thinning property, with a tremen- dously large viscosity at a low stress level.

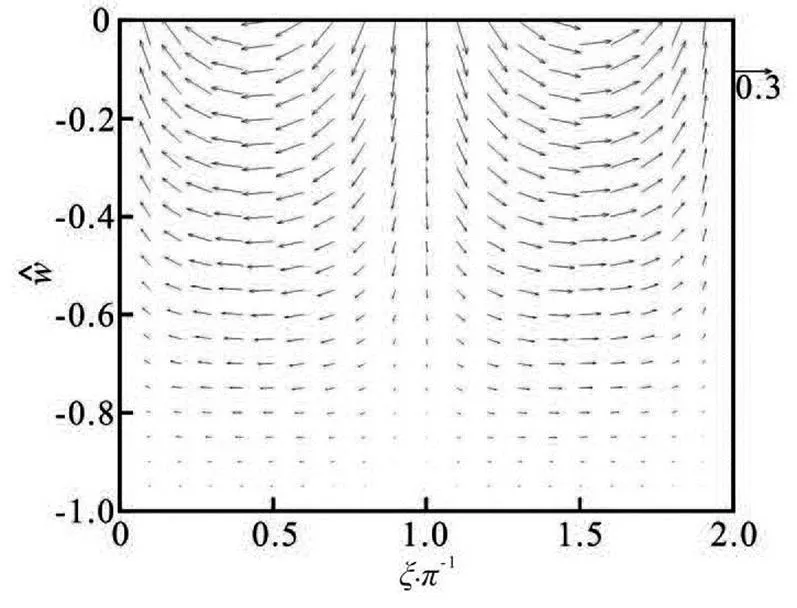
Fig.3 Two-dimensional plot of the flow field for with

Both Figs.4 and 5 reflect the first-order free sur- face displacement over a wave period for different va- lues of the flow index, the pressure magnitudein Fig.4 butin Fig.5. It can be seen that the wave amplitude decreases with the decrease of of. The positive maximum value is reached at, and the negative maximum value occurs at, as shown in Fig.4. These results also confi- rm the phenomena in Figs.2 and 3.

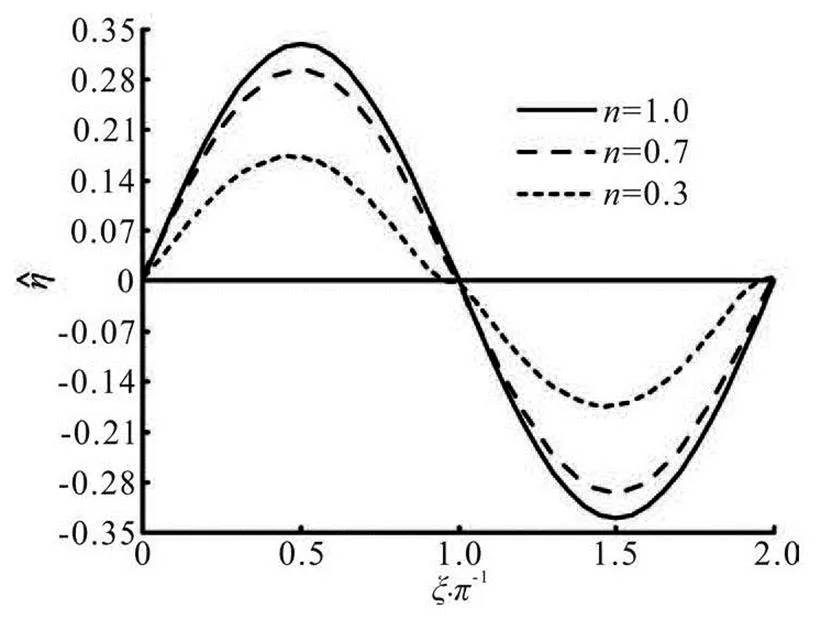
Fig.4 Wave height as a function of for

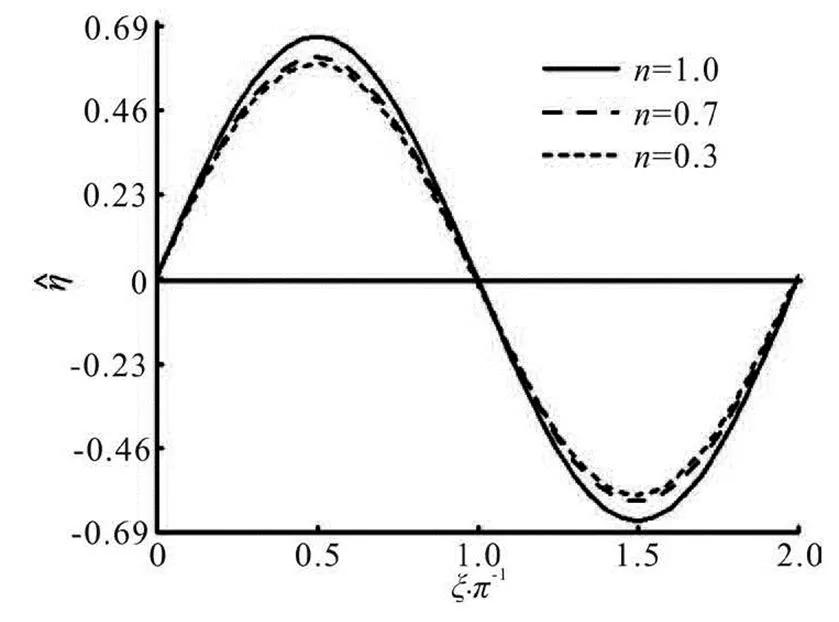
Fig.5 Wave height as a function of for ,

When the pressure loading is doubled to2.0, the wave amplitude foris raised linearly withby a factor of 2, the amplitude forincreases more dramatically to more than three times.

Figure 6 presents the mass transport velocityfor the Newtonian fluid, it consists of the following two components: the mean Eulerian velocityand the Stoke’s drift. It is observed from the Fig.6 that the mass transport near the bed increases dramatically, however, it is backward in the upper part of the fluid.

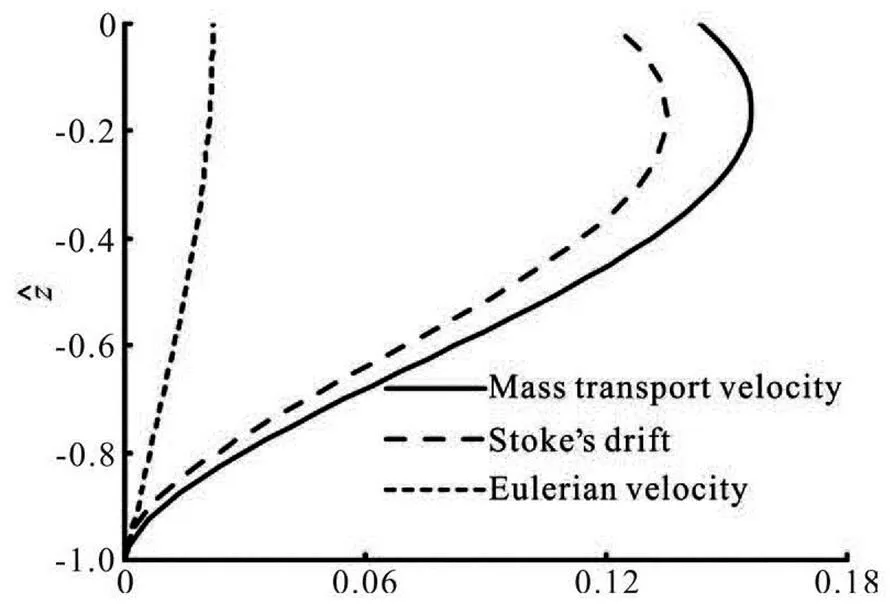
Fig.6 Profile of mass transport velocity in the muddy flow for , where

The mass transport velocities for various values of the flow indexare compared in Fig.7, in which the pressure loadis equal to 1.0 and 2.0, respecti- vely. It is shown that at the same depth, the larger the flow index, the faster that the mass transport increa- ses. Additionally, at a given depth, the mass transport velocity produced by a pressure loadincrea- ses by at least 4 times larger than that produced by.

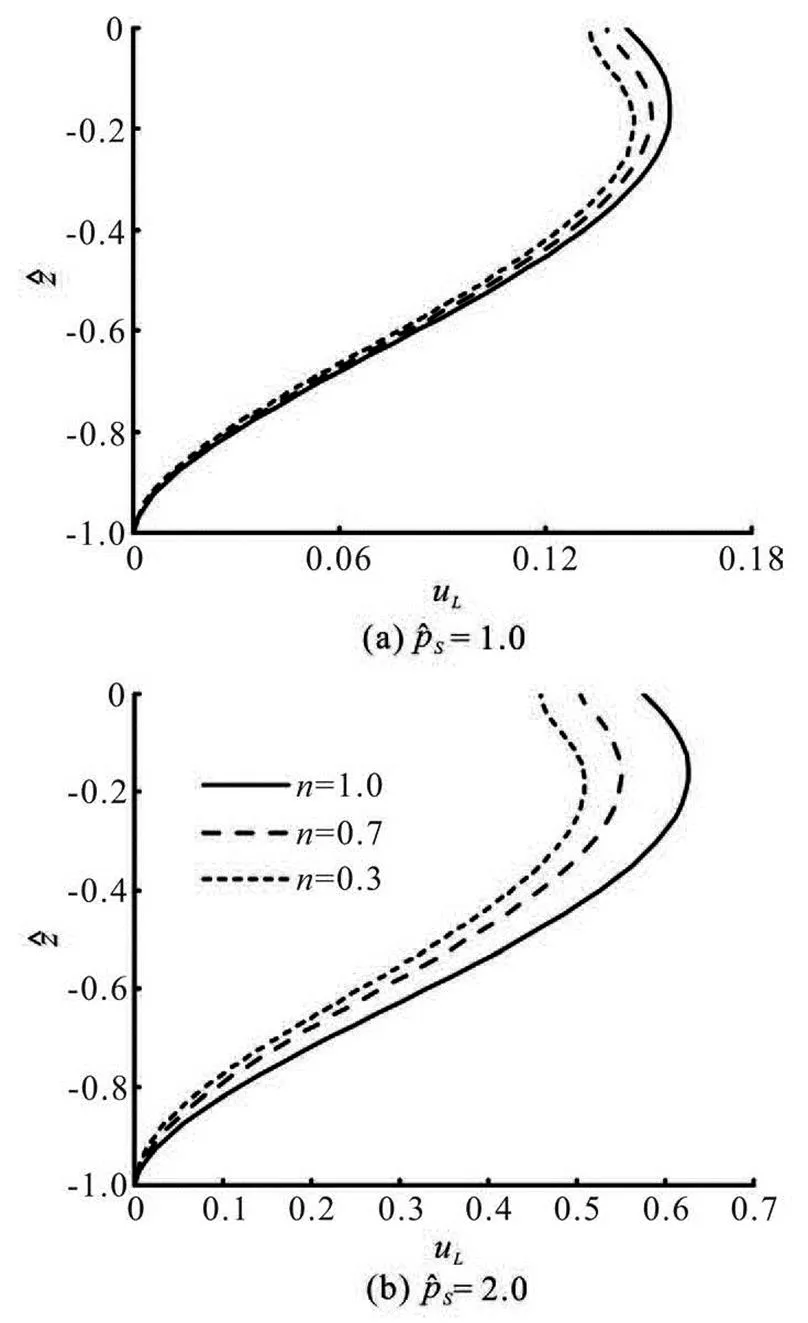
Fig.7 Profile of mass transport velocity as a function of , where

In order to verify the results of the present model, the calculated results are compared with the experime- ntal and numerical results of Sakakayama and Bijker[16], as shown in Fig.8. The laboratory experime- nts were performed in a wave flume of 24.5 m long, 0.5 m wide and 0.57 m deep. Water was used as the upper layer, and a mixture of water and mud was used as the lower layer. The initial thickness of the mud layer was 0.009 m and the water depth was 0.3 m. The wave period in the tests was 1 s and the duration of the wave action was approximately 1 min to 3 min.

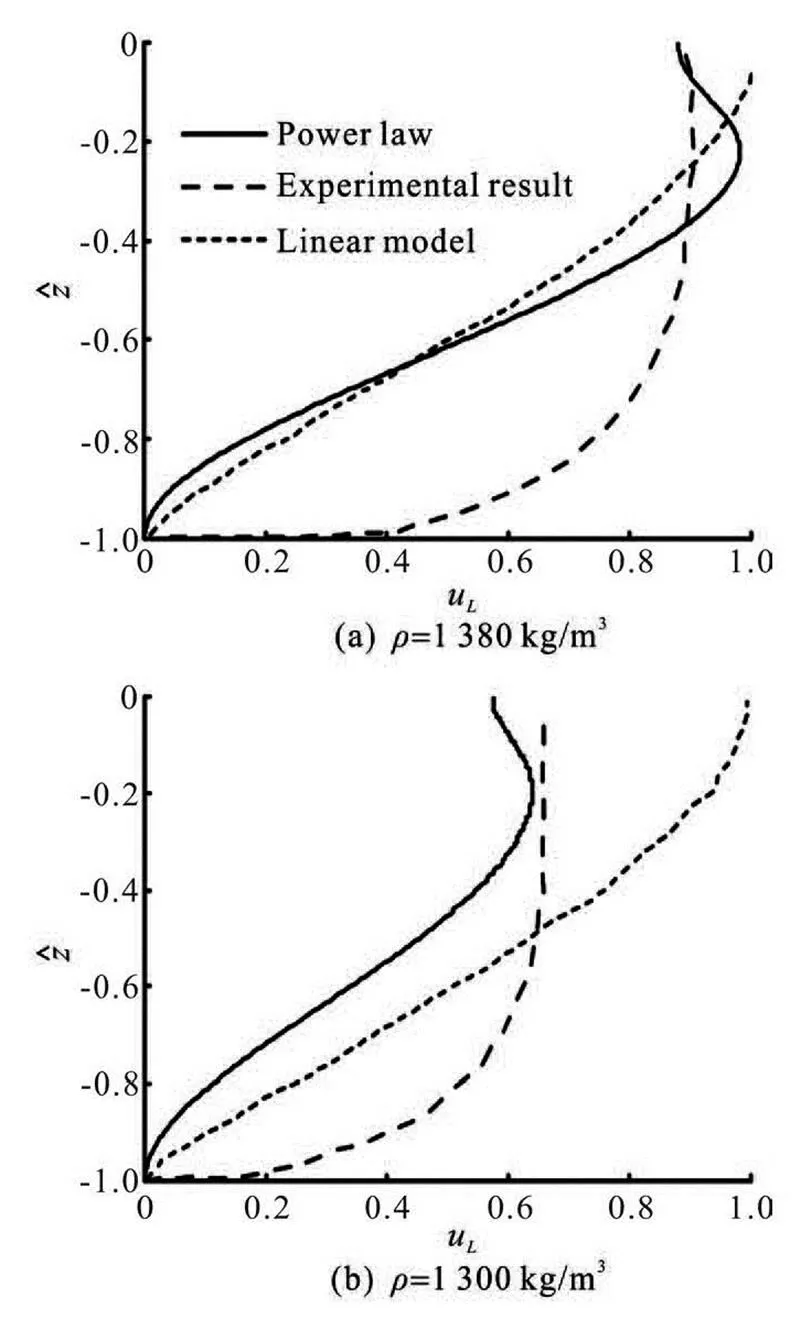
Fig.8 The mass transport velocity in the mud layer

Figure 8 shows that, generally speaking, one sees a good agreement between the measured velocities and the calculated results by the present model. In par- ticular, the results of the present model are an impro- vement from the results of Sakakayama and Bijker[16]. It is apparent that the mass transport velocities near the bottom obtained from both of the models are sma- ller than the experimental results, because the viscosi- ty in both models is constant. However, the viscosity decreases in a real mud with a downward increase in depth, consequently, the mud at a deeper level moves more quickly than the calculated results by the mode- ls.

Figures 9 and 10 illustrate how the net discharge rate varies withand, respectively. For the di- fferent flow index, the discharge rate increases whenincreases from 1.0 to 2.0 while it diminishes whenincreases from 0.6 to 1.2. Therefore, com- pared with, the pressure loadimposes an op- posite effect on the discharge rate. Specifically, by means of either increasingor decreasing, a similar value is obtained for the discharge rate, as is indicated by Eq.(45).

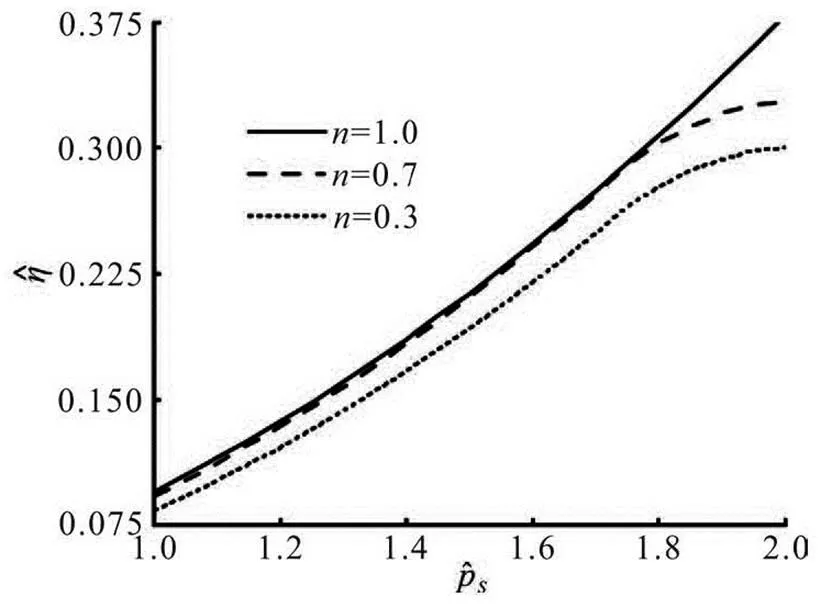
Fig.9 Discharge rate as a function of and , where

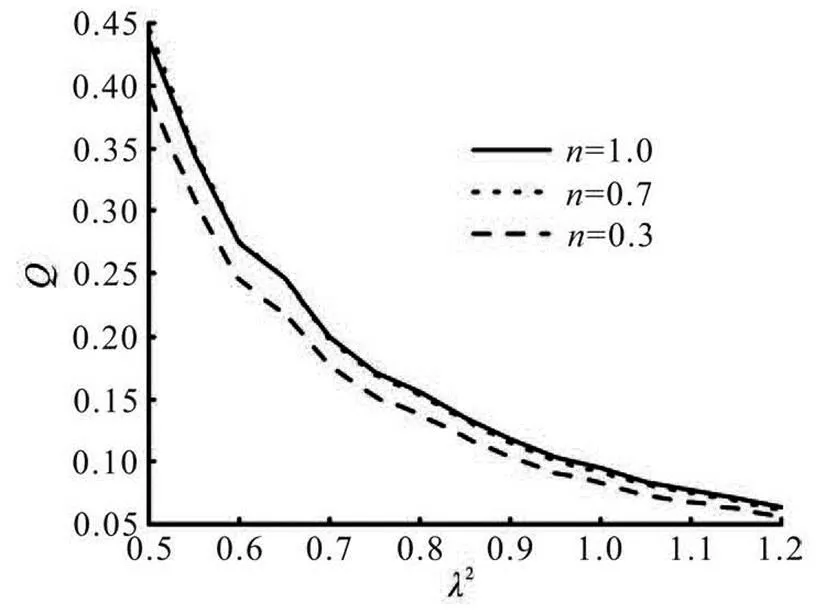
Fig.10 Discharge rate as a function of and , where

5. Conclusions

In this paper, the mass transport velocity in a thin layer of a muddy fluid is presented. Based on an Eulerian coordinate system, the power-law model is adopted to describe the relationship between the stress and the shear rate. According to the assumptions of shallowness and small deformation, a perturbation analysis is conducted up to the second order. The sen- sitivity of the fluid motion, which includes the first- order wave height and the second-order mass transport velocity and the net discharge rate, is discussed. The main results are as follows:

However, the present study is only the first step to understand the interaction of wave-mud, and future work will consider the real rheological properties of the soft mud to study the wave damping and the mass transport in the mud.

References

[1] NGUYEN K. C., SHINTAN T. and UMEYAMA M. Effe- cts of diffusive interface on mass transport by internal waves propagating in a two-layer fluid system[J]. Journal of Applied Mechanics, 2013, 69(2): 1529-1536

[2] NG C. O. Mass transport in a layer of power-law fluid for- ced by periodic surface pressure[J]. Wave Motion, 2004, 39(3): 241-259.

[3] LIU P. F., CHAN I. C. On long propagation over a fluid- mud seabed[J]. Journal of Fluid Mechanics, 2007, 579: 467-480.

[4] HU Y., GUO X. and LU X. et al. Idealized numerical si- mulation of breaking water wave propagating over a vis- cous mud layer[J]. Physics of Fluid, 2012, 24(11): 802- 805.

[5] YANG Feng-chao, CHEN Xiao-peng. Numerical simula- tion of two-dimensional viscous flows using combined fi- nite element-immersed boundary method[J]. Journal of Hydrodynamics, 2015, 27(5): 658-667.

[6] NG C. O. Mass transport in gravity waves revisited[J]. Journal of Geophysical Research, 2004, 109(12): 1-13.

[7] LEE T. C., TSAI D. S. and JENG D. S. et al. Ocean waves propagating over a porous seabed of finite thickness[J]. Ocean Engineering,2002, 29(5): 1577-1601.

[8] NG Chiu-on, FU Sau-chung and BAI Yu-chuan. Mass transport in a thin layer of bi-viscous mud under surface waves[J]. China Ocean Engineering, 2002, 16(4): 423- 436.

[9] NIU Xiao-jing, YU Xi-ping. A numerical method for flows of fluids with complex viscoelasticity[J]. Chinese Journal of Hydrodynamics, 2008, 23(3): 331-337(in Chinese).

[10] BECKER J. M., BERCOVICI D. Permanent bedforms in a theoretical model of wave–sea-bed interactions[J]. Nonli- near Processes in Geophysics,2000, 201(7): 31-35.

[11] ZHANG Xue-yan, NG Chiu-on. Mud-wave interaction: A viscoelastic model[J]. China Ocean Engineering, 2006, 20(1): 15-26.

[12] XIA Y. Z., ZHU K. Q. A study of wave attenuation over a Maxwell model of a muddy bottom[J]. Wave Motion, 2010, 47 (8): 601-615.

[13] XIA Yue-zhang, ZHU Ke-qin. On a fractional-order Maxwell model of seabed mud and its effect to surface wave damping[J]. Applied Mathematics and Mechanics (English Edition), 2011, 32(11): 1357-1366.

[14] NIU Xiao-jing, YU Xi-ping. Visco-elastic-plastic model for muddy seabed[J]. Journal of Tsinghua University (Science and Technology), 2008, 48(9): 1417-1421(in Chinese).

[15] LONGET-HIGGINS M. S. Mass transport in water waves[J]. Philosophical Transactions of the Royal So- ciety, 1953, 245: 535-581.

[16] SAKAKIYAMA T., BIJKER E. W. Mass transport veloci- ty in mud layer due to progressive waves[J]. Journal of Waterway, Port, Coastal, and Ocean Engineering, 1989, 115(4): 614-633.

[17] NG C. O. Water waves over a muddy bed: A two-layer Stokes’ boundary layer model[J]. Coastal Engineering, 2000, 40(3): 221-242.

[18] TIAN Qi. The research on properties and motions of mud in estuary[D]. Doctoral Thesis, Tianjin, China: TianJin University, 2010(in Chinese).

[19] PANG Qi-xiu. Formation and motion characteristics of fluid mud and counter measurements[D]. Doctoral The- sis, Tianjin, China: TianJin University, 2011(in Chinese).

[20] BERCOVICI D., BECK J. M. Pattern formation on the in- terface of a two-layer fluid: Bi-viscous lower layer[J]. Wave Motion, 2001, 34(1): 431-452.

[21] QI P., HOU Y. J. Mud mass transport due to waves based on an empirical model rheology model featured by hyste- resis loop[J]. Ocean Engineering, 2006, 33(16): 2195- 2208.

10.1016/S1001-6058(16)60608-X 2016,28(1):66-74