A Predator-prey Particle Swarm Optimization Approach to Multiple UCAV Air Combat Modeled by Dynamic Game Theory

Haibin Duan,Pei Li,and Yaxiang Yu

A Predator-prey Particle Swarm Optimization Approach to Multiple UCAV Air Combat Modeled by Dynamic Game Theory

Haibin Duan,Pei Li,and Yaxiang Yu

—Dynamic game theory has

Although finding the Nash equilibrium in a two-playergame may be easy since the zero-sum version can be solved in polynomialtime by linearprogramming,this problem has been proved to be indeed PPAD-complete[17?18].So the problem of computing Nash equilibria in games is computationally extremely difficult,if not impossible.Based on the analogy of the swarm of birds and the school of fi sh,Kennedy and Eberhart developed a powerful optimization method,particle swarm optimization(PSO)[19?20],addressing the social interaction,ratherthan purely individualcognitive abilities.As one of the most representative method aiming at producing computational intelligence by simulating the collective behavior in nature,PSO has been seen as an attractive optimization tool for the advantages of simple implementation procedure, good performance and fast convergence speed.However,it has been shown that this method is easily trapped into local optima when coping with complicated problems,and various tweaks and adjustments have been made to the basic algorithm over the past decade[20?22].To overcome the aforementioned problems,a hybrid predator-prey PSO(PP-PSO)was firstly proposed in[21]by introducing the predator-prey mechanism in the biological world to the optimization process.

Recently,bio-inspired computation in UCAVs have attracted much attention[23?25].However,the game theory and solutions to the problem of task assignment have been studied independently.The main contribution of this paper is the developmentof a game theoretic approach to dynamic UCAV air combat in a military operation based on the PP-PSO algorithm.The dynamic task assignment problem is handled from a game theoretic perspective,where the assignmentscheme is obtained by solving the mixed Nash equilibrium using PP-PSO ateach decision step.

The remainder of the paper is organized as follows:Section II describes the formulation of the problem,including the attrition model of a military air operation and its game theoretic representation.Subsequently,we propose a predator-prey PSO forthe mixed Nash equilibrium computing oftwo-player,noncooperative game in Section III.An example of an adversary scenario of UCAV combat involving two opposing sides is presented in Section IV to illustrate the effectiveness and adaption of the proposed methodology.Concluding remarks are offered in the last section.

II.A DYNAMIC GAME THEORETIC FORMULATION FOR UCAV AIR COMBAT

A.Dynamic Model of UCAV Air Combat

There are two combatsides in the UCAV air combatmodel. Specifically,the attacking side is labeled as Red and the defending force as B lue.Each side consists of differentcombat units,which are made up of different numbers of combat platforms armed with weapons.Each unitis fully described by its location,number of platforms and the average number of weapons per platform.Thus,the state of each unit attime k isrepresents the unitlocation,corresponds to the number ofplatforms ofthe i th unitattime k,andto the number of weapons on each platform in the i th unitof X.The number of platforms for the moving units changes according to the following attrition equations

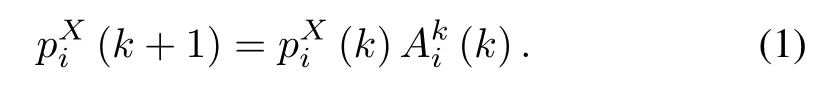
The term in(1)represents the percentage of platforms in the i th unitof X force,which survive the transition from time k to k+1.For each unitin force X,this percentage is dependenton the identities ofthe attacking and the attacked units determined by the choice of target control,and is expressed as

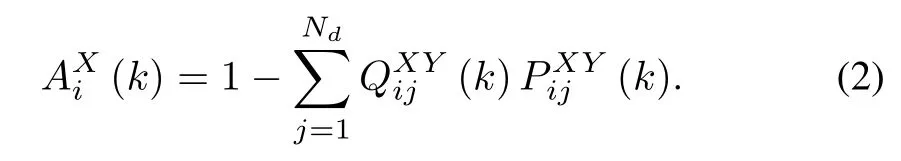
It is assumed in(2)that Ndunits of Y fire at the i th unit of X.The engagement factor QXYij(k)of the j th unit of Y attacking the i th unit of X at time k is computed from

whereβXYijrepresents the probability that the j th unit of Y acquires the i th unit of X as a target,and is calculated by

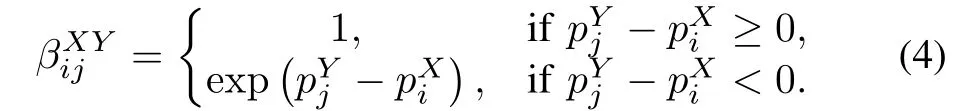
The attrition factor PXYij(k)in(2)representsthe probability of the platforms in the i th unit of X being destroyed by the salvo of sYj(k)fired from the j th unit of Y at time k,and is computed as follows

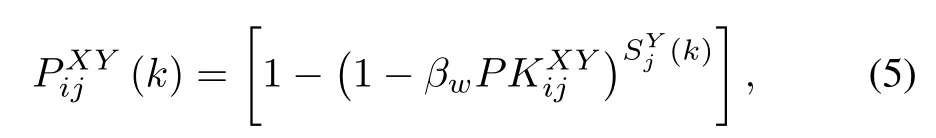
where the term 0≤βw≤1 represents the weather impact which reduces the kill probability according to the weather condition,i.e.,1 corresponds to ideal weather condition while 0 corresponds to the worst weather condition.P KXYijis the probability of i th unitof X being completely destroyed by the j th unit of Y under ideal weather and terrain conditions.

In the equation mentioned above sYiis the average effective kill factor when the j th unit of X attacks the i th unit of Y with salvo cYi(k),and is calculated from

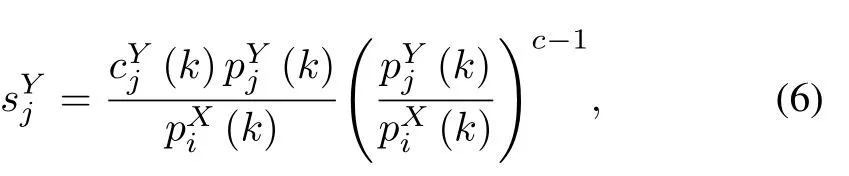
where cYiis the salvo size of j th combat unit of Y and c is a constant referred to as Wes coefficient.

The controlvector for each unitfor both sides is chosen as

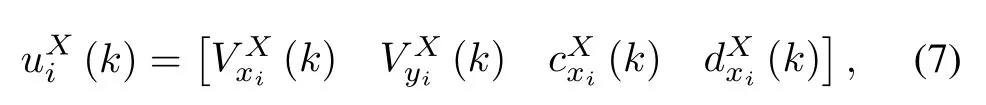
where VxXi(k)and VyXi(k)are respectively the relocating control corresponding to the x-coordinate and y-coordinate,many weapons should fire.The numberofweapons is updated according to

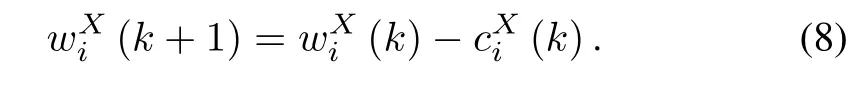
The state equations of each unit engaged in an air combat are defined as

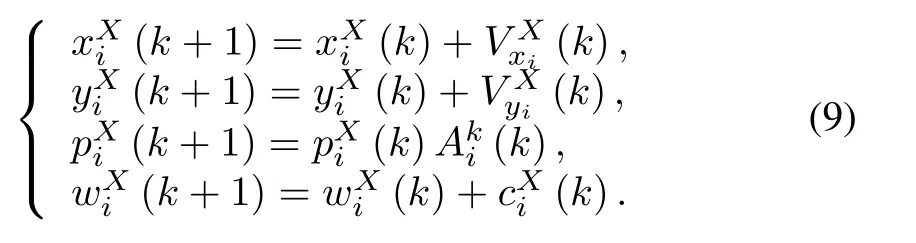
B.Game Theoretic Formulation for UCAV Air Combat

The problem of dynamic task assignmentin the air combat is modeled from a game theoretic perspective in this paper. Suppose Red consists of N R units(UCAVs)and it fires C R missiles during each attack or defense.There are N B units in the B lue force,whose salvo size is also a constant C B.At each decision making step k,both sides decide on which units of its own side should be chosen to attack and which units of the opponent should be chosen as targets,with the purpose of maximizing its own objective function.Each combination of attacking and attacked units is seen as a pure strategy in the game.Foreach side,the numberofpure strategies is calculated as

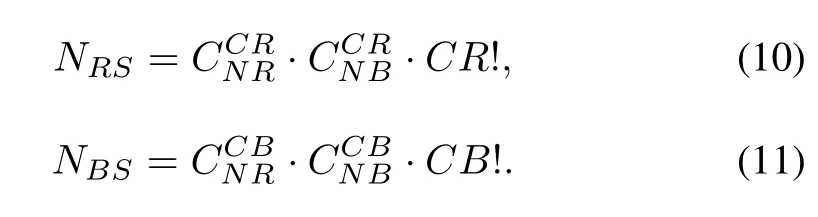
The payoff matrix for both sides is an NRS×NBSmatrix, expressed as

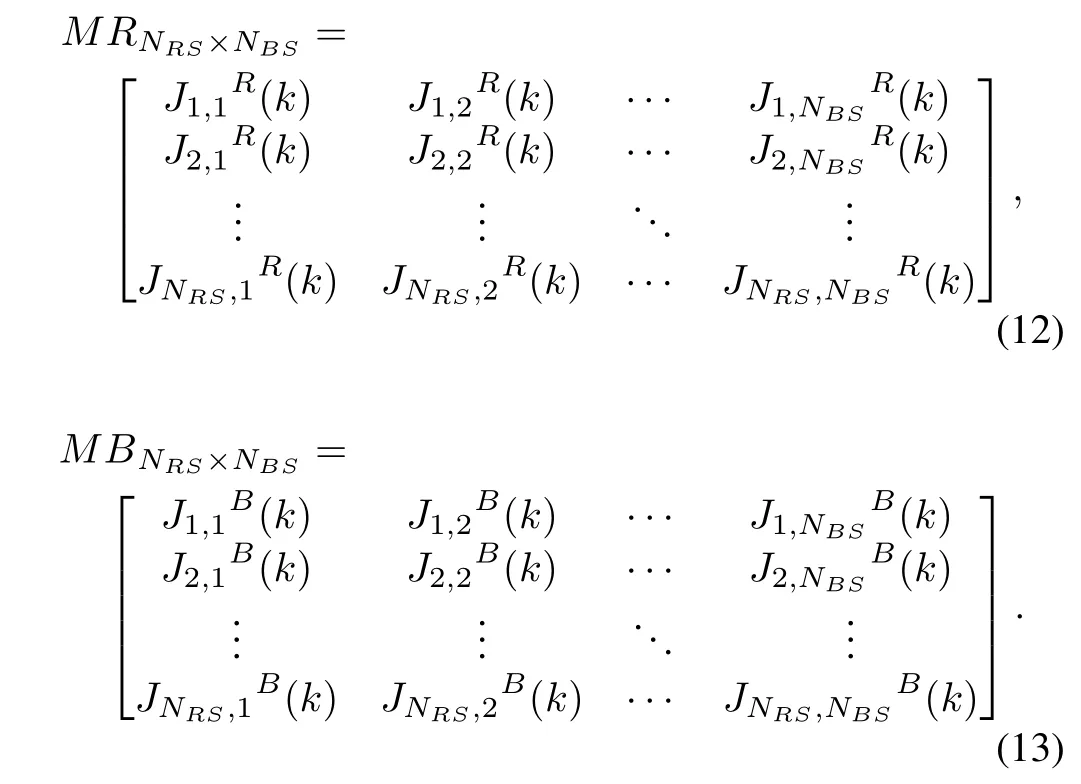
Each entry JRi,j(k)in M R corresponds to the payoff of Red when it takes the i th pure strategy against the j th pure strategy of B lue.Forthe attacking force of Red,the objective function JRi,j(k)is calculated as

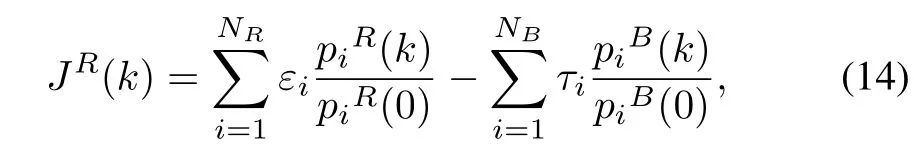
whereεandτare weightcoefficients.The objection function for the defense of B lue is calculated,by the same token,as

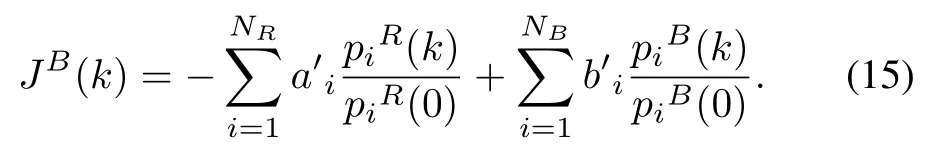
From a game theoretic pointofview,the cooperative UCAV task assignment problem is for the tagged side,Red,to maximize its own payoff ateach decision step,by calculating a mixed Nash equilibrium for the NRS×NBSmatrix game.

III.PREDATOR-PREY PSO FOR THE MIXED NASH SOLUTION

A.Predator-prey PSO

In the gbest-model of PSO,each particle has information of its current position and velocity in the solution space[21]. And ithas the bestsolution found so far of itself as pbest and the bestsolution of a whole swarm as gbest.The gbest-model can be expressed as

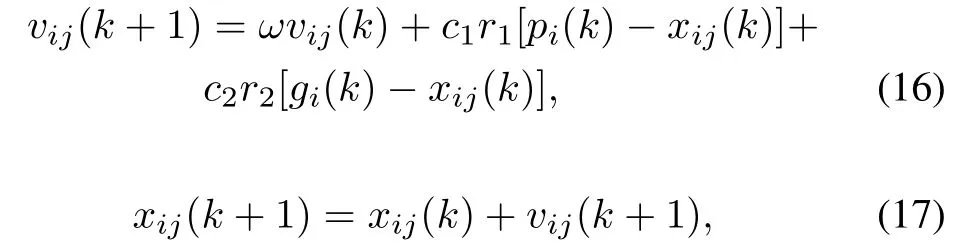
where vij(k)and xij(k)respectively denote the velocity and position of the i th particle in the j th dimension at step k,and c1and c2are weight coefficients,r1and r2are random numbers between 0 and 1 to reflect the stochastic algorithm nature.The personal best position picorresponds to the position in the search space where particle i has the minimum fitness value.The global best position denoted by girepresents the position yielding the bestfitness value among all the particles.

Unfortunately,the basic PSO algorithm is easy to fall into local optima.In this condition,the concept of predator-prey behavior is introduced into the basic PSO to improve the optima finding performance[26?28].This adjustment takes a cue from the behavior of schools of sardines and pods of killer whales.In this model,particles are divided into two categories, predator and prey.Predators show the behavior of chasing the center of preys'swarm;they look like chasing preys.And preys escape from predators in the multidimensional solution space.After taking a tradeoff between predation risk and their energy,escaping particles would take different escaping behaviors.The velocities of the predator and the prey in the PP-PSO can be defined by

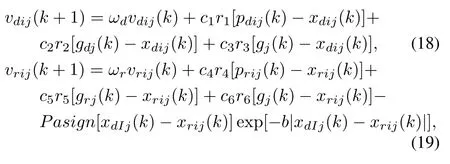
where d and r denote the predator and prey,respectively,pdiis the best position of predators,priis the best position of preys,g is the best position which all the particles have ever found.Andωdandωrare defined as

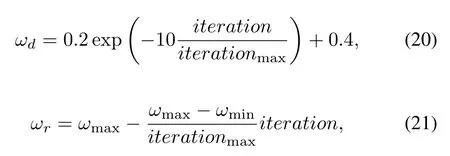
whereωdandωrare the inertia weights ofpredators and preys, which regulate the trade-offbetween the global(wide-ranging) and local(nearby)exploration abilities of the swarm and are considered critical for the convergence behavior of PSO. iterationmaxrepresents the maximum number of iterations andωmaxandωmindenote the maximum and minimum value ofωr,respectively.And the definition of I is given by the following expression

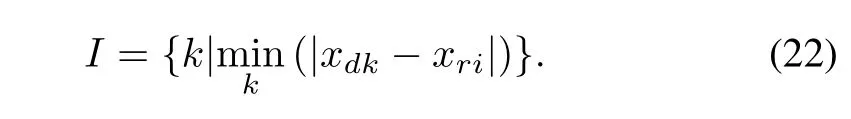
Then I denotes the number ofthe i th prey’s nearestpredator. In(18),P is used to decide if the prey escapes or not(P=0 or P=1),and a and b are the parameters thatdetermines the difficulty of the preys escaping from the predators.The closer the prey and the predator,the harder the prey escapes from the predator.Moreover,a and b are shown as

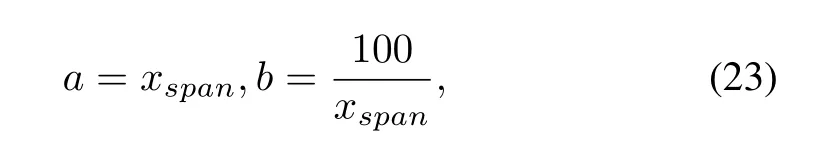
where xspanis the span of the variable.

B.Nash Equilibrium

As a competitive(non-cooperative)strategy of multiobjective multi-criterion system first proposed by Nash[29], Nash equilibrium is basically a local optimum:a strategy profile(s1,s2,···,sn)such that no player can benefit from switching to a different strategy if nobody else switches,?i,?s'i∈Sj

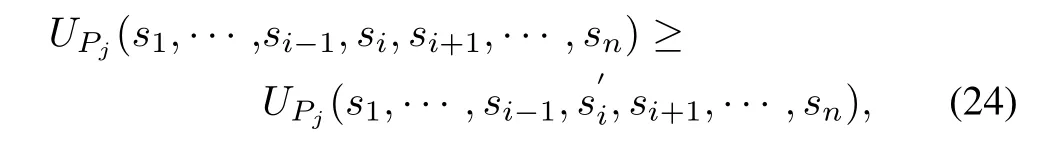
where UPjdenotes the expected payment of person j,sjand Sjrespectively denote the i th strategy of player j and the set of strategies.Note that every dominant strategy equilibrium is a Nash equilibrium,but not vice versa.Every game has one Nash equilibrium at least.In this paper,the expected payment is substituted by the objective function which is used to calculate the payoff matrixes denoted by M Am×nand M Bm×n.We define the vector of mixed strategies form=NRSand n=NBS.So,for each mixed strategy Xi,the Nash equilibrium solution(X?,Y?)must satisfy the given conditions

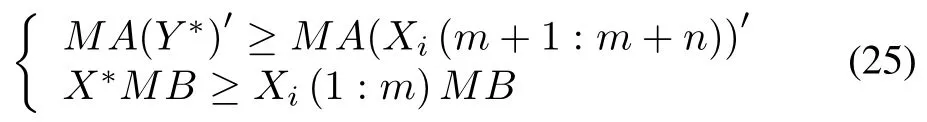
C.Proposed Approach for the Mixed Nash Equilibrium

For utilizing the proposed algorithm to compute Nash equilibrium here,we give the fitness functions as

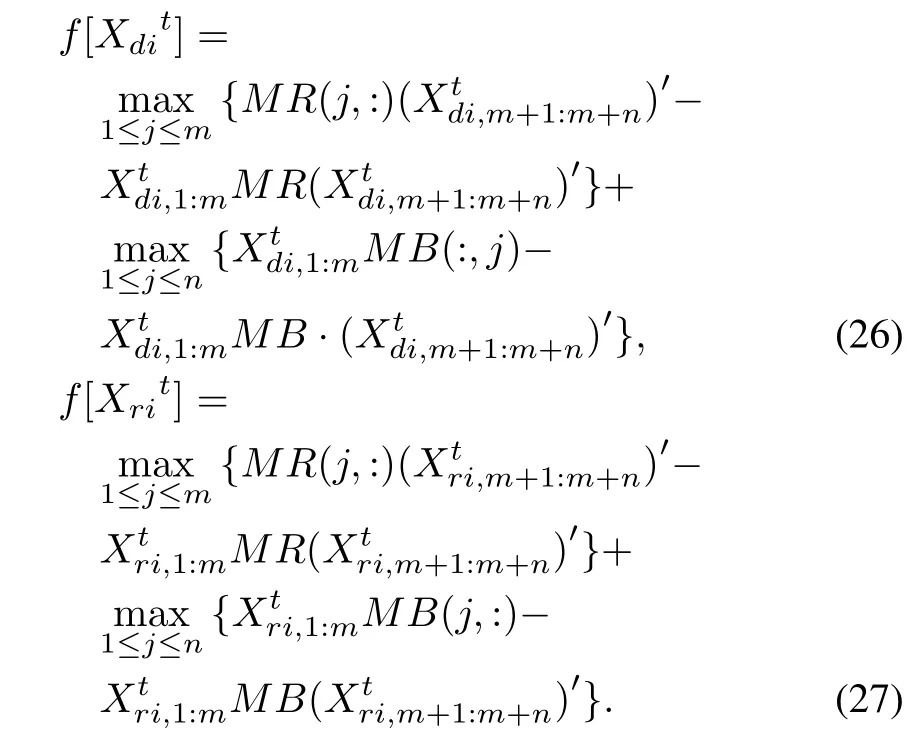
In the last two expressions,Xdi,1:m(k)means the mixed strategies which are produced by the i th predator for the A force and the B force,respectively.Similarly,Xri,1:m(k) and Xri,m+1:m+n(k)denote the mixed strategies which are produced by the i th prey for the A and B forces.Note that the proposed variables must satisfy the following conditions:

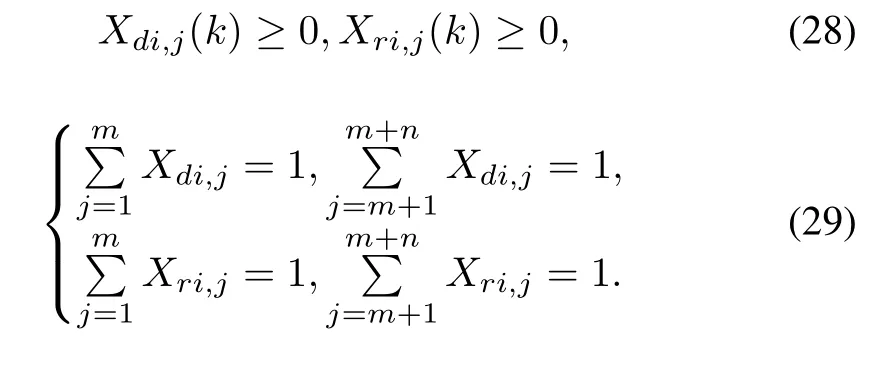
Importantly,the mixed Nash equilibrium corresponds to the minimum of the fi tness function and the optimal or the sub-optimal solution will be the closest to zero.The detailed procedure of PP-PSO for the mixed Nash equilibrium computing is demonstrated in Fig.1.

Fig.1 Procedure of Nash equilibrium computing based on the PPPSO.

To validate the effectiveness of the proposed method,here we illustrated the Nash equilibrium computing both for zerosum game and non-zero-sum game using two simple examples. For a fair comparison among these two method,they use the same maximum iteration number Nmax=100,the same population size m=30,and the same up and lower bounds for inertia weightsωmax=0.9,ωmin=0.2.Besides,in our proposed PP-PSO,the numbers of predators and preys are set md=10,mr=20,respectively.

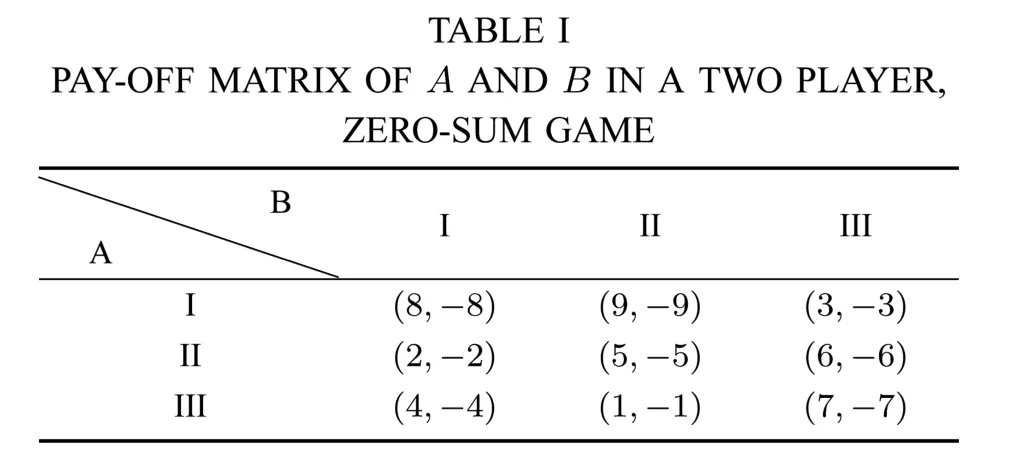
Example 1.Consider two-person,zero-sum game and nonzero-sum game illustrated by Tables I and II[30].

?

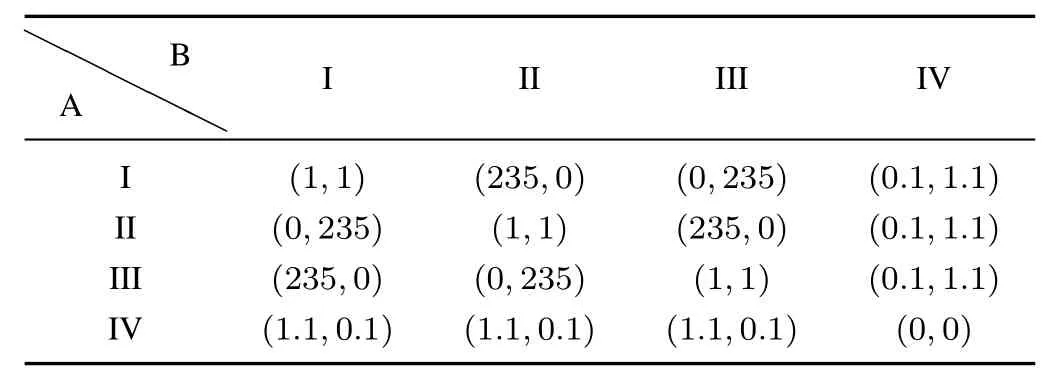
TABLE II PAY-OFF MATRIX OF A AND B IN A TWO PLAYER, NON-ZERO-SUM GAME

As we can see from the above two tables,the first column and the fi rst row represents the strategies of player A and B, respectively.For example,in the zero-sum game,each player has three strategies,which are specified by the number of rows and the number of columns.The payoffs are provided in the interior.The first number is the payoff received by the column player;the second is the payoff for the row player. To reduce statistical errors,each algorithm is tested 100 times independently for these two games.Evolution curves for the two-player,zero sum game are depicted in Figs.2～4.Besides, the simulation results are illustrated from the perspective of average fitness value,best fitness value ever found(Tables III and IV),the minimum error and times thatthe results satisfied that error≤0.01,where error is defined as the following expressions:

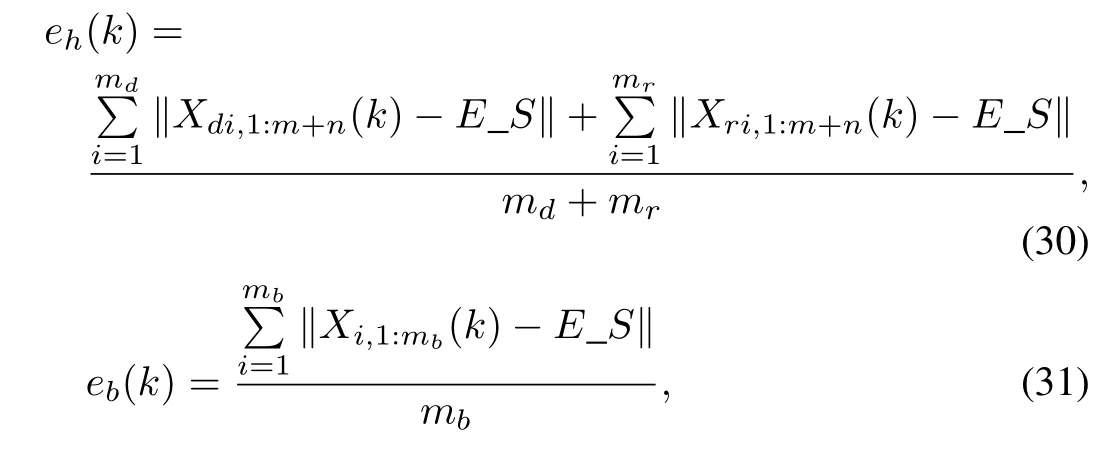
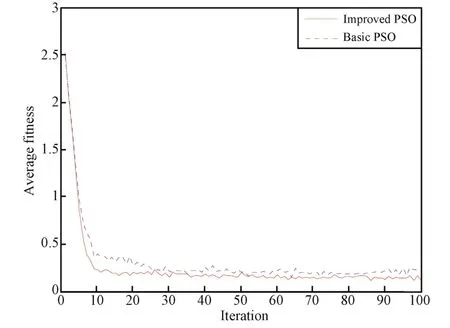
Fig.2. Comparison results of average fitness values for the two player,zero-sum game.

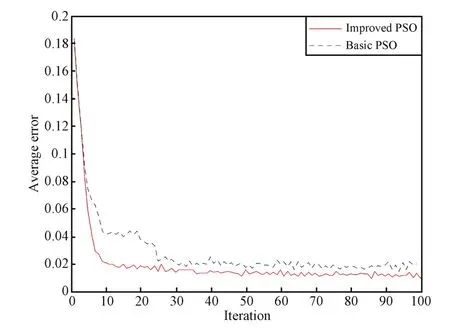
Fig.3. Comparison results ofaverage errors forthe two player,zerosum game.

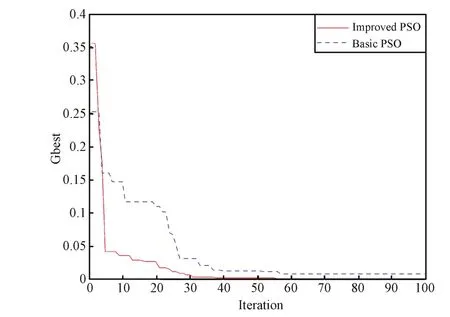
Fig.4. Comparison results of global best solutions for the two player,zero-sum game.

where eh(k)and eb(k)denote the error of the basic PSO and our proposed PP-PSO,E S represents the mixed Nash equilibrium solution of the game that the players participate in.Note￡ that for the zero-su?m game shown in Table I,

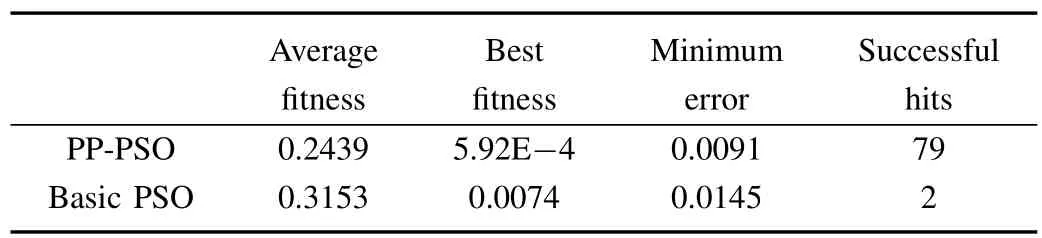
TABLE III COMPARISON RESULTS FOR THE TWO PLAYER,ZERO-SUM GAME

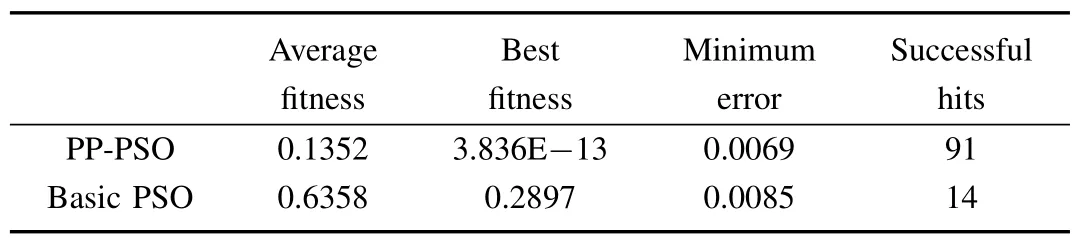
TABLE IV COMPARISON RESULTS FOR THE TWO PLAYER, NON-ZERO-SUM GAME

It is reasonable to conclude from the simple example demonstrated above that the proposed PP-PSO outperforms the basic PSO in terms of solution accuracy,convergence speed,and reliability for Nash equilibrium computing.So itis appropriate to use this method to solve the problem of multiple UCAV air combat modeled by dynamic game theory in the following section.

IV.GAME THEORETIC APPROACH TO UCAV AIR COMBAT BASED ON PP-PSO

A.Experimental Settings

To validate the effectiveness of the dynamic game theoretic formulation for UCAV air combat,a computational example is performed based on Matlab 2009b using our proposed PPPSO.Consider an adversary scenario involving two opposing forces here.The attacking force is labeled as Red team,while the defending force is labeled as B lue team.The missionof the B lue force is transporting military supplements from its base to the battlefront while the task of the Red force is attacking and destroying the aerotransports of the B lue force at least 80%and then returning to their air base.

As shown in Fig.5,the B lue force consists of one transportation unit,which is represented by the solid square,and two combatunits.They are on the way back to the base after accomplishing a military mission.The Red force consists of three combatunits and aims to destroy the B lue transportation unit.The Red force is also programmed to return the base after the mission.For simplification of the problem,each unit ofboth sides is assumed to consistofthe same type of UCAVs, and each UCAV is equipped with a certain number of air-toair missiles.Assume that the speed of Red force is nearly 0.25 km/s while the speed of B lue force is nearly 0.2 km/s, and the state variables will be updated every 2 minutes.So the positions of the Red force and the B lue force willchange 30 km and 24 km,respectively at each step.The configuration parameters used in the simulation for the Red force and the B lue force are listed in Table V and Table VI,respectively.

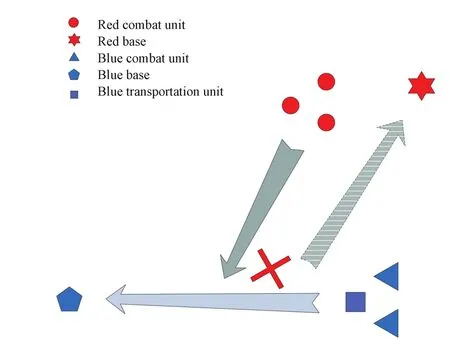
Fig.5.Scenario of cooperative UCAV task assignment.

TABLE V INITIAL CONFIGURATION OF Red FORCE

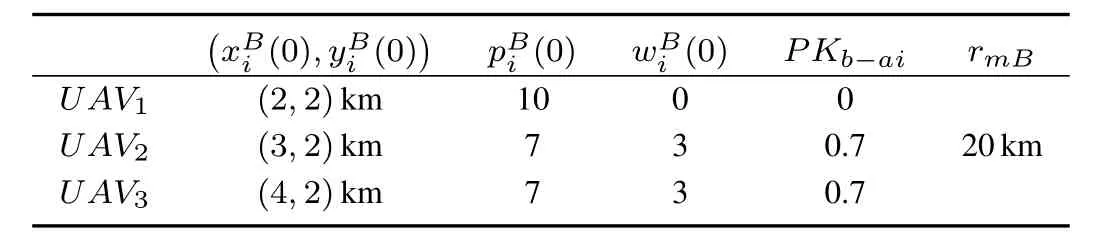
TABLE VI INITIAL CONFIGURATION OF B lue FORCE

In the simulation,the objective functions of the two forces are chosen as

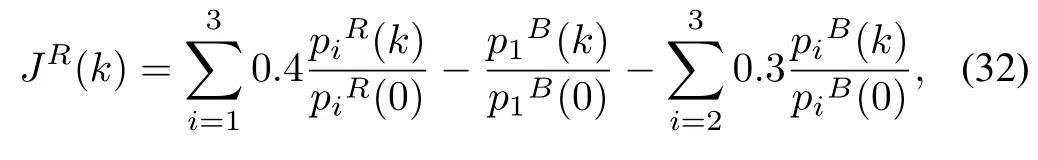
B.Experimental Results and Analysis

Fig.6 presents the flying trajectories for both sides in the air military operations,which result from the proposed game theoretic formulation of task assignmentin a dynamic combat environment and the PP-PSO based solution methodology. The Red force starts from near its base and launches attacks to eliminate the B lue transportation force,which is on the way returning to its base after a military mission.The task assignmentscheme for both sides are calculated based on the proposed approach described above.

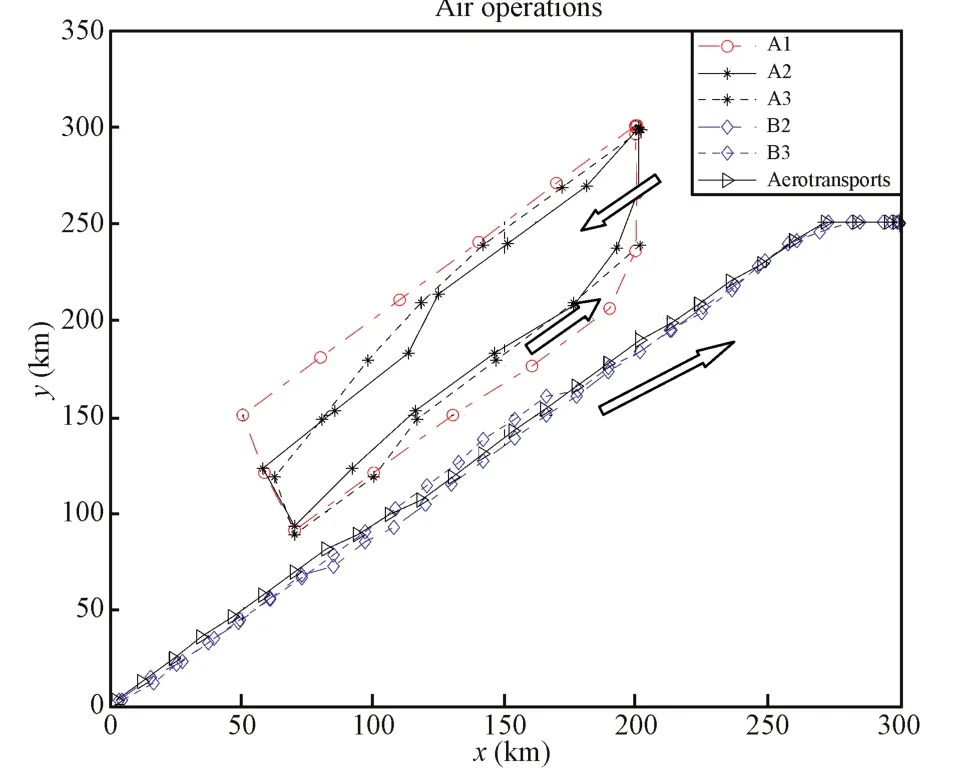
Fig.6.Resulting trajectories of both sides from the proposed approach.

The detailed evolution and convergence behavior with time of platform numbers in combating units are shown in Fig.7. The combating units of both sides start to fight at the 9th time step.After 3 time steps of engagement,this air military operation ends up at the 11th time step,with Red defeating the B lue force and the surviving forces ofboth sides returning to their own bases.At the end of the combat,the Red force manages to inflict more than 90%of the platforms in B lue's transportation unit,78%of platforms in B2,and 70%of platforms in B3.Meanwhile,the Red team pays a price for the victory.The first unit R1 and the third one R3 suffer a slight damage and 30%platforms are destroyed in the attack. However,the second unit R2 of the Red force suffer a serious damage,with more than 60%of the platforms being destroyed in the engagement with the B lue force.The result can be explained from Fig.8,where snapshots of the dynamic task assignmentresults atSteps 9,10,and 11 are given.Itillustrates that the engagement of both sides has a different pattern at each time step and proves the task assignment process to be a dynamic process with time.Atthe 9th and 10th time steps,the second unit R2 of the Red force takes actions in accordance with the resulting mixed Nash equilibrium and chooses thefirst and second units of B lue force as targets,respectively. However,the B lue force insists on attacking R2 by the first unit B1,which is the most powerful unit of its 10 combat platforms.Consequently,R2 suffers the most serious damage in the three units of Red.

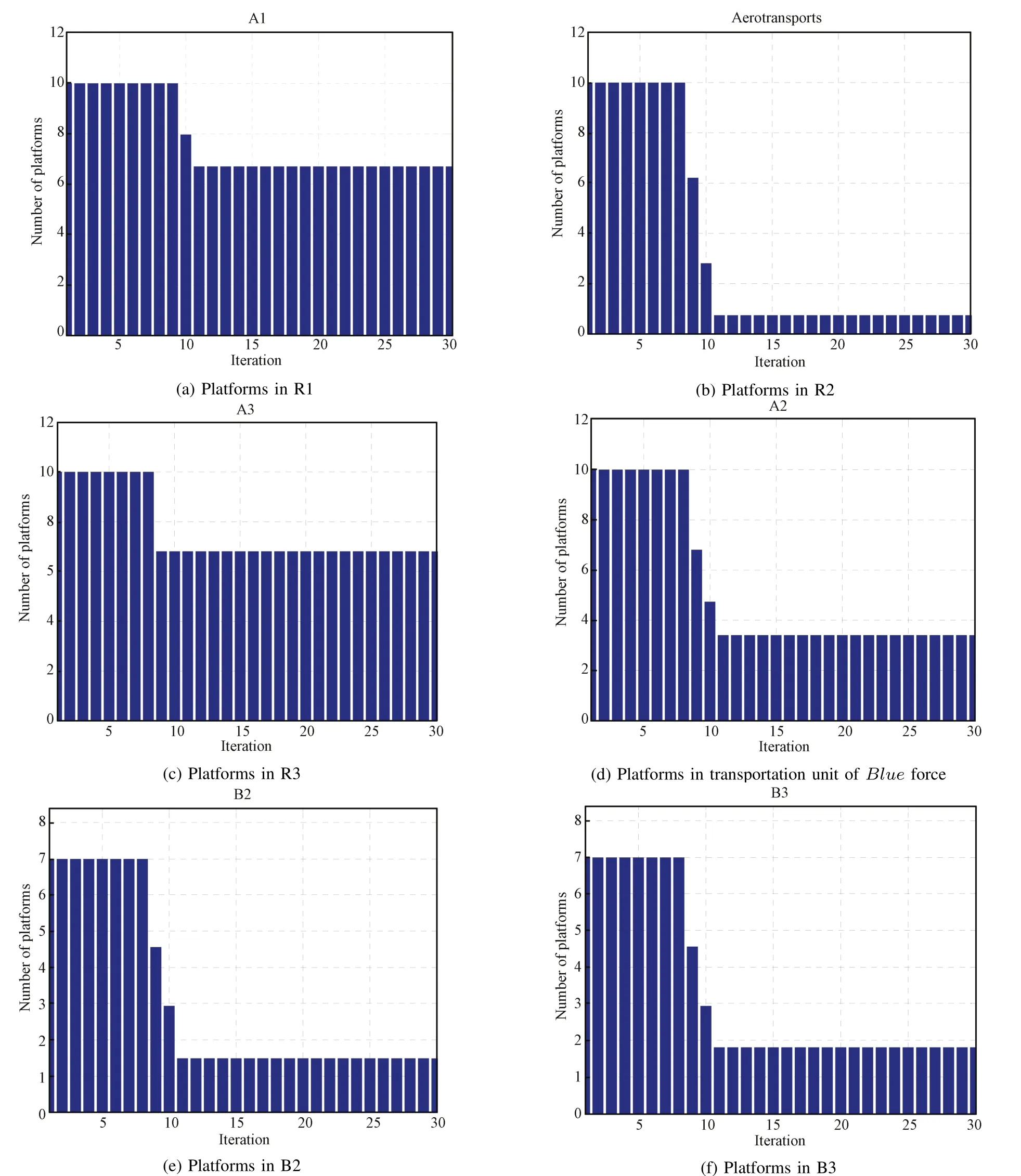
Fig.7.Number of platforms.

It is important to note that both the attacking side and the defense side take advantage of the proposed approach to acquire the assignment scheme over the engagement duration. Therefore,the engagement outcome mainly depends on the initial configuration of each force.The Red force has an advantage in performances and numbers of weapons,whichimplies the possible result of B lue's defeat.The experimental results are coincident with the theoretical analysis and verify the effectiveness and feasibility of the proposed approach.

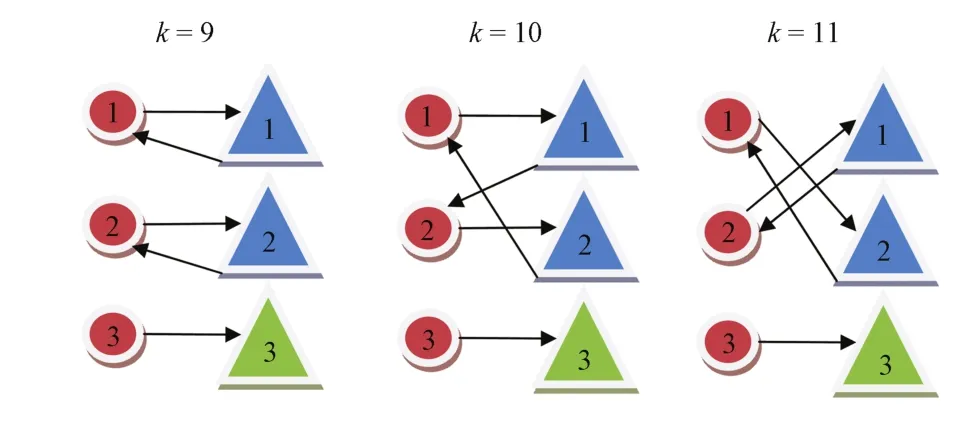
Fig.8.Snapshots of dynamic task assignment results.

V.CONCLUSIONS

This paper developed a game theoretic method for UCAV combat,which is based on the PP-PSO model.By considering both the adversary side and the attacking side as rational game participants,we represented the task allocation scheme as an optional policy set of both sides,and the cooperative task allocation results of both sides were achieved by solving the mixed Nash equilibrium using PP-PSO.An example of military operation involving an attacking side Red and a defense side B lue was presented to verify the effectiveness and adaptive ability ofthe proposed method.Simulation results show that the combination of game theoretic representation of the task assignment and the application of PP-PSO for the mixed Nash solutions can effectively solve the UCAV dynamic task assignment problem involving an adversary opponent.

REFERENCES

[1]Richards A,Bellingham J,Tillerson M,How J.Coordination and control of multiple UAVs.In:Proceedings of the 2002 AIAA Guidance,Navigation,and Control Conference.Monterey,CA:AIAA,2002.145?146

[2]Alighanbari M,Kuwata Y,How JP.Coordination and controlofmultiple UAVs with timing constraints and loitering.In:Proceedings of the 2003 American Control Conference.Denver,Colorado:IEEE,2003. 5311?5316

[3]Li C S,Wang Y Z.Protocol design for output consensus of portcontrolled Hamiltonian multi-agent systems.Acta Automatica Sinica, 2014,40(3):415?422

[4]Duan H,Li P.Bio-inspired Computation in Unmanned Aerial Vehicles. Berlin:Springer-Verlag,2014.143?181

[5]Duan H,Shao S,Su B,Zhang L.New developmentthoughts on the bioinspired intelligence based control for unmanned combat aerial vehicle. Science China Technological Sciences,2010,53(8):2025?2031

[6]Chi P,Chen Z J,Zhou R.Autonomous decision-making of UAV based on extended situation assessment.In:Proceedings of the 2006 AIAA Guidance,Navigation,and Control Conference and Exhibit.Colorado, USA:AIAA,2006.

[7]Ruz J J,Arelo O,Pajares G,de la Cruz J M.Decision making among alternative routes for uavs in dynamic environments.In:Proceedings of the 2007 IEEE Conference on Emerging Technologies and Factory Automation.Patras:IEEE,2007.997?1004

[8]Jung S,Ariyur K B.Enabling operationalautonomy forunmanned aerial vehicles with scalability.Journal of Aerospace Information Systems, 2013,10(11):516?529

[9]Berger J,Boukhtouta A,Benmoussa A,Kettani O.A new mixed-integer linear programming model for rescue path planning in uncertain adversarial environment.Computers&Operations Research,2012,39(12): 3420?3430

[10]Duan H B,Liu S.Unmanned air/ground vehicles heterogeneous cooperative techniques:current status and prospects.ScienceChina Technological Sciences,2010,53(5):1349?1355

[11]Cruz Jr J B,Simaan M A,Gacic A,Jiang H,Letelliier B,Li M,Liu Y.Game-theoretic modeling and control of a military air operation. IEEE Transactions on Aerospace and Electronic Systems,2001,37(4): 1393?1405

[12]Dixon W.Optimaladaptive controland differential games by reinforcement learning principles.Journal of Guidance,Control,and Dynamics, 2014,37(3):1048?1049

[13]Semsar-Kazerooni E,Khorasani K.Multi-agent team cooperation:a game theory approach.Automatica,2009,45(10):2205?2213

[14]Gu D.A game theory approach to target tracking in sensor networks. IEEE Transactions onSystems,Man,and Cybernetics,Part B:Cybernetics,2011,41(1):2?13

[15]Duan H,Wei X,Dong Z.Multiple UCAVs cooperative air combat simulation platform based on PSO,ACO,and game theory.IEEE Aerospace and Electronic Systems Magazine,2013,28(11):12?19

[16]Turetsky V,Shinar J.Missile guidance laws based on pursuit-evasion game formulations.Automatica,2003,39(4):607?618

[17]Porter R,Nudelman E,Shoham Y.Simple search methods for finding a Nash equilibrium.Games and Economic Behavior,2008,63(2): 642?662

[18]Chen X,Deng X,Teng S-H.Settling the complexity of computing twoplayer Nash equilibria.Journal of the ACM,2009,56(3):Article No. 14

[19]Kennedy J,Eberhart R.Particle swarm optimization.In:Proceedings of the 1st IEEE International Conference on Neural Networks.Perth, Australia:IEEE,1995.1942?1948

[20]Eberhart R,Kennedy J.A new optimizer using particle swarm theory. In:Proceedings of the 6th International Symposium on Micro Machine and Human Science.Nagoya:IEEE,1995.39?43

[21]Higashitani M,Ishigame A,Yasuda K.Particle swarm optimization considering the concept of predator-prey behavior.In:Proceedings of the 2006 IEEE Congress on Evolutionary Computation.Vancouver,BC, Canada:IEEE,2006.434?437

[22]Liu F,Duan H B,Deng Y M.A chaotic quantum-behaved particle swarm optimization based on lateral inhibition for image matching. Optik-InternationalJournalforLightandElectronOptics,2012,123(21): 1955?1960

[23]Edison E,Shima T.Genetic algorithm for cooperative UAV task assignment and path optimization.In:Proceedings of the 2008 AIAA Guidance,Navigation and Control Conference and Exhibit.Honolulu, Hawaii:AIAA,2008.340?356

[24]Duan H,Luo Q,Shi Y,Ma G.Hybrid particle swarm optimization and genetic algorithm for multi-UAV formation reconfiguration.IEEE Computational IntelligenceMagazine,2013,8(3):16?27

[25]Liu G,Lao S Y,Tan D F,Zhou Z C.Research status and progress on anti-ship missile path planning.Acta Automatica Sinica,2013,39(4): 347?359

[26]Duan H B,Yu Y X,Zhao Z Y.Parameters identification of UCAV flightcontrolsystem based on predator-prey particle swarm optimization. Science China Information Sciences,2013,56(1):1?12

[27]Duan H,Li S,Shi Y.Predator-prey based brain storm optimization for DC brushless motor.IEEE Transactions on Magnetics,2013,49(10): 5336?5340

[28]Pan F,Li X T,Zhou Q,Li W X,Gao Q.Analysis of standard particle swarm optimization algorithm based on Markov chain.ActaAutomatica Sinica,2013,39(4):381?389

[29]Nash J F.Equilibrium points in n-person games.Proceedings of the National Academy of Sciences of the United States of America,1950, 36(1):48?49

[30]Yu Qian,Wang Xian-Jia.Evolutionary algorithm for solving Nash equilibrium based on particle swarm optimization.Journal of Wuhan University(Natural Science Edition),2006,52(1):25?29(in Chinese)

Haibin Duan Professor atthe Schoolof Automation Science and Electrical Engineering,Beihang University,China.He received his Ph.D.degree from Nanjing University of Aeronautics and Astronautics in 2005.His is the Head of Bio-inspired Autonomous Flight Systems(BAFS)Research Group. His research interests include multiple UAVs cooperative control,biological computer vision and bioinspired computation.Corresponding author of this paper.

Pei Li Ph.D.candidate atthe Schoolof Automation Science and Electrical Engineering,Beihang University,China.He received his bachelor degree from Harbin Engineering University in 2012.He is a member of BUAA Bio-inspired Autonomous Flight Systems(BAFS)Research Group.His research interests include multiple UAV cooperative controland game theory.

Yaxiang Yu Master student at the School of Automation Science and ElectricalEngineering,Beihang University,China.She received her bachelor degree from Beihang University in 2007.She was once a technician at the Changhe Aircraft Industries Group Co.,Ltd.from 2007 to 2008.She is a member of BUAA Bio-inspired Autonomous Flight Systems (BAFS)Research Group.Her research interests include multiple UAV cooperative control and bioinspired computation.

I.INTRODUCTION

ame theory has received increasingly intensive attention as a promising technique for formulating action strategies for agents in such a complex situation,which involves competition againstan adversary.The priority of game theory in solving control and decision-making problems with an adversary opponenthas been shown in many studies[12?15]. A game theory approach was proposed for target tracking problems in sensor networks in[14],where the target is assumed to be an intelligent agent who is able to maximize filtering errors by escaping behavior.The pursuit-evasion game formulations were employed in[16]for the development of improved interceptor guidance laws.Cooperative game theory was used to ensure team cooperation by Semsar-Kazerooni et al.[13],where a team of agents aimed to accomplish consensus over a common value for their output.

Manuscript received July 24,2013;accepted July 18,2014.This work was supported by National Natural Science Foundation of China(61425008, 61333004,61273054),Top-Notch Young Talents Program of China,and Aeronautical Foundation of China(2013585104).Recommended by Associate Editor Changyin Sun

:Haibin Duan,Pei Li,Yaxiang Yu.A predator-prey particle swarm optimization approach to multiple UCAV air combat modeled by dynamic game theory.IEEE/CAA Journal of AutomaticaSinica,2015,2(1):11?18

Haibin Duan,Pei Li,and Yaxiang Yu are with the Science and Technology on Aircraft Control Laboratory,School of Automation Science and Electrical Engineering,Beihang University(BUAA),Beijing 100191,China(e-mail:hbduan@buaa.edu.cn;peilibuaa@asee.buaa.edu.cn; yaxiangyu03@asee.buaa.edu.cn).

considerable attention as a promising technique for formulating controlactions for agents in an extended complex enterprise that involves an adversary.At each decision making step,each side seeks the best scheme with the purpose of maximizing its own objective function.In this paper,a game theoretic approach based on predatorprey particle swarm optimization(PP-PSO)is presented,and the dynamic task assignmentproblem for multiple unmanned combat aerial vehicles(UCAVs)in military operation is decomposed and modeled as a two-player game ateach decision stage.The optimal assignment scheme of each stage is regarded as a mixed Nash equilibrium,which can be solved by using the PP-PSO.The effectiveness of our proposed methodology is verified by a typical example of an air military operation that involves two opposing forces:the attacking force RReeeddd and the defense force BB lluueee.

Index Terms—Unmanned combat aerialvehicle(UCAV),game theory,air combat,predator-prey,particle swarm optimization (PSO),Nash equilibrium.

C OMPARED to unmanned combat aerial vehicles (UCAVs)that perform solo missions,greater efficiency and operational capability can be realized from teams of UCAVs operating in a coordinated fashion[1?5].Designing UCAVs with intelligent and coordinated action capabilities to achieve an overallobjective is a major partof multiple UCAVs control in a complicated and uncertain environment[6?10]. Actually,a military air operation involving multiple UCAVs is a complex dynamic system with many interacting decisionmaking units which have even conflicting objectives.Modeling and controlof such a system is an extremely challenging task, whose purpose is to seek a feasible and optimal scheme to assign the limited combat resource to specifi c units of the adversary while taking into account the adversary's possible defense strategies[8,11].The difficulty lies notonly in thatitis often very difficult to mathematically describe the underlying processes and objectives of the decision makerbutalso in that the fitness of one decision maker depends on both its own control input and the opponent's strategies as well.