交替方向Galerkin方法在偏積分微分方程中的應用

王 佳, 黎麗梅, 王 易, 王怡芬, 歐陽欣

(湖南理工學院 數(shù)學學院, 湖南 岳陽 414006)

交替方向Galerkin方法在偏積分微分方程中的應用

王 佳, 黎麗梅, 王 易, 王怡芬, 歐陽欣

(湖南理工學院 數(shù)學學院, 湖南 岳陽 414006)

用交替方向Galerkin方法研究二維帶有弱奇異核的偏積分微分方程的數(shù)值解, 在空間方向上, 采用線性有限元, 時間方向上采用向后歐拉方法, 積分項用一階卷積求積逼近, 該方法既具有交替方向存儲量少, 計算量低, 又具有有限元高精度的特點.

偏積分微分方程; 交替方向隱式方法; 向后歐拉方法; 有限元方法

引言

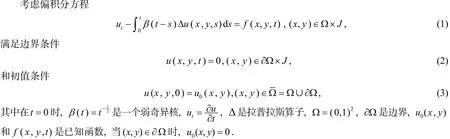
此問題常出現(xiàn)在帶有粘彈性流體模型及帶有記憶功能的熱傳導方程中, 因此討論這類偏積分微分方程的數(shù)值求解具有非常重要的意義. 近年來有許多文獻研究它們的數(shù)值解(例如Sanz-senrna[1], Lòpez-Marcos[2], Chen et al[3], Tang[4], Sun[5], Xu[6,7], G. Fairweather[8],W. Mclean, V. Thomée[9,10]). 他們有的用有限元法[3,6,7,11], 有的用差分法[1,4,5], 有的用樣條配置法[8], 但很少用交替方向有限元方法. 交替方向有限元法最大的優(yōu)點是能把多維問題轉化為一維問題來計算, 大大地減少了計算量. 本文主要是利用交替方向有限元法研究二維偏積分微分方程的數(shù)值解, 在空間方向上采用有限元, 時間方向上使用后歐拉方法, 積分項采用一階卷積求積逼近.

1 預備知識

2 Galerkin交替方向的格式

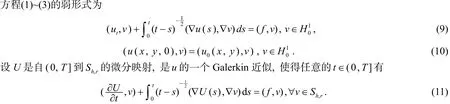
3 數(shù)值例子

初值用U0=W0來逼近, 在T=1時, 用交替方向有限元方法計算出的結果列于表1和表2中. 在表1和表2中, 我們分別選時間步長k=h和k=h2, 來得到相應的誤差和收斂率.

表1 在k=h時的誤差和收斂率

表2 在k=h2時的誤差和收斂率

4 結論

本文用交替方向有限元方法對形如式(1)的偏積分微分方程進行了數(shù)值求解. 在求解過程中, 空間方向上采用有限元, 時間上采用向后歐拉方法, 積分項用一階卷積求積逼近. 用這種離散格式對偏積分微分方程進行數(shù)值求解, 在誤差和精度方面都達到了令人滿意的結果, 并且計算也非常簡便. 這說明用交替方向有限元方法求偏積分微分方程的數(shù)值解是切實可行的.

[1] J. M. Sanz-sern.A numerical method for a partial integro-differential equation[J]. SLAM J. Numer. Anal, 1988(25): 319～327

[2] J. C. Lòpez-marcos.A difference scheme for a nonlinear partial integro-differential equation[J]. SIAM J.Numer.Anal, 1990(27): 20～31

[3] C. Chen, V. Thomée, L. B. Wahlbin.Finite element approximation of a parabolic integro-differential equation with a weakly singular kernel[J]. Math. Comput, 1992(58): 587～602

[4] T. Tang.A finite difference scheme for a partial integro-differential equation with a weakly singular kemel[J]. Appl. Numer. Math, 1993(2): 309～319

[5] Z. Sun, X. Wu.A fu1lly discrete difference scheme for a diffusion-wave systym[J]. Appl. Numer. Math, 2006(109): 193～209

[6] D. Xu.Uniform L behavior for time discretization of a Volterra equation with completely monotonic kernel II:convergence[J]. SIAM J. Nnmer. Anal, 2006 (46): 231～259

[7] D. Xu.Stability of the difference type methods for linear Volterra equation in Hilbert spaces[J]. Numer. Math, 2008(109): 571～595

[8] A. K. Pani, G. Fairweather, R.I.Fernandes.ADI orthogonal spline collocation methods for parabolic partial integro-differential equations[J]. IMA J.Numer,.Anal, 2010(30): 248～276.

[9] W. Mclean, V. Thomée.Numerical solution via laplace transforms of a fractional order evolution equation[J]. J. integr. Equ. Appl, 2009(22): 57～94

[10] W. Mclean, V. Thomée.Maximum-norm error analysis of a numerical solution via laplace transforms and quadrature of a fractional-order evolution eqution[J]. IMA. J. Numer. Anal, 2010(30): 208～230

[11] J. E. Dendy.An analysis of some Galerkin schemes for the solution of nonlinear time dependent problems[J]. SIAM J. Numer. Anal, 1975(12): 541～565

Application of Alternating Direction Galerkin Method in Partial Integral Differential Equation

WANG Jia, LI Li-mei, WANG Yi, WANG Yi-fen, OU Yang-xin
(College of Mathematics, Hunan Institute of Science and Technology, Yueyang 414006,China)

Alternating direction implicit Galerkin method are formulated for the two-dimensional partial intergro-differential equations with a weakly singular kernel. These techniques are based on the finite element method in space and the backward Euler in time in combination with order one convolution quadrature approximating the integral term. The method has not only less storage and low computational characteristics, but also has high precision characteristics with finite element method.

partial intergro-differential equations; alternating direction implicit method; backward Euler method; finite element method

O241.8

: A

: 1672-5298(2015)04-0015-05

2015-10-02

湖南省大學生研究性學習和創(chuàng)新性實驗計劃項目(湘教通[2014]248號)

王 佳(1995? ), 男, 湖南衡南人, 湖南理工學院數(shù)學學院2012級本科生. 主要研究方向: 計算數(shù)學