Quintic spline smooth semi-supervised support vector classication machine
Xiaodan Zhang,Jinggai Ma,Aihua Li,and Ang Li
1.School of Mathematics and Physics,University of Science and Technology Beijing,Beijing 100083,China;
2.Department of Mathematical Sciences,Montclair State University,New Jersey 07043,USA
Quintic spline smooth semi-supervised support vector classication machine
Xiaodan Zhang1,*,Jinggai Ma1,Aihua Li2,and Ang Li1
1.School of Mathematics and Physics,University of Science and Technology Beijing,Beijing 100083,China;
2.Department of Mathematical Sciences,Montclair State University,New Jersey 07043,USA
A semi-supervised vector machine is a relatively new learning method using both labeled and unlabeled data in classication.Since the objective function of the model for an unstrained semi-supervised vector machine is not smooth,many fast optimization algorithms cannot be applied to solve the model.In order to overcome the difculty of dealing with non-smooth objective functions,new methods that can solve the semi-supervised vector machine with desired classication accuracy are in great demand. A quintic spline function with three-times differentiability at the origin is constructed by a general three-moment method,which can be used to approximate the symmetric hinge loss function.The approximate accuracy of the quintic spline function is estimated. Moreover,a quintic spline smooth semi-support vector machine is obtained and the convergence accuracy of the smooth model to the non-smooth one is analyzed.Three experiments are performed to test the efciency of the model.The experimental results show that the new model outperforms other smooth models,in terms of classication performance.Furthermore,the new model is not sensitive to the increasing number of the labeled samples,which means that the new model is more efcient.
semi-supervised,support vector classication machine,smooth,quintic spline function,convergence.
1.Introduction
Using the support vector machine(SVM)[1]to obtain an accurate classier requires a large number of labeled samples.In many applications[2],labeled samples are scarce. Manual labeling for the purposes of training SVM is often a slow,expensive,and error prone process.By contrast,unlabeled samples can be cheaply and automatically collected.Therefore,in machine learning it is important to utilize unlabeled data sufciently.The design of semisupervisedsupportvectormachine(S3VM)[3–7]is based on applying the margin maximization principle to both labeled and unlabeled data.Because of the practicality of S3VM,the semi-supervised classication problem has attracted wide attention of many researchers[8].
Since the objective function of the unconstrained optimization problem of S3VM is not smooth,most existing fast algorithms[9,10]cannot be used for solving the S3VM problem.With this regard,smoothing methods are developedand applied to solve the unconstrainedproblem. Chapelle et al.[11]established a smooth semi-supervised vector machine model.They replaced the symmetric hinge loss function by the Gaussian function.Liu et al.[12]constructed a smooth semi-supervised vector machine model based onthe polynomialfunctions.Yang et al.[13]applied anewsmoothingstrategytoaclass ofS3VMsandobtained a class of smooth S3VMs.
In this paper,a quintic spline function with three-times differentiability at the origin is constructed by a general three-moment method,which plays an important role in approximating the symmetric hinge loss function.Corresponding numerical calculations show that the quintic spline function has a better approximation precision than that of both the Gaussian function and the cubic spline function.Additionally,aconvergencetheoremis proposed, which proves that the solution of the new smooth S3VM (SS3VM)converges to the solution of the original nonsmooth one.Finally,three experiments are performed to test the efciencyof the model.The classication accuracy of the new model is compared with that of other smooth modelsmentionedin this paper.The sensitivityto the parametric variation of the new model is analyzed.The results indicate that the new model has a better classication performance.
2.S3VM model
We considertheproblemofclassifying[14–17]m labeled samples and l unlabeled samples in the n-dimensional real space Rn,represented by an m×n matrix A and an l×n matrix B,respectively.Let Aibe the ith row of A,treatedas a point in Rn.The membership of each point Aiin the classes 1 or–1 is determined by a given m×m diagonal matrix D with 1 or–1 along its diagonal.Precisely,a S3VM model is given by the following quadratic program:

where ω is the normal to the boundingplanes:xTω+b= ±1,with x,ω∈Rn,and b∈R.Note that each ei(i= 1,2)is a columnvectorwith all 1 entries,where e1∈Rm, e2∈Rl.Also,c and c?are positive weights and ξ1and ξ2are slack vectors with ξ1∈Rm,ξ2∈Rl.We further set

where Λ(t)=max(0,1?t)is called the hinge loss function and Λ(|t|)=max(0,1?|t|)is called the symmetric hinge loss function[18].If x∈Rn,Λ(x)=(Λ(x1), Λ(x2),...,Λ(xn))T.By substituting ξi(i=1,2)dened by(2)into(1),the S3VM model(1)can be converted into an unconstrained optimization model as

However,the objective function in(3)is not differentiable, which precludes the use of many fast optimization methods.To improve non-differentiability,we modify(3)as
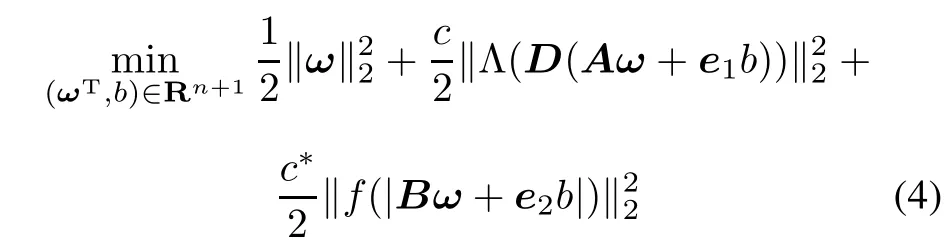
where f(x)is an arbitrary smooth function at the origin and is used to approximate the symmetric hinge loss function Λ(|t|).Although this amendment has little effect on the original problem,it avoids the non-differentiability of the original model(3).Below we study the SS3VM based on the quintic spline function.
3.Construction and analysis of the spline symmetric hinge smooth function
3.1Construction of the quintic spline function
Defnition 1For k>1,m,n∈Z+,let x0=?1/k, x1=0,x2=1/k be a set of nodes and s(x,k)be a piece-
wise function in the following form:

The s(x,k)is called an n-spline with m times differentiability at the origin for Λ(|x|)if it satises following conditions:
(i)Both s0(x,k)and s1(x,k)are polynomials in x of degree n;
(ii)s(d)(x0,k)=0,d=2,3,...,m,s′(x0,k)=1,and s(x0,k)=1?1/k;
(iii)s(d)(x2,k)=0,d=2,3,...,m,s′(x2,k)=?1, and s(x2,k)=1?1/k;
Next we will give the quintic spline function.
Theorem 1Let k> 1 and x0= ?1/k,x1=0, x2=1/k be a set of nodes.Then there exists a unique quintic spline s(x,k)with the third derivative at the origin approximating Λ(|x|).The function must have the following expression:

ProofWe prove this conclusion by the general threemoment method[19].
Let s(x,k)be a quintic spline with the third derivative at the origin,which satises the conditions in Denition 1. We derive the equation for s(x,k)on[?1/k,1/k].Set s(4)(xi,k)=Mi(i=0,1,2).For each x∈[?1/k,0], we have s(x,k)=s0(x,k).Since s0(x,k)is a polynomial of degreeve on[?1/k,0],s(4)0(x,k)is a linearfunction satisfyingTherefore,
Let the aboveequation be integratedfour times,then we can obtain that

where a1,a2,a3,and a4are integration constants.According to the condition(ii)in Denition 1,we can determine


By successive integration,we get

where b1,b2,b3,and b4are integrationconstants.Based on the condition(iii)in Denition 1,it follows

In this way,we show that s(x,k)is a piecewise dened polynomial of degreene with parameters M0,M1,and M2on[?1/k,1/k].Now we apply the condition(iv)in Denition 1:

then the following matrix equation is obtained:


Finally,the unique quintic spline s(x,k)with the third derivative at the origin approximating Λ(|x|)is constructed.On the interval[?1/k,1/k],it can be expressed as(5). □
Similarly,a cubic spline with the second differentiability at the origin approximating Λ(|x|)is shown as

In order to show the differences between different smooth functions more clearly,we present the following smooth performance comparison diagram.
As shown in Fig.1,the quintic spline function with a greater k value is getting closer to the symmetric hinge loss function than that one with a smaller k.In Section 5, we will discuss further dependence of classication accuracy on the parameter k.
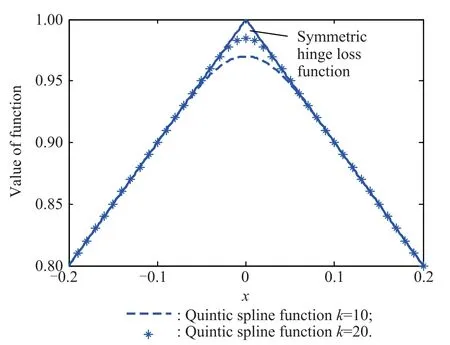
Fig.1 Effect images of the quintic spline function approximating Λ(|x|)when k=10 and k=20
As shown in Fig.2,the quintic spline function is closer to the symmetric hinge loss function than the other functions.Especially,in terms of keeping the parameter k unchanged,the quintic spline function is closer to the symmetric hinge loss function than the general cubic spline function.

Fig.2 Effect images of the different smooth functions approximating Λ(|x|)
3.2Approximate precision of quintic spline functionIn this section,we prove two important properties of s(x,k),which will be applied in the next section to provide the convergenceanalysis of the model.
Theorem 2Let Λ(|x|)be the symmetric hinge loss function.Then,for x∈R and k>1,
(i)0≤s(x,k)≤Λ(|x|);

ProofObviously,if x>1/k or x≤1/k,both inequalities(i)and(ii)are true,since s(x,k)=Λ(|x|).Itremains to show that the inequalities are true on the interval(?1/k,1/k).
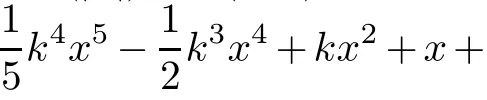
Therefore,λ(x,k)is also an increasing function on(?1/k,0).The minimum is obtained at x =?1/k,λ(?1/k,k)=0.Thus 0≤s(x,k)≤Λ(|x|),when x∈(?1/k,0).
Furthermore,s(x,k)is a decreasing function on (0,1/k).Similar to therst part,the inequality(i)also holds on(0,1/k).

Similarly,if x∈(0,1/k),the above equation is true as well.Therefore,for every x∈R,the(ii)holds. □
4.Convergence analysis of the model
In this section,the convergence theorem of the SS3VM model(4)is presented.We prove that the solution of the SS3VM can closely approximate that of the non-smooth S3VM model.
Defnition 2Let A∈Rm×n,B∈Rl×n,x∈Rn, η∈Rn,μ∈Rn,c,c?∈R,and k>1.

Theorem 3Two real functions h(x)and g(x,k)are dened as above.Then
(i)There exists a solutionˉx of minh(x)and a solutionof ming(x,k)such that
(ii)Let Uhbe the set of the solutions of minh(x),then there exists convergent subsequence{ˉxkn}of{ˉxk}satisfying

In addition,for arbitrary x∈Rn,by inequality(ii)in Theorem 2,we can have



5.Algorithm for the SS3VM model
The Broyden-Fletcher-Goldfarb-Shanno(BFGS)algorithm[20]is suitable for unconstrained optimization problems whenthe objectivefunctionand its gradientvaluecan easily be obtained.The BFGS method is the most widely used one among various quasi-Newton methods.

Step 1Initialization(ω0,b0)=p0∈Rn+1,H0=I, set max=500,i=0,and eps=10?5.
Step 2If i≤max,calculate vi=??(pi).
Step 4Perform linear search along direction dito get a step length αi>0.
Let

Calculate

Step 5Update Hito get Hi+1:

Step 6Let i=i+1,go to Step 2.
In the BFGS algorithm,?(x)is dened in model(4),αiis determined by the following equations:

where 0<ρ<1/2.
6.Numerical experiments
Experiments are performedon datasets with various scales obtained from the UCI Machine Learning Library.The generalization ability of the classier is applied as a test indicator in order to compare the performance of different SS3VM.Correct rates of unlabeled training samples are used to measure the generalization ability of the classier.
The experimental model is dened by(4)where the function f(x)is taken as the Gaussian function,the cubic spline function,the polynomial function,and the quintic spline function given in(6)respectively.For the ease of notation,when f(x)is taken as the Gaussian function,the SS3VM model is named as GSS3VM.Correspondingly, when f(x)is taken as an n-spline function,the SS3VM model is specied as nSS3VM.For example,the SS3VM based on a quintic spline is expressed as 5SS3VM.When f(x)is taken as a polynomial function,the SS3VM model is expressed as PSS3VM.
6.1Experiment to test the wine quality
The considered dataset is made of 1 599 samples.All samplesarelabeledandseparatedintotwoparts:labeledorunlabeled.The labeled part consists of therst 200 samples of the dataset and the rest samples are processed as unlabeled.Each sample contains 11 physicochemicalproperties andone sensoryattribute.The physicochemicaltesting information includes thexed acidity,volatile acidity,citric acid,residual sugar,chlorides,free sulfur dioxide,total sulfur dioxide,density,pH,sulphates,and the alcohol respectively.The sensory data represent the quality which is graded by experts between 0(very bad)and 10(very excellent).The wine quality is divided into two categories: excellent or poor.If the quality score is greater thanve, the wine quality is considered as excellent.Otherwise,the wine quality is poor.

Table 1 Training accuracy of the different smooth S3VM
Table 1 shows that 5SS3VM achieves a higher correct rate under the same conditions.The value of c and c?have some effect on the correct rate of SS3VM.Choosing the value of c and c?properly may improve the correct rate of SS3VM effectually.At the end of this experiment,we study the effect of the parameter k on the classication accuracy of 5SS3VM.Here,the values of both c and c?are selected to be three in the 5SS3VM model.
As can be seen from Fig.3,the parameter k has an inuence on the classication accuracy.The accuracy of 5SS3VM is increasing as the value of k is increasing,unless k reaches a certain level.When the value of k is big enough,the accuracy will keep unchanged.Thus,we should select suitable values of k for different datasets.

Fig.3 Effect of the parameter k on the classifcation accuracy of 5SS3VM
6.2Experiment on the wilt dataset
Thewilt dataset involvesdetectingdiseasedtrees inQuickbird imagery.The dataset is made of 4 339 samples.All samples are labeled.Theve properties of the testing information are GLCM Pan,Mean G,Mean R,Mean NIR, and SD Pan respectively.The wilt dataset is divided into two categories:diseased trees class and other land cover. In this experiment,we also study the effect of proportion of labeled samples on the classication accuracy.Here,we select 20%,30%,and 50%samples to be labeled respectively.And the rest are processed as unlabeled.The classication performances are shown in Table 2.In this experiment,performances of the four SS3VM models are very similar,but overall,5SS3VM is still the best.However,Table 2 shows that the proportion of labeled samples has an inuenceon the correctrate of SS3VM,but not signicant. When the number of labeled samples is large,the classication accuracy cannot be improvedgreatly.It implies that wecan useonlya smallamountoflabeledsamples toguarantee the classication accuracy.

Table 2 Training accuracy of the different SS3VMs(wilt dataset)
6.3Experiment on banknote authentication
The banknote authentication dataset is made of 1372 samples.Data are extracted from images taken for the evaluation of an authentication procedure for banknotes.Wavelet transform tools are used to extract features from images. The four statistical features of the wavelet transformed image are variance,skewness,curtosis,and entropy of images,respectively.The banknote-like specimens are dividedintotwo categories:genuineorforged.Similar tothe wilt dataset,this dataset is labeled too.In the experiment, the effect of proportion of labeled samples and the values of c and c?on the classication accuracy is tested.The classication performances are shown in Table 3.It shows that when dealing with different proportions of the labeled samplesandvariousvaluesofcandc?,the5SS3VMmodel outperforms 3SS3VM and GSS3VM.When dealing with the greater values of c and c?(c=c?=12,c=c?=20), 5SS3VM has a training advantage than PSS3VM.The above results demonstrate that the 5SS3VM model is feasible and effective,and has good features compared with other SS3VM models.

Table 3 Training accuracy of different SS3VMs(banknote authentication dataset)
7.Conclusions
In this paper,a quintic spline symmetric hinge approximation functionwith three-times differentiabilityat the origin is constructed by a general three-moment method.The approximation accuracy of the quintic spline function to the symmetrichingeloss functionis analyzed.A quinticspline smooth semi-support vector machine is obtained.The convergence of the smooth model to the non-smooth one is proved.In three experiments,the classication accuracy and sensitivity to the parametric variation of 5SS3VM are analyzed.The numerical experiments show that the new model has a better classication performance.It is signicant to propose the 5SS3VM model because it adds a new choice when applying SS3VM.
[1]N.Y.Deng,Y.J.Tian.New method in data mining:support vector machine.Beijing:Science Press,2004.(in Chinese)
[2]M.Mozer,M.I.Jordan,T.Petsche,et al.Advances in neural information processing systems.Cambridge:MIT Press,1997.
[3]G.Fung,O.L.Mangasarian.Semi-supervised support vector machines for unlabeled data classifcation.Optimization Methods and Software,2001,15(1):29–44.
[4]J.Long,Y.Li,Z.Yu.A semi-supervised support vector machine approach for parameter setting in motor imagery-based brain computer interfaces.Cognitive Neurodynamics,2010, 4(3):207–216.
[5]S.Reddy,S.Shevade,M.N.Murty.A fast quasi-Newton method for semi-supervised SVM.Pattern Recognition Letters,2011,44(10):2305–2313.
[6]L.Angelini,D.Marinazzo,M.Pellicoro,et al.Semisupervised learning by search of optimal target vector.Pattern Recognition Letters,2008,29(1):34–39.
[7]M.Kalakech,P.Biela,L.Macaire,et al.Constraint scores for semi-supervised feature selection:a comparative study.Pattern Recognition Letters,2011,32(5):656–665.
[8]Y.Q.Liu,S.Y.Liu,M.T.Gu.Polynomial smooth classication algorithm of semi-supervised support vector machines. Computer Science,2009,36(7):179–181.(in Chinese)
[9]A.Astorino,A.Fuduli.Nonsmooth optimization techniques for semi-supervised classication.IEEE Trans.on Pattern Analysis and Machine Intelligence,2007,29(12):2135–2142.
[10]D.P.Liao,B.Jiang,X.Z.Wei,et al.Fast learning algorithm with progressive transductive support vector machine.Systems Engineering and Electronics,2007,29(1):87–91.(in Chinese)
[11]O.Chaplle,A.Zien.Semi-supervised classication by low density separation.Proc.of the 10th International Workshop on Artifcial Intelligence and Statistics,2005.
[12]Y.Q.Liu,S.Y.Liu,M.T.Gu.Polynomial smooth semisupervised support vector machine.Systems Engineering—Theory and Practice,2009,29(7):113–118.(in Chinese)
[13]L.M.Yang,L.S.Wang.A class of smooth semi-supervised SVM by difference of convex functions programming and algorithm.Knowledge Based Systems,2013,41(2):1–7.
[14]Y.J.Lee,O.L.Mangasarian.SSVM:a smooth support vector machine for classication.Computational Optimization and Applications,2001,22(1):5–22.
[15]Y.B.Yuan,J.Yan,C.X.Xu.Polynomial smooth support vector machine.Chinese Journal of Computers,2005,28(1):9–17.(in Chinese)
[16]D.R.Musicant,A.Feinberg.Active set support vector regression.IEEE Trans.on Neural Networks,2004,15(2):268–275. [17]S.Park,B.Zhang.Co-trained support vector machines for large scale unstructured document classication using unlabeled data and syntactic information.Information Processing &Management,2004,40(3):421–439.
[18]J.Wu.Support vector machines learning algorithm research based on optimization theory.Xi’an:Xidian University,2009. (in Chinese)
[19]X.D.Zhang,S.Shao,Q.S.Liu.Smooth support vecter machine model based on spline function.Jornal of University of Science and Tecnology Beijing,2012,34(6):718–725.(in Chinese)
[20]J.Z.Xiong,H.Q.Yuan,H.Peng.A general formulation of polynomial smooth support vector machines.Journal of Computer Research and Development,2008,45(8):1346–1353.
Biographies

Xiaodan Zhang was born in 1959.She is a professor of mathematics in School of Mathematics and Physics,University of Science and Technology Beijing.In 2009,she was a visiting professor at DIMACS,Rutgers University,USA.Her research interests include data mining and dynamical systems.
E-mail:bkdzxd@163.com

Jinggai Ma was born in 1987.She received her B.S. degree from the Hebei Normal University ofScience and Technology in 2011,and M.S.degree in mathematics from the University of Science and Technology Beijing in 2014.
E-mail:abcdef 7110@126.com

Aihua Li was born in 1956.She is a professor at Montclair State University located in New Jersey, USA.She received her Ph.D.degree in mathematics from the University of Nebraska-Lincoln in 1994. Her research interests include commutative algebra, graph theory,discrete dynamical systems,and computational mathematics.
E-mail:lia@mail.montclair.edu

Ang Li was born in 1991.He received his B.S.degree from the University of Science and Technology Beijing in 2013,and pursues his graduate study in mathematics at the same university since then.
E-mail:siwang744@gmail.com
10.1109/JSEE.2015.00070
Manuscript received April 17,2014.
*Corresponding author.
This work was supported by the Fundamental Research Funds for University of Science and Technology Beijing(FRF-BR-12-021).
 Journal of Systems Engineering and Electronics2015年3期
Journal of Systems Engineering and Electronics2015年3期
- Journal of Systems Engineering and Electronics的其它文章
- Planning failure-censored constant-stress partially accelerated life test
- Optimizing reliability,maintainability and testability parameters of equipment based on GSPN
- Ensemble feature selection integrating elitist roles and quantum game model
- New family of piecewise smooth support vector machine
- Articial bee colony algorithm with comprehensive search mechanism for numerical optimization
- Priority probability deceleration deadline-aware TCP
