New family of piecewise smooth support vector machine

Qing Wu,Leyou Zhang,and Wan Wang

1.School of Automation,Xi’an University of Posts and Telecommunications,Xi’an 710121,China;

2.School of Mathematics and Statistics,Xidian University,Xi’an 710126,China;

3.School of Computer Science and Technology,Xi’an University of Posts and Telecommunications,Xi’an 710121,China

New family of piecewise smooth support vector machine

Qing Wu1,*,Leyou Zhang2,and Wan Wang3

1.School of Automation,Xi’an University of Posts and Telecommunications,Xi’an 710121,China;

2.School of Mathematics and Statistics,Xidian University,Xi’an 710126,China;

3.School of Computer Science and Technology,Xi’an University of Posts and Telecommunications,Xi’an 710121,China

Support vector machines(SVMs)have been extensively studied and have shown remarkable success in many applications. A new family of twice continuously differentiable piecewise smooth functions are used to smooth the objective function of unconstrained SVMs.The three-order piecewise smooth support vector machine(TPWSSVMd)is proposed.The piecewise functions can get higher and higher approximation accuracy as required with the increase of parameter d.The global convergence proof of TPWSSVMdis given with the rough set theory.TPWSSVMdcan efciently handle large scale and high dimensional problems.Numerical results demonstrate TPWSSVMdhas better classication performance and learning efciency than other competitive baselines.

support vector machine(SVM),piecewise smooth function,smooth technique,bound of convergence.

1.Introduction

The support vector machine(SVM)is an effective and intelligent machine learning method and has drawn much attention in recent years[1–5].It can solve classication problems and nonlinear function estimation problems in theelds of pattern recognition and machine learning[6–14].

The SVM minimizes the empirical classication error and maximizes the geometric margin.It offers a hyperplane that maximizes the margin between two classes.By introducing slack variables,the soft margin SVM cannd a hyperplanethat splits the examples as cleanly as possible [1,2,4].Maximizing the margins between two classes can be described as a quadratic programming(QP)problem. However,the objectivefunctionof the unconstrainedSVM model is non-smooth at zero.Hence,a lot of good optimization algorithms cannot be used tond the solution. To overcome the above disadvantage,Lee and his partners proposedtouse theintegralofthesigmoidfunctiontoget a smooth support vector machine(SSVM)for classication model in 2001[15].They had done the headmost work of the smooth technique in the SVM.It is a signicant result to the SVM since many famous algorithms can be used to solveit.In2005,Yuanproposedtwopolynomialfunctions, namely,the smooth quadratic polynomial function and the smooth forth polynomial function,which result in a forth polynomial smooth support vector machine(FPSSVM) model and a quadratic polynomial smooth support vector machine(QPSSVM)model[16,17].Soon after,Yuan used a three-order spline function T(x,k)to smooth the objective function of the unconstrained optimization problem of the SVM and obtained a three-order spline smooth support vector machine model(TSSVM)[18].In 2013,a twice continuously differentiable piecewise smooth function ?(x,k)with smoothing parameter k＞0 is proposed to approximatethe plus function,which issues a piecewise smooth support vector machine(PWSSVM)model[19]. However,these approximate functions are constructed separatelyand are in lack of generalization.Furthermore,the efciency or the precision of the algorithms are limited. How to seek better smoothing functions to improve the efciency and the precision is a challenging topic.

Based on ?(x,k),generalized smooth functions are presented.That is a parameterized family of twice continuously differentiable three-order piecewise smooth functions ?d(x,k).And a three-order piecewise smooth support vector machine(TPWSSVMd)is proposed.With the increase of the parameter d,the smooth piecewise functions have better approximation performance.Compared to the other smooth approximation functions,our smooth functionsare a family of smooth functionsrather than only one function.The smooth functions T(x,k)and ?(x,k)are the special cases of the proposed family of piecewise smoothfunctions?d(x,k).Furthermore,thesmoothprecision has been improvedobviously.The globalconvergence proof of TPWSSVMdis given with the rough set theory. The fast Newton-Armijo algorithm[20–22]can be used to solve TPWSSVMd.Experimental results show the great superiority of our scheme in terms of training speed and classication performance.

The rest of the paper is organized as follows.In Section 2,we state pattern classication and describe the TPWSSVMdmodel.The approximation performance of the smooth functions to the plus function is compared in Section 3.The convergence performance of TPWSSVMdis presented in Section 4.In Section 5,we describe the fast Newton-Armijo algorithm.Section 6 shows the experiment results and comparisons.At last,a brief conclusion is given.

In this paper,unless otherwise stated,all vectors will be column vectors unless transposed to row vectors by a prime superscript“T”.For a vector x in the n-dimensional real space Rn,the plus function x+is dened as(x+)i= max(0,xi).The inner product of two vectors x,y in the n-dimensional real space is given as xTy.For a matrix A∈Rm×n,the p-norm will be denoted by‖·‖p.A column vector of those of n-dimension will be denoted by e. If ? is a real valued function,the gradient of ? is represented by??(x)at x which is a row vector and the Hessian matrix of ? is represented by?2?(x)at x.

2.TPWSSVMd

Consider a given data set which consists of m training pointsin then-dimensionalrealspaceRn.Itis represented by an m×n matrix A,according to membership of each point Aiin the class 1 or class–1 as specied by a given m×m diagonal matrix D with 1 or–1 along its diagonal. For this problem,the standard SVM with a linear kernel is given by the following quadratic program

where υ is a positive penalty parameter,e is a vector of 1 s.w and γ are the normal vector and the corresponding bias term of the SVM hyperplane respectively.The second term in the objective function of(1)is the 1-norm of the slack variable y with weight υ.Replacing eTy with 2-norm vector y and adding the term1 2γ2can induce strong convexity,which has little or no effect on the problem. Then the SVM model is transferred to the following problem

Let y=(e?D(Aw?eγ))+,where(·)+replaces negativecomponentsofa vectorbyzeros.ThentheSVMmodel (2)can be converted into the following unconstrained optimization problem

which is a strongly convex minimization problem and has a global unique solution.The function(·)+is a continuous but non-smoothfunction.Therefore,the objective function of(3)is non-smooth.Many optimization algorithms based on derivatives and gradients cannot solve the optimization problem(3)directly.

In 2001,Lee et al.[15]employed the integral of the sigmoid function p(x,k)to approximate the nondifferentiable function x+as follows:

where ln(·)is the natural logarithm,ε is the base of natural logarithmand k is a smoothing parameter.They got the SSVM model.

In 2005,Yuan et al.[16,17]proposed two polynomial functions as follows:

where k＞0.Using the above smooth functions to proximate plus function x+,they got two smooth polynomial support vector machine models(FPSSVM and QPSSVM). Theory analysis and numerical results showed FPSSVM and QPSSVM were more effective than SSVM[15].

In 2007,a three-order spline function[18]was introduced as

With this function,a smooth SVM model TSSVM is obtained.However,the efciency or the precision of these smooth SVMs is limited.

In order to solve the above problem,Wu et al.proposed a new piecewise-smooth function ?(x,k)to approximate the plus function.It is given as follows:

In this paper,we extend T(x,k)and ?(x,k)to a family of three-order piecewise smooth functions ?d(x,k)with smoothing parameter k＞0 to approximate the function x+.

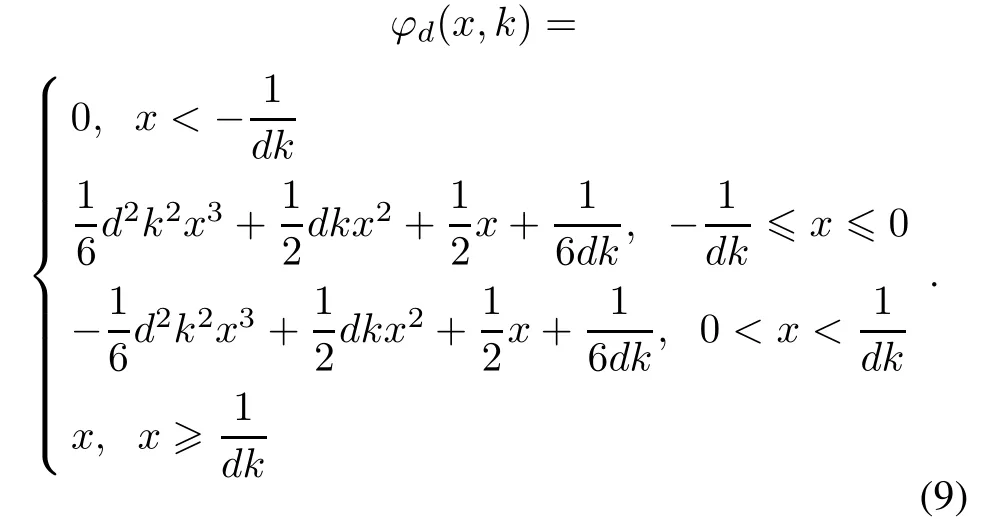
and

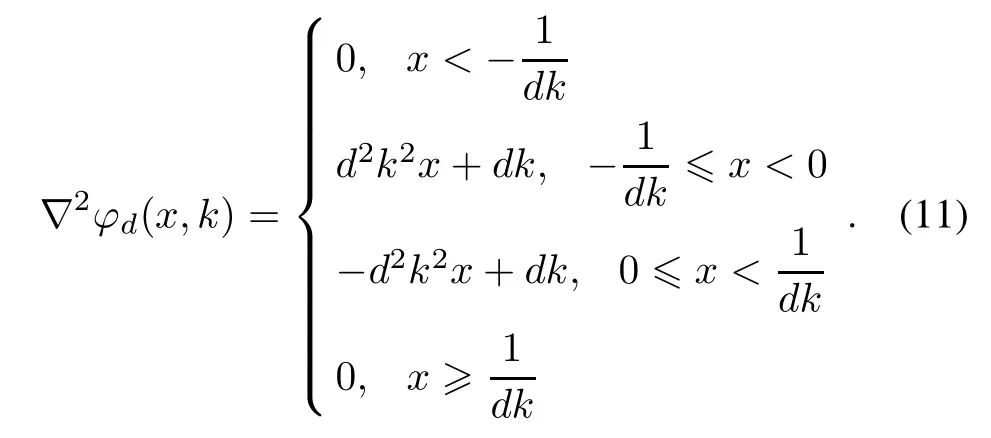
The solution of the problem(3)can be obtained by solving the following smooth unconstrained optimization problem with the smoothing parameter k approaching positive innity.

Thus,we develop a new smooth approximation for problem(3)and get a TPWSSVMdmodel.

3.Approximation performance comparison of smooth functions

In this section,we will analyze the approximation performance of the smooth functions above.

Lemma 1[15] The integral of the sigmoid function p(x,k)is dened as(4),and x+is a plus function.We can obtain the following conclusions easily:

(i)p(x,k)is arbitrary order smooth about x;

(ii)p(x,k)≥x+;

Lemma 2[16] The quadratic polynomial function q(x,k)and the fourth polynomial function h(x,k)are denedas(5)and(6)respectively.Thefollowingconclusions can be obtained:

(i)q(x,k)is one order smooth about x,h(x,k)is twice order smooth about x;

(ii)q(x,k)≥x+,h(x,k)≥x+;

Lemma 3[18]The three-orderspline function T(x,k) is dened as(7).The following conclusion are easily obtained:

(i)T(x,k)is twice order smooth about x;

(ii)T(x,k)≥x+;

Theorem 1The piecewise approximation functions ?d(x,k)dened as(9)have the following properties:

(i)?d(x,k)is twice order smooth about x;

(ii)For any x∈R,?d(x,k)≥x+;

ProofAccording to the formulae(10)and(11),one can easily obtain property(i)above.

Now we prove the inequality ?d(x,k)≥(x)+.

Without loss of generality,we only prove

Now we consider three cases.

Table 1 Approximation accuracy of different smooth functions

Fig.1 Comparison of approximation performance of different smooth functions

4.Convergence analysis of TPWSSVMd

In this section,the convergence of TPWSSVMdis proposed.By the rough set theory,we prove that the solution of TPWSSVMdcan closely approximate the optimal solution of the original model(3)when k approaches positive innity.

Theorem 2Let A∈Rm×n,b∈Rm×1,and dene real function f(x)and gd(x,k)as follows:

where ?d(·,k)is dened in(9),k＞0,d=1,2,3,... Then the following results can be achieved:

(i)f(x)and gd(x,k)are strongly convex functions;

Proof(i)For arbitrary k＞0,f(x)and gd(x,k)are strongly convex functions because‖·‖2is a strongly convex function.

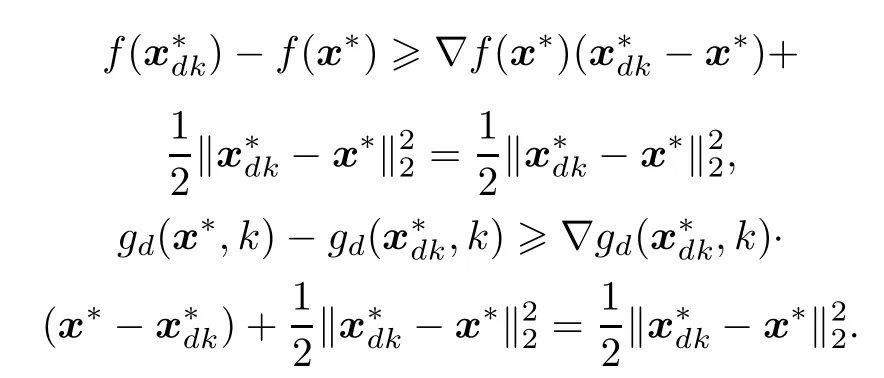
Add the two formulas above and notice that ?d(x,k)≥x+,then we can get

According to Theorem 1,we get to know that

5.Newton-Armijo algorithm for TPWSSVMd

The objective function of(12)is twice continuously differentiable,so we can apply the Newton-Armijo method [15,20,21]to solve TPWSSVMd.The Newton-Armijo method is a fast solution method for optimal problems.It can be described as follows.

Step 1Start with any(w0,γ0)∈Rn+1,τ and set i=0.

Step 2Compute Φid= Φd(wi,γi,k)and gi=?Φd(wi,γi,k).

Step 3If‖gi‖2≤ τ or λi≤ 10?12,then stop, andaccept(wi,γi).Otherwise,computeNewtondirection pi∈Rn+1from the following linear system

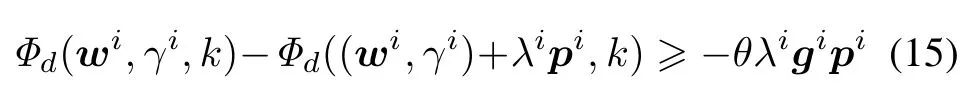
Step 5Replace i by i+1 and go to Step 2.

Whatweneedtosolveis alinearsystem(14)insteadofa quadraticprogram.Itis easytoget thatthe Newton-Armijo algorithm has the globally optimization solution[20–22]. PWESSVM describedabovecan be extendedto solve nonlinear problems with the kernel technique in[15].

6.Numerical implementation and comparison

To show the effectiveness and speed of TPWSSVMd, we perform some experiments to compare the performance numerically between SSVM,FPSSVM,TSSVM and TPWSSVMd.QPSSVM can not be solved by a Newton-Armijo algorithm,which is in lack of the second order derivative.In fact,the classication capacity of FPSSVM is slightly better than QPSSVM[16,17].Hence QPSSVM is not compared in this section.All the experiments are run on a personal computer with a 2.66 GHz and a maximum of 2 Gbytes of memory available for all processes.The computer runs Windows 2007 with Matlab 7.10.The codes of four models are written in Matlab language.We perform tenfold cross-validation on each dataset.For the nonlinear data,we apply the Gaussian kernel.With the change of the parametersd,TPWSSVMdhas different performances.

Table 2 Experimental results for TPWSSVMdon NDC datasets (ν=0.1,k=1,d=1,2,3,4)

The second experiment is used to compare the performance numerically between SSVM,FPSSVM,TSSVM, TPWSSVM3and TPWSSVM4.We use the NDC datasets to test theve algorithms.The test samples also account for 5%of the training samples.Table 3 shows that TPWSSVM4has the highest training accuracy and testing accuracyformassivelysized datasetswith slightdifference in the CPU time.

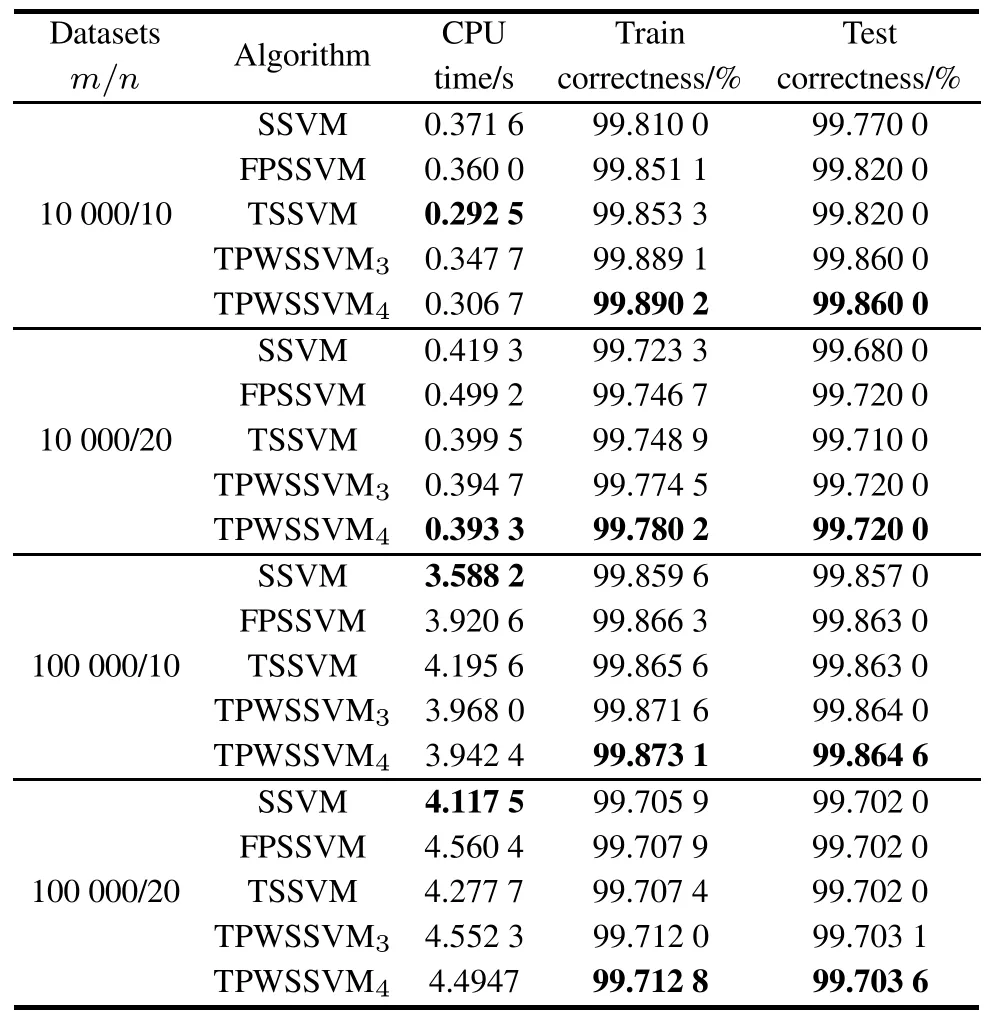
Table 3 Experimental results for four algorithms on NDC datasets (ν=0.1,k=1)

The third experiment is designed to demonstrate the effectiveness of TPWSSVMdthrough the nonlinear“tried and true”checkerboard dataset[24].The checkerboard dataset is generated by uniformly distributing the regions [0,1]×[0,1]to 1002=10 000 points and labeling two classes“white”and“black”by 4×4 grids as Fig.2 shows.

Fig.2 Checkerboard dataset

The training correctness is 98.28%.The test accuracy of TPWSSVM4is 97.49%on a 9 000 points dataset. FPSSVM,TSSVM and TPWSSVM3solve the same problem with 0.96 s,1.09 s and 1.07 s,respectively.The test accuracies of them are 97.38%,97.36%and 97.47%,respectively.SSVM obtain the train accuracy of 98%with 5.67 s,with the testing accuracy of 97.30%.

In the rest trials,the training set is randomly selected from the checkerboard with different sizes.The remaining samples are used as test samples.We compare the classication results of TPWSSVM3,TPWSSVM4,TSSVM, FPSSVM and SSVM with the same Gaussian kernel function.

Table 4 shows that TPWSSVM4can deal with the nonlinear massive problems quickly with the best classication performance.

Table 4 Experimental results for four algorithms on checkerboard datasets

7.Conclusions

In this paper,a family of twice continuously differentiable piecewise-smooth functions are proposed to smooth the unconstrained objective function of SVM,which issues a PWESSVMdmodel.The approximation accuracy of the family of piecewise functions can be as high as required with the increase of the parameter d.The numerical results illustrate that PWESSVMdhas better classication performance for linear and nonlinear massive and high dimensional problems.

[1]V.N.Vapnik.The nature of statistical learning theory.New York:Springer Verlag,1995.

[2]C.J.C.Burges.A tutorial on support vector machines for pattern recognition.Data Mining and Knowledge Discovery, 1998,2(2):121–167.

[3]G.Fung,O.L.Mangasarian.Data selection for support vector machine classiers.Proc.of the Sixth ACM SIGKDD International Conference on Knowledge Discovery and Data,2000: 64–70.

[4]A.Christmann,R.Hable.Consistency of support vector machines using additive kernels for additive models.Computational Statistics and Data Analysis,2012,56(4):854–873.

[5]L.Yao,X.J.Zhang,D.H.Li,et al.An interior point method for 1/2-SVM and application to feature selection in classication.Journal of Applied Mathematics,2014,2014:1–16.

[6]N.Cristianini,J.S.Taylor.An introduction to support vector machines and other kernel-based learning methods.Cambridge:Cambridge University Press,2000.

[7]Y.B.Yuan.Forecasting the movement direction of exchange rate with polynomial smooth support vector machine.Mathematical and Computer Modelling,2013,57(3–4):932–944.

[8]J.Zheng,B.L.Lu.A support vector machine classier with automatic condence and its application to gender classication.Neurocomputing,2011,74(11):1926–1935.

[9]J.Y.Zhu,B.Ren,H.X.Zhang,et al.Timeseries prediction via new support vector machines.Proc.of the International Conference on Machine Learning and Cybernetics,2002:364–366.

[10]X.F.Yuan,Y.N.Wang.Parameter selection of support vector machine for function approximation based on chaos optimization.Journal of Systems Engineering and Electronics,2008, 19(1):191–197.

[11]T.Joachims.Text categorization withsupport vector machines: learning with many relevant features.Proc.of the 10th European Conference on Machine Learning,1998:137–142.

[12]L.M.R.Baccarini,V.V.R.Silva,B.R.D.Menezes.SVM practical industrial application for mechanical faults diagnostic.Expert Systems with Applications,2011,38(6):6980–6984.

[13]A.Christmann,R.Hable.Consistency of support vector machines using additive kernels for additive models.Computational Statistics and Data Analysis,2012,56(4):854–873.

[14]G.Wei,X.D.Yu,X.W.Long.Novel approach for identifying Z-axis drift of RLG based on GA-SVR model.Journal of Systems Engineering and Electronics,2014,25(1):115–121. [15]Y.J.Lee,O.L.Mangarasian.SSVM:a smooth support vector machine for classication.Computational Optimization and Applications,2001,20(1):5–22.

[16]Y.B.Yuan,J.Yan,C.Xu.Polynomial smooth support vector machine.Chinese Journal of Computers,2005,28(1):9–17. (in Chinese)

[17]Y.B.Yuan,T.Z.Huang.A polynomial smooth support vector machine for classication.Lecture Note on Artifcial Intelligence,2005,3584:157–164.

[18]Y.B.Yuan,W.Fan,D.Pu.Splinefunction smoothsupport vector machine for classication.Journal of Industrial and Management Optimization,2007,3(3):529–542.

[19]Q.Wu,W.Q.Wang.Piecewise-smooth support vector machine for classication.Mathematical Problems in Engineering,2013,2013:1–7.

[20]D.P.Bertsekas.Nonlinear programming.Belmont:Athena Scientic,1999.

[21]C.Xu,J.Zhang.A survey of quasi-Newton equations and nuasi-Newton methods for optimization.Annals of Operations Research,2001,103(1–4):213–234.

[22]J.E.Dennis,R.B.Schnabel.Numerical methods for unconstrained optimization and nonlinear equations.Englewood Cliffs:Prentice-Hall,1983.

[23]D.R.Musicant.NDC:normally distributed clustered datasets. http://www.cs.wisc.edu/～musicant/data/ndc,1998.

[24]T.K.Ho, E.M.Kleinberg.Checkerboard dataset. http://www.cs.wisc.edu/～musicant/data/ndc/,1996.

Biographies

Qing Wu was born in 1975.She received her M.S. and Ph.D.degrees in applied mathematics from Xidian University in 2005 and 2009.Now she is an associate professor at the School of Automation, Xi’an University of Posts and Telecommunications. Her research interests include pattern recognition, machine learning and data mining.

E-mail:xiyouwuq@126.com

Leyou Zhang was born in 1977.He received his Ph.D.degree in applied mathematics from Xidian University in 2009.Now he is an associate professor at the School of Mathematics and Statistics in Xidian University.His research interests include data mining and information security.

E-mail:lyzhang77@qq.com

Wan Wang was born in 1989.She received her B.S.degree in mathematics and applied mathematics from Weinan Normal University in 2012.Now, she is a master candidate in Xi’an University of Posts and Telecommunications.Her research interests include machine learning and optimization theory and computation.

E-mail:wcf2ww@163.com

10.1109/JSEE.2015.00069

Manuscript received May 29,2014.

*Corresponding author.

This work was supported by the National Natural Science Foundation of China(61100165;61100231;51205309;61472307),the Natural Science Foundation of Shaanxi Province(2012JQ8044;2014JM8313; 2010JQ8004),the Foundation of Education Department of Shaanxi Province(2013JK1096),and the New Star Team of Xi’an University of Posts and Telecommunications.