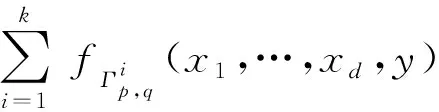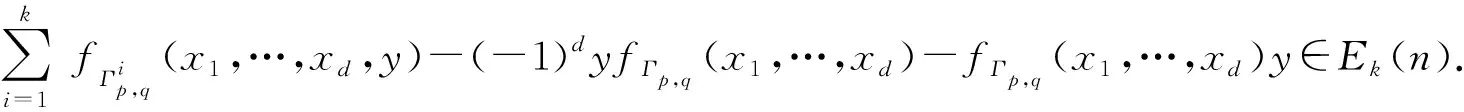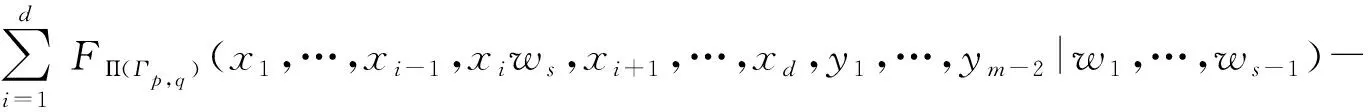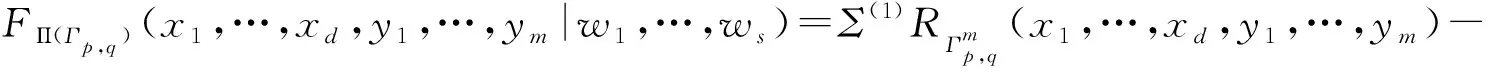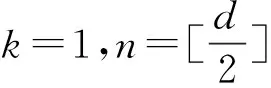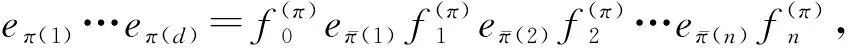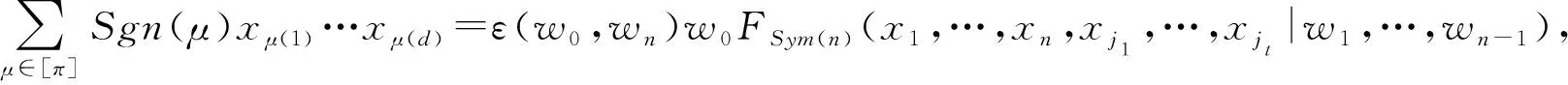矩陣環(huán)的歐拉恒等式與標(biāo)準(zhǔn)多項(xiàng)式恒等式

馮怡君,曹明,魏亞萍,游松發(fā)

(湖北大學(xué)數(shù)學(xué)與計(jì)算機(jī)科學(xué)學(xué)院,湖北 武漢 430062)

0 引言

令Γ是有多重邊的有限有向連通圖,其頂點(diǎn)集V(Γ)={1,…,k},邊集E(Γ)={e1,…,ed},σ,τ是E(Γ)到V(Γ)的映射,并定義σ(es)=i,τ(es)=j,即i,j分別是es的起點(diǎn)和終點(diǎn),es是從頂點(diǎn)i到頂點(diǎn)j的有向邊.對i∈V(Γ),令φ+(i)=|{es|σ(es)=i}|,φ-(i)=|{es|τ(es)=i}|,且γ(i)=max{φ+(i),φ-(i)}.若π∈Sym(d)(作用在{1,…,d})上的對稱群),且τ(eπ(i))=σ(eπ(i+1))(?i=1,…,d-1),則稱eπ(1)eπ(2)…eπ(d)是Γ的一條歐拉路,具有歐拉路的有向連通圖稱為歐拉圖.眾所周知,連通圖Γp,q有從p到q的歐拉路,當(dāng)且僅當(dāng)下列兩個(gè)條件之一成立:

a)p=q時(shí),φ+(i)=φ-(i)(?i=1,…,k);

b)p≠q時(shí),φ+(p)=φ-(p)+1,φ-(q)=φ(q)+1,且φ+(i)=φ-(i)(?i∈{1,…,k}(〗p,q}).

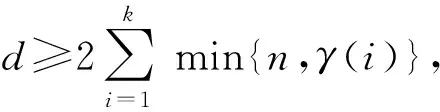
推論0.1[1]令Γp,q是歐拉圖,且|V(Γp,q)|=k,|E(Γ)|=d,若d≥2kn,則fΓp,q(x1,…,xd)=0是Mn(F)的恒等式.

若令Gk(n)={Γp,q|Γp,q是歐拉圖,且|V(Γ)|=k,|E(Γ)|≥2nk}是滿足推論1.2的歐拉圖類,由推論0.1知,?Γp,q∈Gk(n),fΓp,q=0是Mn(C)的恒等式,記Ek(n)=〈fΓp,q|Γp,q∈Gk(n)〉是由fΓp,q生成的多項(xiàng)式集,顯然Ek(n)中元都是Mn(C)的恒等式,且Ek(n)是C〈X〉=C〈x1,x2,…〉的一個(gè)T-理想,其中C〈X〉=C〈x1,x2,…〉是X上的自由結(jié)合代數(shù).

1 主要結(jié)果

定理1.1若Γp,q∈Gk(n),則FΠ(Γp,q)(x1,…,xd,y1,…,ym|w1,…,ws)∈Ek(n).

定理1.1的證明對二元正整數(shù)對(m,s)用歸納法(運(yùn)用文獻(xiàn)[2]中所用歸納法的類型).其中(m,s)的歸納順序規(guī)定為:(m1,s1)<(m2,s2)?m1

情形1若?wi,使Length(wi)≥3,不失一般性,令ws=wym-2ym-1ym,由于FΠ(Γp,q)(x1,…,xd,y1,…,ym|w1,…,ws)=FΠ(Γp,q)(x1,…,xd,y1,…,ym-3,ym-2ym-1ym|w1,…,ws-1,wym-2ym-1ym),又(m-2,s)<(m,s),由歸納假設(shè)有FΠ(Γp,q)(x1,…,xd,y1,…,ym|w1,…,ws)∈Ek(n).

情形2若?wi,使Length(wi)=2,不失一般性,令ws=ym-1ym,我們有

由歸納假設(shè)可知,右邊3個(gè)和項(xiàng)均是Ek(n)中元,即FΠ(Γp,q)(x1,…,xd,y1,…,ym|w1,…,ws)∈Ek(n).

(1)

1)τ(el)=i時(shí),xl是X={x1,…,xd}中先于yρ(t)的最后一個(gè)變元,

2)i=ρ時(shí),X={x1,…,xd}中沒有先于yρ(t)的變元.

式中Σ(1)跑遍m=m1+…+mk的所有k個(gè)非負(fù)整數(shù)分解;Σ(2)跑遍Y的單項(xiàng)的所有非空字的劃分,其中?i∈{1,…,r}使Length(wi)≥2;Σ(3)跑遍所有的字u,v及{yi1,…,yit}的單項(xiàng)的劃分,其中yi1,…,yit不在u,v中出現(xiàn),uv≠1且uv關(guān)于yj(j=1,…,m)的次數(shù)為1或0,ε(u,v)=±1是根據(jù)uFΠ(Γp,q)(x1,…,xd,yi1,…,yit|w1,…,wr)v中單項(xiàng)關(guān)于x1,…,xd,y1,…,ym的置換的奇偶性而確定的符號.

推論1.1若Γp,q∈Gk(n),則FΠ(Γp,q)=0是Mn(C)的恒等式.

推論1.3的證明直接由推論1.1和1.2可以獲證.

定理1.2令Γp,q是歐拉圖,若?t,u∈V(Γ)(t,u可相同),使從t到u的邊至少有n條,則fΓp,q(X)∈〈Sn(X)〉,其中Sn(X)是n次標(biāo)準(zhǔn)多項(xiàng)式,〈Sn(X)〉是由Sn(X)生成的T-理想.

均是Γp,q的歐拉路

1)w0(π)=w0(μ)且wn(π)=wn(μ),

2)?v∈Sym(n-1),使wi(μ)=wv(i)(π)(i=1,…,n-1),

由定理1.2立即有

推論1.4若歐拉圖Γp,q有2n-重邊,則fΓp,q是Mn(C)的恒等式,且fΓp,q∈〈S2n(X)〉.

這一結(jié)論顯示,歐拉恒等式生成的T-理想,均可由標(biāo)準(zhǔn)多項(xiàng)式生成.

[1] Szigeti J, Tuza Z S, Revesz G. Eulerian polynomial identities on matrix rings[J]. J Algebra,1993,161:90-101.

[2] Chang Q. Some consequences of the standard polynomial[J]. Proc Amer Math Soc,1988,104:707-710.

[3] Giambruno G, Sehgal S K. On a polynomial identity forn×nmatrices[J]. J Algebra,1989,126:451-453.

[4] Domokos M. Eulerian polynomial identities and algebras satisfying a standard identity[J]. J Algebra,1994,169:913-928.

[5] Rowen L H. Polynomial identities in ring theory[M]. New York: Academic Press,1980.

[6] You Songfa, Zheng Yumei, Hu Donggang. Eulerian graph and polynomial identites on matrix rings[J]. Advance in Math,2003,32:425-428.