Dynamics and Predictive Control of Gas Phase Propylene Polymerization in Fluidized Bed Reactors*

Ahmad Shamiri**, Mohamed azlan Hussain, Farouq sabri Mjalli, Navid Mostoufiand Seyedahmad Hajimolana

1Department of Chemical Engineering, University of Malaya, Kuala Lumpur 50603, Malaysia

2Training Center, Razi Petrochemical Company, Bandar Imam 161, Iran

3UM Power Energy Dedicated Advanced Centre (UMPEDAC), University of Malaya, Kuala Lumpur 50603, Malaysia

4Petroleum and Chemical Engineering Department, Sultan Qaboos University, Muscat 123, Oman

5Process Design and Simulation Research Center, School of Chemical Engineering, College of Engineering, University of Tehran, Tehran 11155/4563, Iran

Dynamics and Predictive Control of Gas Phase Propylene Polymerization in Fluidized Bed Reactors*

Ahmad Shamiri1,2,**, Mohamed azlan Hussain1,3, Farouq sabri Mjalli4, Navid Mostoufi5and Seyedahmad Hajimolana1

1Department of Chemical Engineering, University of Malaya, Kuala Lumpur 50603, Malaysia

2Training Center, Razi Petrochemical Company, Bandar Imam 161, Iran

3UM Power Energy Dedicated Advanced Centre (UMPEDAC), University of Malaya, Kuala Lumpur 50603, Malaysia

4Petroleum and Chemical Engineering Department, Sultan Qaboos University, Muscat 123, Oman

5Process Design and Simulation Research Center, School of Chemical Engineering, College of Engineering, University of Tehran, Tehran 11155/4563, Iran

A two-phase dynamic model, describing gas phase propylene polymerization in a fluidized bed reactor, was used to explore the dynamic behavior and process control of the polypropylene production rate and reactor temperature. The open loop analysis revealed the nonlinear behavior of the polypropylene fluidized bed reactor, justifying the use of an advanced control algorithm for efficient control of the process variables. In this case, a centralized model predictive control (MPC) technique was implemented to control the polypropylene production rate and reactor temperature by manipulating the catalyst feed rate and cooling water flow rate respectively. The corresponding MPC controller was able to track changes in the setpoint smoothly for the reactor temperature and production rate while the setpoint tracking of the conventional proportional-integral (PI) controller was oscillatory with overshoots and obvious interaction between the reactor temperature and production rate loops. The MPC was able to produce controller moves which not only were well within the specified input constraints for both control variables, but also non-aggressive and sufficiently smooth for practical implementations. Furthermore, the closed loop dynamic simulations indicated that the speed of rejecting the process disturbances for the MPC controller were also acceptable for both controlled variables.

model predictive control, fluidized bed reactor, propylene polymerization, Ziegler-Natta catalyst

1INTRODUCTION

Modeling and control of polymerization process in fluidized bed reactors such as polypropylene production are challenging issues in process control engineering. This is due to many factors such as the high non-linearity of the process dynamics involving complicated reaction mechanisms, complex flow characteristics of gas and solids, various heat and mass transfer mechanisms and the interaction between the process control loops. Many studies were reported on the modeling and control of ethylene polymerization processes using various types of algorithms [1-6]. However, there is little work on the modeling and control of gas phase propylene polymerization in fluidized bed reactors.

The schematic of an industrial gas-phase fluidized bed polypropylene reactor with control design is shown in Fig. 1. The feed gas stream provides monomer, hydrogen and nitrogen, and at the same time agitates and fluidizes the bed through the distributor and also removes the heat of polymerization reaction. Polymerization occurs in the fluidized bed in the presence of Ziegler-Natta catalyst and triethyl aluminum co-catalyst. The unreacted gas exits the top of the reactor and is then compressed and cooled before being fed back into the bottom of the fluidized bed. The polymer production rate in this system is limited by heat removal from the circulating gas since the polymerization reaction is highly exothermic. To maintain acceptable polymer production rate, which is an important goal for industry, it is necessary to keep the bed temperature above the dew point of the reactants to avoid gas condensation and below the melting point of the polymer to prevent particle melting, agglomeration and consequent reactor shut down. For these reasons, process stabilization for propylene polymerization in a fluidized bed reactor is a challenging problem to be addressed through an efficient control system design.

Most of the reactor design and control problems are associated with achieving adequate production rate and heat removal from the reactor. The steady-state and dynamic behavior of the reactor is influenced by many process variables such as the superficial gas velocity, feed gas temperature, monomer concentration, catalyst activity and catalyst feed rate. Choi and Ray [1] used a dynamic model considering bubble and emulsion phases in the bed in the first attempt to describe the dynamics of polypropylene production. They showed that a PI feedback control scheme can be used to control the process transients, but it was limited by the recycle gas cooling capacity. Dadebo et al. [2] showed that for the temperature control of industrial gas phase polyethylene reactors, the nonlinear error trajectory controller (ETC) exhibited significantly superior responses in terms of speed, damping and robustness compared with an optimally-tuned proportionalintegral derivative (PID) controller over a wide range of operating conditions. Ali et al. [3] proposed a non-linear process model based control (modified generic model control) for the control of liquid propylene polymerization. The controller manipulated the hydrogen flow rate and cooling water flow to follow the setpoints for cumulative melt index and reaction conversion. They showed that the proposed controller has good setpoint tracking and disturbance rejection properties and it was superior to the conventional generic model control and proportional-integral (PI) control algorithms. Ibrehem et al. [4] modeled the process in four phases namely: bubble, cloud, emulsion and solid phases with polymerization reactions occurring in the emulsion and solid phases to describe the olefin polymerization in fluidized bed reactor. They implemented neural-networks based predictive controller (NNMPC) to control the system and showed that the performance of the NNMPC was superior to the PID controller in terms of the setpoint tracking. Summary of relevant studies in olefin polymerization and its control are listed in Table 1. The summary shows that most of the control studies are related to polyethylene and only three of them are related to polypropylene.

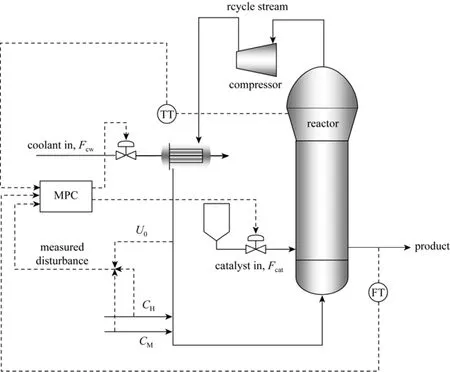
Figure 1Simplified schematic of an industrial gas-phase fluidized bed polypropylene reactor with a model predictive control (MPC) designTI—temperature transmitter; FT—mass flow transmitter

Due to nonlinearities in the process dynamics and difficulties involved in the control of the gas phase propylene polymerization fluidized bed reactor, an efficient process control scheme is vital for stable and efficient operation of the process. The most commonly used controllers in industrial applications are proportional-integral (PI) controllers [23]. A more intelligent and efficient process control scheme, model predictive control (MPC) algorithm, is gradually becoming popular in the process industries due to their ability to handle process interactions, constraints on manipulated and output variables and time delays as well as their ability to control nonlinear processes [25]. The unified framework of MPC and its capacity to incorporate various practical control objectives and requirements have found extensive acceptance in the chemical process industries. However, linear model predictive control (LMPC) algorithms are incapable to handle the complexities encountered in nonlinear processes. Nonlinear model predictive control (NMPC) has good capability in improving control and operation of nonlinear processes such as these polymerization processes. The basic principle of NMPC is the same as LMPC with the exception that the model describing the process dynamics is nonlinear [12, 14]. Successful applications of NMPC on polymerization reactors have been reported, which is also capable of dealing with unanticipated changes in the process dynamics through the state estimator. Summary of relevant studies in olefin polymerization and its control are listed in Table 1.

Based on our knowledge it is the first time that a multiple-input, multiple output (MIMO) model predictive control (MPC) strategy as a centralized MPC technique is used to control the polypropylene production rate and reactor temperature for setpoint tracking and disturbance rejection. Furthermore, a two-phase model with comprehensive kinetics for propylenehomo-polymerization in a fluidized bed reactor that considers the presence of particles in the bubbles and excess gas in the emulsion phase with polymerization reaction in both phases is also considered [26-29].

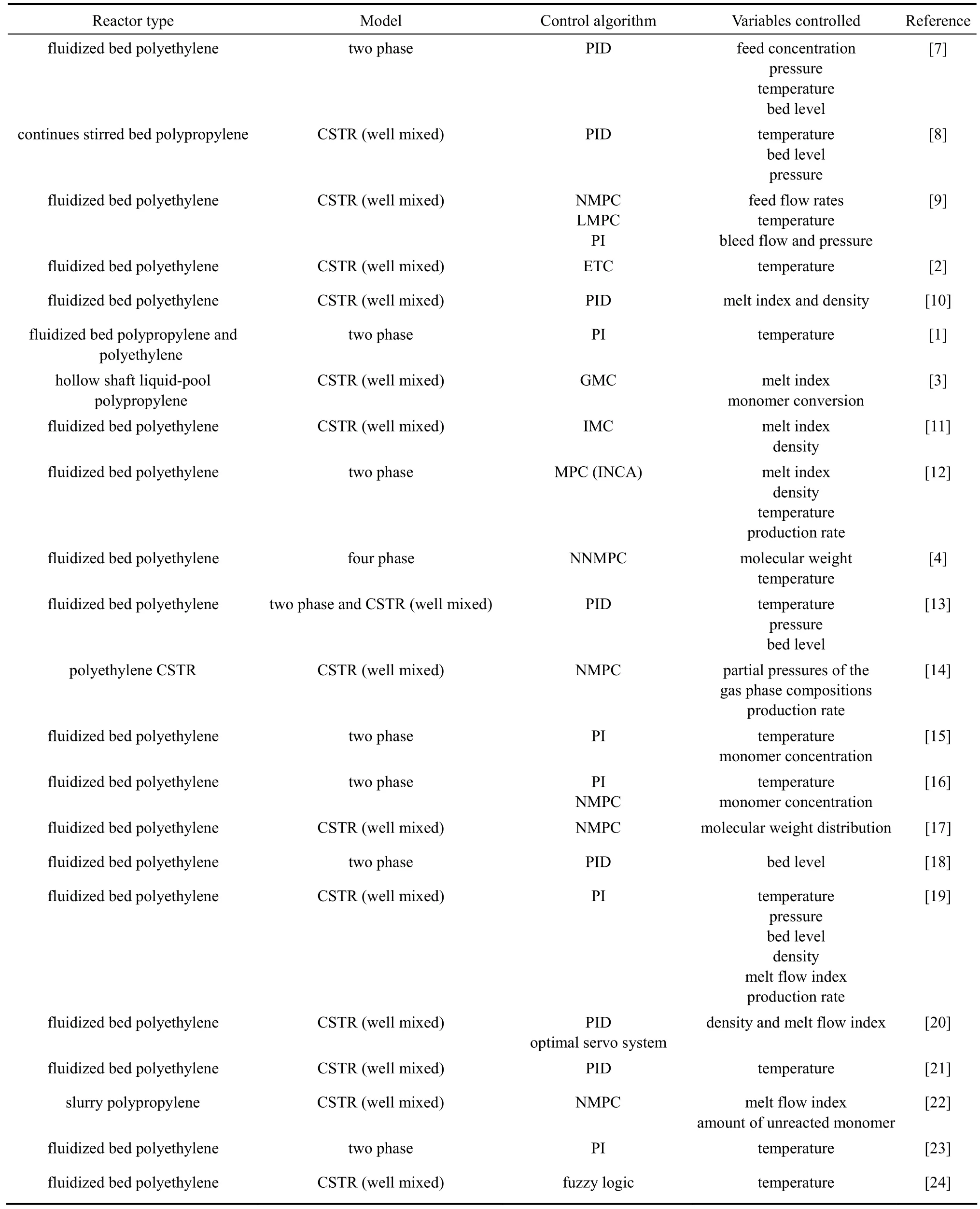
Table 1Summary of control studies in olefin polymerization

2MATHEMATICAL MODEL OF PROPYLENE POLYMERIZATION

2.1Reactor model

In the present study, the kinetic model of propylene homo-polymerization over a Ziegler-Natta catalyst (based on the kinetic model developed by Shamiri et al. [30]) and the dynamic two-phase flow structure proposed by Cui et al. [27, 28] were combined and implemented to provide a more realistic understanding of the phenomena encountered in the reactor hydrodynamics.

The two-phase model presented in this work assumes that all particles have the same mean diameter of 500×10?6m [1, 2, 4, 13, 26]. Polypropylene particles of such size are Geldart B, thus, the constants of this type of particles were chosen and shown in Table 2. It is worth noting that the same approach was adopted in similar modeling attempts [13, 31] and provided good prediction of the reactor performance.

The correlations required for estimating bubble volume fraction in the bed, voidage of emulsion and bubble phases, gas velocities in emulsion and bubble phases and mass and heat transfer coefficients for the improved two-phase model are summarized in Table 2. Fluidized bed reactors are able to produce a broad range of polypropylene.

Table 2Correlations and equations used in the two-phase model

The UNIPOL Polypropylene Technology is a simple and delicate processing system, comprising of either one or two gas-phase fluidized-bed reactors. To produce homopolymers and random copolymers, a single reactor is used [36]. In this work a single reactor is used to produce propylene homopolymers. Characterization of polymer properties was modeled using the population balance and the method of moments [30, 37].

Assuming that the only significant consumption of monomer is by the propagation reaction and hydrogen by transfer to hydrogen, the following expressions for the consumption rate of component (monomer and hydrogen) can be obtained:

For monomer:

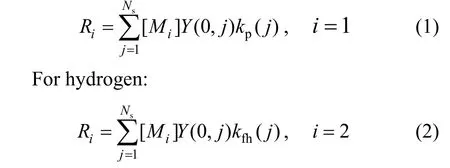
The total polymer production rate for each phase can be then calculated from

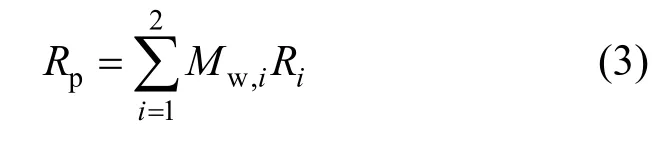
in which Riis the instantaneous rate of reaction for monomer and hydrogen. The reaction rate constants were taken from literature and are listed in Table 3.

The assumptions made in developing the equations of the improved two phase model are summarized below:

(1)The polymerization reactions occur in both bubble and emulsion phases.

(2) The emulsion phase is considered to be perfectly mixed, and it may contain more gas at higher gas velocities than at the minimum fluidization condition. A better mixing between two phases occurs when the superficial gas velocity increases in a fluidized bed due to more solid particles entering bubbles and more gas entering the emulsion phase [13, 18, 27, 28, 31].

(3) The bubbles are assumed to be spherical with uniform size and rise up through the bed in plug flow at constant velocity.

(4) Mass and heat transfer resistances between gas and solids in the emulsion and bubble phases are negligible (i.e., low to moderate catalyst activity) [40].

(5) Radial concentration and temperature gradients in the reactor are negligible due to the agitation produced by the up-flowing gas.

(6) Elutriation of solids at the top of the bed is negligible.

(7) Constant particle size exists throughout the bed [1, 2, 4, 13, 26].

(8) The direction of mass transfer was assumed to be from bubble to emulsion phase.

Based on these assumptions, the following dynamic material balances were derived for all the components in the bed.

For bubbles:

The energy balances can be expressed as

For bubbles:

Table 3Reactions rate constants

For emulsion:

The initial conditions for solution of the model equations are as follows:

2.2Heat exchanger model

As shown in Fig. 1, the external gas cooler is a countercurrent single-pass shell and tube heat exchanger with the recycle gas on the tube side and cooling water on the shell side. A linear first-order dynamic model obtained by imposing first order dynamics on the heat removal rate with a corresponding time constant, τ, to yield a linear dynamic model was considered for simulation of the heat removal system [2] given as

where q is the dynamic heat removal rate, and qssis the steady state heat removal rate given as

where Fgis the gas flow rate, Cpgis the gas heat capacity and Teis the temperature of the gas entering the heat exchanger, which is also the reactor temperature. Tinis the outlet temperature of the gas from heat exchanger, which is also the temperature of the gas entering the reactor, given as

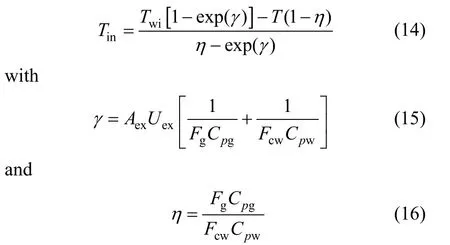
Twiis the temperature of cooling water entering the heat exchanger, Aexis the contact area and Uexis a heat transfer coefficient. Fcwand Cpware the flow rate and heat capacity of the cooling water, respectively.

3MULTIPLE-INPUT, MULTIPLE OUTPUT (MIMO) MODEL PREDICTIVE CONTROL STRATEGY

MPC is an optimization-based control strategy which is well suited for constrained, multivariable processes. The model predictive controller predicts the future behavior of the actual system over a time interval defined by the prediction horizon. The simplified diagram of the MPC algorithm shown in Fig. 2 indicates that a process model is used in MPC in order to predict the controlled variable and in this system the process model is used in parallel to the plant. The predicted controlled variable is fed back to the controller where it is used in an on-line optimization procedure, which minimizes an appropriate cost function to determine the optimal input to the plant acting as the manipulated variable. The optimization problem is solved subject to constraints on input and output variables and also constraints imposed by the nonlinear model equations. The controller output is implemented in real time and then at the next sampling time. The difference between the plant measurement ypand the process model output ymis also fed to the controller to eliminate steady state offset and compensate modeling uncertainties. The cost function usually is specified as a sum of quadratic future errors between the reference trajectory and predicted plant output, and the predictedcontrol effort along the prediction horizon.

Figure 2Model predictive control system

Table 4Operating conditions and physical parameters considered in this work for modeling fluidized bed polypropylene reactors

Due to its ability and simplicity the Model Predictive Control (MPC) algorithm is implemented to control the gas phase propylene polymerization process in this fluidized bed reactor. The MIMO based MPC controller used in this work takes into account both the output and manipulated variables and minimizes the following cost functions V(k) as given by [41, 42]

where k is the current sampling interval, k+i is a future sampling interval (within the prediction horizon), P is the prediction horizon, nyis the number of plant outputs,is the weight for output j, [yj(k+i)?rj(k+i)] is the predicted deviation at future instant k+i, M is the control horizon, nmvis the number of manipulated variables (inputs), Δuj(k+ i ?1) is the predicted adjustment (i.e., move) in manipulated variable j at future (or current) sampling interval (k+i?1), andis the weight for input j.

The cost function is also subjected to inequality constraints of the manipulated and output variables given below:

Manipulated variable constraint is given as:

Manipulated variable rate constraint is given as

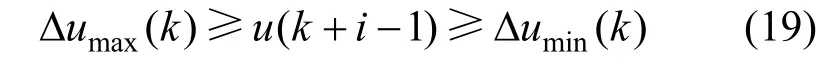
Output variable constraint is given as:

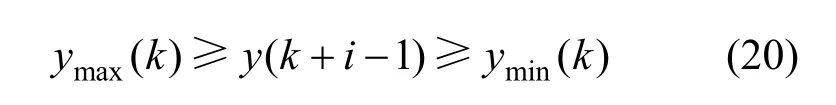
Depending on the problem formulation, parameters such as the control horizon, prediction horizon and weighting matrices in the optimization formulation has to be finalized to obtain the best performance for the predicted output.

In this study, a MIMO system is controlled by the centralized MPC techniques. This system takes the reactor temperature (Te) and production rate (Rp) as controlled variables, with the catalyst feed rate (Fcat) and cooling water flow rate (Fcw) as manipulated variables , and the hydrogen concentration (CH) , propylene concentration (CM) and superficial gas velocity (U0) as measured disturbances. The improved two phase model is written in MATLAB and implemented in S-functions in order to be accessed by Simulink.

4RESULTS AND DISCUSSION

4.1Open loop analysis of the propylene polymerization fluidized bed reactor

To demonstrate the non-linearity of the reactor, the process was simulated at the operating conditions given in Table 4 to explore the effect of step change in the superficial gas velocity, catalyst feed rate, cooling water flow rate and hydrogen and propylene concentrations on the emulsion phase temperature and polypropylene production rate. The results of the open-loop simulations are shown in Figs. 3 to 7.

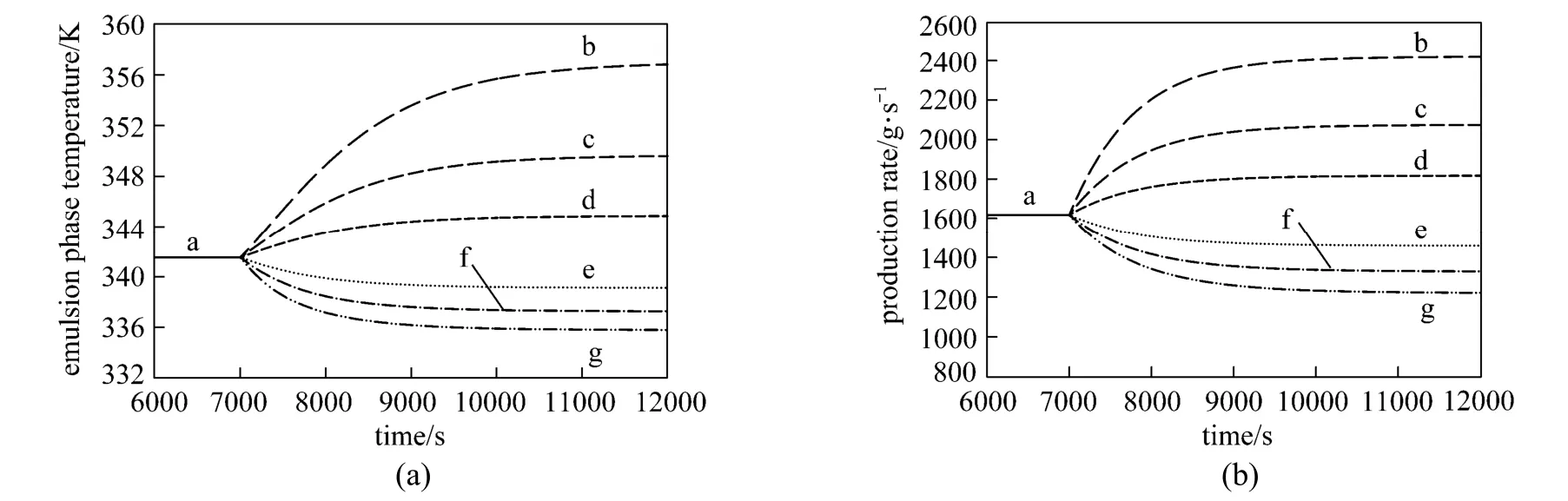
Figure 3Effect of step change in U0on (a) the emulsion phase temperature and (b) production rate (Fcat=0. 3 g·s?1, CM= 0.9 mol·L?1and CH=0.015 mol·L?1)U0/m·s?1: a—0.4; b—0.25; c—0.3; d—0.35; e—0.45; f—0.5; g—0.55

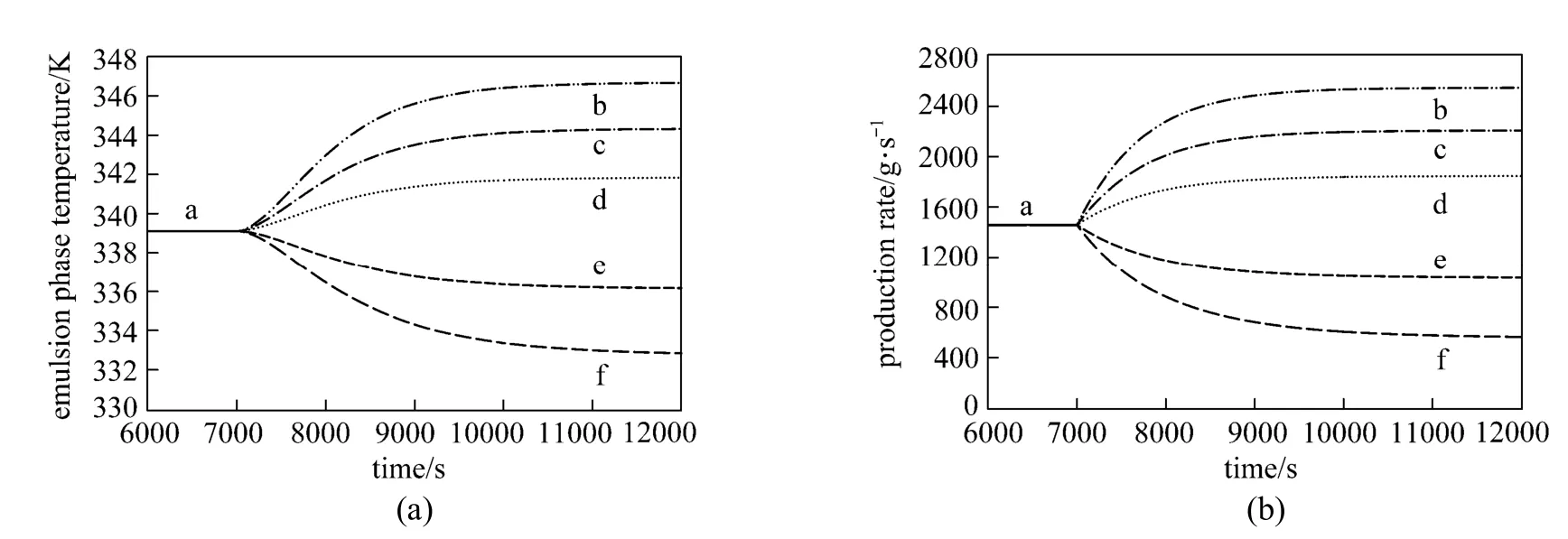
Figure 4Effect of step change in the catalyst feed rate on (a) the emulsion phase temperature and (b) production rate (U0=0.45 m·s?1, CM=0.9 mol·L?1and CH=0.015 mol·L?1)Fcat/g·s?1: a—0.3; b—0.6; c—0.5; d—0.4; e—0.2; f—0.1

As shown in Fig. 3 (a) and 3 (b), the superficial gas velocity was changed from the nominal value (0.4 m·s?1) using increments of 0.05 m·s?1in both positive and negative directions. The superficial gas velocity has a significant effect on the emulsion phase temperature and production rate even for small changes in the superficial gas velocity which indicates that it is an important parameter for the heat removal and consequently the control of reactor temperature and production rate. Although one can manipulate the fluidizing gas velocity to control the reactor temperature and production rate but changes in fluidization characteristics (e.g. solids entrainment) may occur when the gas velocity is varied [1] which is also difficult to control in practice and thus the fluidizing gas velocity is not used as the manipulated variable.

This test clearly shows that the negative steps in superficial gas velocity have more significant effect than the corresponding positive steps for both output variables (emulsion phase temperature and production rate) and produce non-symmetrical responses. The variation of the emulsion phase temperature and polypropylene production rate as the superficial gas velocity change deviates from the linear behavior. For such nonlinear relationships, the use of conventional controllers tends to produce poor control of the process variables, thus justifying the use of a more efficient control scheme to properly regulate the effect of superficial gas velocity on the process variables.

The effect of step changes in the catalyst feed rate on the emulsion phase temperature and production rate is depicted in Fig. 4 (a) and 4 (b). Once the emulsion phase temperature and polypropylene production rate reached steady state conditions at catalyst feed rate of 0.3 g·s?1, the catalyst feed rate was changed to show the effect of manipulating this variable on the process dynamics. Small step changes in the catalyst feed rate result in significant changes in the reactor temperature and polymer production rates. The slightly symmetrical nature of these profiles due to the systematic positive and negative variations in the catalyst flow rate indicates the slightly nonlinear relationships. In this case, using a conventional controller can be acceptable provided that the effect of disturbances, measurement noise, modeling uncertainty and process interaction are not pronounced.

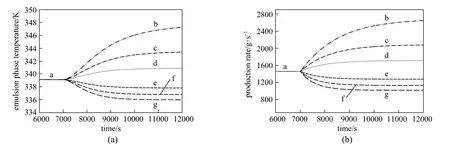
Figure 5Effect of step change in the hydrogen feed concentration on (a) emulsion phase temperature and (b) production rate (U0=0.45 m·s?1, Fcat=0. 3g·s?1and CM=0.9 mol·L?1)CH/mol·L?1: a—0.015; b—0; c—0.005; d—0.01; e—0.02; f—0.025; g—0.3

Figure 6Effect of step change in the propylene feed concentration on (a) the emulsion phase temperature and (b) production rate (Fcat=0. 3 g·s?1, U0=0.45 m·s?1and CH=0.015 mol·L?1)CM/mol·L?1: a—0.7; b—1; c—0.9; d—0.8; e—0.6; f—0.5; g—0.4

In the industry, the properties of polypropylene are controlled by varying the monomer and hydrogen feed rates. Increasing the hydrogen to propylene ratio in the reactor leads to increased chain transfer and to lower molecular weight. Changes in monomer and hydrogen feed rates also act as disturbances to the reactor temperature and polymer production rate. To explore these effects, positive and negative steps were introduced in the hydrogen and propylene feed concentrations by 0.005 mol·L?1and 0.1 mol·L?1respectively. The effect of a step change in the hydrogen concentration in the feed on the emulsion phase temperature and production rate predicted by the model is shown in Fig. 5 (a) and 5 (b). The initial hydrogen feed concentration was set at 0.015 mol·L?1and step changes was introduced from the steady state conditions. As can be seen, hydrogen concentration has highly nonlinear relationship with the reactor temperature and polymer production rate. Increasing the hydrogen concentration leads to enhancing the chain transfer reaction rate and consequently lowers the degree of polymerization due to the shorter polymer chain length.

The effect of varying the feed propylene concentration on the emulsion phase temperature and production rate is shown in Fig. 6 (a) and 6 (b). The propylene concentration was changed from the nominal value of 0.7 mol·L?1. By increasing the feed propylene concentration, the emulsion phase temperature and production rate increases. Increasing the propylene concentration leads to enhancing the reaction rate and consequently the degree of polymerization. This observation, in addition to the ones discussed previously, show nonlinear behavior as inferred from the produced dynamic profiles. Such observations indicate that the process model under investigation needs special attention in terms of the control algorithm used.

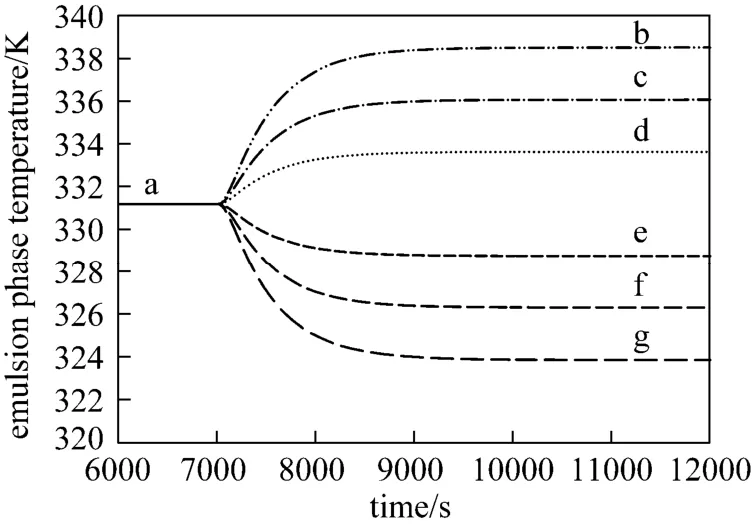
Figure 7Effect of step change in the cooling water flow rate on the emulsion phase temperature (Fcat=0. 3 g·s?1, U0=0.45 m·s?1, CM=0.9 mol·L?1and CH=0.015 mol·L?1)Fcw/g·s?1: a—3×105; b—1.5×105; c—2×105; d—2.5×105; e—3.5×105; f—4×105; g—4.5×105

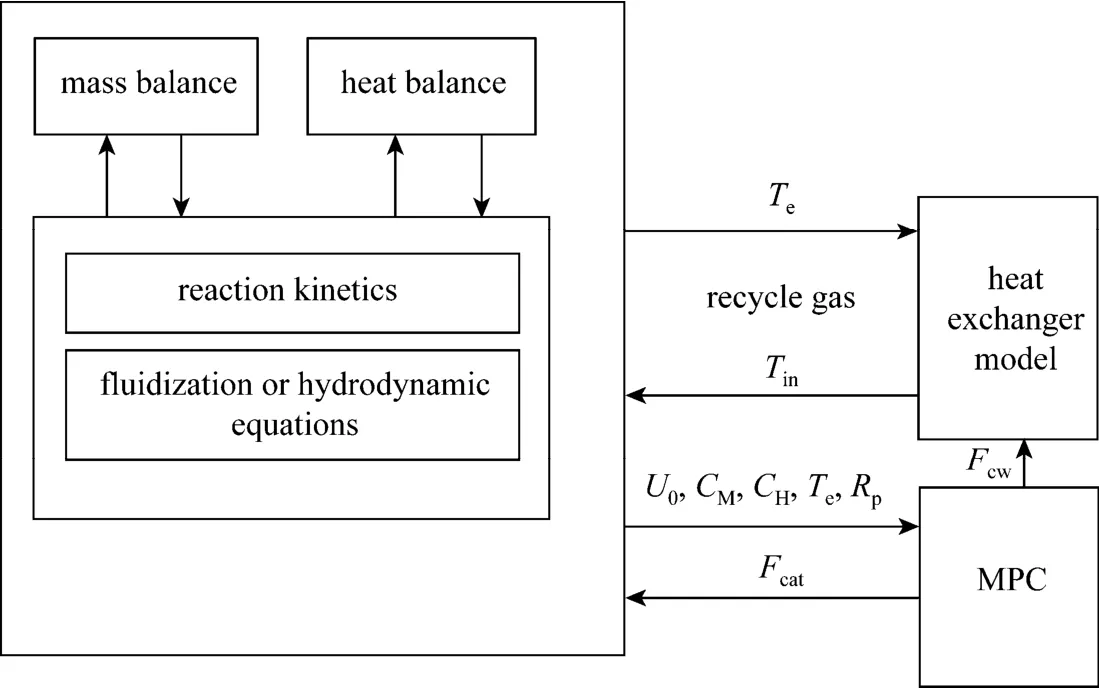
Figure 8A simplified schematic of the process sub-models and control system of the gas phase propylene polymerization fluidized bed reactor

Figure 7 illustrates the effect of step changes in the cooling water flow rate on the emulsion phase temperature. By changing the cooling water flow rate from an initial value of 3×105g·s?1, the emulsion phase temperature changes significantly and shows strong dependency. This indicates that it has an important role on the heat removal and on the control of the fluidized bed polymerization rector temperature.

4.2Closed loop performance of the model predictive controller scheme

A simplified schematic of the process sub-models and control system of the gas phase propylene polymerization fluidized bed reactor is shown in Fig. 8.

4.2.1MPC controller design

The results presented in the previous section show the nonlinear behavior of the system as inferred from the produced dynamic profiles. Such observations imply that the process model under investigation needs special attention in terms of the control algorithm to be used for this process. Despite the fact that the superficial gas velocity, catalyst feed rate and hydrogen and propylene concentrations have significant effect on the output variables, based on actual process experience, not all of them are suitable to be selected as manipulated variables. In the industrial fluidized-bed olefin polymerization reactor, the temperature is usually controlled by manipulating the cooling water flow rate of an upstream heat exchanger which is used to remove the heat of the exothermic polymerization reaction from the recycle gas stream [2], and changes to the catalyst feed rate can be used to control the polymer production rate [11]. Based on this approach, Fcatand Fcwwere selected as manipulated variables and Rpand Tewere used as control variables to design the centralized MPC in this work (see Fig. 1). In this case, superficial gas velocity (U0), propylene concentration (CM), and hydrogen concentration (CH) were classified as the disturbance variables.

To ensure good performance of the MPC controller, the tuning parameters must be appropriately tuned. The tuned parameters suggested by Shridhar and Cooper [43] were used as the starting values but the exact values used in this work were the result of further fine tuning based on actual control performance. In addition to the selection of controller tuning parameters, appropriate values were chosen for the input/output variables constraints and imposed on the system based on practical experience. The values of the upper and lower limits of the constraints for the Fcat?Rpprofile are: 0≤Fcat≤100%, ?20%≤ΔFcat≤20% and for the Fcw?Teprofile are: 0≤Fcw≤100%,?20%≤ΔFcw≤20%. The control system has a sampling time of 15 s, a prediction horizon of 20, a control horizon of 2, an output variables weight of 0.005 for Rpand 0.0005 for Te. The manipulated variables weights selected were 0.1 for Fcatand 0.1 for Fcw.

4.2.2Setpoint tracking

It is interesting to see how the nonlinear polypropylene fluidized bed reactor behaves under advanced and conventional control algorithms. Hence the closed loop performance of the MPC scheme in tracking a series of setpoint changes for emulsion phase temperature and production rate in the polymerization reactor was evaluated. For this purpose, a series of setpoint changes in opposite directions were introduced for the controlled variables. The magnitude of the setpoints introduced for these variables were typical of the respective nominal operating ranges. The commonly used conventional controllers in industrial applications are proportional integral (PI) controllers due to their relative simple design, simple control structure and moderate cost [23]. Therefore, for comparison purposes, a conventional PI controller, tuned using the standard Ziegler-Nichols (Z-N) [44] open loop tuning method, was included in this simulation work. The PI controller tuning parameters were calculated based on an analysis of the open loop process reaction curve for a particular operational region of the process, where the open loop response was approximated by a first order plus dead time (FOPDT) dynamic model [K=?0.3 (process gain), τ=890 s (process time constant) andα=80 (process dead time) for the Teprofile, and K=42.5 (process gain), τ=988 s (process time constant) and α=5 (process dead time) for the Rpprofile].

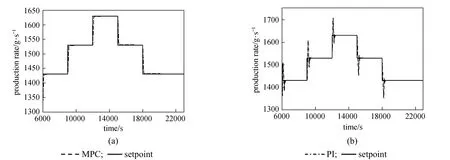
Figure 9Comparison of the performance between the MPC and the PI controller (Kc=7, τI=46.6666, τD=0) in tracking series of setpoint changes in the Rploop

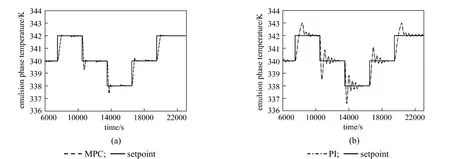
Figure 10Comparison of the performance between the MPC and the PI controller (Kc=?34, τI=271.5654, τD=0) in tracking series of setpoint changes in the Teloop

The parameters tuned using Ziegler and Nichols [44] method were used as starting values but the exact values used in this work were the result of further fine tuning.

Figures 9 and 10 show the performance of the MPC as compared to the PI controller in tracking the series of setpoint changes for Rpand Teprofiles, respectively. The MPC controller is able to track the changes in the setpoints for both profiles. The quality of the setpoint tracking as demonstrated by the MPC in terms of its ability to attain minimal overshoot and minimize the effect of process variables interaction is acceptable. In contrast, the PI controller produced noticeable overshoots for both loops, in addition to the obvious effect of process variables interaction for the Teloop. This illustrates the failure of the decentralized PI controller to track the setpoints for both loops due to loop interactions as well as the process nonlinearity.

The controller moves for MPC and PI controllers in tracking these series of setpoint changes for the Rpand the Teprofiles are shown in Figs. 11 and 12, respectively. It can be seen that the PI controller moves are vigorous for the Rpprofile. Although the controller moves observed for the Teprofile (Fig. 12) are less vigorous and physically realizable, such controller moves typically are not desired during practical implementations due to possible ‘wear and tear’ which can severely shorten the life span of the actuator. In general, the MPC is able to not only produce controller moves which are well within the specified input constraints, but also the controller moves produced are non-aggressive and smooth for practical implementations. The high quality control performance of the MPC is attributed to its ability to handle constraints in the inputs, of which the conventional PI controller was unable to achieve due to the high degree of interaction between these process variables. To summarize, Table 5 shows the integral absolute error (IAE) for the two controllers in tracking the series of setpoint changes for both controlled variables and the performance of the MPC is also superior.

4.2.3Disturb ance rejection

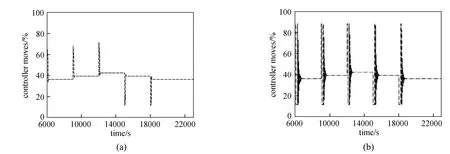
Figure 11Comparison of the corresponding controller moves between the MPC and the PI controller for the Rpprofile MPC; PI

Figure 12Comparison of the corresponding controller moves between the MPC and the PI controller for the Teprofile MPC; PI

Table 5Integral absolute error (IAE) for the MPC and the PI controller in tracking series of setpoint changes for the production rate (Rp) and the emulsion phase temperature (Te) profiles

The results thus far have demonstrated the good performance of the MPC in handling the servo process control problem for the polymerization reactor as compared to the conventional controller. However, for a particular controller to be practically useful in the process industry, the controller must additionally be able to handle regulatory problems effectively. In this case, three variables i.e., hydrogen concentration (CH), superficial gas velocity (U0) and propylene concentration (CM) were identified as the measured disturbance variables. The disturbance variables were introduced one at a time to observe their individual effect on the Rpand Teprofiles. Each disturbance variable was increased by 15% of its nominal value (superficial gas velocity from 0.4 m·s?1to 0.46 m·s?1, hydrogen concentration from 0.01 mol·L?1to 0.0115 mol·L?1and propylene concentration from 0.8 mol·L?1to 0.92 mol·L?1) at the time of 13000 s. Figs. 13 to 15 show the performance of the MPC in rejecting the effect of such changes on the Rpand Teprofiles. Generally, the MPC controller was able to reject these disturbances in an efficient manner. As a general observation, the superficial gas velocity had the largest effect on both the Rpand Teprofiles. On the contrary, hydrogen and propylene concentrations have negligible effect on both of the profiles.

5CONCLUSIONS

A two-phase dynamic model describing the gas phase propylene polymerization in a fluidized bed reactor was used to investigate the dynamic behavior and control on the polypropylene production rate and reactor temperature. The hydrodynamics of the fluidized bed reactor of polypropylene production was based on the dynamic two-phase concept of fluidization. Results of the open loop analysis revealed that the catalyst feed rate and gas superficial velocity have significant effect on the transient behavior of the polypropylene fluidized bed reactor and the process shows nonlinear behavior, especially by the variation of the superficial gas velocity.

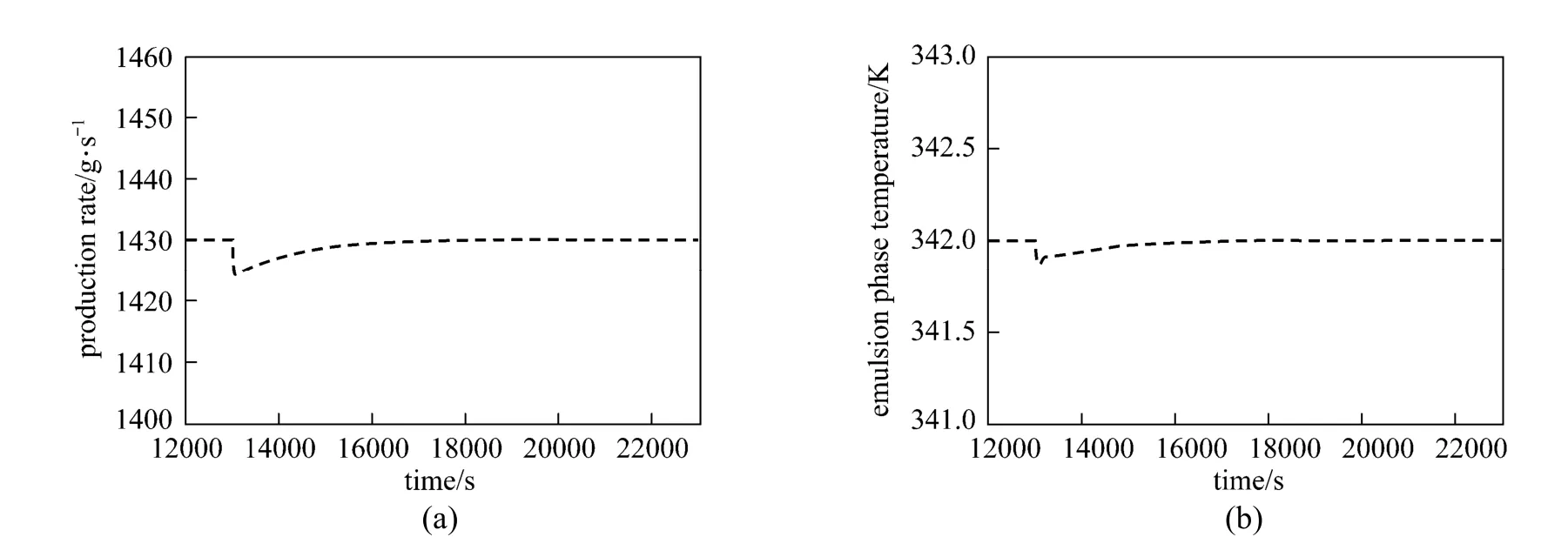
Figure 13Performance of the MPC controller in rejecting the effect of superficial gas velocity (U0) on the Rpand Teprofiles (a 15% increase in the superficial gas velocity was introduced at time=13000)

Figure 14Performance of the MPC controller in rejecting the effect of hydrogen concentration (CH) on the Rpand Teprofiles (a 15% increase in hydrogen concentration was introduced at time=13000 s)

Figure 15Performance of the MPC controller in rejecting the effect of propylene concentration (CM) on the Rpand Teprofiles (a 15% increase in the propylene concentration was introduced at time=13000 s)

Two control algorithms namely, the conventional PI and MPC were tested for the stabilization of the process during setpoint and disturbances changes. The closed-loop simulations for setpoint changes revealed that the MPC is able to track the changes in the setpoint effectively with minimal overshoot while the PI controller produces oscillatory response for the reactor temperature and production profiles. The PI controller produces overshoots for both Rpand Teloops, in addition to the obvious effect of loop interaction for both loops while the MPC moves were shown to be non-aggressive and sufficiently smooth for practical implementations. By introducing changes in the disturbance variables, where each disturbance variable was increased by 15% of its nominal value, the closed loop dynamic simulations indicated that the speed of disturbance rejection for the MPC controller was acceptable for both the Rpand Teprofiles. In conclusion, the results demonstrated excellent performance of the MPC in handling servo and regulatory process controlproblems for this polymerization reactor.

NOMENCLATURE

A cross sectional area of the reactor, m2

Aexheat transfer area of the heat exchanger, m2

CHhydrogen concentration, kmol·m?3

CMpropylene concentration, kmol·m?3

Cpispecific heat capacity of component i, J·kg?1·K?1

Cpgspecific heat capacity of gaseous stream, J·kg?1·K?1

Cp,polspecific heat capacity of solid product, J·kg?1·K?1

Cpwspecific heat capacity of the cooling water, J·kg?1·K?1

Dggas diffusion coefficient, m2·s?1

Dtreactor diameter, m

dbbubble diameter, m

dpparticle diameter, m

Fggas flow rate, kg·s?1

Fcatcatalyst feed rate, kg·s?1

Fcwcooling water flow rate, kg·s?1

H height of the reactor, m

Hbebubble to emulsion heat transfer coefficient, W·m?3·K?1

Hbcbubble to cloud heat transfer coefficient, W·m3·K?1

Hcecloud to emulsion heat transfer coefficient, W·m3·K?1

ΔHRheat of reaction, J·kg?1

j active site type

kds(j) spontaneous deactivation rate constant for a site of type j

kf(j) formation rate constant for a site of type j

kfh(j) transfer rate constant for a site of type j with terminal monomer M reacting with hydrogen

kfm(j) transfer rate constant for a site of type j with terminal monomer M reacting with monomer M

kfr(j) transfer rate constant for a site of type j with terminal monomer M reacting with AlEt3

kfs(j) spontaneous transfer rate constant for a site of type j with terminal monomer M

kh(j) rate constant for reinitiating of a site of type j by monomer M

khr(j) rate constant for reinitiating of a site of type j by cocatalyst

ki(j) rate constant for initiation of a site of type j by monomer M

kp(j) propagation rate constant for a site of type j with terminal monomer M reacting with monomer M

kggas thermal conductivity, W·m?1·K?1

kp(j) propagation rate constant for a site of type j with terminal monomer M reacting with monomer M

Kbcbubble to cloud mass transfer coefficient, s?1

Kbebubble to emulsion mass transfer coefficient, s?1

Kcecloud to emulsion mass transfer coefficient, s?1

M monomer (propylene)

[Mi] concentration of component i in the reactor, kmol·m?3

[Mi]inconcentration of component i in the inlet gaseous stream, kmol·m?3

Mwmonomer molecular weight, kg·kmol?1

NSnumber of active site types

P pressure, Pa

q dynamic heat removal rate, J·s?1

qsssteady state heat removal rate, J·s?1

r number of units in polymer chain

R instantaneous consumption rate of monomer, kmol·s?1

Riinstantaneous rate of reaction for monomer i, kmol·s?1

R(j) rate at which monomer M is consumed by propagation reactions at sites of type j

RemfReynolds number at minimum fluidization velocity, Remf= Umfρgdp/μg

Rpproduction rate, kg·s?1

Rpbbubble phase production rate, kg·s?1

Rpeemulsion phase production rate, kg·s?1

Rvvolumetric polymer phase outflow rate from the reactor, m3·s?1

t time, s

T temperature of the gas entering the exchanger, K

Tintemperature of the inlet gaseous stream, K

Twitemperature of the cooling water entering the heat exchanger, K

U0superficial gas velocity, m·s?1

Ubbubble velocity, m·s?1

Ueemulsion gas velocity, m·s?1

Uexoverall heat transfer coefficient of the heat exchanger, J·K?1·s?1·m?2

Umfminimum fluidization velocity, m·s?1

V reactor volume, m3

Vbvolume of the bubble phase, m3

Vevolume of the emulsion phase, m3

Vpvolume of polymer phase in the reactor, m3

Vpbvolume of polymer phase in the bubble phase, m3

Vpevolume of polymer phase in the emulsion phase, m3

VPFRvolume of PFR, m3

Y(n,j) n th moment of chain length distribution for living polymer produced at a site of type j

γ dimensionless variable defined in Eq. (14)

δ volume fraction of bubbles in the bed

εbvoid fraction of bubble for Geldart B particles

εevoid fraction of emulsion for Geldart B particles

εmfvoid fraction of the bed at minimum fluidization

η dimensionless variable defined in Eq. (14)

μ gas viscosity, Pa·s

ρ density, kg·m?3

ρggas density, kg·m?3

ρpolpolymer density, kg·m?3

Subscripts

1 propylene

2 hydrogen

b bubble phase

e emulsion phase

g gas mixture property

i component type number

in inlet

j active site type number

mf minimum fluidization

pol polymer

PP polypropylene

ref reference condition

REFERENCES

1 Choi, K.Y., Ray, W.H., “The dynamic behaviour of fluidized bed reactors for solid catalysed gas phase olefin polymerization”, Chem. Eng. Sci.,40(12), 2261-2279 (1985).

2 Dadebo, S.A., Bell, M.L., McLellan, P.J., McAuley, K.B., “Temperature control of industrial gas phase polyethylene reactors”, J. Process Contr.,7(2), 83-95 (1997).

3 Ali, M.A.H., Betlem, B., Weickert, G., Roffel, B. “Non-linear model based control of a propylene polymerization reactor”, Chem. Eng. Process.,46(6), 554-564 (2007).

4 Ibrehem, A.S., Hussain, M.A., Ghasem, N.M., “Mathematical model and advanced control for gas-phase olefin polymerization influidized-bed catalytic reactors”, Chin. J. Chem. Eng.,16(1), 84-89 (2008).

5 Zheng, Z.W., Shi, D.P., Su, P.L., Luo, Z.H., Li, X.J., ‘Steady-state and dynamic modeling of the base multireactor olefin polymerization process’, Ind. Eng. Chem. Res.,50(1), 322-331(2011).

6 Luo, Z., Cao, Z., Su, Y., “Monte carlo simulation of propylene polymerization (i) effects of impurity on propylene polymerization”, Chin. J. Chem. Eng.,14(2), 194-199 (2006).

7 Vahidi, O.S.M., Mirzaei, A., “Control of a fluidized bed polyethylene reactor”, Iran. J. Chem. Chem. Eng.,27(3), 87-101 (2008).

8 Choi, K.Y., Ray, W.H., “The dynamic behavior of continuous stirred-bed reactors for the solid catalyzed gas phase polymerization of propylene”, Chem. Eng. Sci.,43(10), 2587-2604 (1988).

9 Ali, E., Al-Humaizi, K., Ajbar, A., “Multivariable control of a simulated industrial gas-phase polyethylene reactor”, Ind. Eng. Chem. Res.,42(11), 2349-2364 (2003).

10 McAuley, K.B., MacGregor, J.F., “Optimal grade transitions in a gas phase polyethylene reactor”, AIChE J.,38(10), 1564-1576 (1992).

11 McAuley, K.B., Macgregor, J.F., “Nonlinear product property control in industrial gas-phase polyethylene reactors”, AICh E J.,39(5), 855-866 (1993).

12 Van Brempt, W., Backx, T., Ludlage, J., Van Overschee, P., De Moor, B., Tousain, R., “A high performance model predictive controller: Application on a polyethylene gas phase reactor”, Control Eng. Pract.,9(8), 829-835 (2001).

13 Sarvaramini, A., Mostoufi, N., Sotudeh-Gharebagh, R., “Influence of hydrodynamic models on dynamic response of the fluidized bed polyethylene reactor”, Int. J. Chem. React. Eng.,6(1), 1542-1580 (2008).

14 Seki, H., Ogawa, M., Ooyama, S., Akamatsu, K., Ohshima, M., Yang, W., ‘Industrial application of a nonlinear model predictive control to polymerization reactors’, Control Eng. Pract.,9(8), 819-828 (2001).

15 Ali, E.M., Abasaeed, A.E., Al-Zahrani, S.M., “Improved regulatory control of industrial gas-phase ethylene polymerization reactors”, Ind. Eng. Chem. R es.,38(6), 2383-2390 (1999).

16 Ali, E.M., Abasaeed, A.E., Al-Zahrani, S.M., “Optimization and control of industrial gas-phase ethylene polymerization reactors”, Ind. Eng. Chem. R es.,37(8), 3414-3423 (1998).

17 Ali, E.M., Ali, M.A.H., “Broadening the polyethylene molecular weight distribution by controlling the hydrogen concentration and catalyst feed rates”, ISA T.,49(1), 177-187 (2010).

18 Hassimi, A., Mostoufi, N., Sotudeh-Gharebagh, R., “Unsteady-state modeling of the fluidized bed polyethylene reactor”, Iran. J. Ch em. Eng.,6(1), 23-39 (2009).

19 Chatzidoukas, C., Perkins, J.D., Pistikopoulos, E.N., Kiparissides, C.,“Optimal grade transition and selection of closed-loop controllers in a gas-phase olefin polymerization fluidized bed reactor”, Chem. Eng. Sci.,58(16), 3643-3658 (2003).

20 Sato, C., Ohtani, T., Nishitani, H., “Modeling, simulation and nonlinear control of a gas-phase polymerization process”, Comput. Chem. Eng.,24(2-7), 945-951 (2000).

21 Salau, N.P.G., Neumann, G.A., Trierweiler, J.O., Secchi, A.R., “Dynamic behavior and control in an industrial fluidized-bed polymerization reactor”, Ind. Eng. Chem. Res.,47(16), 6058-6069 (2008).

22 Bolsoni, A., Lima, E.L., Pinto, J.C., “Advanced control of propylene polymerizations in slurry reactors”, Braz. J. Chem. Eng.,17(4-7), 565-574 (2000).

23 Ghasem, N.M., “Dynamic behavior of industrial gas phase fluidized bed polyethylene reactors under PI control”, Chem. Eng. Technol.,23(2), 133–145 (2000).

24 Ghasem, N.M., “Design of a fuzzy logic controller for regulating the temperature in industrial polyethylene fluidized bed reactor”, Chem. Eng. Res. Des.,84(2), 97-106 (2006).

25 Gu, B., Gupta, Y.P., ‘Control of nonlinear processes by using linear model predictive control algorithms’, ISA T.,47(2), 211-216 (2008).

26 Shamiri, A., Hussain, M.A., Mjalli, F.S., Mostoufi, N., Shafeeyan M.S., “Dynamic modeling of gas phase propylene homopolymerization in fluidized bed reactors”, Chem. Eng. Sci.,66(6), 1189-1199 (2011).

27 Cui, H., Mostoufi, N., Chaouki, J., “Characterization of dynamic gas-solid distribution in fluidized beds”, Chem. Eng. J.,79(2), 133-143 (2000).

28 Cui, H., Mostoufi, N., Chaouki, J., “Gas and solids between dynamic bubble and emulsion in gas-fluidized beds”, Powder Technol.,120(1-2), 12-20 (2001).

29 Shamiri, A., Hussain, M.A., Mjalli, F.S., “Two phase dynamic model for gas phase propylene copolymerization in fluidized bed reactor”, Defect. Diffus. Forum, 312-315, 1079-1084 (2011).

30 Shamiri, A., Hussain, M.A., Mjalli, F.S., Mostoufi, N., “Kinetic modeling of propylene homopolymerization in a gas-phase fluidized-bed reactor”, Chem. Eng. J.,161(1-2), 240-249 (2010).

31 Kiashemshaki, A., Mostoufi, N., Pourmahdian, S., Sotudeh-Gharebagh, S., “Two phase modeling of a gas phase polyethylene fluidized bed reactor”, Chem. Eng. Sci.,61(12), 3997-4006 (2006).

32 Lucas, A., Arnaldos, J., Casal, J., Puigjaner, L., “Improved equation for the calculation of minimum fluidization velocity”, Ind. Eng. Ch em. Proc. Dev. Des.,25(2), 426-429 (1986).

33 Kunii, D., Levenspiel, O., Fluidization Engineering, 2nd edition, Boston, MA, Butterworth-Heinmann (1991).

34 Mostoufi, N., Cui, H., Chaouki, J., “A comparison of two- and single-phase models for fluidized-bed reactors”, Ind. Eng. Chem. R es.,40(23), 5526-5532 (2001).

35 Hilligardt, K., Werther, J., “Local bubble gas hold-up and expansion of gas/solid fluidized beds”, German Chem. Eng.,9(4), 215-221 (1986).

36 Cai, P., Chen, L., van Egmond, J., Tilston, M., “Some recent advances in fluidized-bed polymerization technology”, Particuology,8,(6)578-581 (2010).

37 Shamiri, A., Hussain, M.A., Mjalli, F.S., Mostoufi, N., “Improved single phase modeling of propylene polymerization in a fluidized bed reactor”, Comput. Chem. Eng.,36(6), 35-47 (2012).

38 McAuley, K.B., MacGregor, J.F., Hamielec, A.E., “A kinetic model for industrial gas-phase ethylene copolymerization”, AIChE J.,36(6), 837-850 (1990).

39 Luo, Z.H., Su, P.L., Shi, D.P., Zheng, Z.W., “Steady-state and dynamic modeling of commercial bulk polypropylene process of hypol technology”, Chem. Eng. J.,149(1-3), 370-382 (2009).

40 Floyd, S., Choi, K.Y., Taylor, T.W., Ray, W.H., “Polymerization of olefins through heterogeneous catalysis. III. Polymer particle modelling with an analysis of intraparticle heat and mass transfer effects”, J. Appl. Polym. Sci.,32(1), 2935-2960 (1986).

41 Mjalli, F.S., Al-Asheh, S., “Neural-networks-based feedback linearization versus model predictive control of continuous alcoholic fermentation process”, Chem. Eng. Technol.,28(10), 1191-1200 (2005).

42 Seborg, D.E., Edgar, T.F., Mellichamp, D.A., Process Dynamics and Control, 2nd edition, John Wiley & Sons, New Jersey (2004).

43 Shridhar, R., Cooper, D.J., “A tuning strategy for unconstrained SISO model predictive control”, Ind. Eng. Chem. Res.,36(3), 729-746 (1997).

44 Ziegler, J.G., Nichols, N.B., Rochester, N.Y., “Optimum settings for automatic controllers”, Trans. ASME,64(8), 759-768 (1942).

10.1016/S1004-9541(13)60565-0

2012-02-17, accepted 2013-01-12.

* Supported by the Research Grants of the Research Council of Malaya.

** To whom correspondence should be addressed. E-mail: a.shamiri@um.edu.my