Time-dependent variational approach to solve multi-dimensional time-dependent Schr¨odinger equation
Mingrui He(何明睿), Zhe Wang(王哲), Lufeng Yao(姚陸鋒), and Yang Li(李洋),
1Department of Basic Courses,Naval University of Engineering,Wuhan 430033,China
2Key Laboratory for Laser Plasmas(Ministry of Education)and School of Physics and Astronomy,Shanghai Jiao Tong University,Shanghai 200240,China
Keywords: time-dependent variational approach,above-threshold ionization,high harmonic generation
1.Introduction
The rapid development of laser technology brings powerful ultrashort intense light sources into laboratories.[1-3]The frequency domain of the modern laser covers a broad range from mid-infrared to the x-ray regime, while the intensity of the laser pulses is routinely achieved over 1016W/cm2.Atoms, molecules, and condensed matter interacting with the intense light sources exhibit various nonlinear phenomena, including above-threshold ionization (ATI),[4-6]highorder harmonic generation (HHG),[7-11]and nonsequential double ionization.[12,13]All these phenomena are not accessible through perturbation theory.
In the non-relativistic regime, numerically solving the time-dependent Schr¨odinger equation(TDSE)is the most rigorous nonperturbative method to simulate the intense laseratom interactions, which in principle gives the most faithful reproduction of the concerned physical scenarios.However, as the computational resources required by solving TDSE grow exponentially with respect to the number of degrees of freedom, most discussions of full-dimensional systems are restricted to the single-active-electron (SAE)approximations.[14-16]Even within SAE, accurate solutions under extreme conditions are still challenging.They demand enormous computer resources for two-and three-dimensional models of atoms and molecules.Nowadays,efficient methods to solve TDSE are still under active development using different bases under different given physical conditions.[17-19]
The curse of dimensionality is more severe when SAE fails, if, for example, doubly excited states are important.A formal consistent way is to treat all electrons as active indistinguishable particles.Directly solving TDSE beyond simple multielectron species, such as He and H2, is extremely difficult, due to exponential increase in computational cost.For example,when simulating full dimensional He onL2(R6)using a basis{e1,e2,...,en}?L2(R), one needs to discretize,store,and apply the Hamiltonian H in this basisHi1...id j1...jd=〈ei1?...eid|H|ej1?...ejd〉.The tensor productsHi1...id j1...jdconsists ofn12complex numbers, thus applying it requiresn12complex mutiplecations.However, to represent a physical situation to a satisfying accuracy, the discretization must be chosen high enough, i.e.,nmust be chosen to be large enough, which is limited by the available computational resources, especially for high-dimensional problems.To subjugate this difficulty, various theoretical methods, including the time-dependent density-functional theory (TDDFT) and the multiconfiguration time-dependent Hartree-Fock (MCTDHF)method have been proposed,which provide efficient resorts for quantum mechanics to treat multi-electron systems asab initioas possible.[20-22]In the MCTDHF method, the total wavefunction of the multi-electron system is expressed as a superposition of the chosen number of time-dependent spin-orbitals prepared for each electron.It provides a compact and computationally less demanding description of the multi-electron atoms and molecules interacting with the intense light sources.The mathematical idea is to discretize a state in the configuration space of each electron.The electronelectron correlation,i.e.,the interaction between each configuration space is approximated by low-rank approximation.An improved description of the electron correlation is achieved by adding more configurations in the singular value decompositions.
In this paper, inspired by the methodology of MCTDHF method for multielectron problems and math behind, we formulate an efficient method to solve multi-dimensional TDSE within single-electron approximation.Using two-dimensional(2D) TDSE as an example, we treat each spatial degree of freedom as a distinguishable quasi-particle.Then the 2D total electronic wavefunction is expressed as a linear combination of a direct product of one-dimensional (1D) wavefunctions with different expansion coefficients.Both the expansion coefficients and the 1D wavefunctions are simultaneously propagated in time based on the time-dependent variational principle,[21,23,24]which provides an adequate representation of the temporal evolution of the total wavefunction with appreciably less computational demand.We implement this approach to numerically simulate the strong-field ionization of the argon atoms induced by the linearly polarized laser pulse and circularly polarized laser pulse.With the increasing number of decomposing 1D wavefunctions, the obtained photoelectron momentum distributions(PEMDs)show increasingly better agreement with these simulated by numerically solving the TDSE directly.Moreover, we investigate the high harmonic generation (HHG) from a 1D non-Born-Oppenheimer hydrogen molecular ion.The obtained spectrum is in good agreement with the TDSE calculation.This provides an accurate and efficient method to simulate the laser-atom interaction within extreme electromagnetic conditions, which generally demands large computer power.
2.Numerical methods
2.1.Argon atom

We first consider the strong-field ionization of 2D model argon atom exposed to a strong laser field.The 2D-TDSE reads [atomic units (a.u.) are used throughout unless stated otherwise]The soft-core parameterεis set to be 0.39 to correctly reproduce the ground-state energy of the argon atom.Equation(2)is separable except for the soft Coulomb potential.In our timedependent variational treatment, each spatial degree of freedom is regarded as a quasi-particle.It represents that we treat the two dimensions as independent degrees of freedom,while these two dimensions are not really independent because of the potential function.Therefrom,we separate the total Hamiltonian according to their spatial components as
together with the soft Coulomb potential(3)being the particleparticle interaction term.
Analogy to the MCTDHF method,we rewrite the total 2D wavefunction as a superposition of 1D wavefunction products
We callχ(x,t) andφ(y,t) the 1D orbitals ofx-particle andy-particle,respectively,andcij(t)being the expansion coefficients.We would like to mention that,similar to performing eigenvalue decomposition on the square matrix,only whennequals the grid number ofψ(x,y,t), the sum of the products of 1D wavefunction can produce exact 2D wavefunctionψ(x,y,t).Hereχ(x,t)andφ(y,t)are simulated by imaginarytime propagation,and orthonormalization is imposed on these 1D orbitals
With these assumptions at hand, we can derive the equations of motion for the 1D orbitalsχ(x,t)andφ(y,t)as well as the expansion coefficientscij(t)based on the time-dependent variational principle.[21,23]The results read
where the operators ?Q(x)= 1-∑p|χp〉〈χp| and ?Q(y)= 1-∑μ|ψμ〉〈ψμ| are projectors onto the orthogonal complement of the occupied orbital space, which guarantee the orthonormality of orbitals during time propagation;ρx,ρy,andρxyare the one-body and two-body reduced density matrices,respectively;(?Wxy)μνand(?Wyx)pqare mean-field potentials,given by
The fourth-order Runge-Kutta method is employed to numerically propagate the equations of motion.The initial wavefunction is prepared by imaginary-time propagation.[25]To obtain the PEMD,the total 2D wavefunction is split into two parts at the end of every time step by an absorbing function,[26,27]and the “ionized part” is first transformed into momentum space and then propagated under the Volkov Hamiltonian analytically to the end of the pulse.[26]
2.2.Hydrogen molecular ion
The second example is HHG from H+2molecular ion subject to a linearly polarized laser field.The motions of the nuclei and electron are restricted in the polarization direction of the laser field.Then the HamiltonianH(z,R,t)can be modeled by
wherezandRare the electronic coordinate as measured from the nuclear center of mass and the internuclear distance, respectively.The soft-core parameterεnnandεneare set to be 1.0 and 0.03, respectively.The electronic reduced mass is given byμe=2M/(2M+1) withMbeing the proton mass.The effective charge isqeff= (2M+2)/(2M+1).Similar to Eq.(2), we can decompose Eq.(14) into a set of singleparticle Hamiltonians and the particle interaction term.The total wavefunctionψ(z,R,t) is expanded accordingly.Then the equations of motion can be derived.Details are omitted here.HHG spectra are computed as the squared modulus of the Fourier-transformed electric dipole acceleration.In order to reduce the background level of the HHG spectra,the dipole acceleration is multiplied by a Hanning window function before the Fourier transform.
3.Results and discussion
We first consider the strong-field ionization of the argon atom subject to a linearly polarized few-cycle laser pulse with the wavelength of 1200 nm, the peak intensity of 2×1014W/cm2and the pulse duration of 8TwithTbeing the optical cycle period of the laser pulse.The electric fieldE(t)of the laser pulse is defined as
Hereω=2π/Tis the angular frequency.N0=8 is the total number of the laser optical cycles.E0=0.0755 is the amplitude of the electric field corresponding to the peak laser intensity of 2×1014W/cm2.With this intensity, the Keldysh parameter[28]γ<1, i.e., in the tunneling regime.Hereγ=[Ip/(2Up)]1/2, withUp=E20/(4ω2) being the ponderomotive potential.
We employ two treatments to solve the 2D-TDSE: (1)The approximation method with the 2D electron wavefunctionΨ(x,y,t)given by Eq.(6),usingn1D wavefunctions for bothxandydirections.Figures 1(a)-1(e)present the obtained PEMD for different numbersn.(2) Numerically exact solution of the TDSE with split-operator spectral method[29]by discretizing 2D electron wavefunction in Cartesian grid ranges from-819 a.u.to 819 a.u.for both directions with the grid size of ?x=?y=0.4 a.u.The obtained PEMD is shown in Fig.1(f),which works as a reference.
For smalln,liken=1,the calculated PEMD is not credible,and the interference structures cannot be identified in the spectrum.With increasingn,the PEMD simulated by the approximation method shows increasingly better agreement with the reference result in Fig.1(f).Whenn=30, the obtained PEMD(as shown in Fig.1(e))has no obvious difference with the reference result.By performing eigenvalue decomposition on the potential functionV(x,y),we obtain a simple criterion for selecting suitablen.For Ar atom,asnincreases,the diagonal elements of the feature matrix rapidly decrease.Set the threshold 10-10andn=30.
In order to compare the numerical efficiency of the present method with the commonly used 2D representation of the wave function on grid,we first analyze the required memory size.Denoting the number of grid points along each direction bym, the required memory size for the expansion of Eq.(6)can be expressed as 2mn+n2and that for the the conventional method asm2.Typically, the conditionn ?mis satisfied.Thus the required memory size for the 2D electron wavefunction in the present method is much smaller than that in the conventional method for achieving a good agreement.However,due to the 2D potential functionV(x,y)used in the temporal propagation, the memory size cannot be reduced in a further step.Moreover,thanks to the small size of the wavefunction,one can expect that the computational efficiency can be significantly improved.Numerical propagation of Eqs.(9)-(11)is much faster.The only price to pay is that Eqs.(10)and(11)are nonlinear,time step smaller than that in the common method should be adopted in order to have a stable propagation.Nevertheless, the computation time is 30% of the common method.
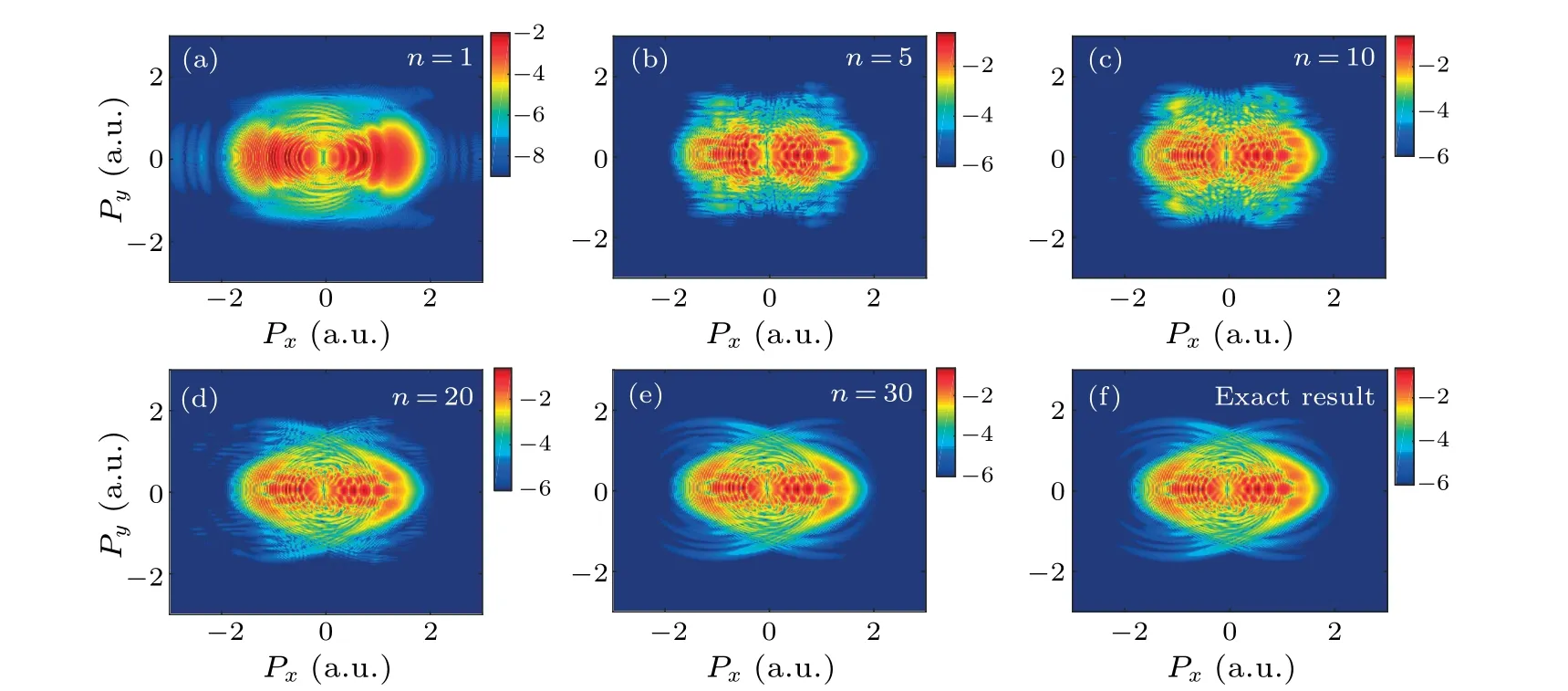
Fig.1.The photoelectron momentum distribution(PEMD)of Ar atoms induced by the linearly polarized laser pulse,simulated by the approximation method[(a)-(e)]and the precise split-operator spectral method(f).The number n of the one-dimensional wavefunctions in the approximation method is(a)1,(b)5,(c)10,(d)20,and(e)30.The wavelength of the laser pulse is 1200 nm and the intensity is 2×1014 W/cm2.The pulse duration is 8 optical cycles.The color scale is logarithmic.
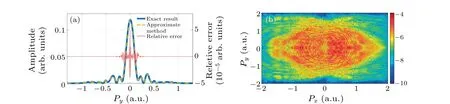
Fig.2.(a) Left longitudinal coordinate: The transverse momentum distribution of the PEMD at the cut px =Up extracted from Fig.1(e) (orange dashed curve) and Fig.1(f) (blue curve).Right longitudinal coordinate: the relative error of the two curves (red curve).(b)The difference plot with logarithmic color scale.
Evident interference structures can be identified in Fig.1(e).The nearly horizontal fork-like interference fringes are the strong-field photoelectron holography.[30]In previous studies, both the inherent structural information and the ultrafast electronic dynamical information can be retrieved from the phase of the interference fringes,[5,31,32]which requires our approximation method to provide correct interference fringe locations as carried out with the traditional TDSE solving method (including the split-operator spectral method).To make an intuitive comparison, we cut slices from Figs.1(e)and 1(f) atpx=Up, respectively.The corresponding transverse momentum distributions are shown in Fig.2(a), where the approximate result (orange dashed curve) almost exactly coincides with the reference result (blue curve).The relative error between these two curves,as shown by the red curve in Figs.2(a), is in the order of 10-4and below.Furthermore, a differential approach is used to compare the overall difference between Figs.1(e) and 1(f).The difference plot is defined as DP(px,py) =|Da(Px,Py)-Dref(Px,Py)|, whereDa(Px,Py)andDref(Px,Py)are the photoelectron distribution corresponding to the approximation method withn=30 and the reference result,respectively.As shown in Fig.2(b),the amplitude of DP(px,py) has been as low as 10-4and the interference fringes in the PEMD have barely any location shift.
Besides the one-dimensional linearly polarized laser pulse, we investigate the tunneling ionization of argon atoms induced by a circularly polarized laser pulse.The laser parameters of this circularly polarized laser pulse,including the wavelength,peak intensity,and pulse duration are the same as the linearly polarized laser pulse.Here,the electric fieldE(t)of this laser pulse is defined as
Similarly,we employ both the approximation method and the split-operator spectral method to solve the 2D TDSE.For the approximation method, the numbernof the one-dimensional wavefunctions used in Eq.(6) increases from 1 to 30, corresponding to PEMDs presented in Figs.3(a)-3(e).Clearly,with increasingn, the corresponding PEMD shows increasingly better agreement with the reference result in Fig.3(f),which is calculated by the split-operator spectral method.By using the differential approach (as used in Fig.2(b)) to compare these two treatments,we confirm that forn=30,the approximate result is almost identical to the reference result.It demonstrates that the approximation method is accurate and computationally efficient.
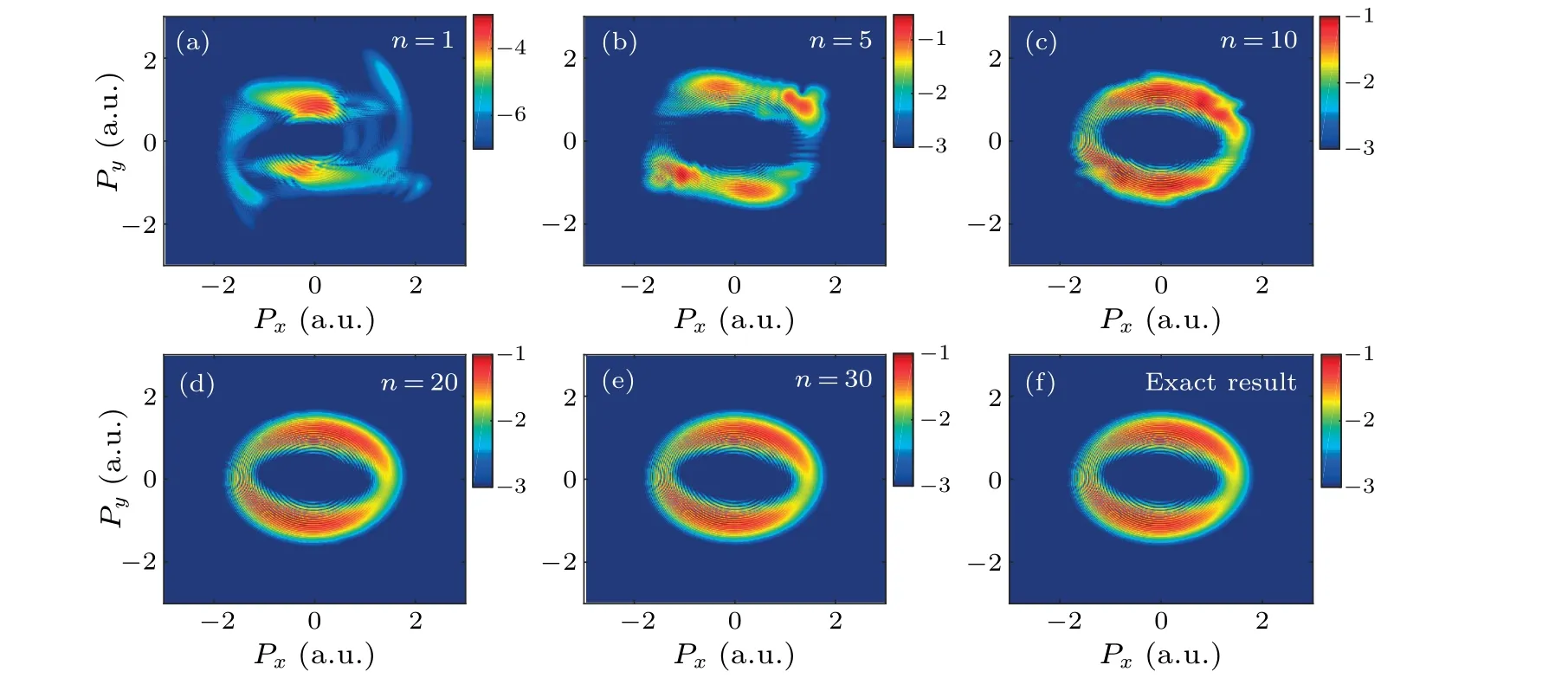
Fig.3.PEMDs of Ar atoms induced by the circularly polarized laser pulse.(a)Simulated by the approximation method with the onedimensional wavefunctions number n=1, (b)n=5,(c)n=10,(d)n=20,(e)n=30.(f)Calculated result with the split-operator spectral method.The color scale is logarithmic.
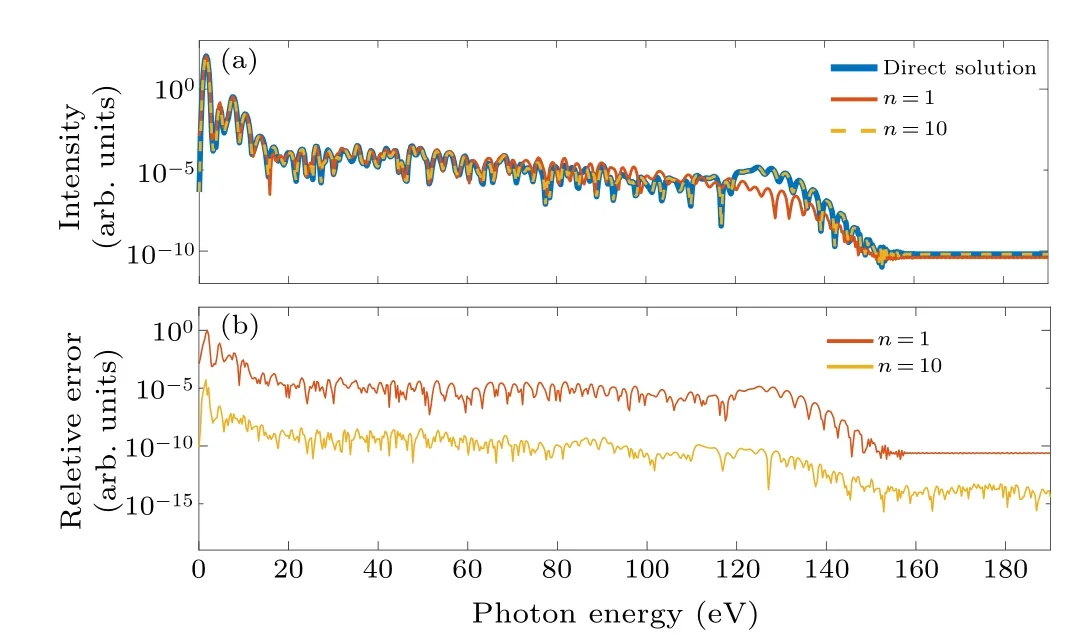
Fig.4.(a)The high-order harmonic spectrum from H+2 molecular ion,using the approximation method with n=1 (the red solid curve) and n=10(the yellow dashed curve),and the direct solution of the TDSE(the blue solid curve).(b)Relative error between the direct solution and the approximation method with n=1 (the red curve) and n=10 (the yellow curve).
In the above discussion, we calculate the PEMD of the tunneling ionization of the Ar atom.Both the split-operator spectral method and the approximation method are used to numerically solve the 2D TDSE and to obtain the real-time propagation of the electron wavefunction.The“ionized part”of the electron wavefunction is separated from the total timedependent electron wavefunction and transformed into momentum space at the end of each time step to simulate the PEMD,and thus sizable computational demanding is required.In the subsequent discussion, we investigate the HHG of 1D non-Born-Oppenheimer hydrogen molecular ion subject to the linearly polarized laser pulse given by Eq.(15).Here,we treat both the 1D electron and the 1D nuclear motion as two distinguishable quasi-particles.Similarly to calculating the PEMD, we numerically solve this 2D-TDSE and trace the temporal evolution of the electron wavefunction, where our approximation method can efficiently reduce the computational cost.Then the HHG spectrum is calculated as the modulus squared of the Fourier transform of the dipole accelerationa(t)= d2〈ψ(t)|z|ψ(t)〉/dt2, which is computational less demanding compared to simulating PEMD.
Figure 4(a)presents the HHG spectra from the H+2molecular ion simulated by the approximated method and the direct method (solving TDSE directly), and Fig.4(b) presents the relative error between these two methods.For the approximation method, the result shows an improvement with increasing numbernof the one-dimensional wavefunctions.Whenn=10,the spectrum displays remarkable agreement with the direct solution.Note that Figs.1(c)and 3(c)demonstrate that,forn=10,the approximation method is not accurate enough.This indicates that calculating PEMD requires more 1D wavefunctions to simulate the temporal evoluting electron wavefunction in Eq.(6).
4.Conclusion
In summary, we have demonstrated an approximation method to solve the 2D TDSE and utilize this method for exactly solvable systems.In this approach, the 2D electron wavefunction is expanded in terms of the multiplication of two serials of 1D wavefunctions.The equation of motion for the expansion coefficients and 1D wavefunctions are derived.Employing this approximation method to the investigation of the atom and molecule irradiated by the intense laser field,the PEMD and high-harmonic spectrum can be accurately and computationally simulated efficiently.Moreover, this framework is highly flexible,and thus it would enable more efficient simulations of the laser-matter interaction.For example,it can be straightforwardly extended to solve real three-dimensional TDSE for atoms and molecules in intense laser fields.By writing the three-dimensional wavefunction in Cartesian coordinates asψ(x,y,z), analogously to Eq.(6), we can write the wavefunction as a linear combination of lower-dimensional wave function productsψ(x,y,z)=∑ni j ci j(t)χi(x,y,t)φj(z,t).The derived equations of motion can be directly applied.Note that in this case, separation of the wavefunction into three quasi-particles according to three directions is not recommend,because in this case the coulomb potential would be a threeparticle interaction term and will highly complicate the equations of motion.Moreover,our approximation method can use OpenMP with shared memory for parallel computing,and it is more difficult to imply MPI computing with distributed memory than directly solve the time-dependent Schr¨odinger equation.
Acknowledgments
Project supported by the National Natural Science Foundation of China(Grant Nos.12204545 and 12274294)and the Program for NUE independent research and development.
- Chinese Physics B的其它文章
- Diamond growth in a high temperature and high pressure Fe-Ni-C-Si system: Effect of synthesis pressure
- Si-Ge based vertical tunnel field-effect transistor of junction-less structure with improved sensitivity using dielectric modulation for biosensing applications
- Speeding-up direct implicit particle-in-cell simulations in bounded plasma by obtaining future electric field through explicitly propulsion of particles
- Temperature-induced logical resonance in the Hodgkin-Huxley neuron
- Energy-distributable waterborne acoustic launcher for directional sensing
- Structural stability and ion migration of Li2MnO3 cathode material under high pressures

