An Improved Singularity Free Self-Similar Model of Proton Structure Function
Baishali Saikiaand D.K.ChoudhuryDepartment of Physics,Gauhati University,Guwahati 781 014,Assam,India
2Physics Academy of North-East,Guwahati 781 014,Assam,India
1 Introduction
Although renormalization group equation of quantum if eld theory[1]exhibits self-similarity,[2]it is not yet established rigorously in QCD,the accepted fundamental quantum field theory of strong interaction.However,because of its wide applicability in other areas of physics,[3]study of self-similarity in the structure of the proton is worth pursuing.In this spirit,Lastovicka[4]in 2002, first suggested the self-similarity as a possible feature of multipartons specially in the kinematical region of small Bjorken x,which in later years was pursued in Refs.[5–15].Specifically,how quarks and gluons share the momentum fractions of the proton was studied in Refs.[11–12],behavior of double parton distribution functions,longitudinal structure function FL[14]and Froissart bound.[15]
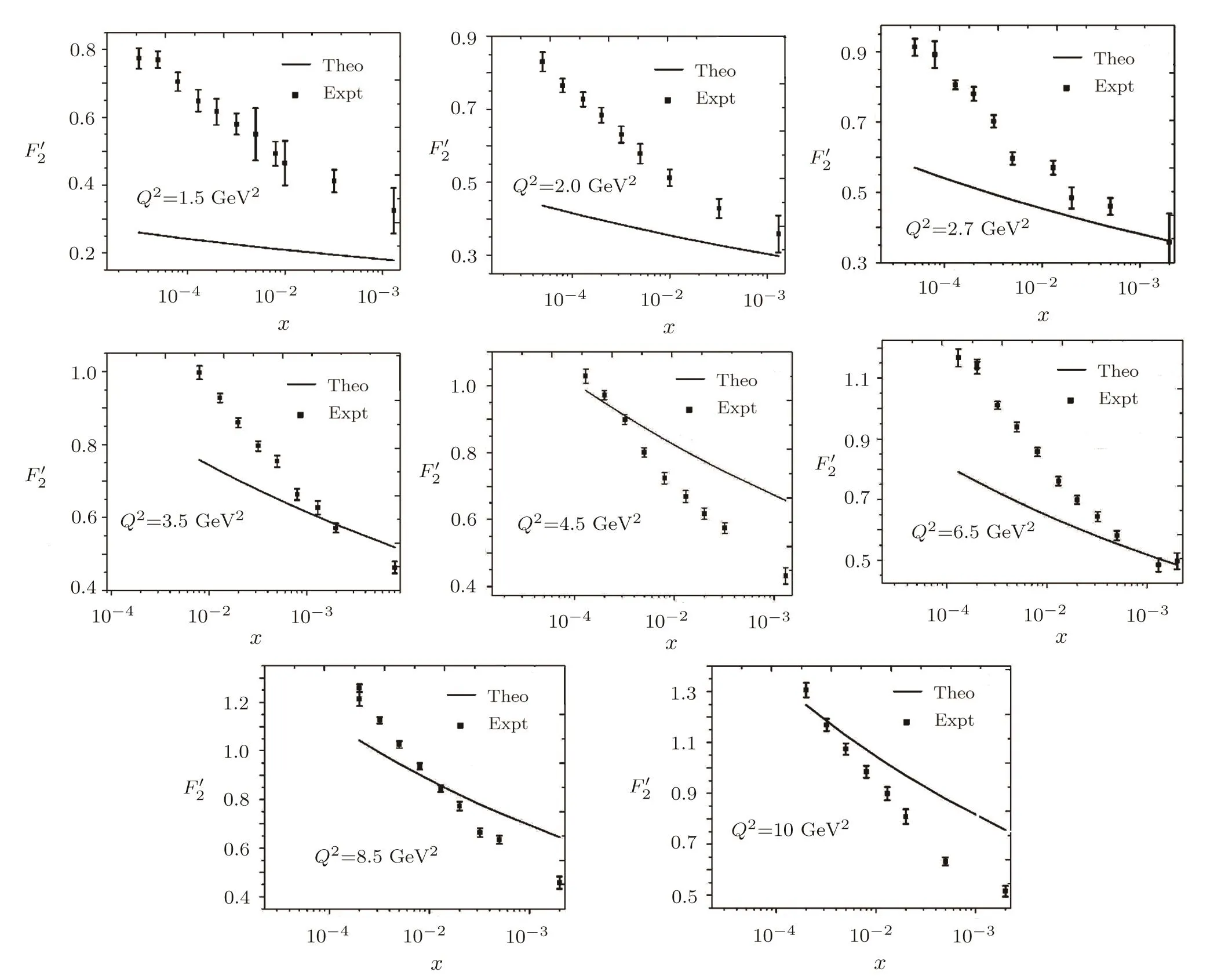
One of the limitations of the phenomenological analysis of Ref.[4]is that it has a singularity at x ~ 0.019,[11?12]which is well within the kinematical range of x;0 In the present paper,we therefore make a re-analysis of the model of Ref.[4],demanding it to be singularity free in the entire x-range;0 The self-similarity based model of the proton structure function of Ref.[4]is based on Parton Distribution Function qi(x,Q2)where qiis the virtualities of the quark hit by the photon.In Refs.[13,15],it has been shown that if one assumes that the TMDPDF has similar formula like Lastovicka used,[4]one can obtain the same form of structure function although the two models are different.Such identical form of the PDF of structure function has been obtained because the relation between unintegrated parton distribution function(uPDF)and the TMD with PDF are assumed to be identical,which is in general may not be true.With such assumption,we follow the reformulated model[13,15]of Ref.[4](Model 1,Model 1A)and see its possible consequences.Choosing the magni fication factors(1/x)andit is written as:[13,15](reformulated Lastovicka model) where i denotes a quark fl avor.Here D1,D2,D3are the three fl avor independent model parameters whileis the only fl avor dependent normalization constant.M2(=1 GeV2)is introduced to make(PDF)qi(x,Q2)as defi ned below(in Eq.(2))dimensionless.The integrated quark densities then de fi ned as: As a result,the following analytical parametrization of a quark density is obtained by using Eq.(2):[12](Model 1A) where is fl avor independent.Using Eq.(3)in the usual Definition of the structure function F2(x,Q2),one can get or it can be written as whereEquation(5)involves quarks and anti-quarks as in Ref.[4]we use the same parametrization both for quarks and anti-quarks. From HERA data,[17?18]Eq.(6)was fi tted in Ref.[4]with in the kinematical region, We note that the parameters in Eqs.(7)and(8)are same as Ref.[4].We call it to be the reformulated version of Model 1 except the Definition of Eq.(1)because it is PDF not TMD,which occurs in the Definition of structure function in Ref.[4]. The de fi ning equations of the model of Ref.[4](Eqs.(1)–(4)above)do not ascertain the numerical values and signs of the parameters Djs.These are determined from data[17?18]leading to the set of Eq.(7)in the kinematic range(Eq.(8)).However,the phenomenological analysis has one inherent limitation:due to the negative value of D3,Eq.(6)develops a singularity at x0v 0.019[11?12]as it satis fi es the condition 1+D3+D1log(1/x0)=0,contrary to the expectation of a physically viable form of structure function. Rede fi ning the model parameters Djs bys(j=1,2,3)and(PDF)qi(x,Q2)by(x,Q2)and also structure function F2(x,Q2)by(x,Q2)in the present analysis,we observe that it can be made singularity free under the following speci fic conditions: Case 1 Ifin Eq.(1)then the PDF Eq.(3)and the Structure Function Eq.(6)will be of the form: Case 2 In this casein Eq.(1)then the corresponding expressions for the PDF and Structure Function in this limit are respectively: Case 3 In this case,in Eq.(1)then the corresponding PDF and the Structure Function are set in the form: respectively. Case 4 This is the most general case for the singularity free model of Parton Distribution Function(PDF)Eq.(3)and Structure Function Eq.(6)under the condition thatare positive. To determine the parameters of the modelwe use recently compiled HERA data[16]instead of earlier data[17?18]used in Ref.[4].Following this procedure of Ref.[4],we make χ2-analysis of the data and find the following results.Case 1We note that=1 is ruled out since it will make the structure function Eq.(10)x-independent.In Table 1 we show the results.From the χ2-analysis,it is obtained that the model in case 1 is con fi ned well with data for 0.35 GeV2≤Q2≤70 GeV2and 6.62×10?6≤x≤0.08.andare taken to be zero in this limit.Here the number ofdata points is 222. Table 1 Results of the fi t of case 1;Eq.(10). Case 2 The parametersare determined(given in Table 2)in the similar manner as in case 1 and the range of validity has been obtained as:0.35 GeV2≤Q2≤27 GeV2and 6.62× 10?6≤ x≤0.032.As in case 1,here too D2=1 is ruled out since it will make Eq.(12)x-independent.The number ofdata points is 174. Table 2 Results of the fi t of case 2;Eq.(12). Case 3 Here,parameters are best fi tted in the range:0.35 GeV2≤ Q2≤ 15 GeV2and 6.62×10?6≤x≤ 0.02 and given in Table 3.The number ofdata points is 146. Table 3 Results of the fi t of case 3;Eq.(14). Case 4 Parametersare determined and given in Table 4 and obtained in a more restrictive range:0.85 GeV2≤Q2≤10 GeV2and 2×10?5≤x≤0.02.The number ofdata points is 95. Table 4 Results of the fi t of case 4;Eq.(16). In Fig.1,we plotof the present model(Model 2)for case 4 as a function of x for eight representative values of Q2(Q2=(1.5,2,2.7,3.5,4.5,6.5,8.5,10)GeV2)in the phenomenologically allowed range 0.85 GeV2≤Q2≤10 GeV2.We also show the corresponding available data from Ref.[16]. It shows that as the model parameters have lesser restrictive constraint except for the positivity,the range of validity shrinks from Q2=120 GeV2to Q2=10 GeV2.Thus our analysis indicates that the phenomenological range of validity of the present version of the model is more restrictive:0.85 GeV2≤Q2≤10 GeV2and 2×10?5≤ x ≤ 0.02 to be compared with Eq.(8)of the previous version of Ref.[4].Also,the individual χ2at Q2=8.5 GeV2and 10 GeV2is minimum to be compared with Q2=4.5 GeV2and 10 GeV2,which is quite larger than that of 10 GeV2.It is same for Q2=1.5 GeV2too.Basically,our results valid in small area in between Q2of 8.5 GeV2and 10 GeV2.But due to the unavailability of the experimental data points,the di ff erence can not be shown explicitly. We also observe the following features of the model compared to data:at Q2=1.5 GeV2data overshoots the theory.But as Q2increases,the theoretical curve comes closer to data.At Q2=10 GeV2,on the other hand,the theory exceeds data.Main reason of this feature is that the x-slope of the model is less than that of the data.Speci fically,due to positive D3,the growth of the structure function with Q2becomes faster than a linear growth as can be seen from Eq.(4)i.e. at higher values of Q2>1 GeV2to be compared with of Ref.[4],which is faster than data.This is the major limitation of the present singularity free version of the model,which calls for further improvement. Fig.1 Comparison of the structure function(Model 2)Eq.(16)as a function of x in bins of Q2for case 4 with measured data of F2from HERAPDF1.0.[16] Let us discuss a possible way of removing the short coming of the models under discussion.As noted in Ref.[4],this approach has taken the notion of selfsimilarity to parametrize Parton Distribution Function(PDF)and eventually the structure function.However,the variables in which the supposed fractal scaling of the quark distributions and F2(x,Q2)occur are not known from the underlying theory.In Ref.[4],the choice of 1/x is presumably because of the power law form of the quark distributions at small x found in Gl¨uck–Reya–Vogt(GRV)[19]distribution.However,this form is not derived theoretically but rather follows from the power law distributions in x assumed for the input quark distributions used by the GRV distribution for the QCD evolution.The choice of 1/x as the proper scaling variable is therefore not established from the underlying theory.Instead,if log1/x is chosen as the scaling variable[20]then asymptotic Froissart saturation like[21]behavior can be achieved in such self-similar model.[15]Same is true for the magni fication factor M1=as occurred in de fi ning TMD(Eq.(1)).In the present case,a proper choice of M1seems necessary to allow an expression of proper singularity free version of the models. The magni fication factor M1can be considered as special case of a more general form: Only in a speci fic case,where α1=1 and all other coefficients cases vanish lead to the original M1as de fi ned in Eq.(1). The de fi ning TMD therefore can be generalized to instead of Eq.(1),such that the generalized TMD will take the form If,on the other hand,αi(i=0,1,2,...,n)vanish or negligibly small thenbecome where Taking only the two terms of Eq.(20),can be written as and the corresponding TMD(Eq.(19))becomes Assuming the convergence of the polynomials as occurred in Eq.(23),we obtain:(Model 3) After integration overit yields the desired PDF Using Eq.(25)in Eq.(5),the usual Definition of structure function,it gives with the condition that as the equality will yield an undesired singularity. The above model of structure function(Model 3)has new 7 independent parameters B1,B2,to be fi tted from data and compared with the previous models(Models 1 and 2).If the model parametersandsatisfy the additional condition then the resultant TMD becomes:(Model 4) while the integration overleads to the PDF And the corresponding structure function is which is completely free from singularity except for≥1.Such singularity is,however,consistent with the usual Regge expectation.[22?26]The model has now got 4 parameters: Furthermore,if the magni fication factor 1/x is also generalized to(1/x?1)for large x as suggested in Ref.[13]then one has got TMDPDF,PDF and structure function as: which leads to Generalizing the magni fication factor?M1as in Eq.(22)and taking only the two terms and assuming the convergence of the polynomials occurring in the expression as in Eq.(23),we obtain the generalized TMD as:(Model 5) And hence corresponding PDF(ˉqi)and structure function(ˉF2)will be Imposing the condition will lead to corresponding TMD,PDF and structure function as:(Model 6) Corresponding PDF and corresponding structure function which is our improved form and also has slower logarithmic raise in Q2with the large x behavior consistent with QCD.[23?27]Equations(31)and(40)are the main results,which are singularity free and have the logarithmic rise in virtually Q2. In this section,we make a comparison of structure function of Models 4 and 6 since only these two have logarithmic Q2rise in PDF and structure function.Model 6 is the large x extrapolation of Model 4. To determine the parameters of Model 4 and Model 6,we have used the compiled HERA data[16]as used in earlier work(Model 2).We make χ2-analysis of the data and obtain the phenomenological range of validity of Q2and x. For Model 4,the fi tted parameters are given in Table 5.The range of validity is found within:1.2 GeV2≤Q2≤ 800 GeV2and 2×10?5≤ x≤ 0.4.The number of data points of?F2is 284.Similarly for Model 6,the range of validity is:1.2 GeV2≤Q2≤1200 GeV2and 2×10?5≤ x≤ 0.4,which is quite larger in comparative to earlier works(Models 1 and 2).The fi tted parameters for Model 6 are given in Table 6.The number of data points ofis 302. In Figs.2 and 3,we plotandof Models 4 and 6 respectively as a function of x for few representative values of Q2 We note that some experimental values cannot be well described by Model 4 in Fig.2.Figure 2 shows the model 4 is suitable for small x but not the large x.The main reason is:the model 4 is by construction for small x whereas the model 6 is extrapolated to large x.From Fig.2,this feature can be seen prominently:as the experimental values of Q2increase the corresponding experimental ranges of x also increase.At Q2=150 GeV2,x range is 6 10?1whereas at Q2=800 GeV2,the corresponding range goes up to x 6 0.4,which is well above the small x-range.Thus at higher Q2,the agreement is less than that of lower Q2.However,in Fig.3,where the model 6 is applied,the experimental agreement at high Q2is better. The above analysis indicates that a singularity free version of a self-similarity based model in Proton is possible if proper choice of magni fication factor is made.It has allowed such a wider phenomenological range of validity in Q2than that of the model of Ref.[4].It has also logarithmic rise in virtually Q2instead of power law. Fig.2 Comparison of the structure function(Model 4)Eq.(31)as a function of x in bins of Q2with measured data of F2from HERAPDF1.0.[16] Fig.3 Comparison of structure function(Model 6)Eq.(40)as a function of x in bins of Q2with measured data of F2from HERAPDF1.0.[16] Table 5 Results of the fi t of Model 4;Eq.(31). Table 6 Results of the fi t of Model 6;Eq.(40). In the present paper,we have made a reanalysis of a structure function(x,Q2)based on self-similarity using the more recently compiled HERA data.[16]The present study is based on the notion that a physically viable model of Proton should be fi nite in the x-range;0 Our first analysis,however,indicates that the range of validity of such singularity free version of the model is much narrower in Q2:0.85 GeV2≤Q2≤10 GeV2to be compared with that of Ref.[4]. We have then explored the possible way of improving the model phenomenologically.As noted in Ref.[15],this approach of Ref.[4]has taken the notion of self-similarity to parametrize Parton Distribution Function(PDF)and eventually the structure function.However,the variables in which the supposed fractal scaling of the quark distribution and F2(x,Q2)occurs are not known from the underlying theory.In Ref.[4],the choice of 1/x is presumably because of the power law form of the quark distributions at small x found in Gl¨uck–Reya–Vogt(GRV)[19]distribution.However,this form is not derived theoretically but rather followed from the power law distribution in x assumed for the input quark distribution used by the GRV distribution for the QCD evolution.A more plausible variable appears instead to be ln(1/x)as has been used by Block etal,.[20]which is consistent with Froissart bound.[21]It also results in similar Froissart bound in the self-similar model.[15] In this spirit,we have modi fi ed magni fication factor M1properly so as to yield a singularity free version of the model,which has also logarithmic rise of Q2instead of power law as in Ref.[4].The phenomenological range of validity is also much larger:1.2 GeV2≤Q2≤800 GeV2than the previous singularity free version:0.85 GeV2≤Q2≤10 GeV2.A parameter free extrapolation to large x increases the phenomenological range further 1.2 GeV2≤Q2≤1200 GeV2. We now report the possible prediction of the model. (i)Using this model,one can obtain the corresponding form of gluon distribution which then can be used to calculate the Longitudinal Structure Function FL(x,Q2),using the Altarelli and Martinelli equation[28]as an improvement of our earlier result of model 1.[14] (ii)It can also predict the corresponding partial momentum fraction carried by quarks and gluons in Proton and test how far such pattern di ff ers from the QCD based models.[20] Let us end this section with a comment regarding the theoretical limitation of the present work: As noted in the introduction,self-similarity is not a general property of QCD and is not established properly,either theoretically or experimentally.In this work,we have merely made a use of fractal techniques to parametrize a multivariable function like structure function as a method of generalization as in Ref.[4].We have shown,under speci fic condition among the de fi ning parameters,a slower logarithmic rise in Q2of structure function is achievable,which is closer to QCD expectation than the earlier power law growth of Ref.[4]and has a wider phenomenological range of x and Q2.It implies,in a limited kinematical range,the notion of self-similarity makes some sense.However,unlike perturbative QCD where the corresponding Lagrangian is well de fi ned,Feynman rules are derivable and the asymptotic freedom can be established by using the Renormalization Group Equation leading to such logQ2terms,it is beyond the scope of the present work and hence can not be considered as a first principle result. Acknowledgments Final part of this work was completed when one of us(DKC)visited the Rudolf Peirels Center of Theoretical Physics,University of Oxford.He thanks Professor Subir Sarkar for hospitality and useful discussion.We also thank Dr.Kushal Kalita for useful comments.One of the authors(BS)acknowledges the UGC-RFSMS for fi nancial support. References [1]M.Gell Mann and F.Low,Phys.Rev.D 95(1954)1300. [2]D.V.Shirkov,Sov.Phys.Dokl.27(1982)197;K.Kr¨oger,Phys.Reports 323(2000)81. [3]Xu Cai and Long Guo,Chin.Phys.Lett.26(2009)088901;Jian-Chao Cai,etal.,Chin.Phys.Lett.27(2010)024705;Yu Zhou,Zu-Guo Yu,and Yee Leung,Chin.Phys.B 20(2011)090507;Ching-Hung Yuen and Wong Kwok-Wo,Chin.Phys.B 21(2012)010502;Chao Wang,Wan-Ting Xiong,and You-Gui Wang,Chin.Phys.Lett.29(2012)128903;Hui-Lin Shang,Acta Physica Sinica 61(2012)180506;Chuan-Feng Li and Feng Bi,Chin.Phys.Lett.30(2013)010306;Jian-Chao Cai,Chin.Phys.B 23(2014)044701. [4]T.Lastovicka,Euro.Phys.J.C 24(2002)529,hepph/0203260. [5]D.K.Choudhury and Rupjyoti Gogoi,hep-ph/0310260;hep-ph/0503047. [6]D.K.Choudhury and Rupjyoti Gogoi,Ind.J.Phys.80(2006)823. [7]D.K.Choudhury and Rupjyoti Gogoi,Ind.J.Phys.81(2007)607. [8]A.Jahan and D.K.Choudhury,hep-ph/1106.1145. [9]A.Jahan and D.K.Choudhury,Proceedings of the 3rd International Workshop on Multiple Partonic Interactions at the LHC,(2012)145;DOI:10.3204/DESY HUMBERG-PROC-2012-03/94. [10]A.Jahan and D.K.Choudhury,Ind.J.Phys.85(2011)587,hep-ph/1101.0069. [11]A.Jahan and D.K.Choudhury,Mod.Phys.Lett.A 27(2012)1250193,hep-ph/1304.6882. [12]A.Jahan and D.K.Choudhury,Mod.Phys.Lett.A 28(2013)1350056,hep-ph/1306.1891. [13]D.K.Choudhury and A.Jahan,Int.J.Mod.Phys.A 28(2013)1350079,hep-ph/1305.6180. [14]A.Jahan and D.K.Choudhury,Commun.Theor.Phys.61(2014)644,hep-ph/1404.0808. [15]A.Jahan and D.K.Choudhury,Phys.Rev.D 89(2014)014014,hep-ph/1401.4327. [16]H1 and ZEUS Collaborations,F.D.Aaron,etal.,J.High Energy Phys.1001(2010)109,hep-ex/0911.0884. [17]H1:C.Adlo ff,etal.,Euro.Phys.J.C 21(2001)33,hepex/0012053. [18]ZEUS:J.Breitweg,etal.,Phys.Lett.B 487(2000)53,hep-ex/0005018. [19]M.Gl¨uck,E.Reya,and A.Vogt,Euro.Phys.J.C 5(1998)461;hep-ph/9806404 [20]M.M.Block,L.Durand,P.Ha,and D.W.McKay,Phys.Rev.D 84(2011)094010,hep-ph/1108.1232. [21]M.Froissart,Phys.Rev.123(1961)1053. [22]T.Regge,Nuovo Cim.14(1959)951. [23]Richard D.Ball,Emanuele R.Nocera,and Juan Rojo,arXiv:hep-ph/1604.00024. [24]R.G.Roberts,The Structure of the Proton:Deep Inelastic Scattering,Cambridge University Press,Cambridge(1994). [25]R.Devenish and A.Cooper-Sarkar,Deep Inelastic Scattering,Oxford University Press,Oxford(2004). [26]F.J.Yndurain,Theory of Quark and Gluon Interactions,Springer Verlag,Berlin(1992)p.129. [27]S.J.Brodsky and G.R.Farrar,Phys.Rev.Lett.31(1973)1153. [28]G.Altarelli and G.Martinelli,Phys.Lett.B 76(1978)89.2 Formalism
2.1 Proton Structure Function Based on Self-Similarity
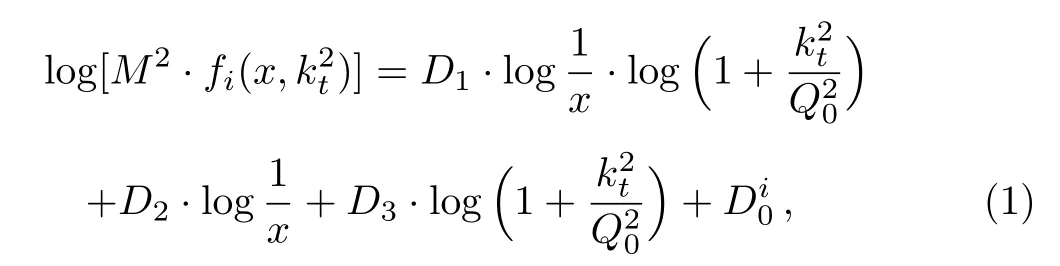
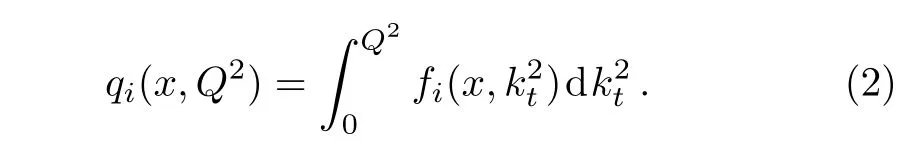
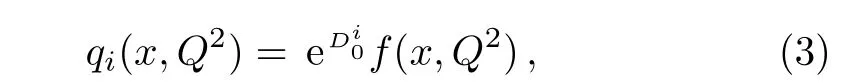
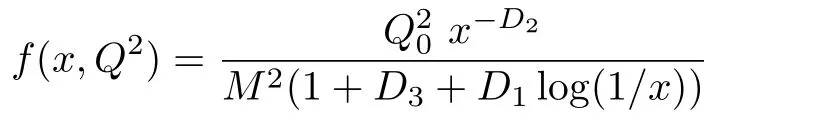
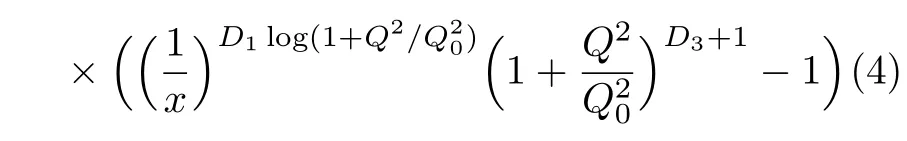
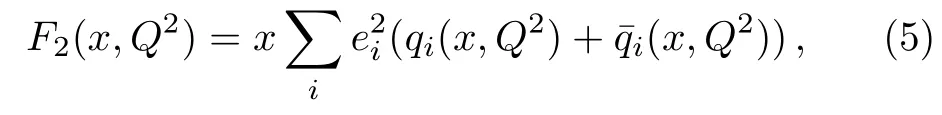
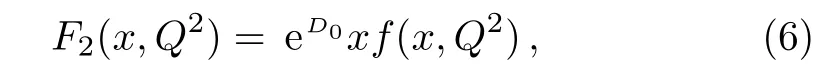

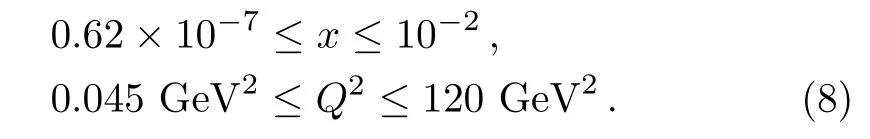
2.2 Singularity Free Structure Function(Model 2)
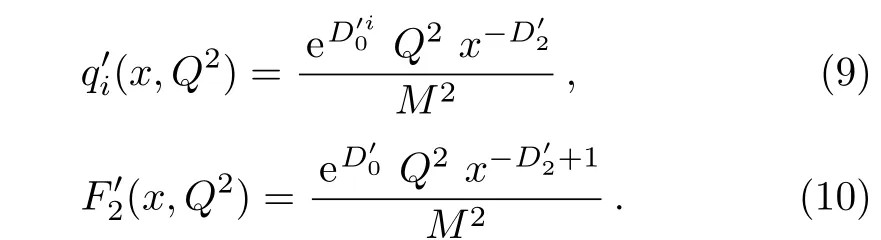
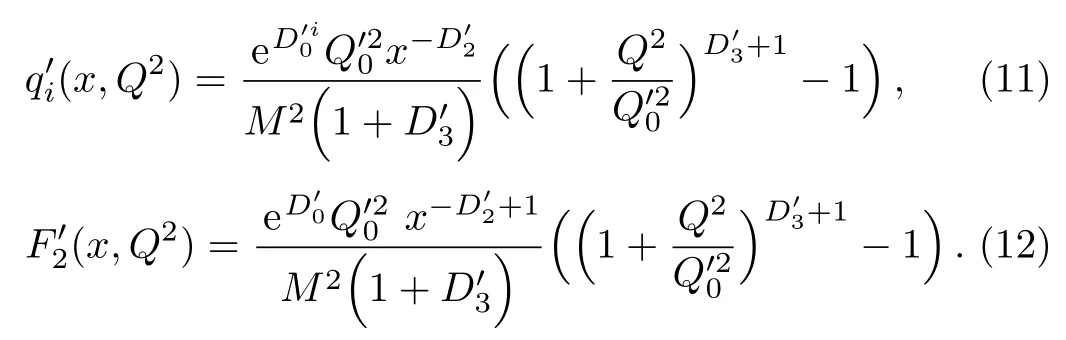
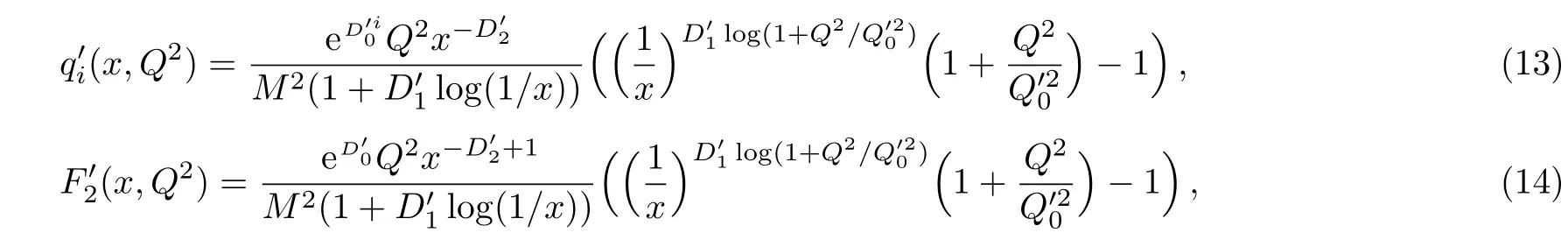
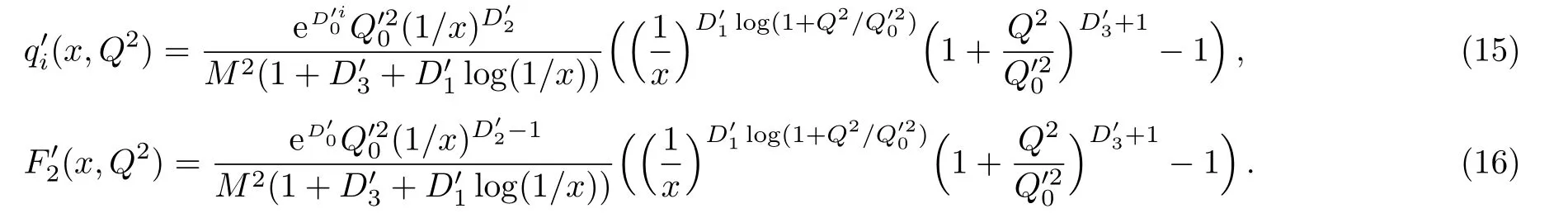
3 Results
3.1 Analysis of Singularity Free Model(Model 2)




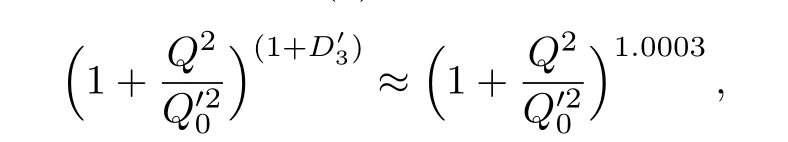
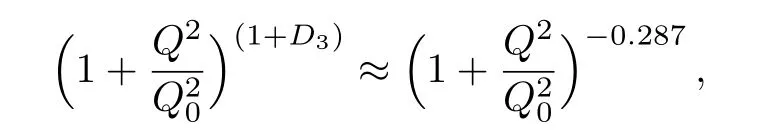
4 An Improved Singularity Free Model
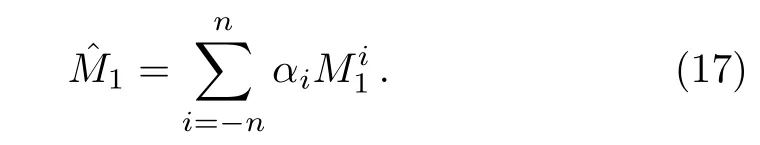

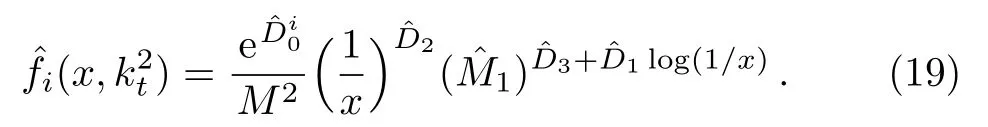
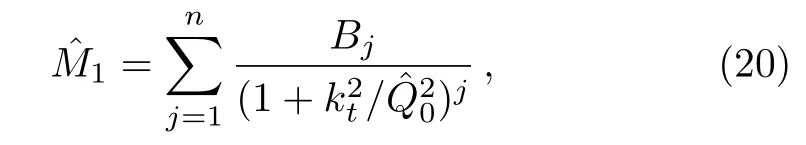

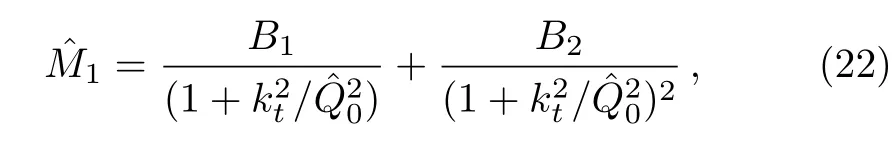

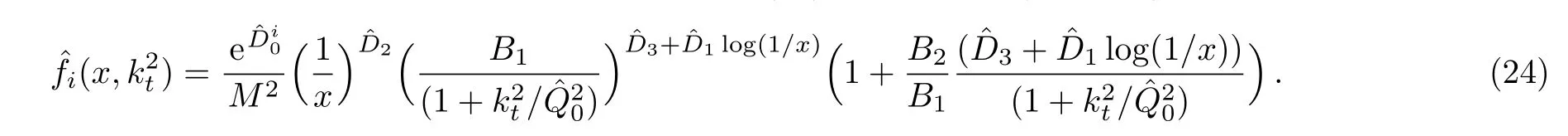
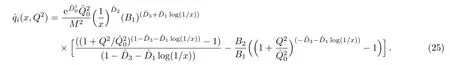
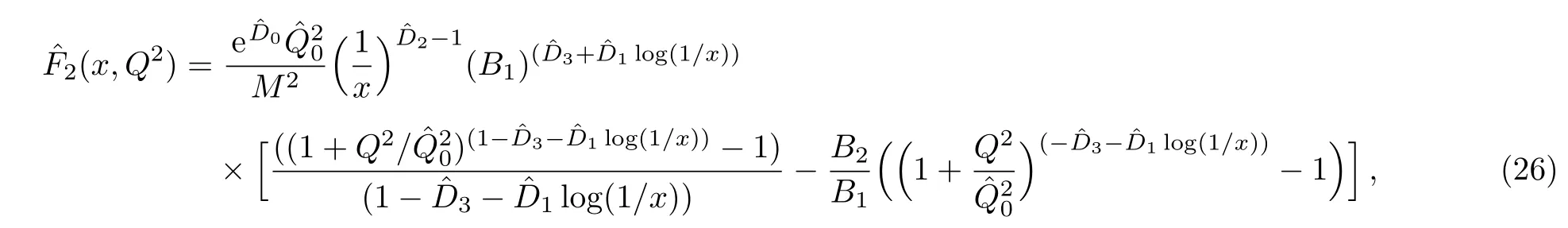


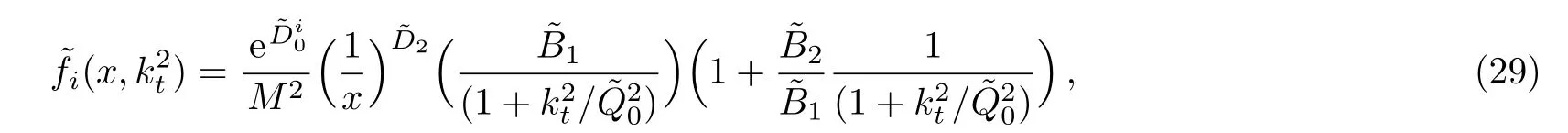
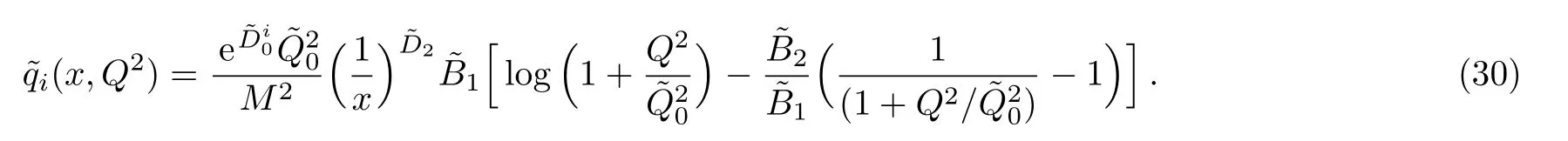
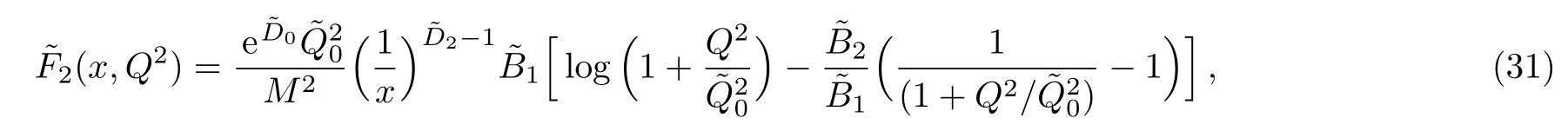
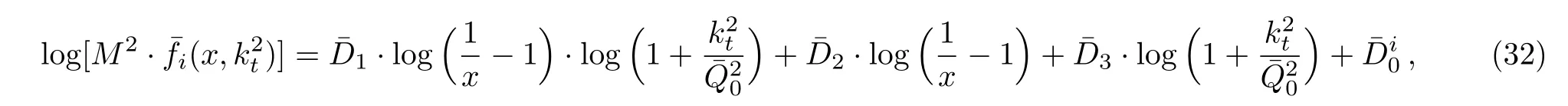
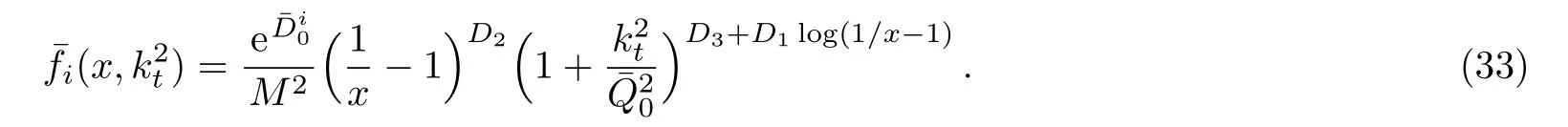
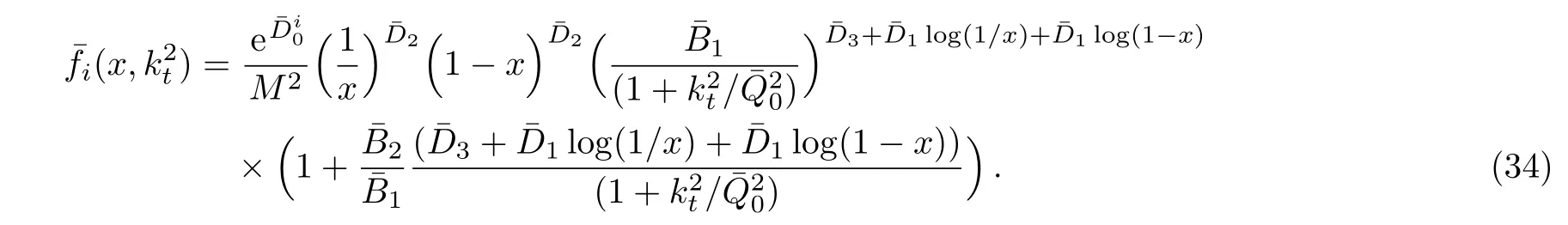
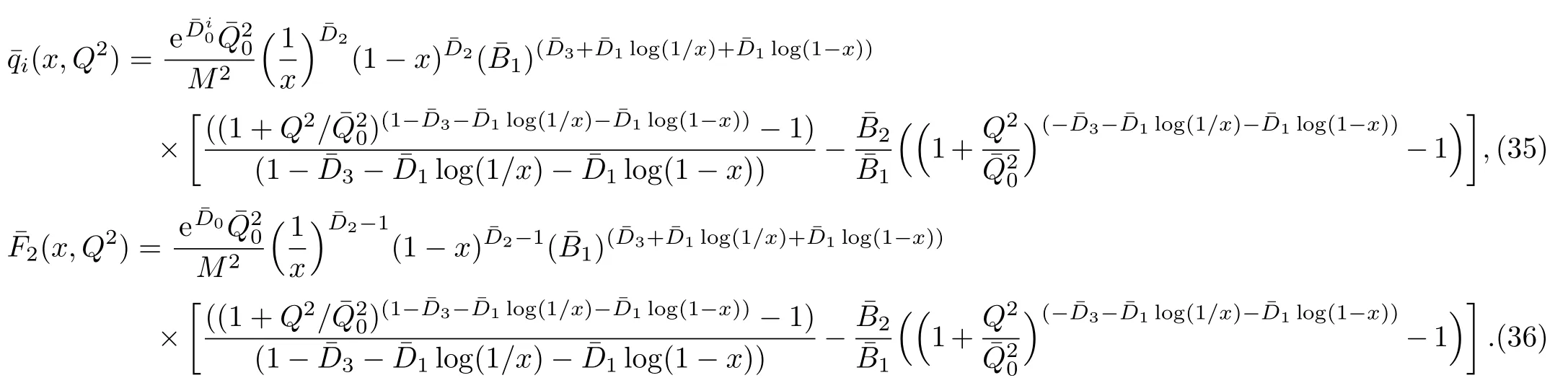
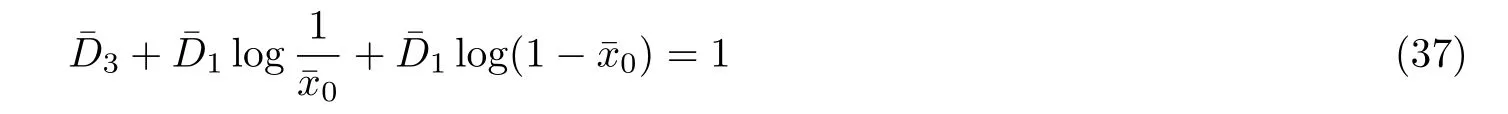
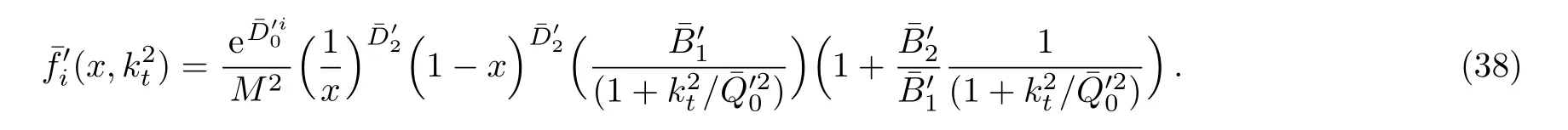
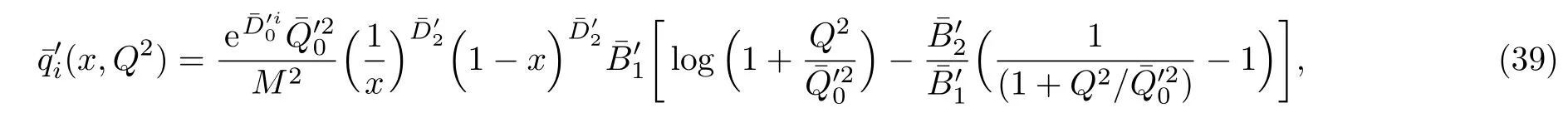
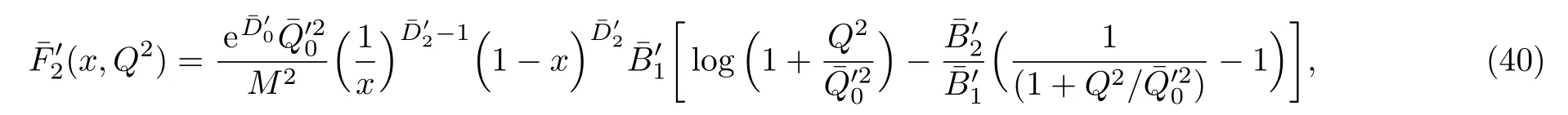
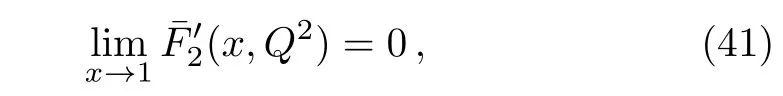
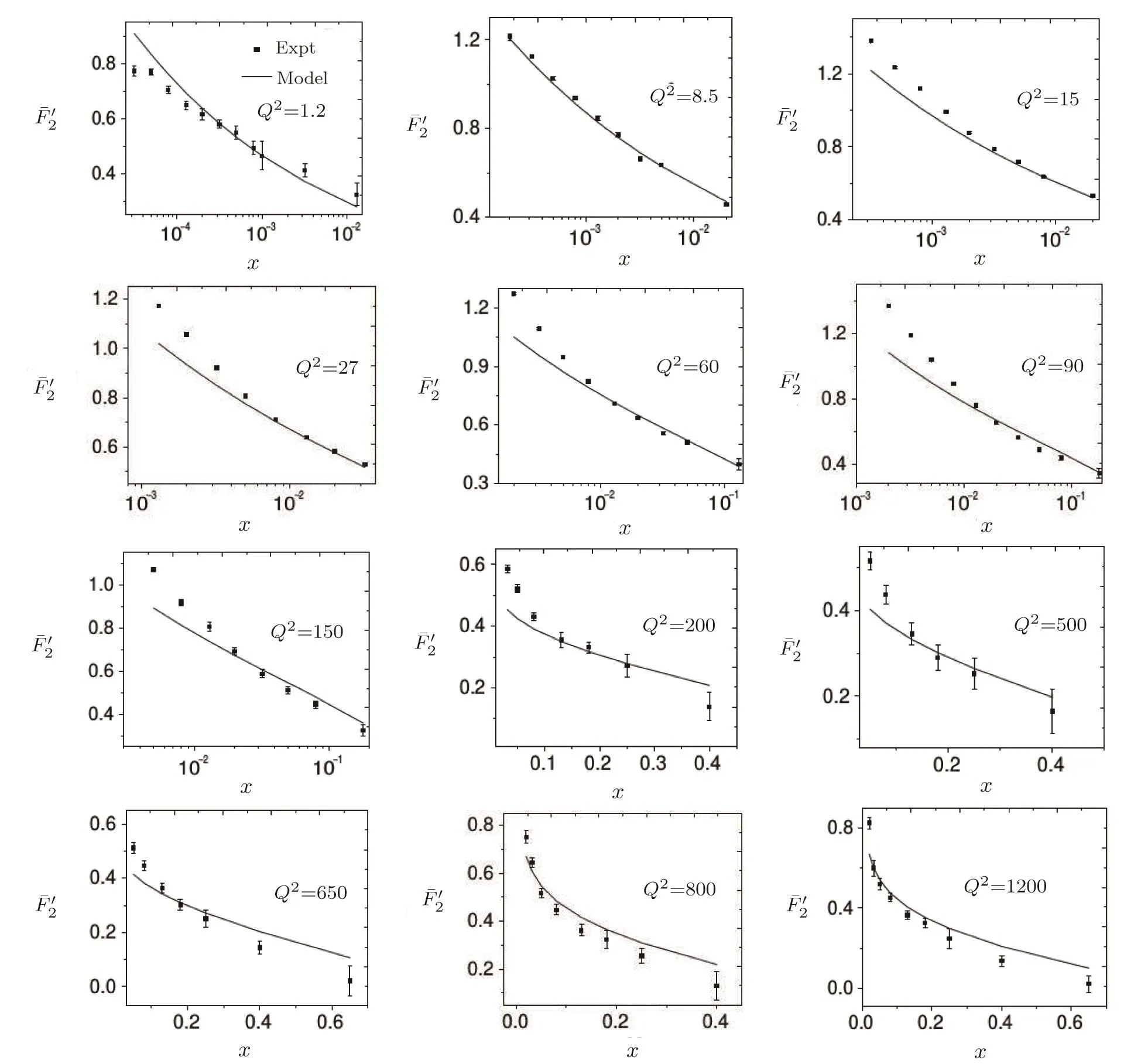
5 Comparison of the Structure Function of Models 4 and 6 with Data and Determination of the Model Parameters
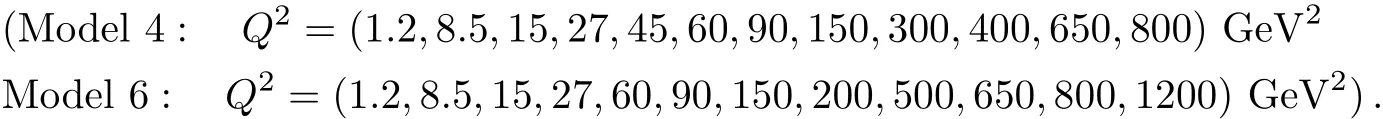
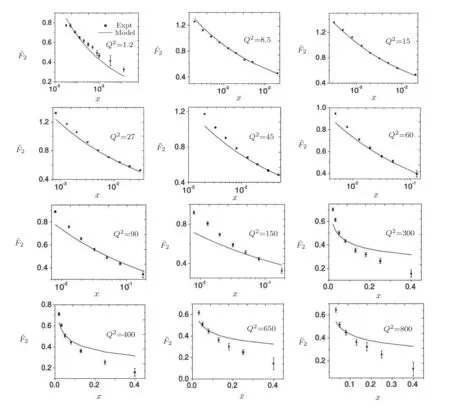


6 Summary
 Communications in Theoretical Physics2017年1期
Communications in Theoretical Physics2017年1期
