Feedback control for stochastic finite-time/fixed-time synchronization of stochastic coupled nonlinear systems

Hongxiao Hu·Wenjing Yang·Zhengtao Ding

Abstract A novel feedback control is proposed to investigate the stochastic finite-time/fixed-time synchronization between two stochastic coupled nonlinear systems(SCNSs).Based on graph theory and Lyapunov function methods,some effective stochastic finite-time/fixed-time synchronization criteria for SCNSs are established.Finally,the examples are included to demonstrate our analytical results.

Keywords Stochastic finite-time synchronization·Stochastic fixed-time synchronization·Stochastic settling time

1 Introduction

Over the past decades, coupled nonlinear systems (CNSs)have attracted significant attention due to their extensive applications in variety of real systems, such as communication networks, social networks, microgrids, biological systems and so on [1–4].As one of the most important dynamical behaviors of CNSs,synchronization indicates two or more equivalent or nonequivalent systems by adjusting each other can reach to a common dynamical behavior.It has a broad application in practice such as electronic systems[5, 6], secure communication [7], neural networks [8].At the same time,many different types of synchronization have been put forward to CNSs such as Quasi-synchronization[9],lag synchronization[10,11],anti-synchronization[12],exponential synchronization[13,14].As we know,all kinds of these synchronization are investigated over an infinity time interval.Nevertheless, in a large number of practical engineering fields, the CNSs might always be desired to reach synchronization as fast as possible in a finite time interval.Generally,synchronization over a finite time interval is more physically realizable compared with the concerning infinite time[15,16].There are two concepts of synchronization over finite time interval, i.e.finite-time synchronization [17–20]and fixed-time synchronization[21–23].

Moreover, due to the variability and uncertainty of the system environment, CNSs are affected by various types of environmental noises, which may destroy the dynamical behaviors of CNSs [24].Therefore, it is necessary to study synchronization of CNSs with stochastic perturbations.In fact, there are many researches related to the synchronization of SCNSs[25–27].In[25],some sufficient criteria were obtained to guarantee the synchronization of SCNSs in the sense of mean-square asymptotical synchronization by using the Lyapunov function methods.Applying Lyapunov method along with the Kirchhoff’s Matrix Tree Theorem, the exponential synchronization of SCNSs with time-varying coupling structure on networks were studied and two sufficient criteria were obtained by [26].Unfortunately, to the best of the authors knowledge, the stochastic finite-time/fixed-time synchronization for SCNSs has not been properly investigated so far.

Summarizing the above discussions,in this paper,we aim to deal with the stochastic finite-time/fixed-time synchronization problems for SCNSs by using feedback control.The remainder of this paper is organized as follows.Section2 introduces some preliminaries and the model descriptions.Then, stochastic finite-time/fixed-time synchronization of SNSCs are considered by Sect.3.Finally,Sect.4 gives some simulation examples.

2 Preliminaries and problem formulation

Denotem-dimensional Brownian motion byB(t) =vec[Bi(t)]m,t≥0.Let E[·] denote the expectation of the stochastic process.Letz(t):=z(t,z0)bendimensional It? process ont≥0 with the initial valuez(0)=z0∈Rn,which satisfies the following stochastic nonlinear system(SNS):

whereΥ∈C1(Rn;Rn),Φ∈C2(Rn;Rn×m),Υ(0) = 0,Φ(0)=0.For H ∈C2(Rn,R+),we denote[24]

where

Lemma 1 (See [28])LetH ∈C2(Rn,R+)be a radially unbounded positive definite function.If there is a positive scalar c such that

and

for all z∈Rn{0},where μ: R+→R+is a positive continuous differentiable function with the derivative μ′(s)≥0for any s>0and

then for any z0∈Rn we haveP(τz0<∞)=1and

where τz0is the stochastic settling time of z(t,z0),i.e.τz0=inf{t≥0:z(t,z0)=0},z(t,z0)is the solution of(1).

Lemma 2LetH ∈C2(Rn,R+)be a radially unbounded positive definite function.If there is a constant α> 0such that

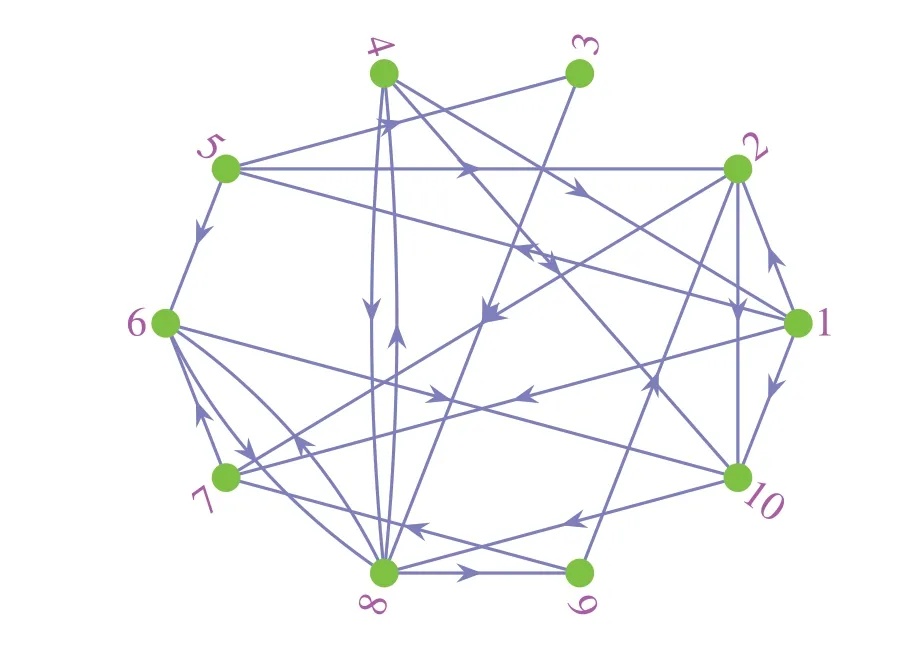
where0

ProofWe choosec=αandμ(u) =upin Lemma 1.By(5),(2)and(3)are satisfied.Sinceit follows from(4)that(6)holds.By Lemma 1,the proof is completed.■

Lemma 3LetH ∈C2(Rn,R+)be a radially unbounded positive definite function.If there are two constants α,β>0such that

where0 1,then the result in Lemma 1 is true and the inequality(4)is replaced by

ProofWe choosec= 1 andμ(u) =αup+βuqin Lemma 1.By(7),(2)and(3)are satisfied.Since

it follows from(4)that(8)holds.By Lemma 1,the proof is completed.■

Let L = {1,2,...,N}, we introduce a directed graphG=(L,E), whereEare the vertices set and the arcs set,respectively.We define(i,j) ∈Eif vertexitoj.LetB=[bi j]N×Nbe the weight matrix.(j,i) ∈Efori,j∈L if and only ifbi j> 0.A weighted digraph(G,B)is strongly connected if and only if the weight matrixBis irreducible.The Laplacian matrixLof(G,B)is defined as

Lemma 4 (see[29])Let ci be the cofactor of the ith diagonal element of L.If N≥2,then we have

where Ki j:Rmi×Rm j→Rare the arbitrary functions,Q is the set of all spanning unicyclic graphs of digraph(G,B),W(Q)is the weight of Q,and CQ stands for the directed cycle of Q.Particularly,ci is a positive constant for all i∈L,when B is irreducible.

Lemma 5For any y∈Rn and0

In this paper,we consider the following drive system,which is defined on the digraph(G,B)withN(N≥2)vertices:

fori∈L, whereYi(t) ∈Rmi,fi: Rmi→Rmiis a continuously nonlinear function,k>0 is the coupling strength,B= [bi j]N×Nis the unknown weight configuration matrix of the system(9),Hi j:Rmi×Rm j→Rmiis the influence of thejth vertex on theith vertex.ui(t) ∈Rmiis the feedback controller,σi(Y1,Y2,...,YN)∈Rmi×nidescribes the unknown coupling of the complex networks.ωi(t) ∈Rnioscillates randomly around its unknown average value,i.e.

fori∈L, whereαiis a constant vector,?i(t) ∈Rni×nican be arbitrary known bounded matrix, andBi(t) is anidimensional Brownian motion.

The response system is considered as following:

fori∈L, whereZi(t) ∈Rmiis the response state of theith node.For convenient writing, letY(t) = vec[Yi(t)]N,Z(t)=vec[Zi(t)]Nandκ(t)=Y(t)-Z(t).

Let the synchronization errorsκi(t) =Yi(t)-Zi(t)fori∈L.Then we can obtain the error dynamical system as follows

Definition 1 Drive system(9)is said to be stochastic finitetime synchronized onto response system (10), if the error dynamical system(11)admits a solution for any initial dataκ0∈Rn, and any solutionκ(t,κ0), the stochastic settling timeτκ0=inf{t≥0:κ(t,κ0)=0},is finite almost surely,that is P(τκ0<∞)=1;Furthermore,

Definition 2 Drive system(9)is said to be stochastic fixedtime synchronized onto response system (10), if the drive network (9) is stochastic finite-time synchronized onto the response network(10)and there exists a constantTmax> 0 such that E[τκ0] ≤Tmax, for allκ0∈Rn, whereτκ0is the stochastic settling time of the solution of error dynamical system(11)with initial valueκ0.

In this paper,some assumptions are given as following:(A1) Fori∈L, there exitsδi> 0 such that functionfi:Rn→Rnsatisfies

(A2) For anyi,j∈L,there exitπi,ξi>0,such that

for any(ζi,ζ j),(?i,? j)∈Rmi×Rm j.

(A3) For anyi,j∈L, there areβi≥0,ai j≥0 andri j≥0 such that‖αi‖≤βi,

forYi,Zi∈Rmi,Y=vec[Yi]N,Z=vec[Zi]N.

For convenience,we denote

3 Main results

3.1 Stochastic finite-time synchronization for SCNSs

In order to achieve the stochastic finite-time synchronization,the controllers are designed as following

fori∈L, wherehi> 0 anddi> 0 are control gains,0<θ< 1 is a tunable constant,forz=vec[z j]mi∈Rmi.

We introduce the following assumption for the functionψ.

(A4)For anyi∈L,there existsμi>0 such that for anyj=1,2,...,mi,

Theorem 1Supposing Assumptions(A1)–(A4)are satisfied.If B is irreducible and there are positive constants hi such that

Then,drive system(9)and response system(10)arrive stochastic finite-time synchronization under controller(13)with stochastic settling time τ satisfying

where

ProofConsider the Lyapunov function given by

One obtains

By Assumptions(A1)–(A3),we can show that

Since

It follows from Assumption(A4)and Lemma 5 that

Consequently,by(18)and(19),we get

It follows from the strongly connected property of the weighted digraph(G,B) that ?C> 0.Consequently, by the inequality(14),yields

By the definition of ?ci,we can obtain that ?ciis the cofactor of theith diagonal element of ?L:= diag[ξi]N·L.Then it follows from Lemma 4 that

By Lemma 2,the proof is completed.■For the special case, suppose thatπi=ξi=λ≥0 for alli∈L.Then Assumption (A2) can be replaced by the following assumption.

(A′2)there is a nonnegative constantλsuch that

for anyi,j∈L and(ζi,ζ j),(?i,? j)∈Rmi×Rm j.

Corollary 1Supposing Assumptions(A1)–(A4)are satisfied with Assumption(A2)replaced by Assumption(A′2).If B is irreducible and there exist constants hi>0such that

Then drive system(9)and response system(10)arrive stochastically finite-time synchronization under controller(13)with stochastic settling time τ satisfying

Remark 1IfHi j(ζi,ζ j)=Λ(ζ j-ζi)forζi,ζ j∈Rm,i,j∈L.Then Assumption(A′2)is satisfied withλ=‖Λ‖.

Theorem 2Suppose Assumptions(A1),(A3)and(A4)hold,H(ζi,ζ j) =ζ j-ζi for ζi,ζ j∈Rm,i,j∈L.If B is irreducible and there are positive constants hi such that

Then drive system(9)and response system(10)arrive stochastically finite-time synchronization under controller(13)with stochastic settling time τ satisfying

where

ProofLet,it has

Based on the Lemma 4,yields

Therefore,

By Lemma 2,the proof is completed.■

Theorem 3Suppose Assumptions(A1)–(A4)are satisfied.If there exist constants hi>0such that

Then drive system(9)and response system(10)are stochastically finite-time synchronization under controller with stochastic settling time τ satisfying

where

ProofLetIt has

It follows from the condition(22)that

By Lemma 2,the proof is completed.■

Remark 2The topological structure of the(G,B) is not requested in Theorem 3.Hence, the strongly connected digraph is not necessary in this theorem.

3.2 Stochastic fixed-time synchronization

In this section,to achieve the control goal of stochastic fixedtime synchronization,we design the controller as following

where 01 and the control gainshi,γi,di>0.

Theorem 4Suppose Assumptions(A1)–(A4)are satisfied.If B is irreducible and there are positive constants hi such that

Then,drive system(9)and response system(10)are stochastically fixed-time synchronization under controller(23)with stochastic settling time τ satisfying

ProofConstruct a Lyapunov function as (16) and take the same discussion as the Theorem 1,we can obtain

By Lemma 4 and(24),yields

By Lemma 3,the proof is completed.■

Corollary 2Supposing all of Assumptions(A1)–(A4)are satisfied with Assumption(A2)replaced by Assumption(A′2).If B is irreducible and there are positive constants hi such that

Then,drive system(9)and response system(10)are stochastically fixed-time synchronization under the controllers(23)with a stochastic settling time τ,which satisfies

Remark 3For the special case,we can chooseHi j(ζi,ζ j)=Λ(ζ j-ζi)forζi,ζ j∈Rm,i,j∈L.Then Assumption(A′2)is satisfied withλ=‖Λ‖.

Especially,choosingH(ζi,ζ j)=ζ j-ζiforζi,ζ j∈Rmand taking the same discussion with the Theorem 2,we have

Theorem 5Suppose Assumptions(A1),(A3)and(A4)hold,H(ζi,ζ j)=ζ j-ζi for ζi,ζ j∈Rm.If B is irreducible and there exist constants hi>0such that

Then,the drive-response systems(9)and(10)are stochastically fixed-time synchronized under the controllers(23)with stochastic settling time τ satisfying

Corollary 3Suppose Assumptions(A1)–(A4)hold.If there exist positive constants hi such that

Then,the drive-response systems(9)and(10)are stochastically fixed-time synchronized with stochastic settling time τ satisfying

Remark 4Exponential synchronization,whose convergence time is infinite, was studied for SCNSs by [25, 26].In this paper, the stochastic finite-time and fixed-time controllers are introduced to synchronize SCNSs,which means that the system can achieve better performance.

Remark 5If we takeψi(v)=vfori∈L andv∈Rm,then the controllers(13)and(23)can be degraded into

and

which have been studied in [30, 31], respectively.WhenHi j(ζi,ζ j) =Λ(ζ j-ζi)fori,j∈L andζi,ζ j∈Rm,the fixed-time synchronization for SCNSs(9)and (10)without considering the topological structure of(G,B) are studied by[30,31].Therefore,our results are more richer than their.

4 Numerical example

In this section, some numerical examples are presented to demonstrate validity of the proposed criteria.

The isolated node is a R?ssler-like system [32] or a 3Dneural network[33]described by:

(1)The R?ssler-like system is presented as

wherev=[v1,v2,v3]T∈R3is the state vector,

(2)the 3Dneural network is given as

wherev=[v1,v2,v3]T∈R3is the state vector,

In this section,we denoteN=10 and L={1,2,...,10}.The derive-response complex dynamical network is defined as

Fig.1 Digrph(G,B)with ten vertices

and

whereYi,Zi∈R3fori∈L.Fori∈L,choosing

withY10+1=Y1, the coupling strengthk= 1,?i(t) =diag[1,1,1],αi=[1,1,1]T,the control functionψi(v)=vfori= 1,2,...,10 andv∈R3and the weight matrixBis irreducible(see Fig.1)with

Therefore,

By the analysis in[32],we have

where ˉδ= 0.492.Letζi=vi-wiand?i= tanh(vi)-tanh(wi)fori=1,2,3,for the ?f,we have

where ?δ= 4.875.Consequently, we haveΔ= diag[ˉδI5,?δI5].By the analysis in[31],we obtain

and

where‖eN+1(t)‖:=‖e1(t)‖.Hence,fori=1,2,...,N-1,ai j=2 andri j=4 whenj=i,i+1,aN N=aN1=2,rN N=rN1=4,elseai j=ri j=0.Then we have

We can choose

then the conditions(20)and(25)hold.Therefore,by Corollaries 1 and 2, the drive systems (27) and (28) reach stochastically finite-time and fixed-time synchronization.

Fig.2 The trajectory of the total synchronization error ‖κ(t)‖ of the complex system without control with initial values of the nodes Yi(0)=0.1·i[10,10,10]T and Zi(0)=0.1·i[1,1,1]T for i ∈L

Fig.3 The trajectories of the total synchronization error‖κ(t)‖of the complex systems(27)and(28)with initial values of the nodes Yi(0)=0.1·i ·[10,10,10]T and Zi(0)=0.1·i ·[1,1,1]T for i ∈L

The trajectories of the total synchronization error‖κ(t)‖of complex systems (27) and (28) without the control inputs are showed in Fig.2.In the following,two examples present the numerical results of the stochastic finite-time and fixed-time synchronization for the derive-response complex dynamical networks(27)and(28),respectively.

Stochastic finite-time synchronization:Let the parametersd= 10 andθ= 0.3.By Corollary 1, the derive-response complex dynamical network can achieve stochastic finitetime synchronization with a stochastic settling timeτ,which satisfies E[τ]≤5.35 with initial values of the nodesxi(0)=0.1·i·[10,10,10]Tandyi(0)=0.1·i·[1,1,1]Tfori∈L(see Fig.3).

Fixed-time synchronization:Fori=1,2,...,N,letγi=40,di= 10,p= 0.3 andq= 1.25.Then, by Corollary 2, the systems (27) and (28) can achieve stochastic fixedtime synchronization with a stochastic settling timeτ,which satisfies E[τ]≤0.996 under controller(23)(see Fig.4).

Fig.4 200 trajectories of the total synchronization error‖κ(t)‖of the complex systems (27) and (28).The initial values of the nodes are chosen from[-10,10]randomly

Data availability Data sharing is not applicable to this article as no new data were created or analyzed in this study.

Declarations

Conflict of interest We declare that we do not have any commercial or associative interest that represents a contradict of interest in connection with the work submitted