Visualizing and witnessing first-order coherence,Bell nonlocality and purity by using a quantum steering ellipsoid in the non-inertial frame
Huan Yang(楊歡), Ling-Ling Xing(邢玲玲), Ming-Ming Du(杜明明),Min Kong(孔敏), Gang Zhang(張剛),?, and Liu Ye(葉柳)
1School of Electrical and Photoelectronic Engineering,West Anhui University,Lu’an 237012,China
2College of Electronic and Optical Engineering,Nanjing University of Posts and Telecommunications,Nanjing 210003,China
3School of Physics and Optoelectronic Engineering,Anhui University,Hefei 230039,China
Keywords: quantum steering ellipsoid,first-order coherence,Bell-nonlocality,purity
1.Introduction
As a basic concept in the physical world, coherence arises from quantum superposition and is essential for the quantum information sciences, including quantum interference and multipartite entanglement.[1,2]It also plays a vital part in the fields of quantum metrology,[3]low-temperature thermodynamics,[4-6]solid-state physics[7]and so on.Meanwhile,coherence can also be used to depict the interference capability of interacting fields in quantum optics research.[8-12]Beyond this, there have been various efforts to ascertain the interrelations between coherence and correlations,[13-20]and these relations are essential for predicting the coherent transfer in researched quantum systems.Various coherence measures have been established to quantify coherence.Examples include first-order coherence(FOC)[13](which is a basisindependent measure)and thel1norm of coherence(which is a basis-dependent measure).[21]It should be emphasized that there is a relationship between FOC and thel1norm of coherence.For a single-qubit state, the FOC of a state is equal to thel1norm of coherence quantified on the optimal basis.In principle, quantum correlations include various forms, such as quantum entanglement, Einstein-Podolsky-Rosen (EPR)steering and Bell nonlocality(BN).Among these, BN(quantum entanglement) is the strongest (weakest) quantum correlation.Coherence is one of the important bases for generating quantum correlations; even conceptually, coherence is more fundamental than quantum correlations, including BN.One can detect the BN of a system by violating some Bell-type inequalities,[22-32]especially the Clauser-Horne-Shimony-Holt (CHSH) inequality.[30-34]It deserves to be emphasized that not all entangled states can possess BN.[35]Horodeckiet al.have derived the sufficient and necessary conditions for BN for arbitrary bipartite states.[36]
In the field of quantum information science, the construction of three-dimensional pictures of different quantum states is an important avenue for investigating quantum correlations.[37]A Bloch vector provides a simple and intuitive representation of any single-qubit state.[37]However,for a two-qubit state, 15 parameters of the state need to be described,introducing amazing complexity and difficulty for the geometric description of a two-qubit state.Fortunately,Jevticet al.[38]proposed a scheme in which a quantum steering ellipsoid (QSE) is used to visualize any two-qubit state.To clarify, there is a remarkable phenomenon in which measuring the subsystem of an entangled state can remotely steer the state of the other subsystem.This phenomenon is called EPR steering.[39,40]If one performs all possible local operations on one qubit,all Bloch vectors of the other qubit’s steered states form a QSE in the Bloch sphere.[38]Any bipartite state can correspond to a QSE.In particular, not all QSEs can faithfully express a two-qubit state.The sufficient and necessary condition for a QSE to denote a bipartite state was derived by Milneet al.[41]It is worth mentioning that the QSE provides an intuitive depiction and indication for quantum correlations.Examples include steered coherence,[42-44]discord,[38,45-47]entanglement[38,41,48]and EPR steering.[49-54]Zhanget al.[55]experimentally verified the QSE of two-qubit states and also demonstrated volume monogamy relations of the QSE.[56]Recently,Duet al.[57]investigated quantum phase transitions in theXXZmodel through a QSE.However,these efforts are limited to inertial systems.[42-45,57]
The non-inertial frame provides nontrivial tools for understanding relativistic quantum information and black holes,and is a rapidly developing field.[58]Relevant explorations in the non-inertial frame have been widely carried out.[59-74]There has been a lot of effort made to investigate nonlocality under non-inertial frames.[75-78]Friiset al.[75]explored entanglement of accelerated fermions.Smithet al.[76]analyzed tripartite nonlocality of non-inertial observers.Subsequently,Tianet al.[77,78]investigated nonlocality, entanglement and measurement-induced nonlocality under the Unruh effect.Of particular note is that each actual system is inevitably coupled with the surrounding environment.This coupling can accelerate the degeneration of quantum nonlocalities and set obstacles for achieving various quantum information tasks.For this reason, explorations of quantum nonlocalities in non-inertial frames suffering from different noise channels have been extensively performed.[79-86]Nevertheless, use of a QSE to visualize nonlocality under non-inertial frames is still lacking,especially when considering the collective influences of noninertial frames and noise channels in the QSE formalism.Such an investigation may provide a more visual tool to ascertain the influences of relativistic motion and external noise on different quantum correlations.
Encouraged by this,we visualize the FOC,BN and purity in a non-inertial frame by utilizing a QSE, and also explore them when the particle suffers from a depolarizing channel or a non-coherence-generating channel(NCGC).Our results reveal that FOC, BN and purity can be visualized and detected by the parameters of the QSE.Particle acceleration induces shrinking and movement of the QSE.These peculiarities are responsible for the results that the BN and purity are reduced with increase in the acceleration.Note that FOC can be revived by higher acceleration due to the trait that the QSE can puncture the center of the Bloch sphere under a higher acceleration.The condition of FOC disappearance(or recovery)can be attained through the QSE.The depolarizing channel results in monotonic shrinking of the QSE,and it finally degenerates into a point at the center of the Bloch sphere.The results imply that the coherence,BN and purity monotonously decrease as noise strength increases.Under the influence of the NCGC,the periodic oscillation of the QSE visualizes the periodic oscillations of the BN and purity with growing noise parametersθandφ.The FOC is invariant with different values ofθsince the center of the QSE cannot move with the change ofθ.Moreover, the BN is more fragile after considering the additional effects of a depolarizing channel and NCGC because the depolarizing channel and the NCGC can reduce the size of the QSE.Under the additional influences of a depolarizing channel and NCGC,the conditions for FOC disappearance are invariant because the condition for the QSE to achieve the center of the Bloch sphere cannot be influenced by the depolarizing channel and the NCGC.
Section 2 of this paper briefly describes QSE theory.In Subsection 3.1,we characterize and capture the FOC,BN and purity of a system in the QSE formalism.The collective influences of the depolarizing channel and the NCGC on the FOC,BN and purity are explored in Subsections 3.2 and 3.3,respectively.Finally,conclusions are drawn.
2.The QSE
Alice and Bob collectively possess bipartite statesρ,
whereIis the identity operator,σ=(σ1,σ2,σ3) denotes the vector of the Pauli matrix.Mnm= Tr(ρσn ?σm) (m,n=1,2,3),a= Tr(ρσ ?I),b= Tr(ρ·I ?σ).According to Ref.[38], if we perform all possible local measurements on Bob,the QSE of Alice(i.e.,?A)can be constructed by all the vectors of Alice’s steered states.One can use center?Aand ellipsoid matrix ?Ato characterize ?A:
The orientations and lengths of the semiaxes of ?Aare reflected by the eigenvectors of ?Aand the arithmetic square root of eigenvalues of ?A, respectively.One can also obtain the QSE of Bob(?B),namely,
3.Visualizing and detecting the FOC, BN and purity via the QSE
3.1.Under the influence of a non-inertial frame
Of particular note is that the ellipsoid ?Bcannot puncture the Bloch sphere.The maximally obese statescorrespond to the state with the largest ellipsoid volume at the centerc=(0,0,Ξ).can be expressed by
Its matrix form is
The maximally obese state is very useful and can bind many quantum nonlocalities for two-qubit states,such as the entanglement and BN.[48]The largest volume ellipsoid of Bob for the centerc=(0,0,Ξ)can be represented as

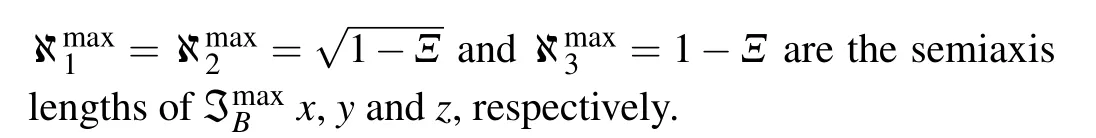
Now, let us consider that Alice and Bob (as two observers) collectively possessin Minkowski space-time.Alice remains stationary and Bob moves with uniform acceleration.As a consequence,the Unruh effect will appear.Meanwhile,we assume that Alice possesses a detector which is sensitive only to mode|n〉A(chǔ)(the mode of Minkowski space-time that corresponds to Alice)and Bob possesses another detector which is sensitive only to mode|n〉B(the mode of Minkowski space-time that corresponds to Bob).We then let Alice remain stationary while Bob moves with a uniform acceleration.Considering a fermionic field system, from the accelerated perspective of Bob the Minkowski vacuum state is found to be a two-mode squeezed state[87]
with acceleration parameterγ=(e-2πωc'/a+1)-1/2.Here,ais the acceleration of Bob,ωis the frequency of the Dirac particle andc'is the speed of light in a vacuum.0<γ <π/4 corresponding to 0<a <∞.{|0〉I}and{|0〉II}indicate Rindler modes in regions I and II,respectively.The only excited state is given by[87]
Using Eqs.(10) and (11), the state of Eq.(8) is transformed into
Due to the fact that Bob is causally disconnected from region II, the physically accessible information is encoded in mode A(described by Alice)and mode I(described by Bob).Tracing over the mode in region II,we obtain
We calculate the QSE of Bob in the form
The central coordinate of the QSE on thez-axis is
Thex,yandzsemiaxis lengths of the QSE are ?1,?2and ?3,respectively.Namely,

The FOC for the bipartite systemρABis
This result implies that the FOC of the whole bipartite system can be directly visualized by the distance from the center of the QSE ?Bto the center of the Bloch sphere.D2ABdisappears only if ?Breaches the center of the Bloch sphere,which provides an avenue to witness the FOC.We also visualize the maximal CHSH violation[30-33]ofρABthrough ?B,i.e.,
The BN ofρABisBN(ρAB)=max{0,β(ρAB)-2}.It is revealed that the BN ofρABcan be intuitively characterized and detected by ?1or ?2.Using ?B,one can visualize the purity ofρAB,namely,
which establishes the connection between purity and the QSE.It is straightforward that the purity can reach 0.25 only if the QSE degenerates into a point at the center of the Bloch sphere.Equation(20)can also be rewritten as
The results obtained above provide visual tools to investigate and detect the FOC,BN and purity under a non-inertial frame.For clarity, we herein use Fig.1 to depict the geometric parameters of the QSE,FOC,BN and purity with respect to the acceleration parameterγ.Under the Unruh effect, lengths of?1, ?2and ?3degenerate with increasingγ, as shown in Fig.1(a).According to the result of Eq.(19), one can reveal that the shrinkage of ?Bvisually reflects the reduction in BN in Fig.1(b).The BN cannot be detected if the semiaxis of ?BsatisfiesThe critical case corresponds to.In the critical case,the shape of ?BwithΞ=0.4 is plotted in Fig.2(green ellipsoid).
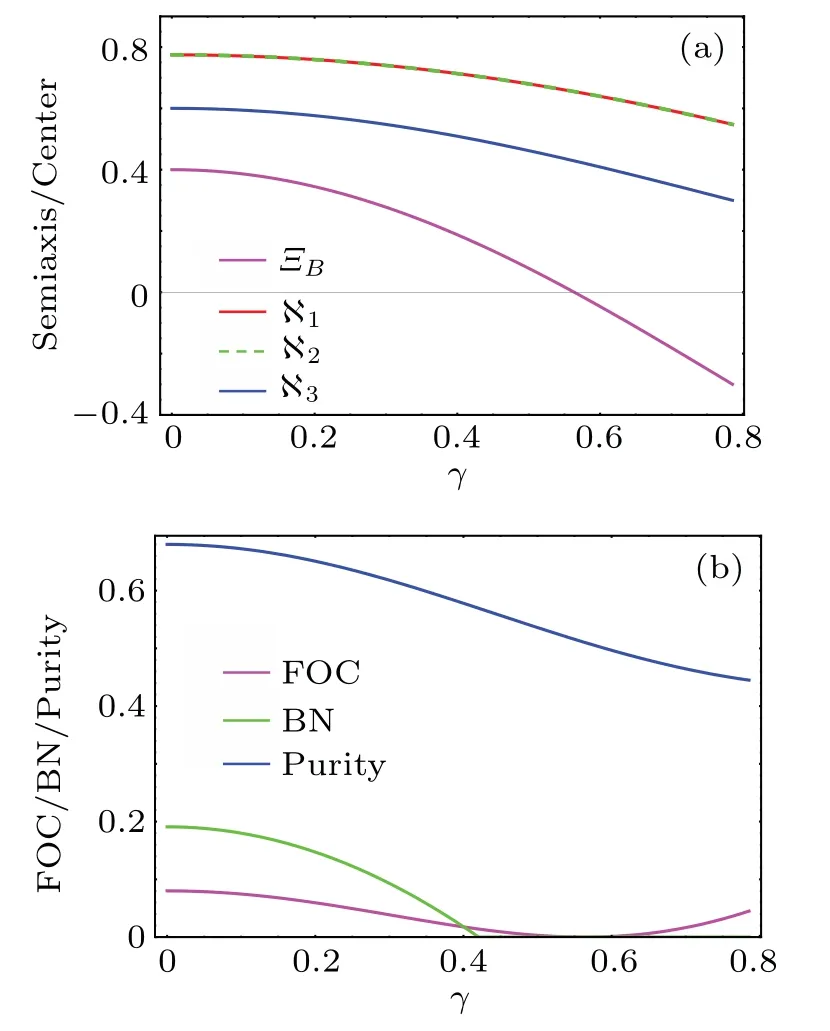
Fig.1.(a) The dependence of semiaxis length and ΞB on γ.(b) The dependence of the FOC,BN and purity on γ. Ξ =0.4.
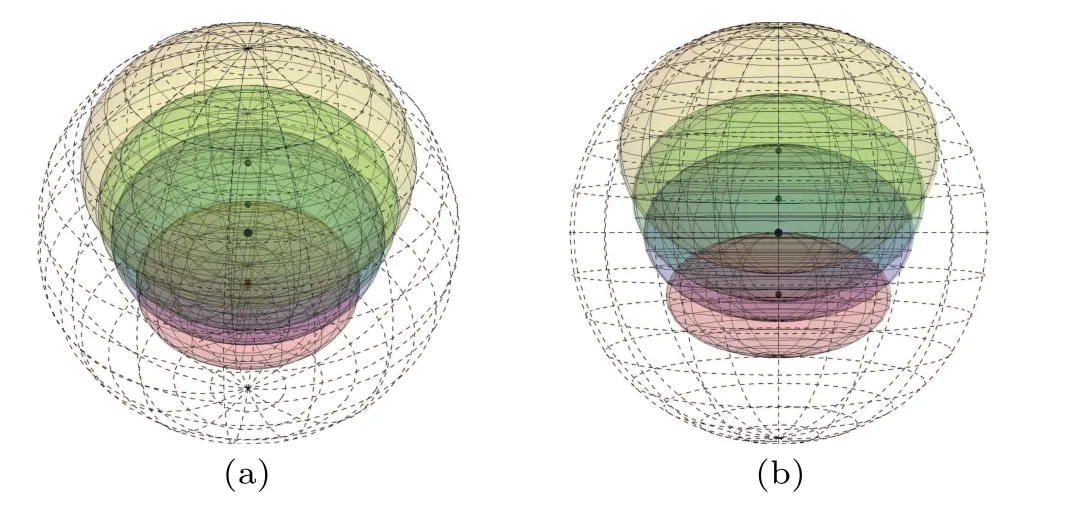
Fig.2.The shape of ?B: (a) stereoscopic view, (b) front perspective.The yellow ellipsoid represents the initial ?B with γ =0.The green QSE and blue QSE are ?B with γ =0.4205 (corresponding to the case when the BN suddenly disappears in Fig.1(b))and γ =0.5639(corresponding to the case when the FOC suddenly disappears in Fig.1(b)),respectively.The red ellipsoid represents the final ?B with γ =π/4. Ξ =0.4.
As seen in Figs.1(a)and 2,the Unruh effect induces the result that the ?Band its center move along the negative orientation of thez-axis asγincreases.Note that the FOC is only associated with the centerΞBof ?B.Therefore, the movement of the center of the QSE is responsible for the detection of the FOC.Namely,FOC first degenerates and suddenly disappears; subsequently, it revives under the strong Unruh effect.The revival of the FOC in Fig.1(b) due to the center of the ?B,ΞB, can puncture the center of the Bloch sphere in Fig.1(a).The phenomenon is different from the peculiarity of the BN.Using the QSE parameters in Eq.(14), one can see and easily obtain that FOC will suddenly disappear ifγ=arccos[(1-Ξ)/(1+Ξ)]/2 and will revive in the interval of arccos[(1-Ξ)/(1+Ξ)]/2<γ ≤π/4.The blue ellipsoid in Fig.2 is the shape of ?Bcorresponding to the case of FOC disappearance.We also provide the final ?B(corresponding toγ=π/4,as red ellipsoid plotted)under the non-inertial frames in Fig.2.These results indicate that the QSE cannot degenerate into a point under the non-inertial frame as the acceleration parameterγincreases, meaning that the purity ofρABdecays with decreasing ?Band cannot reach 0.25 in Fig.1(b).
3.2.The collective effects of the non-inertial frames and depolarizing channel
Exotic environments unavoidably influence the quantum systems in a realistic scenario.Herein,we consider Bob in the state of Eq.(13)coupled to a depolarizing channel,which can be described by the Kraus operators
andp=1-e-γ0t.Hence,the non-zero matrix elements of the output state ?ρAB-Dread as
The QSE of Bob has the form
For each subsystem,FOC is visualized by
The FOC for bipartite systems is
Similarly, the maximal CHSH violation and the purity of ?ρAB-Dare visualized by ??B-D,i.e.,
The BN is BN(?ρAB-D)=max{0,β(?ρAB-D)-2}.Hence,the FOC, BN and purity under a depolarizing channel can be visualized and captured by ??B-D.Equation (30) can also be rewritten as
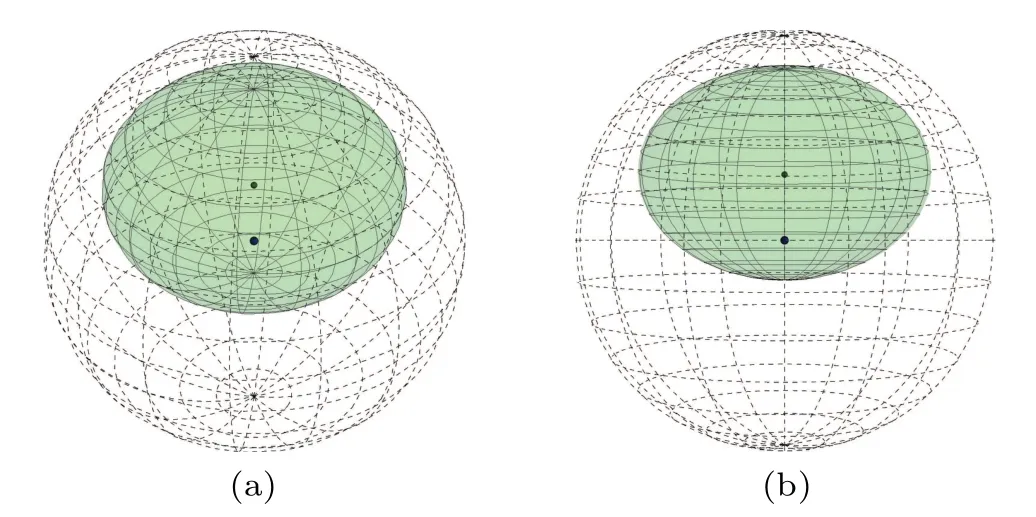
Fig.4.The ??B-D corresponding to the case when the BN suddenly disappears under the depolarizing channel: (a)stereoscopic view,(b)front perspective. Ξ =0.4,γ =0.2.
To visualize and capture the FOC,BN and purity under a depolarizing channel we plot the dependence of the QSE parameters,FOC,BN and purity on the depolarizing channel parameterpin Fig.3.Figure 3(a)shows that the semiaxis lengths linearly degrade with increasingp.This characteristic leads to a linear decrease of the BN in Fig.3(b).The semiaxis length?1-Drapidly shrinks to■which causes a sudden disappearance of the BN in this case,and one can use the traits of the QSE to determine that detection of the BN cannot be realized.Figure 4 visually displays the shape of ??B-Dfor the disappearance of the BN(Ξ=0.4 andγ= 0.2).The center of ??B-Dmoves along the negative orientation of thez-axis aspstrengthens, as displayed in Fig.3(a).It deserves to be emphasized that the center of ??B-Dcannot puncture the center of the Bloch sphere, and ??B-Dfinally degenerates into a point at the center of the Bloch sphere.These traits are different from those in Fig.1(a).According to the characteristics of the QSE,one can conjecture that the purity of ?ρAB-Ddegrades with decreasing ??B-D,finally reaching 0.25 in Fig.3(b).Meanwhile,the system’s FOC monotonously decreases with increasingpand reduces to zero atp=1 in Fig.3(b).One can always witness existence of FOC via the QSE(except atp=1).
Next let us turn to visualize the influences of the Unruh effect on the FOC,BN and purity when considering a depolarizing channel.We give the QSE parameters,FOC,BN and purity with respect toγin Fig.5.In comparison with the results in Fig.1(without considering the influence of a depolarizing channel),it can be found that the depolarizing channel cannot affect the trends of the QSE,FOC,BN and purity in Fig.5.Of particular note is that the BN more easily disappears(the critical case corresponds toγ=arcsec[2-2Ξ(1-p)])if we additionally consider the effect of the depolarizing channel.The reason for this can be visually explained using the QSE.That is, the size of the QSE is smaller when considering the effect of a depolarizing channel (as revealed in Eqs.(16) and (26))and the semiaxis of ??B-Dmore easily reaches 2/2 under the Unruh effect.In particular,note that the depolarizing channel cannot affect the condition of the disappearance of FOC (the critical case corresponding toγ=arccos[(1-Ξ)/(1+Ξ)]/2)ifp/=1.This phenomenon can be visually interpreted by the fact that the condition for the center of the QSE reaching the center of the Bloch sphere is not affected by the depolarizing channel.
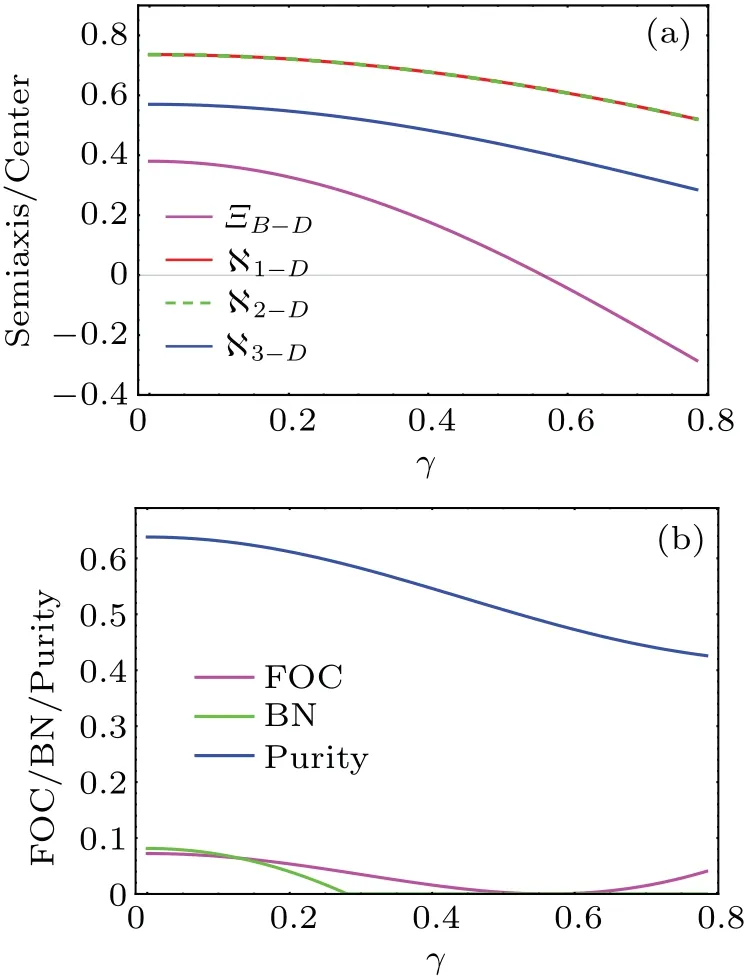
Fig.5.(a)The dependence of semiaxis lengths and ΞB-D on γ.(b)The dependence of the FOC,BN and purity on γ. Ξ =0.4, p=0.05.
3.3.The collective influences of the non-inertial frames and the NCGC
The NCGC is defined as a completely positive tracepreserving map which does not generate quantum coherence from an incoherent state.[88]Incoherent operation is a strict subset of the NCGC.[88]The Kraus operators of a rank-2 NCGC are[88]
Here,θ,φ,ηandξare all real numbers.For simplicity,ηandξare supposed to be zero in this paper.The channel with the form of Eq.(32) is not an incoherent channel unless sinφcosφsinθcosθ=0.[88]Assuming Bob’s state ofρABcoupled to the NCGC,the final two-qubit state is ?ρAB-N,namely,
The QSE of Bob is given by
For each subsystem,the FOC is
Based on this result,one can attain the FOC of ?ρAB-Nby using the geometrical parameters of ??B-N,namely,
In the QSE formalism,the maximal CHSH violation of ?ρAB-Nis
where ?maxand ?secare the longest and the second longest semiaxes of ??B-N, respectly.The BN is BN(?ρAB-N) =max{0,β(?ρAB-N)-2}.The purity of ?ρAB-Nis
that is,
To begin with,we visualize and capture the FOC,BN and purity with different channel parametersθin Fig.6.From this figure we can see that the semiaxis lengths ?1-Nand ?3-Nperiodically oscillate under the NCGC.The period of oscillation is equal toπ.However, the length of theysemiaxis?2-Nis invariant withθ.Thereby, ??B-Nperiodically and alternately changes between a three-dimensional ellipsoid and a one-dimensional ellipse.We see that the BN first disappears,then revives and reaches a maximum atθ=nπ(n=0,1,2,...)(corresponding to the maximal lengths of thexandzsemiaxes).It is straightforward to show that the centerΞB-Nof ??B-Nis invariant in this case,and one can always witness the existence and invariance of FOC via the QSE,as described in Fig.6(b).The periodical oscillations of ?1-Nand ?3-Nvisualize a periodic oscillation in the purity of ?ρAB-N.
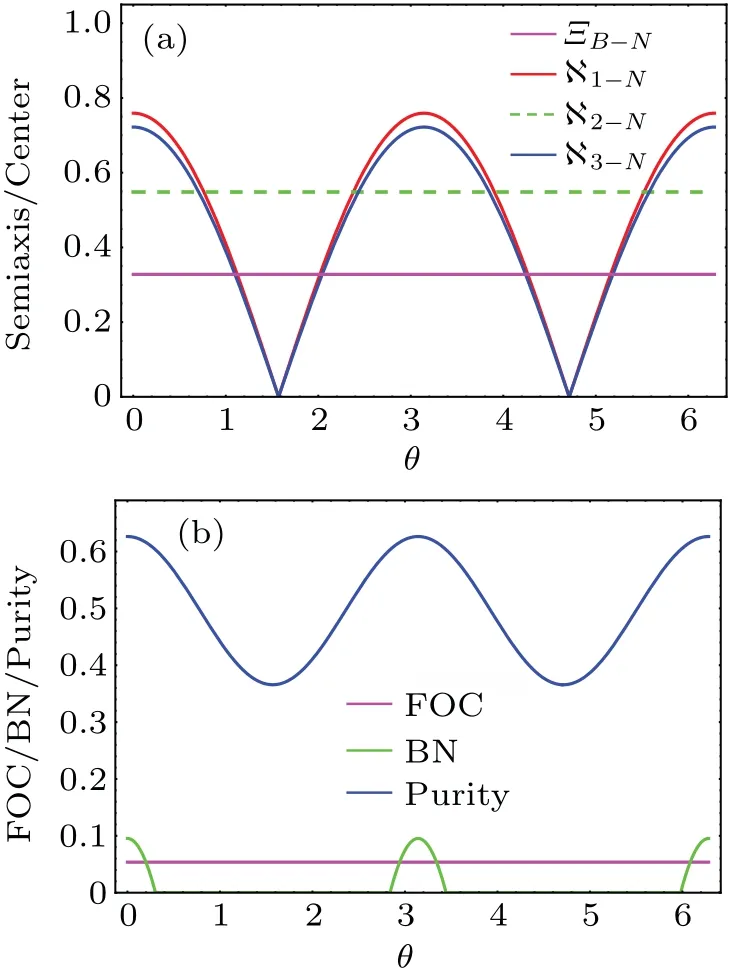
Fig.6.The dependence of semiaxis length and ΞB-N on the channel parameter θ.(b) The dependence of the FOC, BN and purity on θ.Ξ =0.4,γ =0.2,and φ =π/20.
Next, we further visualize the FOC, BN and purity for various values ofφ.One can see from Fig.7 that the length of thexsemiaxis is invariant.?2-Nand ?3-Nperiodically oscillate and achieve a maximum ifφ=nπ/2.Notably, the center of ??B-Nis not invariant with various values ofφ, and the center of ??B-Npunctures the center of the Bloch sphere atφ=nπ/2.One can use the trait of the QSE to visualize and determine that the invariance of the FOC cannot occur, and the FOC periodically oscillates and reaches zero atφ=nπ/2 in Fig.7(b)(the results are remarkably different from those in Fig.6(b)).Also,the tendency of the purity in Fig.7(b)is fully correlated with the trait of FOC due to the periodic oscillations of ?2-N,?3-NandΞB-Nin Fig.7(a).
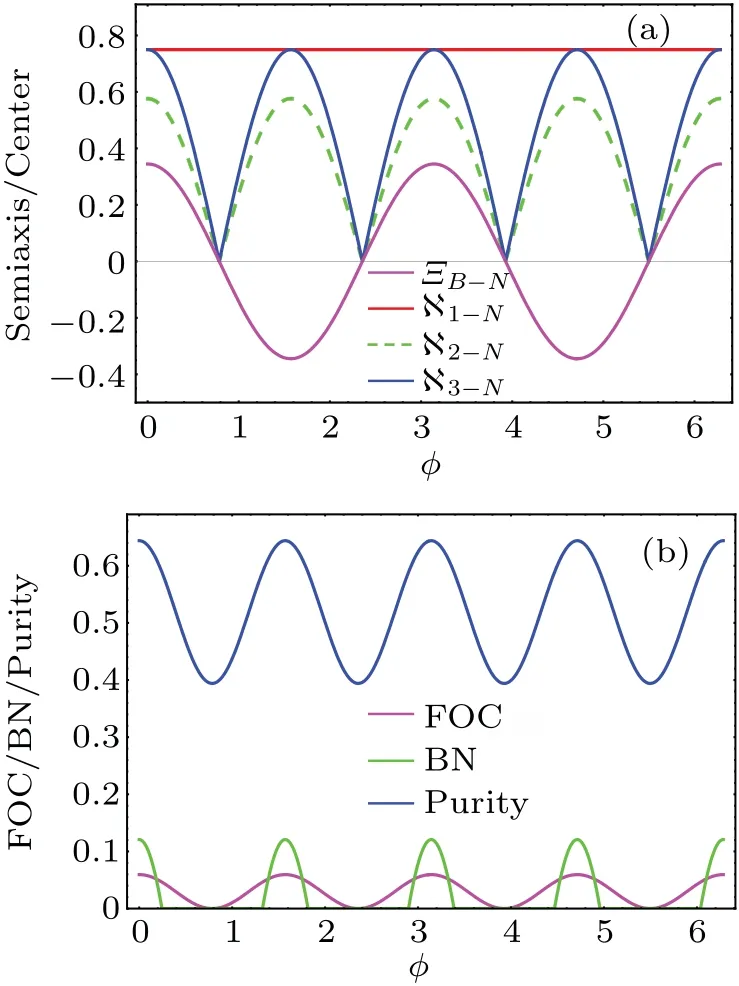
Fig.7.(a)The dependence of semiaxis length and ΞB-N on the channel parameter φ.(b)The dependence of the FOC,BN and purity on φ.Ξ =0.4,γ =0.2,and θ =π/20.
Finally, we direct our attention to explore the influences of the Unruh effect on the FOC, BN and purity under the NCGC.The dependence of the QSE parameters, FOC, BN and purity onγare demonstrated in Fig.8.Comparing Fig.8 with Fig.1, it can be concluded that the NCGC cannot influence the tendencies of the QSE, FOC, BN and purity.However, the NCGC can reduce the size of the QSE (as uncovered in Eqs.(16) and (36)), which means that the BN disappears at a weakerγunder the additional effect of the NCGC,as shown by the green curve in Fig.8(b).Beyond this, one can reveal from Eqs.(15) and (35) and Figs.1 and 8 that the condition ofΞB-N=0 (when the QSE reaches the center of the Bloch sphere) is not influenced by the NCGC if cos2φ/=0.For this reason,the NCGC cannot affect the condition of the disappearance of FOC(the critical case corresponding toγ=arccos[(1-Ξ)/(1+Ξ)]/2)in this scheme.
4.Conclusions
We obtain the form of the QSE under the non-inertial frame, and also derive the QSE of the system coupled to the depolarizing channel and the NCGC,respectively.The FOC,BN and purity are visualized and detected via the QSE.To be specific,the distance from the center of the QSE to the center of the Bloch sphere visualizes the FOC of a bipartite system.The lengths of thexandysemiaxes visualize the BN of the system.The shape of the QSE and its position dominate the purity of system.Beyond this, the conditions for the disappearance of the FOC and BN can be directly obtained by the characteristics of the QSE,and one can capture the FOC,BN and purity by using the shape and position of the QSE.That is,FOC will suddenly disappear if and only if the QSE moves to the center of the Bloch sphere, no matter what shape the QSE is.The BN will disappear if and only if the length of thexorysemiaxis is equal to 2/2, no matter where the QSE is in the Bloch sphere.The purity can reach 0.25 if and only if the QSE degenerates into a point at the center of the Bloch sphere.Under a non-inertial frame,the QSE moves along the negative orientation of thez-axis and shrinks with enhancing acceleration.This characteristic visualizes the decrease of the BN and purity.Notably,due to the result that the center of the QSE can puncture the center of the Bloch sphere if the acceleration is strong,the vanished FOC can revive at high acceleration.Considering the depolarizing channel,the QSE monotonically shrinks and finally degenerates into a point at the center of the Bloch sphere.This phenomenon is responsible for the monotonous degeneration of the FOC,BN and purity.Under the effect of the NCGC,the shape of the QSE periodically oscillates with increasing channel parametersθandφ.These traits visualize the periodical oscillations of the BN and purity with increasingθandφ.It deserves to be emphasized that the center of the QSE is invariant with variousθ, which reflects the invariance of FOC.Moreover, our results reveal that the depolarizing channel and NCGC can decrease the size of the QSE,and cannot influence the condition for the QSE reaching the center of the Bloch sphere(ifp/=1 or cos2φ/=0).That is to say, the BN is more fragile when considering the additional effects of a depolarizing channel and the NCGC.The condition for the disappearance of FOC is invariant when considering the depolarizing channel and the NCGC as additional influences.
Acknowledgements
Project supported by the National Natural Science Foundation of China (Grant No.12175001), the Natural Science Research Key Project of the Education Department of Anhui Province of China (Grant No.KJ2021A0943), the Research Start-up Funding Project of High Level Talent of West Anhui University(Grant No.WGKQ2021048),an Open Project of the Key Laboratory of Functional Materials and Devices for Informatics of Anhui Higher Education Institutes(Grant No.FMDI202106), the University Synergy Innovation Program of Anhui Province(Grant No.GXXT-2021-026)and the Anhui Provincial Natural Science Foundation (Grant Nos.2108085MA18 and 2008085MA20).
- Chinese Physics B的其它文章
- Corrigendum to“Reactive oxygen species in plasma against E.coli cells survival rate”
- Dynamic decision and its complex dynamics analysis of low-carbon supply chain considering risk-aversion under carbon tax policy
- Fully relativistic many-body perturbation energies,transition properties,and lifetimes of lithium-like iron Fe XXIV
- Measurement of the relative neutron sensitivity curve of a LaBr3(Ce)scintillator based on the CSNS Back-n white neutron source
- Kinesin-microtubule interaction reveals the mechanism of kinesin-1 for discriminating the binding site on microtubule
- Multilevel optoelectronic hybrid memory based on N-doped Ge2Sb2Te5 film with low resistance drift and ultrafast speed

