二項(xiàng)式定理應(yīng)用問題綜析

吉林師范大學(xué)數(shù)學(xué)與計(jì)算機(jī)學(xué)院 張語航

二項(xiàng)式定理:

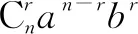
1 二項(xiàng)式定理在展開式中的應(yīng)用

1.1 求展開式中的特定項(xiàng)

求展開式中的特定項(xiàng)時(shí),通常直接運(yùn)用通項(xiàng)公式.具體步驟為:先根據(jù)題中已知條件確定指數(shù)并找到等量關(guān)系,列出方程;然后對(duì)方程求解,求出r的值;最后將r的值代入通項(xiàng)公式中,進(jìn)一步求出特定項(xiàng).

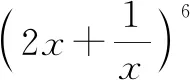
解：二項(xiàng)式展開式的通項(xiàng)為

故展開式的第3項(xiàng)為240x2,常數(shù)項(xiàng)為160.

1.2 求展開式中特定項(xiàng)的系數(shù)

例2求(x2+1)(x-2)7的展開式中x3的系數(shù).

解：在展開式中,x3的來源有兩個(gè).

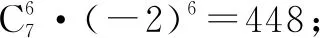
所以,x3的系數(shù)是448+560=1 008.

1.3 求展開式中各項(xiàng)系數(shù)的和或差

求二項(xiàng)式展開式各項(xiàng)系數(shù)的和或差時(shí),通常采用賦值法[2],即根據(jù)具體情況對(duì)二項(xiàng)式中的a,b元素賦予確定的值,尤其是特殊的值,如-1,0,1等.

例3若(1-2x)7=a0+a1x+a2x2+……+a7x7,求(1)a1+a2+……+a7;(2)a1+a3+a5+a7;(3)a0+a2+a4+a6.

解：(1)賦值法.

令x=1,代入二項(xiàng)展開式,得

(1-2)7=a0+a1+a2+……+a7=-1.

①

令x=0,代入二項(xiàng)展開式,得

(1-0)7=a0=1.

所以1+a1+a2+……+a7=-1.

故a1+a2+……+a7=-2.

(2)令x=-1,代入二項(xiàng)展開式,得

(1+2)7=a0-a1+a2-a3+a4-a5+a6-a7=37=2 187.

②

由①-②,可得

(3)由①+②,可得

1.4 求展開式中系數(shù)的最值

解：設(shè)展開式中第r+1項(xiàng)的系數(shù)最大,則

2 解決整除性問題

在使用二項(xiàng)式定理解決整除問題時(shí),關(guān)鍵是要在二項(xiàng)式的構(gòu)造上有所創(chuàng)新.通常將相關(guān)式(數(shù))的底數(shù)寫成除數(shù)與某個(gè)數(shù)字的和或差的形式,再根據(jù)二項(xiàng)式定理展開解決問題即可.

例5證明:34n+2+52n+1能被14整除.

證明：對(duì)原式變形,得

上式為14的倍數(shù),能被14整除,所以結(jié)論得證.

3 求余數(shù)問題

用二項(xiàng)式定理解決余數(shù)問題要考慮到余數(shù)的范圍,若a=c·r+b,用r來表示除數(shù),則b為余數(shù),余數(shù)一般要小于除數(shù),即b的范圍為b∈[0,r).

例6求9192除以100的余數(shù).

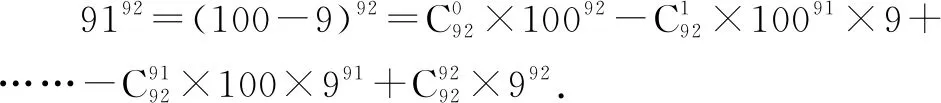
由于展開式的前92項(xiàng)均能被100整除,因此只需求最后一項(xiàng)除以100的余數(shù).

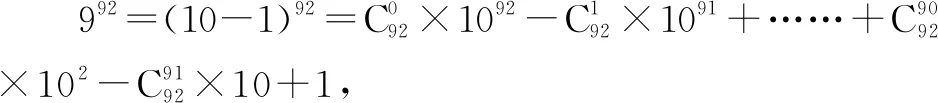
4 求近似值問題

例7求1.037精確到小數(shù)點(diǎn)后2位的值.

解：1.037=(1+0.03)7

=1+0.21+0.018 9+……

≈1.23.

所以1.037精確到小數(shù)點(diǎn)后2位的值為1.23.

5 證明組合數(shù)恒等式問題

證明：在二項(xiàng)式展開式中,令a=3,b=1,得

6 證明不等式問題

在應(yīng)用二項(xiàng)式定理證明不等式有關(guān)問題時(shí),通常與放縮法一起使用[3],放縮的實(shí)質(zhì)是對(duì)其展開式進(jìn)行取舍,將相等關(guān)系轉(zhuǎn)化為不等關(guān)系.

例9當(dāng)n∈N*且n≥2時(shí),求證:3n>2n-1(n+2).

證明：由二項(xiàng)式定理,可得

故3n>2n-1(n+2).

由上可知,二項(xiàng)式定理在解題中有著廣泛的應(yīng)用.在高中數(shù)學(xué)中,二項(xiàng)式定理比較常見的題型就是利用二項(xiàng)展開式的通項(xiàng)公式解決特定項(xiàng)、展開式中各項(xiàng)系數(shù)的和或差等問題,除此之外,運(yùn)用二項(xiàng)式定理來解決二項(xiàng)式系數(shù)或各項(xiàng)系數(shù)最值等問題也偶爾出現(xiàn).只有多積累、多運(yùn)用,才會(huì)完成從量變到質(zhì)變的蛻變.