函數(shù)零點問題的求解路徑分析

江蘇省溧陽中學(xué) 韓 俊

眾所周知,極限與導(dǎo)數(shù)(微積分)緊密相關(guān),很多導(dǎo)數(shù)問題與極限思想都息息相關(guān).蘇教版教材在高中數(shù)學(xué)課程中不涉及極限的知識,這給很多涉及導(dǎo)數(shù)的函數(shù)問題的求解帶來了重重困難.例如,含參的函數(shù)零點討論問題,這是近些年來函數(shù)壓軸的常見題型,筆者就借此題型來分享幾個含參函數(shù)零點問題的解題感悟.

1 引例

1.1 分析

①

數(shù)形結(jié)合,如圖1我們發(fā)現(xiàn):

圖1

再細(xì)想,一來學(xué)生對函數(shù)圖象的趨勢(極限思想)不一定能準(zhǔn)確把握,二來作為解答題,這樣的解答似乎略顯蒼白,因此,需要用文字和數(shù)學(xué)表達(dá)式來準(zhǔn)確證明上面的結(jié)論,即用零點存在定理來證明零點的存在性.那么,如何取點就變成了學(xué)生解決此題的難點.許多學(xué)生“為題消得人憔悴”,但依舊不得.重新審視此題,筆者略談一二,希望能夠給此類題型提供一些解題思路.

1.2 解析

再考慮非特值:

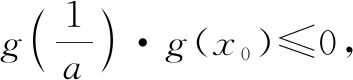
1.3 總結(jié)

從上述解題過程看,找到使得函數(shù)值異號的點大致可以選擇以下三種路徑.

路徑一:把代數(shù)式中已經(jīng)能判定符號的式子取出,再將剩余部分視作“零”,通過解方程找到所需定號的“點”.

2 三種路徑在壓軸題中應(yīng)用

經(jīng)過上題的研究,筆者有些“眾里尋他千百度,驀然回首,那人卻在,燈火闌珊處”之感.下面利用這三種路徑來解決如下高考壓軸題.

當(dāng)a≤0時,ax-1≤0.所以,當(dāng)x∈(0,1)時,f′(x)>0,f(x)單調(diào)遞增;當(dāng)x∈(1,+∞)時,f′(x)<0,f(x)單調(diào)遞減.故f(x)max=f(1)=a-1<0,此時函數(shù)f(x)無零點,不合題意.

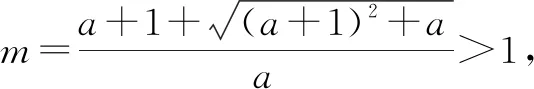
綜上,a 的取值范圍為(0,＋∞)．

評析：通過該題的解析不難發(fā)現(xiàn),在討論當(dāng)0＜a＜1時,可先利用路徑二由x＞1得到,再利用路徑三由ex≥x＋1的變形式elnx≥lnx＋1得到lnx≤x－1,進(jìn)而得到lnx＜x,用x替換x,得lnx＜2 x,則f(x)＞ax－1－2(a＋1)x ＝,則存在使得f(m)＞0．

3 結(jié)束語

通過上文兩題所述,大多數(shù)的函數(shù)“找點”問題都可從上述三種路徑中摸索出一些解題思路,雖不一定能“眾里尋他千百度,驀然回首,那人卻在,燈火闌珊處”,但也希望通過此文為一些“為題消得人憔悴”的朋友們,在解決此類問題時點亮一絲“燈火”．

正如波利亞所說：“如果你有一個念頭,你就夠幸運的了;如果你走運的話,你或許能找到另一個念頭;真正糟糕的事是,我們根本就沒有念頭,1001ba1001ba,這時任何一個可能指明問題新方向的問題,都值得歡頌,因為它可以引起我們的興趣,可以使我們繼續(xù)工作,繼續(xù)思索．”所以,解題永無止境,收獲永無止境,愿看過此文的朋友在解決壓軸題時,總能經(jīng)歷三境,不斷升華．