繁星樹線圖的完美匹配數(shù)
葉銀珠,陳海燕
(集美大學(xué)理學(xué)院,福建 廈門 361021)
圖的完美匹配不僅在圖論和計算科學(xué)中起著重要的作用,而且在統(tǒng)計物理和量子化學(xué)中占有重要的地位.在統(tǒng)計物理中,完美匹配被稱為dimer構(gòu)型[1],在量子化學(xué)中,完美匹配被稱為Kekulé結(jié)構(gòu)[2-4].眾所周知,計算圖的完美匹配數(shù)是一個NP-hard問題[5-7],受到學(xué)者高度的關(guān)注.
給定一個圖G=(V,E),圖G的線圖用L(G)表示,是頂點(diǎn)集V(L(G))=E(G)的圖,其中L(G)中的頂點(diǎn)e和f相鄰當(dāng)且僅當(dāng)e和f是G中相鄰的邊.Sumner[8]和Vergnas[9]證明了每個具有偶數(shù)個頂點(diǎn)的連通無爪圖至少有一個完美匹配.因為每個線圖都是無爪的,所以具有偶數(shù)條邊的連通圖的線圖一定有完美匹配.Dong等[10]給出了偶數(shù)條邊樹的線圖完美匹配數(shù)表達(dá)式.本文主要利用此表達(dá)式來確定一類繁星樹線圖的完美匹配數(shù)的最大值和最小值.
令G=(V,E)是頂點(diǎn)數(shù)為n,邊數(shù)為m的圖,對于v∈V,v的度表示為dG(v)或d(v).若dG(v)=1,則頂點(diǎn)v稱為G的懸掛點(diǎn),其關(guān)聯(lián)的邊稱為懸掛邊.邊子集M?E稱為G的一個匹配,如果M中沒有兩條邊關(guān)聯(lián)同一個頂點(diǎn).一個匹配M稱為G的一個完美匹配,如果G的每個頂點(diǎn)都與M中的一條邊相關(guān)聯(lián).G的完美匹配數(shù)用M(G)表示.對任意圖G,令p(G)表示G的具有偶數(shù)條邊的分支數(shù).令S1,k表示k+1個頂點(diǎn)的星形樹.一棵樹T被稱為繁星,如果它可以通過在一棵星形樹的懸掛點(diǎn)添加懸掛邊得到.
給定任何非負(fù)整數(shù)k,定義
(2k)!!=(2k-1)!!=(2k-1)(2k-3)…3·1,
其中0!!=(-1)!!=1.
引理1[10]設(shè)T是頂點(diǎn)集為{v1,v2,…,vn}的一棵樹,其中n>1且為奇數(shù),那么
1 繁星樹線圖的完美匹配數(shù)

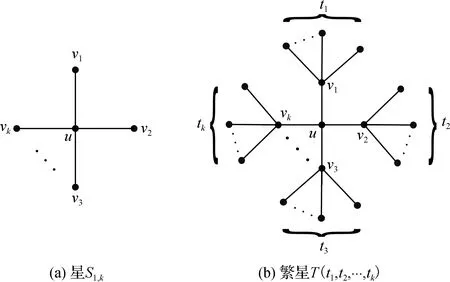
圖1 星和繁星Fig.1 Star and blossomed star
定理1設(shè)k和l是兩個正整數(shù),對任意T=T(t1,t2,…,tk)∈Tk,l有
其中r表示t1,t2,…,tk中偶數(shù)的個數(shù).
證明?v∈V(T),很顯然若dT(v)≤2,則p(T-v)!!=1.因此只需要考慮p(T-u)和p(T-vi)(i=1,2,…,k).T-u有k個分支,每個分支的邊數(shù)分別為t1,t2,…,tk,所以p(T-u)=r.T-vi有ti+1個分支,其中ti個為孤立點(diǎn),剩下的一個分支有l(wèi)+k-ti-1條邊,所以
由引理1得
證畢.

2 繁星樹線圖完美匹配數(shù)的最小值

πi,j(T(t1,…,ti,…,tj,…,tk))=
T(t1,…,ti-2,…,tj+2,…,tk),ti≥2;
θi,j(T(t1,…,ti,…,tj,…,tk))=
T(t1,…,ti-1,…,tj+1,…,tk),ti≥1.

(i) 若ti與tj有同樣的奇偶性,則
M(L(T))≥M(L(πi,j(T))).
(ii) 若ti與tj有不同的奇偶性,則
M(L(T))≥M(L(θi,j(T))).
證明對(i),由πi,j的定義和定理1易得
(1)
當(dāng)ti和tj都是偶數(shù)時,式(1)等于
當(dāng)ti和tj都是奇數(shù)時,式(1)等于
所以只要ti與tj同奇偶,都有
M(L(T))≥M(L(πi,j(T))),
(i)得證.
對(ii),由θi,j的定義和定理1可得
(2)
當(dāng)ti為偶數(shù),tj為奇數(shù)時,式(2)等于
當(dāng)ti為奇數(shù),tj為偶數(shù)時,式(2)等于
因此M(L(T))≥M(L(θi,j(T))).(ii)得證.
令

?i,j,|ti-tj|≤2}.





0≤x≤k-b且與k-b同奇偶};


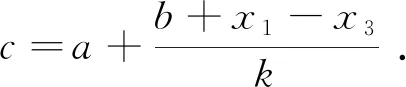
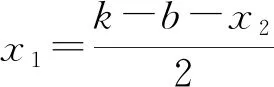
當(dāng)b+x1-x3=k,即c=a+1,這時



M(L(T*))=f(x)=

M(L(T*))=f(x)=
證明注意到k+l是偶數(shù),由l=ka+b得,當(dāng)a是偶數(shù)時,k-b一定是偶數(shù),當(dāng)a是奇數(shù)時,b一定為偶數(shù).所以由引理3和定理1,結(jié)論馬上得證.

(i) 若a是偶數(shù),
M(L(T))≥
(ii) 若a是奇數(shù),
M(L(T))≥

(i) 當(dāng)a是偶數(shù)時,由引理4,當(dāng)0≤x 所以當(dāng)0≤a≤k-b時,x=a是f(x)在其定義域內(nèi)的最小值點(diǎn),即 (ii) 當(dāng)a是奇數(shù)時,由引理4,當(dāng)0≤x 所以當(dāng)a≥k-1時,f(x)在整個定義域上是增函數(shù). 當(dāng)b-1≤a≤k-1, 當(dāng)a≤b-1, 結(jié)論得證. φi,j(T(t1,…,ti,…,tj,…,tk))= T(t1,…,ti+tj,…,0,…,tk),ti,tj≥1. 證明令r,r′分別表示T-u,φi,j(T)-u中偶數(shù)條邊的分支個數(shù),則由φ-變換的定義得 所以由定理1可得, 因此M(L(T))≤M(L(φi(T))).結(jié)論得證. 定理4設(shè)k和l是兩個正整數(shù),對任意T=T(t1,t2,…,tk)∈Tk,i,有 M(L(T(t1,t2,…,tk)))≤ 注:定理3和定理4證明過程中借助了一系列變換,但這些變換不是嚴(yán)格單調(diào)的,除了證明中給出的繁星達(dá)到最值外,還可能存在其他繁星達(dá)到最值,因此存在下面的問題. 問題:分別確定出定理3和定理4中等號成立的所有極圖.



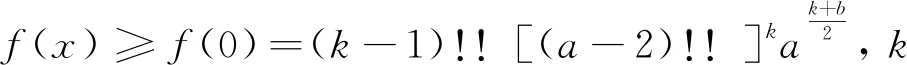
3 繁星樹線圖完美匹配數(shù)的最大值




