Mottness,phase string,and high-Tc superconductivity
Jing-Yu Zhao(趙靖宇) and Zheng-Yu Weng(翁征宇)
Institute for Advanced Study,Tsinghua University,Beijing 100084,China
Keywords: mechanism of high-Tc superconductivity,doped Mott insulator,emergent organizing principle
1. Introduction
As a revolutionary idea in the twentieth century, the gauge symmetry principle dictates the fundamental interactions between the elementary particles, which is completely characterized[1,2]by a nonintegrable phase factor
whereAμis the gauge potential andPstands for path ordering. In stark contrast to the real elementary particles with gauge interactions in high-energy physics, we will point out in this article that a novel world of elementary particles with gauge interactions can also emerge in a condensed matter system of strongly correlated electrons purely based on the nonrelativistic quantum mechanics with long-range entanglement.In the low-energy regime of such a many-body system, the characterization of electronic single-particle excitations can be qualitatively different from the conventional Landau’s quasiparticles in the so-called Landau paradigm[3,4]which has been a pillar stone of the modern condensed matter physics.In other words,the most elementary excitations can become some fractionalized objects other than electron-like. Gauge interactions also arise naturally among these fractional particles. Such elementary particles with a novel gauge structure constitute the precise mathematical description for a class of many-body systems known as the doped Mott insulator as illustrated in Fig.1,in which a nonintegrable phase factor similar to Eq.(1)emerges as a new organizing principle. It is protected by the Mott gap,which is caused by the local interaction to split the single-band of the electron into the so-called lower and upper Hubbard bands,respectively.[5]
At half-filling, the filled lower Hubbard band is charge neutral,which is known as the Mott insulator. Its spin degrees of freedom remain unfrozen, which can be adiabatically connected to the Heisenberg antiferromagnet in the large Mott gap limit. The doped Mott insulator will be quite different from a semiconductor as the dopants — doped holes in the lower Hubbard band or doped electrons in the upper Hubbard band—can strongly interact with the many-body spin background of the Mott insulator. Thirty five years ago, P. W. Anderson seminally proposed[6,7]that the doped Mott insulator lies in the core physics of the high-Tccuprate. The presence of a Mott gap>1.5 eV in the cuprate superconductors has been well established experimentally today.[8]
The state-of-the-art experiments in condensed matter physics have provided a rich variety of means to investigate the realistic materials like the cuprate. In principle, it is an overdetermined problem as so many different experimental probes are available to “interrogate” the same compounds from spin, charge, and electron channels, from transport to spectroscopies, from low energy to high energy, from low doping to high doping.[9]This is presumably an advantage of condensed matter physics over high energy physics where extremely high energy accelerators are needed in order to smash atoms or nuclei or so into more elementary constituents. Nevertheless, a great experimental complexity so far observed in the cuprate phase has actually contributed to more confusions instead of clarifying the fundamental nature of the high-Tcproblem based on the conventional wisdoms.
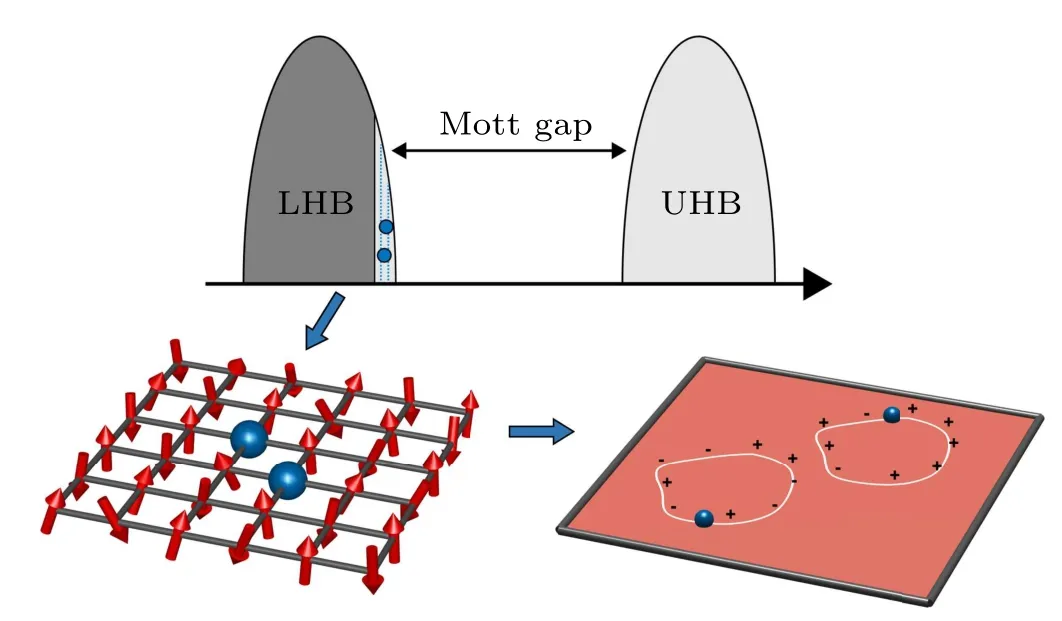
Fig. 1. The Mott gap due to a local interaction splits the single band of the electrons into the upper Hubbard band(UHB)and lower Hubbard band(LHB).A nonintegrable phase factor as a product of signs(cf. Fig.2),will be generally picked up by a dopant moving in the spin background,which is composed of the electrons in the filled LHB.The novel quantum interference of such a phase-string effect will replace the conventional Fermi statistics in the Landau paradigm as a new organizing principle, which dictates the essential physics of the doped Mott insulator.
A full understanding of the Mott physics(dubbed“Mottness”) is thus essential to provide the correct key ideas and theoretical framework in solving the high-Tcproblem. In particular, the aforementioned fractionalized particles and gauge structure of the Mottness identified in a rather simple and exotic duality world should be properly translated back to the extremely complex real world of the electrons in order to explain the experiment. In this article, we will briefly review a recent systematic effort in examining the non-perturbative,strongly correlated nature of the Mottness mainly from the concept of phase-string.[10–12]Alternative approaches to the Mottness have been reviewed elsewhere.[5,13,14]For a gapped bulk system without gapless modes, the general problem of quantum long-range entanglement has been also systematically investigated and classified based on the concept of topological order.[15]
Since the Mottness is based on a lattice model, e.g., a large-UHubbard model or thet–Jmodel or the like, which mainly involves the local hopping and strong interactions of the electrons, exact numerical algorithms will be available as another powerful machinery in the study. Of course, to truly access the long-wavelength, low-energy physics, large-scale numerics may be required which is still an NP hard problem due to an exponentially large Hilbert space with the increase of the sample size. However,with a relatively large Mott gap as revealed in experiment,the unique Mott properties can emerge already at a length scale comparable to the lattice constant,which is well accessible by a finite-size numerical simulation.In the following,we will first present a precise organizing principle of the Mottness based on thet–Jand Hubbard models and then show that nontrivial physical consequences with nonperturbative nature can indeed occur at any finite-size lattices,which may be thus properly examined numerically.
2. Organizing principle of the Mottness
A doped Mott insulator has been widely recognized as a strongly correlated system where perturbative approaches fail.How to establish a correct description for the Mott physics has been one of the most challenging and difficulty issues of the condensed matter physics in the past three decades. In the following,two organizing principles for the Mottness will be presented, which underlie the basic understandings of the nature of strong correlations and high-Tcsuperconductivity presented in this article.
Fermi statistics of the electrons and the corresponding sign structure of quantum many-body wave functions, which enforce the Pauli exclusion principle, are the foundation of Landau’s Fermi liquid description in the traditional condensed matter physics. However,such a basic law will be fundamentally changed once the Mott gap is opened up by interaction,leading to a new and novel sign structure that is to be elaborated as follows.
2.1. Sign structure of the Mottness: Phase-string
Without loss of generality, let us first focus on thet–Jmodel,which is equivalent to the Hubbard model atU/t ?1 limit on a bipartite lattice [Udenotes the onsite Coulomb repulsion andtthe nearest neighbor (NN) hopping integral]. An exact theorem, which holds true for arbitrary dimensions, electron concentration, and temperature, has been established.[16,17]When a doped charge carrier moves from A to B in Fig.2,it will always pick up a nontrivial phase factor

where{c}represents the closed loops of all the dopants and spins, with a positive weightW[{c}]≥0 depending on the coupling constants,temperature,and dopant concentration.[17]The conventional Fermi statistical sign structure,(?1)Nex({c}),withNexdenoting the number of exchanges of the whole electrons as identical particles,[18]is significantly reduced toτcτhhcin Eq.(3),in which the residual Fermi statistical signs are for dopants only as given by

Fig.2. Phase-strings as products of signs given in Eq.(2),which are picked up by a hole moving from A to B from distinct paths. Here the sign ±depends on the backflow spin σ =±1(as explicitly illustrated for the bluecolored path)exchanged with the hole at each step of hopping.
The phase-string sign structureτccan be also precisely determined in a finite-UHubbard model[19]associated with doped holes and doped electrons, respectively. As illustrated by Fig. 1, the opening of a Mott gap due to the local repulsion between the electrons at half filling will lead to a Mott insulator with the lower Hubbard band filled up by the electrons. When such a Mott insulator is doped by holes or electrons in the lower or upper Hubbard band, the dopants will generally pick up a Berry-phase-like phase-string as given in Eq.(2). In other words,each dopant will induce a many-body response from the background in the form of the phase-string effect,which makes a doped Mott insulator fundamentally distinct from the picture of a doped semiconductor where only the Fermi sign structure Eq. (4) remains withoutτc. Finally, the same sign structureτcis still present in a geometrically frustrated model like thet–t′–Jmodel [witht′the next-nearestneighbor (NNN) hopping integral] or a triangular Hubbard model with merely an additional geometric (non-dynamic)Berry phase appearing in Eq.(3),whose proofs will be given in detail elsewhere. Therefore, in general, the phase-string sign structure is a precise property of a doped Mott insulator with spin rotational symmetry,which is protected by the Mott gap.
It has been previously conjectured by Anderson[20]that an unrenormalizable Fermi-surface phase shift will be induced by each dopant in a doped Mott insulator,which causes an“orthogonality catastrophe”[21,22]and leads to a non-Fermi-liquid behavior of the many-body ground state.The phase-string sign structure identified rigorously in thet–Jand Hubbard models corresponds precisely to such a many-body phase shift. Butτcin Eqs. (2) and (3) is more singular as a nonintegrable phase factor,which is not only prominent near the Fermi surface as originally speculated by Anderson.[20]As a matter of fact, a spin flip can lead to a total sign change inτc. As such, the whole spin background of the Mott insulator becomes effectively long-range entangled with the dopants in a sufficiently long-time, low-energy limit. Thus the phase-string factorτcimplies a very non-perturbative nature of the Mottness that calls for a new methodology drastically different from the conventional many-body approaches.[3,4]
2.2. Mutual duality:An emergent topological gauge structure
The phase-string sign structure outlined above will replace the conventional Fermi sign structure as a new organizing principle of the Mottness. To understand its nontrivial physical implications,in the following a mutual-duality transformation is introduced,[23–25]which can effectively regulate and smoothen the singular hopping term,and reveal a hidden equivalence of the phase-string with a topological gauge structure.



2.3. Numerical verification of the phase-string effect
Based on the above two exact theorems, one may critically compare the ground state results between thet–Jandσ·t–Jmodels. Two models differ only by the presence and absence of the phase-string factorτcin Eqs. (3) and (12), respectively. Thus the pure and singular effect of the sign structure can be accurately singled out and verified by finite-size numerics.
Since the theorem on the phase-string sign structure holds true for any lattices, one can study a 2D sample of sizeN=L×L,or a ladder of sizeN=L×1(chain),N=L×2(twoleg),N=L×3(three-leg),N=L×4(four-leg),....Due to the particle–hole symmetry in the Hubbard model, one may only focus on the hole doped side,with single hole,two holes,... ,up to a finite doping concentrations of dopants.
2.3.1. Single-hole case
It is noted that at half-filling, thet–Jandσ·t–Jmodels reduce to the same Heisenberg model, whose ground state is spin-singlet with long-range antiferromagnetic correlations in a large sample.[28]Single hole injected into such an antiferromagnetic spin background will induce the phase-string sign structure in thet–Jmodel but none in theσ·t–Jmodel. Therefore, the single hole problem is the simplest case to demonstrate the phase-string effect by simply comparing the ground state properties between the two models,which can be calculated by exact diagonalization(ED)and density matrix renormalization group(DMRG)numerical methods. In the following we briefly outline some important results.
In 2D withC4rotational symmetry and open boundary condition(OBC),the single-hole ground state has been shown to have a fourfold degeneracy in a finite sample. In addition to a simple double degeneracy ofSz=±1/2(since one spin-1/2 is removed from the spin-singlet ground state), a novel angular momentum ofLz=±1 has been revealed in ED (L=4)and DMRG (L=6, 8) results.[29]Furthermore, corresponding toLz=±1, a spin current which conservesSz=±1/2 is found in the background. On the other hand, for a 2D sample with periodic boundary condition(PBC),the novel double degeneracy ofLz=±1 will be replaced by a fourfold degeneracy characterized by four total momenta at (±π/2,±π/2)in the ground states. Again the spin currents are found in the background as the backflow associated with the doped hole to generate a finite momentum in the ground state.[29]
Physically the novel quantum numberLzand the spin currents in the ground state are a direct manifestation of the phasestring effect in Eq.(2),which means that accompanying each step of hole hopping,the backflow must be spin-dependent to explicitly exhibit a spin current ifSz ?=0 as shown in the exact numerics. Indeed, once one artificially switches off the phase string in thet–Jmodel to result in theσ·t–Jmodel,the numerical calculations have shown[29]that the novel quantum numberLzand the spin currents all disappear with only the trivial double degeneracy due toSz=±1/2 left in the new ground state under OBC. Furthermore, under PBC, the total momentum reduces to the trivial symmetric point at (0,0) or(π,π) with restoring the translational symmetry without the presence of spin currents in the background.
Similar comparative studies of the single hole in the onedimensional chain,[30,31]two-leg, three-leg, and four-leg ladders, etc.,[26,32–34]as well as in the Hubbard model,[35–37]all have shown that in thet–J(Hubbard)case the doped hole always generates a nontrivial backflow spin current with new quantum number, which involves the many-body spin excitations from the background, while in theσ·t–J(σ-Hubbard)case, the doped hole simply behaves as a Bloch wave (i.e., a Landau-like quasiparticle with translational symmetry),which is essentially decoupled from the half-filled spin background.The presence/absence of the spin current is thus an explicit manifestation of the presence/absence of the phase-string effect in these models.
2.3.2. Two-hole case
The above numerical studies have unequivocally demonstrated that the phase-string sign structure of Eq.(2)has played a crucial role to turn a Landau-like quasiparticle (in theσ·t–Jmodel) into a “twisted” quasiparticle with novel quantum number and an explicit spin current formed by its spin-1/2 partner in a finite-size sample with different geometric shapes of the lattice.
By a sharp contrast, the aforementioned novel degeneracy and underlying spin current disappear when two holes are injected into the antiferromagnetic background, leading to a strong pairing between the holes. The 2D two-hole ground state is a spin singlet state characterized by angular momentumLz=2 mod 4, which is nondegenerate with theC4rotational symmetry of the square sample under OBC.[29]Two-leg and four-leg ladders all show[38]strong binding energies for the two holes in the nondegenerate ground state. In particular,in the two-leg ladder,one may continuously tune the rung(interchain)hopping integral into zero,where the pairing state remains and the phase-string can be analytically sorted out.Then it can be precisely shown[39]that the pairing energy is gained by eliminating the frustration effect due to the phasestring on each individual hole.Simultaneously the spin current is eliminated too there by pairing.
Such a new pairing mechanism due to the phase-string effect can be further directly seen from the fact that when the phase-string is turned off in theσ·t–Jmodel,the pairing vanishes too and the two-hole ground state simply reduces to that of two Landau quasiparticles decoupled from the spin background. Note that in the two-leg and four-leg cases, the undoped spin backgrounds are in short-range antiferromagnetic or the RVB states,and previously Anderson conjectured[6]the so-called RVB pairing mechanism for superconductivity based on thet–Jmodel. However, the above numerical simulations clearly indicate that the RVB is not dominantly responsible for the pairing of dopants,as shown in theσ·t–Jmodel. It is the phase-string induced by the motion of doped holes in thet–Jmodel that forces a strong binding between two holes in order to reduce its frustration effect.
2.3.3. Finite-doping case
As shown by numerical calculations, the strong pairing identified in the two-hole case can persist continuously into a finite-doping regime. Here the pairing mechanism can be well established in a finite-size study as the pairing size is generally small. It thus indicates that either a superconductivity or a phase separation may naturally arise in a finite-doped Mott insulator in the thermodynamic limit.
By DMRG calculation, two-legt–Jladder has been investigated, say, at doping concentrationδ=1/12, 1/8, etc.,
where quasi-long-range pair–pair correlation has been found at largeL. The ground state as a quasi-1D superconducting state known as the Luther–Emery (LE) state has been confirmed.[40]Various pseudogap-like phenomena have been also found when the spin background is artificially tuned into a long-range antiferromagnetic order[41]or partially polarized by Zeeman fields, resulting in a charge-density-wave or pairdensity-wave order with the pairing becoming subleading. For the four-leg ladder, similar complex phase diagram has been also found,[42]in which an NNN hopping integralt′may be further needed to stabilize the LE phase from the stripe and phase separation instabilities.[43]Rich properties have been also reported[44]in the literature for the six-leg case, which is even closer to the 2D limit.
Then it is important to show that once the phase-string sign structure is turned off,the above mentioned pairing,stripe or pair density wave order in the complex phase diagram of thet–Jladders have been found all gone, with the ground states simply behaving like a Fermi gas formed by the dopants on top of a decoupled spin background in theσ·t–Jladders. In other words, it proves[40,45]that the pairing and the various charge ordering states in thet–J(Hubbard)model can all be attributed to the phase-string effect,which induces the essential long-range mutual entanglement between the dopants (holes)and spin background that has been turned off in theσ·t–J(σ-Hubbard)model.
Therefore, the exact numerics have indeed accurately demonstrated that the phase-string sign structure plays an essential role in determining the unconventional long-range and short-range physics of the doped Mott insulator, whereas, as soon as the phase-string is turned off, the anomalies in the Mottness disappear to restore a Fermi liquid behavior similar to a doped semiconductor.
3. Parent state at finite doping: A non-Landau paradigm
In the Mott world,the electrons will be organized according to an emergent law of mutual statistics, i.e., the phasestring sign structure outlined in Subsection 2.1. Without such a novel sign structure, the exact numerics have indicated that the ground state would reduce to a trivial Fermi-gas state composed of the fermionic dopants,which is effectively separated from the spin background of the filled lower Hubbard band,similar to a doped semiconductor. By a sharp contrast,a rich phase diagram including a strong pairing between the dopants will arise once the phase-string sign structure is restored,based on the comparative numerical studies of thet–Jandσ·t–Jmodels(cf. Subsection 2.3).
According to the second theorem presented in Subsection 2.2,the duality transformation of Eq.(8)incorporates the most singular effect of the phase-string in the mutual swap of a dopant with the backflow spin during the hopping. Then the residual effect of the phase-string becomes smoothened after the transformation, which is precisely described by a novel topological gauge structure. To leading order of approximation, assuming a uniform distribution of charge at finite doping, a parent ground state of thet–Jmodel has been constructed as follows:[25,46]

The ground state ansatz in Eqs. (17) and (18) is fundamentally distinct from the original proposal of a single-component RVB state by Anderson.[6]Here|ΦG〉is composed of a two-component RVB structure:|b-RVB〉denotes a neutral RVB spin background, and a BCS-like component is created on the vacuum state|b-RVB〉in terms of a Cooper-like pair of doped holes, ∑i j gi j?ci↑?cj↓. At half filling,|ΨG〉reduces to|b-RVB〉, and the latter recovers the so-called longrange bosonic RVB state,which was first proposed by Liang,Doucot,Anderson[47]to accurately describe a long-range antiferromagnetic state of the Heisenberg model. At finite doping,the vacuum state|b-RVB〉will evolve into a short-range antiferromagnetic state(a spin liquid state)self-consistently.[25,46]Furthermore, in the original electron representation, an intrinsic long-range mutual entanglement between these two components is introduced via the phase-string factor ei?Θin Eq.(17),whose effect will be implemented via the topological gauge fields in the dual representation.
In the following, let us first examine the ground-state ansatz in the one-hole and two-hole cases, by using the variational Monte Carlo (VMC) calculations in comparison with the exact numerical results.
3.1. One-hole and two-hole ground states
The simplest nontrivial case of the doped Mott insulator is the single-hole-doped ground state. In the dual space of Eq.(18)it is simply reduced to

The excellent agreement of the single-hole state in Eq. (20) with finite-size ED and DMRG results outlined in Subsection 2.3, as calculated by the VMC method, including the nontrivial angular momentumLz=±1 in 2D[49]and the momentum structure in the two-leg ladder case,[48]clearly demonstrates that the doped hole in the Mottness gets substantially renormalized by the phase-string effect,whose behavior is fundamentally distinct from the celebrated Landau’s quasiparticle as a new quasiparticle of the doped Mott insulator.Recently a single-hole-doped case under a perturbation of a weak spin–orbit coupling(SOC)has been also examined,[50]which has further shown that the twisted hole with the novel angular momentum in Eq. (21) is critical to properly describe the response to the SOC as indicated by an excellent agreement between the VMC and ED.
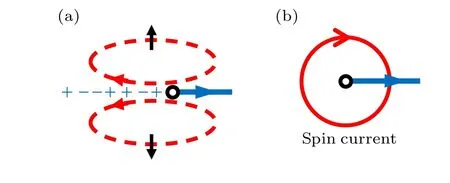
Fig. 3. The composite structure of a renormalized single hole state in Eq.(20). (a)The motion(blue arrow)of a doped hole(black circle)creates a sequence of±signs(phase string)depending on ↑and ↓of the backflow spins. To avoid cancellation in the hopping integral due to the phase-string effect, the backflow spin currents have to bend over in a roton-like pattern(red-dashed)around the hole. (b)Such a roton configuration may be explicitly manifested by a vortex of spin current around the hole as a net effect of an extra Sz=±1/2,characterized by an emergent internal angular momentum of Lz=±1 in agreement with the exact numerics. The original figure is from Ref.[52].
Similarly to Eq. (20), the two-hole ground state ansatz based on Eqs.(17)and(18)may be formally rewritten as[51,52]

The VMC calculation in 2D shows[52]that the two-hole ground state is nondegenerate with an angular momentumLz=2 mod 4 under aC4rotational symmetry,again in agreement with the ED and DMRG results. In particular, a strong binding has been revealed with the pairing mechanism directly connected to the phase-string effect. As shown in Fig. 4,a roton-like spin current pattern originated from the phasestrings has been clearly identified around the two holes. The pairing structure is shown to have a novel dichotomy: namely,an s-wave pairing symmetry is found in|gi j|for the pairing of two twisted quasiparticles ?c,but a d-wave symmetry is shown for the overlap of the ground state with the Cooper-pair order parameter. In particular, the strong binding disappears once the phase-string is turned off in Eq. (21) in the VMC calculation, even though the RVB pairing is still present in the spin background|b-RVB〉. It implies that the BCS-like pairing of doped holes is predominantly attributed to the phasestring effect,[52]instead of the RVB pairing as originally envisaged by Anderson.[6,7]Interestingly the pairing size of the two holes is about 4a0×4a0(a0is the lattice constant),which is much smaller than the spin–spin correlation length in the VMC calculation.[52]
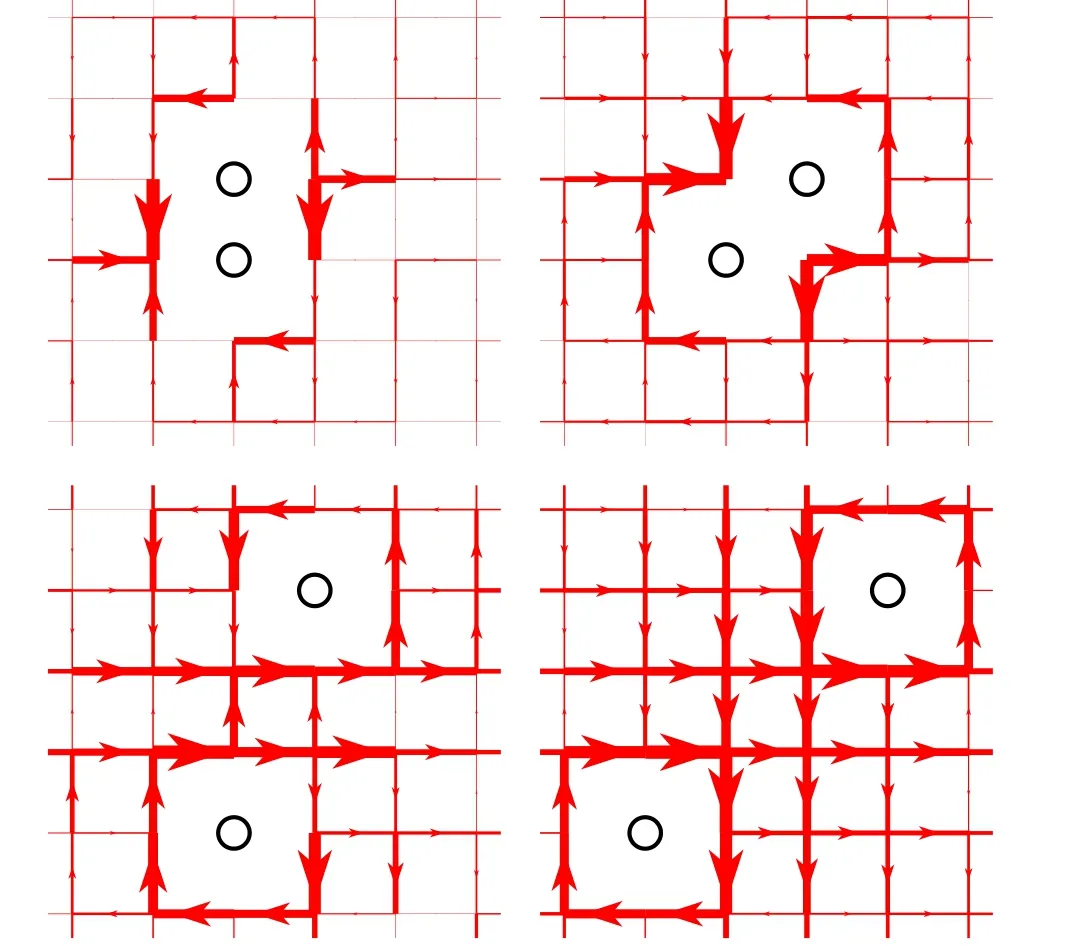
Fig.4. A roton-like spin current pattern around two holes[52] in the pairing ground state of Eq.(22),which contributes to a strong binding between the two holes with a size ~4a0×4a0. The original figure is from Ref.[52].
3.2. Finite doping:Fractionalization protected by multiple hidden ODLROs

in which ?Pswill enforce the single-occupancy constraint∑σ nbiσ= 1 in the spinon state|Φb〉such that|b-RVB〉 ≡?Ps|Φb〉; and ?PBwill further enforcenaiˉσ=nhi nbiσsuch that theSzspin of thea-spinon will compensate that of theb-spinon at a hole site. By applying ?P, the physical Hilbert space is restored in Eq.(25). On the other hand,theU(1)gauge fluctuations associated with the constraint enforced by the projection ?P, that is, the feedback effect on the subsystems in Eq. (25)will get suppressed or Higgsed due to the hidden off-diagonallong-range-orders[54](ODLROs) in the subsystems (see below). The latter provides the rigidity of the spontaneous symmetry breaking to justify this fractionalization scheme selfconsistently.[25,46]
In the dual space, the three subsystems in Eq. (25) are given by[25,46]


Table 1. Fractionalization of the Mottness and the topological gauge fields defined in Eqs. (14)–(16) due to the phase-string sign structure.Here Aextij denotes the external electromagnetic field.
Finally,in this fractionalization formulation of the parent state,the original bare-hole creation operator can be expressed

4. Synthesis
4.1. Phase-string sign structure dictates a new parent state
of the Mottness
In the traditional condensed matter physics, a Fermi liquid state of many-body electrons is considered to be the parent phase, based on which a BCS superconductivity is a spontaneous symmetry breaking or ODLRO state following the Cooper-channel instability of the Fermi liquid. Similarly,other ODLRO states like charge-density-wave and spindensity-wave ordered phases are also the low-temperature states following,say,the Fermi surface nesting instabilities of a Fermi liquid parent state. In general, the quantum behavior of many-body electrons is within the description of the Landau paradigm in which the Fermi statistics or fermionic sign structure has laid down the essential foundation.
The validity of the Landau paradigm is ensured in a weakly correlated system in which the Fermi energy is dominant over the interaction between the electrons. However, a Landau paradigm is expected to be failed if the interaction becomes a dominant force like in the fractional quantum Hall system[60]where the kinetic energy of the electrons gets essentially quenched by strong magnetic fields. The doped Mott insulator discussed in this article corresponds to the limit that the onsite Coulomb repulsionU ?t,which represents another important case of strongly correlated electron systems that the Landau paradigm may break down.
The most striking fact in the doped Mott insulator is that the Fermi sign structure is fundamentally changed to the phase-string sign structure, which is due to the restricted Hilbert space in the presence of a Mott gap. Such a gap splits the single band of the electrons into the lower and upper Hubbard bands(cf. Fig.1). Distinct from a trivial semiconductor,for doped holes in the lower Hubbard band or doped electrons in the upper Hubbard band,their statistical signs are no longer purely fermionic but also include exotic mutual statistics,i.e.,the phase-string, which is originated from the braidings between the dopants and spins in the charge-neutral background,i.e.,the filled lower Hubbard band. In general,each worldline of the dopants will be always weighed by a nontrivial phasestring sign factor (2) in a way precisely like the nonintegral phase factor Eq.(1)due to a gauge potential.[1,2]
In the original RVB theory[6,7]of the doped Mott insulator, the effect of the Hilbert space restriction due to the Mott gap has been implemented by enforcing a Gutzwiller projection in the large-Ulimit. However, the crucial phase-string sign structure,which can be rigorously identified in thet–Jand Hubbard models as the direct consequence of the Hilbert space restriction,is omitted,although a possible nontrivial response of the many-body background of the (doped) Mott insulator to each injected dopant has been conjectured.[7,20]Without correctly incorporating the phase-string effect,the underlying physics would deviate from that of the true Mottness just like that a theory of the conventional metal would deviate from the Landau’s Fermi liquid description should the Fermi statistics be omitted.
Here the phase-string is very singular as a product of signs±,which depends on the spins exchanged with the dopant as it moves forward. A strong phase interference of different paths connectingAandBin Fig. 2 is easily visualized. In particular,each spin-flip on one path can result in a total sign change or the reverse of a constructive/destructive quantum interference between the paths. As such, each dopant becomes entangled effectively with all the neutral spins of the Mott insulator and vice versa. So the Mottness is probably one of the most challenging non-perturbative problems of many-body quantum mechanics. Especially a long-range quantum mutual entanglement is involved with infinite degrees of freedom in the thermodynamic limit.
Nevertheless, such an extreme strong correlation problem of the Mottness can get substantially simplified mathematically by a mutual-duality transformation. In such a dual world, the many-body electrons are fractionalized into more elementary constituents with the singular interference effect of the phase-string being exactly mapped onto three smooth topological gauge fluxes. In this new world, the matters of the fractionalized particles of infinite numbers can further experience spontaneous symmetry breaking to acquire ODLROs to gain partial rigidity,such that the internalU(1)symmetries accompanying the fractionalization get suppressed (Higgsed)simultaneously. In other words,the electrons and phase-string sign structure can self-organize themselves into an emerging world of true elementary particles that are only weakly coupled via the topological(mutual Chern–Simons)gauge fields.The validity of the fractionalization with a novel gauge structure is thus protected by the Mott gap together with the hidden ODLROs at lower temperatures.
4.2. A complex phase diagram with antiferromagnetism, superconductivity, and Fermi liquid as lowtemperature instabilities of the parent phase
The significantly reduced fermion signs due to Mottness imply the destruction of the Fermi-liquid normal state at least in the small doping concentration regime of the cuprate. Here the Fermi-liquid state is replaced by a new parent state due to the phase-string sign structure, with the multi-ODLROs characterized by a mean-field phase diagram[46]as shown in Fig.5(a).Such a parent state characterized by Eq.(18)is composed of the following essential components atT=0:(I)It reduces to a long-range RVB state at half filling that can highly accurately describe the AFLRO ground state of the Heisenberg model.(II)It is a d-wave superconducting state at finite dopingδ<δ?. (III)Atδ>δ?,?s=0 for the b-RVB order parameter of theb-spinons such that|Φb〉describes a Curie–Weiss paramagnetic spin background.
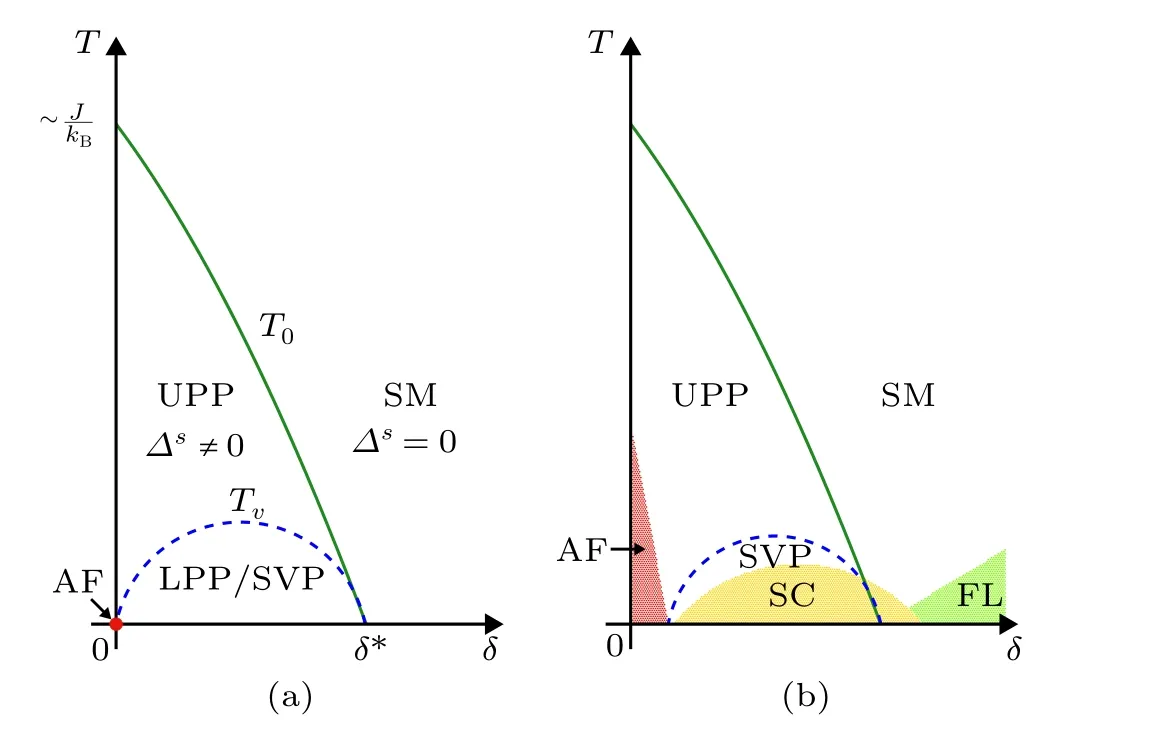
Fig.5. (a)The phase diagram of the parent phase,[25,46] in which the pseudogap phase with the bosonic RVB order parameter ?s ?= 0 is separated into the upper (UPP) and lower (LPP) by the holon Bose-condensation at T =Tv. The LPP is also known as the spontaneous vortex phase (SVP).Beyond T >T0,?s =0 and the spin background reduces to a Curie–Weiss paramagnet with a strange-metal(SM)behavior of the dopants. (b)The antiferromagnetic(AF),superconducting(SC),and Fermi liquid(FL)as lowtemperature instabilities of the parent phase in(a).
In such a parent phase diagram, theT= 0 superconducting state will be phase-disordered onceT>0+by thermally excitedb-spinons, each of which carries a supercurrent vortex formed by the holon condensate due to the mutual Chern–Simons gauge fieldAsi j. The corresponding state is called[61–63]the lower pseduogap phase(LPP)or spontaneous vortex phase(SVP)with a characteristic temperature scaleTvof the holon Bose condensation as shown in Fig.5(a). A true superconducting instability may further occur in the LPP/SVP at a finite transition temperature[59]

such that theT= 0 superconducting phase coherence can persist over toT On the other hand, by going beyond the mean-field parent state, the AFLRO in Fig. 5(a) may be restored not only atδ= 0, but also within a sufficiently low but finite doping regime, whereEg→0 to recover the gapless spin wave excitation.[10,64]HereEg=0 means the Bose-condensation of theb-spinons, which also implies the charge localization due to the vortex condensation associated with the spinons. It is consistent withTc→0 according to Eq. (32). Namely, the AFLRO phase and superconducting phase do not overlap as controlled by the gapless and gapped spin-1 excitations, respectively. As such,how an AFLRO/insulating phase at dilute doping evolves into a short-range RVB/superconducting phase can be systematically investigated based on the parent pseudogap state by carefully considering the gauge fluctuation effects ofAsandAh. Atδ>δ?,theb-spinon RVB order parameter?s=0. In such a Curie–Weiss paramagnetic spin background of|Φb〉,the holons can no longer propagate coherently due to the strong destructive quantum interference of the phase-string.Only can a Landau quasiparticle effectively propagate coherently as a collective mode, which is immune from the destructive phase-string effect in this regime. A Fermi liquid behavior with full Fermi surface can be recovered in an RPA scheme beyond the parent mean-field-theory description.[65]Finally atT>T0with?s=0, the incoherent propagation of the holons under the frustration of the phase-string effect via the random gauge potentialAsi jhas been shown to lead to a linear-Tresistivity.[10,66]In other words, the strange metallic behavior observed in the cuprate may be the consequence that the two hidden ODLROs,i.e.,the b-RVB order and the holon condensation in the parent state of Eq. (18), are “melted” in the high-temperature phase of Fig.5(a). The cuprate superconductor is widely considered to be a class of realistic materials of strong correlation, in which the Mott gap opens up as clearly observed by experiment.[8]At half-filling of the electrons, the Mott gap will render the electronic system to be an antiferromagnetic Mott insulator, and the superconductivity arises when additional charge dopants, holes or electrons, are injected into such a Mott insulator, resulting in a doped Mott insulator. A global phase diagram including high-Tcsuperconductivity,pseudogap,and strange metal phases has been well established experimentally in which the doping concentration and temperature seem to be two essential parameters that can be fine-tuned to result in an exceptional complexity in the phase diagram.[9]Novel excitations revealed by the spectroscopies,thermodynamic,and transport measurements should provide direct probes of the elementary particles predicted by the Mottness. In contrast to the high-energy accelerators to test the Standard Model of the elementary particles in nature, these experimental measurements in the high-Tccuprate have already generated a body of overly rich data in the past three decades that are capable of“overdetermining”the microscopic theory. Furthermore, the finite-size exact numerics can provide another powerful and unique verification of the ground state and excitations predicted by the concrete models of the Mottness. Especially,the lattice shape,doping concentration,and the coupling parameters are all artificially adjustable to explore a much wider phase space beyond the experimental reach to test the theoretical structure of the Mottness. In this sense,the fractionalization dual world due to the strong correlation of the Mottness can be straightforwardly verified or falsified by both the experimental measurements and numerical experiments. The Mott physics provides a striking example to illustrate“more is different” or the emergent phenomenon in manybody quantum mechanics.[67,68]A single band of electrons in the presence of the onsite Coulomb repulsion would behave generally as a Fermi liquid[3,4]in the limit that the Fermi energy is dominant over the interaction. But in the opposite limit oft ?U, a Mott gap opens up and the low-energy physics inside the gap will be completely changed. Here the Fermi statistics is replaced by the phase-string sign structure as the new organizing principle. The latter is equivalent to a mutual semionic statistics between the fractionalized coordinates in the restricted Hilbert space of the Mottness. In this brief review,a consistent picture based on a systematic study has been presented, in which the key emphasis is on that the new elementary particles with weakly-coupled mutual Chern–Simons gauge fields are the faithful representation of the Mottness in a dual world. In particular, near the half-filling, these quantum constituents form multiple hidden ODLROs in the thermodynamic limit. It is effectively a rigid system with lowenergy gaps or short-range orders,but is short of having a true ODLRO atT>0+. It resembles a pseudogap state with a gapless quasiparticles emerging in portions(Fermi arcs)of the Brillouin zone as a collective mode of the elementary particles. Antiferromagnetically ordered phase, superconducting phase,and the Femi liquid phase may be regarded as the lowtemperature instabilities of such a parent state at different doping regimes. As such,a series of sharp and unique predictions can be explicitly made for the high-Tccuprate based on the Mottness. Acknowledgments Stimulating discussions with Shuai Chen, Donna Sheng,Jan Zaanen, and Jia-Xin Zhang are acknowledged. A partial support of this work by the National Key R&D Program of China(Grant No.2017YFA0302902)is also acknowledged. This brief review is an extension of a contribution to the volume of Festschrift for the Yang Centenary in celebration of Prof. C.N.Yang’s 100th birthday.4.3. Experimental and numerical comparisons
5. Conclusion
- Chinese Physics B的其它文章
- Magnetic properties of oxides and silicon single crystals
- Non-universal Fermi polaron in quasi two-dimensional quantum gases
- Purification in entanglement distribution with deep quantum neural network
- New insight into the mechanism of DNA polymerase I revealed by single-molecule FRET studies of Klenow fragment
- A 4×4 metal-semiconductor-metal rectangular deep-ultraviolet detector array of Ga2O3 photoconductor with high photo response
- Wake-up effect in Hf0.4Zr0.6O2 ferroelectric thin-film capacitors under a cycling electric field

