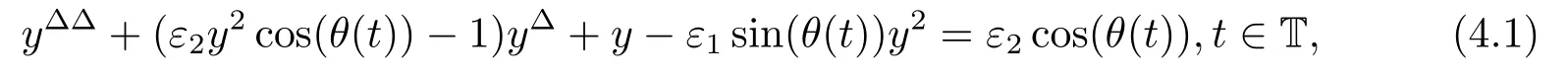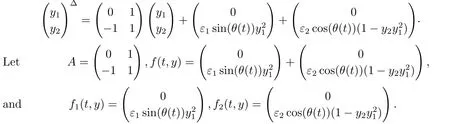Existence and Uniqueness Theorems of Almost Periodic Solution in Shifts δ±on Time Scales
HU Meng (胡猛), WANG Lili (王麗麗)
(School of Mathematics and Statistics, Anyang Normal University, Anyang 455000, China)
Abstract: In this paper, by using the theory of calculus on time scales, the properties of almost periodic functions in shifts δ± and the contraction mapping principle, the existence and uniqueness theorems of almost periodic solution in shifts δ± of some nonlinear and linear dynamic equations on time scales are established, and the specific expressions of the solutions on finite and infinite intervals are given, respectively.Finally, we applying the obtained results to study the existence of almost periodic solution in shifts δ± of a perturbed dynamic equation with small positive parameters.
Key words: Almost periodic solution in shifts δ±; Existence and uniqueness theorem of solution; Nonlinear equation; Linear equation; Time scale.
1.Introduction
In recent years, with the development of the theory of time scales,[1?2]the existence of almost periodic solutions of dynamic equations on time scales received many researchers’special attention[3?6].In [3], the authors defined an almost periodic time scale T satisfies the condition “t±s ∈T,?t ∈T, s is the translation constant”.Under the condition all almost periodic time scales are additive,unbounded above and below.However,there are many time scales don’t satisfy the condition,for example,={qn:q >1 is a constant and n ∈Z}∪{0}which is neither closed under the operations t±s nor unbounded below.In order to solve the problem, in [7], with the aid of the shift operators δ±, we studied almost periodicity in shifts δ±on time scales, and give three definitions, that is, almost periodic time scale in shifts δ±,almost periodic function in shifts δ±and ?-almost periodic function in shifts δ±.
The purpose of this paper is to study the existence and uniqueness theorems of almost periodic solution in shifts δ±of some nonlinear and linear dynamic equations on time scales,and the specific expressions of almost periodic solutions in shifts δ±on finite and infinite intervals will be given, respectively.Furthermore, we applying the obtained results to study the existence of almost periodic solution in shifts δ±of a perturbed dynamic equation with small positive parameters.
Consider the following dynamic equations on time scales
and

where t ∈T and T is an almost periodic time scale in shifts δ±; A(t) is a continuous almost periodic matrix function in shifts δ±; f(t) and f(t,x(t)) are continuous ?-almost periodic vector functions in shifts δ±.
2.Preliminaries
Let T is a nonempty closed subset (time scale) of R.The forward and backward jump operators σ,ρ:T →T and the graininess μ : T →R+are defined, respectively, by
σ(t)=inf{s ∈T:s>t}, ρ(t)=sup{s ∈T:s A point t ∈T is called left-dense if t > inf T and ρ(t) = t, left-scattered if ρ(t) < t,right-dense if tt.If T has a left-scattered maximum m, then Tk= T{m}; otherwise Tk= T.If T has a right-scattered minimum m,then Tk=T{m}; otherwise Tk=T. A function f : T →R is right-dense continuous provided it is continuous at right-dense point in T and its left-side limits exist at left-dense points in T.If f is continuous at each right-dense point and each left-dense point, then f is said to be a continuous function on T. A function p : T →R is called regressive provided 1+μ(t)p(t)0 for all t ∈Tk.The set of all regressive and rd-continuous functions p : T →R will be denoted by R = R(T,R).We define the set R+=R+(T,R)={p ∈R:1+μ(t)p(t)>0,?t ∈T}. If r is a regressive function, then the generalized exponential function eris defined by er(t,s)=expfor all s,t ∈T, with the cylinder transformation Let p,q :T →R are two regressive functions, define Lemma 2.1[1]Assume that p,q :T →R are two regressive functions, then Lemma 2.2If α ∈R and α ∈R+, then eα(t,σ(s))≥1+α(t ?σ(s)),?t ≥σ(s). ProofSince α ∈R+, then eα(t,σ(s)) > 0 for all t,s ∈T.Assume that t,s ∈T,and t ≥σ(s).Let y(t) = α(t ?σ(s)), then αy(t)+α = α2(t ?σ(s))+α ≥α = y?(t).Since y(σ(s))=0,then y(t)≤α(t,σ(τ))α?τ =eα(t,σ(s))?1,that is,eα(t,σ(s))≥1+y(t)=1+α(t ?σ(s)).This completes the proof. Remark 2.1If α ∈R and α>0, by Lemma 2.2, for all t ≥σ(s). A comprehensive review on the shift operators δ±on time scales can be seen in [8-11]. Let T?be a non-empty subset of the time scale T and t0∈T?be a fixed constant,and define operators δ±: [t0,+∞)×T?→T?.The operators δ+and δ?associated with t0∈T?(called the initial point) are said to be forward and backward shift operators on the set T?, respectively.The variable s ∈[t0,+∞)Tin δ±(s,t) is called the shift size.The values δ+(s,t) and δ?(s,t) in T?indicate s units translation of the term t ∈T?to the right and left,respectively.The sets D±:= {(s,t) ∈[t0,+∞)T×T?: δ±(s,t) ∈T?} are the domains of the shift operators δ±, respectively.Hereafter, T?is the largest subset of the time scale T such that the shift operators δ±:[t0,+∞)×T?→T?exist. Definition 2.1[7]Let T is a time scale with the shift operators δ±associated with the initial point t0∈T?.The time scale T is said to be almost periodic in shifts δ±if there exists p ∈(t0,+∞)T?such that (p,t)∈D±for all t ∈T?, that is, Definition 2.4[3]Let x ∈Rn, and A(t) is an n×n rd-continuous matrix function on T,the linear equation is said to admit an exponential dichotomy if there exist positive constants k,α, a projection P and the fundamental solution matrix eA(t) of (2.1), satisfying where ∥·∥is the Euclidean norm. Similarly to the proof of the proposition 4.4 in [12], we can obtain the following lemma. where E is a relatively dense set, and eA(t) is the fundamental solution matrix of (2.1). Let APS(T) is the set of all almost periodic solutions in shifts δ±of the equation (1.1). We first consider the case of T is unbounded above and below, and t ∈(?∞,+∞)T. Theorem 3.1Assume that the linear equation (2.1) admits exponential dichotomy,and f is Lipschitz with respect to the second argument, that is, Therefore, then, by Lemma 2.5, Using the Cauchy-Schwarz inequality, then, by Lemma 2.1 and Remark 2.1, Similarly, we can obtain From the inequalities (3.2) and (3.3), and Definition 2.2, x(t) is an almost periodic solution in shifts δ±of (1.1).Define then φ has a unique fixed point.In fact, then This implies that φ has a unique fixed point, that is, the equation (1.1) has a unique almost periodic solution in shifts δ±.This completes the proof. Similarly to the proof of Theorem 3.1, we can obtain the following results. Corollary 3.1Assume that the conditions of Theorem 3.1 hold.The almost periodic solution in shifts δ±of the equation (1.1) on [t0,+∞)T, where eA(t) is the fundamental solution matrix of (2.1). where eA(t) is the fundamental solution matrix of (2.1). ProofThe proof of the existence of almost periodic solution in shifts δ±of the equation(1.2)is similar to that in Theorem 3.1,so we omit it here.Moreover,∥A∥and ∥f∥are bounded,then by the Picard method of successive approximations and the uniqueness of limit, or by Gronwall’s inequality, we can prove that (3.4) is the unique almost periodic solution in shifts δ±of the equation (1.2).This completes the proof. Corollary 3.3Assume that the conditions of Theorem 3.2 hold.The almost periodic solution in shifts δ±of the equation (1.2) on [t0,+∞)T, where eA(t) is the fundamental solution matrix of (2.1). Consider a perturbed dynamic equation with small positive parameters ε1and ε2. Let T be an almost periodic time scale in shifts δ±, μ(t) be bounded, sin(θ(t)) and cos(θ(t)) be ?-almost periodic functions in shifts δ±on T. By using the transformation y =y1,=y2, the equation (4.1) can be written as Since A is a constant matrix and the real part of the eigenvalues of A are nonzero,y?(t)=A(t)y(t) admits exponential dichotomy. Define S={y ∈APS(T):∥y∥≤ζ}, where ζ is a positive constant. According to Theorem 3.1, the equation (4.1) has a unique almost periodic solution in shifts δ±.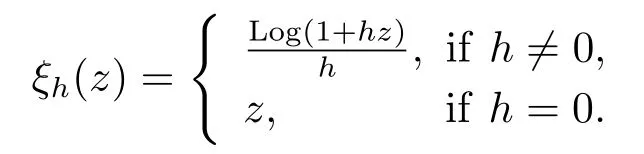





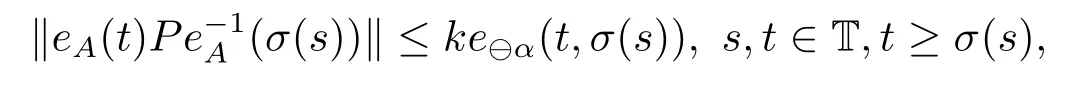


3.Main Results

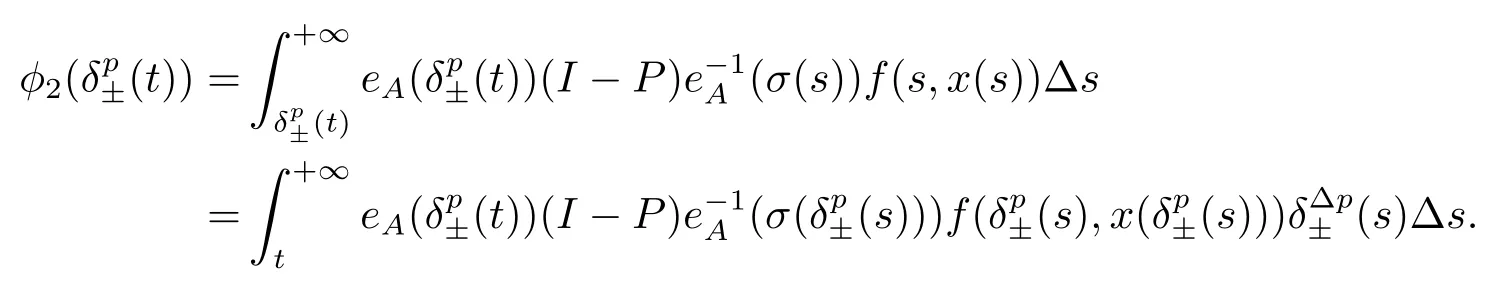

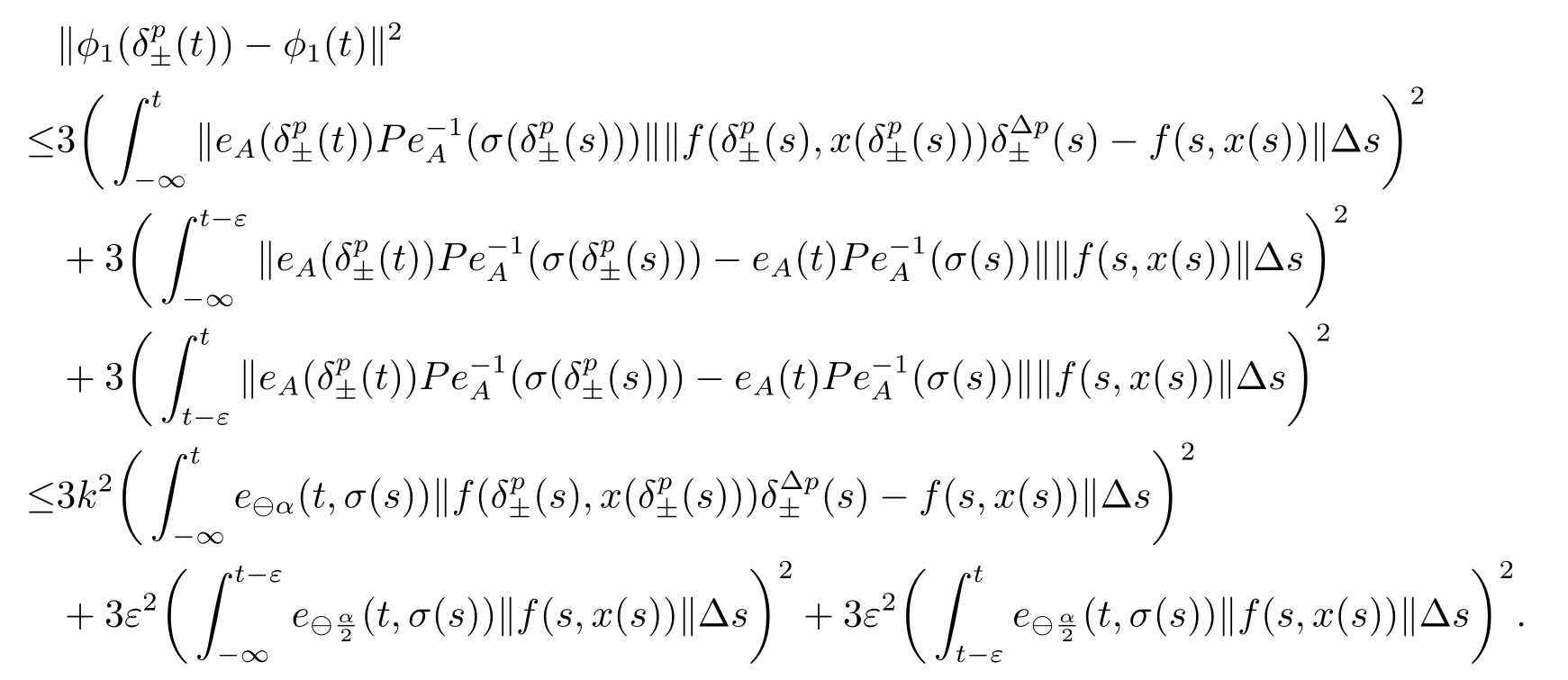
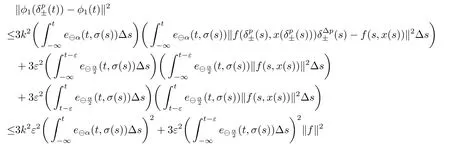

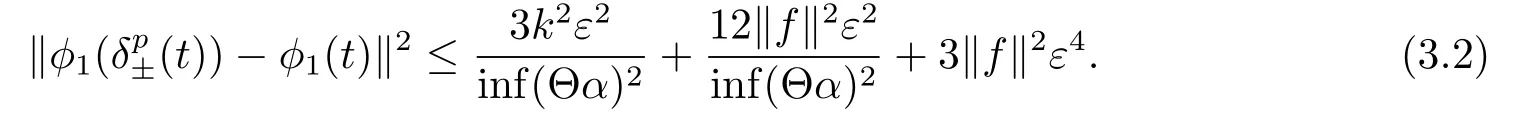

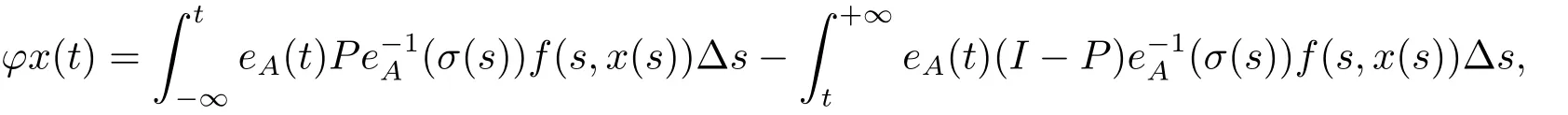


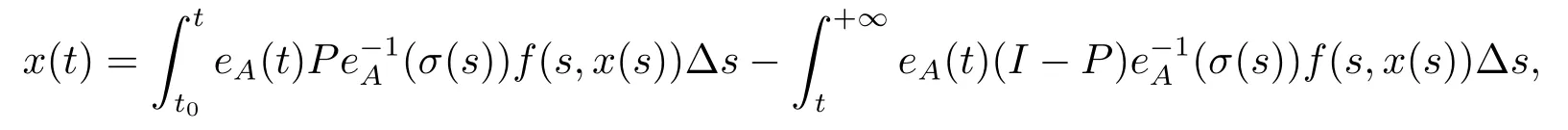


4.An Application