A Note on the Distance Signless Laplacian Spectral Radius

WANG Yanna(王燕娜), ZHOU Bo(周波)

(1.Basic Courses Department, Guangdong Communication Polytechnic,Guangzhou 510650, China; 2.School of Mathematical Sciences,South China Normal University, Guangzhou 510631, China)

Abstract: We propose three graft transformations that decrease the distance signless Laplacian spectral radius of graphs, and then determine the unique graph having the smallest distance signless Laplacian spectral radius over all cacti with n vertices, k cycles and at least one pendant vertex.

Key words: Distance signless Laplacian spectral radius; Graft transformation; Cactus;Pendant vertex

1.Introduction

We consider simple, finite, undirected and connected graphs.For a graph G with u ∈V(G), let NG(u) be the set of neighbors of u in G.The degree of a vertex u in G, denoted by degG(u), is the cardinality of NG(u).The vertex u is a pendant vertex of G if degG(u) = 1.A cactus is a connected graph in which any two cycles have at most one common vertex.

Let G be a connected graph.For u,v ∈V(G),the distance between u and v in G,denoted by dG(u,v),is the length of a shortest path connecting them in G.In particular,dG(u,u)=0.The distance matrix of G is defined as D(G) = (dG(u,v))u,v∈V(G).For u ∈V(G), the transmission of u in G,denoted by TrG(u),is the sum of distances from u to all other vertices of G, i.e., TrG(u)=Let Tr(G)be the diagonal matrix of vertex transmissions of G.The distance signless Laplacian matrix of G is defined as Q(G)=Tr(G)+D(G).The distance signless Laplacian spectral radius (DSLSR for short) of G, denoted by μ(G), is the largest eigenvalue of Q(G).

The spectral properties of the distance matrix have been studied extensively.[1]The spectral properties of the distance signless Laplacian matrix have been studied to some extent.[2?7]

Bose et al.[8]determined the cactus with minimum distance spectral radius among all cacti with given number of cycles.In this article,we propose three graft transformations that decrease the DSLSR of graphs under less restrictions, and as applications, we determine the unique graph that minimizes the DSLSR over all cacti on n vertices with k cycles and at least one pendant vertex, where 0 ≤k ≤

2.Preliminaries

Let G be a connected graph.Note that Q(G) is nonnegative and irreducible.By Perron-Frobenius theorem, μ(G) is simple, and there is a unique positive unit eigenvector corresponding to μ(G), which is called the DSL-Perron vector of G, denoted by x(G).Let V(G)={v1,··· ,vn} and x=(xv1,··· ,xvn)T∈Rn.Then

If x is unit and x has at least one nonnegative component, then by Rayleigh’s principle,we have μ(G) ≥xTQ(G)x with equality if and only if x = x(G).For x = x(G) and each u ∈V(G), (μ(G)?TrG(u))xu= ∑v∈V(G)dG(u,v)xv, which is called the DSL-eigenequation of G at u.

Lemma 2.1[4]Let G be a connected graph with η being an automorphism of G, and x the DSL-Perron vector of G.Then η(vi)=vjimplies that xvi=xvj.

An edge of a graph G is called a pendant edge if it is incident to a pendant vertex.For e ∈E(G), let G ?e be the subgraph of G obtained by deleting e.

Let G be a graph with u,v ∈V(G) and vv1,··· ,vvf∈E(G) and uv1,··· ,uvfE(G).Let G′=G ?{vvi:i=1,...,f}+{uvi:i=1,...,f}.Then we say that G′is obtained from G by moving edges vv1,··· ,vvfat v from v to u.

3.Graft Transformations Decreasing DSLSR

In this section,we propose three graft transformations that decrease the DSLSR of graphs.

Theorem 3.1Let G be a connected graph with an induced complete graph Ktsuch that G ?E(Kt) consists of vertex-disjoint connected graphs H1,··· ,Ht.Suppose that V(Kt)∩V(Hi) = {wi} for i = 1,··· ,t, |V(Hi)| ≥2 for i = 1,2, and w1has a pendant neighbor, say v1, in H1.Let G′be the graph obtained from G by moving all edges at w2except the edges in E(Kt) from w2to w1.Then μ(G)>μ(G′).

ProofLet x = x(G′).As we pass from G to G′, the distance between a vertex of V(H2) {w2} and a vertex of H1is decreased by 1, the distance between a vertex of V(H2){w2} and w2is increased by 1, and the distance between any other vertex pair is decreased or remains unchanged.Thus

If t=2, then w1w2is a pendant edge in G′, so, by Lemma 2.1, we have xv1=xw2, from which, together with (3.1), we have μ(G)>μ(G′).

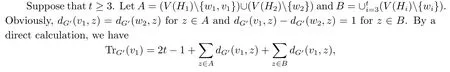
So

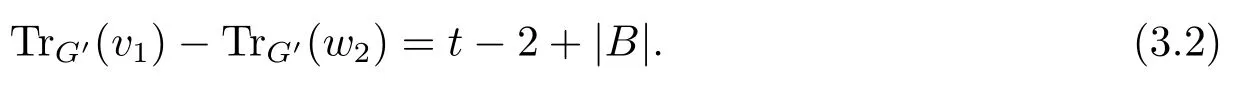
From the DSL-eigenequations of G′at v1and w2, we have

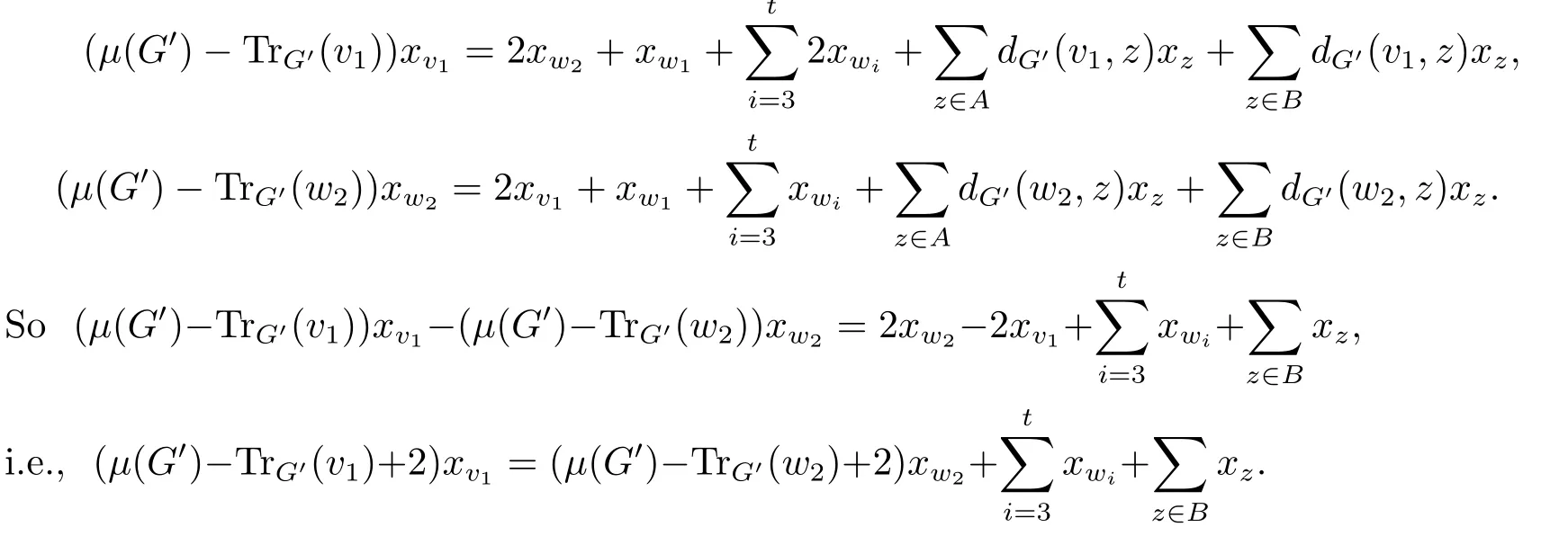
Thus

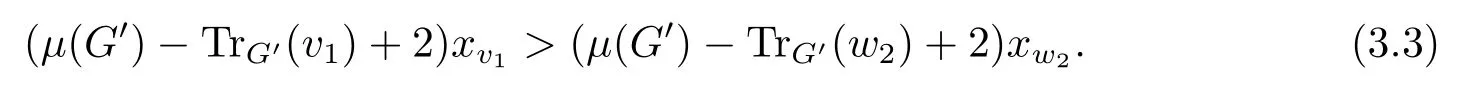
From (3.2), one has TrG′(v1) ?TrG′(w2) = t ?2 + |B| > 0, so μ(G′) ?TrG′(w2) + 2 >μ(G′)?TrG′(v1)+2>0.It follows from (3.3) that xv1≥xw2.By (3.1), μ(G)>μ(G′).This completes the proof.

As an immediate consequence of the previous theorem, we have the following result in[7]: Let G be a connected graph with a cut edge uv that is not a pendant edge satisfying that u has a pendant neighbor.Let G′be the graph obtained from G by moving all edges at v except uv from v to u.Then μ(G)>μ(G′).

Theorem 3.2Let G be a graph consisting of two nontrivial connected graphs G1and G2sharing a unique vertex u such that E(G) = E(G1)∪E(G2).Suppose that u has a pendant neighbor w in G1, u has neighbor v of degree at least two in G2satisfying that, for any z ∈V(G2){u,v}, dG(u,z)dG(v,z).Let G′be the graph obtained from G by moving all the edges at v except uv from v to u.Then μ(G)>μ(G′).

ProofLet x=x(G′).By Lemma 2.1, we have xw=xv.

Let S = {z ∈V(G2){u,v} : dG(u,z)?dG(v,z) = 1}.Let z be a neighbor of v in G2different from u.As dG(u,z)dG(v,z) = 1 and dG(u,z) ≤dG(u,v)+dG(v,z) = 2, one has dG(u,z)=2.So z ∈S and S?.

Note first that, as we pass from G to G′, the distance between a vertex of S and a vertex of V(G1) is decreased by 1, and the distance between a vertex of S and v is increased by 1.In the following, we show that the distance between any other vertex pairs is decreased or remains unchanged.

It is evident that the distance between any two vertices in V(G1)∪{v}remains unchanged as we pass from G to G′.

Suppose that z1,z2∈V(G2){u,v}.Let P be a shortest path from z1to z2in G.Clearly,P is also a path of G2.If v lies outside P, then P is also a path connecting z1and z2in G′.Suppose that v lies on P.If u lies outside P, then the path obtained from P by replacing v with u is a path connecting z1and z2in G′.Otherwise, u lies on P.In this case, uv appears to be an edge on P.So the path obtained from P by deleting v is a path connecting z1and z2in G′.So the distance between any two vertices in V(G2){u,v} remains unchanged or is decreased as we pass from G to G′.

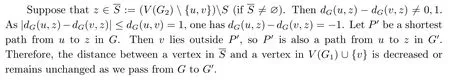
Therefore, we have

and thus μ(G)>μ(G′).The proof is completed.

Theorem 3.3Let G be a graph consisting of two nontrivial connected graphs G1and G2sharing a unique vertex u such that E(G)=E(G1)∪E(G2).Suppose that u has a pendant neighbor w in G1, and suppose that NG2(u) = {v1,v2}, degG2(vi) ≥2 for i = 1,2, v1and v2are not adjacent, and for any w ∈V(G2){u}, dG2(v1,w)dG2(v2,w).Let G′be the graph obtained from G by moving all the edges at viexcept uvifrom vito u for each i=1,2.Then ρ(G)>ρ(G′).

ProofLet x=x(G′).By Lemma 2.1, we have xw=xv1=xv2.

4.DSLSR of Cactus

In this section, we determine the unique graph that minimizes the DSLSR over all cacti with n vertices, k cycles and at least one pendant vertex.

Let C(n,k) be the class of all cacti on n vertices and k cycles, whereLet C0(n,k)∈C(n,k) be the cactus consisting of k triangles and n ?2k ?1 pendant edges with a common vertex.

Theorem 4.1Suppose that G ∈C(n,k) and G has at least one pendant vertex, whereThen μ(G)≥μ(C0(n,k)) with equality if and only if G ～=C0(n,k).

ProofIt is trivial if n=2.Suppose that n ≥3.

Let w be a pendant vertex of G, and u be its unique neighbor.As n ≥3, one has degG(u)≥2.Let v1be any a vertex adjacent to u except w.

Claim 1Either v1is a pendant vertex, or u and v1lie on a triangle with degG(v1)=2.

Suppose first that uv1is a cut edge.We show that v1is a pendant vertex.Suppose that this is not true.Let G′be the graph obtained from G by moving all the edges at v1except uv1from v1to u.Obviously, G′is a cactus with n vertices, k cycles and at least one pendant vertex.By Theorem 3.1, μ(G)>μ(G′), a contradiction.So v1is indeed a pendant vertex.

If n ≥7, then, as the maximum row sum of Q(C0(n,1)) is 4n ?6, we have from [9, p.24,Theorem 1.1] that μ(C0(n,1))≤4n ?6μ(C0(n,1)).

By a direct calculation, we have

μ(C0(6,1))≈16.7148,μ(C0(5,1))≈12.5826 andμ(C0(4,1))≈8.3723.

Thenμ(Cn)>μ(C0(n,1))for n ≥6,andμ(Cn)<μ(C0(n,1))for n=4,5.The result follows.