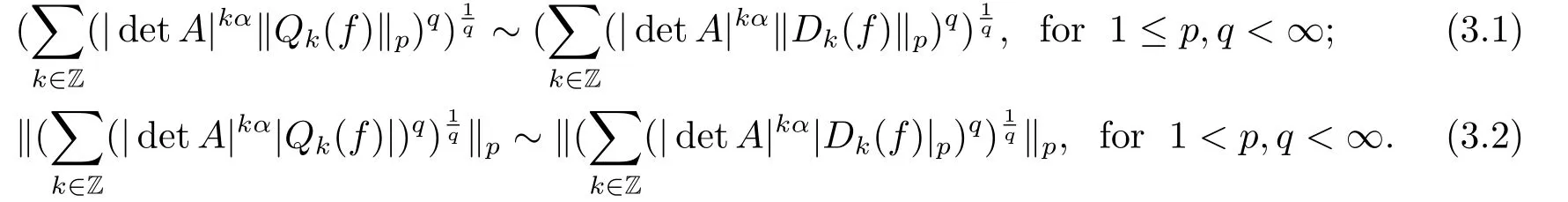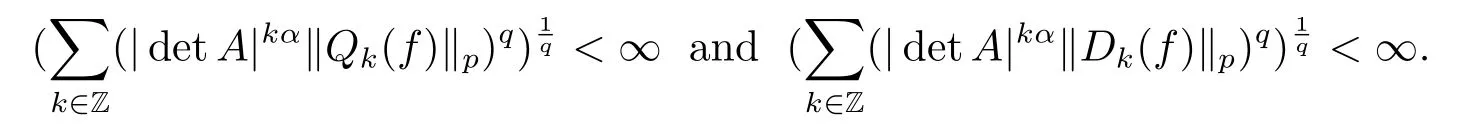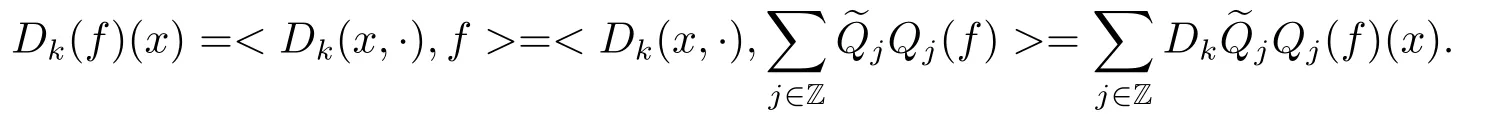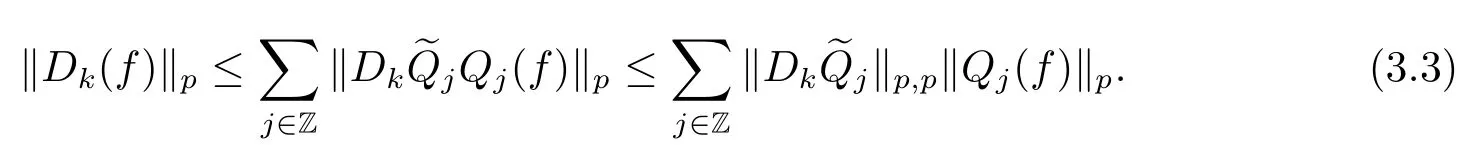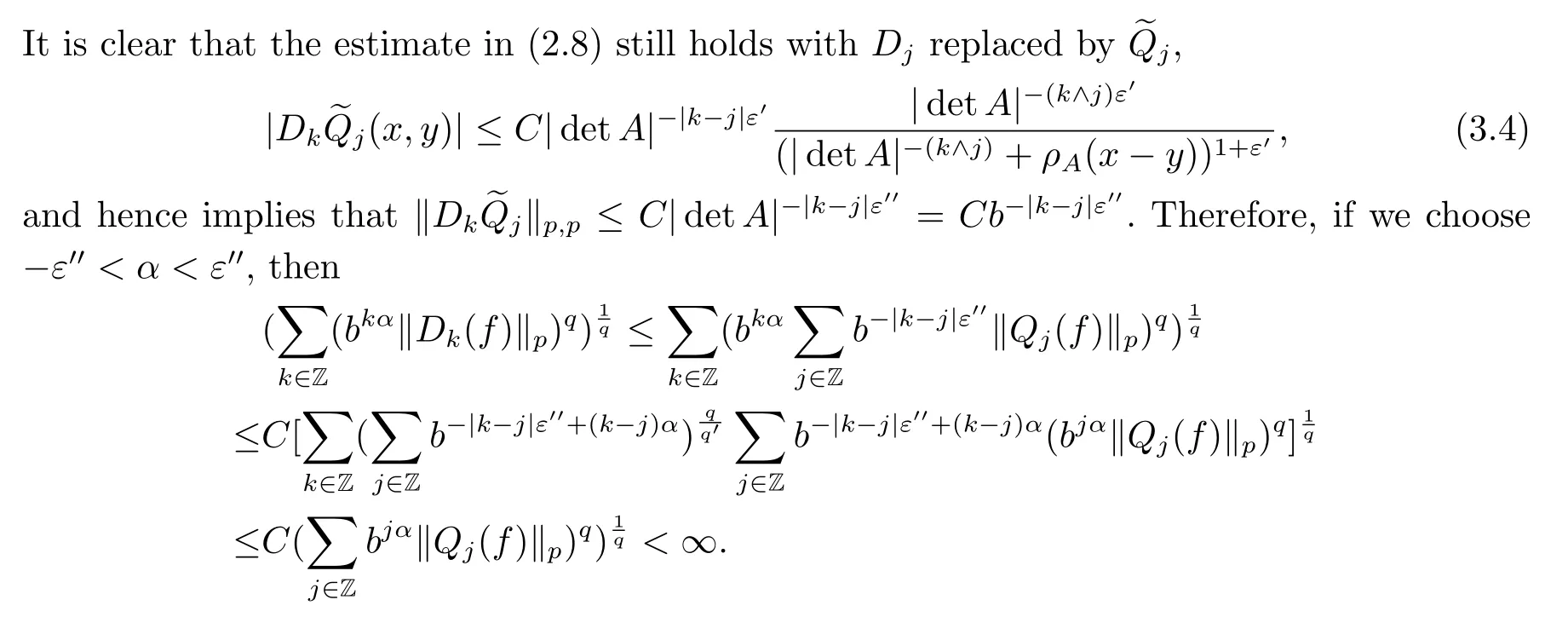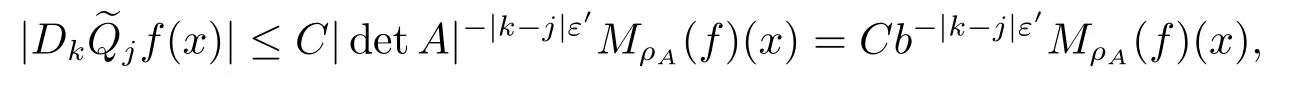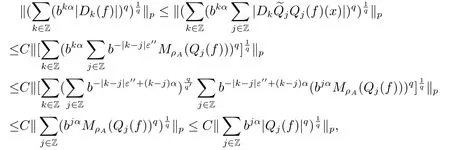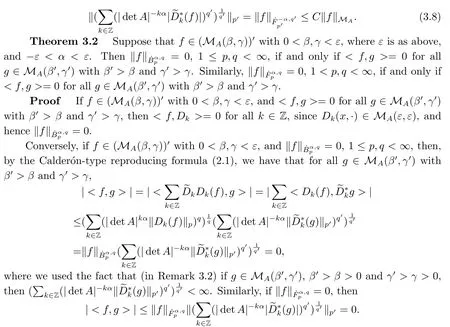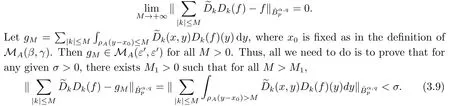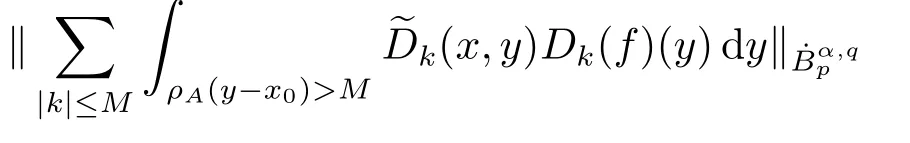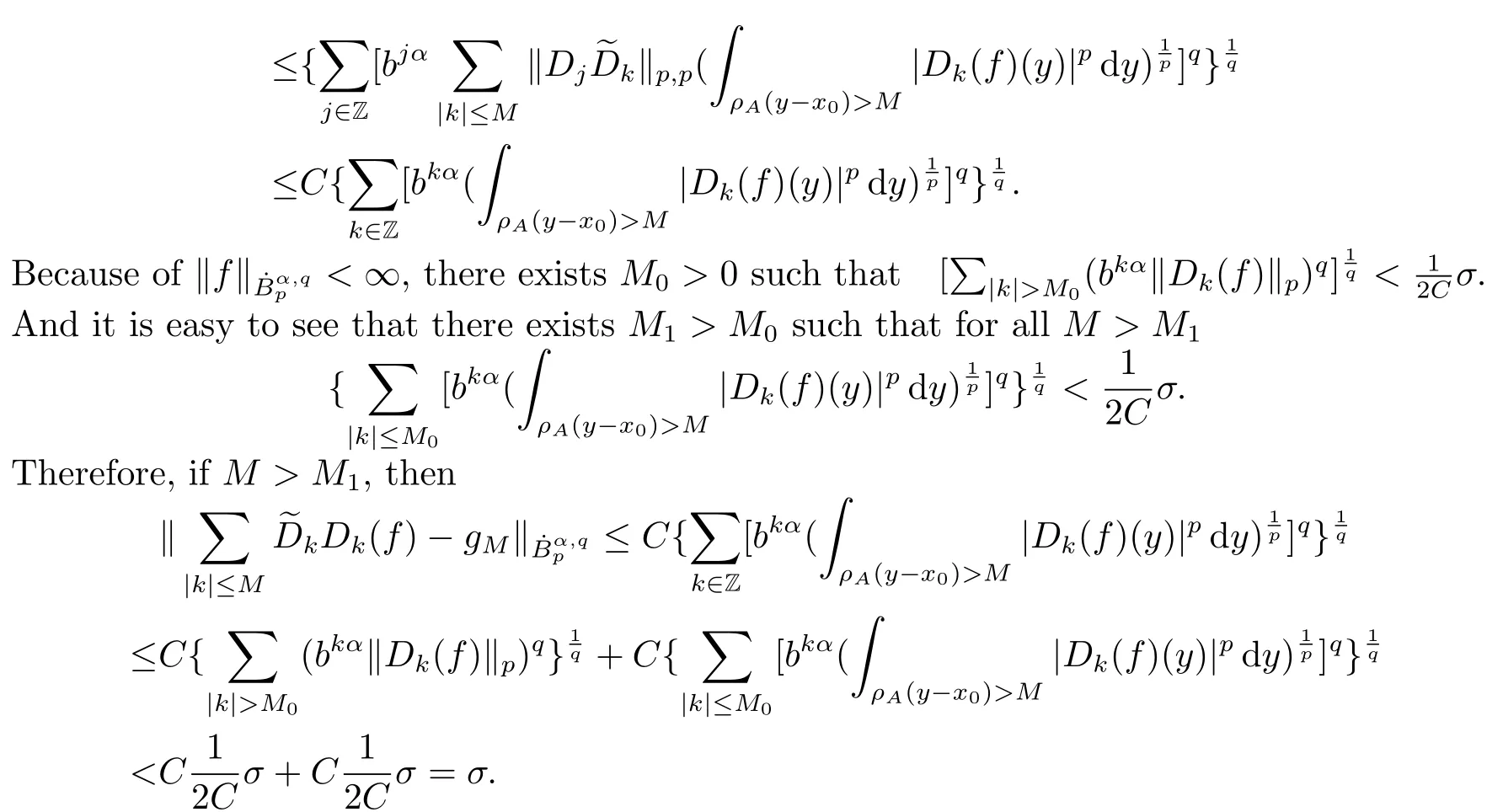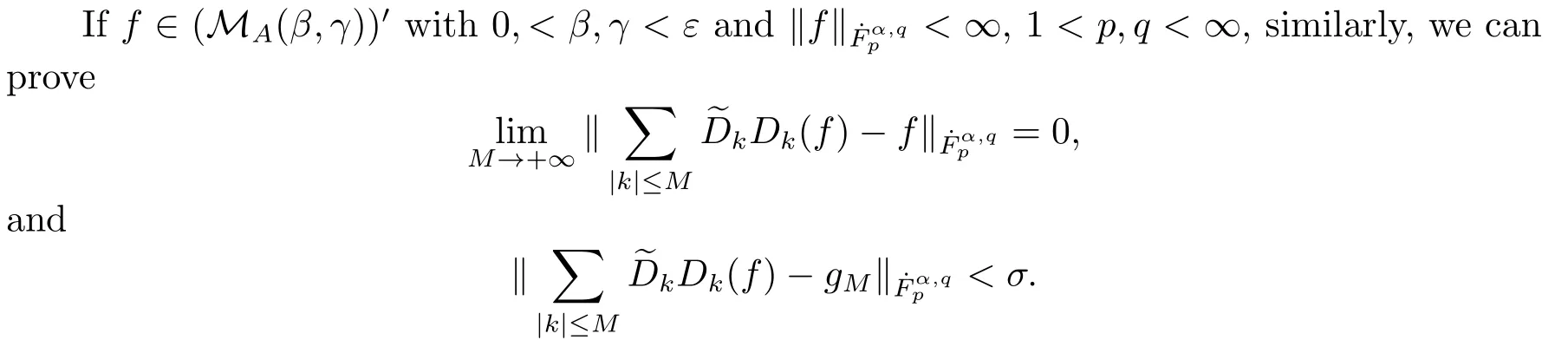A Characterization of the Anisotropic Besov and Triebel-Lizorkin Spaces
SHANG Qinming(尚欽明), ZHAO Kai(趙凱)
( 1.School of Data Science, Qingdao Huanghai University, Qingdao 266427, China;2.School of Mathematics and Statistics, Qingdao University, Qingdao 266071, China)
Abstract: Based on the properties of the anisotropic spaces and Littlewood-Paley theory, using the operators families of approximation to the identity, the Calder′on-type reproducing formula for anisotropic spaces is obtained.Then, by the Calder′on-type reproducing formula, the authors characterize the anisotropic Besov and Triebel-Lizorkin spaces.All these results are obtained without using Fourier transform and convolution.
Key words: Anisotropic; Calder′on reproducing formula; Besov space; Triebel-Lizorkin space; Characterization
1.Introduction
It is well known that the theory of function spaces constitute an important part of harmonic analysis.In a sense, the Calder′on reproducing formula plays an important role in characterizations for spaces.In 2003, Bownik[1]introduced the anisotropic Hardy spaces and discussed some properties of them.Then, he and his cooperator discussed the Besov and Triebel-Lizorkin spaces associated with an expansive dilation A,and obtained the atomic and molecular decompositions of these spaces[2?3].The atomic and molecular decompositions of the anisotropic Hardy spaces were studied in [4-5].The anisotropic Herz type Hardy spaces and Herz spaces were also discussed[6?7].Other characterizations of function spaces,in especial Besov and Triebel-Lizorkin spaces, can be found in[8-13]etc.But all these results for anisotropic spaces were worked by the Fourier transform and convolution.In this paper,motivated by HAN and his cooperator’s work for spaces of homogeneous type[14?15], by the Littlewood-Paley theory, using the operators families of approximation to the identity, we obtain a Calder′on-type reproducing formula for anisotropic spaces.Then, by the Calder′ontype reproducing formula, we characterize the anisotropic Besov spacesand Triebel-Lizorkin spacesAll these results we obtained just only use the operators families of approximation to the identity, any where is not used the Fourier transform and convolution.
For convenience,we recall some definitions and properties of anisotropic spaces associated with general expansive dilations.
Definition 1.1[1]A real n×n matrix A is an expansive matrix, sometimes called shortly a dilation, if minλ∈σ(A){|λ|}>1, where σ(A) is the set of all eigenvalues of matrix A.
Definition 1.2[1]A quasi-norm associated with an expansive matrix A is a measurable mapping ρA:Rn→[0,+∞) satisfying

where h ≥1 is a constant.
Note that the quasi-norm associated with an expansive matrix A induces a quasi-distance making Rna space of homogeneous type.Here we only list a few basic results in the following.
If we let
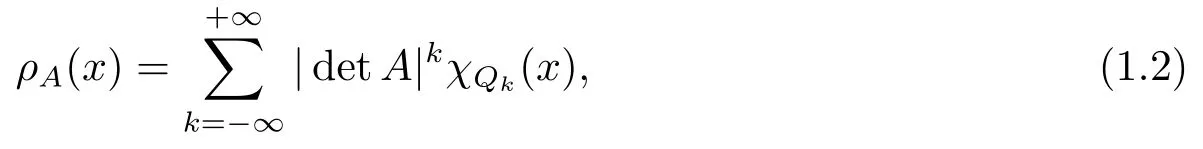
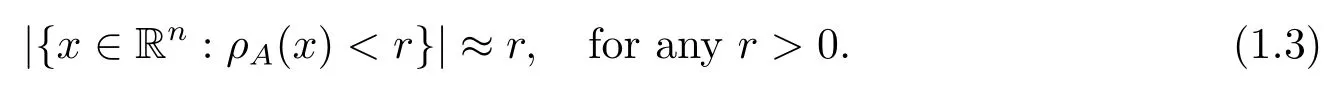
Let B = B(ρA) be the collection of all ρA-balls: BρA(x,r) = {y ∈Rn: ρA(y ?x)
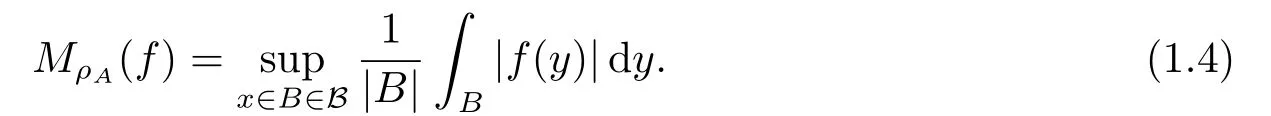
The Hardy-Littlewood maximal operator MρAis weak type(1,1)and bounded on Lp(Rn),1 < p < ∞; and also have the Fefferman-Stein vector valued inequality as (1.5) bellow.For details, we refer to [1-3] etc.Suppose that 1 < p < ∞and 1 < q ≤∞.Then for any{fk}∈Lp(Rn) there exists a constant C >0 such that
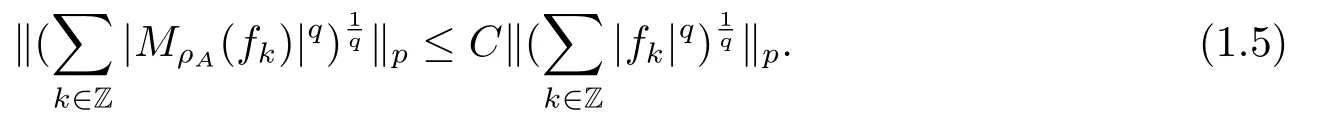
2.Calder′on Type Reproducing Formula
We begin by recalling the definition of the Calder′on-Zygmund operator with respect to a dilation A and a quasi-norm ρA.
Definition 2.1[1]Let T : S(Rn) →S′(Rn) be a continuous linear operator.We say that T is a Calder′on-Zygmund operator (with respect to a dilation A and a quasi-norm ρA) if there exists a continuous function K(x,y) defined on Rn×Rn{x=y}, satisfying the following conditions: for some constant C >0 and ε>0,
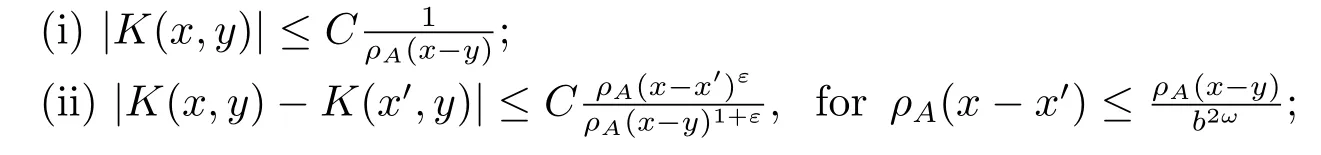
(iii) Property(ii)also holds with x and y interchanged;where b=|det A| and ω is as above.Moreover, the operator T can be represented by
(v) T can be extended to a continuous linear operator on L2(Rn) with ∥T∥≤C.If a continuous linear operator T satisfies the conditions(i)through(iv),we say T ∈CZK(ε).
Definition 2.2Fix two exponents 0<β ≤1 and γ >0.A function f defined on Rnis said to be a “test” function of type (β,γ,r,x0) centered at x0∈Rnwith width r > 0 and dilation A, if f satisfies the following conditions:
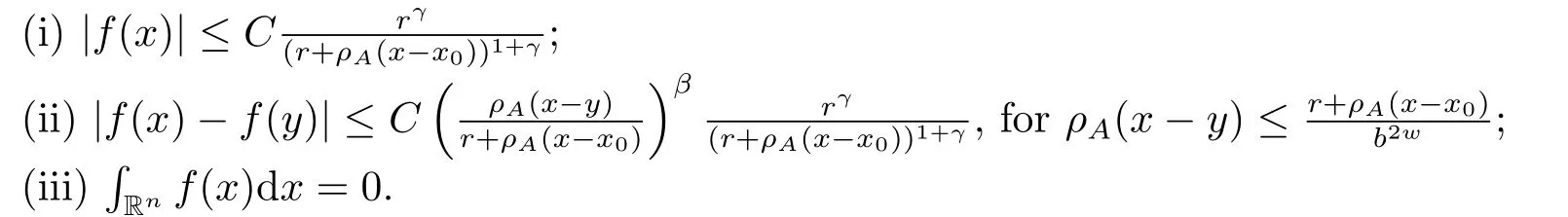
The collection of all test functions of type (β,γ,r,x0) will be denoted by MA(β,γ,r,x0).If f ∈MA(β,γ,r,x0), then the norm of f in MA(β,γ,r,x0) is defined by
(iv) ∥f∥MA=inf{C :(i) and (ii) hold }.
Since,for x0∈Rnand r >0,MA(β,γ,r,x0)=MA(β,γ,1,0)with equivalent norms,we can use MA(β,γ)instead of MA(β,γ,1,0)for simple.The dual space of MA(β,γ)is written as (MA(β,γ))′.

With the above definitions, since the quasi-norm associated with an expansive matrix A induces a quasi-distance making Rna space of homogeneous type, similar to [15], we can easily to prove the result as follows.Here we omit the details.

In order to establish the Calder′on-type reproducing formula associated with an expansive dilation A, we introduce the following family operators with dilation A.
Definition 2.4A sequence {Sk}k∈Zof operators is called to be an approximation to the identity associated with a dilation A, if Sk(x,y), the kernel of Sk, are functions from Rn×Rninto C satisfying: For any k ∈Z, and x,x′,y and y′in Rn, there exsit 0<ε ≤1 and C >0 such that
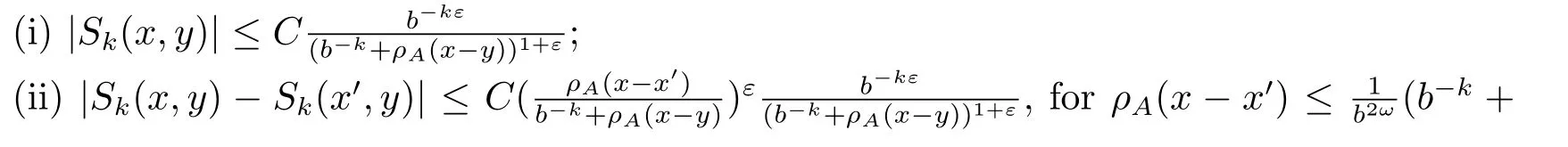
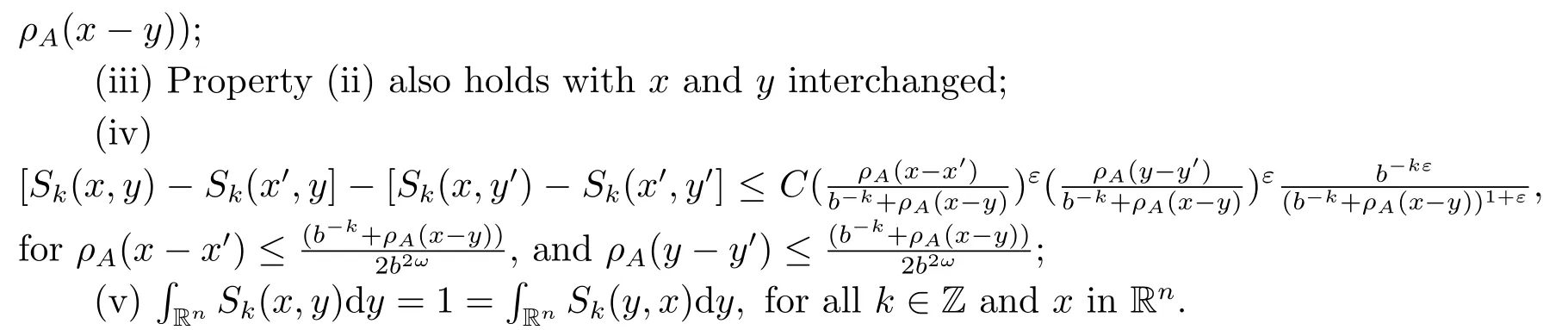
We now can use these family operators to establish the Calder′on-type reproducing formula associated with an expansive dilation A.

By the duality argument and Theorem 2.2, we can obtain the following theorem.
Theorem 2.3Suppose that{Dk}k∈Zis as in Theorem 2.2.Then there exists a family of operators {}k∈Zwhose kernels satisfy (2.2),(2.3) and (2.4), such that for all f ∈(MA(β,γ))′,
where the series converges in (MA(β′,γ′))′with β′>β and γ′>γ.
To prove Theorem 2.2, we need the following lemma.

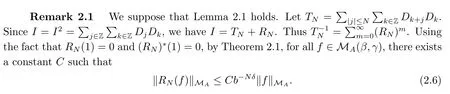
Therefore, we have
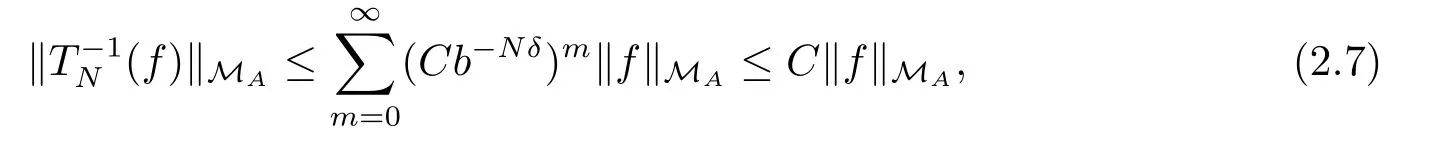
due to b=|det A|>1 and we can choose N large enough.
Proof of Lemma 2.1We prove Lemma 2.1 briefly.Similar to HAN’s work in [14],the following important estimates holds: for 0<ε′<ε, there exists a constant C such that
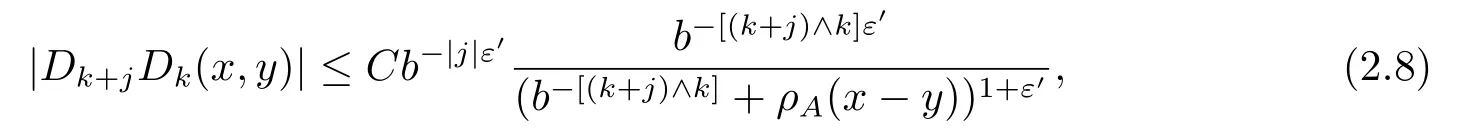
where a ∧c=min{a,c}.Then we have
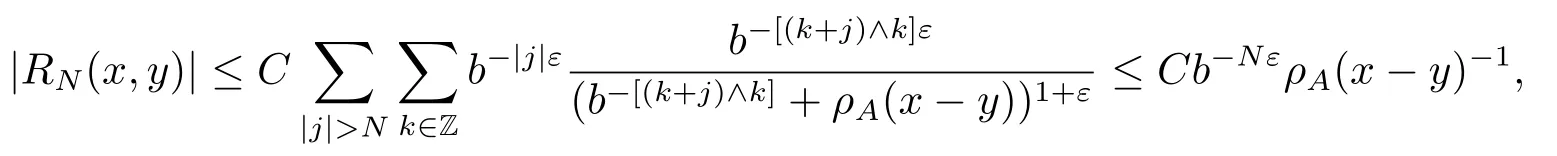
which shows (i) in Lemma 2.1.
For (iii), by (2.8) and (i) in Lemma 2.1, similar to [10,14-15], we can prove that
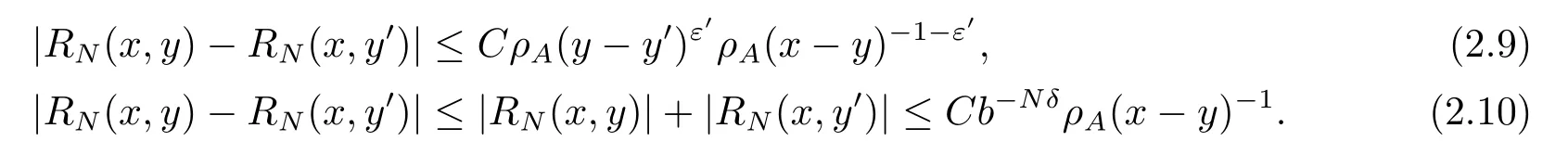
Taking the geometric mean between (2.9) and (2.10), we obtain (iii) in Lemma 2.1.
Similar to (iii), we can prove (ii).For (iv), similarly, we also can obtain

Hence, taking the geometric mean between (2.11) and (2.12), (iv) holds.

On the other hand, for η <ε, there are

Taking the geometric mean between(2.13)and(2.14),and between(2.13)and(2.15),we have
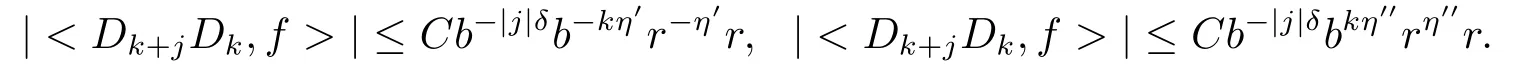
Set r =bk0.Thus
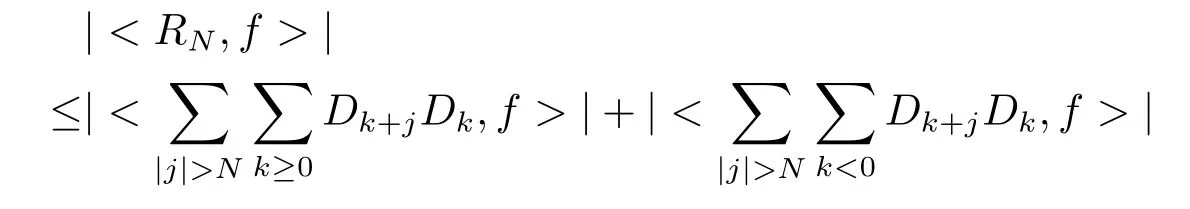

which shows (v) in Lemma 2.1, and hence Lemma 2.1 holds.
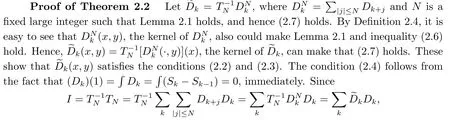
all we need is to prove that the series in (2.1) converges in the norm of Lpand MA(β′,γ′).
First,suppose that f ∈MA(β,γ).Then the convergence of the series in(2.1)in MA(β′,γ′)is equivalent to
Note that
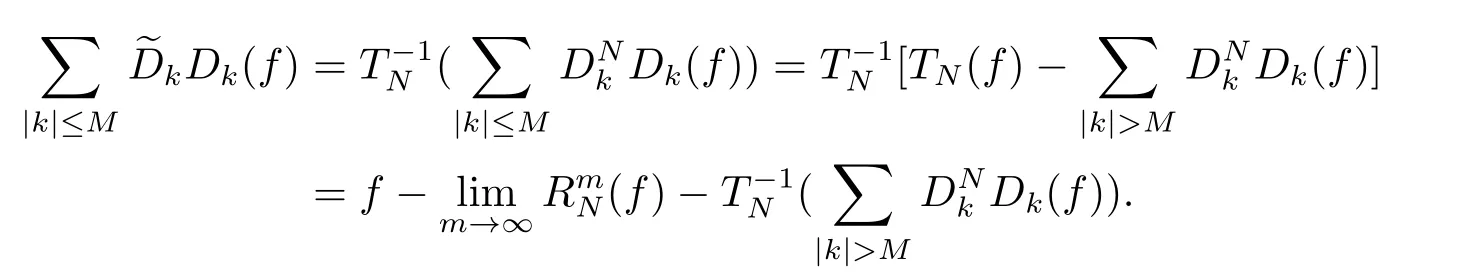
Therefore, to show (2.16), it suffices to prove
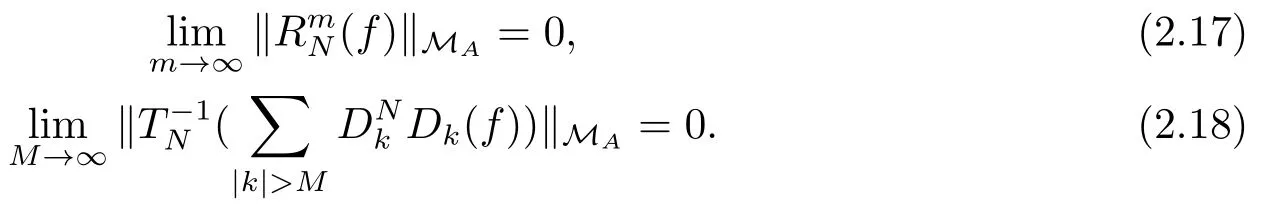
By (2.6), and N is large enough to guarantee Cb?Nδ<1, we have
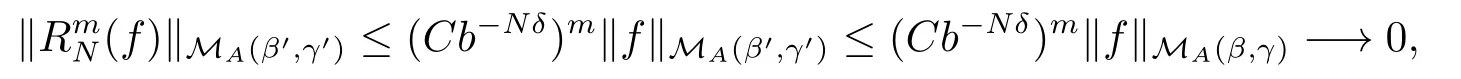
which gives (2.17).To prove (2.18), we claim that
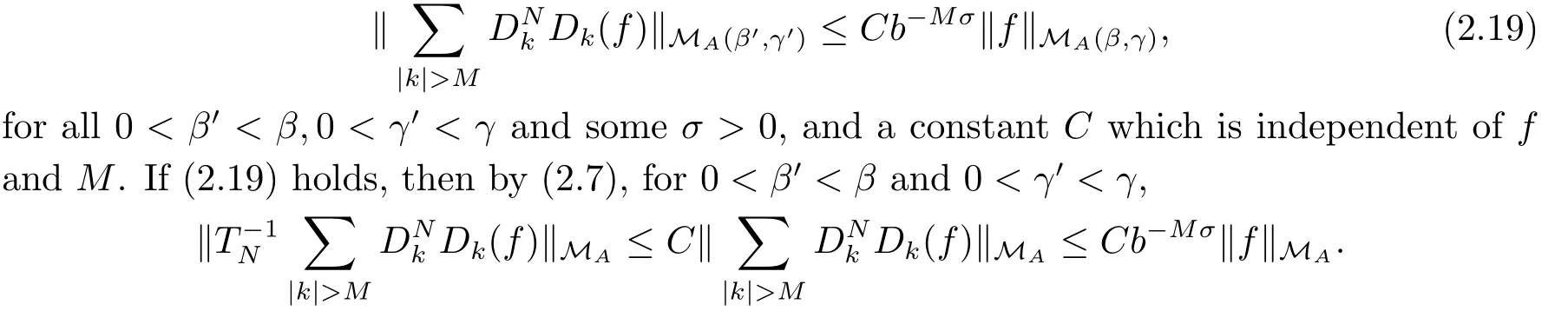
Thus, (2.18) holds.
To prove (2.9), it suffices to show that for 0 < β′′< β and 0 < γ′< γ, there exists a constant C which is independent of f, M and some σ >0 such that
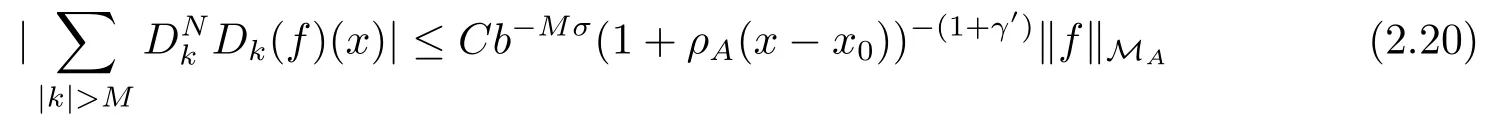
and
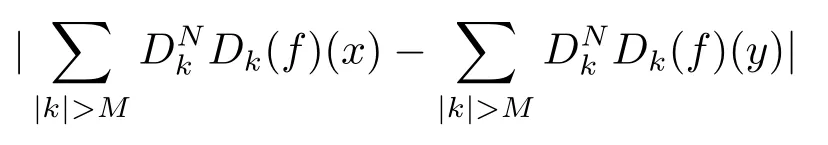
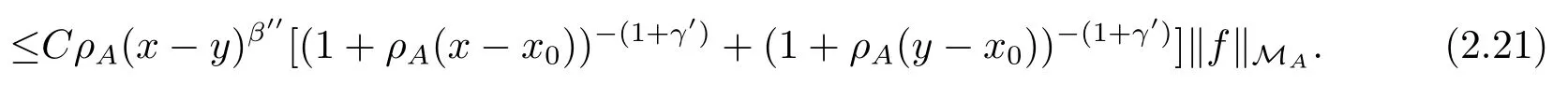
In fact, if (2.20) holds, we have
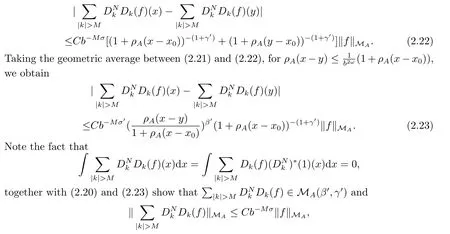
which gives (2.19).It remains to prove (2.20) and (2.21).
For (2.20), noting that Ek=Dk, it is easy to check that Ek(x,y), the kernel of Ek,satisfies the conditions(i), (ii)and(iii)in Definition 2.4 with ε replaced by ε′,0<ε′<ε,and Ek(1)=0.Consider first the case ρA(x ?x0)≤b, by Ek(1)=0, then
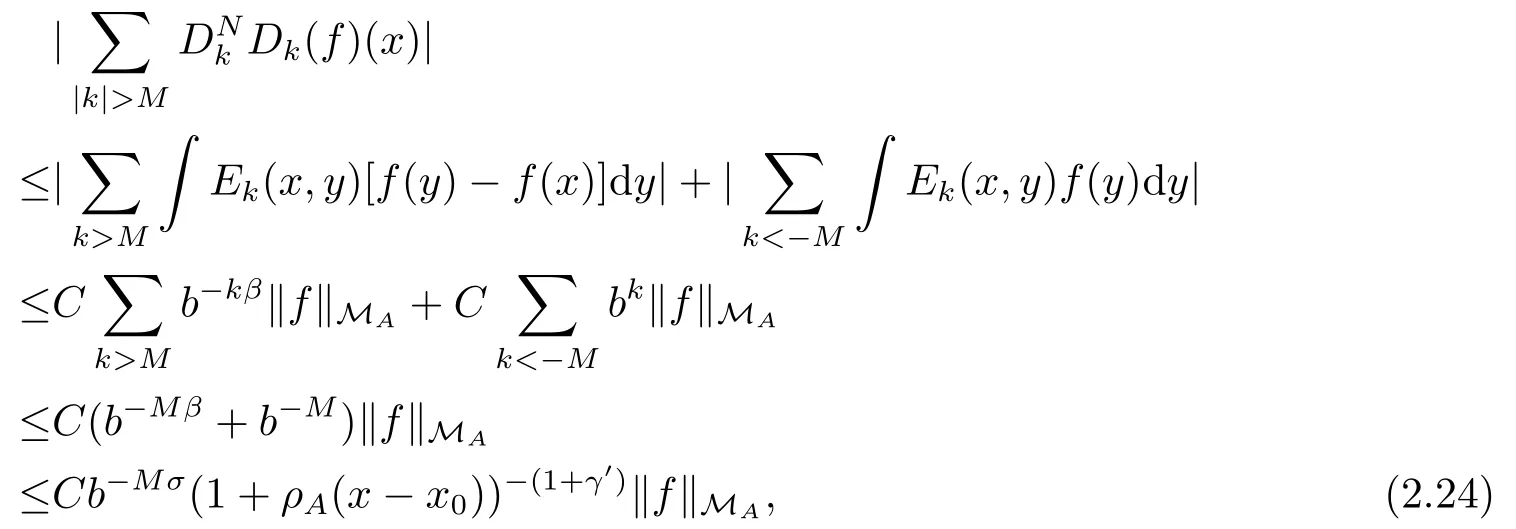
where σ > 0 is a constant and 0 < γ′< γ.This proves (2.20) for ρA(x ?x0) ≤b.If ρA(x ?x0)>b, then
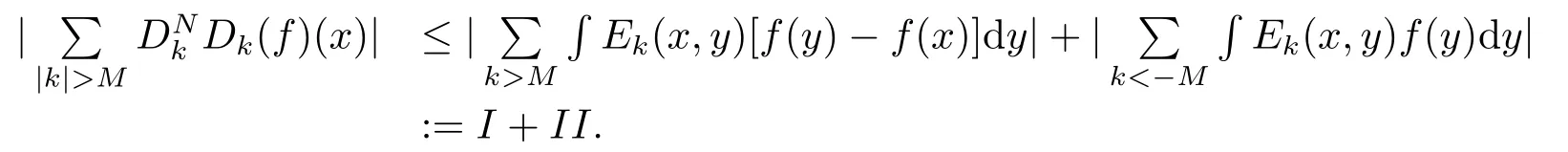
Since ρA(x ?y) ≤Cb?k< Cb?Mfor k > M and hence ρA(x ?y) < 1, if M is larger than logbC.Thus
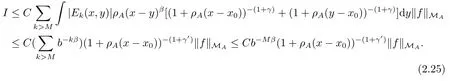
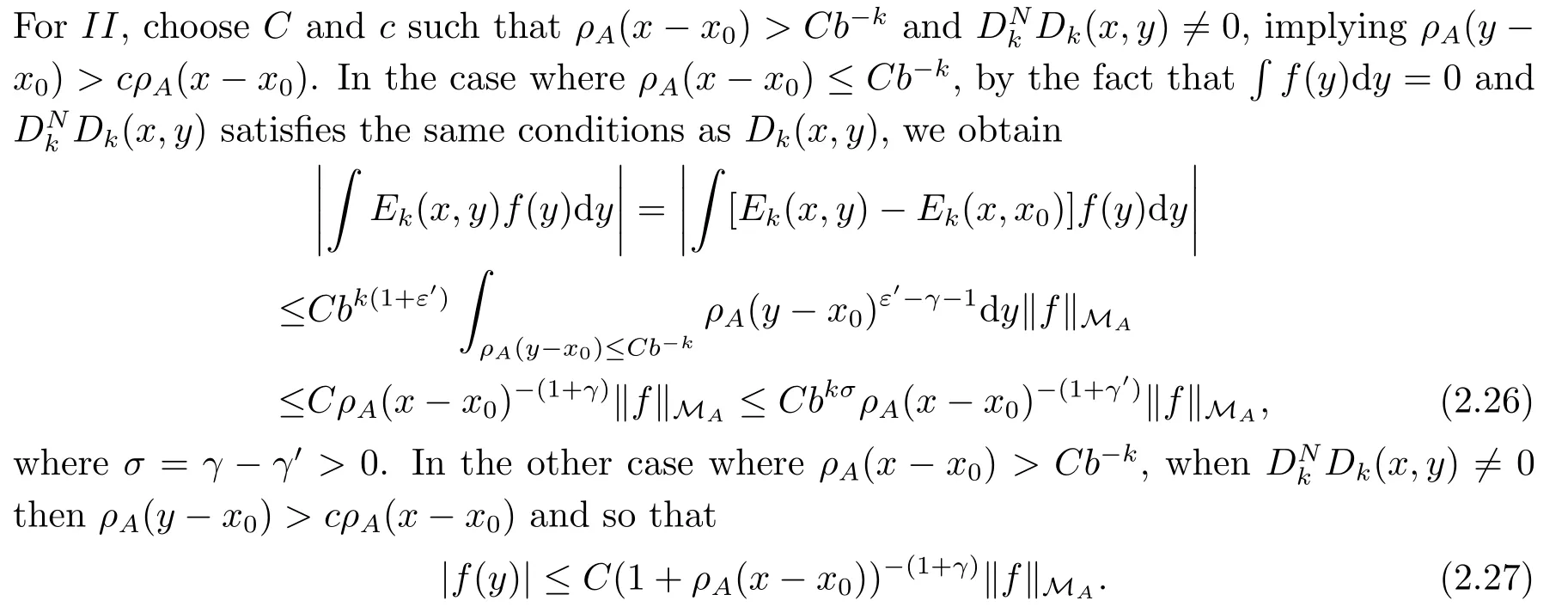
Thus
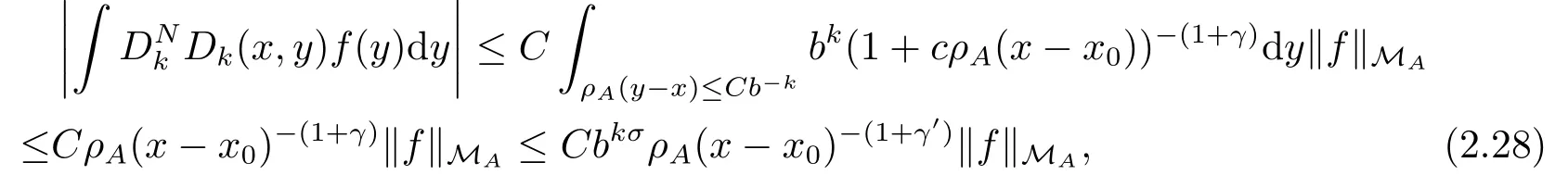
where σ =γ ?γ′>0.Combining (2.26) and (2.28) shows
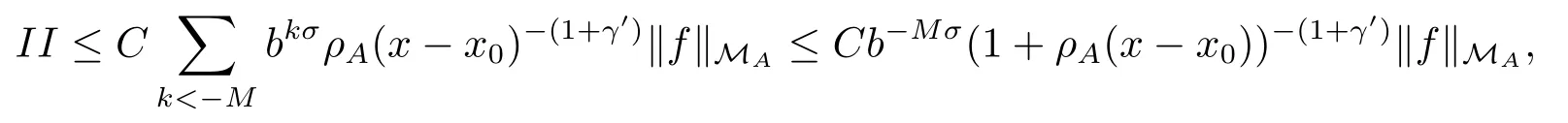
which together with (2.24) and (2.25) implies (2.20).

and
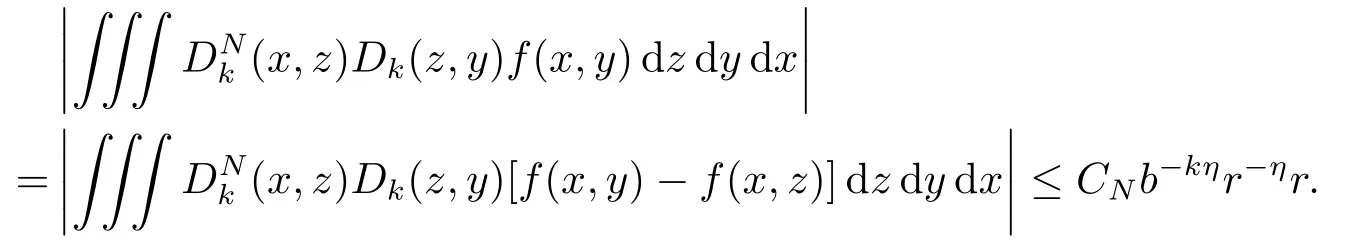
Thus,
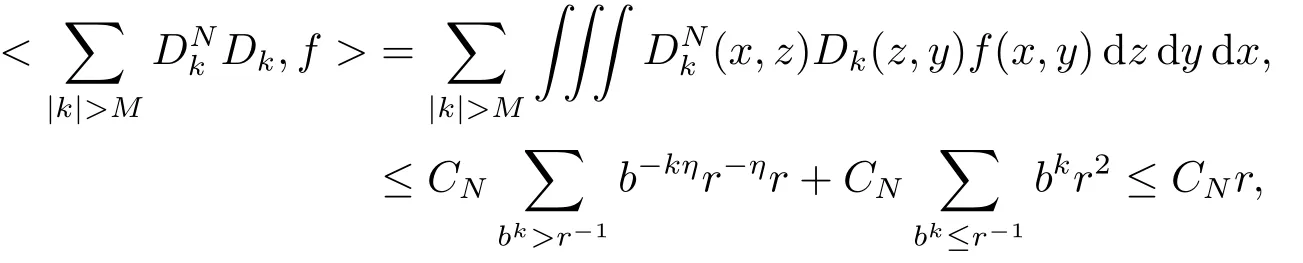
Finally,to see that the series in(2.1)converges in Lpfor 1 With the help of the Calder′on-type reproducing formula in Section 2, in this section, we use the operator family of approximations to the identity to define the Besov and Triebel-Lizorkin spaces associated with a dilation A. Theorem 3.1Suppose that {Sk}k∈Zand {Pk}k∈Zare approximations to the identity defined in Definition 2.4.Set Dk=Sk?Sk?1and Qk=Pk?Pk?1.Then for all f ∈(MA(β,γ))′with 0 < β,γ < ε, where ε is the regularity exponent of the approximations to the identity,and ?ε<α<ε, there are ProofFor (3.1), without loss of generality we may assume that Since Dk(·,y) ∈MA(ε,ε), by the Calder′on-type reproducing formula in (2.5), there exists a family of operators {Qj}j∈Zsuch that Thus Changing Qkand Dk, we can complete the same proof for the other inequality in (3.1). For (3.2), by (3.4), we can obtain where MρA(f) is the Hardy-Littlewood maximal operator of f.Thus, using the Fefferman-Stein vector valued maximal function inequality (1.5) for 1 which shows one inequality in (3.2).The other inequality in (3.2) can be proved similarly.The proof of Theorem 3.1 is completed. The proof of Theorem 3.2 is completed. Hence Using the method of the proof of Theorem 3.1, we have Hence, (3.9) holds. This completes the proof of Theorem 3.3. By Theorem 3.3 and Remark 3.2, we can obtain the following result immediately.
3.Besov and Triebel-Lizorkin Spaces with A Dilation A