Dynamics and near-optimal control in a stochastic rumor propagation model incorporating media coverage and L′evy noise
Liang’an Huo(霍良安) and Yafang Dong(董雅芳)
Business School,University of Shanghai for Science and Technology,Shanghai 200093,China
Keywords: rumor propagation,near-optimal control,popular science education,media coverage,L′evy noise
1. Introduction
In recent years, with the rapid development of the Internet, information exchange between individuals has become more rapid and convenient. As a kind of information with negative influence, the spreading speed and influence range of rumors has grown exponentially. In serious cases, rumors also harm social stability, which should cause all society to be highly vigilant.[1-3]With the outbreak of COVID-19,there have been many rumors, such as “You can prevent the virus with multiple layers of masks”, “A patient flees from Peking Union Medical College Hospital” and so on. These rumors spread wildly on the Internet, resulting in the inability to allocate and use material resources such as masks, and also caused strong negative effects and social panic,which largely hindered the timely prevention and control of the epidemic.Therefore, it is necessary to minimize the negative impact of rumor propagation by studying the optimal control theory of the rumor propagation process.
As for the propagation process,many scholars have done relevant studies.In 1965,Daley and Kendal proposed the classic rumor propagation model (DK model),[4]which brought a breakthrough for further research on rumor propagation.Later,Maki and Thomson further improved the DK model into the MK model.[5]On this basis, scholars have proposed and studied many extended propagation models.[6-8]With the development of science and technology, the Internet and other complex networks have penetrated into people’s lives and become an important platform for rumor propagation. Therefore, many scholars began to study the influence of complex network topology on the rumor propagation process. Zanette studied the dynamics of an infectious disease-like model of rumor propagation in a small-world network,[9]while Albertet al.studied the tolerance of complex networks to errors.[10]Doeret al.analyzed how rumors spread in social networks and simulated the propagation process of rumors in different network topologies.[11]Liuet al.proposed a Susceptible-Hesitated-Infected-Removed (SHIR) model to study the dynamics of competitive dual information diffusion.[12]Donget al.proposed a new model for the rumor spreading process in online social networks.[13]Zhaoet al.extended the SHIR model as in epidemic disease modeling to investigate the propagation dynamics of information online.[14]Zhuet al.proposed a rumor propagation model with nonlinear functions and time delay in social networks.[15]
The models involved in the above articles are all deterministic, but uncertainty is inherent in most real-world systems,such as changes in national policies and the involvement of media coverage(that is,the numbers of ignorant and spreaders may change suddenly after the involvement of media coverage). The L′evy jumping process is a discontinuous function with right continuity and left limit, which can better describe this mutation. Therefore, it is of great value to study the impact of the L′evy jumping process on the dynamics of rumor propagation. The stochastic model constructed by the combination of a deterministic model and L′evy noise can better describe the propagation process of rumors in the real world. In recent years, the stochastic propagation model of rumors has also increasingly attracted scholars’ attention. Some scholars have considered L′evy noise, but they mainly studied the dynamic propagation behavior of rumors.[16,17]Dauhooet al.converted the deterministic rumor model into a stochastic rumor model by using the stochastic coefficient representing the influence of the system,proving the existence and uniqueness of global and local solutions.[18]Jiaet al.studied a random rumor propagation model and obtained that the threshold of the random model under the influence of white noise was less than that of the deterministic model.[19]Lvet al.studied a random delayed rumor propagation model.[20]Ankuret al.introduced a random rumor model into a social network containing expert intervention,and drew the conclusion that noise might be one of the reasons for the persistence of rumors in a stochastic environment.[21]
The purpose of studying the dynamic process of rumor transmission is to better control rumors and reduce their negative impact. Therefore, how to control the spread of rumors has become an issue of concern to an increasing number of scholars.Amineet al.studied a new rumor propagation model and theoretically proved the existence of optimal control.[22]Chenet al.discussed the control of rumor propagation in an emergency and analyzed the stability of the model.[23]The literature contains some research in this area. For example,Huiet al.aimed to study the rumor spreading mechanism on social network platforms during the transmission of COVID-19,and to take education as a control measure for rumor spreading.[24]Wanget al.studied the extent to which media reports before the crisis effectively refuted rumors,and evaluated the impact of media reports before the crisis on the effectiveness of rumor refutation in the experiment.[25]Based on the nonlinear dynamics model, Huoet al.analyzed the rumor propagation process and studied the influence of media coverage and government emergency strategies on the information propagation dynamics after emergencies.[26]
There are two possible reasons for the spread of rumors.First of all, as false information, rumors are extremely misleading and provocative. Some people do not have enough knowledge to distinguish between true and false information,which leads people to listen to rumors and propagate them into facts. Secondly,when a rumor is generated and propagated in an emergency, there is no corresponding real information released in time to refute the rumor,which leads to the constant spread of the rumor. In this case, popular science education and media coverage are two effective methods to prevent the crisis of rumor spreading. Popular science education can improve people’s knowledge level and the ability to identify rumors,and directly transform the ignorant into the immune. In this way, the source of rumor propagation can be reasonably controlled and the path of rumor propagation can be further cut off to weaken the influence of rumors. Media coverage can refute rumors in a targeted way and reduce the probability of rumors propagating,which can not only let people know the truth in time,but also guide people to choose the right behavior and prevent overreaction. In addition,the exact solution of the equation of state and the adjoint equation is difficult to obtain and the exact control is also difficult when the stochastic factors are considered.Therefore,it is of great practical significance to study the approximate optimal control of the rumor propagation model.
Based on the above analysis and actual situation,a rumor spreading model that joins the L′evy process can describe the dynamic process of rumor propagation more accurately. Most researchers use deterministic models when conducting rumor spreading research,and rarely consider random factors. In addition,some researchers only conduct research on the process,and rarely mention control strategies. Therefore, this paper proposes a stochastic model combining media coverage and L′evy noise to describe the dynamic process of rumors spread in the real world. By introducing two control strategies,popular science education and media coverage, an optimal control problem is proposed to minimize the influence of rumors spread and control costs.
The structure of this paper is as follows. Section 2 introduces the preparatory knowledge and establishes the stochastic ignorant-spreader-recovered(ISR)model;Section 3 and 4 give the necessary and sufficient conditions for near-optimal control; Section 6 carries on the numerical simulation; and Section 7 summarizes the whole paper.
2. Model formulation
In the classical ISR model of rumor propagation,[27]nodes in social networks are divided into three categories: ignorant(I)is a node without any information about the rumor,spreader(S)is the node that accepts the rumor and propagates it, and recovered (R) is the node that fnially decides to stop propagating rumors after contact with rumors. In social networks,rumors propagate among people in accordance with the rules of mass action. The ignorant node has not contacted the rumor and will not propagate it,but it may become a spreader by contacting the spreader nodes.
The propagation process of rumors can be described as follows:
(i) The main propagation model of rumors is communication after the interaction of individual opinions, that is,the information exchange between individuals through telephone, instant messaging software, face-to-face conversation and other means.
(ii)Assume that a spreader propagates rumors with a certain probability when they meet an ignorant person. Media coverage can specifically refute rumors by releasing facts,thus gradually reducing the probability of rumor propagation and finally reaching a stable value.
(iii) When the spreader meets the recovered or another spreader,they lose the motivation to spread rumors.
(iv) Rumors spread within a certain community, and the total number of people is variable. Those who initially enter the community are ignorant.
The total population isN=I+S+R. Due to the contact between different types of individuals,information is transmitted and diffused,and then the types of individuals are changed,as shown in Fig.1.
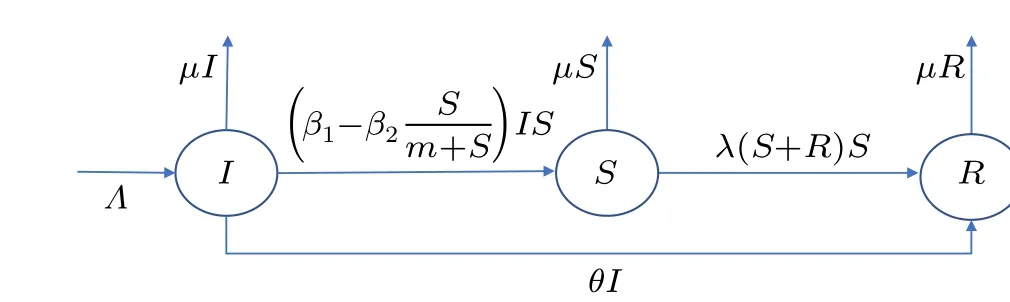
Fig.1. Schematic diagram of a rumor under the influence of popular science education and media reports.
We develop this problem on the basis of a deterministic ISR model[28]as follows:


Generally, a L′evy process ~L(t) consists of the sum of a linear drift, a Brownian motionB(t) and a superposition of centered independent Poisson processes with different jump sizesλ(dv) which is the rate of arrival intensity of the Poisson process with a jump of sizev. According to the L′evy-Ito decomposition theorem,[29]we get

In the above model, when rumors spread to a certain scale, they may endanger social harmony and stability, and bring huge losses to the related people. Therefore,it is necessary to study how to control the propagation of rumors. The reason why rumors are widely spread may be that some people are unable to distinguish between true and false information due to their insufficient knowledge reserve, so they take rumors as facts to propagate.Another reason may be that there is no corresponding real information about the breaking event to refute the rumor,so the rumor keeps propagating.
Under such circumstances,popular science education and media reports are the most effective ways to curb the spread of rumors. On the one hand, popular science education can improve a person’s cognitive level so as to directly transform the ignorant into the immune. Popular science education stops rumors from spreading in the first place and reduces the number of the ignorant while increasing the number of the immune.On the other hand,media coverage can also be a targeted refutation of rumors. By increasing media coverage,the truth can be publicized in a timely manner and public opinion can be actively guided so as to reduce the number of spreaders and the negative impact of rumor propagation. Reasonable coverage and time for media coverage and popular science education can reduce the number of spreaders and ignorants to a lower level. Therefore, we introduce education and media controlu(t)=(uθ(t),um(t))into the stochastic ISR model(3)as follows:
whereumanduθrepresent the control variables for the influence of science popularization education and media coverage,respectively. LetUad?Rbe a bounded nonempty closed set.uθ,um:[0,1]×Ω →Uis called admissible, if it is anFt-adapted process with values inUad.
The purpose of optimal control is to minimize the negative effects caused by the propagation of rumors and maximize the positive social utility. This paper chooses the following aspects to consider the social utility of the propagation of untrue information:
(I) Minimize the number of ignorant individualsIand spreadersSof rumors.
(II)Minimize the cost of variable control in the process.
We define the associated objective function as

3. Analysis of near-optimal control for stochastic ISR model
Before we study near-optimal control,we give some preliminary knowledge as follows; let (Ω,F,(Ft)0≤t≤T,P) be a complete filtered probability space on a finite time horizon[0,T], and we assume that (Ft)0≤t≤Tis the natural filtration andF=Ft. If the control processu:[0,T]×Ω →Uis anFt-adapted process with values inU,then it is called admissible.We useUadto denote the set that consists of all admissible controls;|·|denotes the form of an Euclidean space;fxis the partial derivative offwith respect tox;χsdenotes the indicator function of a setS;andX+Yis the set{x+y:x ∈X,y ∈Y}for any setsXandY.

Definition 1[32]Ifu*(·) attains the minimum ofJ(0,x0;u(·)), then an admissible controlu*(·) is called optimal control.
Definition 2[32]For any givenε >0, if|J(0,x0;uε(·))-V(0,x0)|≤ε, an admissible controluε(·) is calledε-optimal control.
Definition 3[32]A family of admissible controls{uε(·)}parameterized byε >0 and any elementuε(·) in the family are called near-optimal control,if|J(0,x0;uε(·))-V(0,x0)|≤δ(ε)holds for a sufficiently smallε >0,whereδis a function ofεsatisfyingδ(ε)→0 asε →0. The estimateδ(ε)is called an error bound. Ifδ(ε)=cεkfor somec,k >0,thenuε(·)is called near-optimal with orderεk.
Lemma 1 Ekeland’s principle.[33]Let (Q,d) be a complete metric space andF(·):Q →Rbe a lower-semicontinuous and bounded from below. For anyε >0, we assume thatuε(·)∈Qsatisfies

(H3)The control setUis convex.
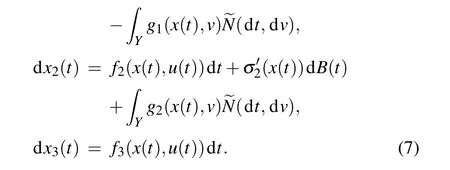
Under hypotheses(H1)and(H2),the adjoint equation admits a unique adapted solution. By Mazur’s theorem,[34]we can then obtain the existence of optimal control under hypothesis(H3).
3.1. Sufficient conditions of near-optimal controls
In order to obtain sufficient conditions of near-optimal controls, we give the following lemmas for the moment estimation of the state and adjoint equation. For convenience,letx(t) = (x1(t),x2(t),x3(t))T= (I(t),S(t),R(t))T,u(t) =(um(t),uθ(t));then we get

3.1.1. Some priori estimates of the ignorant, spreader and recovered
Then we give some prior estimates of the ignorant,spreader and recovered. The following lemma illustrates the boundedness ofεmoment estimates for the ignorant,spreader and recovered.


The second moment estimate of the adjoint Eq. (10) is given in the following lemma.
Lemma 3 For anyum(t),uθ(t),u′m(t),u′θ(t)∈Uad, we have




Using Gronwall’s inequality,we can derive Eq.(11)from the above inequality. Then the proof is complete.
3.1.2. Sufficient conditions for near-optimal controls
In this section,we define the Hamiltonian functionH(t,x(t),u(t),p(t),q(t),r(v)),H:[0,T]×R3+×Uad×R3+×R2+×R2+→R,


According to Eqs.(31)and(23),we can obtain

Therefore,from Eq.(38)and hypothesis(H2),we get
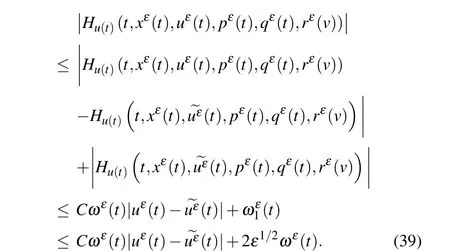
According to lemma 3 and the definition of ~d, the expected conclusion can be obtained from Eqs. (30) and (39) and Holder’s inequality.
3.2. Necessary conditions for near-optimal controls
In this section, we discuss the necessary conditions of near-optimal control. First, we give the following priori estimates to the ignorant, spread and recovered persons of the system to get our results.
In order to give the following lemma, we first define a metric on the admissible control fieldUad[0,T]as follows:
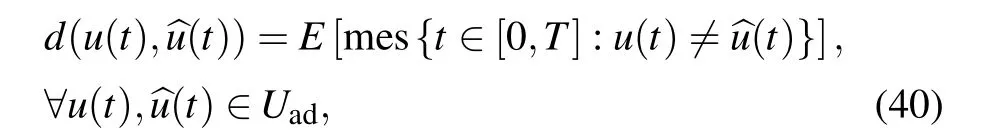
where mes stands for the Lebesgue measure. SinceUadis closed,it can be proven thatUadis a complete metric space underd.[34]The problem of moment estimation of the distance between two state variables is discussed by using the distance of the defined control variables.
Lemma 4 For allk ≥0 and 0<l <1 satisfyingkl <1, andu(t),^u(t)∈Uad, along with the corresponding trajectoriesx(t),x′(t), there exists a positive imprecise parameterC=C(k,l)such that



The proof is complete,which is the result of the estimation of the state Eq.(6).
For the result of moment estimation of the adjoint equation,we have the following lemma.
Lemma 5 Let hypotheses (H2) and (H3) hold. For any 0<l <1 and 1<k <2 satisfying (1+l)k <2, there exists a positive imprecise parameterC=C(l,k) such that for anyu(t),^u(t)∈Ualong with the corresponding trajectoryx(t),^x(t)and the solutionp(t),q(t),r(v),(^p(t),^q(t),^r(v))of the adjoint equation,we have



4. Numerical simulations
In this section, we use MATLAB to perform numerical simulations and use these numerical examples to illustrate the impact of popular science education, media reports and L′evy noise on the dynamics of rumor spreading.We set the parameter values as follows:Λ=0.25,μ=0.15,β1=0.6,β2=0.4,λ=0.2,θ=0.2,σ=0.009.
According to Milstein’s method,[37]we can get the corresponding discretization equation of the state Eqs.(4)and(10)as follows:
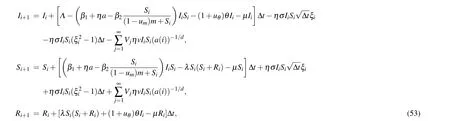
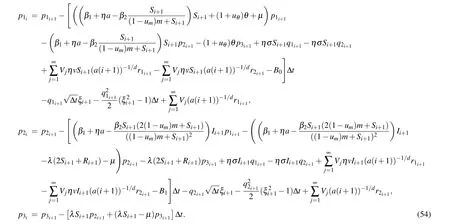
The intensity of L′evy noise can affect the rumor propagation process. Figure 2 depicts the influence of L′evy noise on the rumor propagation process.r(v)stands for response intensities. As shown in the figure,the trend chart of the number of spreaders over time is different under different response intensitiesr(v). The greater the value ofr(v),the faster the value ofS(t)decreases. Therefore, we can reduce the ultimate spread scale of rumors by strengthening external intervention. For example, when rumors spread wildly and even cause bad social impact,the government should promptly popularize relevant knowledge about rumors to guide people to correctly view the content of rumors,and relevant media should also increase their reporting efforts. In this way,the number of spreaders of rumors can be reduced by strengthening external intervention.
We also simulated the time evolution diagram of the number of people in different states during rumor propagation under four different control conditions: (1)um=0,uθ=0 represents the uncontrolled situation;(2)um=0,uθ/=0 represents the situation where only popular science education control is added;(3)um/=0,uθ=0 represents the situation where only media coverage control is added; and(4)um/=0,uθ/=0 represents the situation where both media coverage and popular science education control are added. As can be seen from Fig. 4, when media coverage and popular science education control are added at the same time,the peak value and number of spreaders drop sharply, and the influence scope of rumors becomes smaller. Compared with the other three conditions,the rumor propagation process is easier to control, indicating that this situation is nearoptimal control. For example, in the early days of the COVID-19 outbreak,many people were not familiar with the specific case of novel coronavirus. It was rumored that “symptoms such as fever and cough were signs of infection with COVID-19”. The rampant propagation of this rumor was bound to cause public panic. In order to prevent this crisis,the government provided the latest research on COVID-19 in official news and educated the public through multiple media channels. Popular science education allowed people to learn more about the symptoms of COVID-19 infection, which directly reduced the number of the ignorant and enabled them to convert directly to the immune. Media coverage directly reduced the number of communicators through targeted refutation of the rumor.
In addition, it can be seen from Figs. 3-5 that the dynamic optimal control is effective. Both the control of popular science education and the control of media coverage decline faster than the situation without control. Under the control of government and media intervention,the number of spreaders declines faster than in the absence of control. For example,during the COVID-19 outbreak,the public listened to the rumor that “Shuanhuanglian could prevent the novel coronavirus”,so they rushed to buy Shuanhuanglian,causing chaos in the market. The government quickly educated the public about the novel coronavirus treatment, and many media outlets debunked the rumor. The double control increased the number of people immune to the rumor. Taking a closer analysis,we can see that when the media coverage control strategy is added, the control effect is good but not great. When the government science education control strategy is added, the control effect is significantly improved. This simulation result shows that the government science education control strategy is more effective than the media coverage control strategy.
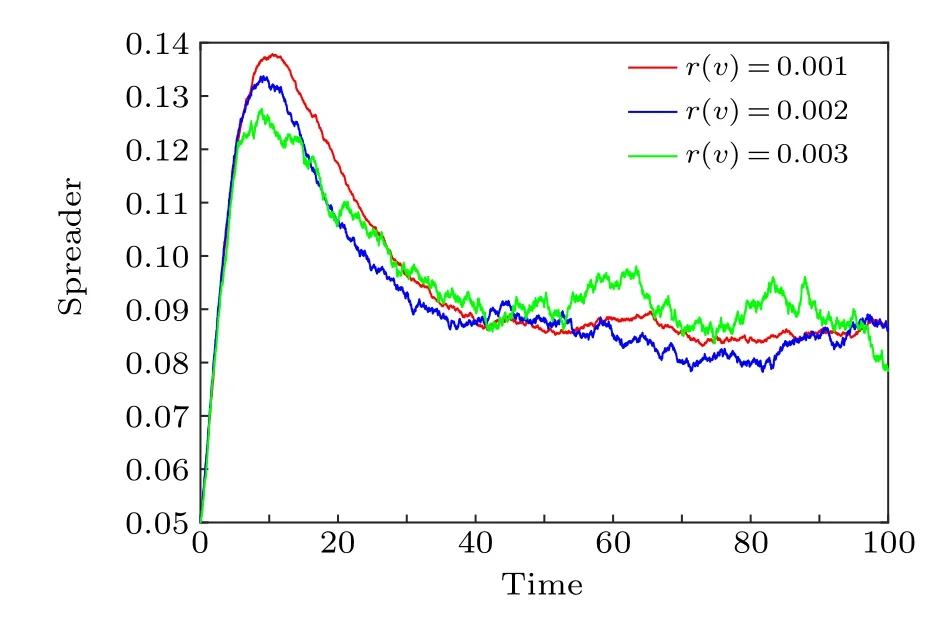
Fig.2. Path of S(t)under different response intensities r(v).

Fig. 3. Path of I(t) for the stochastic ISR model with initial (I0,S0,R0)=(0.8,0.2,0.05).

Fig. 4. Path of S(t) for the stochastic ISR model with initial (I0,S0,R0)=(0.8,0.2,0.05).

Fig. 5. Path of R(t) for the stochastic ISR model with initial (I0,S0,R0)=(0.8,0.2,0.05).
As for the near-optimal control,it can be seen from Fig.6 that solutionsp1,p2, andp3of adjoint Eq. (10) converge to zero in the end, indicating that the objective function reaches the minimum value.
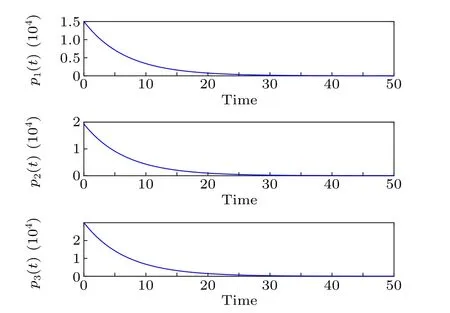
Fig. 6. Path of p1, p2, p3 for the stochastic ISR model with initial(I0,S0,R0)=(0.8,0.2,0.05).
5. Conclusion
This paper studies the problem of near-optimal control of rumor propagation. We first construct a stochastic model that includes media reports and L′evy noise. Then,in order to minimize the impact of rumor propagation and control costs,we introduce two control strategies: popular science education and media coverage. Using the Hamiltonian function and Pontryagin maximum principle, the necessary and sufficient conditions for the model to be close to the optimal control are obtained.Finally,we verify the effects of popular science education,media report control and noise control through numerical simulations. The results show that popular science education and media coverage can effectively control the spread of rumors, and these two control strategies can reduce the cost of rumor dispelling to the lowest level. At the same time,L′evy noise will also affect the process of rumor propagation.The louder the noise, the faster the attenuation speed of the spreader. In this paper,we assume that the parameters are precisely known,but may not be true due to various uncertainties.The influence of uncertain parameters and time delay on the rumor control process is worthy of further study.
Acknowledgments
Project supported by the Program for Professor of Special Appointment(Eastern Scholar)at Shanghai Institutions of Higher Learning,and the Project for the Natural Science Foundation of Shanghai,China(Grant No.21ZR1444100),and the Project for the National Natural Science Foundation of China(Grant Nos.72174121,71774111,71871144,and 71804047).
- Chinese Physics B的其它文章
- Surface modulation of halide perovskite films for efficient and stable solar cells
- Graphene-based heterojunction for enhanced photodetectors
- Lithium ion batteries cathode material: V2O5
- A review on 3d transition metal dilute magnetic REIn3 intermetallic compounds
- Charge transfer modification of inverted planar perovskite solar cells by NiOx/Sr:NiOx bilayer hole transport layer
- A low-cost invasive microwave ablation antenna with a directional heating pattern

