Tetrapartite entanglement measures of generalized GHZ state in the noninertial frames

Qian Dong(董茜) R.Santana Carrillo Guo-Hua Sun(孫國華) and Shi-Hai Dong(董世海)

1Centro de Investigaci′on en Computaci′on,Instituto Polit′ecnico Nacional,UPALM,CDMX 07738,Mexico

2Catedr′atica CONACyT,Centro de Investigaci′on en Computaci′on,Instituto Polit′ecnico Nacional,UPALM,CDMX 07738,Mexico

3Research Center for Quantum Physics,Huzhou University,Huzhou 313000,China

4Laboratorio de Informaci′on Cu′antica,CIDETEC,Instituto Polit′ecnico Nacional,UPALM,CDMX 07700,Mexico

Keywords: tetrapartite,generalized GHZ state,entanglement measures,dirac field,noninertial frames

1. Introduction

The concept of entanglement introduced by Einstein,Podolsky,Rosen[1]and Schr¨odinger[2,3]in 1930s has become an important topic in quantum information since the shared entangled qubits support us to perform some quantum mechanical forms of communication,e.g.,quantum dense coding and quantum teleportation.[4-10]This is because the non-locality is one of its most important characteristics. Among the different kinds of description for the degree of the entanglement, the negativity[11,12]and its relevant whole entanglement measures including the algebraic and geometric averages[13]are often used to study the degree of the entanglement. The von Neumann entropy[14-16]is also applied to study the entanglement property of the entangled quantum system. Up to now,a number of authors have worked out the bipartite and tripartite systems except for many multipartite systems.[10,17-24]In recent years, many endeavors were devoted to the inertial quantum properties,and a lot of interesting contributions in the noninertial frames have been made,[21,25-39]in which the general relativity,quantum field theory and quantum information theory have been combined.[13,21]This is because the non-negligible effects of relative motion have occurred in noninertial frame on quantum dynamics. Moreover, the relativistic field theory provides not only a complete theoretical framework but also an essential theory for many potential experimental setups. From these works mentioned above,it is recognized that the entanglement is degraded when the observer is moving in an acceleration. Since the tripartite entangled state was studied,[30]a lot of papers focused on some certain states, e.g., the GHZ state, the W-state and other relevant entangled states. Along with this line,we have carried out the entanglement measures of the tripartite and tetrapartite systems initialed in the pure or mixed states such as the GHZ,the W-class and the Werner states in noninertial frame.[40-47]Among them, the tripartite entanglement measures for a generalized GHZ state including a polar angleθhave been explored in the noninertial frame.[44]In this work,we are going to investigate the tetrapartite entanglement measures of a generalized GHZ state when the observers are moving in a uniform acceleration. Four different cases, i.e., the observer accelerated from one to four will be studied. The corresponding negativity,the algebraic and geometric averages as well as the von Neumann entropy will be calculated accordingly.

This work is organized as follows. We present in Section 2 the corresponding density matrix of the tetrapartite system initialed in a generalized GHZ state. In Section 3, starting with the density matrix, the negativity (1-1, 2-2 and 1-3 tangles), the algebraic and geometric averagesπ4andΠ4are calculated. The von Neumann entropy is studied in Section 4.We finally present the conclusions in Section 5.

2. Tetrapartite entanglement from one to four accelerated observers

The initial generalized entangled GHZ state to be considered here has the form

The subscripts A,B, C and D denote Alice, Bob, Charlie and David,respectively. This state becomes maximally entangled GHZ case whenθ=π/4. Its degree of entanglement depends on the controllable angleθ, but it is not entangled any more whenθ=0 andθ=π/2.

To study its entanglement property in the noninertial frames,as shown in Refs.[48-50],we use the Rindler coordinates to describe a family of observers in a uniform acceleration.Dividing Minkowski space-time into inaccessible regions I and II makes the accelerating observers in region I naturally disconnect from their analogous counterparts located in region II.The Minkowski vacuum state can be expressed by a product of two-mode squeezed states of the Rindler vacuum.In this work, using a single-mode approximation[21,38,40]rather than the general non-single-mode approximation,[51,52]in which Shi and his co-authors have first constructed the vacuum and one-particle structure states in the Kruskal modes and then studied the quantum coherence in a curved space time and the Bell correlation via quantum partially collapsing measurement, the transformations between both the coordinated systems for the fermion field can be expressed as the following form:[21,27,38,40]

As mentioned above,the observers are confined to move in the region I so that it is natural to trace out the part of the antiparticle state in region II.We shall study this entanglement system in four different cases.

1) When David is accelerated and its density matrixρABCDI=|ψg〉A(chǔ)BCDI·ABCDI〈ψg| can be calculated. For simplicity,we only write out explicitly its nonzero elements

In what follows,we are going to make use of these results to calculate the negativity and von Neumann entropy.

3. Negativity and whole entanglement measures

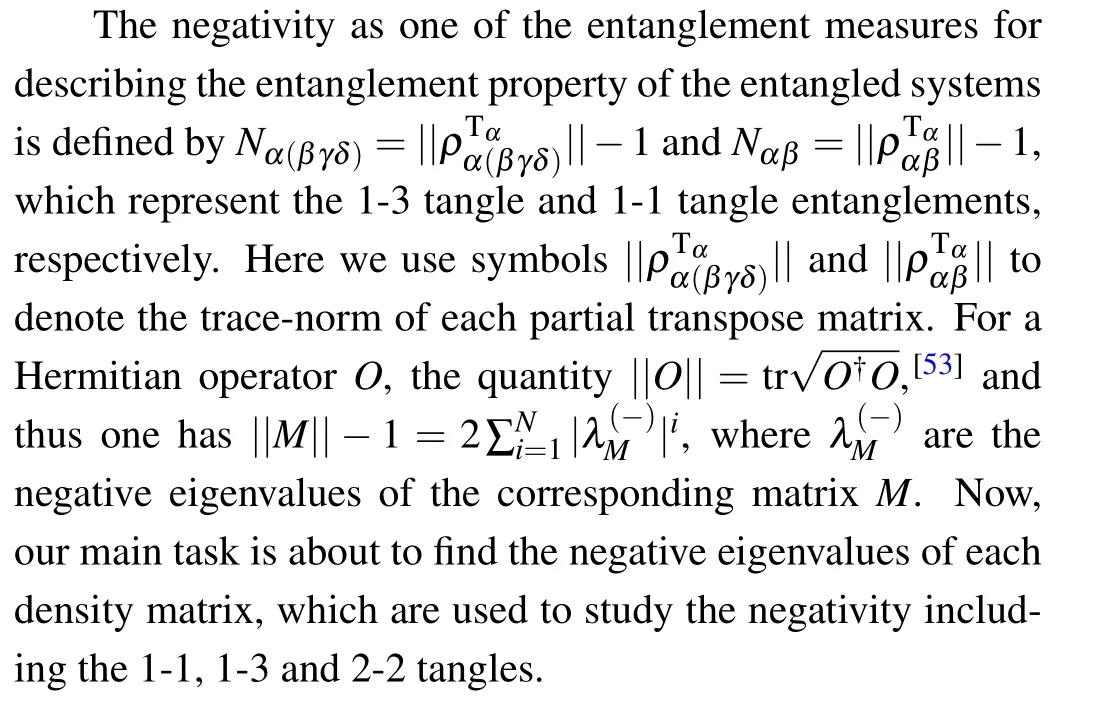
After tedious calculation,the explicit expressions of 1-3 tangles are given by

where

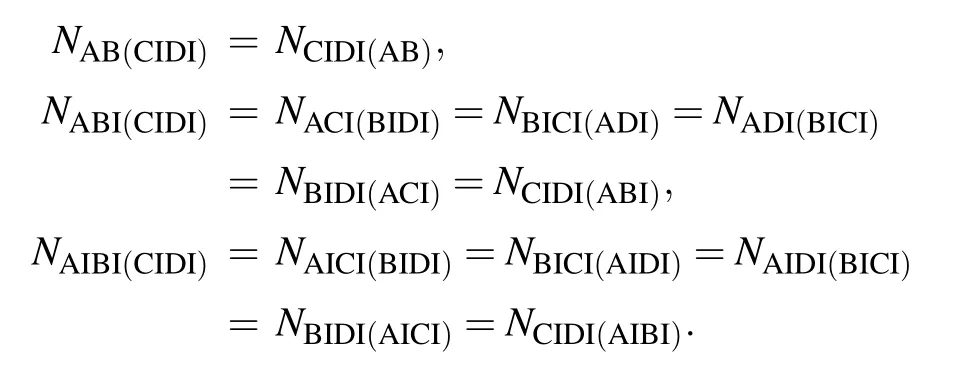
Except for these, we observe that all 1-1 tangles, which include theNκζ,NκIζandNκIζI[κ,ζ ∈(A,B,C,D)],are equal to zero. This implies that there is no any entanglement between any two qubits. This result is different from other cases such as the initial entangled W-class state,[38,39,46]in which the entanglement 1-1 tangles are never equal to zero.

As shown in Fig. 1 about the 1-3 tangles, we find that they first increase withθand then decrease, but they always decrease with the increasing acceleration parameterr. How to explain this phenomenon? As we know, the degree of entanglement for the whole entangled system becomes weaker as the acceleration parameterrincreases so that the entangled tetrapartite system becomes more disordered and less stable.We also notice that the entanglement of all them has never been disappeared even in the particular caser →π/4. On the other hand, we observe that theNA(BCDI)is symmetric with respect toθ=π/4,but there is no such a symmetry for other negativitiesNB(ACIDI),NCI(ABDI),NBI(ACIDI)andNAI(BICIDI).

Based on the obtained negativity, let us study the whole entanglement measures. One of them is called the algebraic averageπ4. Among the four components,the respective definition has the following form:[54]

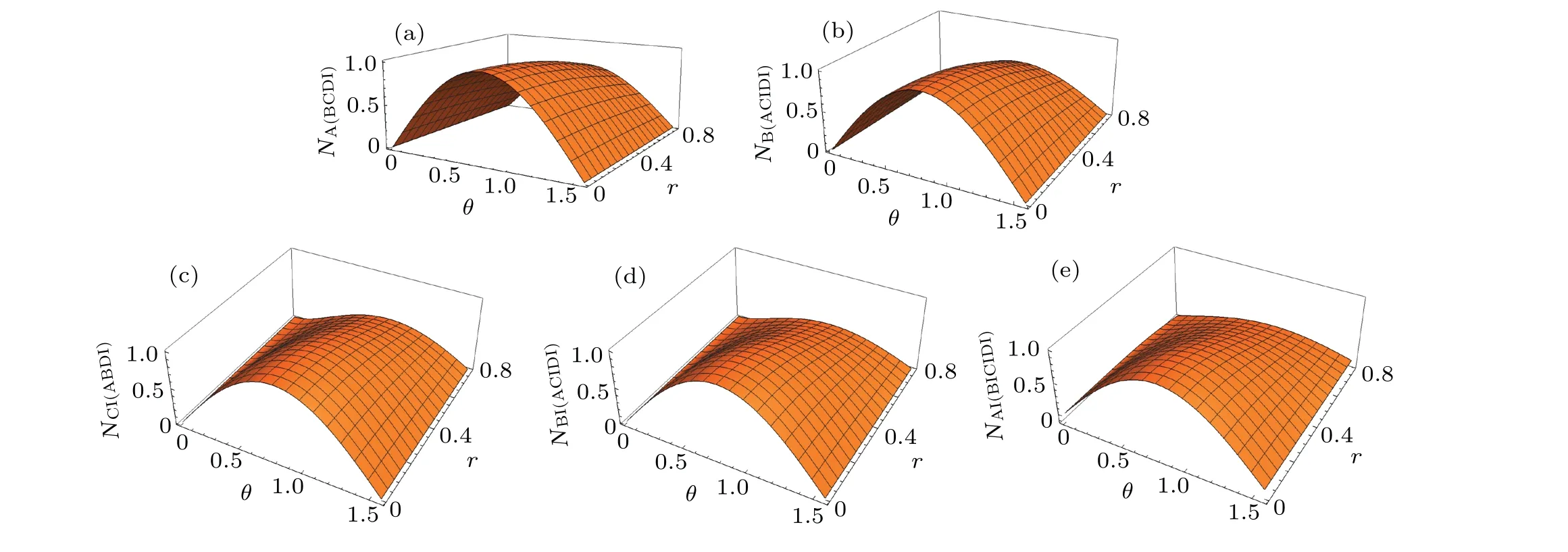
Fig.1. The 1-3 tangles NA(BCDI),NB(ACIDI),NCI(ABDI),NBI(ACIDI) and NAI(BICIDI) shown in(a)-(e),respectively.

Fig.2. Algebraic average πA(BCDI),πDI(ABC),πA(BCIDI)),πCI(ABDI),πA(BICIDI),πBI(ACIDI) and πAI(BICIDI).

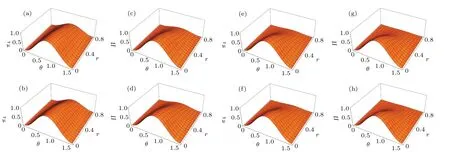
Fig.3. Algebraic average measure π4 and geometric average measure Π as the functions of both angle θ and acceleration parameter r: (a)and(b)for only one observer accelerated; (c)and(d)for two observers accelerated; (e)and(f)for three observers accelerated; (g)and(h)for all observers are accelerated.

We show the algebraic and geometric averagesπ4andΠ4in Fig. 3 and notice that the difference between them is very small. This means that eitherπ4orΠ4can be used to describe the entanglement property of this system. How to explain this phenomenon? It is known from Eqs.(13)-(16)that two(two accelerated qubits)and three(one or three accelerated qubits)of algebraic averagesπκ,πζ,π?andπξare equal to each other if considering the symmetric properties of the negativity. This results in a small difference between the algebraic average and the geometric average. In particular,they are totally equal for the particular case, i.e., the four qubits are accelerated simultaneously.

4. The von Neumann entropy

To know the information measure for an entangled quantum system,let us finally study the von Neumann entropy[56]

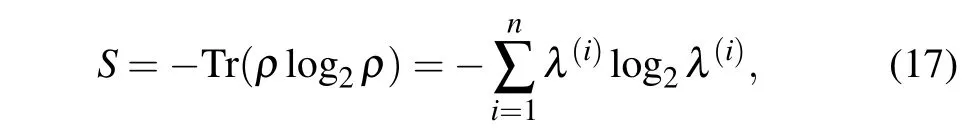
whereλ(i)denotes thei-th nonzero eigenvalue of the density matrixρ.

In what follows,we are going to present eigenvalues of all bipartite,tripartite subsystems and tetrapartite systems,i.e.,

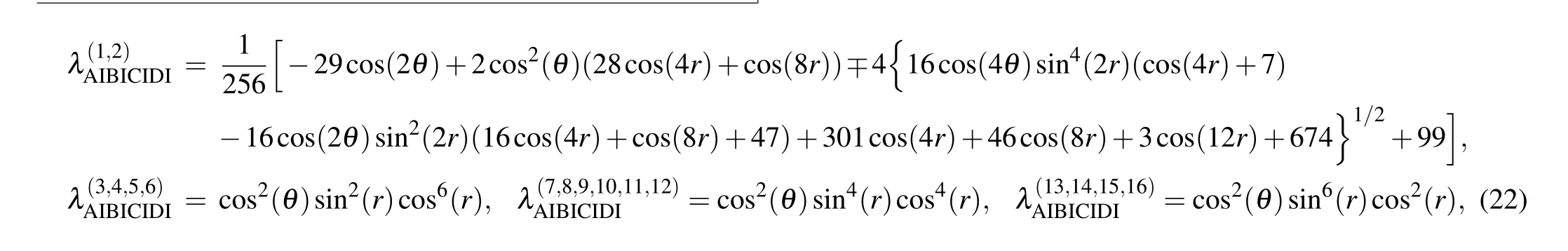
Fig. 4. The von Neumann entropies SABCDI, SABCIDI, SABICIDI and SAIBICIDI plotted as the functions of both parameters.

As displayed in Fig.4,we see that the von Neumann entropy becomes larger with the increasing number of accelerated observers. This is because the entangled system becomes more disordered and less stable as the accelerated observers increase and the quantum correlation among them becomes stronger. In general, the entropy increases with the increasing accelerationrbut does not always increase with it. For example, as illustrated in Fig. 5, we notice that the entropiesS3-0nonandS2-0nonare totally independent of the acceleration parameterr. Here we denote the number of the accelerated observers by the subscripts 0,1,2,3-non. Let us explain this. As we know, the entropiesS3-0nonandS2-0noncorrespond to a particular case,i.e.,without acceleration,and thus it is not strange that they are independent of the accelerationr.On the other hand, we observe forθ ＞π/8 that theS3-3nonandS2-2nonfirst increase with the acceleration parameterrand then decrease with it, butS3-2non,S3-1non, andS2-1nonalways increase with the acceleration parameterr. How to explain this kind of phenomenon? When the tetrapartite system is reduced to a tripartite system with all three accelerated observers,these entropies first reach a maximum value and then decrease when the accelerationrincreases. This implies that the stability of this entangled system is closely related with the controllable angel. This system will pass through a most disordered state and then gradually decreases with the increasingr. However,this did not occur only if one of three qubits,sayS3-2non,S3-1non,andS2-1non,was not accelerated. In addition, we find that the von Neumann entropySABCDI,SABCIDI,SABICIDIandSAIBICIDIalways decrease with the controllable angleθ, while the entropiesS3-3non,S3-2non,S3-1nonandS3-0nonfirst increase with the angleθand then decrease with it, butS3-0nonandS2-0nonare symmetric to the variableθ.Let us explain these interesting phenomena. For a fixed accelerationr/=0,as shown in Fig.4,the von Neumann entropy of the whole entangled system changes gradually from the most disordered state(the controllable angleθ ?0)to a stable state(θ ?π/2). On the contrary, that of the tripartite system in which one of four qubits disappears is different from that of the whole tetrapartite case(see Fig.5). These tripartite entropies will arrive to the most disordered state aroundθ ≈π/4 (exactlyπ/4 for the particular casesS3-0nonandS2-0non)when the controllable angelθincreases from the initial value of zero and then becomes more stable when it reaches toθ ≈π/2.This can also be explained by the fact that the initial GHZ state becomes maximally entangled whenθ=π/4 as mentioned in Section 2. This means that the degree of entanglement in tripartite case is totally different from the tetrapartite case when one of the qubits disappears.

Fig.5. The von Neumann entropies S3-3 non,S3-2 non,S3-1 non,S3-0 non,S2-2 non,S2-1 non and S2-0 non.

5. Concluding remarks

In this work, we have calculated the negativity (say the 1-1, 2-2 and 1-3 tangles) of the generalized tetrapartite GHZ state. Based on these results, the algebraic average and geometric averageπ4andΠ4are computed. It is seen that all 1-1 tangles are equal to zero. This is different from the entangled W-class case,[38,39]in which there exists an entanglement sudden death. When compared between the arithmetic averageπ4and the geometric averageΠ4,it is found that their difference is very small. This implies that one of them can be used to describe this entangled system.

As far as the von Neumann entropy,we have noticed that it increases with the increasing number of accelerated qubits and first increases and then decreases with the angleθ. Generally speaking,the von Neumann entropy for the tetrapartite system increases with the acceleration parameterrbut that of the tripartite, sayS3-3nonandS2-2non, does not always increase with it. TheS3-0nonandS2-0nonare independent of the acceleration parameterrand symmetric to variableθ.

Before ending this work,we are going to give a few useful remarks. Firstly, compared the present results with those of the tripartite case,[44]it is found that the results obtained here are more complicated than those in the tripartite case.For example,the expressions of the respective density matrix in tetrapartite entangled system become more complicated because of the increasing number of qubits. This is the reason why we do not write them out explicitly in this work unlike the tripartite case.[44]On the other hand,the 1-3 and 2-2 tangles do not exist at all for the tripartite case. Undoubtedly,the results obtained in this work will reduce to those of tripartite case when one of entangled qubits,say David,disappears.Secondly,the von Neumann entropy in tetrapartite system becomes larger than that in tripartite case because of the increasing of the number of qubits. Thirdly,with respect to the recent study in Refs. [51,52], it is possible to consider in the future how to carry out the entanglement properties of this system when the general non-single-mode approximation is used.

Acknowledgement

This work was partially supported by the 20210414-SIPIPN,Mexico.