Gilbert damping in the layered antiferromagnet CrCl3

Xinlin Mi(米鋅林), Ledong Wang(王樂棟), Qi Zhang(張琪), Yitong Sun(孫藝彤),Yufeng Tian(田玉峰), Shishen Yan(顏世申), and Lihui Bai(柏利慧)

School of Physics,State Key Laboratory of Crystal Materials,Shandong University,Jinan 250100,China

We theoretically and experimentally studied the Gilbert damping evolution of both acoustic and optical magnetic resonance modes in the layered flake CrCl3 with an external magnetic field H applied in plane. Based on a Lagrangian equation and a Rayleigh dissipation function, we predicted that the resonance linewidth ΔH as a function of microwave frequency ω is nonlinear for both acoustic and optical modes in the CrCl3 flake, which is significantly different from the linear relationship of ΔH ∝ω in ferromagnets.Measuring the microwave transmission through the CrCl3 flake,we obtained the ω–H dispersion and damping evolution ΔH–ω for both acoustic and optical modes. Combining both our theoretical prediction and experimental observations,we concluded that the nonlinear damping evolution ΔH–ω is a consequence of the interlayer interaction during the antiferromagnetic resonance,and the interlayer Gilbert dissipation plays an important role in the nonlinear damping evolution because of the asymmetry of the non-collinear magnetizaiton between layers.

Keywords: Gilbert damping,antiferromagnetic resonance(AFMR),CrCl3

1. Introduction

Antiferromagnets (AFMs) allow designing high-speed and robust spintronic devices due to the advantages of zero net magnetization and high resonant frequency up to THz.[1–6]Studies on spin-transfer torque[7–11]and anisotropic magnetoresistance[12,13]explored the rich physics and advanced the potential applications by controlling and detecting the magnetic order in antiferromagnets. Further development and applications of devices based on antiferromagnetic materials require a more comprehensive understanding of antiferromagnetic dynamics. But different from ferromagnetic dynamics, there is little known about antiferromagnetic dynamics[14–16]due to the more complex internal structures and higher resonant frequencies requiring terahertz techniques to detect.[1,17,18]

To describe the magnetization dynamics of antiferromagnetic systems, a key issue is to find the proper form of damping. Damping represents the dissipation of energy in the magnetic system, which affects the response speed of magnetic devices. It is inextricably linked to many magnetic phenomena such as spin pumping, spin transfer, and domain wall motion,[19,20]and plays an important role in the study of magnetic dynamics. In ferromagnetic systems,there have been a lot of detailed studies on magnetization dynamics with damping,[21–29]and a complete theory has been formed to describe the ferromagnetic dynamics.[22,25]Generally speaking,the magnetization dynamics in a ferromagnetic system is determined by the Landau–Lifshitz–Gilbert (LLG)equation[22,25]

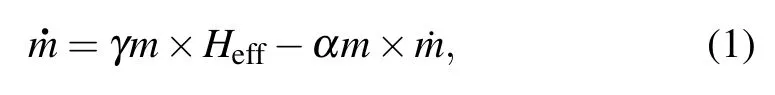
whereHeffis the effective field including the external field,the exchange field and the anisotropy field.γis the gyromagnetic ratio.αis the Gilbert damping constant. The first term on the right-hand side of Eq. (1) determines the precessional motion of the magnetic moment in the ferromagnet around the effective field. The second term is the Gilbert damping which makes the direction of the magnetic moment gradually align to the effective field. The linewidth of the ferromagnetic resonance derived from the LLG equation shows a linear relationship with frequency ΔH–ω,[30]which produces a good agreement with extensive experiments in the ferromagnetic systems.[30–33]So the magnetic damping in ferromagnets is usually investigated by linewidths due to the linear relationship between ferromagnetic resonance linewidths and damping.[30–33]

Although there has been a great deal of research in antiferromagnetic dynamics, there is still not a universally accepted dynamic equation until now. In the 1950s, Kittel applied the Landau–Lifshitz equation to the two sublattices of antiferromagnet and calculated the resonance frequencies of AFMs.[34,35]Following the classical Lagrangian approach that has previously been employed for FMs by Gilbert,[22]Kamraet al.used Lagrangian equations with Rayleigh dissipation to describe the antiferromagnetic dynamics in 2019,[36]and successfully predicted the enhancement of the dissipation rate of ferrimagnets at the compensation point, which has agood agreement with recent experiments.[36,37]The same theory was used by Yuanet al.to find a significant effect of the dissipation moment on the magnon lifetime and domain wall motion.[38]These studies are all for the case of collinear magnetization with an external magnetic field less than the spinflop field. In a non-collinear magnetization case,the damping process would be expected to be different because the asymmetry between the sublattices has an impact on dynamical spin exchange interaction during the antiferromagnetic resonance(AFMR).For example,in a layered antiferromagnet CrCl3,the magnetization from each layer can be easily aligned to a noncollinear case by an external magnetic field due to the relative weak coupling.[39]

In this work, we studied the damping evolution of both acoustic and optical magnetic resonance modes in CrCl3,again starting from the Lagrangian equation with Rayleigh dissipation.[22,36,38]The equations depicting the antiferromagnetic dynamics were established following the method of establishing the LLG equations in ferromagnets using the Lagrangian approach.[22]We obtained the same antiferromagnetic dynamics equations with Kamra and Yuan’s works.[36,38]The Gilbert damping parameter was represented by a 2×2 matrix containing intralayer as well as interlayer damping terms.Then,we applied this theory to describe the antiferromagnetic resonance in CrCl3.[39]The expressions of the linewidths of the optical and acoustic modes were obtained, which predict the linewidth evolution of the optical and acoustic modes with frequency. They both have a non-linear growth but the growth trend of the optical mode is much faster than the acoustic mode. Our experimental data also proved this point. Combining both of our theoretical prediction and experimental observations,we concluded that the nonlinear damping evolution ΔH–ωis a intrinsic nature during the antiferromagnetic resonance and the interlayer Gilbert dissipation plays an important role in the non-linear growth of linewidth because of the asymmetry of the non-collinear magnetization between layers.

2. The theory of antiferromagnetic dynamics

We consider the simplest antiferromagnet with two sets of sublattices,whose magnetizations are described byM1andM2,respectively.Here we describe this system in the frame of the Lagrangian classical field theory,with introducing the socalled Rayleigh dissipation functional. Then the Lagrangian equation describing the antiferromagnetic system is given by

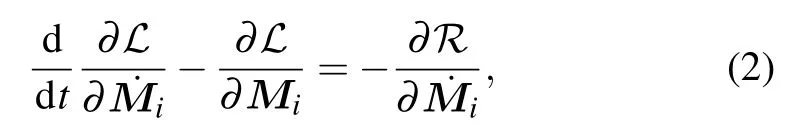
whereL=T ?Uis the Lagrangian,andTandUare the kinetic energy and potential energy of the antiferromagnetic system,respectively. The Rayleigh dissipation functionR,which describes the energy dissipation in the magnetization motion,has the following form in the antiferromagnetic system:

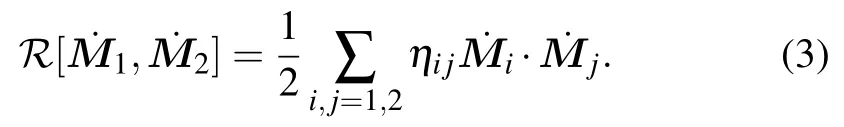
The parameter matrixηijquantities the intralayer and interlayer dissipation rate of each sublattice magnetization motion, and the interlayer dissipation may derive from the spin pumping effect between adjacent layers in AFMs.[38,40]For the antiferromagnet with two sublattices,the potential energy,whereHiis the effective field applied to thei-th sublattice magnetization,and the Lagrange equation can be simplified to

The kinetic energy of a spin comes from the Berry phase caused by spin motion.[41]For an antiferromagnet with two sublattices, the kinetic energy can be rewritten asT=, whereAiis the magnetic potential corresponding to thei-th sublattice magnetization,which is decided by ?×Ai=Mi.[38]Replacing the kinetic energy term with the above expression in Eq.(4),we can get

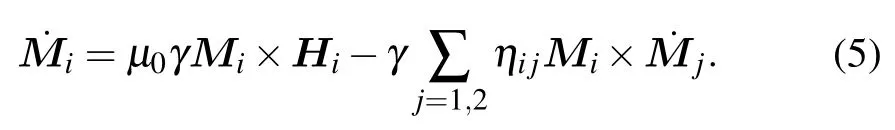
We find that Eq.(5)has exactly the same form as the LLG equation,with the following transformation:

where we have made a simplification|M1|=|M2|=M0,which is very reasonable for antiferromagnets. So far we have obtained the equation describing the antiferromagnetic dynamics, which is equivalent to the theory applied in two-sublattice ferrimagnets at the compensation point in Kamra’s work or Yuan’s theory for AFM system with two sublattices.[36,38]

But there are still too many parameters in the matrixα.Here we proceed to simplify. Firstly,due to the high symmetry of the two sets of sublattices in the antiferromagnet, this requires that theαmatrix is symmetric and the diagonal elements must be equal,namely,α11=α22,α12=α21.Secondly,according to the second law of thermodynamics, the entropy of an isolated system does not decrease, so the energy of a system without external energy input does not increase. This implies that the eigenvalues and the elements of the damping matrixαmust be non-negative.

When there is only one set of magnetic moments, the termγηijMi×˙Mjwhich describes the interaction between the two sets of magnetic moments no longer exists and theequation naturally evolves into the LLG equation in ferromagnet systems.[22]And if we setη=O,Eq.(5)becomes an equation for an undamped magnetization system,which is equivalent to the Landau–Lifshitz equation in ferromagnets.

Then we apply the theory developed above to describe the antiferromagnetic dynamics in the layered antiferromagnet CrCl3. In the macro approximation, we assume that the magnetization direction is uniform within each layer in CrCl3,and useM1andM2to represent the total magnetic moment of the two different sublattices. As for the selection of the effective field, we use the same form as in the Liu’s paper,[39]which has been shown to be well suited to describe the antiferromagnetic dynamics in CrCl3. Thus,the LLG equation in CrCl3has the following form:[34,35,39]

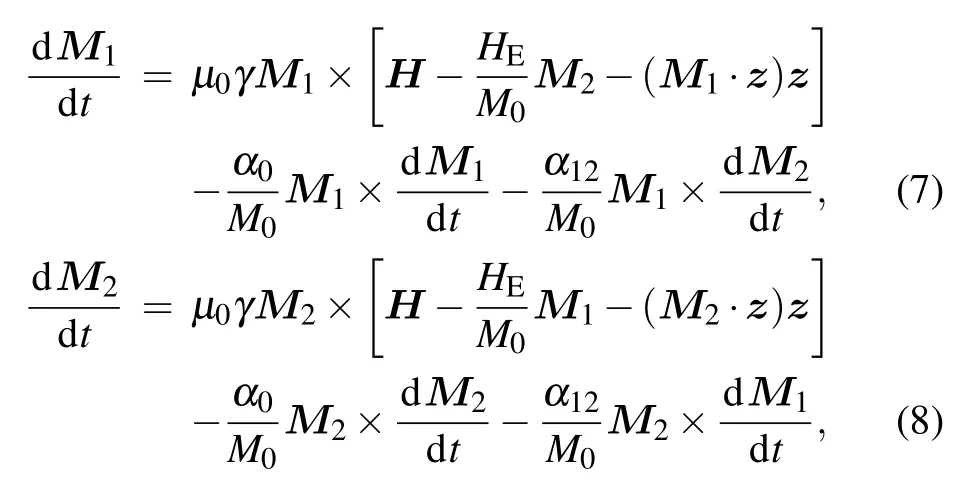
whereHEis the interlayer exchange field andM0is the saturation magnetization,|M1|=|M2|=M0.γis the gyromagnetic ratio andzis along the crystal c axis perpendicular to sample plane. Andα0=α11=α22is the Gilbert damping parameter in the layer,α12=α21is the Gilbert damping parameter between layers,andH=H0+?is the external magnetic field,whereH0is the static magnetic field and?is the rf magnetic field.

3. The linewidth in the antiferromagnetic resonance

In the work of Kamra and Yuan,[36,38]they discussed the damping of the right-handed mode and left-handed mode in AFMR when the external magnetic field was applied to the direction of magnetization.[36,38]Different from the situation they discussed, here we discuss the damping of the optical mode and acoustic mode in CrCl3. When the magnetic fieldH0is applied in the layer plane and perpendicular to the direction of magnetization,Eqs.(7)and (8)are symmetric around the direction of the external magnetic field. Under a linear approximation, we can solve Eqs. (7) and (8) to obtain two independent modes(optical mode and acoustic mode),which can be excited by the microwave field in certain conditions.[39]The optical and acoustic modes will form a Lorentzian resonance curve. Their resonant frequenciesωOandωAhave the relationship with magnetic field as follows:[39]

whereφis the angle of deflection of the magnetization direction under the external magnetic field and has the relationship sinφ=H/2HE. This was the work of Liuet al.,[39]but the effect of damping was neglected in their work and the damping evolution ΔH–ωwas not further investigated. We have found the appropriate damping to describe the dissipation of AFM dynamics in CrCl3, and in this way we obtain the linewidth ΔHas a function of the microwave frequency. Here we do not consider a broaden line width independent of the resonance frequency,which is originated from the multi-domain state as inhomogenous in the real sample.

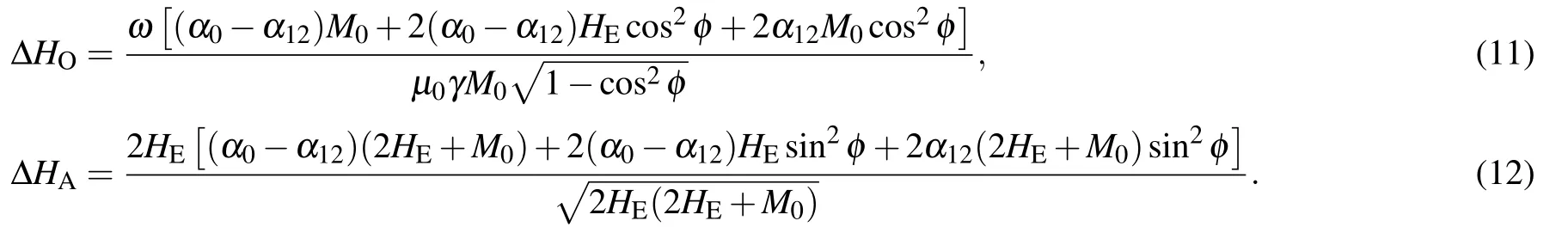
Equations(11)and (12)constitute the main conclusions of this paper and demonstrate that(i)the variation of linewidth ΔHwith frequency in antiferromagnets is not a simple linear relationship, which is very different from the linear relationμ0ΔH=μ0ΔH0+αω/γin ferromagnets,[30]and(ii)the linewidth variation is still different between the optical and acoustic modes, with the linewidth of the optical mode increasing faster than the acoustic mode.

To gain further insight into the results presented in Eqs.(11)and (12), we plot the damping evolution ΔH–ωof the optical and acoustic modes in Fig.1. The parameters employed in the figure areμ0HE=95 mT,μ0M0=330 mT andγ=28/2πGHz/T, which can well reflect the characteristics of antiferromagnets with the weak interlayer coupling,such as CrCl3. The damping parameterαis around 10?2in ferromagnets,such as YIG,and we therefore chooseα0andα12to be on the same order of magnitude. And here we do not consider the effect of the non-uniform linewidth.As shown in Fig.1(a),the linewidths of the optical and acoustic modes both grow nonlinearly with the increase of frequency,but there is a clear difference between them. For the acoustic mode,the linewidth still has a certain value at zero-frequency and grows more slowly,while for the optical mode, the linewidth increases dramatically from zero and surpasses the acoustic mode at around 4.5 GHz. To further investigate the effect of different damping parametersα0,α12on the linewidth,we fixα0and changeα12in the Figs. 1(b) and 1(c). We do the opposite in Figs. 1(d)and 1(e), and find that in the acoustic mode, the growth rate of linewidth increases with the growth ofα0orα12, and the linewidth at the zero-frequency increases with the growth ofα0, but reduces with the growth ofα12. Whenα0=α12, the linewidth at the zero-frequency will disappear. In the optical mode,the linewidth increases with the growth ofα0as it does in the acoustic mode. But with the growth ofα12,it grows at low frequencies and decreases at high frequencies. Moreover,the linewidth at the zero-frequency is always zero. Then we can get the conclusion that the nonlinear damping evolution ΔH–ωis a consequence of the interlayer interaction during the antiferromagnetic resonance, which is not decided byα0orα12and the interlayer Gilbert dissipation also plays an important role in changing the value of the nonlinear linewidth.We notice that the new damping termα12will have the effect only when the sublattice is asymmetric, according to the theory of karma.[36]But in our work, the operation of applying an external magnetic field perpendicular to the direction of magnetization has broken the centrosymmetry, so here the new damping termα12always exists.

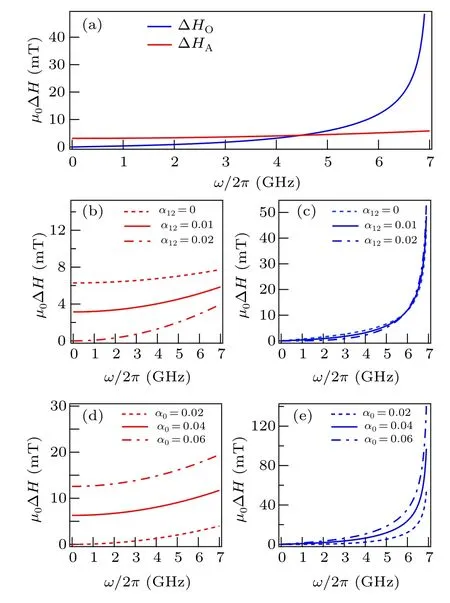
Fig.1. The linewidth ΔH as a function of the frequency for the optical mode and acoustic mode. The curves in blue and red depict the optical and acoustic modes,respectively. (a)The curves are calculated according to Eqs.(11)and(12)by setting α0=0.02,α12=0.01. For(b)and(c)α0=0.02,α12=0,0.01 and 0.02 correspond to dashed,solid and dash-dotted curves,respectively.α12=0.02,α0=0.02,0.04 and 0.06 correspond to dashed,solid and dash-dotted curves for(d)and(e),respectively.

4. Experimental results

Based on the above theoretical model, we conducted experiments to investigate the resonance frequency and the damping evolution ΔH–ωof the optical and acoustic modes in antiferromagnet CrCl3. To measure the AFMR signal of the antiferromagnet CrCl3, an external magnetic fieldH=H0+?was applied to the CrCl3/Pt bilayer to drive the antiferromagnetic resonance. The microwave field component?in they–zplane was applied by placing a coplanar waveguide along thex-axis. The static magnetic fieldH0was applied along they-axis. The microwave power was 100 mW and the modulation frequency used for lock-in measurement was 8.33 kHz. Thus,the optical mode and the acoustic mode were driven byhyandhz,respectively.[39]In our experiments,the CrCl3/Pt strip was placed along thex-andy-axis. The microwave transmission intensity was simultaneously measured as a DC voltage through a diode. To perform measurements at low temperatures,the device was placed in a cryogenic chamber.

Fig. 2. (a) Evolution of the AFMR in CrCl3 measured by DC voltage through a diode. The dispersion (b) and the damping evolutions (c) of the optical and acoustic modes in CrCl3. The damping evolutions with different α12 of the optical(d)and acoustic modes(e)in CrCl3. The blue curve and the red curve in(b)are plotted according to Eqs.(9)and(10),respectively.The blue and the red curves in(c)–(e)are plotted according to Eqs.(11)and(12),respectively. And the dashed curves different from solid curves are the parameter α12=0.

The evolution of AFMR in CrCl3is measured in DC voltage by sweeping magnetic field at fixed frequencyωas shown in Fig.2(a).

Figure 2(b) shows the results in which the resonant frequencies of the optical and acoustic modes are as a function of the magnetic fieldH. We use Eqs. (9) and (10) to fit the resonance frequencies.[39]These fits are shown by the red and blue lines in Fig.2(b),which represent the optical and acoustic modes,respectively,with fit parameters ofμ0HE=95 mT,μ0M0=330 mT andγ/2π=28 GHz/T.As shown in Fig.2(b),with the choice of the above parameters, the fitted curves agree well with our experimental data, both for the optical and acoustic modes. And this result has been confirmed by the work of Liuet al.[39]But the damping is neglected in their work which is very important to the antiferromagnetic dynamic.

Here we further study the damping evolution ΔH–ωof the optical and acoustic modes,which are shown in Figs.2(c)–2(e). Then we use Eqs. (11) and (12) with different nonuniform linewidth terms ΔHO0and ΔHA0to fit the linewidth of the optical and acoustic modes. The parametersHEandM0are fixed, which have been obtained from fitting the resonant frequency above.[39]These fits are shown by the red and blue solid lines in Figs. 2(c)–2(d), which represent the optical and acoustic modes, respectively. The fit parameters employed areα0=0.02,α12=0.013, ΔHO0=3.18 mT and ΔHA0=1.30 mT.As shown in Figs.2(c)–2(e),in the range of 3 GHz to 7 GHz, our theory agrees very well with the experimental data for the optical, and for acoustic modes, there is a small deviation between the experimental data and the theoretical prediction which may originate from our experiment with large error bar,but the trend of variation between the theoretical and experimental data is the same. The optical and acoustic modes both show a non-linear increase in linewidth with increasing frequency. Moreover, our theory and experiments also show that the optical mode will have a dramatic increase in linewidth with increasing frequency.But for acoustic mode,the increasing trend is more gentle than optical mode as shown in Fig. 2(c). So at high frequencies, the linewidth of optical mode will be much larger than acoustic mode. To further study the role ofα12in damping, we setα12=0 in the red and blue dash lines as a contrast in Figs.2(d)and 2(e),and other parameters are the same as the solid lines.But there is no very huge difference between the dashed lines and solid lines in Figs. 2(d) and 2(e). Although our theory predicts thatα12has a significant effect on linewidth, further experiments are needed to verify that.

5. Summary

In this work, we have theoretically and experimentally investigated the Gilbert damping evolution ΔH–ωof optical and acoustic mode with frequency in the layered antiferromagnet flake CrCl3. We discovered that the linewidths of both optical and acoustic modes have a nonlinear positive correlation with frequency in AFMs, which is different from the linear relationship in ferromagnets. We developed suitable damping from the Lagrange equation with the Rayleigh dissipation functional to account for the linewidth of the optical and acoustic modes and predicted nonlinear ΔH–ωrelationship for both optical and acoustic modes, which is in agreement with our experimental observations. Combining both our theoretical prediction and experimental observations, we concluded that the nonlinear damping evolution ΔH–ωis a intrinsic nature,which is derived from the interlayer interaction during the antiferromagnetic resonance. Our work provides a method for extracting damping parameters from antiferromagnetic linewidths, allowing a quantitative measure of the magnitude of dissipation in antiferromagnetic resonances.

Acknowledgements

Project supported by the National Natural Science Foundation of China (Grant No. 11774200), the Shandong Provincial Natural Science Foundation, China (Grant No. ZR2019JQ02), and the Youth Interdisciplinary Science and Innovative Research Groups of Shandong University.