Scaling of rise time of drive current on development of magneto-Rayleigh-Taylor instabilities for single-shell Z-pinches
Xiaoguang Wang(王小光), Guanqiong Wang(王冠瓊),Shunkai Sun(孫順凱), Delong Xiao(肖德龍),Ning Ding(丁寧), Chongyang Mao(毛重陽), and Xiaojian Shu(束小建)
Institute of Applied Physics and Computational Mathematics,Beijing 100094,China
In fast Z-pinches, rise time of drive current plays an important role in development of magneto-Rayleigh–Taylor(MRT)instabilities. It is essential for applications of Z-pinch dynamic hohlraum(ZPDH),which could be used for driving inertial confinement fusion (ICF), to understand the scaling of rise time on MRTs. Therefore, a theoretical model for nonlinear development of MRTs is developed according to the numerical analysis. It is found from the model that the implosion distance L=r0 ?rmc determines the development of MRTs,where r0 is the initial radius and rmc is the position of the accelerating shell. The current rise time τ would affect the MRT development because of its strong coupling with the r0. The amplitude of MRTs would increase with the rise time linearly if an implosion velocity is specified. The effects of the rise time on MRT, in addition, are studied by numerical simulation. The results are consistent with those of the theoretical model very well. Finally,the scaling of the rise time on amplitude of MRTs is obtained for a specified implosion velocity by the theoretical model and numerical simulations.
Keywords: magneto-Rayleigh–Taylor instability,rise time,Z-pinch,magnetohydrodynamic
1. Introduction
TheZ-pinch dynamic hohlraum(ZPDH)is one of potential configurations to achieve fusion ignition.[1–7]It is formed after an annular high-atomic-numberZ-pinch plasma is accelerated by an axial current and then impacts onto a low density foam cylinder.[2,8–11]A high opacityZ-pinch plasma can trap the radiation generated in the impaction process and acts as a hohlraum wall, and its ability to reduce the radiation loss to vacuum is vital for applications of inertial confinement fusion(ICF).
Magneto-Rayleigh–Taylor (MRT) instabilities will occur at outer surface of aZ-pinch plasma when it is accelerated by the azimuthal magnetic field produced by the axial drive current.[12–18]They can slow down the plasma and disturb the plasma density and momentum distributions,[13,15,19]thus weakening the radiating shock and reducing theZpinch plasma’s capability of trapping x-ray radiation in the hohlraum.[20,21]Therefore, it is strongly expected that development of MRT instabilities can be controlled to an acceptable extent by appropriate measures in ZPDH driven ICF.
Peak and rise times of drive current play important roles in implosion dynamics ofZ-pinch plasmas, as well as development of MRT instabilities.[6,15]In engineering, long rise time is preferred very much in constructing a large current pulse power generator for ICF.Therefore,effects of rise time of drive current are important topic in community ofZ-pinch driven ICF.Recently, Slutz studied the scaling of magnetized liner inertial fusion(MaglIF)with the rise time by numerical simulation.[22]It shows that the required energy and preheat energy for a given fusion gain will increase with the rise time.In ZPDH applications, the development of MRT instabilities should be considered to determine a suitable rise time besides the overall energy balance. In this paper,we focus on the former.
Lots of works have been carried out on MRT instabilities inZ-pinch community.[6,15–17,23–34]In compared experiments of foil and wire-arrayZ-pinches onZmachine,[35]it is thought that one of possible reasons for lower stability of copper foil is a longer period for MRT developing in run-in phase compared to a wire array. The linear theoretical analysis of single mode indicates that the perturbation amplitude of MRT is only related to the implosion distance over which the accelerating plasma shell takes.[36,37]Some experiments show that large radiusZ-pinches are inherently susceptible to the MRT instability.[38,39]A long rise time is required for matching the large radius because of their strong coupling. Therefore, the long rise time would result in more unstable MRTs. However,the conclusions mostly result from observing indirect parameters,such as the peak and pulse width of x-ray radiation. The scaling of rise time on the nonlinear development of MRTs is still an interesting topic for single shell implosion.
Therefore,effects of implosion parameters on the nonlinear development of MRT instabilities and their dependence on the rise time of drive current are studied in the run-in phase of a single shell implosion by theoretical analysis and simulation.It is found that the amplitude of MRTs before stagnation willincrease with the rise time linearly if an implosion velocity is specified. Finally,a scaling of the rise time on MRTs is given.
This paper is organized as follows.In Section 2,we introduce the physical model for numerical simulation. Firstly,the development characteristic of MRTs is numerically analyzed in Section 3. Then,in Section 4,a theoretical model for nonlinear development of MRTs in thin shell implosion is developed according to the numerical analysis. Section 5 presents the results of simulation about the effect of rise time on MRTs,which are consistent with the theoretical model. Section 6 gives the conclusions.
2. Physical models
The MRT instability inr–zcross section is taken into account, because it is most severe in the run-in phase of the plasma implosion. Although wire array loads are generally employed so far, they may transform into plasma shells with load current larger than 30–50 MA due to the increase of wire diameter and decrease of inter-wire gaps.[40]The process of early plasma formation and ablation of the wire array are beyond the scope of this article. We focus on the run-in phase inZ-pinches. Therefore, a plasma shell of uniform density is taken as the initial condition in our study. The control equations are compressible resistive magnetohydrodynamic (MHD) equations, including the continuity equation,the momentum equation,the energy equation and the magnetic field equation,which are written as follows:
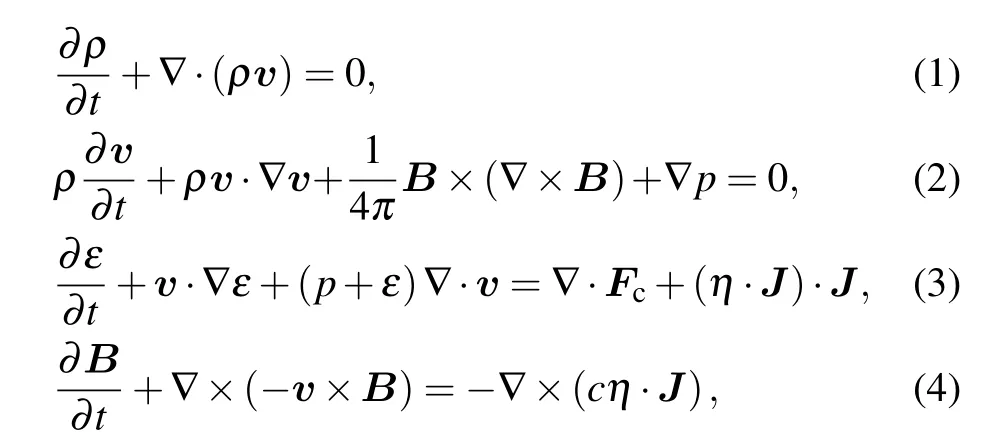
whereρis the mass density,υis the velocity,Bis the magnetic field,Jis the current density,ηis the resistivity,cis the speed of light in vacuum,pis the pressure,andεis the internal energy. The limited energy flux
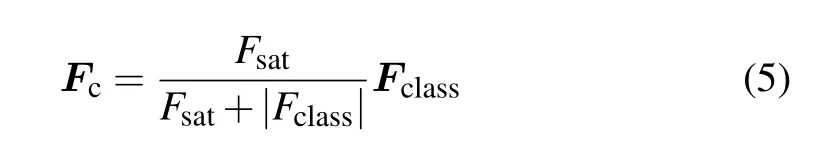
is utilized in the energy equations,and the classical energy flux is
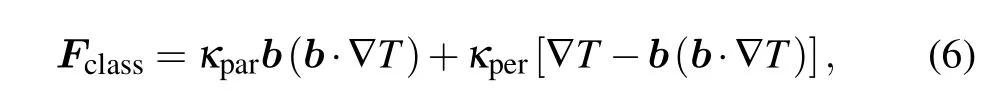
whereTis the temperature,κparandκperare the parallel and normal thermal conductivity coefficients respectively,bis the unit vector along theB.The saturated thermal conduction flux iswithciobeing the isothermal speed of sound andφ <1 a free parameter. Typically, the plasma temperature is from 1 eV to 100 eV,and the density is tens of mg/cm3in the run-in phase. Therefore, the Braginskii heat conductivity coefficients and the Spitzer resistivity are employed in the model.[41]The ideal equation of state is utilized to close the MHD equations, where the adiabatic indexΓ=1.4. The effective ionizationZeff=5 is employed in this study. The temperatureTis calculated byp=(Zeff+1)nikBT,wherekBis the Boltzmann constant andniis the ion number density.In our model we neglect radiation loss for simplicity because it is relatively small compared to the material energy(kinetic energy plus internal energy)of the plasma in the run-in phase.This approximation will not result in the severe variation of the implosion dynamics and the corresponding MRT development.
The azimuthal magnetic field at the outer boundary is

whereI(t) is the drive current,rbis the position of the outer boundary, andcis the speed of light in vacuum. In experiments,drive currents are determined by both the pulse power generator and the plasma impedance in implosion because they are strongly coupled inZ-pinches.In order to simplify the issues and to obtain a similar implosion dynamics, the drive current used is taken as[6,15]
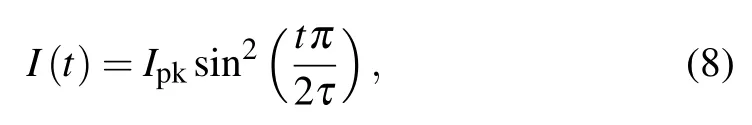
which is similar to the experimental measurements. Here,Ipkis the current peak andτis the rise time. The coupling of the imploding plasma to the pulse power generator is neglected.However,the plasma impedance(including the resistivity)and the current distribution are calculated consistently in the physical model. The initial current is distributed only at the outer surface of the plasma shell.
The open source code PLUTO,[42]which has been successfully used for simulating MRT instabilities, is utilized to solve the above equations in thin aluminum liner experiments on the 7–8 MA facility.[43]
The thin shell model[6,15]is a commonly used approximation for theZ-pinch implosions without considering the 2D phenomena. In the model,the dimensionless parameter

is the peak of the normalized acceleration, which determine the imploding dynamic with the current shape together. Heremlis the mass per unit length of the plasma shell andr0is the initial radius. The parameterξis termed as pinch constant in this paper.
It is challenging to distinguish the effect of the rise time from the other parameters because they are strongly coupled inZ-pinch implosions. For example,the rise timeτwould increase with the initial radiusr0if the pinch constantξis kept constant. We address this issue by developing a theoretical model and numerically studying the effects of the rise time on MRT instabilities in a similarZ-pinch dynamic system.
Typically, the plasma temperature is~100 eV, and the density is tens of mg/cm3in the run-in phase ofZ-pinch implosions. The magnetic Reynold numberRm=vAl0/η ~100 and the Peclet numberPt=l0v/κper~1018under the conditions,whereρ0is the initial density,l0~1.0 cm is the characteristic scale,andis the Alfven velocity. The resistivity and thermal conduction could be ignored in Eqs.(1)–(4).Then the control equations will be reduced to ideal magnetohydrodynamic equations. The initial velocity is zero in our simulations. TheZ-pinch implosions will be in Euler similarity according to Eqs.(6)–(8)and(11)in Ref.[44]if the accelerationg(t)of the plasma shell. The initial density profile and pressure profiles, in addition, are identical. Therefore, same pinch constantsξand current shapesI(t)/Ipkare provided in our simulations to get the identical acceleration. The initial plasma temperature and density are both uniform for the same pressure profile. The original width of plasmaδr0are 0.1 cm for all the cases,which leads tor0/δr010 in our simulations.The initial temperature is 10000 K in our simulations.[45]Note that the temperature is involved in our simulations for calculating the resistivityη,which determines the current skin depthλskin. Usually,λskinis much smaller thanl0so that the dynamics are still similar for MRT instabilities. We makeξ=5.0 in simulations for obtaining the optimized implosion kinetic energy.
The perturbation amplitude of MRT instabilities is calculated by

whereAiis the amplitude of each mode from Fourier analysis.According to Ref.[46],the perturbation spectrum is analyzed by calculating the radial density integral and subtracting its mean:

where the density integral is divided by the max densityρm=maxand the position of plasma shellrmc, in order to obtain a quantity with units of length. We define the radial center of mass as the position of the accelerating plasma shell as expressed by Eq.(11).
3. Development characteristics of MRT
In order to develop a theoretical model of MRTs,the development characteristics of MRT is firstly analyzed in a single shellZ-pinch by simulation. A plasma shell, with temperature 10000 K and density 0.41 mg/cm3, is taken as the initial load.[47]The original shell widthδr0is 0.1 cm. The initial radiusr0=2.0 cm,Ipk=10 MA,ml=0.5 mg/cm andτ=100 ns, which makeξ=5.0. We simulate the MRT development by seeding 0.5% random density perturbation initially.Figure 1 shows the perturbation amplitude and the dominant wavelength(at which the amplitude is the largest in the spectrum)as a function of the normalized time. The decrease of perturbation amplitude before acceleration is mainly due to the plasma expansion. After that, it begins to grow exponentially in the run-in phase, which is in agreement with the aluminum foil experiments on the MAIZE machine at University of Manchester[48]and on the pulse power generator at CAEP.[43]

Fig.1.The perturbation amplitude(circle)and dominant wavelength(squaredot-dashed line)of the MRT instability as a function of time for r0=2.0 cm,Ipk=10 MA,ml=0.5 mg/cm and τ=100 ns. The dot-dashed(red),dashed(blue) and solid (green) lines present the fitting results by exp(γtn) in the snowplow,thin-shell and break-through regimes,respectively.
We divide the run-in phase into three regimes according to the perturbation development and implosion characteristics:the snowplow regime, the thin-shell regime and the breakthrough regime, as shown in Figs. 1 and 2. We obtain the growth ratesγ(normalized to 1/τ)of the perturbation,which are 6.3,21.7,and 7.0 in different regimes,respectively,by fitting the simulation data with exp(γtn)function wheretn=t/τis the normalized time. In the snowplow regime, the magnetic fields accelerate and sweep the plasma like a piston at the interface as shown in Figs. 2(a) and 2(d) when the skin depth is much smaller than the initial width of the plasmaδr0.The growth rate is small due to the stabilization of accretion effects and smaller acceleration at the early time. The implosion will be in the thin-shell regime after the magnetic piston goes aboutδr0, i.e., sweeping all of the plasma shell. It is found from Fig. 2(e) that the width of the plasmaδris approximate to current skin depthλskinin thin-shell regime. The growth rate becomes larger. However,the perturbation amplitude of the MRT instability is smaller than its dominant wavelength,which is almost constant in the two regimes. Namely,the development is in linear approximately. The skin depth is about 260μm,which is also the characteristic scales of magnetic field and density profile. The dominant wavelength is around 400μm. The modes with the wavelength smaller than skin depth are stabilized possibly by the gradients of density and magnetic field. It is inferred that the dominant wavelength is affected by the skin depth in snow-plow and thinshell regimes.
The magnetic field would break and penetrate through the plasma shell when the perturbation amplitude develops comparable to or larger than the width of plasm shellδr,which is approximate to the skin depth. Then,the implosion goes into the break-through regime. The amplitude is also comparable to and larger than the dominant wavelength. Under the condition, the development of MRTs will be dominated by nonlinear coupling. It can be observed from Fig.2(c),where bubble merging occurs associating with field breaking through. The dominant wavelength increases with the amplitude dramatically as shown in Fig. 1, which means that the multi-mode development of MRTs may be in bubble-merger regime(or in self-similar growth).[49–51]
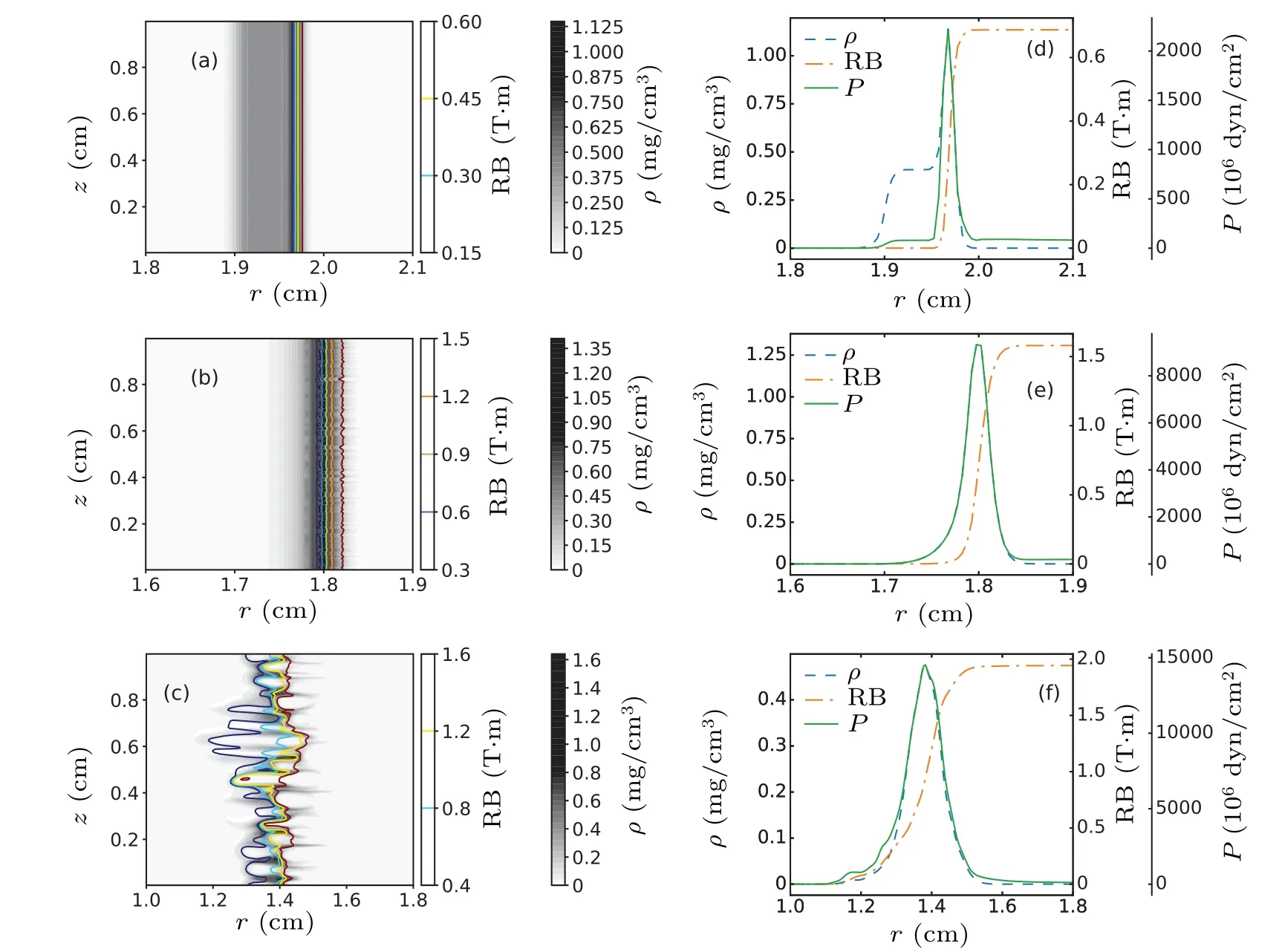
Fig.2. Distributions of the plasma density ρ (gray map)and the RB=Bθr(color contour lines)at(a)t =0.4(snow-plow),(b)t =0.7(thinshell)and(c)t =0.9(break-through),(d)–(f)the radial profiles of the ρ,RB and pressure P by averaging along z direction corresponding to(a)–(c),respectively. It can be found from(e)that the skin depth is λskin ~263μm.
4. Model for MRT development
According to the development characteristics,we develop a model for MRT development in thin shell implosion to obtain the scaling of rise time on MRTs. The implosion distance isL=r0?rmc,which is normalized byLn=L/r0. The timet, velocityvand accelerationgare normalized bytn=t/τ,vn=vτ/r0andgn=gτ2/r0. The wave numberkand the amplitudeAof MRTs are normalized bykn=kr0andAn=A/r0.For theZ-pinch implosion,the RT growth function is defined as

As shown in Section 3,the amplitude is smaller than the dominant wavelength in snow-plow and thin-shell regimes. In addition,the dominant wavelength is almost constant. Thus the MRT instability grows approximately in linearity for most period in the two regimes. Then its amplitude is

The approximate solutions of the snow-plow model with drive current shape sin2(tπ/2)are[15]
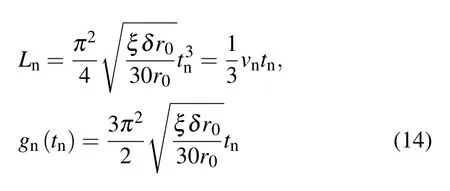
forLn<1/3.Substituting Eqs.(13)and(15)into Eq.(14),the amplitude of MRTs in the snowplow regime can be approxi-mately written as

The approximate solution of the thin-shell is[6,15]

According to Eqs.(13),(14)and(17),the amplitude of MRTs in the thin-shell regime is
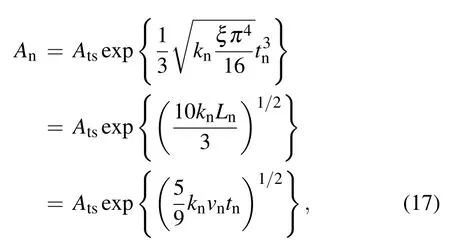
whereAtsis the amplitude at the beginning of the thin-shell regime.
The multi-mode development of MRTs in the breakthrough regime is in self-similar growth. We estimate the bubble amplitude of the MRTs by utilizing the multimode turbulence mix width equation[14,52]
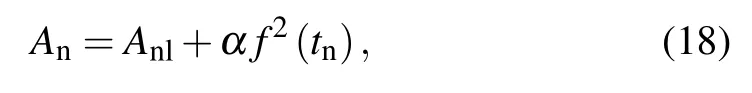
which is based on self-similar growth or bubble merger models. Here,αis a dimensionless coefficient,α=0.06 for Atwood numberAtwood=1.0,andAnlis the nonlinear saturated amplitude beyond which the MRT instability would go into self-similar growth. Inserting Eqs.(12)and(16)into Eq.(18)yields the amplitude of MRTs:
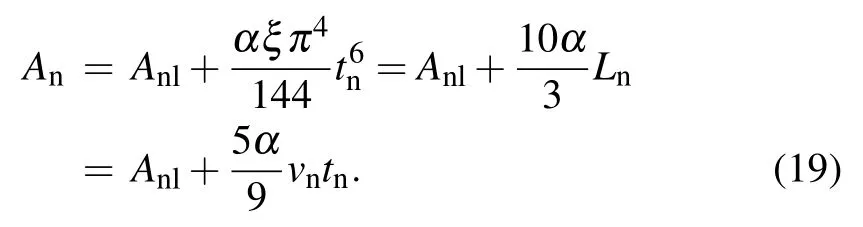
Finally,the development of MRTs can be expressed as


wherettsis the time at the beginning of the thin-shell regime,Lnlis the implosion distance where the perturbation amplitude reachesAnl,andtnlis the corresponding normalized time.

Fig. 3. The perturbation amplitudes from Fourier analysis of simulation data(dashed line)and theoretical estimation(solid and dot-dashed lines) as a function of implosion distance for r0 = 2.0 cm (a) and r0=3.0 cm(b)with τ =100 ns,Ipk=10 MA and ξ =5.0.
The comparison between the theoretical and simulated results is given for the implosions withr0=2.0 cm andr0=3.0 cm forτ=100 ns,Ipk=10 MA andξ=5.0 in Fig.3.The implosion distanceLis given by the simulation.The simulatedresults indicate the dominant wavelength is around 400 μm in snow-plow and thin-shell regimes. Thus, the single modes withkn=42 forr0=2.0 cm andkn=70 forr0=3.0 cm are estimated by the theoretical model. The initial amplitude is about 2.0×10?4r0. It shows that the model is in agreement with the simulation very well in the snowplow and thin-shell regime. It is also a good approximation at the beginning of the break-through regime. Then, the simulations are beyond the theoretical results. This is because the dominant wavelength becomes larger than the amplitude again in some period due to dramatic bubble merging as shown by Figs.1 and 2. As a result,the MRT development becomes approximately exponential inf(tn) again at that time. Similar phenomena were observed in aluminum foil experiments.[48,53]The model also could estimate the amplitude of MRTs qualitatively in the regime if theαis multiplied by a coefficient~1.85,i.e.,makingα=0.11,as shown by the dash-dotted lines in Fig.3.
It is found from the model that the development of MRTs is only related to the implosion distanceL(or the initial radius). Usually,the nonlinear amplitudeAnlis hundreds of micrometers as mentioned in Section 3. The implosion distanceLis taken from mm to cm for the thin shell implosion,which is much larger thanAnl. Therefore, the implosion distance in the break-through regime will determine the development of the MRTs, especially for the large radiusr0. From another perspective,the perturbation amplitude increases linearly with the implosion timetfor identical implosion velocityv. The scaling

could be obtained from Eq. (21) withAn=A/r0andvn=vτ/r0. Usually,tnis constant for the same pinch constantξand normalized implosion distanceLn. The implosion timetis equal to the current rise timeτwhentn=1. It is concluded from Eq. (22) that the MRT amplitude will increase linearly with the rise timeτif an implosion velocity is specified.
5. Numerical results
5.1. Effects of the implosion parameters on MRTs
The effects of the implosion parameters on the MRT development are also studied in the similarZ-pinch dynamic system by simulation according to the theoretical model in this section. Firstly,we make a research on the effect of perturbation seed. It is found that the instability amplitude of MRTs increases linearly with the initial amplitude in the thin-shell regime. Then the current peak’s effect on MRT in the run-in phase is studied by changing it from 5 MA to 50 MA. The matched mass is adopted to keep the pinch constantξ=5.0.The MRT instabilities show similar development for different current peaks in our simulations. The reason is clearly such that the implosion dynamics(acceleration process)in the similar system is almost identical though the peak current is varied. However, it should be noted that the effects of current peak on the process of plasma formation are not considered in the paper, which could affect the developments of MRTs by changing the perturbation seed, the temperature and density profile.[36,54]
With other parameters corresponding to Fig. 1, effect of the current rise timeτon the development of MRTs is studied.The matched massmlis used to keepξ=5.0 in the simulation. It is found that the MRTs develop similarly for different rise times with the same initial radiusr0and pinch constantξ.Figure 4 presents that the growth rates for different rise times in the three regimes are almost identical. The different initial perturbations evolved in early expansion before the acceleration may account for the small difference. The mean growth ratesγare obtained by averaging the results in Fig. 4, which are 6.1,20.9 and 8.3 in the three regimes,respectively.

Fig.4. With other parameters corresponding to Fig.1,the current rise time τ is changed from 50 ns to 350 ns, and the matched masses ml are used to keep ξ =5.0. The fitting growth rates vs the rise time in the snowplow(SP),thin-shell(TS)and break-through(BT)regimes are presented.
The similar results are also found forr0=1.0 cm and 3.0 cm as depicted in Figs.5(a)and 5(b). However,it is found that the amplitude and dominant wavelength of MRTs before stagnation increase with the initial radiusr0from 1.0 cm to 3.0 cm. The amplitude increases from 0.1 cm to 0.54 cm,and the dominant wavelength increases from 0.07 cm to 0.3 cm.The average growth ratesγin the snow-plow regime are 5.43 and 6.82 forr0=1.0 and 3.0 cm. The growth rates in the thinshell regime are 18.3 and 23.5,and the average growth rate in the break-through regime is 8.1 forr0=3.0 cm. The development period of MRT in this regime is very short in the case of small radiusr0=1.0 cm,so the growth rate is not given. It is obvious that the initial radiusr0of the plasma shell plays a key factor for MRT development in theZ-pinch. In other words,the implosion distanceLdetermines the amplitude of MRTs.

Fig. 5. The amplitude as a function of time for different current rise times τ with r0=1.0 cm(a)and r0=3.0 cm(b). The pinch constant is kept ξ =5.0 by utilizing matched masses. The other parameters correspond to Fig.1.

Fig.6. (a)and(b)The perturbation amplitude as a function of time for different pinch constants with the rise times 50 ns and 150 ns, respectively. The pinch constant is changed by adjusting the mass ml.
The effect of pinch constant is also investigated by only adjusting the mass withIpk=10 MA,r0=1.0 cm andτ=50 ns or 150 ns. Figure 6 shows the perturbation amplitude as a function of time for different pinch constants with the rise times 50 ns (Fig. 6(a)) and 150 ns (Fig. 6(b)). The growth rateγincreases with pinch constantξ(i,e,peak of normalized acceleration) as expected. However, longer period is needed for the same implosion distance with smallerξ. Finally, the perturbation amplitude of MRTs may be identical for the same implosion distance. Corresponding to Fig.6,Fig.7 shows the amplitude as a function of the implosion distanceLfor different pinch constants. As predicted by the theoretical model,the amplitudes are only related to the implosion distanceLwhenξis larger than 2.5.It also supports that the implosion distanceLplays an important role in the development of MRTs. It is demonstrated that the results are consistent with the prediction of the theoretical model very well.
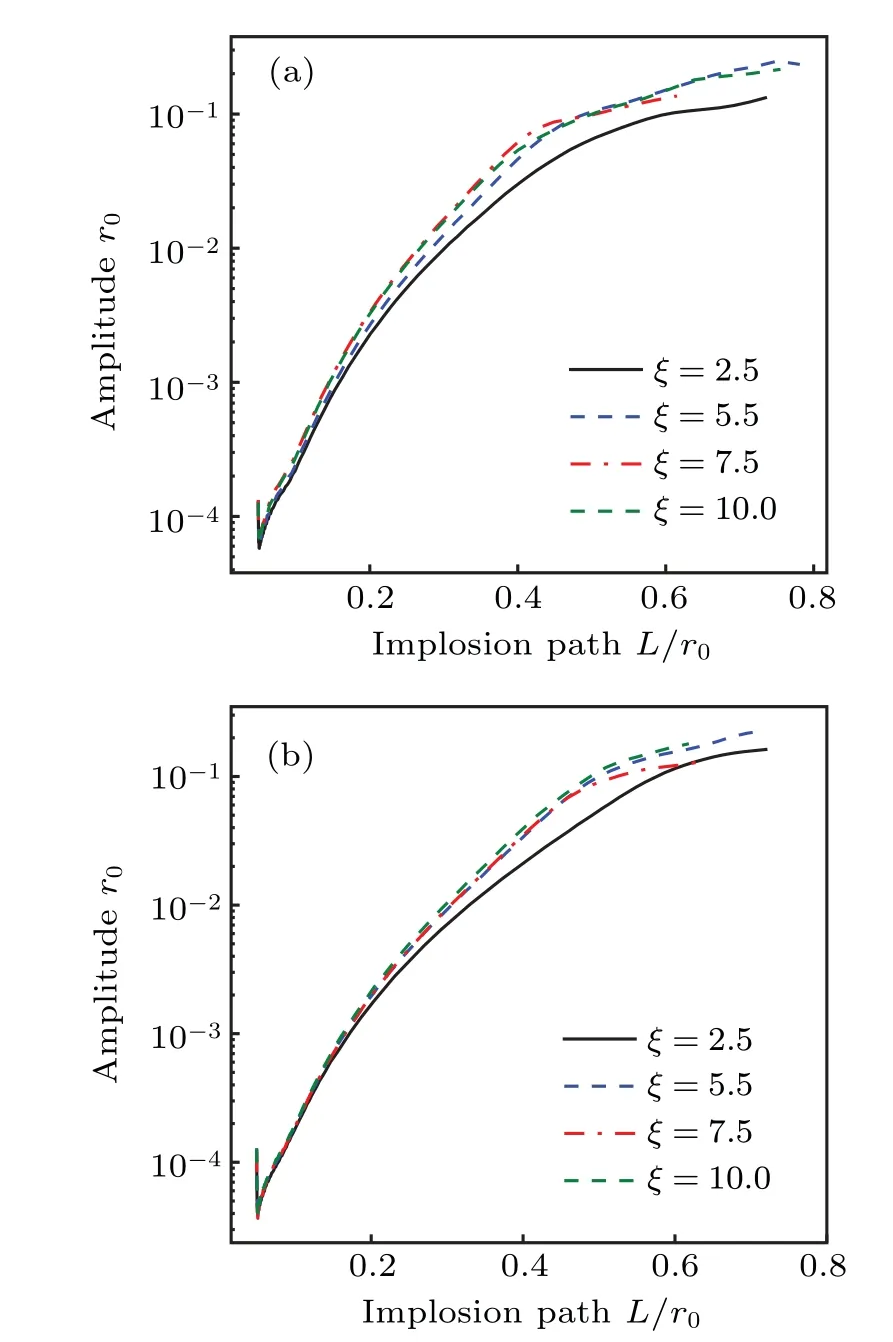
Fig. 7. Corresponding to Fig. 6, the perturbation amplitude as a function of the implosion distance L for different pinch constants with the rise times 50 ns(a)and 150 ns(b).
5.2. Scaling of rise time on MRTs
In fact,high plasma implosion velocity is needed to generate high temperature radiation for ZPDH application and others. Clearly, the implosion velocity is approximately proportional to the ratio of the initial radius to the rise time provided the same pinch constant. So longer rise time requires larger radius if the identical implosion velocity and massmlare kept. Consequently,the perturbation amplitude would increase with the rise time according to the theoretical model.
In order to validate it, we also study the effect of rise time on the MRT instabilities by simulation, keeping identical pinch constantξ, implosion velocityvand the mass per unit lengthml. Figure 8 presents the amplitudeAstgbefore the stagnation as a function of the rise timeτ. The matched radiuses are used to keepvfandξconstant. It is found that the amplitude of MRTs increases with the rise timeτlinearly,i.e.,Astg∝aτ,whereais a coefficient in cm/μs and is about 1.63 from the result of Fourier analysis. The amplitudes of spikebubble,which is the distance from the outmost tip of spikes to the innermost tip of bubbles, are also given, since the perturbation amplitude of Fourier analysis may not be exact enough when it is larger than the radial position of the plasma in this paper. Usually,the latter is twice the Fourier analysis or even larger.
It is obtained from the theoretical model thata=5αv/9?1.87 cm/μs, where the implosion velocityv=30.6 cm/μs is given by the simulation in Fig. 8. It is shown that the theoretical result agrees with the simulation very well.
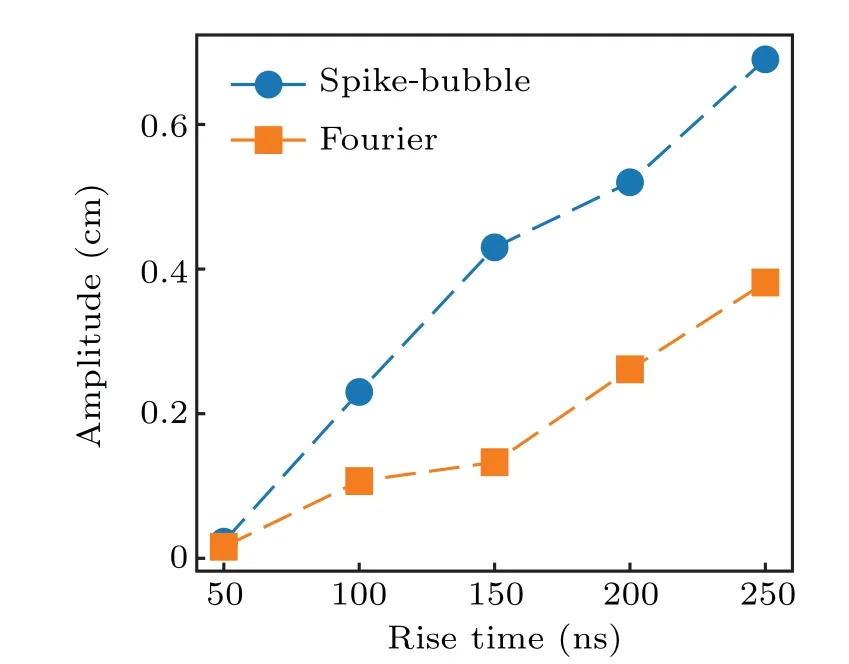
Fig.8. The perturbation amplitude as a function of the rise time τ before stagnation. The square-dashed line is the amplitude obtained by Fourier analysis. The circle-dashed line is the spike-bubble amplitude.Note that the matched radii are used to keep v and ξ identical.The other parameters correspond to Fig.1.
6. Conclusions
In summary,the development characteristics of MRTs are firstly analyzed by simulation for a single shell implosion. In the analysis,we divide the run-in phase into three regimes according to the perturbation characteristics and implosion dynamics: the snow-plow regime, the thin-shell regime and the break-through regime. The perturbation amplitude of MRTs grows exponentially with time in the run-in phase. It is found that the perturbation amplitude is smaller than the dominant wavelength in the snowplow and thin-shell regimes,so the development of MRTs is nearly linear. Usually,the perturbation amplitude is comparable to or larger than the dominant wavelength in the break-through regime. In addition,the dominant wavelength increases with the perturbation amplitude.The development of MRTs is in self-similar (nonlinear coupling) in this regime. However, it will return to the linear regime for some period due to dramatic bubble-merging, which leads to the dominant wavelength larger than the perturbation amplitude.
According to the numerical analysis,a theoretical model for nonlinear development of MRTs in thin shell implosion is developed. The model is in agreement with the numerical results very well in the snowplow and thin-shell regimes. In the breaking-through regime, the model could qualitatively predict the numerical results by modifying the coefficientαof RT mix width equation.
It is seen from the theoretical model that the implosion distanceLdetermines the amplitude of MRT instabilities. The result is not affected by the pinch constants very much. The rise time,however,could also affect the MRT development because it couples with the initial radius strongly if an implosion velocity is specified. In ZPDH applications, for example, a high implosion velocity is necessary for the high temperature radiation. The long rise time will lead to large implosion distanceLfor keeping the high implosion velocity.Consequently,the amplitude of MRTs increases with the rise time. According to the model,the amplitude before the stagnation increase with the rise time linearly for a specified velocity. Actually,it will also be true for theZ-pinch radiation source if the high radiation power is required.
Then effects of the rise time on MRTs are also studied by simulations. The results demonstrate that implosion distanceLplays a key factor in development of MRTs. The scaling of rise time on MRTs for a specified velocity is consistent with the theoretical. Finally, a scaling of rise time on MRT developmentis obtained by the theoretical model and simulations,whereα=0.11.
It should be noted that the development of MRTs is more complicated in the break-through regime. At the beginning of the breakthrough regime,the RT mix width equation based on self-similar growth or bubble-merger model is a good approximation. However,the development will return to the linear growth because of dramatic bubble-merging for some period. Therefore, a better model should be developed for the breaking-through regime in future.
In addition, the effects of the peak and rise time on the process of plasma formation in the initial phase of the implosion will affect the MRT development by affecting the perturbation seed, the density profile and the plasma temperature.These issues are beyond the scope of this paper. Furthermore,only the current shape of sin2(πt/2τ)is applied in the paper.The changing of the current shape should also be considered carefully in future. The effects of equation of state and radiation would also affect the temperature of the plasmas insimulations. As a result,the resistivity will change,leading to different skin depths and then affecting the nonlinear amplitudeAnl. These issues should also be considered carefully in future.
Acknowledgements
This work was supported by the National Natural Science Foundation of China (Grant Nos. 11975057,11605013,11775023,and 11705013).
The simulation work in our paper is mainly performed using an open code PLUTO. The authors are grateful to the contributors of the code.
- Chinese Physics B的其它文章
- A broadband self-powered UV photodetector of a β-Ga2O3/γ-CuI p-n junction
- High-sensitive terahertz detection by parametric up-conversion using nanosecond pulsed laser
- High efficiency,small size,and large bandwidth vertical interlayer waveguide coupler
- High-fidelity resonant tunneling passage in three-waveguide system
- An analytical model for cross-Kerr nonlinearity in a four-level N-type atomic system with Doppler broadening
- Determine the physical mechanism and source region of beat wave modulation by changing the frequency of high-frequency waves