Thermal apoptosis analysis considering injection behavior optimization and mass diffusion during magnetic hyperthermia

Yun-Dong Tang(湯云東) Jian Zou(鄒建) Rodolfo C C Flesch(魯?shù)婪駽 C 弗萊施)

Tao Jin(金濤)3, and Ming-Hua He(何明華)4,?

1College of Physics and Information Engineering,Fuzhou University,Fuzhou 350116,China

2Departamento de Automac??ao e Sistemas,Universidade Federal de Santa Catarina,88040-900 Florian′opolis,SC,Brazil

3College of Electrical Engineering and Automation,Fuzhou University,Fuzhou 350108,China

4Fujian Medical University,Fuzhou 350122,China

Keywords: thermal apoptosis analysis, injection behavior optimization, mass diffusion, magnetic hyperthermia

1. Introduction

Magnetic hyperthermia, as a low invasive therapeutic method,[1]has attracted more and more attentions in terms of tumor ablation[2]and heat-induced immunity.[3]Nanofluid containing magnetic nanoparticles (MNPs) needs to be injected into the tumor region prior to the treatment and then dissipates the heat inside tumor region for therapy under the action of an applied magnetic field. The heat dissipated from the MNPs can result in thermal apoptosis for malignant cells due to their sensitivity to high temperature.[4]The malignant cells can be ablated without damaging the healthy cells if the treatment temperature of bio-tissue is in a range between 42°C and 46°C.[5]The treatment temperature for the bio-tissue is a key factor to determine the treatment effect, which strongly depends on many factors,such as the shape of tumor,the dose of nanofluid,the injection location,the properties of nanofluid and bio-tissue,and other injection behaviors during nanofluid injection.[6,7]However, most of the factors are unable to be changed due to their intrinsic characteristics except for the dose and injection location of nanofluid. Therefore,it is necessary to optimize these two items prior to the therapy in order to obtain better treatment temperature distribution for therapeutic target. In addition to the treatment temperature,another important factor, Arrhenius kinetic coefficients,[8]is also really crucial in determining the thermal apoptosis of malignant cells in the region of interest.[9]

Magnetic hyperthermia research involves with many different disciplines, all of which has recently been investigated from different aspects. Some reports in the literature focused on the MNPs heating mechanism due to an applied magnetic field,and also on the validation between the theory results and experimentations.[10,11]In addition, there were also more indepth investigations in previous literature, such as the effects of dipolar interactions on the magnetic hyperthermia,[12]and the influence of aggregation morphology of nanoparticles on thermal conductivity of nanofluid.[13]These researches were further used to obtain the treatment temperature distribution for bio-tissue by considering Pennes bio-heat transfer(PBHT)equation.[14,15]The thermal apoptosis of malignant cells can then be predicted when the treatment temperature is considered as the input of an Arrhenius model.[16-18]Furthermore,several different approaches were also considered for improving the treatment effect in previous work. One example is the use of multiple site injection for treatment,which can improve the homogeneity of nanofluid distribution inside tumor region with respect to the single site injection.[19]However, the tumor shape in this literature was assumed to be of a general ideal sphere, which is also a common assumption made in most of previous work. Salloumet al.tried to determine the optimum parameters of the heat sources for all MNP injection sites by using an optimization algorithm in an irregular tumor model.[6]Nevertheless, in the present work the injection site location of nanofluid for the proposed model before the optimization is not considered. In addition,the diffusion duration after injection can also help to improve the homogeneity of nanofluid distribution for tumor region,which will then benefit the treatment temperature for magnetic hyperthermia.[20]Although the cited reports made essential contributions to different aspects of magnetic hyperthermia,these researches did not still present an effective solution to improve the thermal apoptosis of tumor cells for an irregular tumor model by considering the optimization results of the injection site and nanofluid dose.

The present study focuses on an irregular malignant model, by combining the recent advances in the injection behavior optimization and diffusion duration, thereby improving the therapeutic effect after the injection of nanofluid. The proposed algorithm is used to optimize the injection location and nanofluid dose prior to treatment,and the diffusion time is considered to further improve the uniformity of nanofluid distribution inside tumor region during a hyperthermia therapy.The method of analyzing the malignant ablation is proposed and further applied to three typical tumor cells. In addition,the finite element method is used to solve the partial differential equation for the concentration distribution of nanofluid and the treatment temperature distribution of bio-tissue for the proposed model during therapy. All the research methods proposed in this work can provide references for the formulation of magnetic hyperthermia programs.On this basis,other influencing factors of thermal apoptosis in magnetic hyperthermia can be studied, and they can be widely used in the relevant researches of magnetic hyperthermia.

2. Theory and method

2.1. Physical model

In this work, a symmetric tumor model used to evaluate the thermal apoptosis behavior is proposed as shown in Fig. 1. This model consists of a healthy tissue with a diameter of 25 mm (green), an irregular tumor tissue (yellow), and a nanofluid component with undetermined dose and injection site (black). The parameters of nanofluid need to be optimized prior to being injected into the tumor, which include they-coordinate value (y0), the power dissipation of MNP(QMNP), and the radius of nanofluid dose (R1). In addition,four different points are specified in order to investigate the thermal apoptosis behavior for three different malignant cells during simulation. All of these proposed points have the samex-coordinate value (zero), and have the same distance from each other in this model. Point A is located in the center of nanofluid,and point B is at the edge of nanofluid region.

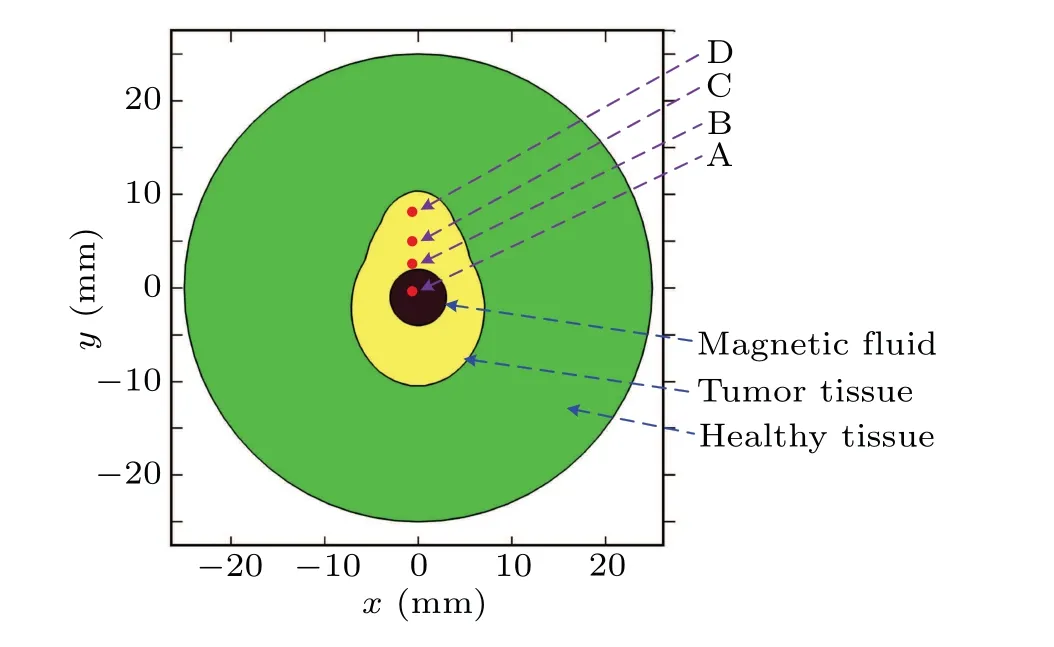
Fig. 1. Proposed geometric model with symmetric tumor for magnetic hyperthermia.

2.2. Mathematical model for numerical simulation

2.2.1. Thermal damage model for malignant cells

The thermal damage to malignant cells is strongly determined by the therapeutic temperature profile during magnetic hyperthermia,which is typically between 42°C and 46°C.In addition, one can also realize that kinetic coefficients should be also responsible for the cytotoxic effects of heat according to an Arrhenius mode at a proper temperature. In the Arrhenius mode,it is supposed that thermally induced cell injury is a first-order irreversible dynamic process,and the cell mortality rateS(τ)due to the heating at temperatureTforτcan be obtained by solving the following equations:[20,21]

whereτis the therapeutic time during heating period,Tis the treatment temperature in unit Kelvin, the universal gas constantRgis generally 8.314 J·mole-1·K-1, and the kinetic parametersEaandArespectively represent the activation energy and the frequency factor for the ablation process, which have to be established before treatment based on experimental data.

Once the thermal damage model is determined, one can obtain the cell mortality rate for tumor cells by using their Arrhenius kinetic coefficients. In this paper,three typical tumor cells are taken for example in the simulation,which are SN12 human renal carcinoma cells,[22]the PC3 human prostate carcinoma cells,[23]and the AT1 subline of Dunning R3327 rat prostate cells.[24]Equations(1)and(2)can describe the thermal apoptosis well enough for the AT1 and SN12,but not for the PC3 since a time delay dependent on therapeutic temperature needs to be considered to improve the accurate results.The time delay for this PC3 case can generally be obtained by a measurement method considering calcein leakage as follows:

wheretdis the time delay in second for the PC3,andbandmare the coefficients due to the fitting experiment for the PC3.Thus,the thermal apoptosis model for the PC3 will come into effect after the time delay has reached to a value obtained from Eq.(1).

2.2.2. Bio-heat transfer model

According to the Arrhenius mode above, the thermal apoptosis of malignant cells is determined by the kinetic coefficients due to the cell characteristics as well as the treatment temperature situation during hyperthermia. Therefore,the treatment temperature should be the only optimization target needed to be improved for the cell ablation,which can be obtained by solving the PBHT equation through using the finite element method. To compensate for the difference between bio-tissue and ideal solution,an improved PBHT model is considered in this work to predict the treatment temperature for the proposed bio-tissue model.[25]In this heat transfer model,the power dissipation of MNPs is considered as an input item,and assumed to just exist within the tumor region at the same time;it can be expressed as follows:[14,26,27]

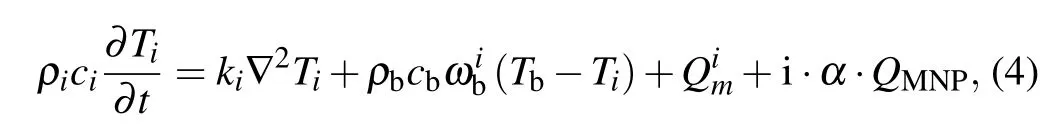
where subscriptiin Eq. (4) can be only zero or “1”, which indicates the healthy tissue or the tumor tissue, respectively;variablesρ,c,krepresent the tissue density,the tissue specific heat, and the thermal conductivity of the tissue, respectively;parametersρb,cb,ωbdenote the blood density,the blood specific heat, and the blood perfusion rate, respectively;Tindicates the absolute temperature of tissue;Tbmeans the blood temperature;Qmis the metabolic heat generation;αis a compensation coefficient for the power dissipation of MNPs when located inside the living tissues;QMNPdenotes the power density of MNPs dissipated from tumor tissue under an action of an applied magnetic field, which can further be expressed asQMNP=φPMNP,withφbeing the volume fraction of MNPs injected into tumor region,parameterPMNPbeing the volumetric heating rate dissipated by an MNP,which can be described by Rosensweig theory for relaxation loss as[28]

It must be particularly pointed out that the thermal characteristics of bio-tissue presented in Eq. (4) will change with the injection since the nanofluid should be considered as a part of the tumor region after the injection. The value of thermal characteristics should depend on the volume fraction of the MNPs,φ,at this time,and is given as follows:

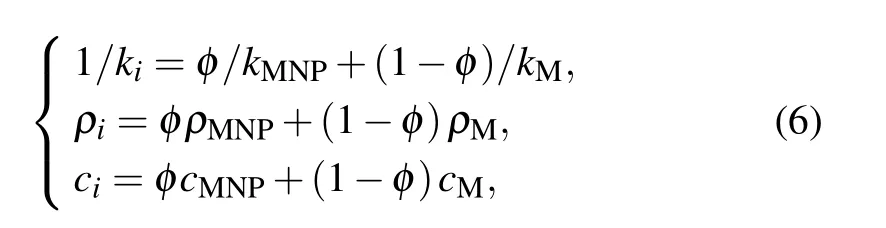
where subscript MNP denotes the thermal property of MNP,and subscript M indicates the malignant tissue. In addition,one can further associate the volume fraction of the MNPs with the nanofluid concentration through the density of MNPs,which can be expressed as

2.2.3. Mass transfer model after injection

The nanofluid concentration is a constant before the injection,but will change with the nanofluid being injected into tumor region. To investigate the optimal dose for treatment,here in this work it is assumed that the nanofluid keeps uniform distribution before the completion of injection and begins to diffuse over the time after the injection due to the pressure inside interstitial tissue. This interstitial pressure is caused by the transport of nanofluid inside bio-tissue, which can be illustrated by Darcy’s law,[29]?Pi=-εμv/K, wherePiis the interstitial flow pressure,εis the porosity of bio-tissue,vis the interstitial flow rate vector, andKis the permeability coefficient. The bio-tissue region in this paper is supposed to be a porous medium including sink and a source, and the mass balance equation for this interstitial flow can be described as

whereLPis the hydraulic conductivity of the capillary wall,S/Vis the surface area per unit volume of bio-tissue for transport in the interstitium,Pbis the blood pressure in the capillary,σsis the average osmotic reflection coefficient,πbis the plasma protein oncotic pressure,andπiis the osmotic pressure of the interstitial fluid. The drainage termφLis related to the differential pressure between interstitial tissue and lymphatic vessels,which is distributed homogeneously in normal tissue,and it is given as follows:[31]

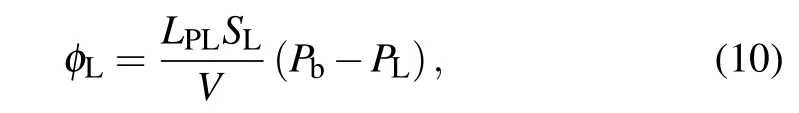
whereLPLSL/Vis the lymphatic filtration coefficient, andPLis the hydrostatic pressure of the lymph.

Substituting Eqs. (9) and (10) into Darcy’s law related to Eq. (8), one can obtain a couple of Laplacian for the interstitial pressure for the healthy region and tumor region as follows:

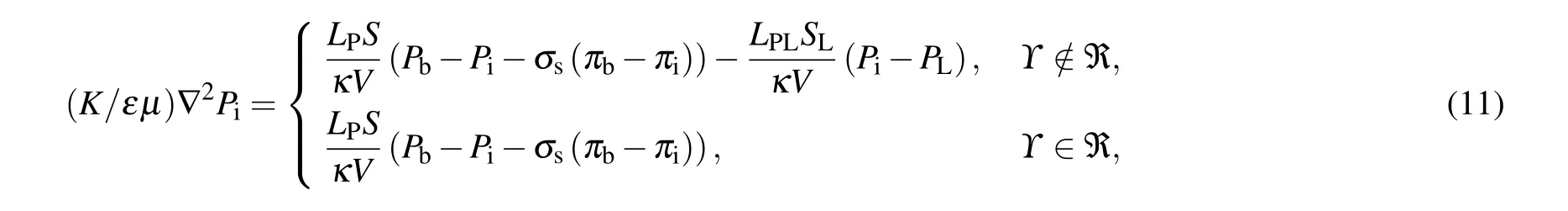
whereΥrepresents the solution domain for the equations,and? refers to the malignant region.

The interstitial flow velocity can be obtained by Darcy’s law after having obtained the interstitial pressure from Eq. (11). The mass transfer equation can then be used for describing the behavior of nanofluid diffusion after injection when the velocity gap between the MNPs and interstitial flow is ignored,[32]

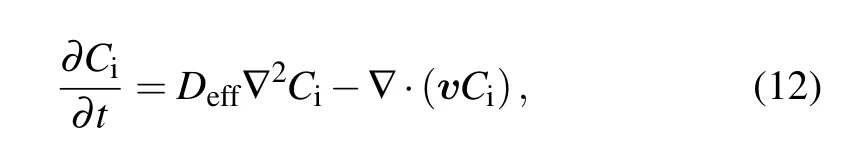
whereCiis the nanofluid concentration inside bio-tissue after injection due to the interstitial pressure,Deffis the diffusion coefficient for the nanofluid in the bio-tissue, which can be estimated by the Stokes-Einstein equation.[33]

2.3. Optimization procedure for injection behavior

The concentration distribution of nanofluid after injection is determined by many factors,the properties of bio-tissue and nanofluid, the diffusion time, and more importantly, the dose and injection site of nanofluid. In order to improve the treatment effect,it is extremely essential to optimize the dose and injection site of nanofluid for an irregular tumor model before therapy. In this work, the injection behavior of the proposed tumor model is optimized by considering simulated annealing (SA) algorithm for a proposed objective function. The optimization aim in this work is to improve the effective treatment temperature area as much as possible for the tumor tissue while minimizing this target for the healthy tissue. For this reason, in this work the treatment temperature area betweenTa1andTa2for tumor region is maximized while minimizing the temperature area lower thanTa1for healthy region. TemperaturesTa1andTa2are regarded as the thresholds of a safe therapy,42°C and 46°C,respectively.

Thus, two dimensionless terms can be used to illustrate this consideration for the treatment as follows:

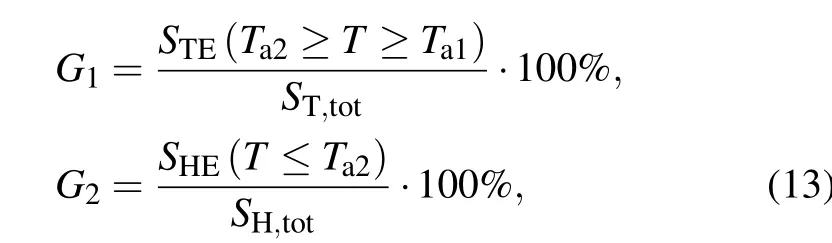
whereSTE(Ta2≥T ≥Ta1) is defined as the tumor area under an effective treatment temperature,ST,totis the whole tumor area,SHE(T ≤Ta2)is the healthy tissue area lower thanTa2,andSH,totis the whole area of healthy region. In order to improve the treatment effect, in this work is proposed an objective function by maximizingG1and minimizingG2at the same time,which can be expressed as

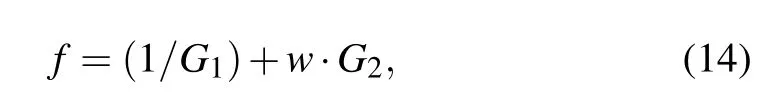
wherewis the weighting coefficient,which is set to be a constant 10, due to the consideration of its relative importance during treatment and their value range during optimal calculation.

The objective function presented in Eq. (14) will obtain a minimal value when the injection dose and site are both optimal by considering the proposed SA algorithm. The injection dose in this proposed model is related to the nanofluid areaD=πR21after injection as well as the power density of MNPsQMNP, while the injection site is determined by theycoordinate value of the injection center.The value of objective function depends on the temperature profile of the proposed model,which is obtained by solving Eq.(4)through using the finite element method and taking Eqs.(5)-(12)as its input at the same time.In this work,the tolerance is set to be 10-10for all values of variables and function during optimization analysis,which can guarantee sufficient time for the convergence of iterations. Thus,one can obtain the optimal injection parameters and treatment temperature for the tumor model when the terminating condition for iterations is reached and the objective function stops changing after several iterations.

3. Boundary condition and model properties

3.1. Boundary condition

In this work, the finite element method is used to solve the partial differential equations(Eqs.(4)and(12))for obtaining the treatment temperature profile and the nanofluid concentration inside bio-tissue. For Eq. (4), Dirichlet boundary condition is applied to the bio-tissue area surface,which is set to be a normal body temperature, 37°C. Newman boundary conditions are applied to the interface of different models for the proposed model. In addition,a constant value,T=37°C,is used as the initial value of this treatment.For Eq.(12),Newman boundary condition is used for all inner interfaces. The initial temperatures of all the tissues are considered to be zero while the initial concentration of the MNPs’ regions are assumed to beC0prior to therapy.

3.2. Model properties

In this subsection the material properties are investigated by using the proposed model, which cover the Arrhenius kinetic coefficients for different tumor cells in Table 1,the thermal properties of the proposed bio-tissue model in Table 2,the magnetic and MNP properties in Table 3, and also the transport properties of nanofluid in Table 4.

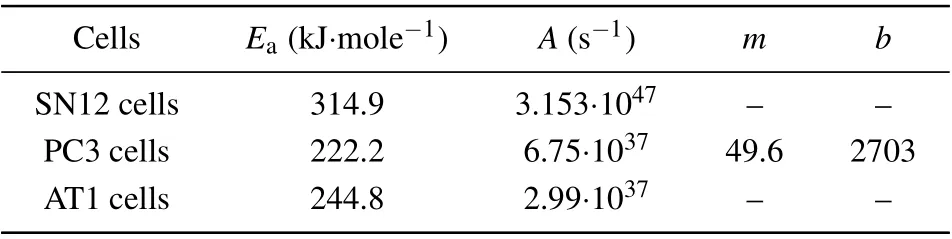
Table 1. Arrhenius kinetic coefficients for different malignant cells.[17,34]

Table 2. Thermal properties for proposed bio-tissue model.[2]

Table 3. Magnetic and MNP properties used in simulations.

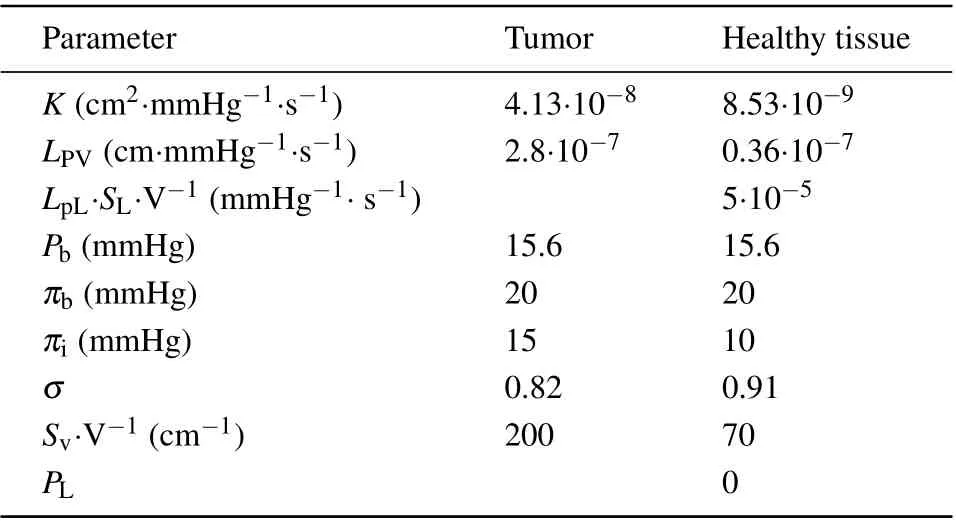
Table 4. Material properties used for modeling transport of MNPs in interstitium.[30,31]

4. Results and discussion

4.1. Optimization results for proposed bio-tissue model

In the process of optimization, the SA algorithm is used to optimize the injection behavior by considering a relatively arbitrary initial value for the proposed geometric model according to its metropolis sample rule.[35]The optimization parameters in this work arey0,QMNP,andR1,which need to be assigned a set of initial values prior to this optimization. Figure 2 shows the convergence curves for the variables and the objective function values obtained by the SA method during the optimization procedure. As shown in Fig.2,the variables and the objective function value both fluctuate dramatically before 100 iterations, and gradually reach their corresponding stable states after 150 iterations. It is worth mentioning that the current optimal valuef0for the objective function is always in a relatively stable state with respect to the current function valuefin the whole process of this optimization.

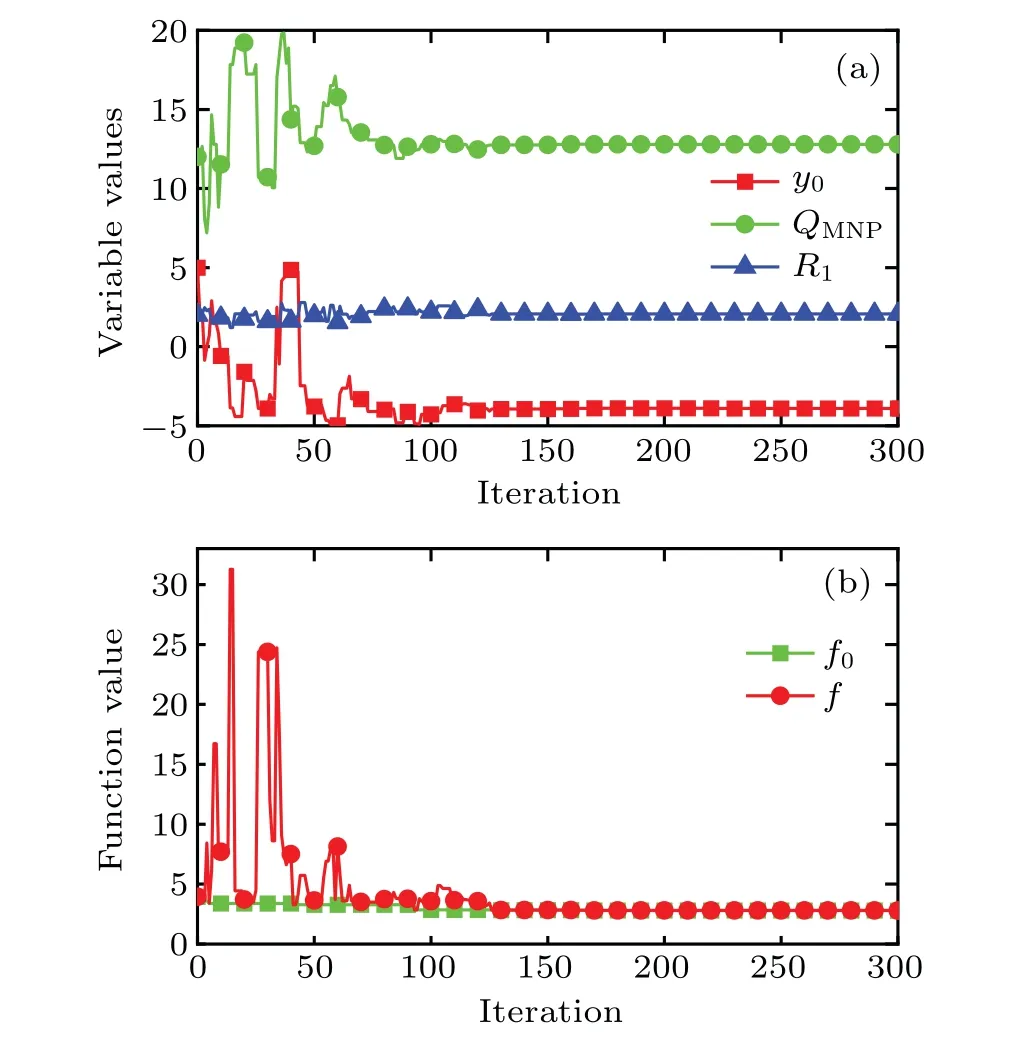
Fig.2. Convergence curves obtained by SA algorithm for(a)iterative variables and(b)objective function value,with QMNP being 105 W·m-3,y0 and R1 being in unit mm.

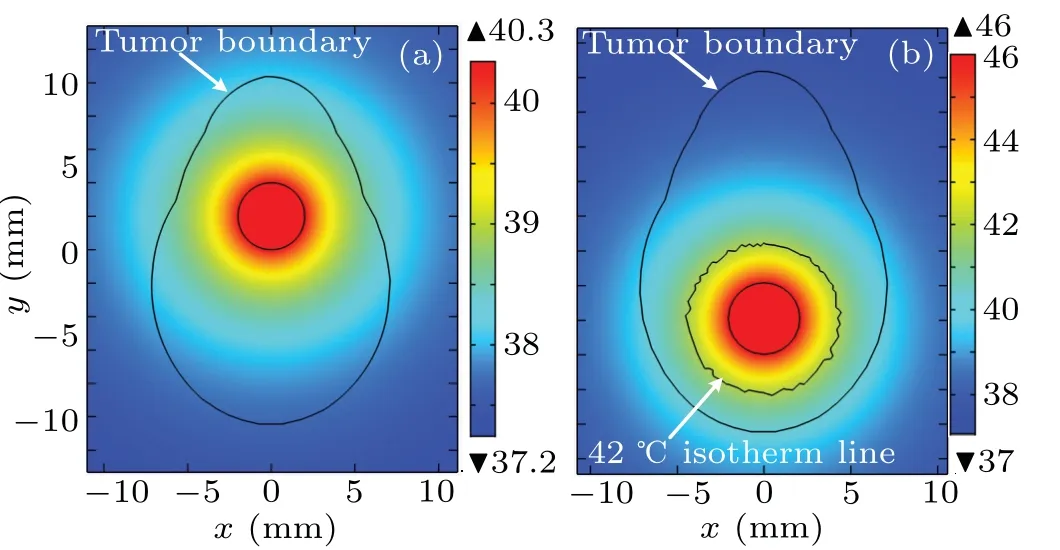
Fig. 3. Temperature distributions from the optimization results of injection behavior with a set of arbitrary initial values: (a) before optimization, (b)after optimization. Axes are in unit mm,and temperatures are in unit °C.

Once the injection behavior is obtained by this optimization, the treatment temperature for the proposed model can be obtained by solving Eq. (4) through using the finite element method. Figure 3 illustrates the treatment temperature distributions from the optimization results of Fig. 2 by using a set of arbitrary intimal values. As shown in Fig. 3(a), the maximum temperature value is only 40.3°C in a steady state before the optimization, which is lower than the threshold of effective therapeutic temperature for magnetic hyperthermia,42°C.As shown in Fig.3(b),what is particularly noteworthy is that the treatment temperature distribution can reache an obviously better situation after the optimization since the effective area for treatment temperature is significantly improved and the maximum temperature value is just limited to 46°C.

4.2. Concentration distributions from optimization results at different diffusion durations

The injection parameters,which includey0,QMNP,andR1after the optimization,can result in an optimal treatment temperature distribution for the proposed bio-tissue model. Nevertheless, this treatment effect can be further improved if the diffusion time is considered for the therapy after the injection according to previous literature.Figure 3 shows the concentration field from the optimization results for the proposed model in different diffusion durations,4 h,8 h,and 16 h. As shown in Fig. 3, the nanofluid diffuses gradually from the injection center and becomes more homogeneous inside tumor region as the diffusion duration is increased. However,the maximum value of nanofluid concentration can be observed in a downward trend over the diffusion duration, which decreases from 0.04 g·cm-3at 4 h to 0.01 g·cm-3at 16 h.

Fig.4. Concentration distributions from optimization results different diffusion durations: (a)4 h,(b)8 h,(c)16 h. Concentration is in units g·cm-3.

4.3. Temperature field distribution considering different concentration distributions due to diffusion duration

Different concentration distributions for nanofluid can result in different treatment temperature profiles inside tumor region when the solution of Eq.(12)is considered as the input of Eq.(4)during magnetic hyperthermia. In this work,the diffusion changes during the heating duration can be ignored due to the different time scales of these two cases.Figure 5 shows the treatment temperature distribution for the proposed model due to different diffusion durations:8 h,16 h,and 16 h with higher dissipation of MNPs. As can be seen, the maximum value of treatment temperature decreases further from the diffusion duration of 8 h in Fig. 5(a) to 16 h in Fig. 5(b) with respect to non-diffusion in Fig. 3(b). Most notably, figure 5(c) shows a better treatment temperature for the case considering the diffusion duration of 16 h when the power dissipation of MNPs is set to be a new critical valueQMNP=5.4·107W·m3for the proposed model. Furthermore,this case with better treatment temperature can then result in a better treatment effect than other cases presented in Fig.5.

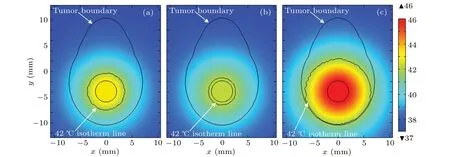
Fig.5. Steady-state temperature distributions in proposed model for different diffusion durations: (a)8 h, (b)16 h, and(c)16 h with higher power dissipation of MNPs. Temperature is in unit °C.

4.4. Tumor cells’ablation for different treatment temperature distributions

Once the treatment temperature distribution over time is determined by solving Eq.(4)through using the finite element method,the apoptosis probability of tumor cell can then be obtained by using Arrhenius model. In this paper, three typical tumor cells are considered for the thermal apoptosis analysis during magnetic hyperthermia. Figure 6 exhibits the apoptosis probabilities of three different tumor cells over time for the proposed point A with considering different concentration distributions due to different durations of diffusion. The critical power dissipationQMNPpresented in Fig. 6 can ensure that the maximum safe value of treatment temperature is 46°C for the proposed bio-tissue model before the nanofluid diffusion,and theQ′MNPcan achieve the same situation after 16 h of nanofluid diffusion. As shown in Fig. 6, the apoptosis probability for all tumor cells at point A can be slightly improved after 16 h of diffusion with a higher critical power dissipation of MNPQ′MNPthan with a criticalQMNPwithout diffusion, which is due to the relatively high treatment temperature within the tumor region. However,this situation can then turns worse when the diffusion duration is increased but the power dissipation of MNP is kept unchanged as can be seen in Fig.6. It can also be concluded that the apoptosis probability of tumor cells is strongly related to the kinetic coefficient of the Arrhenius model, since the maximum value of apoptosis probability can just reach less than 25%for the SN12 case in Fig.6(a)while 100%for the AT1 case in Fig.6(b). As shown in Fig.6(c),the apoptosis of the PC3 case is related not only to the kinetic coefficients but also the time delay due to Eq.(3),which always keeps at 0%before this delay.

The grey line presented in Fig.7 describes the apoptosis probability for the proposed points with the power dissipationQMNPbefore diffusion while the color line shows the apoptosis probability with the power dissipationQ′MNPafter diffusion.As illustrated in Fig. 7, points A and B have the similar results due to their similar treatment temperatures since both of them are located within the range of nanofluid region. However,points C and D each have obviously different probability values before and after the nanofluid diffusion. The main reason for this phenomenon is that points C and D are away from the injection site, so their treatment temperature can be further improved when the diffusion duration and higher power dissipation are considered for therapy.

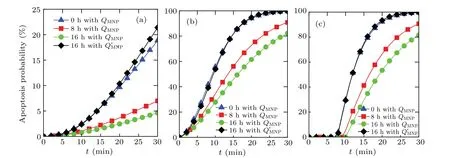
Fig.6. Curves of apoptosis probability versus time of different tumor cells for the proposed point A considering different concentration distributions due to different durations of diffusion,for(a)SN12,(b)AT1,and(c)PC3.

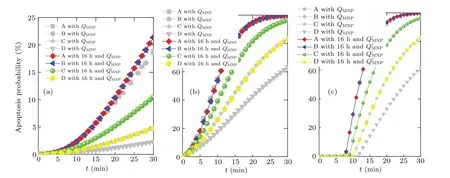
Fig.7. Curves of apoptosis probability versus time of different tumor cells for the proposed points considering different power dissipations of MNP,QMNP,and Q′MNP for(a)SN12,(b)AT1,(c)PC3.

5. Conclusions

In this work, the Arrhenius model is used to investigate the thermal apoptosis behaviors for three different malignant cells,which are assumed to exist in a symmetric tumor model during magnetic hyperthermia. In order to obtain better treatment effect,two methods are proposed by improving the treatment temperature profile for the proposed tumor model, optimizing the injection behavior, and increasing the duration.Simulation results demonstrate that the treatment temperature distribution can be obviously improved when simulated annealing algorithm is used to optimize the location and dose for nanofluid injection,and can also become much better when the increasing duration for nanofluid diffusion is combined with a correct critical power dissipation for MNP. Both of these solutions can finally lead the thermal apoptosis to be improved in all cases of the proposed malignant cells during magnetic hyperthermia. Nevertheless, it is worth mentioning that the malignant apoptosis due to magnetic hyperthermia may also result in a poor treatment effect when the Arrhenius kinetic coefficients of malignant cells are similar to the SN12 cells.Thus, although the method proposed by this paper can contribute to malignant cells in most of cases,it still be a potential topic to improve the treatment effect for some specific tumors with poor kinetic coefficient during hyperthermia.

Acknowledgements

Project supported by the National Natural Science Foundation of China (Grant No. 62071124), the Natural Science Foundation of Fujian Province, China (Grant No. 2020J01464), the Fund from the Education Department of Fujian Province, China (Grant No. JAT190013), the Fund from the Fuzhou University,China(Grant No.GXRC-19044),and the Conselho Nacional de Desenvolvimento Cient′?fico e Tecnol′ogico(BR)(CNPq)(Grant No.309244/2018-8).