State-flipped control and Q-learning algorithm for the stabilization of Boolean control networks

LIU Yang LIU Ze-jiao LU Jian-quan

(1.College of Mathematics and Computer Science,Zhejiang Normal University,Jinhua Zhejiang 321004,China;2.College of Mathematical Medicine,Zhejiang Normal University,Jinhua Zhejiang 321004,China;3.Jinhua Intelligent Manufacturing Research Institute,Jinhua Zhejiang 321032,China;4.School of Mathematics,Southeast University,Nanjing Jiangsu 210096,China)

Abstract:In this paper,the global stabilization of Boolean control networks under state-flipped control with respect to a given subset is addressed.For a given subset of the set of the nodes,the state-flipped control can change the values of some nodes from 1 or 0 to 0 or 1. Considering the flips as controls, Boolean networks under state-flipped control are studied.Combining control inputs with state-flipped controls, the concepts of joint control pair and the state-flipped-transition matrix are proposed. A necessary and sufficient condition is provided to check whether a Boolean control network under state-flipped control can be globally stabilized.An algorithm is developed to find the stabilizing kernel,which is the flip set with the minimal cardinal number.By using the reachable set,another method is provided for global stabilization and joint control pair sequences.Besides,if the system is a large scale network,a model-free reinforcement learning method called Q-learning algorithm,is used for the joint control pair sequences.A numerical example is given to illustrate the theoretical results.

Key words: Boolean control networks; semi-tensor product; state-flippped control; global stabilization; Q-learning algorithm

1 Introduction

By modeling the gene as a binary (on-off) device,Kauffman in 1969 firstly proposed Boolean networks(BNs)for investigating different metabolic behaviors of genes[1]that enable to capture the properties of largescale complex networks [2]. In order to make the BNs applicable to more types of biological networks, control inputs are added into BNs, and they are extended to Boolean control networks (BCNs). Cheng et al.proposed the semi-tensor product (STP) [3], which is a powerful tool in studying BNs (BCNs). Under the framework of STP, BCNs are expressed as finite state discrete time nonlinear dynamic systems with matrix algebra form. On the basis of the matrix algebra form,many properties of BCNs have been investigated, such as stabilization, controllability, observability, fault detection,disturbance decoupling and so on[4-12].

Stabilization problem is an important issue in control theory.In a BCN,stabilization is defined as finding feasible control sequences for any initial state to reach a target fixed point after finite time steps.There are many interesting results in the stabilization problems of BCNs.For example,Li et al.investigated state feedback stabilization for BCNs. Based on the concept of invariant subsets in [13], several necessary and sufficient conditions for set stabilization of BCNs have been presented.By using a minimal number of controllers, Lu et al. studied the pinning stabilization of BCNs in[14].

State-flipped control is a newly control mechanism with little intervention on the system[15-16].It works by changing the value of some nodes in BCNs from 1 to 0, or from 0 to 1, which simulates turning on or off genes in biological systems.Thanks to its ease of operation, many researchers have adopted the state-flipped control. For instance, Rafimanzelat et al. [16] studied the attractor stabilizability of BNs by flipping some nodes of the state in attractors once, after the networks have passed their transient period in the attractors.Rafimanzelat et al.[15]investigated the attractor controllability of BNs by flipping a subset of nodes in the states of several attractors as well. Chen et al. provided the criteria of controllability and stabilization of BCNs by flipping a subset of nodes in some initial states, rather than flip the nodes of the attractors after the system has passed the transient period.More recently,Zhang et al.have applied the flipping mechanism to the stabilization and set stabilization of switched BCNs, which considers flipping a subset of nodes of initial state once[17].In addition, the weak stabilization of BNs with flip sequences is investigated in [18]. Up to now, many researchers have implemented state-flipped control into stabilization and controllability of BNs(BCNs).

Reinforcement learning(RL)is one of the methodologies of machine learning, which is used to describe and solve the problems that agents use learning strategies to maximize returns or achieve specific goals in the process of interacting with the environment. As a breakthrough in reinforcement learning algorithms,Qlearning(QL)algorithm was first proposed by Watkins in 1992 [19].QL algorithm is a model-free RL algorithm,which can be used in the tracking control of autonomous surface vehicles[20],smart grid devices[21],and intelligent intersection traffic signal control [22]and so on.QL can be used to judge some properties of gene regulatory networks,which can reduce the computational complexity to a certain extent compared with the traditional STP method.An important concept inQL is theQtable, which is a mapping table between states-actions and estimated future rewards.Under some conditions,theQtable will converge to aQ?table where we can read the optimal policy from.QL algorithm was applied to probabilistic Boolean control networks(PBCNs),which shows the advantages of the algorithm in the case of model-free[23].It investigated the feedback stabilization problem of PBCNs,and compared the STP method with the value iteration method.Acernese et al. [24] also developed aQL algorithm about self-triggered control co-design for stabilization of PBCNs.

The existing works in the state-flipped control mainly consider flipping a subset of nodes just once,no matter for the initial states or the states in attractors.In this paper, we consider the joint control pair, which consists of a state-flipped control and a control input.When studying the global stabilization of BCN under state-flipped control,we first give a set of nodes that can be flipped,and the actual state-flipped control depended on the subset of the given set.There exist many different joint control pairs, hence we propose the concept of joint control pair sequences.In our joint control pair sequences,sometimes the obtained state-flipped control is with respect to an empty set,which means that we do not need to add state-flipped control for the state and it is enough to just take a control input,i.e.,a normal case in BCNs. The contributions of this paper are summarized as follows:

? We propose the concept of joint control pair which consists of a state-flipped control and a control input,and apply it into BCNs.

? The global stabilization of BCNs under stateflipped control is studied, and several necessary and sufficient conditions are presented.

? For stabilizing a BCN under state-flipped control, aQL algorithm is designed to find the corresponding joint control pair sequence for every initial state.

2 Preliminaries

2.1 Notations

2.2 BCN and its algebraic representation

Consider a BCN as follows:

Definition 1[3]For matricesA ∈Rp×qandB ∈Rs×t, the semi-tensor product (STP) with symbol “”is defined as

2.3 State-flipped control

This subsection introduces the state-flipped control and its algebraic representation.Before introducing the flip function, we need to choose a flip set, which is a subset of the nodes’set of a BCN.It can be specified in random, or it can be a collection of genes that we are able to control in the practical cases.

Definition 2 LetA:={a1,a2,··· ,ar} ?[1 :n].The flip function with respect toAis defined as

Definition 4 LetB:={b1,b2,··· ,bs} ?[1 :n]. The combinatorial flip matrix with respect toBis defined as paper, we first consider that all states in BCN (3) are flipped with respect to all subsets ofB. The new system that all states take one flip transition with respect to one subset ofBand one state transition with control input is called BCN(3)underBstate-flipped control.

Here, we present a brief explanation of two setsAandB. For a given state,Ais the actual flip set, and every element inAcorresponding to the nodes of the given state has to be flipped.However,Bis a combinatorial flip set, and we select a subset ofBdenoted byAto flip.Next,we give a numerical example of a BCN(3)to illustrate the flip matrix and the combinatorial flip matrix.

Example 1 Consider a BCN with three nodes,i.e.n= 3. If a subsetB ?[1 :n] is given byB={2,3}, we can find that all possible flip sets are subsets ofB, denoted byA1= ?,A2={2},A3={3},A4={2,3}. Then, flip matrices with flip setsAi,i=[1:4]can be calculated as

3 Main results

This section focuses on the stabilization of BCN(3)underBstate-flipped control. Several criteria are proposed to judge the stabilization.Note that the global state transition space may be changed under state-flipped control defined in Section 2. Hence, we present a new type of the state transition matrix,which is called stateflipped-transition matrix.

According to ～G,the new system transformed from BCN(3)underBstate-flipped control is

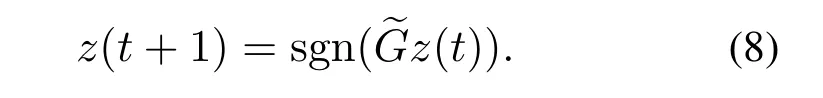
Therefore,z(t)is a Boolean vector with several entries equal to 1 and other entries equal to 0. Setz(0)=x(0) =x0. The state transition between two states is called a state-flipped transition in BCN (3) underBstate-flipped control with the combined action of a stateflipped control and a control input. Here, we use notation (η?A,δi2m) which is called the joint control pair to represent the combined action in one state-flipped transition step of BCN(3).D(z(t+1))represents the set of all states steered fromD(z(t))after one state-flipped transition step.

Definition 7 Given a subsetB ?[1 :n]. For an initial statex0∈Δ2n, letx(k;uk,x0) be the state of BCN(3)at timek,whereuk={u0,u1,··· ,uk?1}is a control input sequence. Letx(k;Λk,x0) be the state of BCN(3)underBstate-flipped control at timek,whereΛkis the joint control pair sequence withkjoint control pairs.

Theorem 1 For any joint control pair sequenceΛt, assume thatx0∈Δ2nis an initial state, then the state reached fromx0after some state-flipped transitions with joint control pairs is always inD(z(t)),i.e.,x(t;Λt,x0)∈D(z(t)).

Now, we give an example to illustrate the validity of Theorem 2.

Example 2 GivenB={2,3}as is mentioned in Example 1.Consider a BCN with three nodes and one control input, i.e.n= 3,m= 1 in [14]. Its algebraic representation is

Next,after introducing matrix ～G,we are able to address the global stabilization of BCN(3)underBstateflipped control based on ～G.We derive the definition ofxdstabilizable for a BCN(3)underBstate-flipped control as follows, where the in-degree of the statexdis greater than 0.

If BCN (3) underBstate-flipped control can achieve global stabilization, we call the setBstabilizing set.

In Definition 8, we need to find properΛtfor the global stabilization. The result of Theorem 2 implies that the reachability between two states can be calculated by ～G.Therefore,we propose Theorem 3 as a prior condition to judge the global stabilizaion of BCN (3)underBstate-flipped control.If the global stabilization under state-flipped control cannot be achieved by a subsetB ?[1 :n]in Theorem 3,then we need to choose another set to replaceB.

Theorem 3 For a given subsetB ?[1 :n]and a statexd=δd2n,BCN(3)underBstate-flipped control is globally stabilizable toxdif and only if the following two statements hold:

1) (～G)dd>0;

2) There exists a positive integerk ∈[1:2n ?1],such that Rowd((～G)k)>0.

If we have verified that BCN (3) underBstateflipped control is globally stabilizable toxd,then BCN(3) can be also globally stabilizable toxdunder stateflipped control for any superset ofB. In order to reduce the control cost, we always expect that the cardinal number ofBachieving global stabilization is as small as possible.A stabilizing setBwith minimal cardinal number is said to be a stabilizing kernel of BCN(3)underBstate-flipped control,and the corresponding minimal “N” in Definition 8 is called stabilizing step.Since the subsetBis given in advance,it is used to prejudge whether BCN (3) underBstate-flipped control can achieve global stabilization to a given state. However, it is possible that a subset ofBmight be a better stabilizing set with smaller cardinal number. Hence, it inspires us to find a stabilizing kernel, which is a subset ofB, to give the state-flipped control. Algorithm 1 is developed to obtain a stabilizing kernel based on the givenB.

Algorithm 1 An algorithm for finding a stabilizing kernel and the corresponding stabilizing step of BCN(3)based on a given set B to achieve global stabilization to δd2n Input: M,B Output: Bγi,k 1: Initialization 2: γ =1 3: i=1 4: Initialize θ and Cγ θ 5: If(MCBγi)dd >0,go to step 6 6: k =1 7: If Rowd[(MCBγi)k]>0,8: return Bγi,k,end 9: else k ←k+1 10:If k ≤2n ?1,go to step 7 11:else i ←i+1 12:If i ≤Cγθ,go to step 5 13:else go to step 14 14:If output is empty,γ ←γ+1 15:If γ ≤θ,go to step 3 16:else end 17:else end 18: else i ←i+1 19: If i ≤Cγθ,go to step 5 20: else γ ←γ+1 21:If γ ≤θ,go to step 3 22:else end

Now, we give several explanations of the notations using in Algorithm 1. The cardinal number of given subsetBisθ, i.e.|B| =θ.Bγiis a subset ofBwith cardinal number beingγ.Cγθis a combinatorial number.IfBγiandkare returned,thenBγiis a stabilizing kernel andkis its corresponding stabilizing step.

Based on the above analysis,for a traditional BCN(3), if it cannot achieve global stabilization to any state,we can consider adding some state-flipped controls. Given a subsetB ?[1 :n], the global stabilization with respect toxdcan be checked by Theorem 3 underBstate-flipped control.Then,Algorithm 1 presents a method for calculating the stabilizing kernel and the stabilizing step.In practical problems,we not only need to judge whether the network can be globally stabilizable,but also need to find the corresponding joint control pair sequences for each state.Thus,another method about reachable set for global stabilization is provided.

In the construction ofkstep reachable set, we can obatin thatEi(d)∩Ej(d) = ?for any positive integersiandjsatisfying 1 ≤i ?=j≤2n ?1. Next,we can calculate thekstep reachable set ofxdto determine whether BCN(3)underBstate-flipped control is globally stabilizable toxd.

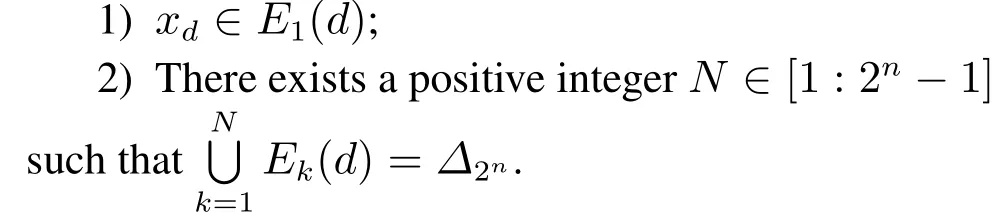
Algorithm 2 An algorithm for finding a joint control pair sequence to steer δj2n to δi2n Intput: δj 2n,δi2n Output: Λ{δj2n,δi2n}1: Initialization 2: k =1 3: If k ≤2n ?1,do step 5 4: else end 5: If[(～G)k]ij >0,then let k?=k,do step 7 6: else k ←k+1,do step 3 7: Calculate Em(i),m ∈[1:k?]8: Find a path P = {x0 = δj 2n →x1 = δp12n →x2 = δp2 2n →···→xk?=δi2n}9: Calculate MHAr,r ∈[1:2θ]10: Find (MHArt)pt+1,pt > 0, then the state-flipped control for xt is η?Art,where t ∈[0:k??1],rt ∈[1:2θ]11: Find(GqtHArt)pt+1,pt = 1,then the control input for xt is ut =δqt 2m,where t ∈[0:k??1],qt ∈[1:2m]12: Λ{δj2n,δi2n} ={(η?Ar0,u0),(η?Ar1,u1),··· ,(η?Ark??1,uk??1)}13: end

If we use BCNs to model large-scale gene regulatory networks, the STP-based approach will have high computational complexity.To this end,we present aQL algorithm,which can be applied in model-free cases and reduces computational complexity, to check whether a BCN(3)underBstate-flipped control is globally stabilizable to a given state.

QL algorithm is a type of model-free reinforcement learning algorithm involving Markov decision processes(MDPs),and especially in this paper we only consider the case without any probability[23-24]. As a reinforcement learning method,QL algorithm can achieve goals through interactive learning and training between agents and the environment. Agents can be sensors,drones,power stations in smart grids,gene nodes in biological networks, and so on. The environment representing everything outside the subject can interact with and impact on the agents. Specifically, the agents and the environment constantly interact. The agents select actions,and in turn,the environment responds to those actions and provides new information to the agents. In the process of interaction,the environment generates rewards, namely specific values, which can reflects the quality of the current action. The essence of reinforcement learning is to find a series of actions that maximize the long-term rewards(return)to achieve a given goal.Besides,a policy is a mapping from states to the probability of choosing each possible action.Simply,a policy can be regarded as a choice of actions for a state at each step.

In this paper,we regard a controller as an agent and the unknown system (the BCN) as the environment. A joint control pair is regarded as an action.The reward is set artificially based on a given goal, and the return is the sum of the rewards. After the qualitative introduction, we introduce some specific notations and necessary explanations for theQL algorithm.

In BCN(1)underBstate-flipped control,Xt ∈Dndenotes the state attaftertstate-flipped transition steps.Xd ∈Dndenotes a given target state. Since both state-flipped controlη?Atand control inputUt ∈Dmare adopted, now we recall joint control pair(η?At,Ut)denoted byJtfor the sake of convenience.

For theQL algorithm,some basic notations are introduced.Λ?(Xt,Xd) denotes the optimal policy (i.e.a joint control pair sequence achieving the given target state with maximal return) fromXttoXd.rtdenotes the reward used to calculate the immediate return value received by the agent, after the agent selects an action from the current state and moves to the next state. The reward function is set in advance according to our goals.With target of steering the BCN underBstate-flipped control to be globally stabilizable toXd, we give the setting of the rewardrt+1as follows:

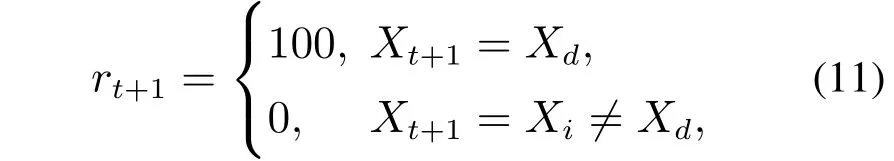
whereXi ∈Dnwithi ∈[1:2n].

Based on the above settings, Algorithm 3 is proposed usingQL method to check the global stabilization of BCN underBstate-flipped control as follows.

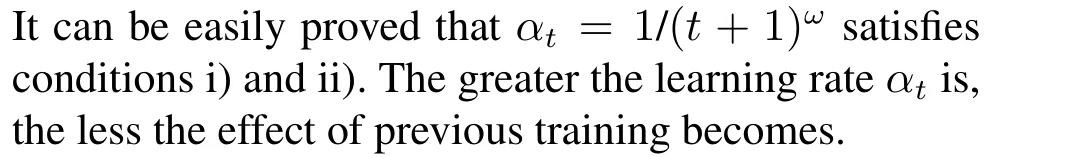
Now, we give the origin ofQtable in Algorithm 3. We setπto be the policy.vπ(Xt)denotes the value function forXt, which can estimate the long-term discounted return to show the performance of agent atXtand under policyπthereafter,namely:

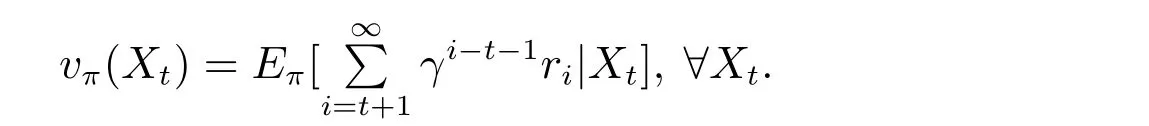
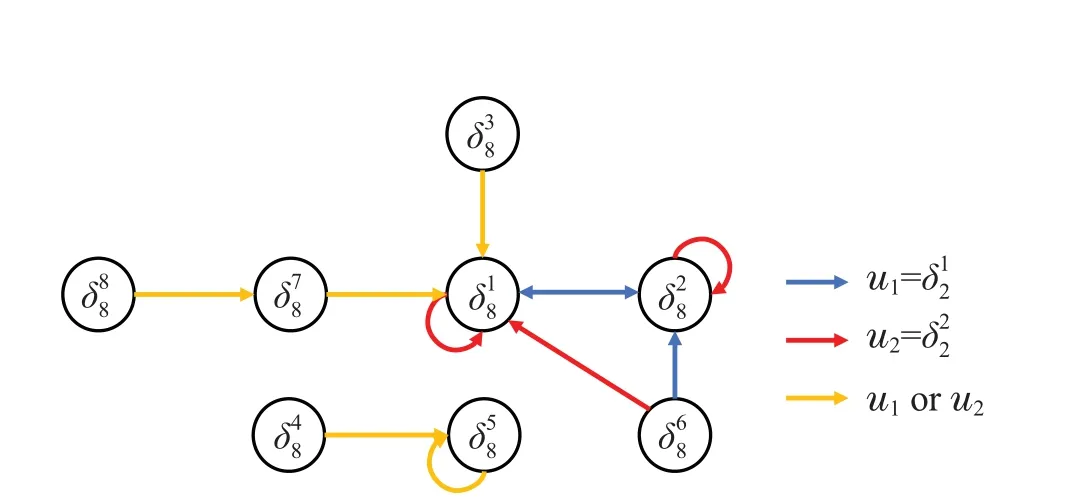
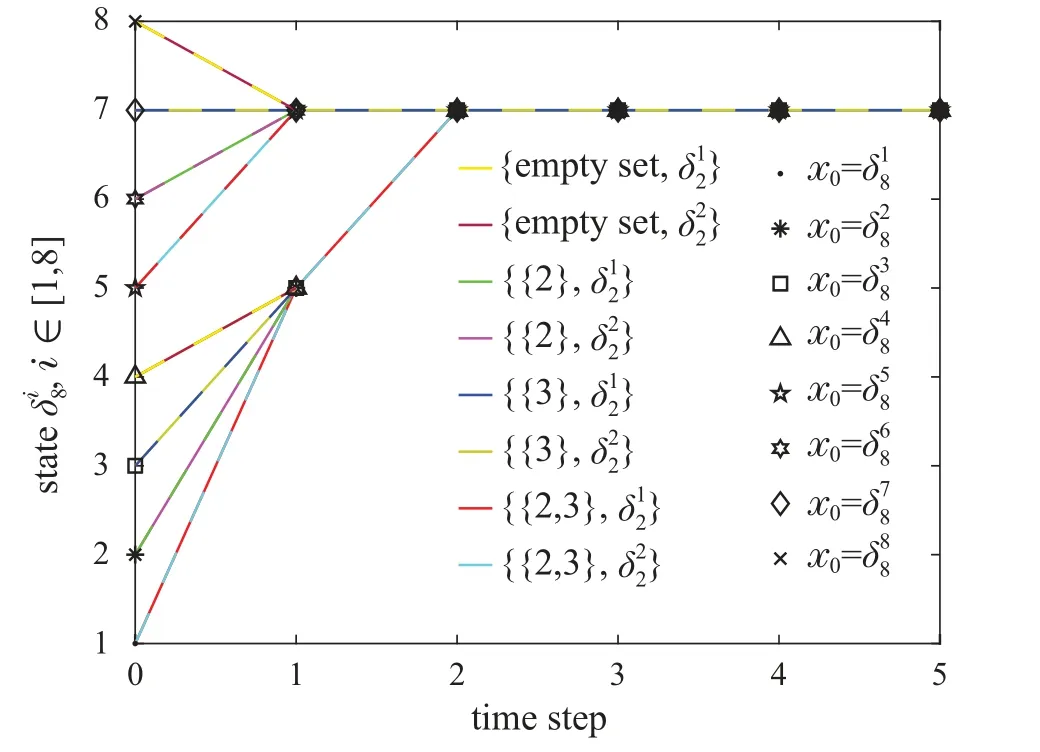
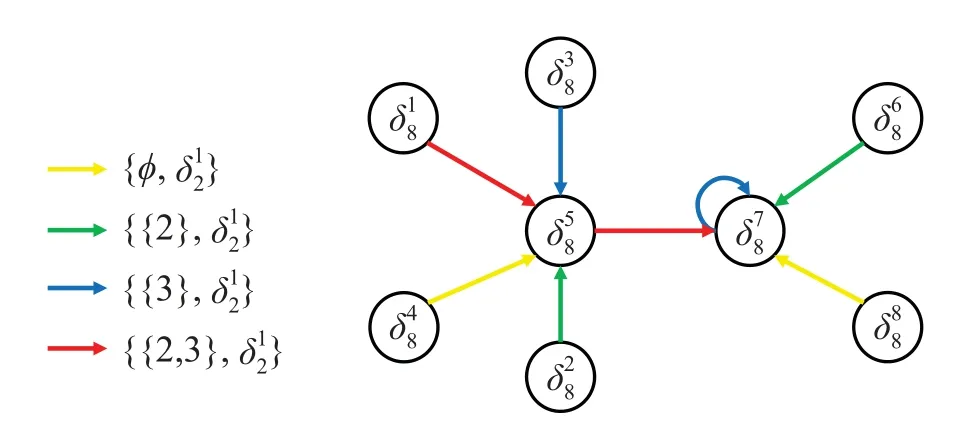
Algorithm 3 Global stabilization of BCN under B state-flipped control using QL method Intput:Xd,N,T,τ,?-greedy,ω Output:Λ?(Xt,Xd),if BCN under B state-flipped control is globally Xd stabilizable 1: Initialization: Q0(Xt,J t,Xd) ←0,?Xt,?Jt, Eτ(Xd)←?2: For ρ=0,1,··· ,N ?1 do 3:Xρ ←rand(Dn)4:αρ ←1/(ρ+1)ω,t ←0,Xt ←Xρ 5:While(t

where P{X|Xt,J}is the conditional probability forXttoXby taking the joint control pairJ. Similarly, we set the action-value functionqπ(Xt,Jt) to be the expected return fromXt,underJtbased on policy

whereQtable is in R2n×2n.Recalling conditions i)and ii),Qtable is convergent and converges toQ?table.Thus, for any initial stateX0, we can useQ?table to estimateq?, and hence we can find the optimal stateflipped transitions toXd.Finally,we can obtain the optimal joint control pair sequenceΛ?(X0,Xd).

After introducing the update rule ofQfactor, we continue to introduce other necessary notations in Algorithm 3:Each episodeρ ∈[0,N ?1]is a complete training process from any initial stateX0to the target stateXd, whereNis the maximal number of episodes we consider.?-greedy strategy is a common algorithmic idea, which refers to choosing the actionJtwith the largestQtin the current view by probability 1??,i.e.Jt=arg maxQt.With probability?,the choice of the action is random. In each episodeρ, we denoteTas the maximum of actions taken by the agent. We setτ=2n?1 andT ?τ.In addition,we denoteEτ(Xd)as the set of states which arrive toXdafter (within)τstate-flipped transition steps.

4 Simulations

In this section,a simple BCN is used to demonstrate the obtained theoretical results.

Example 3 Reconsider BCN(1), the state transition matrix of BCN(9)is given by

Next,we adopt theQL Algorithm 3 to find the joint control pair sequences to steer the BCN under{2,3}state-flipped transition to achieve global stabilization toxd=δ78.Set the reward by(11),and letN=500000,ω=0.51,?=0.3.The convergedQ?table can be ob-

The joint control pairs above and below the arrow are both allowed in the state-flipped transition between two states. Fig. 2 shows the state-flipped transitions considering all joint control pairs of BCN (9) under{2,3}state-flipped transition. For two states, we take any feasible joint control pair composing a state-flipped transition graph of BCN (9) under{2,3}state-flipped control,which is shown in Fig.3.Comparing Fig.1 and Fig.3,note that although BCN(9)is not globally stabilizable by free control sequences,BCN(9)under{2,3}state-flipped control is globally stabilizable to the target stateδ78after adding state-flipped control.

Fig.1 The state transition graph of BCN(9)

Fig.2 All paths about state-flipped transitions of BCN(9)under{2,3}state-flipped control

Fig.3 One of the state-flipped transition graphs of BCN(9)under{2,3}state-flipped control

5 Conclusion

This paper addresses the global stabilization of BCNs under state-flipped control. We propose a BCN added with state-flipped control, called BCN under state-flipped control.The state-flipped-transition matrix is given to judge the reachability of states. Based on the state-flipped-transition matrix, several criteria are proposed for the global stabilization. We design an algorithm for finding a stabilizing kernel and the corresponding stabilizing step. Moreover, aQL algorithm is given for finding the joint control pair sequences to achieve global stabilization.Finally,an example is provided to illustrate the main results.