一道合肥質(zhì)檢試題的推廣

山東省泰安市寧陽(yáng)縣第一中學(xué)(271400) 劉才華

題目已知F是拋物線E:y2=2px(p ＞0)的焦點(diǎn),直線?:y=k(x-m)(m ＞0)與拋物線E交于A,B兩點(diǎn),與拋物線E的準(zhǔn)線交于點(diǎn)N.

(1)若k=1 時(shí),|AB|=求拋物線E的方程;

(2) 是否存在常數(shù)k, 對(duì)于任意的正數(shù)m, 都有|FA| · |FB|=|FN|2? 若存在, 求出k的值; 若不存在,說明理由.

這是合肥市2021 屆高三第一次教學(xué)質(zhì)量檢測(cè)理科數(shù)學(xué)試題第20 題,對(duì)于試題的第(2)問,我們?nèi)菀椎玫饺缦?/p>

命題1F是拋物線E:y2= 2px(p ＞0)的焦點(diǎn), 直線?:y=k(x-m)與拋物線E交于A,B兩點(diǎn),與拋物線E的準(zhǔn)線交于點(diǎn)N,則對(duì)于任意的實(shí)數(shù)m ∈[0,+∞),都有|FA|·|FB|=|FN|2的充要條件是k2=1.

證明由題意得準(zhǔn)線方程為x=則從而

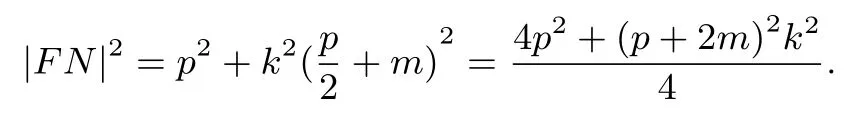
設(shè)A(x1,y1),B(x2,y2), 由

得k2x2-2(mk2+p)x+k2m2= 0. 由題意得k /= 0. 由m ∈[0,+∞)得Δ=8mpk2+4p2＞0,且x1+x2=x1x2=m2. 由拋物線焦半徑公式得|FA|=x1+則

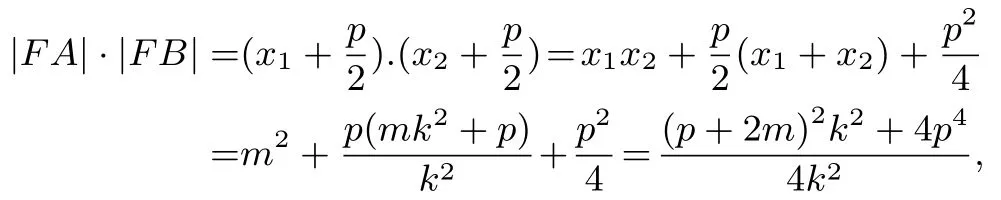
于是|FA| · |FB|=|FN|2?? k2= 1. 則對(duì)于任意的實(shí)數(shù)m ∈[0,+∞), 都有|FA| · |FB|=|FN|2的充要條件是k2=1.

進(jìn)一步思考,對(duì)于橢圓,我們得到如下:

命題2F是橢圓E:=1(a ＞b ＞0)的焦點(diǎn),直線?:y=k(x-m)與橢圓E交于A,B兩點(diǎn),與橢圓E的對(duì)應(yīng)準(zhǔn)線交于點(diǎn)N,橢圓的離心率為e(e≥則對(duì)于任意的實(shí)數(shù)m ∈[-a,a],都有|FA|·|FB|=|FN|2的充要條件是k2=2e2-1.

證明(1) 若F為橢圓E的左焦點(diǎn), 設(shè)橢圓E的半焦距為c, 則F(-c,0), 對(duì)應(yīng)準(zhǔn)線方程為x=從而|FN|2=

設(shè)A(x1,y1),B(x2,y2),由消去y得(a2k2+b2)x2-2ma2k2x+a2(m2k2-b2) = 0,則由m ∈[-a,a]得Δ=4a2b2[(a2-m2)k2+b2]＞0,且

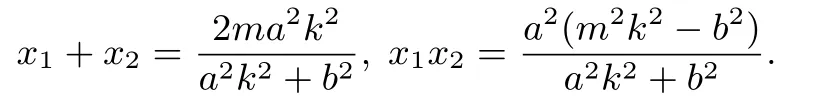
由橢圓的焦半徑公式得|FA|=a+ex1,|FB|=a+ex2,則

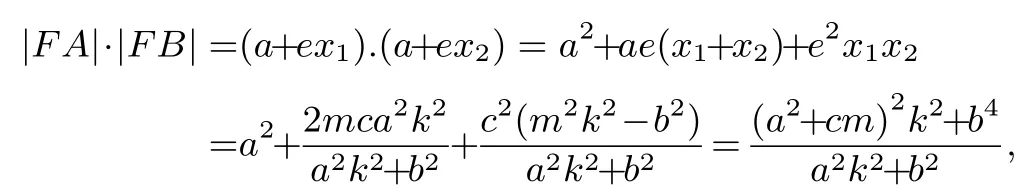
于是

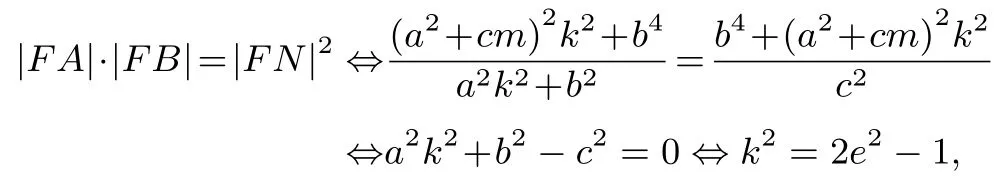
則對(duì)于任意的實(shí)數(shù)m ∈[-a,a],都有|FA|·|FB|=|FN|2的充要條件是k2=2e2-1;

(2)若F為橢圓E的右焦點(diǎn),同理可證,過程從略.

由(1)和(2)知命題2 成立.

對(duì)于雙曲線,我們得到如下

命題3F是雙曲線E:=1(a,b ＞0)的焦點(diǎn),直線?:y=k(x-m)與雙曲線E交于A,B兩點(diǎn),與雙曲線E相應(yīng)的準(zhǔn)線交于點(diǎn)N,雙曲線的離心率為e,則對(duì)于任意的實(shí)數(shù)m ∈(-∞,-a]∪[a,+∞),都有|FA|·|FB|=|FN|2的充要條件是k2=2e2-1.

證明(1)若F為雙曲線E的左焦點(diǎn),設(shè)雙曲線E的半焦距為c,則F(-c,0),對(duì)應(yīng)準(zhǔn)線方程為x=從而

設(shè)A(x1,y1),B(x2,y2),由消去y得(a2k2-b2)x2-2ma2k2x+a2(m2k2+b2) = 0,則由題意得a2k2-b2/= 0. 由m ∈(-∞,-a]∪[a,+∞)得Δ=4a2b2[(m2-a2)k2+b2]＞0,且

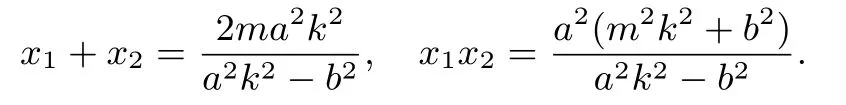
由雙曲線的焦半徑公式得|FA|=-a-ex1,|FB|=-a-ex2,則

于是

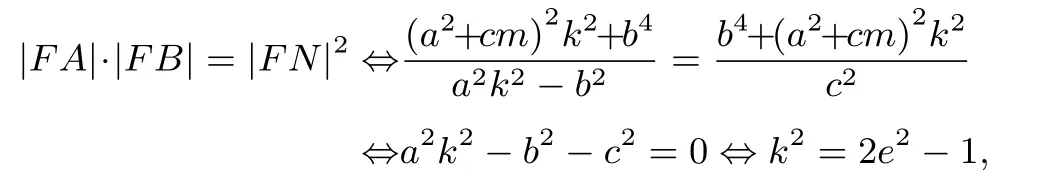
則對(duì)于任意的實(shí)數(shù)m ∈(-∞,-a]∪[a,+∞), 都有|FA|·|FB|=|FN|2的充要條件是k2=2e2-1;

(2)同理可證F為右焦點(diǎn)時(shí)結(jié)論成立. 綜上命題成立.

注意到拋物線的離心率e= 1,所以命題1、命題2 和命題3 有統(tǒng)一形式的結(jié)論,是圓錐曲線中一個(gè)統(tǒng)一的性質(zhì).