AN UPBOUND OF HAUSDORFF’S DIMENSION OF THE DIVERGENCE SET OF THE FRACTIONAL SCHRDINGER OPERATOR ON Hs(Rn)?
(李丹)
School of Mathematics and Statistics,Beijing Technology and Business University,Beijing 100048,China E-mail:danli@btbu.edu.cn
Junfeng LI (李俊峰)?
School of Mathematical Sciences,Dalian University of Technology,Dalian 116024,China E-mail:junfengli@dlut.edu.cn
Jie XIAO (肖杰)
Department of Mathematics and Statistics,Memorial University,St.John’s NL A1C 5S7,Canada E-mail:jxiao@math.mun.ca
Abstract Given n≥2 and,we obtained an improved upbound of Hausdorff’s dimension of the fractional Schr?dinger operator;that is,.
Key words The Carleson problem;divergence set;the fractional Schrdinger operator;Hausdorff dimension;Sobolev space
1 Introduction
1.1 Statement of Theorem 1.1
Suppose that S(R)is the Schwartz space of all functionsf
:R→C such that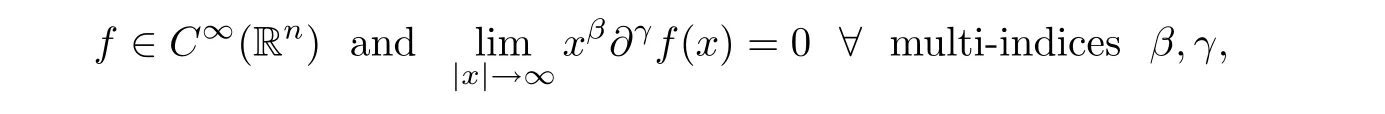

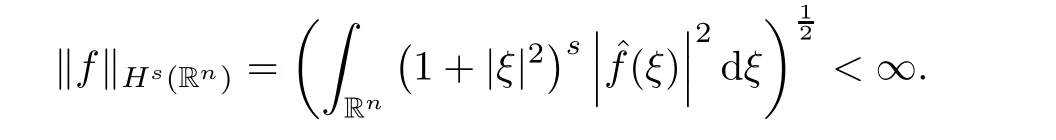
f
stands for the(0,
∞)?α
-pseudo-differential operator de fined by the Fourier transformation acting onf
∈S(R),that is,if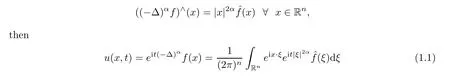
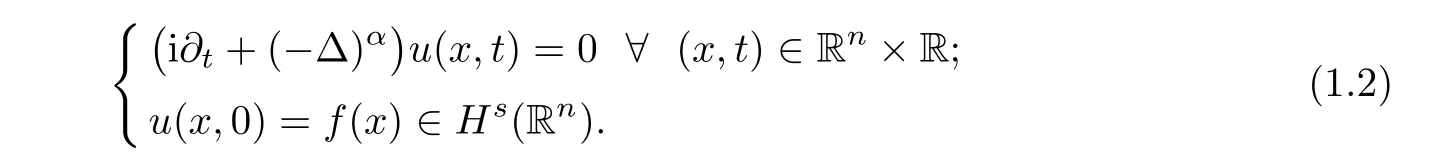
s
such that
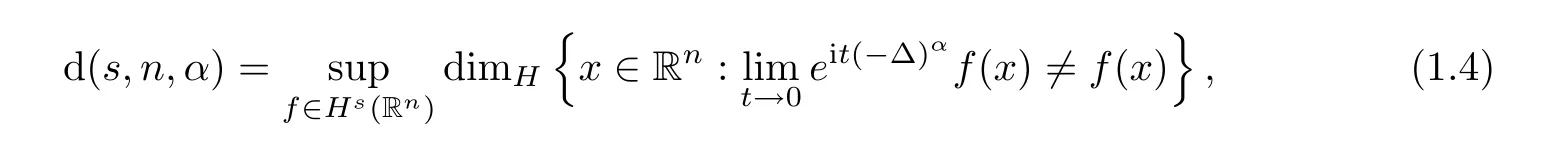

Theorem 1.1
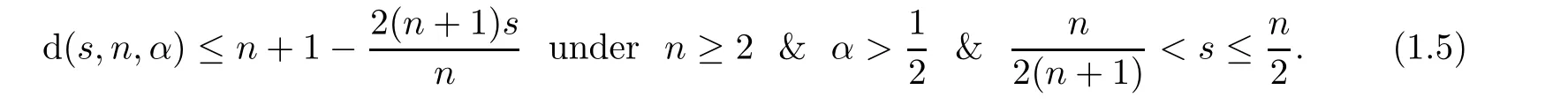
1.2 Relevance of Theorem 1.1
Here,it is appropriate to say more about evaluating d(s,n,α
).In general,we have the following development:
Theorem 1.1 actually recovers Cho-Ko’s[1]a.e.-convergence result

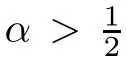
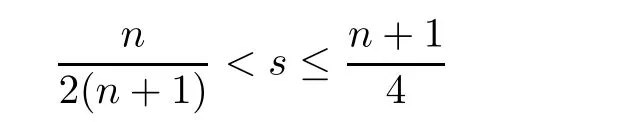
as follows:
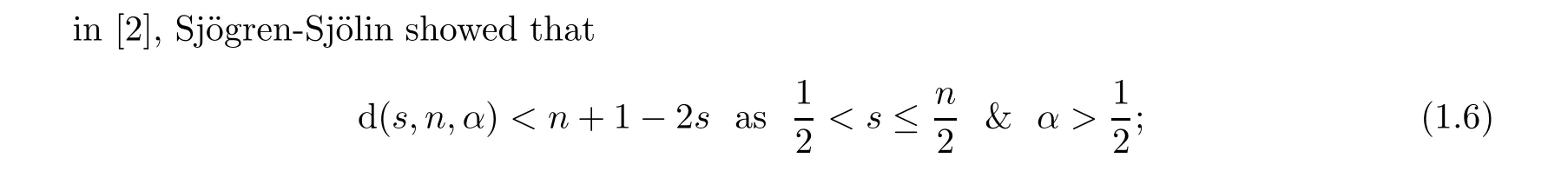
in[3]and[4],it was proved that
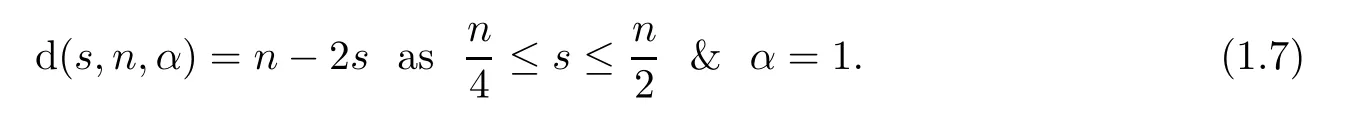
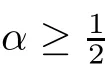

In particular,we have the following case-by-case treatment:

Bourgain’s counterexample in[9]and Luc`a-Rogers’result in[20]showed that
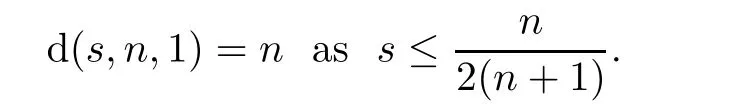

On the one hand,in[5],Du-Zhang proved that
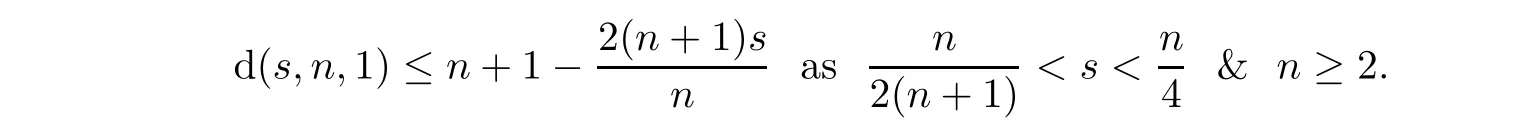
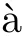
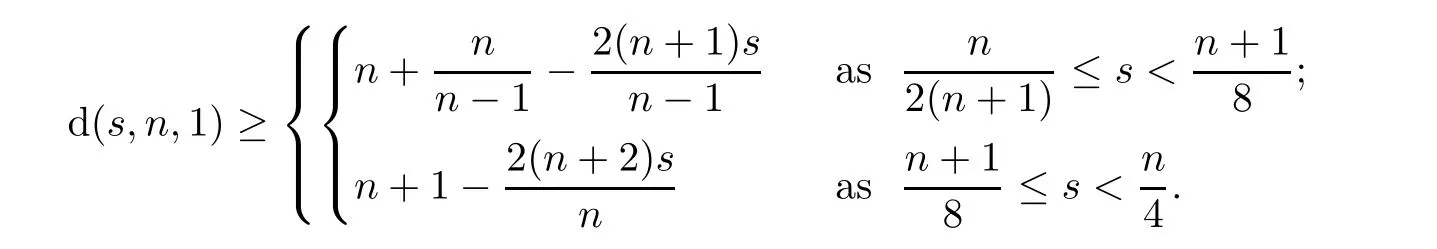
s,n,
1);see also[5,20–23]for more information.
Very recently,Cho-Ko[1]proved that(1.3)holds for
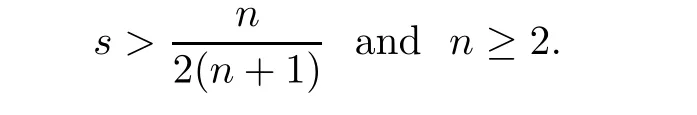
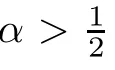

2 Theorem 2.2?Theorem 1.1
2.1 Proposition 2.1 and its Proof
In order to determine the Hausdorff dimension of the divergence set ofe
f
(x
),we need a law forH
(R)to be embedded intoL
(μ
)with a lower dimensional Borel measureμ
on R.Proposition 2.1
For a nonnegative Borel measureμ
on Rand 0≤κ
≤n
,let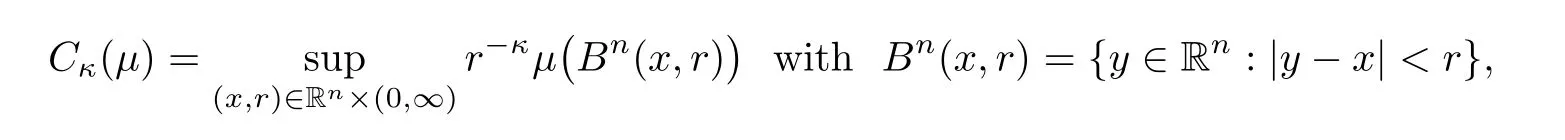
M
(B)be the class of all probability measuresμ
withC
(μ
)<
∞that are supported in the unit ball B=B
(0,
1).Suppose that
t
∈R,then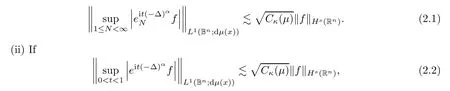
s,n,α
)≤κ
.Proof
(i)(2.1)is the elementary stopping-time-maximal inequality[3,(4)].(ii)The argument is split into two steps.
Step 1
We show the following inequality: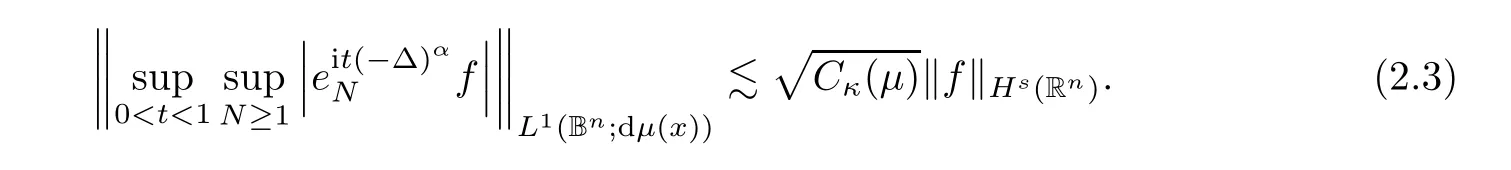
In a similar way as to the veri fication of[3,Proposition 3.2],we achieve
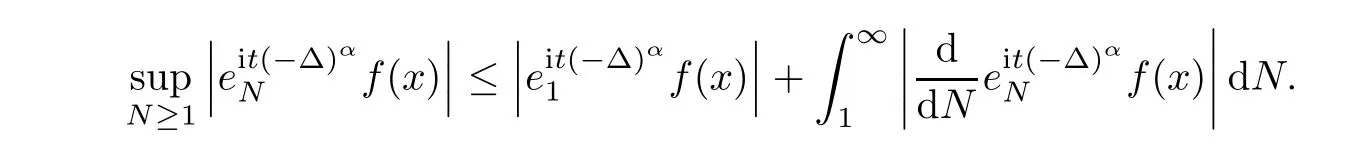
It is not hard to obtain(2.3)if we have the inequalities
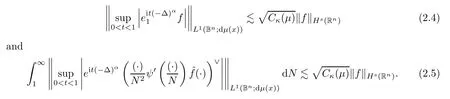
(2.4)follows from the fact that(2.2)implies
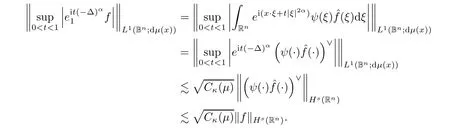
To prove(2.5),we utilize
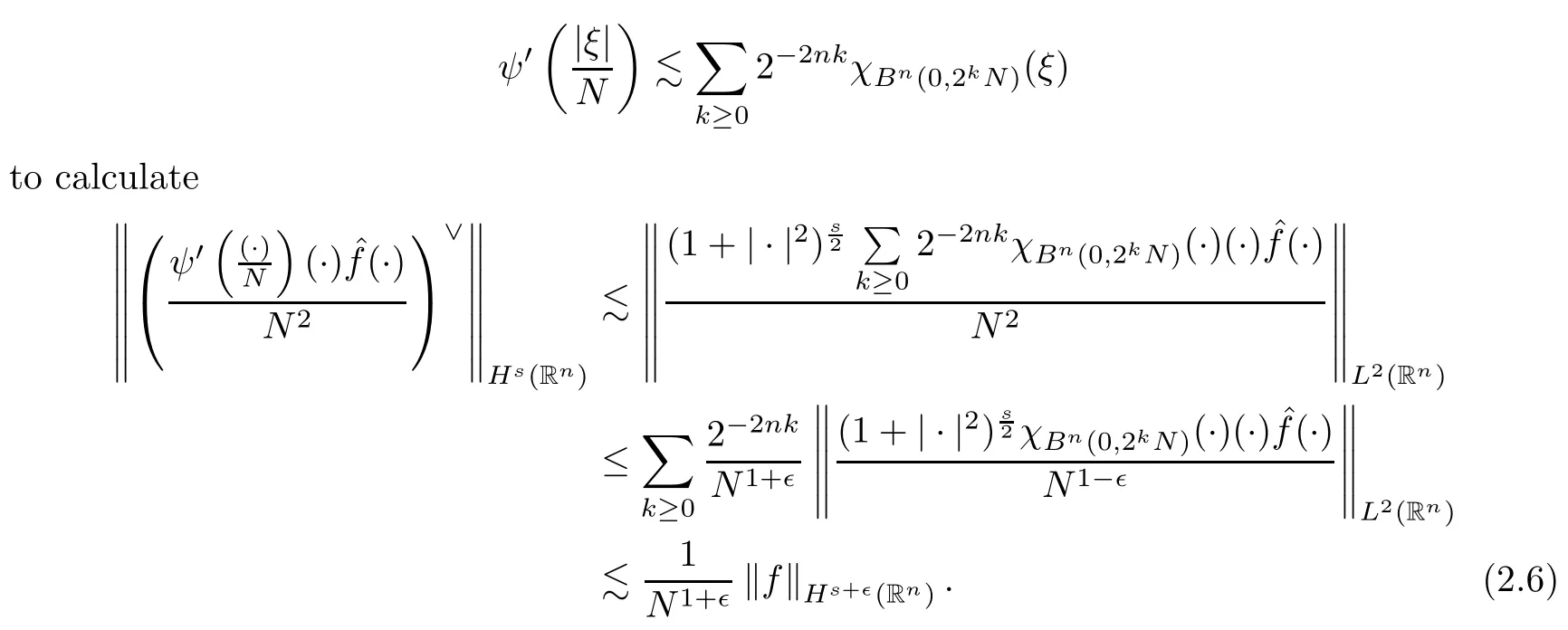
By(2.2)and(2.6),we obtain
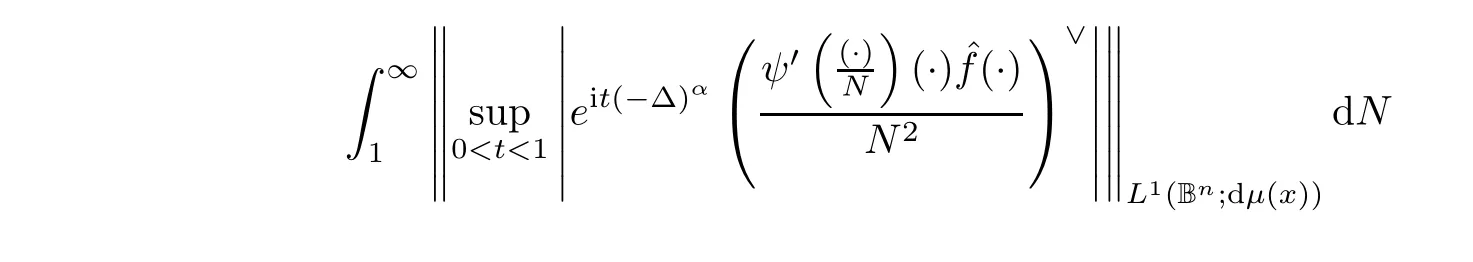
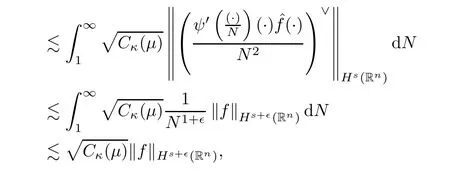
thereby reaching(2.5).
Step 2
We now show that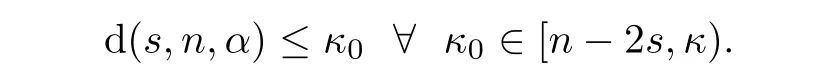
By the de finition,we have

then a combination of(2.3)and(2.1)gives that
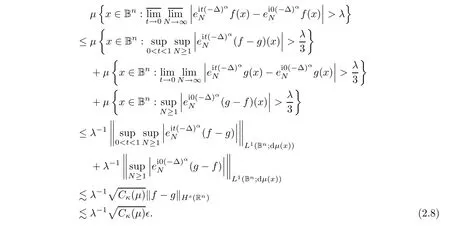
?
→0,and then lettingλ
→∞,we have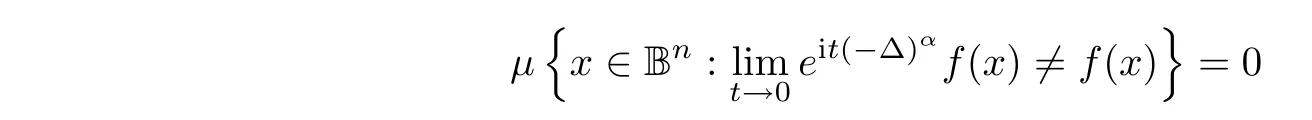
μ
∈M
(B)withκ>κ
.If Hdenotes theκ
-dimensional Hausdorff measure which is of translation invariance and countable additivity,then Frostman’s lemma is used to derive that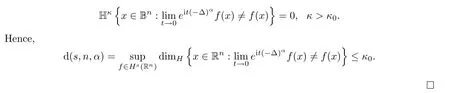
2.2 Proof of Theorem 1.1
We begin with a statement of the following key result,whose proof will be presented in Section 3,due to its nontriviality:
Theorem 2.2
If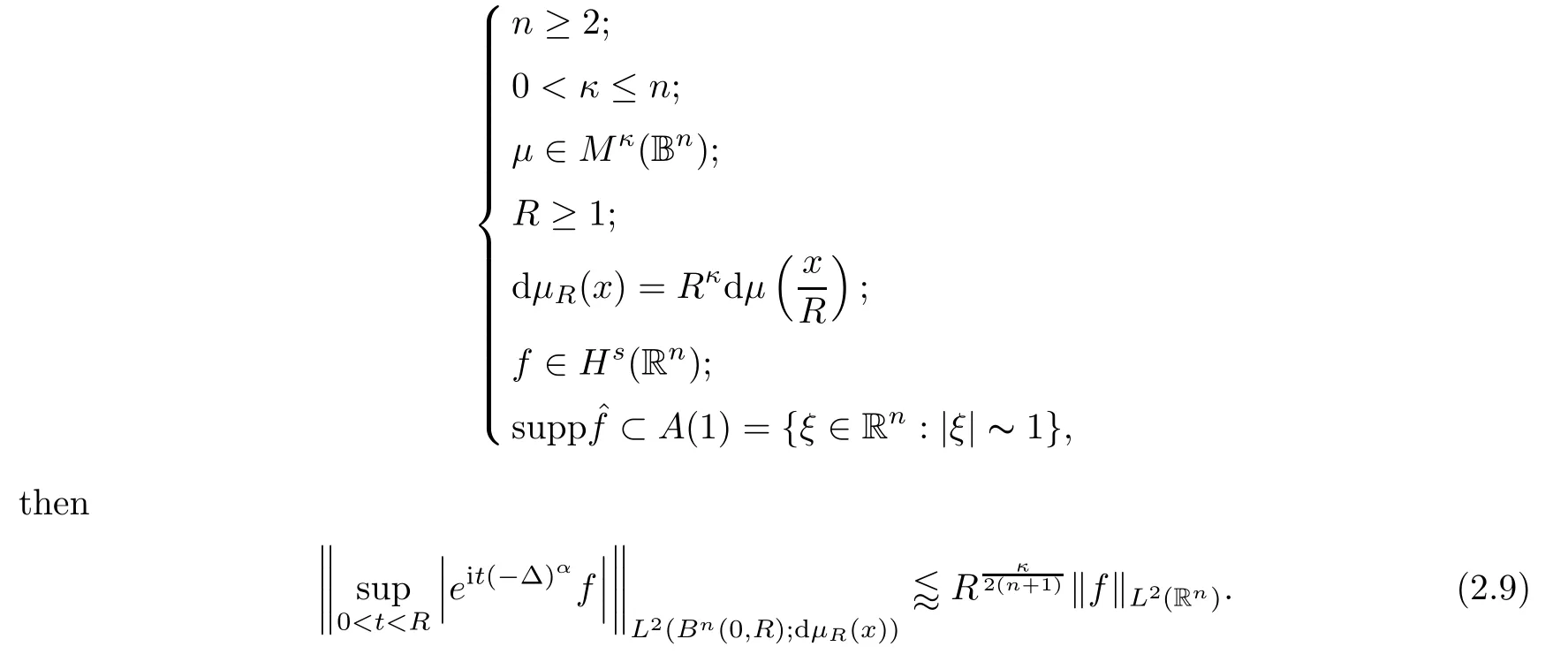
Consequently,we have the following assertion:
Corollary 2.3
If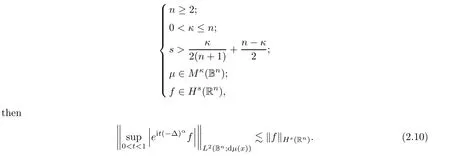
Proof
Employing Theorem 2.2 and its notations,as well as[1](see[10,11,24,25]),we get that
Next,we use parabolic rescaling.More precisely,if

T
=t
andX
=x
,then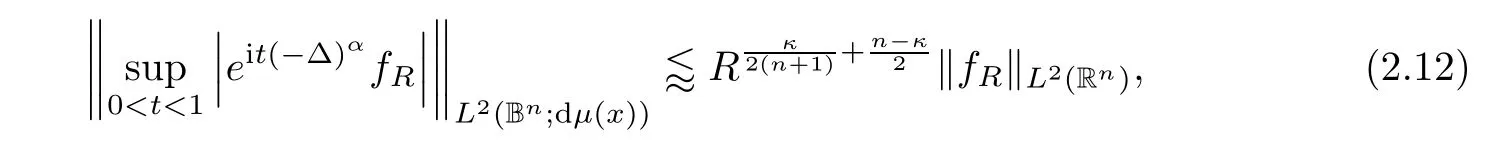
and hence Littlewood-Paley’s decomposition yields that
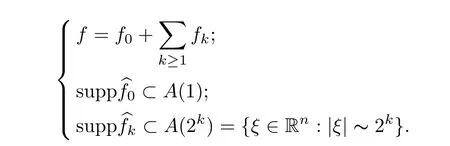
Finally,by Minko wski’s inequality and(2.12),as well as
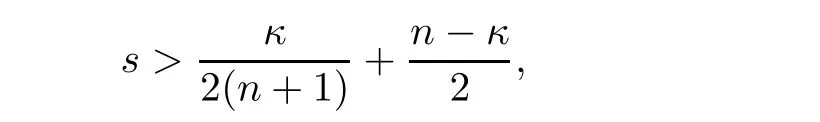
we arrive at
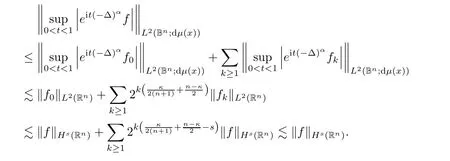
Next we use Corollary 2.3 to prove Theorem 1.1.
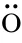

whence(2.2)follows.Thus,Proposition 2.1 yields that
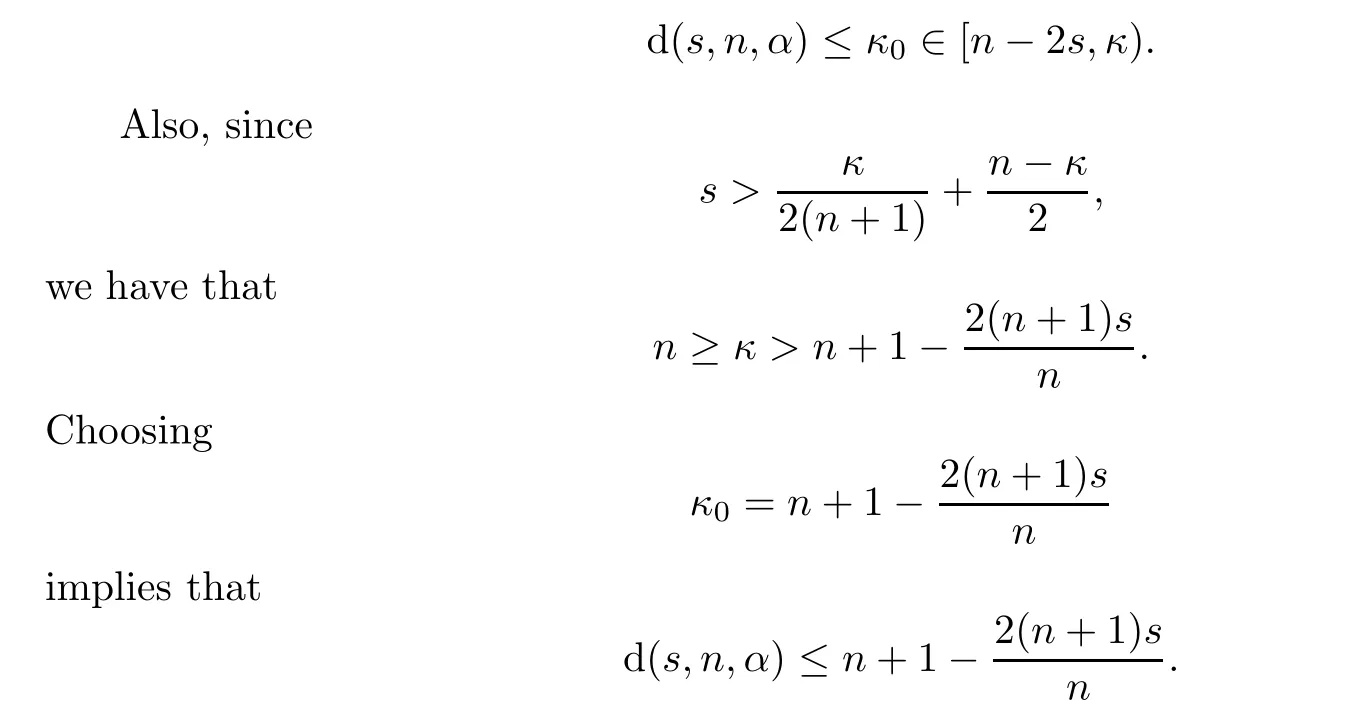
Next,we make the following two-fold analysis:
On the one hand,we ask for
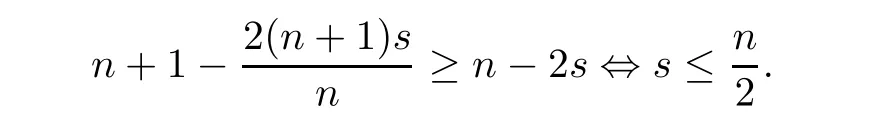
On the other hand,it is natural to request that
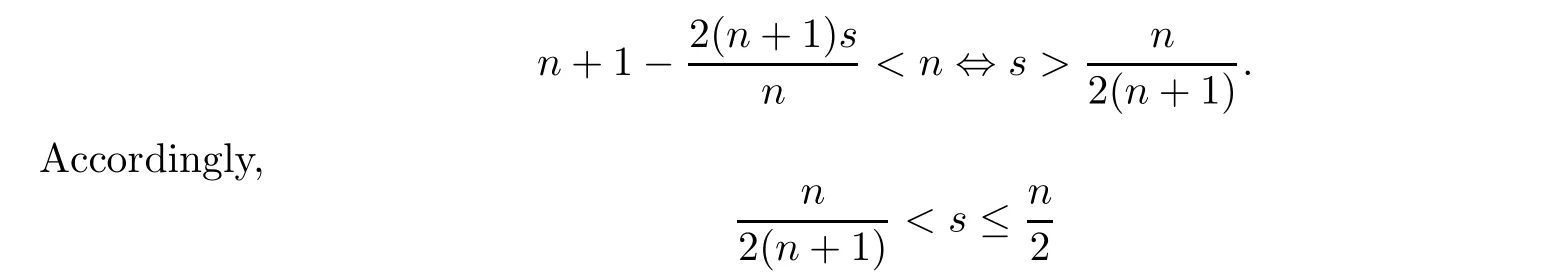
is required in the hypothesis of Theorem 1.1.
3 Theorem 3.1?Theorem 2.2
3.1 Theorem 3.1?Corollary 3.2
We say that a collection of quantities are dyadically constant if all the quantities are in the same interval of the form(2,
2],wherej
is an integer.The key ingredient of the proof of Theorem 2.2 is the following,which will be proved in Section 4:Theorem 3.1
Let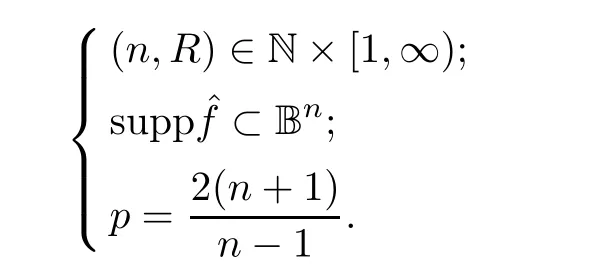
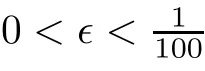

such that if
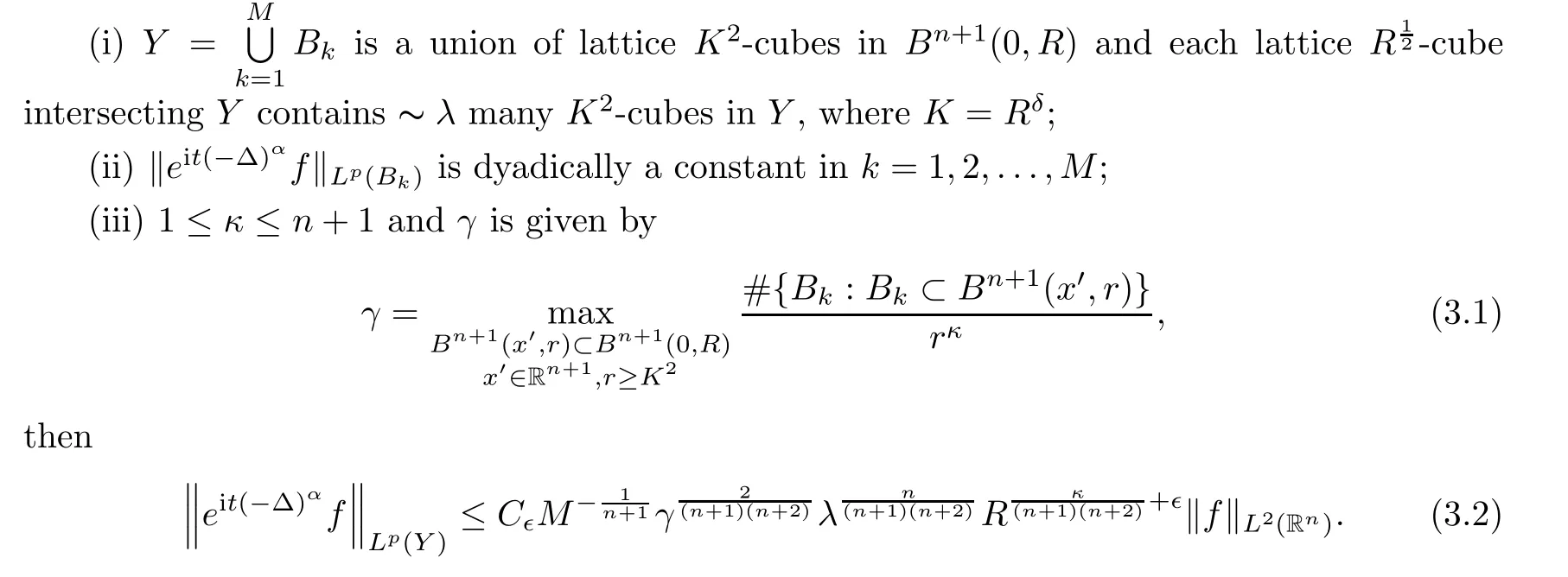
L
-restriction estimate:Corollary 3.2
Let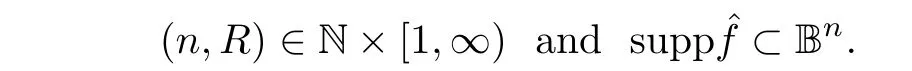
?>
0,there exists a constantC
>
0 such that if
Proof
For any 1≤λ
≤R
,we introduce the notation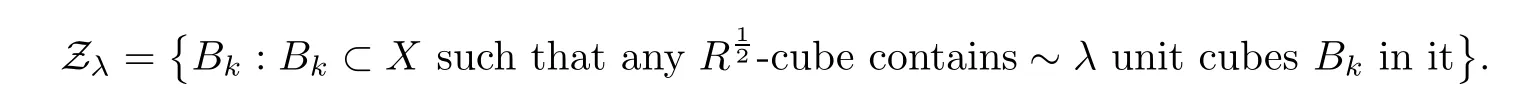
λ
such that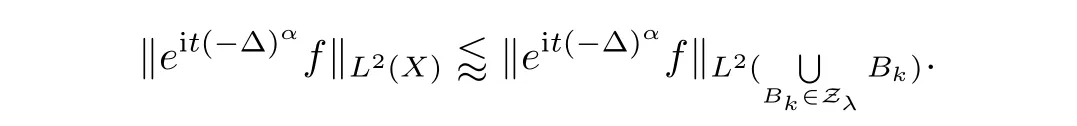
It is easy to see that
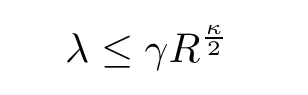
Next,we assume that the following inequality holds(we will prove this inequality later):
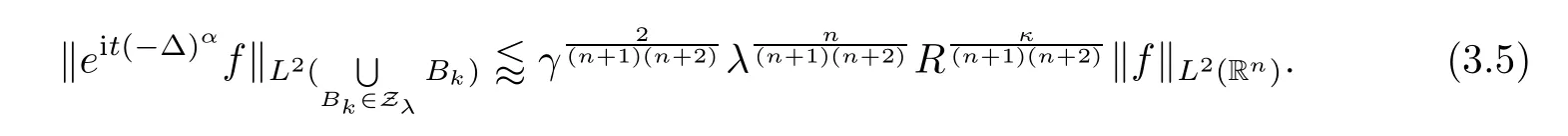
We thereby reach
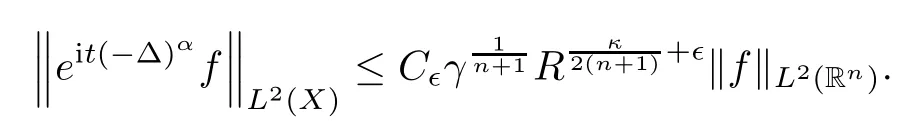
Hence,it remains to prove(3.5).

K
-cube according to the following two steps:Step 1
Letβ
be a dyadic number,let B:={B
:B
?Z
,
and for any latticeK
?cubeB
??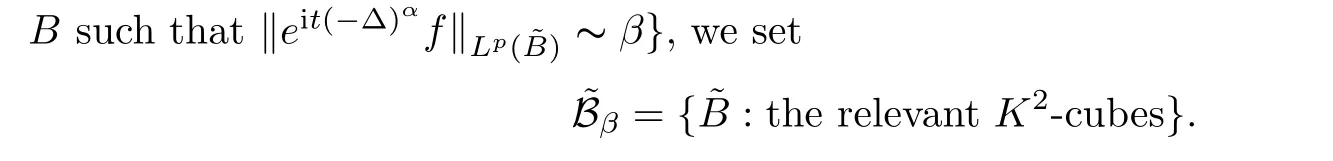
Step 2
Next,fixingβ
,lettingλ
be a dyadic number,and denoting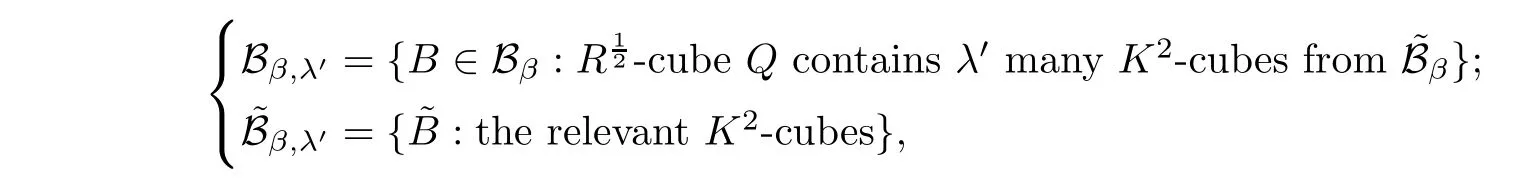
β,λ
}satis fies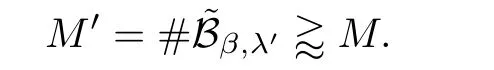
λ
andγ
,we have
which is the desired(3.6).
3.2 Proof of Theorem 2.2
In this section,we use Corollary 3.2 to prove Theorem 2.2.
We have
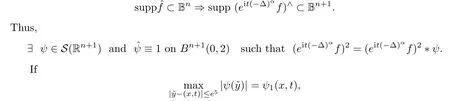
x,t
)∈R,
x,t
),and hence
?>
0,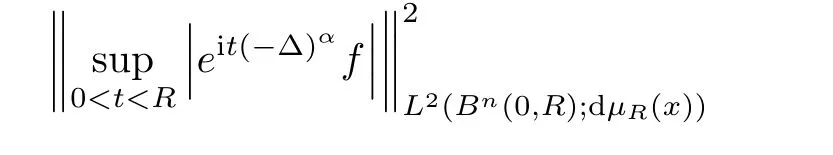

4 Conclusion
4.1 Proof of Theorem 3.1-R?1
In what follows,we always assume that
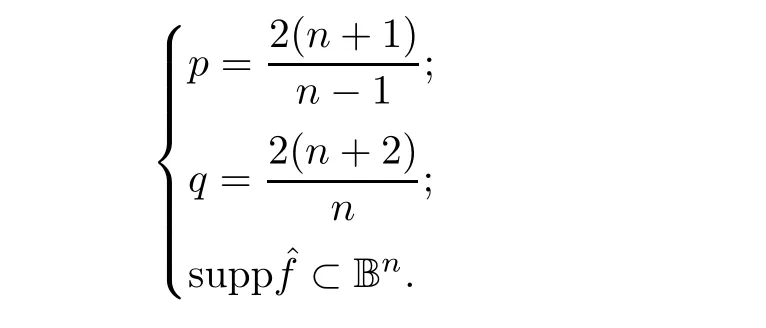
R
?1 is trivial.In fact,from the assumptions of Theorem 3.1,we see that
Furthermore,by the short-time Strichartz estimate(see[26,27]),we get that
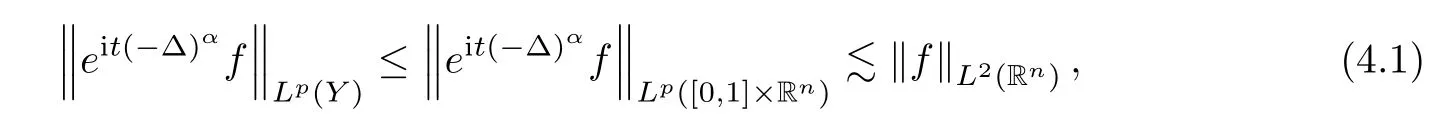
R
?1.4.2 Proof of Theorem 3.1-R?1
First,we decompose the unit ball in the frequency space into disjointK
-cubesτ
.Write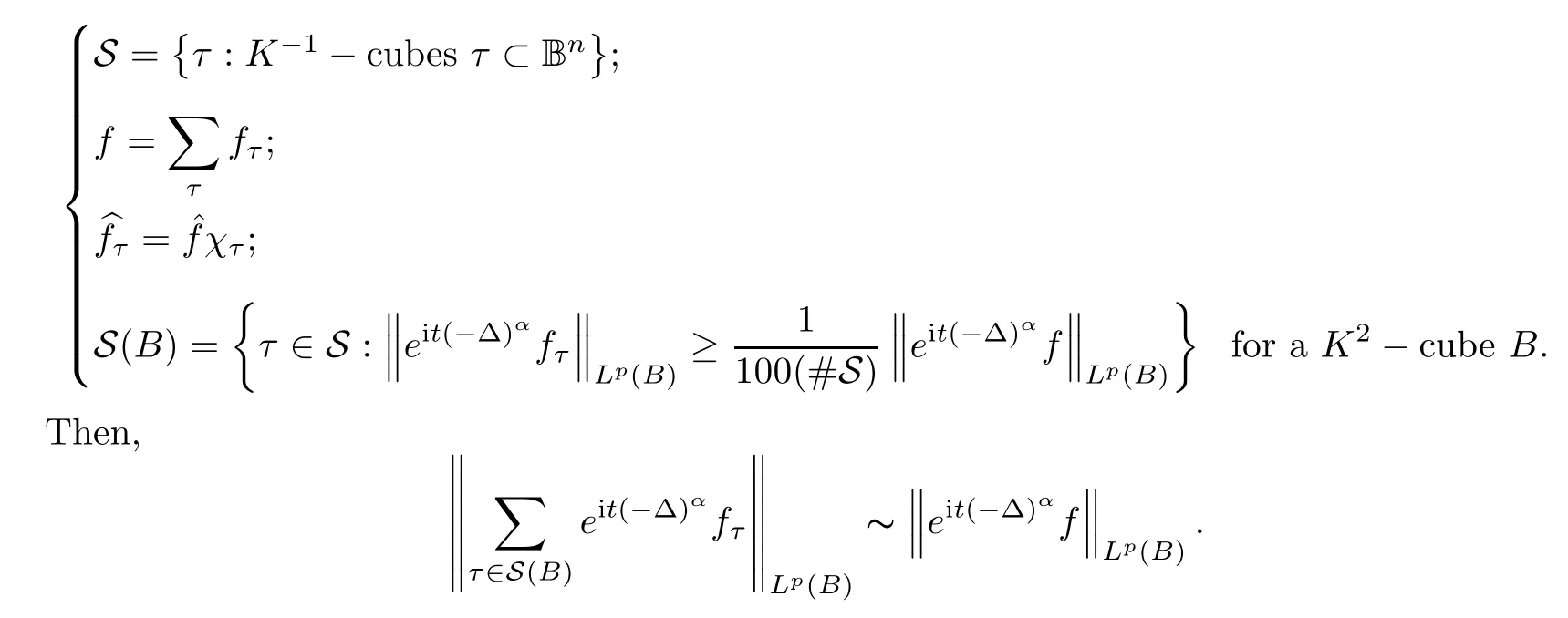
Second,we recall the de finitions of narrow cubes and broad cubes.
We say that aK
-cubeB
is narrow if there is ann
-dimensional subspaceV
such that for allτ
∈S(B
),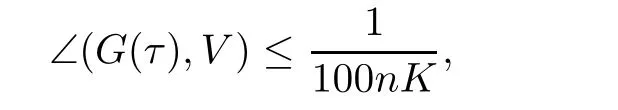
G
(τ
)?Sis a spherical cap of radius~K
given by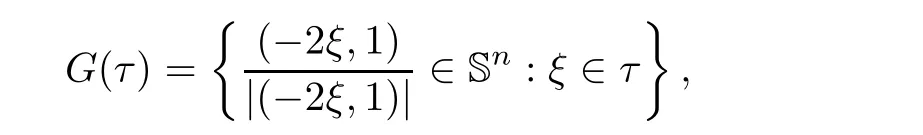
G
(τ
),V
)denotes the smallest angle between any non-zero vectorv
∈V
andv
∈G
(τ
).Otherwise,we say that theK
-cubeB
is broad.In other words,a cube being broad means that the tilesτ
∈S(B
)are so separated that the norm vectors of the corresponding spherical caps cannot be in ann
-dimensional subspace;more precisely,for any broadB
,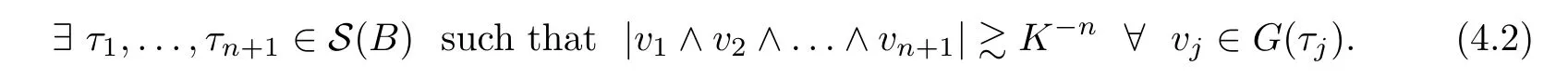
Third,with the setting
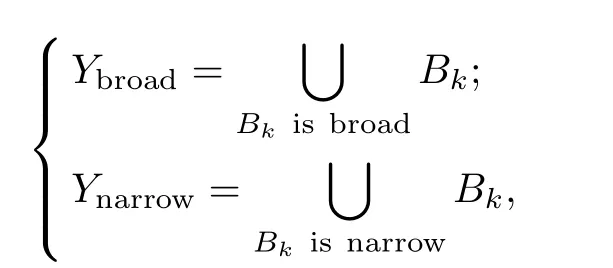
Y
according to the sizes ofY
andY
.Thus,
4.2.1 The broad case

<c
?1 andL
∈N be sufficiently large.We consider a collection of the normalized phase functions as follows:

Next we begin the proof of Theorem 4.1.
Proof
We prove a linear re fined Strichartz estimate in dimensionn
+1 by four steps.
f
are approximately orthogonal,thereby giving us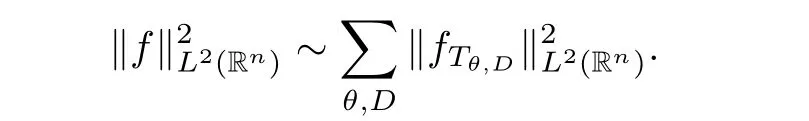
e
f
(x
)toB
(0,R
)is essentially supported on a tubeT
,which is de fined as follows: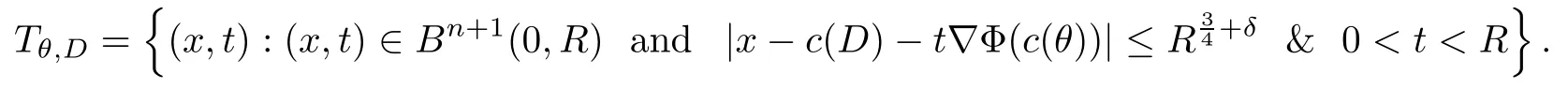
c
(θ
)&c
(D
)denote the centers ofθ
andD
,respectively.Therefore,by a decoupling theorem,we have that
In fact,as in Remark 4.2,we get that
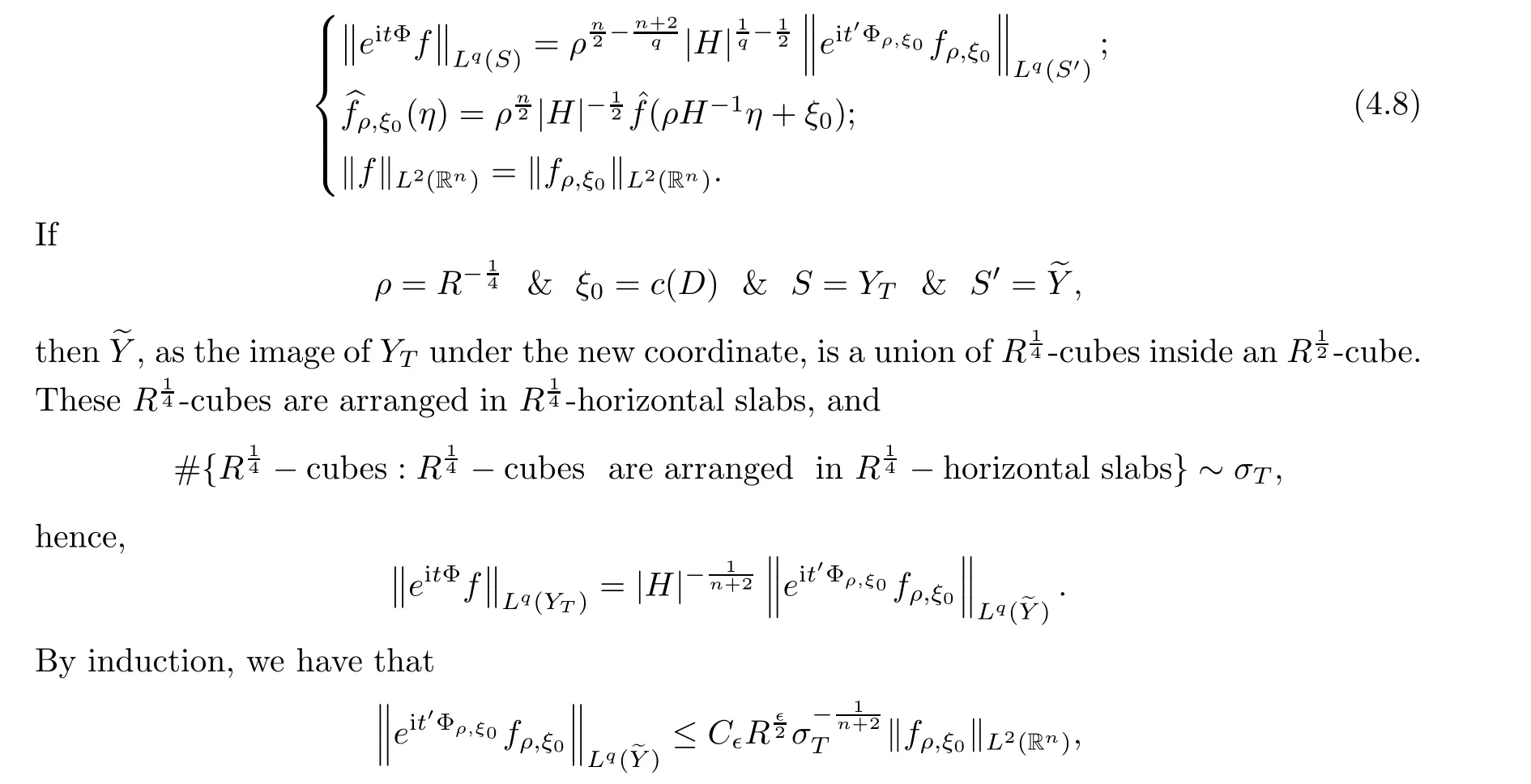
f
=f
,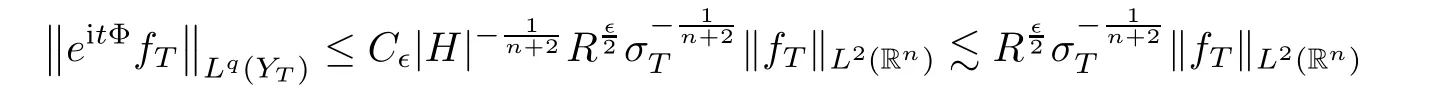
H
|~1),
namely that,(4.7)holds.Third,we shall choose an appropriateY
.For eachT
,we classify tubes inT
in the following ways: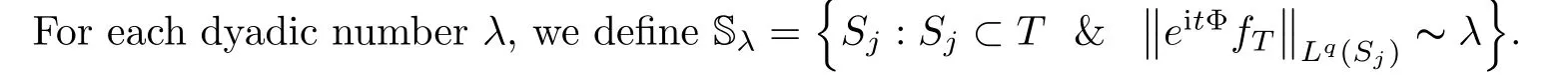
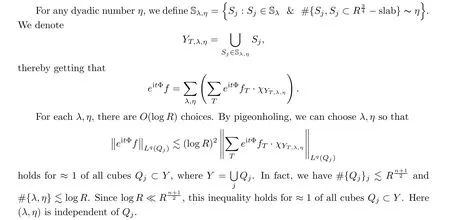


Y
according to the dyadic size of‖f
‖.We can restrict matters toO
(logR
)choices of this dyadic size,so we can choose a set ofT
’s with T such that
Q
?Y
according to the number ofY
that contain them.Denote that
ν
are dyadic numbers,we can use(4.9)to get
thereby finding that

Fourth,we combine all of our ingredients and finish our proof of Theorem 4.1.
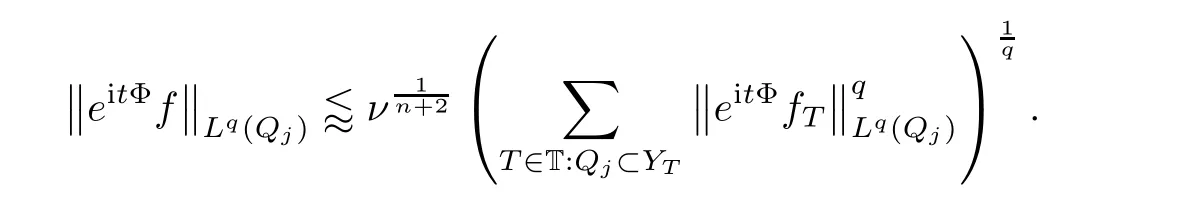
Q
?Y
and using our inductive hypothesis at scaleR
2,we obtain that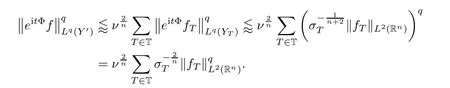
Q
?Y
,since
we get that
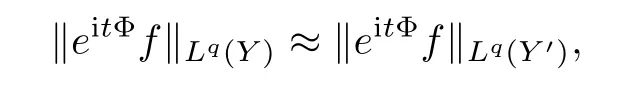
f
‖is essentially constant among allT
∈T to derive that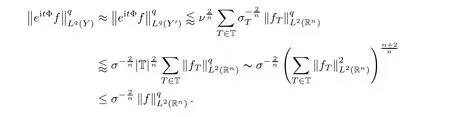
q
-th root in the last estimation produces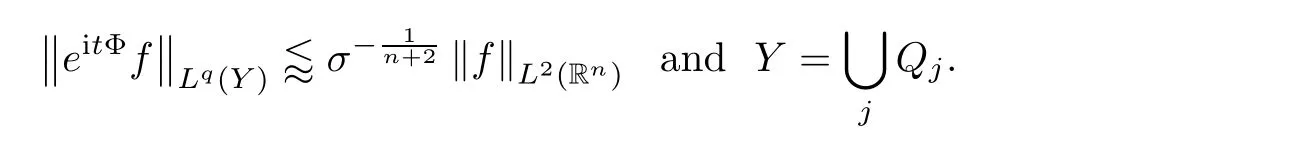
Moreover,Theorem 4.1 can be extended to the following form,which can be veri fied by[22]and Theorem 4.1:
Theorem 4.4
(Multilinear re fined Strichartz estimate in dimensionn
+1.)For 2≤k
≤n
+1 and 1≤i
≤k
,letf
:R→C have frequenciesk
-transversely supported in B,that is,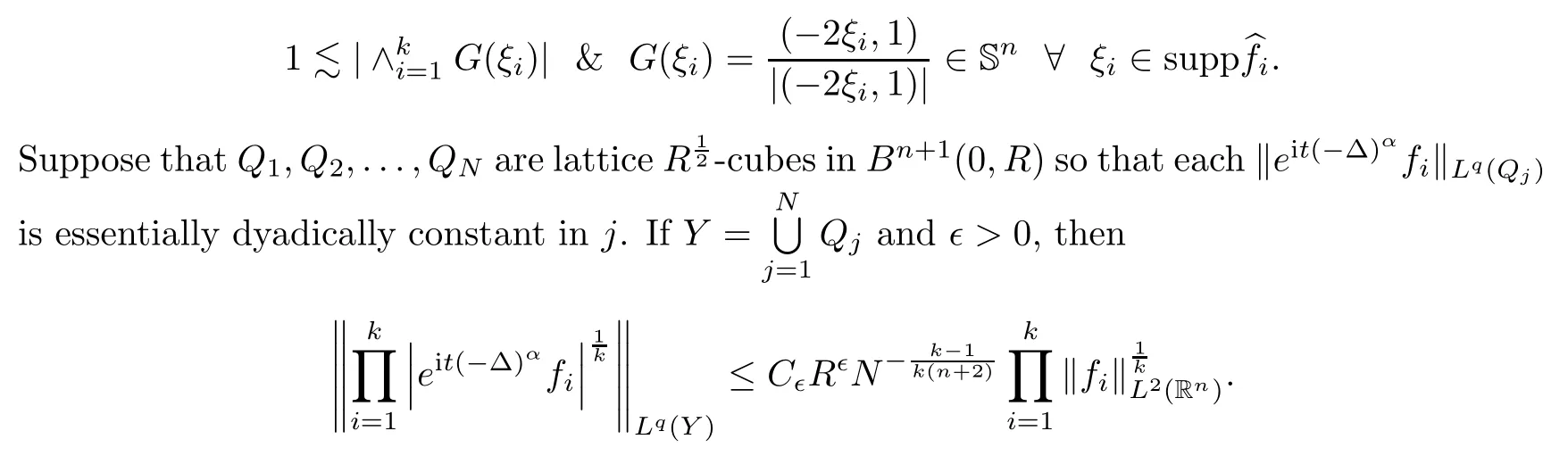
Next,we prove the broad case of Theorem 3.1.


B
∈Y
,
B
into small balls as follows:

γ
,which ensures thatM
≤γR
andγ
≥K
.
4.2.2 The narrow case
In order to prove the narrow case of Theorem 3.1,we have the following lemma,which is essentially contained in Bourgain-Demeter[28]:
Lemma 4.5
Suppose that(i)B
is a narrowK
-cube in Rthat takesc
(B
)as its center;(ii)S denotes the set ofK
-cubes which tile B;(iii)ω
is a weight function which is essentially a characteristic function onB
;more precisely,that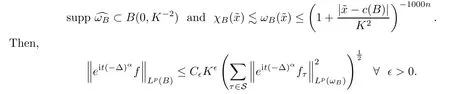
Next,we prove the narrow case of Theorem 3.1.
Proof
The main method we use is the parabolic rescaling and induction on the radius.We prove the narrow case step by step.

Fourth,let
Y
,we can write
O
(R
)‖f
‖can be neglected.In particular,on each narrowB
,we have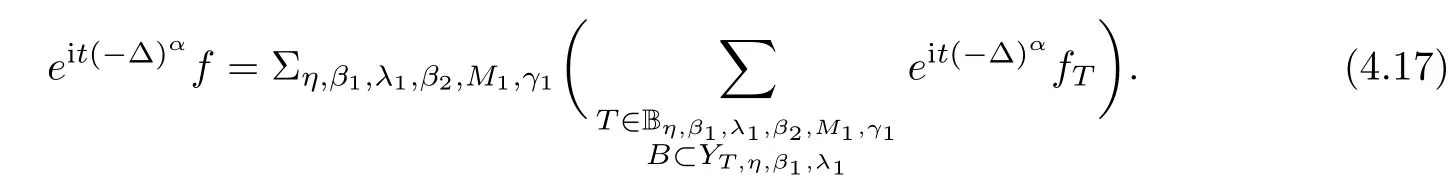
Without loss of generality,we assume that
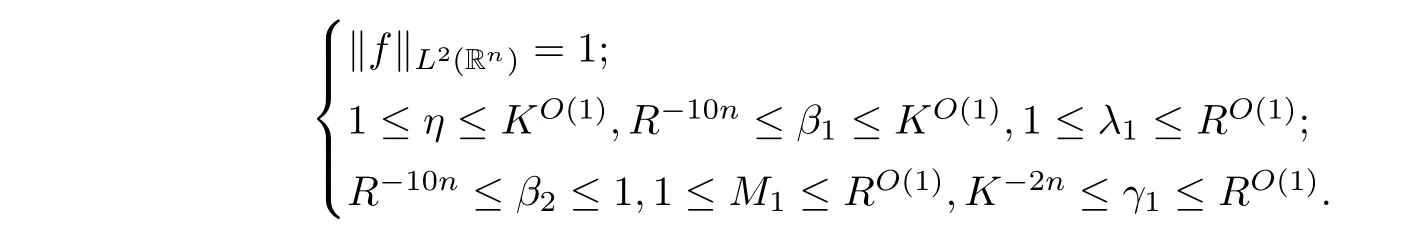
O
(logR
)signi ficant choices for each dyadic number.By(4.17),the pigeonholing,and(4.15),we can chooseη,β
,λ
,β
,M
,γ
such that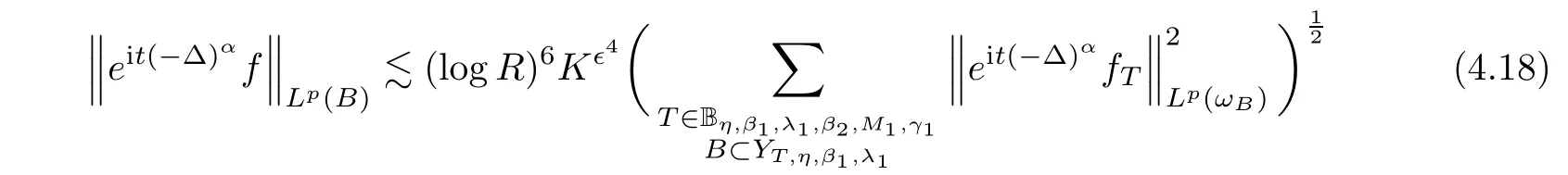
R
)narrowK
-cubesB
.Fifth,we fixη,β
,λ
,β
,M
,γ
for the rest of the proof.Let
Y
?Y
be a union of narrowK
-cubesB
each of which obeys(4.18)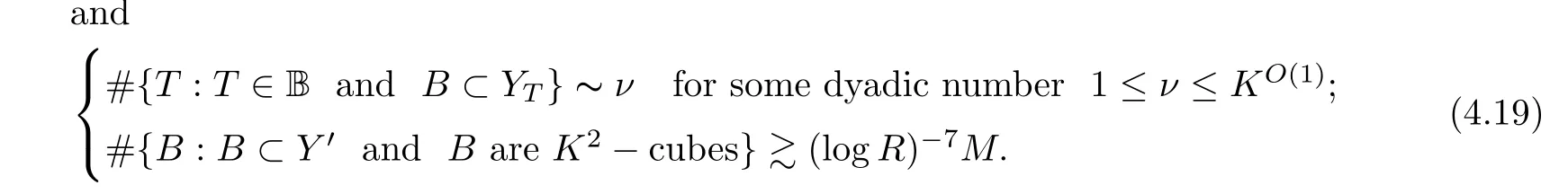
e
f
‖is essentially constant ink
=1,
2,...,M
,in the narrow case,we have that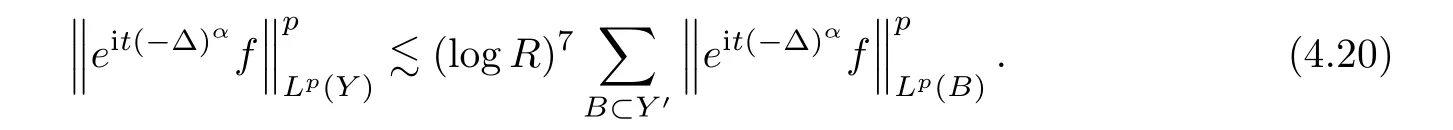
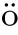

By(4.20)and(4.21),we have

e
f
‖,we apply parabolic rescaling and induction on the radius.For eachK
-cubeτ
=τ
in B,we writeξ
=ξ
+K
η
∈τ
,whereξ
=c
(τ
).In a fashion similar to the argument in(4.6),we also consider a collection of the normalized phase functions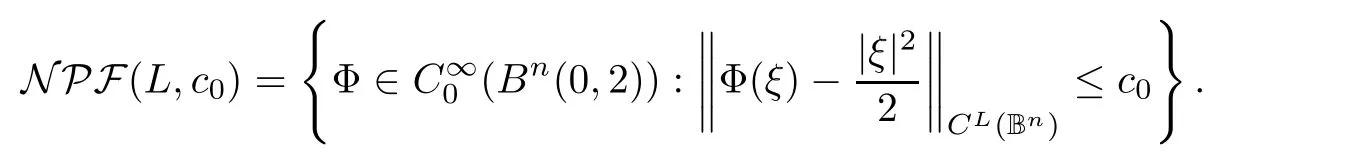
By a similar parabolic rescaling,

More precisely,we have that

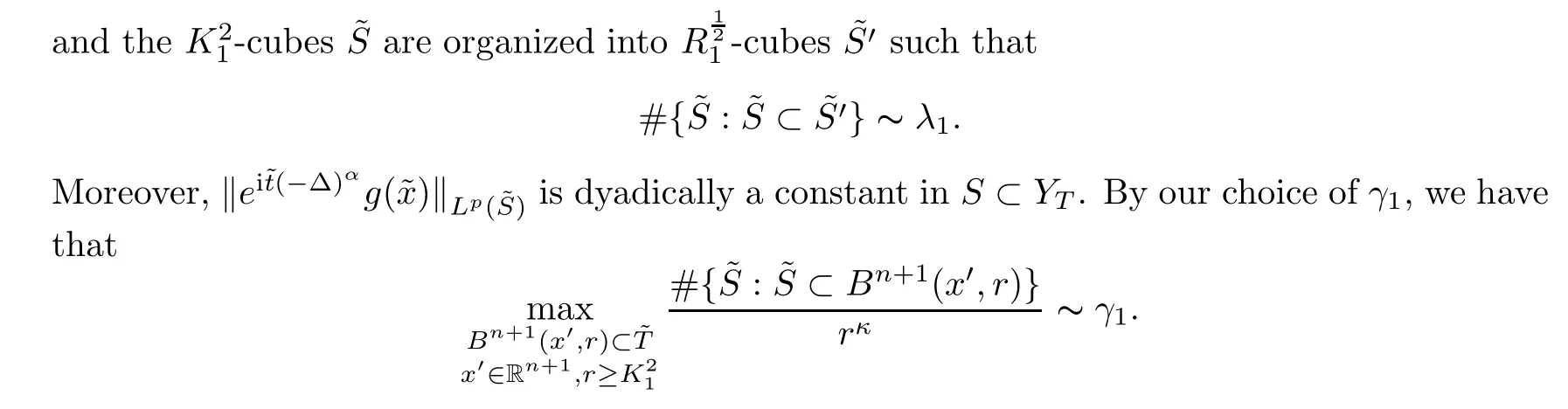
R
,we have that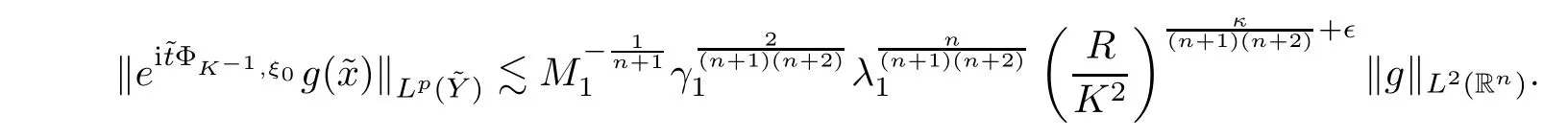
g
‖=‖f
‖,we get that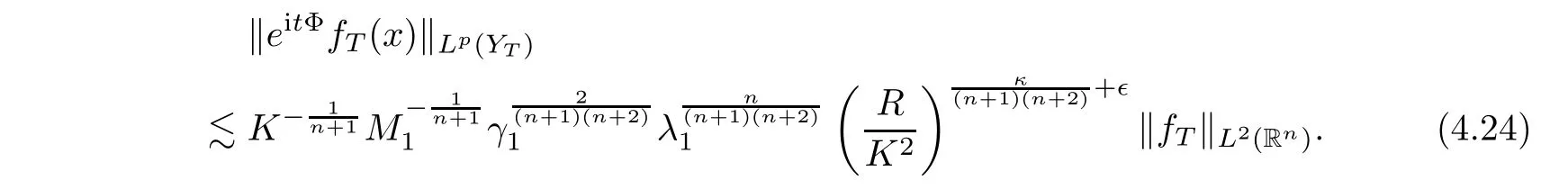
Since(4.24)also holds whenever one replaces Φ with(??),we get that
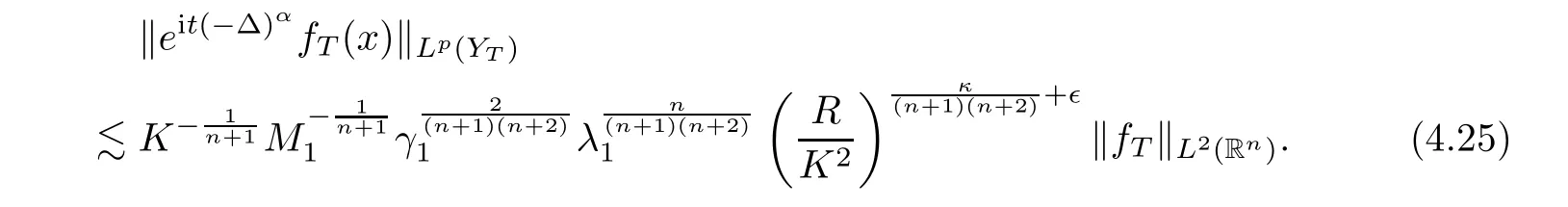
By(4.22)and(4.25),we obtain that
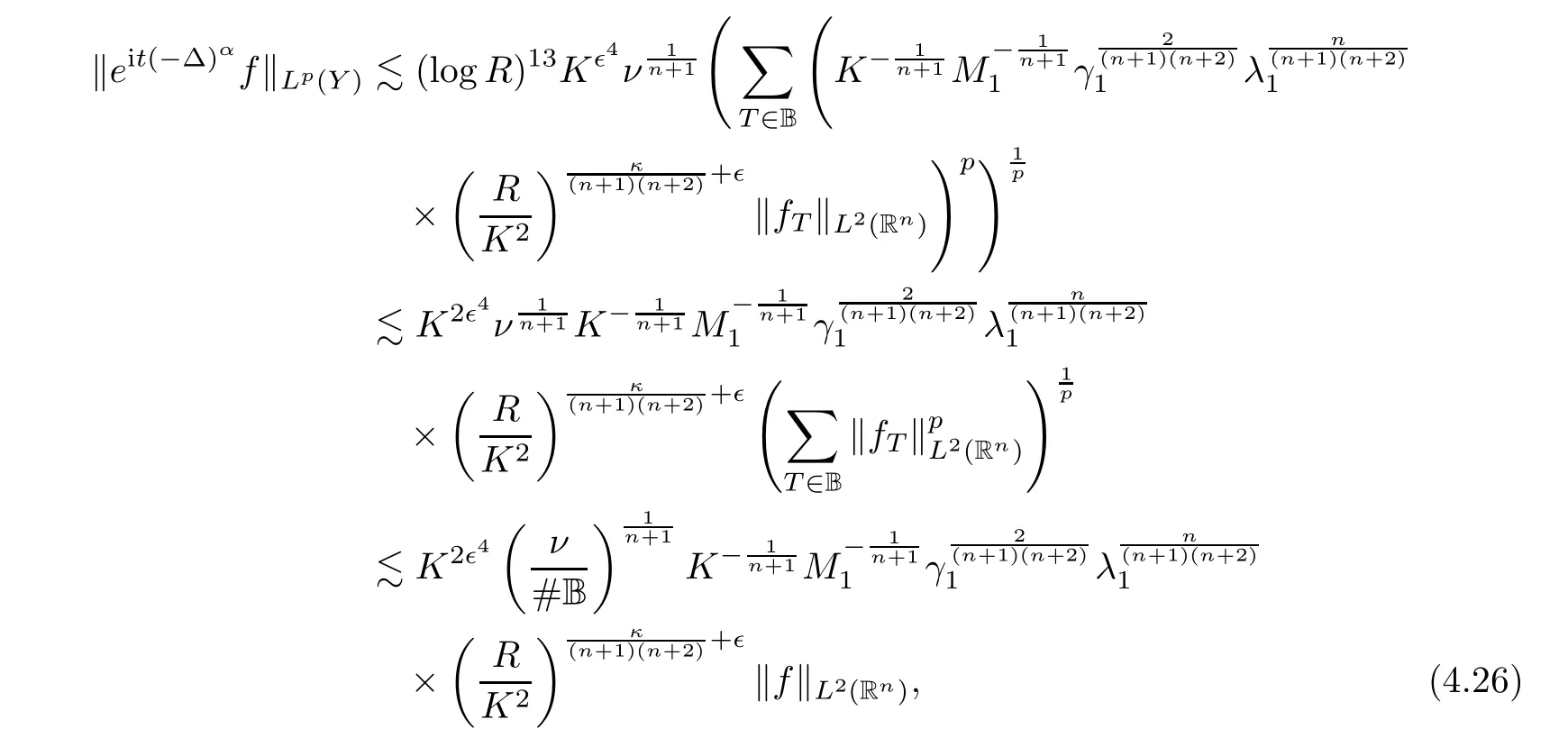
f
‖is essentially constant inT
∈B,and then implies that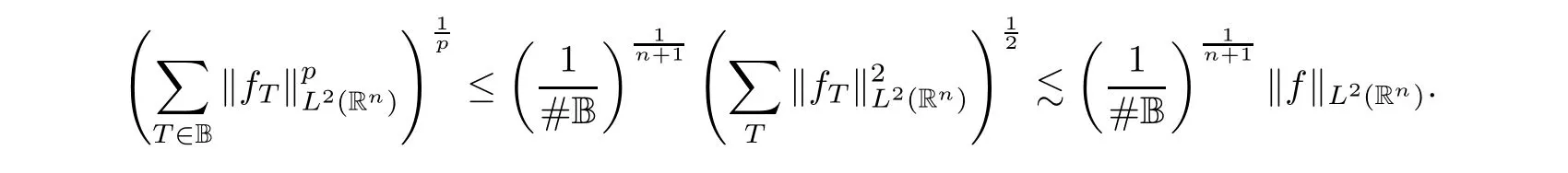
Eighth,we consider the lower bound and the upper bound of
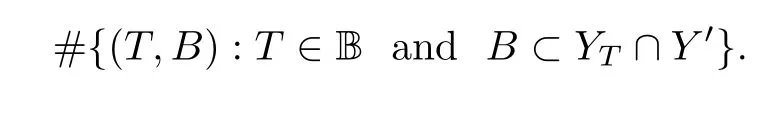
ν
in(4.19),there is a lower bound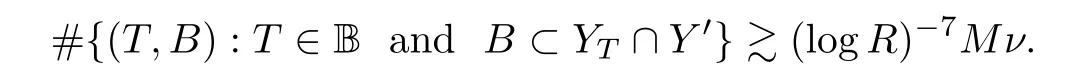
M
andη
,for eachT
∈B,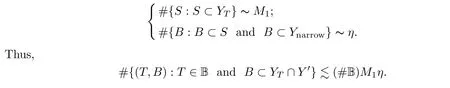
Therefore,we get

γ
andγ
.By our choices ofγ
,as in(4.16)andη
,we get that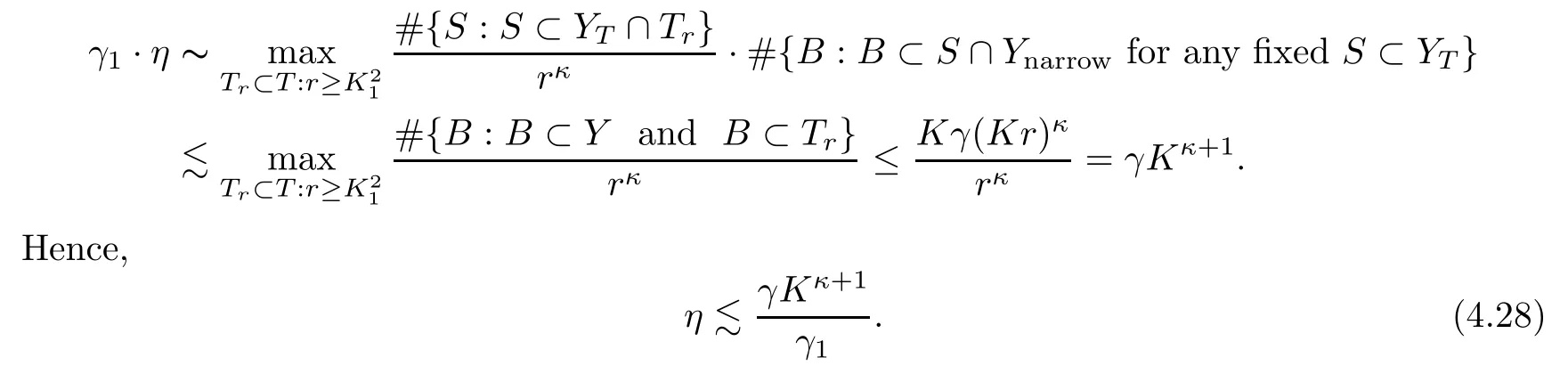
Tenth,we complete the proof of Theorem 3.1.
On the one hand,
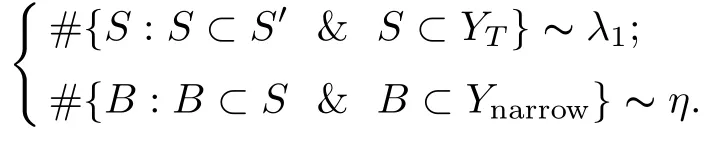
Thus it follows that

Inserting(4.27),(4.29)and(4.28)into(4.26)gives that
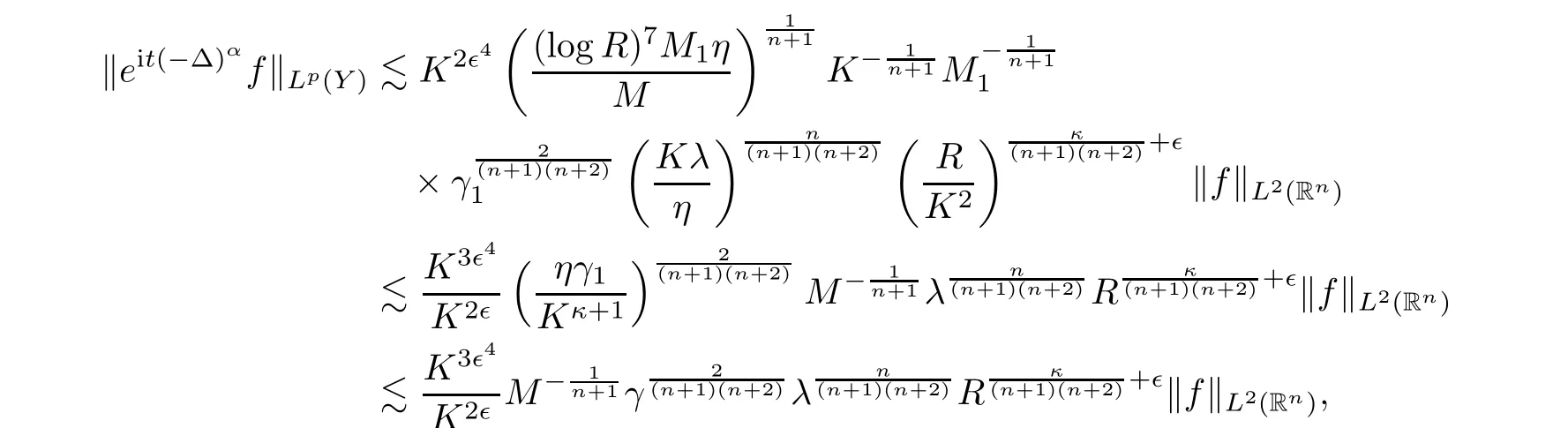

 Acta Mathematica Scientia(English Series)2021年4期
Acta Mathematica Scientia(English Series)2021年4期
- Acta Mathematica Scientia(English Series)的其它文章
- REGULARITY OF WEAK SOLUTIONS TO A CLASS OF NONLINEAR PROBLEM?
- EXISTENCE TO FRACTIONAL CRITICAL EQUATION WITH HARDY-LITTLEWOOD-SOBOLEV NONLINEARITIES?
- A DIFFUSIVE SVEIR EPIDEMIC MODEL WITH TIME DELAY AND GENERAL INCIDENCE?
- ON A COUPLED INTEGRO-DIFFERENTIAL SYSTEM INVOLVING MIXED FRACTIONAL DERIVATIVES AND INTEGRALS OF DIFFERENT ORDERS?
- CLASSIFICATION OF SOLUTIONS TO HIGHER FRACTIONAL ORDER SYSTEMS?
- ENERGY CONSERVATION FOR SOLUTIONS OF INCOMPRESSIBLE VISCOELASTIC FLUIDS?
