CONSTRUCTION OF IMPROVED BRANCHING LATIN HYPERCUBE DESIGNS?

(陳浩)

School of Statistics,Tianjin University of Finance and Economics,Tianjin 300222,China E-mail:chlh1985@126.com

Jinyu YANG (楊金語) Min-Qian LIU (劉民千)?

School of Statistics and Data Science,LPMC&KLMDASR,Nankai University,Tianjin 300071,China E-mail:jyyang@nankai.edu.cn;mqliu@nankai.edu.cn

Abstract In this paper,we propose a new method,called the level-collapsing method,to construct branching Latin hypercube designs(BLHDs).The obtained design has a sliced structure in the third part,that is,the part for the shared factors,which is desirable for the qualitative branching factors.The construction method is easy to implement,and(near)orthogonality can be achieved in the obtained BLHDs.A simulation example is provided to illustrate the effectiveness of the new designs.

Key words Branching and nested factors;computer experiment;Gaussian process model;orthogonality

1 Introduction

Many experiments involve factors that only exist within the levels of another factor.Take printed circuit board(PCB)manufacturing,for example([1]).Here,the surface preparation method is a qualitative factor having two levels:mechanical scrubbing and chemical treatment.Under each of the two levels,there exist two different factors:pressure and micro-etch.More precisely,the factor pressure only exists when the method involves mechanical scrubbing,and micro-etch rate only exists under the level of chemical treatment.Following the de finitions in[1],the factors that only exist within the levels of another factor(like the pressure and the microetch rate)are called nested factors.Accordingly,a factor within which other factors are nested is called a branching factor;these include things such as the surface preparation method for PCB manufacturing.Such experimental situations are often encountered in computer experiments as well,for example,the motivation example of[1].The objective of that example is to optimize a turning process for hardened bearing steel with a cBN cutting tool.There is one branching factor,called the cutting edge shape,which has two levels:chamfer and hone edge.Within the chamfer,two factors(length and angle)are nested,while no factor is nested in the hone edge.In addition,there are six other factors(cutting edge radius,tool nose radius,rake angle,cutting speed,feed and depth of cut),called shared factors,which are common to both the branching and nested factors.

Although experiments with branching and nested factors are commonly encountered,there is little literature on the design construction for such experiments.Taguchi[2]proposed pseudofactor designs by carefully assigning branching and nested factors to the columns of orthogonal arrays(OAs,[3]),where the pseudo-factor is in fact the nested factor.Later,in[4],such designs were called branching designs.However,as stated in[1],Taguchi’s method is not sufficiently general to be applied to computer experiments.Instead,Hung et al.[1]developed branching Latin hypercube designs(BLHDs)to suit computer experiments with branching and nested factors.A BLHD consists of three parts:(i)an OA for the branching factors;(ii)several Latin hypercube designs(LHDs)([5])for the nested factors;(iii)an LHD for the shared factors.An example of a BLHD is given in Table 1(Table 3 in[1]);here the BLHD has eight runs,one branching factor

z

,one nested factor

v

,and two shared factors:

x

and

x

.As pointed out in[1],the same levels of

v

(for example two 1’s)do not have the same meaning.Such a frame of a BLHD looks attractive,however the third part has no sliced structure to accommodate the qualitative branching factor.The superiority of sliced Latin hypercube designs(SLHDs)over ordinary LHDs was proved by both theoretical and simulated results in[6]when being used for computer experiments with both qualitative and quantitative factors.Thus an SLHD is more effective as the third part of a BLHD than an LHD.For an SLHD,not only the whole design,but also its slices achieve the maximum strati fication in any one-dimensional projection.Such a good property ensures that when the third part is collapsed onto the branching factor,each factor in the third part gets maximum strati fication under each level of the branching factor.Take the design in Table 1 as an example;when the third part is collapsed onto

z

,it becomes the following matrix: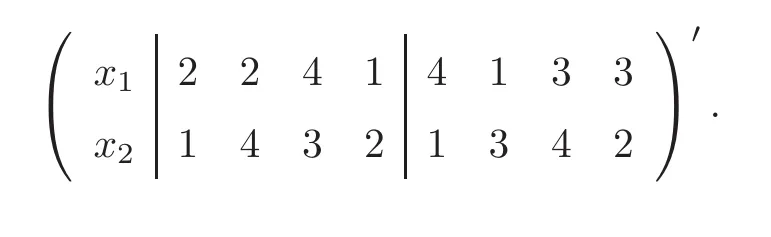

Table 1 An example of a BLHD

It is easy to see that the first column

x

does not get the maximum strati fication under either level of

z

,which can be seen more clearly from the scatter plot in Figure 1(a);that is,when considering the projection on

x

,there are two points falling into either of the intervals[1

/

4

,

2

/

4)and[2

/

4

,

3

/

4).Note that the levels of

x

and

x

in Figure 1 are mapped into[0

,

1)through(

x

?0

.

5)

/

8,where

x

is the

i

th level of factor

x

for

i

=1

,...,

8 and

j

=1

,

2.However,if we exchange the second and seventh elements of

x

in Table 1,then the third part becomes an SLHD with 8 runs,2 factors and 2 slices.Now,the collapsed matrix becomes

Figure 1 (a)Scatter plot of the third part of the BLHD in Table 1;(b)Scatter plot of the third part obtained by exchanging the 2nd and 7th elements of x1in Table 1.The symbols ‘?’and ‘+’represent the four runs from the first and second slices,respectively.

The scatter plot is presented in Figure 1(b),which shows that there is only one point from each slice falling into one of the intervals[0

,

1

/

4)

,

[1

/

4

,

2

/

4)

,

[2

/

4

,

3

/

4)

,

[3

/

4

,

1)in each dimension;that is,each slice gets the maximum strati fication in any 4×1 or 1×4 grid.In this paper,we focus on introducing a sliced structure into the third part of BLHDs,and propose a levelcollapsing method to construct BLHDs.The obtained designs,referred to as improved BLHDs(IBLHDs),have a better structure than existing BLHDs,and can achieve near orthogonality more easily.

The remainder of this paper is organized as follows:Section 2 provides the level-collapsing method for constructing IBLHDs.Section 3 discusses the(near)orthogonality of the IBLHDs.An example for illustrating their effectiveness is presented in Section 4.Section 5 contains some concluding remarks.

2 Construction of IBLHDs

First,we give some de finitions and notation.For any real number

r

,「

r

?denotes the smallest integer greater than or equal to

r

,and for a real vector or matrix

M

,「

M

?is de fined to its elements.A permutation on

Z

is a rearrangement of 1

,...,n

,and all

n

!rearrangements are equally probable.An

n

×

q

matrix is called a Latin hypercube design(LHD),denoted by

L

(

n,q

),if each column is a permutation on

Z

,and these columns are obtained independently.Denote an SLHD with

n

runs,

q

factors and

s

slices by

SL

(

n,q,s

).Next,we propose the level-collapsing method for constructing IBLHDs.Without loss of generality,assume that there is only one branching factor,

z

,with

s

levels,under each of which an

L

(

n

,m

)is nested.In addition,

t

shared factors are involved.

Algorithm 2.1

Step 1

Let

z

=(1

,...,

1

,...,s,...,s

)be the branching factor,where each level

i

appears

n

times for

i

=1

,...,s

.

Step 2

Construct an

SL

(

sn

,m

+

t,s

)by the method in[6],denoted by

S

=(

S

,S

),where

S

includes

m

columns of

S

,and

S

includes the left

t

columns.

For the IBLHD in Table 2,there are two structural differences compared with BLHDs:(i)the third part is an

SL

(

n,t,s

)instead of an

L

(

n,t

),which guarantees that each shared factor gets the maximum strati fication under each level of the branching factor;(ii)the LHDs in the second part are obtained by collapsing some columns of the SLHDs constructed in Step 2,which makes it easier to develop(near)orthogonality between factors.

Table 2 IBLHD with one branching factor

Table 3 IBLHD in Example 3.3

Table 4 Correlations among v1,v2,x1and x2

Remark 2.2

Note that for a BLHD,it may happen that there is no nested factor under some level of the branching factor([1]).In this case,we just need to delete the corresponding LHD in the second part of an IBLHD.

3 Nearly Orthogonal IBLHDs

Orthogonality is a desirable property for experimental designs,because it guarantees that the main effects can be estimated uncorrelatedly under the first-order polynomial model.In this section,we consider nearly orthogonal IBLHDs,in which nested factors are orthogonal to each other,orthogonal to the shared factors for the whole IBLHD,and nearly orthogonal to the shared factors within each slice.

Let us now see some further de finitions.A design is said to be orthogonal if the correlation between any two distinct columns is zero.An

SL

(

n,q,s

)is called a sliced orthogonal LHD(SOLHD,[7–12]),denoted by

SOL

(

n,q,s

),if both the whole design and its slices are orthogonal.From the construction method in Algorithm 2.1,if the original SLHD in Step 2 is an SOLHD,then the obtained IBLHD will inherit the orthogonality to some extent.In this paper,we only take the SOLHDs constructed by Algorithm 1 in[10]as the SLHDs in Step 2 of Algorithm 2.1.Other SOLHDs in the aforementioned literature can also be used of course,and the results will be similar,that is,the resulting IBLHDs are nearly orthogonal.To present the results in Proposition 3.1,we first brie fly introduce Algorithm 1 in[10].

Using

OD

(

m

)’s,Yang et al.[10]constructed

SOL

(2

sm,m,s

)by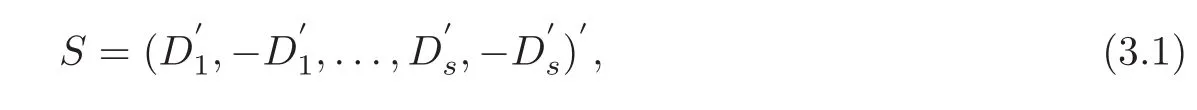

where

D

,...,D

are

OD

(

m

)’s with(

a,b

)

,...,

(

a,b

),respectively,and

a

=2

s

and

b

=?

a

+(2

j

?1)for

j

=1

,...,s

.When projected onto each dimension,each of the 2

m

equally spaced intervals[?2

sm,

?2

s

(

m

?1))

,

[?2

s

(

m

?1)

,

?2

s

(

m

?2))

,...,

[?2

s,

0)

,

[0

,

2

s

)

,...,

[2

s

(

m

?1)

,

2

sm

)contains exactly one point of each slice.

Proposition 3.1

Without loss of generality,assume that there is only one branching factor with

s

levels.If the SLHD

S

=(

S

,S

)in Step 2 of Algorithm 2.1 is an

SOL

(2

sm,m,s

)in(3.1),then(i)the nested factors are orthogonal to the shared factors for the whole IBLHD,and nearly orthogonal to the shared factors within each slice,and the upper bound for the absolute correlations between any nested factor and any shared factor in the

j

th slice is

(ii)the nested factors are orthogonal to each other for both the whole design and its slices.

Before proving Proposition 3.1,we present an obvious lemma with its proof omitted.

Lemma 3.2

Assume that

D

is an

OD

(

m

),where

m

=2and

r

≥1 is an integer,and let

T

=(

T

,...,T

)=(

D

,

?

D

).Then(i)

T

is one permutation on set{?

ma

?

b,

?(

m

?1)

a

?

b,...,

?

a

?

b,a

+

b,...,

(

m

?1)

a

+

b,ma

+

b

},

j

=1

,...,m

;(ii)

T

can be collapsed to one permutation on{1

,...,

2

m

}by linear transformation

where

T

is the

i

th element of

T

,

P

=

b/a

+

m

+1for the negative levels of

T

,and

P

=?

b/a

+

m

for the positive levels of

T

.

Because the inner product is a sum that does not depend on the order of the product pairs,so we can always arrange the order of summation so that the first

m

levels of

A

are negative.Then based on the structure of the

SOL

(2

sm,m,s

)in(3.1),

Therefore,the correlation between

C

and

B

is

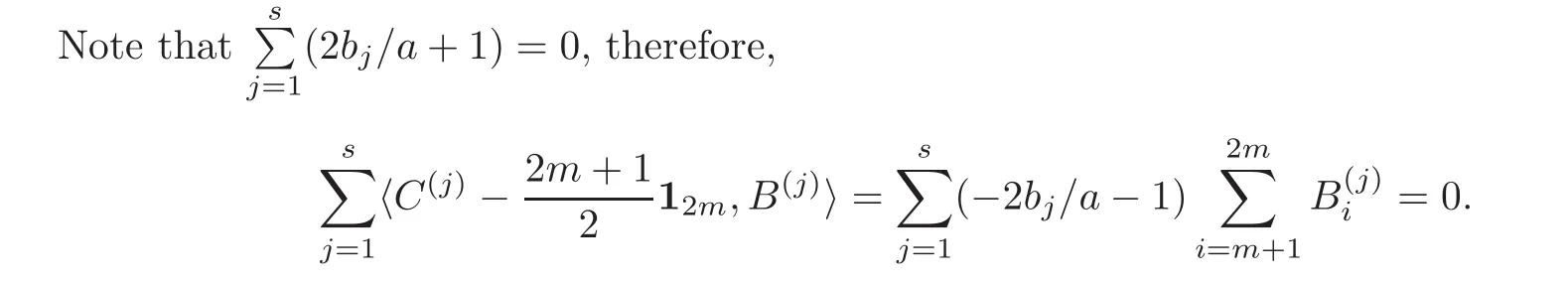
Thus,the nested factors are orthogonal to the shared factors for the whole IBLHD.This completes the proof of(i).

(ii)Denote the columns of any two nested factors in the

j

th slice of the IBLHD by

C

and

C

,respectively,which are collapsed from

A

and

A

by linear transformation based on(3.3),

j

=1

,...,s

.Note that 〈

A

,A

〉=0,and thus,

so corr(

C

,C

)=0.Therefore,the nested factors are orthogonal to each other within each slice.The orthogonality also holds for the whole design.This completes the proof of(ii).Note that in Proposition 3.1,the nested factors are orthogonal to the shared factors for the whole IBLHD,however,if some other SOLHDs are used as the SLHDs in Step 2 of Algorithm 2.1,the nested factors may only be nearly orthogonal to the shared factors for the whole IBLHD.Usually,the values of(3.2)are small,for example,when

m

=8

,s

=3

,a

=6

,b

=?5

,b

=?3

,b

=?1.In this case,the upper bounds(3.2)for the three slices are 0

.

0162

,

0

.

0153 and 0

.

0431,respectively.An illustrative example is given below.

Example 3.3

Consider a computer experiment with 16 runs,one branching factor

z

with two levels?1 and+1,two nested factors

v

and

v

,and two shared factors

x

and

x

.According to Algorithm 2.1 and Proposition 3.1,we take an

SOL

(16

,

4

,

2)from[10]with

a

=4,

b

=?3,

b

=?1,which is

Without loss of generality,the nested factors are assigned to the first two columns of

S

,and after they are collapsed over

z

,the final IBLHD is presented in Table 3.We can compute the upper bounds given in(3.2),which are 0

.

0525 and 0

.

0434 for the two slices.The real correlations between the nested factors and shared factors for the two slices and the whole design are listed in Table 4,which verify the conclusions in Proposition 3.1.Moreover,we can see that the upper bounds(3.2)are attainable.

4 Effectiveness of IBLHDs

In this section,we mainly study the performance of IBLHDs when they are used for building Gaussian process(GP)models.Although integrated analysis has been proven to be better than independent analysis([14]),we insist on using independent analysis in this paper,because different levels of the branching factor often represent remarkably different things,such as the two surface treatment methods in[1].That is to say,the data under one level of the branching factor is probably irrelevant with the data under another one,therefore,they can borrow no strength from one another to improve the fitted model.

where f(x)=(

f

(x)

,...,f

(x))is a vector of pre-speci fied regression functions and β=(

β

,...,β

)is a vector of unknown coefficients.The residual

ε

is assumed to be a stationary GP with zero mean and covariance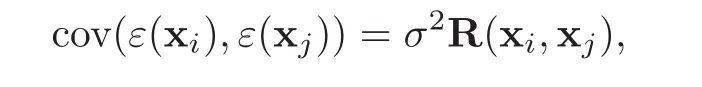

where R(x

,

x)is the Gaussian correlation function,whose popular form is the product exponential correlation function([15])that will be used in this paper:

Here,θ=(

θ

,...,θ

)is a vector of scale parameters.Usually,a maximum likelihood method is adopted to estimate the parameters(β

,σ

,

θ).Following the normality assumption of the GP model,the log-likelihood function of the collected data is

where R(

θ

)is the

n

×

n

correlation matrix with the(

i,j

)th element being R(x

,

x)and F=(f(x)

,...,

f(x)).As is stated in[16],simultaneous maximization over(β

,σ

,

θ)is unstable because R(θ)may be nearly singular and

σ

could be very small.Furthermore,β and θ play different roles:β is used to model overall trend,while θ is a smoothing parameter vector.Thus it is desirable to estimate these things separately.After giving θ,the maximum likelihood estimators(MLE)of β and

σ

can be derived from(4.1)as follows: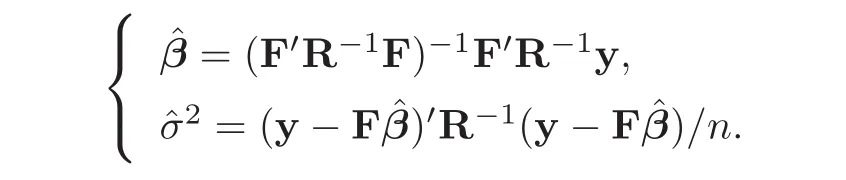

Then the MLE of θ can be obtained as

Finally,the best linear unbiased predictor(BLUP)of

y

at an untried point xis

Next,we present an illustrative example which was implemented using the Matlab toolbox DACE([17]).

Example 4.1

Assume there is a branching factor

z

with two levels,?1 and+1,and under each of these the nested factor

v

has eight levels:1

,...,

8.In addition,three shared factors,

x

,x

and

x

,are involved,and sixteen runs are available.The real response function is assumed to be

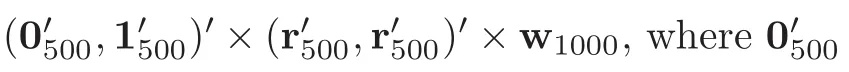
Figure 2 Boxplots of the 1000 RMSPEs corresponding to BLHDs and IBLHDs.

Table 5 Mean and standard deviation values of RMPSEs in Example 4.1

Note that in this section we fit a separate GP model for each level of the branching factor,otherwise we would need a special kernel function.

5 Concluding Remarks

In this paper,we proposed a new method for constructing BLHDs,and showed that the obtained IBLHDs improve the BLHDs in terms of the projection property under each level of the branching factor;that is,not only the whole design but also the slices get maximum strati fication in one-dimensional projection.In addition,if the original SLHDs are orthogonal,then in the obtained IBLHDs,the nested factors are orthogonal to each other,orthogonal to the shared factors for the whole design,and nearly orthogonal to the shared factors within each slice.Furthermore,the example shows that the IBLHDs outperform the BLHDs when used for building a GP model and for predictions at new points.

Note that all the optimization criteria in[1],including maximin distance,minimum correlation and orthogonal-maximin,can be applied on IBLHDs to get corresponding optimal IBLHDs.Although the nested factors are quantitative in both this paper and[1],they can be qualitative sometimes.Chen et al.[12]constructed SLHDs with both the branching and nested factors being qualitative.In addition,we can also construct the second and third parts of an IBLHD using the OA-based idea([18–20]).