Entanglement generation and protection for two atoms in the presence of two parallel mirrors

Yuhong Ye(葉玉洪),Hongwei Yu(余洪偉)and Jiawei Hu(胡佳偉)

Department of Physics and Synergetic Innovation Center for Quantum Effects and Applications,Hunan Normal University,Changsha,410081,China

Abstract We study,in the framework of open quantum systems,the entanglement generation of two atoms in between two parallel mirrors in a thermal bath of quantum scalar fields.We find that the presence of mirrors plays an important role in entanglement generation and protection.The entanglement dynamics is crucially dependent on the geometric configurations of the two-atom system with respect to the mirrors,and the ranges of temperature and interatomic separation within which entanglement can be generated are significantly changed compared with those in a free space.In particular,when the atomic transition wavelength is larger than twice the distance between the two mirrors,the atoms behave as if they were isolated from the environment and the entanglement can persist in the steady state if the atoms are initially entangled and no entanglement can be created if they are initially separable,no matter how the atoms are placed with respect to the mirrors and to each other.This is in sharp contrast to the fact that in a free space,steady-state entanglement is possible only when the two atoms are placed extremely close to each other,while in the presence of one mirror,it is possible when the two atoms placed extremely close to the mirror.

Keywords:quantum entanglement,open quantum systems,quantum and thermal fluctuations

1.Introduction

Quantum entanglement plays a vital role in quantum information technologies[1]such as quantum communication,quantum teleportation,quantum cryptography,quantum computation,and so on.A major challenge in the realization of these quantum based technologies is the decoherence and dissipation induced by the inevitable system-environment couplings.In particular,it has been shown that an entangled quantum system may get disentangled within a finite time via spontaneous emissions even when the environment is a vacuum,which is known as entanglement sudden death[2,3].However,on the other hand,due to the indirect interactions provided by the common bath,in certain circumstances,two initially separable atoms may get entangled[4–13].In particular,it has been shown that,for a two-atom system immersed in a thermal bath,entanglement generation happens for atoms with an appropriate separation in a thermal bath at sufficiently small temperatures,while entanglement sudden death is a general feature if the interatomic separation is nonvanishing[11].That is,steady-state entanglement is possible only when the two atoms are placed extremely close to each other[13].

The studies also show that the entanglement dynamics of a quantum system is crucially dependent on changes of the environment to which it is coupled.It is well-known that vacuum fluctuations can be modified in the presence of boundaries,which leads to novel effects such as the Casimir[14]and Casimir–Polder effects[15],modifications of the spontaneous transition rates[16–22],position-dependent resonance interactions[23,24],electromagnetic shielding in quantum metrology[25],and so on.Then,a question naturally arises as to what happens to the entanglement dynamics of a quantum system if the environment is altered by the presence of reflecting mirrors.Recently,the entanglement dynamics for a two-atom system in the presence of a single reflecting mirror has been investigated,which shows that the presence of a mirror plays an important role in controlling the entanglement dynamics[26–28].Remarkably,it has been shown that,when both of the atoms are placed extremely close the mirror,the two-atom system can behave as if it were isolated from the environment,and the initial entanglement will be preserved no matter how long they are separated[28].

A further question is what happens to the entanglement dynamics if two parallel reflecting mirrors are present.In fact,it has long been known that,the spontaneous emission rate of an excited atom can be completely turned off if its transition dipole moment is parallel to the reflecting mirrors,when the distance between the two mirrors is smaller than half of the transition wavelength[16–19],no matter where the atom is placed between the mirrors.Therefore,novel features which are different from those in a free space and in the presence of a single mirror are expected in the entanglement dynamics of a two-atom system,since it is closely related to the spontaneous transition processes.Here let us note that the entanglement dynamics of a two-atom system in a common cavity has been extensively studied,see,e.g.[29–34].Usually,it is assumed that the atoms interact with a single-mode cavity field[30–32],or a reservoir with some kinds of spectral density,such as the Lorentzian spectral density[33].In the present paper,we assume that the environment the atoms immersed in is a thermal bath of quantum scalar fields with all frequencies in the presence of two parallel reflecting mirrors.The two-point function of the quantum fields in the coordinate space is worked out with the method of images,which facilitates the investigation of how the entanglement dynamics is dependent on the geometric configurations of the twoatom system with respect to the mirrors.In particular,we focus on whether entanglement can be generated at the neighborhood of the initial time for a separable two-atom system,and whether entanglement can persist in the steady state.Hereafter,natural units with?=c=kB=1 are applied.

2.The basic formalism

In this paper,we study the entanglement generation for two atoms immersed in a thermal bath of quantum scalar fields in the presence of two parallel reflecting mirrors.The Hamiltonian of the total system is

Here HAis the Hamiltonian of the two-atom system.We assume that there is no direct interaction between the two atoms,so the Hamiltonian can be written as

where the superscript α(α=1,2)labels the operator of the α th atom,with σi(i=1,2,3)being the Pauli matrices,σ0the 2×2 unit matrix,and ω the energy level spacing of the atoms.HFis the Hamiltonian of the fluctuating massless scalar fields.HIis the Hamiltonian describing the interaction between the atoms and the field,which takes the form in analogy to the electric dipole interaction as[35]

where μ is a dimensionless coupling constant which is supposed to be small,Φ is the field operator,τ is the proper time,and xi(i=1,2)labels the position of the i th atom.

In the weak-coupling limit,the evolution of the reduced density matrix of the two-atom system satisfies the Gorini-Kossakowski-Lindblad-Sudarshan master equation[36,37]

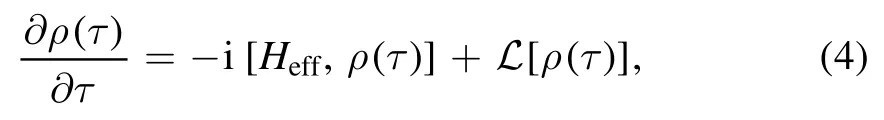
where i is the imaginary unit,

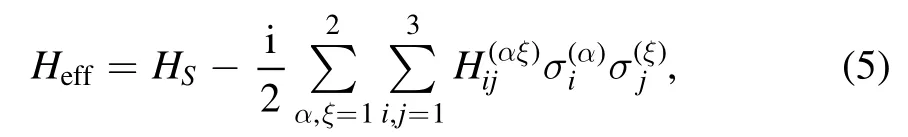
and

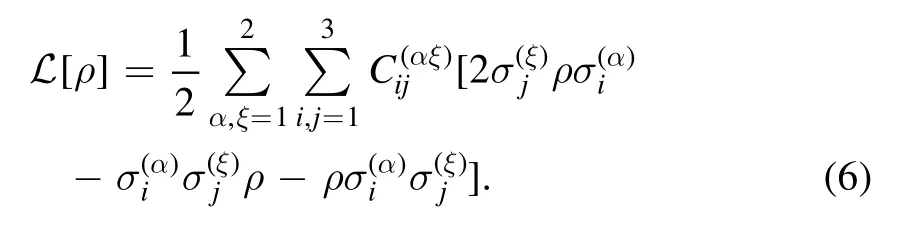
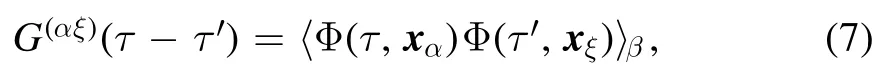
which are given as follows,

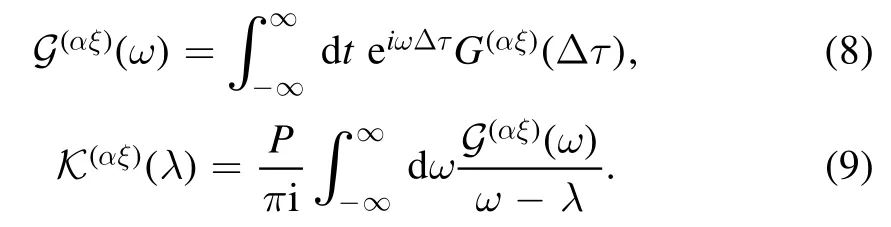
Here P denotes the principal value,andΔτ=τ-τ′.Then,the coefficientscan be explicitly written as

where

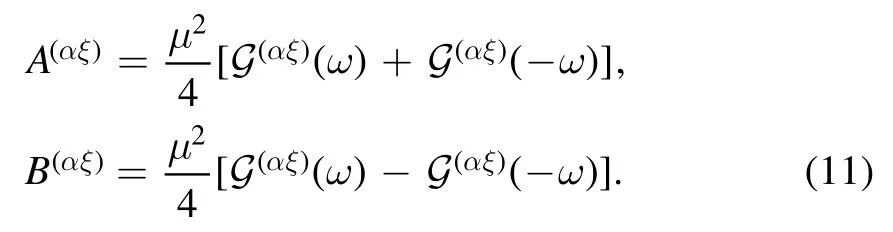
Replacing the Fourier transformG(αξ)(ω)with the Hilbert transformK(αξ)(ω),one obtains

For convenience,we employ the coupled basis{|G〉=|00〉,|E〉=|11〉,|A〉=∣01〉)}to solve the master equation of the two-atom system.The density matrix of the two-atom system can be written as ρ=∑I,JρIJ|I〉〈J|,where ρIJ=〈I|ρ|J〉,I,J∈{G,E,A,S}.First,we rewrite the coefficients equation(10)as

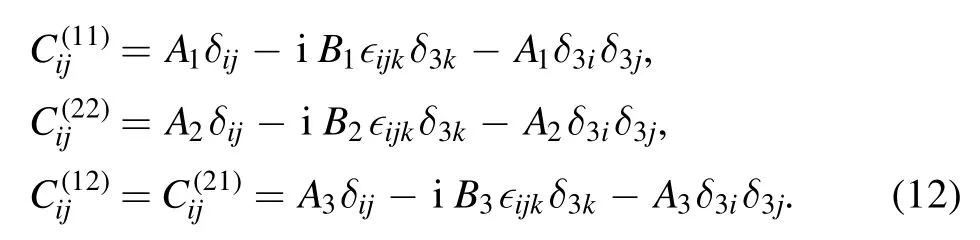
For brevity,we have defined A1=A(11),A2=A(22),A3=A(12)=A(21),and B1=B(11),B2=B(22),B3=B(12)=B(21).Then,a set of equations,which are decoupled from other matrix elements,can be obtained as follows

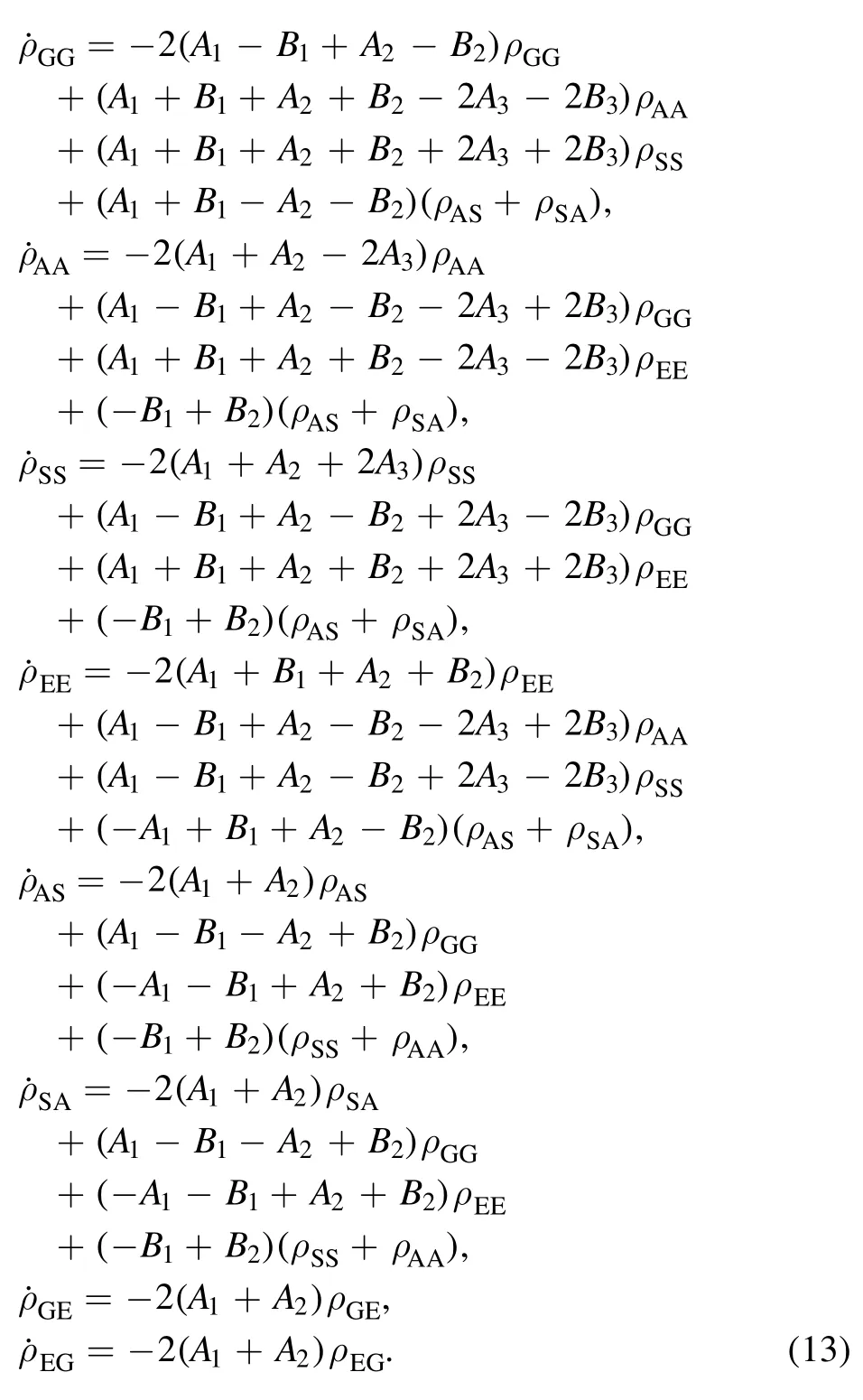
Note that ρGG+ρEE+ρAA+ρSS=1 is satisfied.

3.The condition for entanglement generation

In this section,we investigate whether entanglement can be created between two atoms at the neighborhood of the initial time with the help of the partial transposition criterion[38,39],i.e.a two-atom state ρ(τ)is entangled if and only if the partial transposition of ρ(τ)does not preserve its positivity.We assume that initially the two atoms are in their ground and excited states respectively,i.e.ρ(0)=|1〉〈1|?|0〉〈0|,which is separable.In this case,based on the partial transposition criterion,the two atoms can be entangled at the neighbourhood of τ=0 if and only if the following inequality is satisfied[12,13],

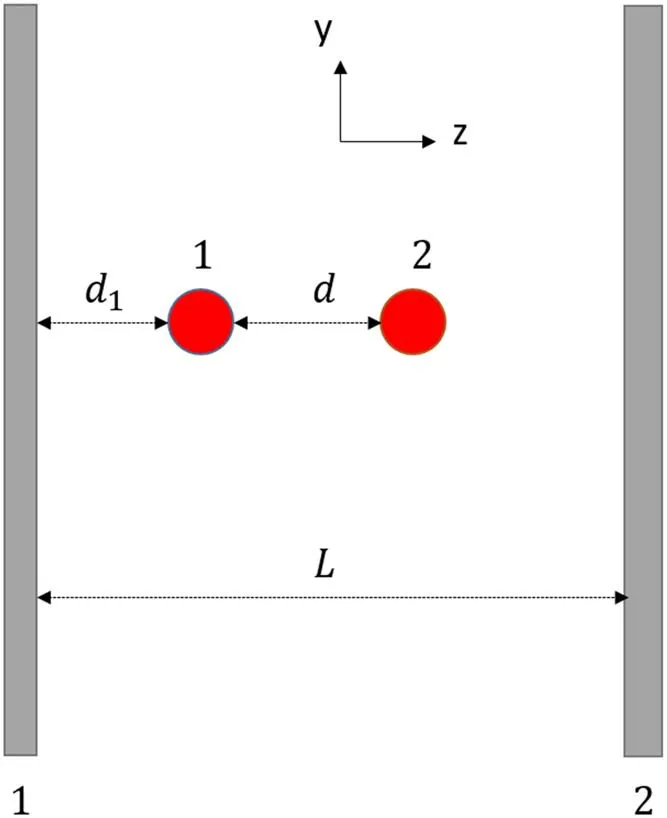
Figure 1.Two atoms separated from each other by a distance d are aligned vertically to two parallel mirrors separated by a distance L.

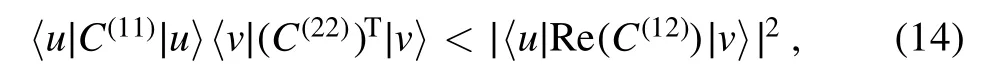
where the superscript T denotes matrix transposition,and ui=vi={1,-i,0}.Substituting the explicit form of C(αξ)into equation(14),one obtains

In this paper,we study the entanglement generation for two atoms coupled with massless scalar fields in a thermal bath at temperature 1/β in the presence of two parallel reflecting mirrors.Without loss of generality,the two mirrors are assumed to be located at z=0 and z=L respectively.We assume that the two atoms are aligned vertically to the mirrors,which are placed at x1=(0,0,d1)and x2=(0,0,d1+d)respectively,where d1is the distance between atom 1 and mirror 1,and d is the interatomic separation,see figure 1.For convenience,we rewrite the distance between the two mirrors as

where is the atomic transition wavelength,k∈Zand0≤θ＜2π.The coefficients Aiand Biare given in appendix,and the explicit expressions are dependent on whether the distance between the two mirrors L is an integer times/2,i.e.whether θ in equation(16)is zero or not.Since the expressions are complicated in a general case,first let us consider some special cases in the following.

Case 1.When the transition wavelength is larger than twice the distance between the two mirrors,i.e.>2L,it can be found with the help of equation(32)that,A1=A2=A3=0,and B1=B2=B3=0,so the condition(15)cannot be satisfied,and thus entanglement can not be created.In fact,in this case,the spontaneous emission is turned off[16–19],so the atoms are locked up in their initial state,and it is natural that entanglement cannot be created in this case.Note that this conclusion does not rely on how the atoms are aligned with respect to the boundaries.Actually,from the definition equation(7),it is clear that the two-point functions G(11)(Δτ)and G(22)(Δτ)(and thus A1,A2,B1,B2)are independent of the relative positions of the two atoms and the alignment with respect to the boundaries,so they are always zero when>2L.Then,according to the Cauchy-Schwarz inequality,|G(12)(Δτ)|2≤G(11)(Δτ)G(22)(Δτ)=0,so G(12)(Δτ)(and thus A3,B3)are also zero when>2L.

A similar case is when one or both of the two atoms are placed extremely close to the mirrors,i.e.when d1→0 or d1+d→L,it can be found from equations(32)and(33)thatA1A2=B1B2==0.Therefore,the condition(15)is not satisfied,and entanglement cannot be created.Actually,when an atom is placed infinitely close to a reflecting mirror,it behaves as if it were isolated from the environment,so there is no environment-induced entanglement.Also,it does not rely on how the atoms are aligned with respect to the boundary.

Case 2.When the transition wavelength is larger than one but smaller than or equal to twice the distance between the two mirrors,i.e.L＜≤2L,it is straightforward to verify that=A1A2.Then,as long as none of the two atoms is placed infinitely close to the mirrors,i.e.d1≠0 and d+d1≠L,then B1B2>0,so the condition(15)can be satisfied,and entanglement can be created at the initial time,no matter how high the environmental temperature is.

Except for the situations discussed in Case 1,the spontaneous emission rates of the atoms are non-zero,i.e.A1A2≠0 and B1B2≠0.Then,the condition(15)can be rewritten as

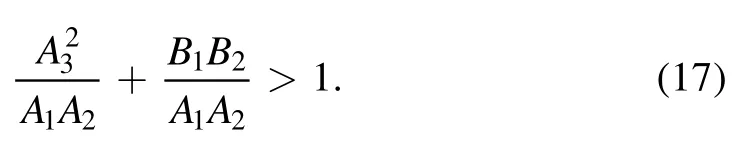
Here let us note that the criterion for entanglement generation can be written as equation(17)only if A1A2≠0.As an example,in Case 1,although A1=A2=A3=0,and B1=B2=B3=0,the limits ofandexist,andis possible.However,it is obvious from equation(13)that the two-atom system is lock up in its initial state,and entanglement generation is impossible.From equations(32)and(33),it can be found thatdepends on the environmental temperature only,which takes the form

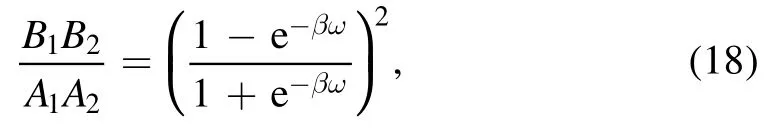
and decreases monotonically as temperature increases,whileis temperature-independent,and it is dependent on the distance between the two mirrors and the positions of the two atoms.When the environment is a vacuum,i.e.β→∞,then entanglement can be generated unlessis zero.Also,if the separation between the two atoms is vanishing,i.e.d→0,thenbecomes 1,and the inequality(17)is always satisfied and entanglement can be created,no matter where the atoms are placed,as long as the environment temperature is not infinite.When the distance between the two mirrors L→∞,but the distance d1between atom 1 and mirror 1 and the interatomic separation d are finite,the coefficients Aiand Biare given in equation(34)in appendix,which reduce to those in the case of a single mirror,see equations(37)–(42)in[27]in the zero-acceleration limit.Furthermore,if d1also approaches infinity,the coefficients are given in equation(35),which reduce to those in a free space[13],as expected.

Since in a general case,the ratiois complicated,in the following,we study its behavior numerically.First,we fix the interatomic separation d,and see how the ratiovaries with the distance between atom 1 and the first mirror d1.Note that since the atoms are aligned vertically to the mirrors,the range of d1is restricted to[0,L-d].As shown in figure 2,the ratiooscillates as d1increases,and it is always positive when the interatomic separation d is small.That is,there is always a critical temperature below which entanglement can be generated no matter where the vertically aligned two-atom system is placed.As d becomes larger,there are zeros of the ratio,i.e.there are positions at which the twoatom system cannot get entangled at the neighborhood of the initial time,even if the environment is a vacuum.When d becomes close to the distance between the two mirrors L(i.e.when the two atoms are close to the two mirrors respectively),is almost unchanged as d1varies,and it is always positive,i.e.entanglement can always be generated below a critical temperature.

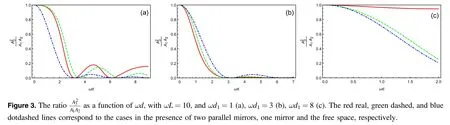
Second,we fix the distance between atom 1 and the first mirror d1,and show how the ratiovaries with the interatomic separation d in figure 3.It is shown that the ratiooscillates with a damping amplitude as d increases.Thus,as temperature increases,the range of d within which entanglement can be created becomes narrower.When d1approaches L,i.e.when both the two atoms are placed close to one of the mirrors,the ratiois close to unity and remains nearly unchanged,so entanglement can always be generated below some critical temperature.

In figures 2 and 3,we have also compared the ratioin the current case with those in the cases of a single mirror and the free space,which in general can be both larger and smaller than those in the other two cases.However,when the atoms are placed close to one of(i.e.d1is large,see figure 3(c))or both of(i.e.d is large,see figure 2(c))the mirrors,the ratioin the two-mirror case is always larger than those in the other two cases.That is,the range of temperature within which entanglement can be created is wider in the two-mirror case compared with the cases of a free space and one mirror.

4.The steady-state entanglement

In the previous section,we reveal that in certain circumstance entanglement can be generated in the presence of two mirrors.Another problem of interest is whether the entanglement can be protected and the system is still entangled in the steady state.Here,we characterize the degree of entanglement with the help of concurrence[40],which ranges from 0,for separable states,to 1,for maximally entangled states.In this paper,for simplicity,the initial density matrix is chosen as of the X shape,i.e.the only nonzero elements are those along the diagonal and anti-diagonal elements in the basis|00〉,|01〉,|10〉,|11〉.The X form will be maintained during evolution[41],and the concurrence can be calculated to be in the following form[9]

where

Moreover,as will be shown that ρGE(∞)is zero,so K2(∞)is negative,andC[ρ(∞)]=max {0,K1(∞)}.

In order to investigate the steady-state entanglement,first we need to work out the steady state of the two-atom system,which can be found by taking the time derivatives in equation(13)to be zero.Since only five of the first six equations in equation(13)are independent,we solve a system of six linear equations composed of five of the first six equations in equation(13)by taking their right-hand sides to be zero,and ρGG+ρEE+ρAA+ρSS=1.

When the determinant of coefficient matrix is nonzero,i.e.

the nonzero density matrix elements of the steady state can be solved as

On the other hand,when the determinantΔ=0,the steady state is also related to the initial state,and might be entangled.Explicit cases will be shown in the following in whichΔ=0 can be achieved.

Case 1.When the interatomic separation d→0,we have A1=A2=A3,and B1=B2=B3.Then it can be found that the nonzero density matrix elements are,

and

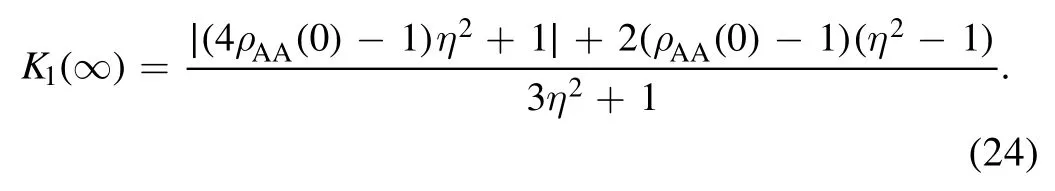
Case 2.When one of the atoms is placed extremely close to a mirror,e.g.atom 1 is placed extremely close to mirror 1,i.e.d1→0,then A1=A3=0,and B1=B3=0.The nonzero density matrix elements can be calculated as

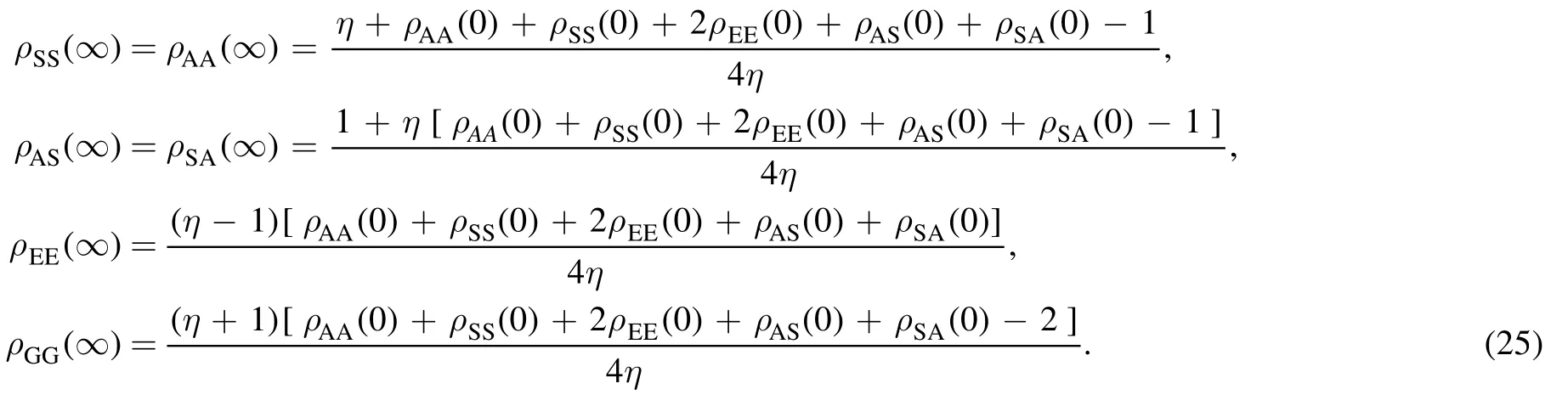
Since ρAA(∞)=ρSS(∞)and ρAS(∞)=ρSA(∞)=0,K1(∞)is negative,thus the steady state cannot be entangled.

Case 3.When both of the two atoms are placed extremely close to the mirrors,then A1=A2=A3=0,and B1=B2=B3=0.From equation(13),it is obvious that the two-atom system does not evolve.So the initial entanglement can persist in the steady state.Note that this condition can also be satisfied when only one mirror is present[28].

Case 4.A similar case to Case 3 is when the transition wavelength is smaller than twice the distance between the two mirrors,i.e.＜2L.In this case,A1=A2=A3=0,and B1=B2=B3=0 are also satisfied,so there exists steadystate entanglement.

Case 5.When the transition wavelength is larger than one but smaller than or equal to twice the distance between the two mirrors,i.e.L＜≤2L,then=A1A2andand the result depends on whether the environment is a vacuum or not.

If the environment is a vacuum,η=1,it can be calculated that

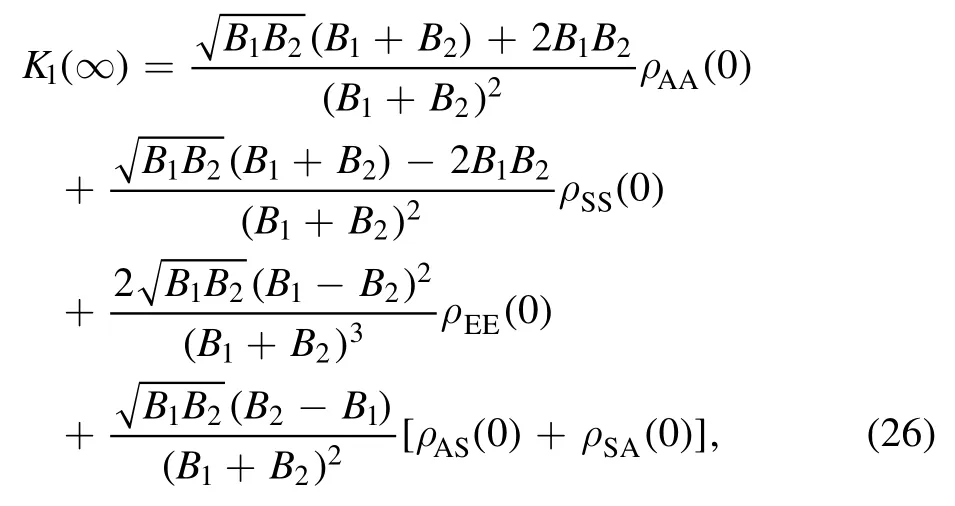
which can be positive depending on the initial state and the value of B1and B2.As an example,if both the two atoms are initially in the excited state,ρEE(0)=1,there exists steadystate entanglement when B1≠B2,i.e.the distance between atom 1 and mirror 1 must be different from that between atom 2 and mirror 2.When B1=B2,equation(26)can be simplified as K1(∞)=ρAA(0).That is,it is required that the initial state satisfies ρAA(0)≠0 to obtain steady-state entanglement.

If the environment is not a vacuum,i.e.η≠1,it can be shown that B1=B2=B3is required to haveΔ=0 and=B1B2satisfied simultaneously,i.e.the distance between atom 1 and mirror 1 must be the same as that between atom 2 and mirror 2.It is obvious that the result should be the same as that has been discussed in Case 1,and the steady state can be entangled.

5.Discussion and summary

We have investigated,in the framework of open quantum systems,the entanglement generation for a two-atom system immersed in a thermal bath in the presence of two parallel reflecting plane mirrors.We have shown that the presence of mirrors plays an important role in entanglement generation,in the sense that the ranges of temperature and interatomic separation within which entanglement can be generated are significantly changed compared with those in a free space.Remarkably,when the atomic transition wavelength is larger than twice the distance between the two mirrors,the atoms behave as if they were isolated from the environment,and the initial entanglement can persist in the steady state but no entanglement can be created if they are initially separable,no matter how the atoms are placed with respect to the mirrors and to each other.This is in stark contrast to the fact that in a free space,steady-state entanglement is possible only when the two atoms are placed extremely close to each other,while in the presence of one mirror,it is possible when the two atoms placed extremely close to the mirror.

It should be pointed out that we have only considered the case in which the two atoms are aligned vertically to the mirrors.The reason is twofold.First,for the parallel alignment case,terms such aswill appear in the infinite summation in the two-point functions.This makes a mere analytical calculation of the two-point functions impossible,let alone the coefficients Aiand Biwhich determine the entanglement generation.So,a study of such case would require numerical computations from at very early stages.Second,more importantly,the main features of the entanglement generation,which have been summarized above,do not depend on how the atoms are aligned with respect to the mirrors.

Nevertheless,there are some unique features of entanglement generation in the case of vertical alignment.The range of temperature within which entanglement can be created is wider in the two-mirror case compared with the cases of a free space and one mirror,when the atoms are placed close to one or both of the mirrors,and entanglement can both be generated and be maintained in the asymptotic regime,when the transition wavelength is larger than one but smaller than or equal to twice the distance between the two mirrors.It can be checked numerically that there are no such features in the case of parallel alignment.

Acknowledgments

We would like to thank Yuebing Zhou for valuable discussions.This work was supported in part by the NSFC under Grants No.11805063,No.11690034,and No.12075084,and the Hunan Provincial Natural Science Foundation of China under Grant No.2020JJ3026.

Appendix.Calculations of the coefficients

In this appendix,we show the details of the calculations of the coefficients Aiand Biof a two-atom system immersed in a thermal bath of quantum scalar fields in the presence of two perfectly reflecting plane mirrors.

The field correlation function can be obtained with the help of the method of images[42],which takes the following form,

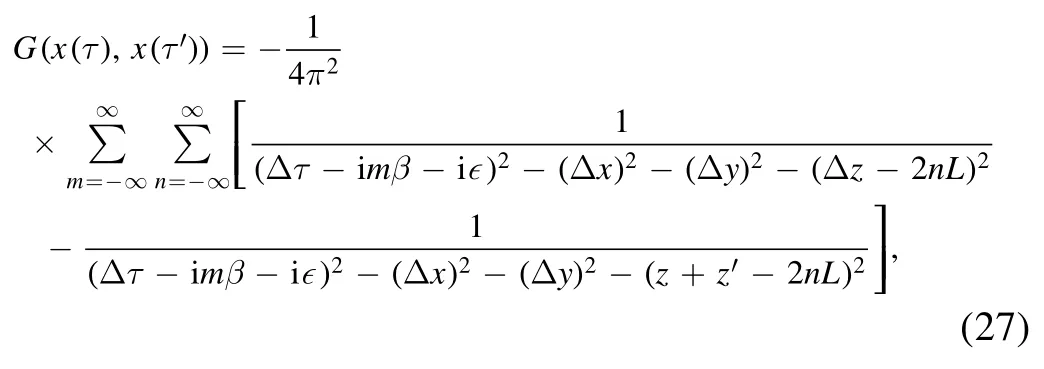
where 1/β is the temperature of the thermal bath.

Allowing for the trajectories of the two atoms,and=(τ,0,0,d1+d),the correlation functions can be written as

The Fourier transforms of the correlation functions above can be obtained as

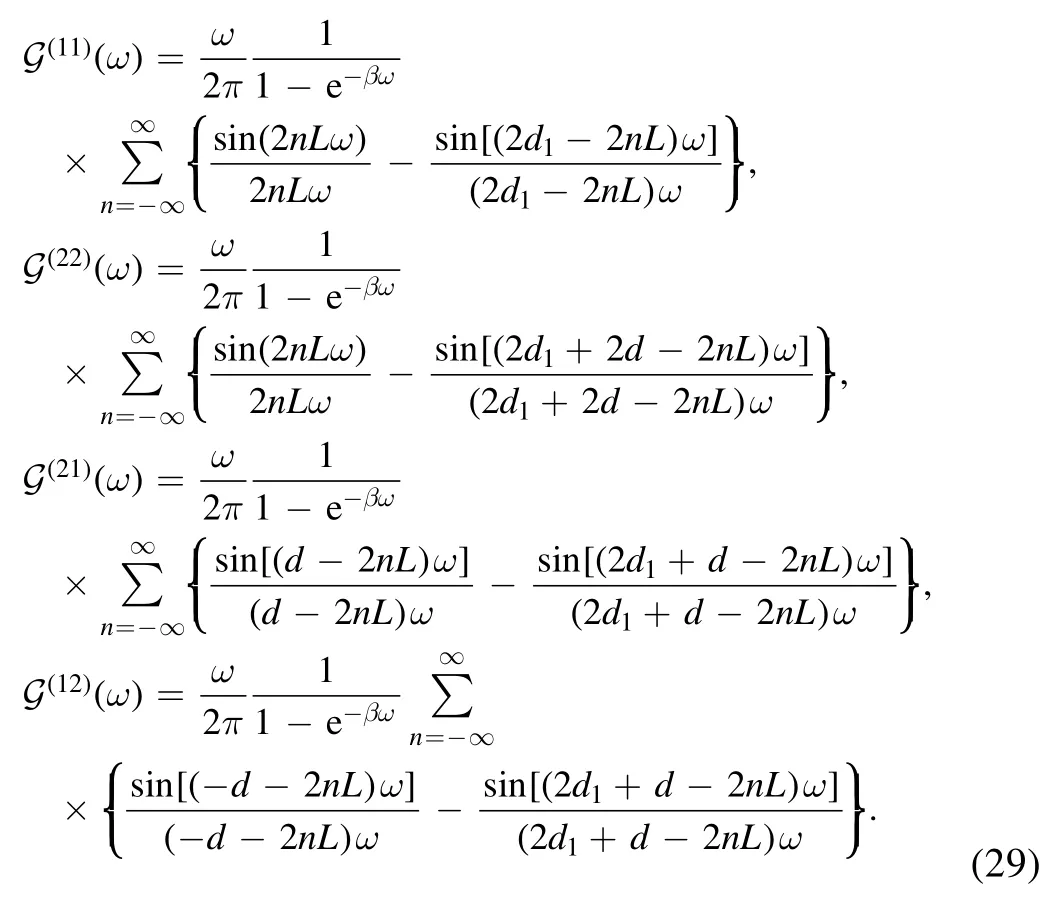
In order to solve the infinite sum over n,we employ the following formulae[43],

with k being a positive integer.For convenience,we rewrite the distance between the two mirrors as

wherek∈Zand 0≤θ＜2π.When θ≠0,the coefficients can be calculated as

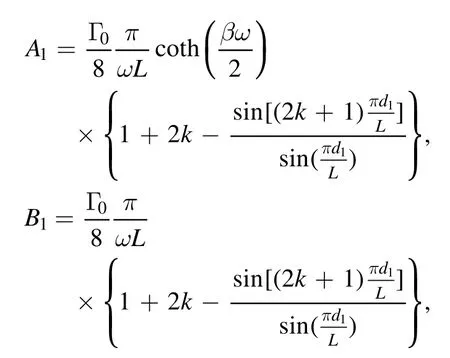
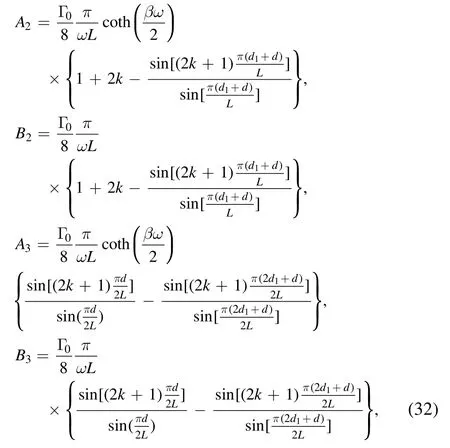
whereΓ0=μ2ω/2π being the spontaneous emission rate.When θ=0,we have

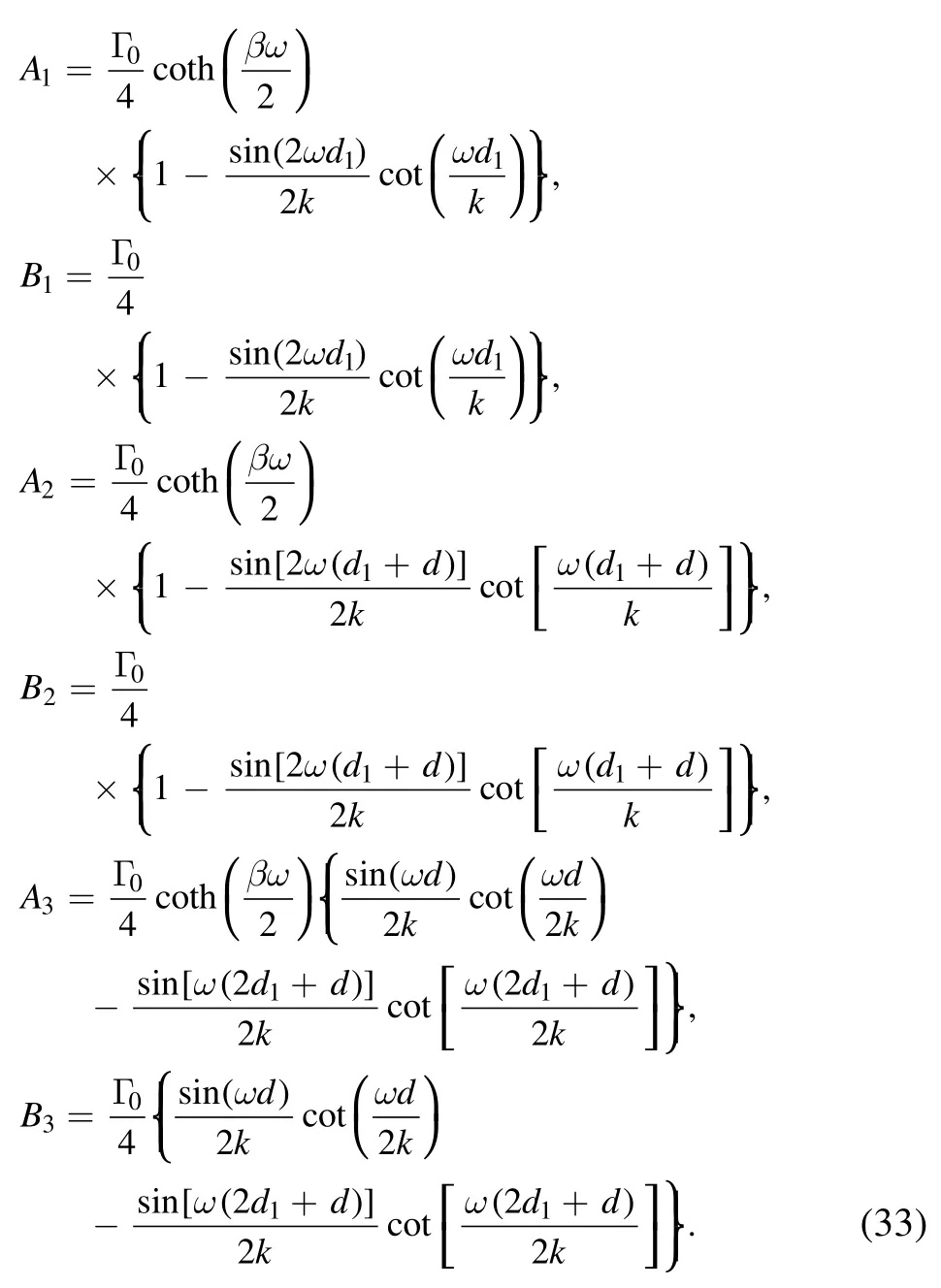
When the distance between the two mirrors L→∞,but the distance between atom 1 and the first mirror d1and the interatomic separation d are finite,then

which reduces to the result in the case of a single mirror,see equations(37)–(42)in[27]in the limit a→0.Furthermore,if d1also approaches infinity,then

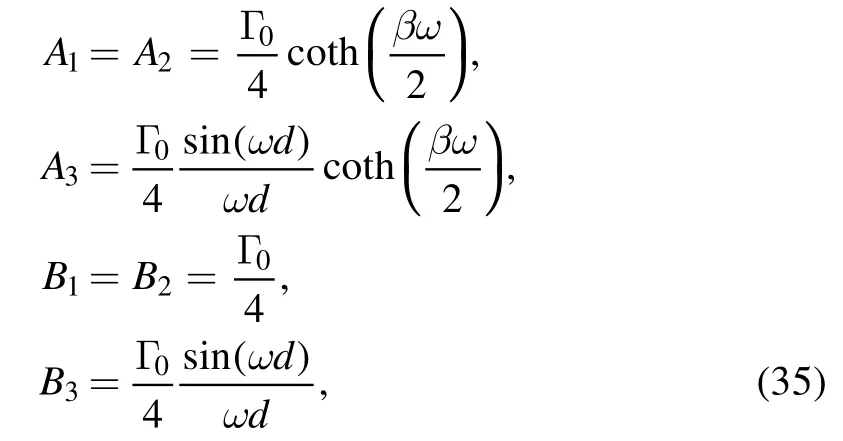
i.e.the result reduces to that in a free space[13].