Controlled quantum teleportation of an unknown single-qutrit state in noisy channels with memory?

Shexiang Jiang(蔣社想), Bao Zhao(趙寶), and Xingzhu Liang(梁興柱)

School of Computer Science and Engineering,Anhui University of Science and Technology,Huainan 232001,China

Keywords: three-dimensional quantum teleportation,fidelity,Pauli noise,memory channel

1. Introduction

Quantum teleportation (QT) is one of the most significant technologies of quantum communication. It uses quantum states as information carriers for remote transmission of information about a physical system without transferring the physical system. The QT was originally proposed by Bennettet al.[1]in 1993. When an EPR (Einstein–Podolsky–Rosen) pair is shared between a sender and a receiver, an unknown single-qubit state is transmitted from the sender to the remote receiver with the help of local operations and classical information. The QT has been validated in several physical experiments.[2,3]Interest in QT has grown considerably since Bennettet al.’s work, and many QT schemes[4–14]have been proposed. A controlled QT (CQT) scheme was devised[15–17]that increased the security of QT by requiring a controller to give permission for the transmission between the sender and the receiver.Bidirectional QT(BQT)schemes have been introduced[18–21]in which two parties,both a sender and a receiver, teleport quantum states as multipartite entangled states in the quantum channel. Other improved QT schemes have been proposed that embrace a variety of communication scenarios, such as bidirectional controlled QT (BCQT),[22,23]cyclic QT,[24]and cyclic controlled QT.[25]

Most of the works mentioned are concerned with teleportation in a two-dimensional (2D) subspace of a quantum system,and teleported quantum information has been limited to qubits. A quantum particle can physically have many degrees of freedom, implying that a quantum system may have more than two dimensions. Researchers[26–30]have thus extended QT to operate in high dimensionally, both in theory and in practice. The authors in Ref. [26] investigated QT for arbitrary high-dimensional photonic quantum states and gave an example of teleportation in a three-dimensional(3D)state.The authors in Ref. [30] implemented BCQT in a 3D quantum system.High-dimensional QT schemes can not only carry more information but also better suppress noise than conventional 2D QT systems.

Quantum noise is an unavoidable phenomenon in physical QT. Noise can decohere a quantum state, in which case the output state received is not consistent with the teleported state. Fidelity describes the distance between two states. In QT schemes that can be realized, it is important to study the effect of noise on the scheme and to determine how to increase the fidelity of the output state. In 2002, Ohet al.[31]proposed a QT scheme for a noisy channel. They found that when the channel was affected by isotropic noise,the fidelity of QT was less than that of classical communication. However, when the noise was modeled by a Lindblad operator,the fidelity was greater than that of classical communication.Since then, many different QT schemes have been proposed with noisy channels.[32–35]Researchers have analyzed the effects of different types of noise on teleportation by calculating the fidelity of teleportation. A variety of techniques have been used to improve fidelity,such as entanglement distillation and weak measurement.

Most of QT research are based on the assumption that a noisy channel used for the transmission of entangled particles is memoryless and that two consecutive uses of the channel are independent. However,when the transmission is realized, there can be a noise correlation between them. A noisy channel with memory was first investigated by Macchiavelloet al.[36]They created a memory model using Pauli noise operators and showed that the memory can enhance the transmission of classical information in the depolarizing channel. Many correlated noise channels were studied after that report, and the effects of the noise correlation between consecutive transmissions on different schemes[37–40]have been thoroughly investigated.Liet al.[39]showed recently that the correlation between two consecutive uses of a channel subject to Pauli noise could be used to improve the fidelity of teleportation. More recently, Zhanget al.[40]proposed a remote state preparation scheme for a Pauli noise channel with memory. They quantified fidelity for five types of noisy channel with memory and found that channel memory can enhance communication.

There are few studies of high-dimensional quantum teleportation in noisy channels with memory. Thus, it is of interest to investigate the effects of memory on the fidelity of high-dimensional quantum teleportation. We propose a CQT scheme for an arbitrary 3D quantum state,which we call 3DCQT.The scheme is first introduced in an ideal environment.We then consider the transmission of entangled particles in four 3D-Pauli-like noisy channels with memory where the noise errors are classified into four types: trit-flip, t-phaseflip, trit-phase-flip, and t-depolarizing. The results show that memory can increase the fidelity of teleportation when there are trit-flip and t-depolarizing errors. When channel memory is very strong,the scheme becomes immune to trit-flip noise.However,for t-phase-flip noise and trit-phase-flip noise,memory can lead to perfect fidelity of teleportation only when the noise parameter is below a certain value. This understanding facilitates to improve the efficiency of teleportation in highdimensional quantum systems. In summary, the proposed scheme possesses the following advantages.

(i)The arbitrary state of a single particle in the 3D quantum system can be expressed as Eq.(1),which is used to analyze the average fidelity of the output state.

(ii) The 3D-CQT scheme is introduced in an ideal environment and is presented for the first time in a 3D-Pauli-like noisy channel with memory.

(iii)For each of four types of channels with memory,the relationships between fidelity and the memory and noise parameters,and the fidelity of classical transmission,are pictorially represented and mathematically formulated.

This paper is organized as follows. In Section 2, some preliminaries related to the work are introduced,including descriptions of qutrits, 3D-Bell state, 3D-GHZ state, and Weyl operators,together with measurement bases and unitary transformations for qutrits. In Section 3, the proposed scheme is presented in an ideal environment. In Section 4,four types of 3D-Pauli-like noise are described using Kraus operators. In Section 5, the scheme is presented in each of four types of Pauli-like noisy channel with memory; the relationships between fidelity and the memory and noise parameters are identified and classical fidelity is analyzed. The work is summarized and conclusions are presented in Section 6.

2. Preliminaries

In this section, some basic preliminaries related to the work are presented,including descriptions of qutrits,3D-Bell state, 3D-GHZ state, unitary transformations for qutrits, and Weyl operators.

2.1. Qutrit,3D-Bell state,and 3D-GHZ state

The information unit in a 3D quantum system is a qutrit,which is analogous to the classical trit. A qutrit is a superposition of computation basis states|0〉,|1〉, and|2〉. It can be expressed as[41]

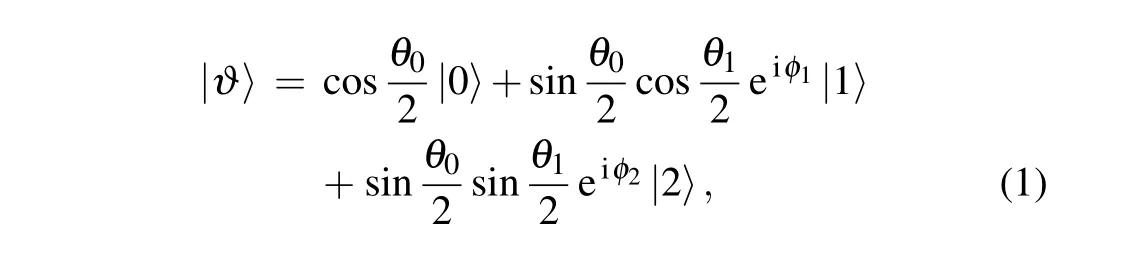
whereθ0,θ1∈[0,π]andφ1,φ2∈[0,2π].

The equation for the general two-particle Bell state in a high-dimensional quantum system is[42]

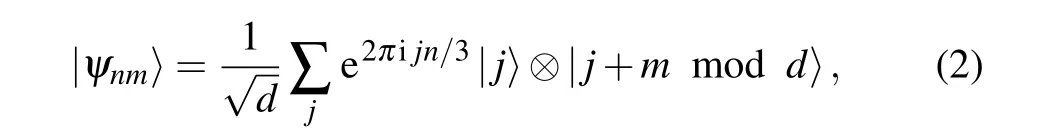
wheren,m,j=0,1,2,...,d ?1. Whend=3, the nine 3D Bell(3D-Bell)states are

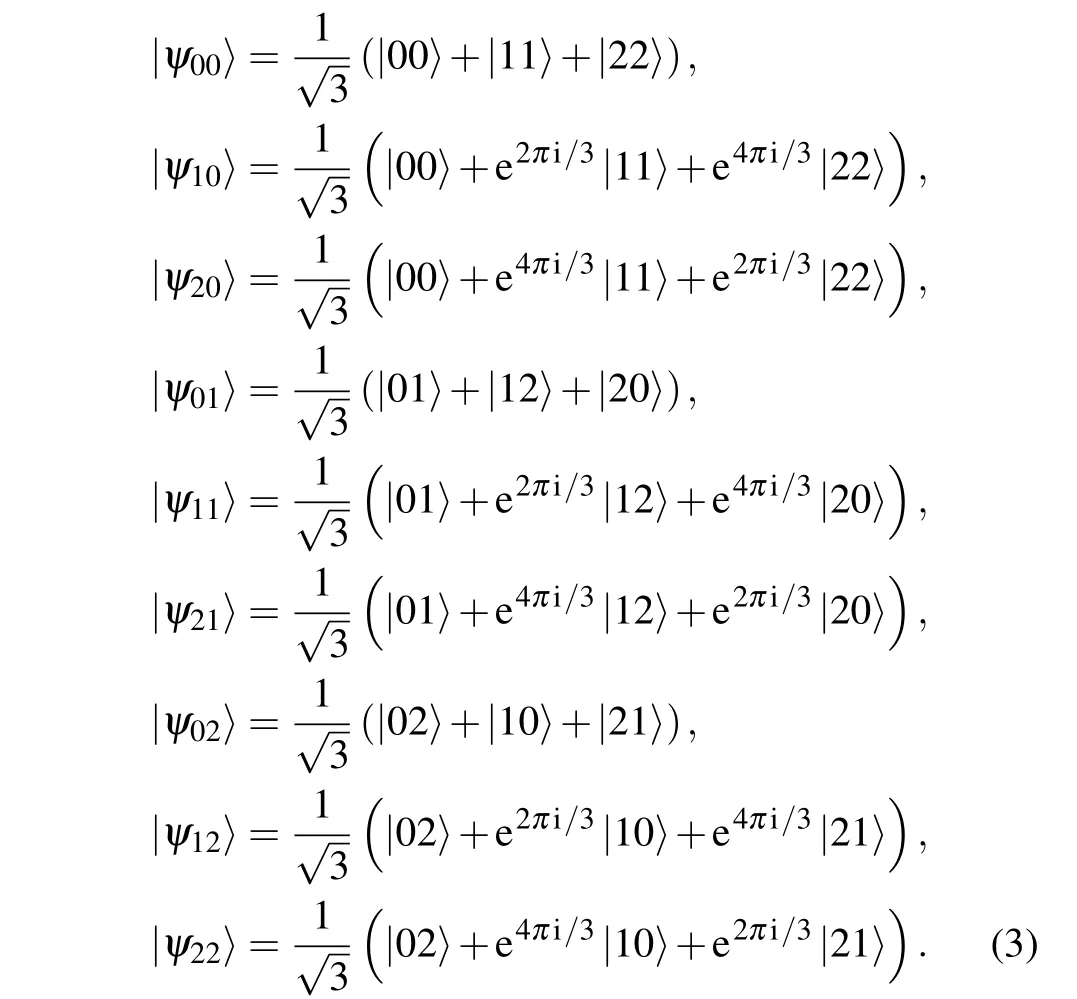
The nine 3D-Bell states have been demonstrated to be discriminable by using one additional single-photon,which is described in detail in Ref. [26]. Thus, they can form a basis{|ψnm〉}that can be used for joint measurement of the twoqutrit state.

The authors in Ref. [43] gives the following expression for ann-particle high-dimensional quantum state:

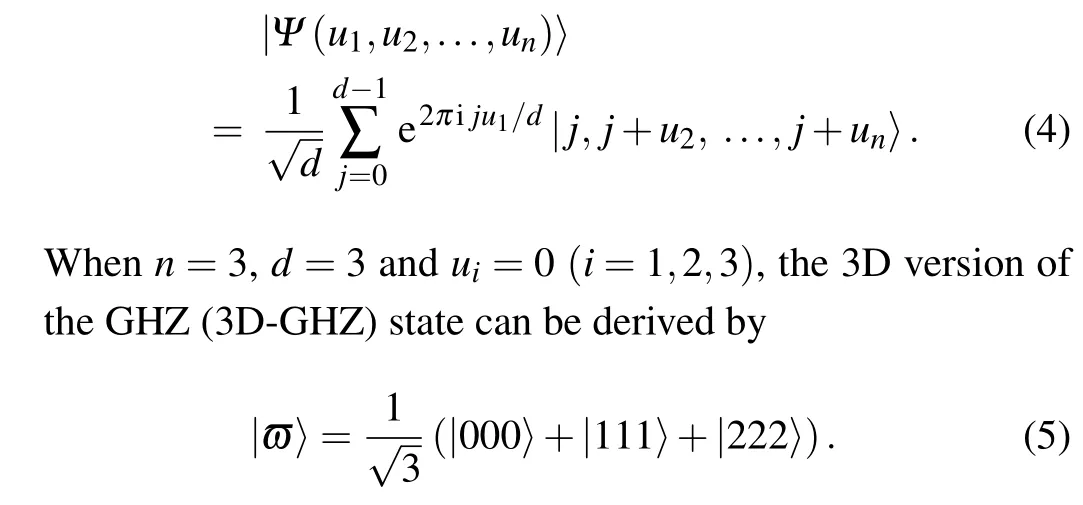
2.2. Measurement bases and unitary operations

In this subsection, some basic measurement bases and unitary operations,which are essential to transmissions of the qutrit state,are introduced.

2.2.1. The 3D-Z-basis and 3D-X-basis

Measurement bases for the 3D quantum system, analogous to theZ-basis andX-basis used for measurement in a 2D quantum system,are defined as

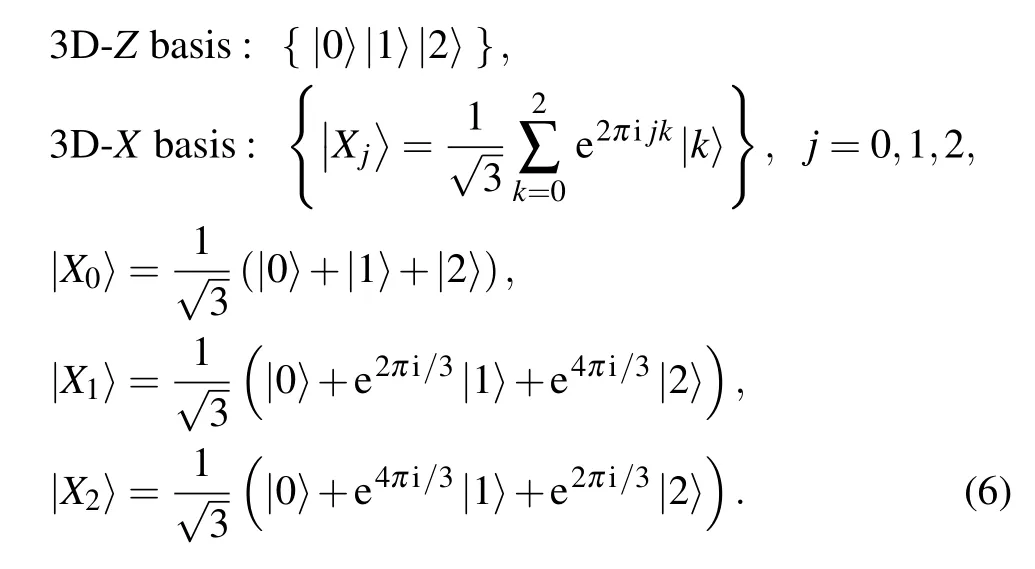
2.2.2. 3D-Hadamard transform

When influenced by the transform, a qutrit state can be changed from an initial computation basis state to a superposition state as follows:

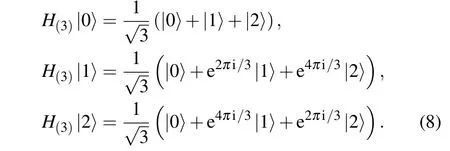
2.2.3. 3D-controlled NOT gate

In a 3D quantum system, a 3D-controlled NOT gate(CNOT(3))can be expressed by

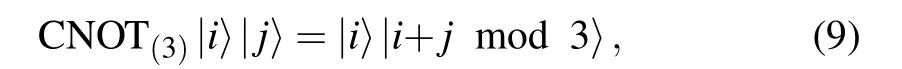
where|i〉is the controlled qutrit, and|j〉is the target qutrit.The following expressions can be derived from Eq.(9):

2.3. Weyl operators

Pauli operators are important operators in a 2D quantum system that are often used as transformations of a qubit state.The analogous operators in a high-dimensional quantum system are Weyl operators, which can be used to transform a high-dimensional quantum state. Weyl operators can be defined as[45]

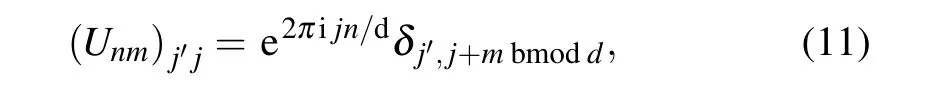
wheredis the dimension of the quantum system, andn,m,j,j＇=0,1,...,d ?1. Whend=3, nine Weyl operators for the 3D quantum system are obtained as

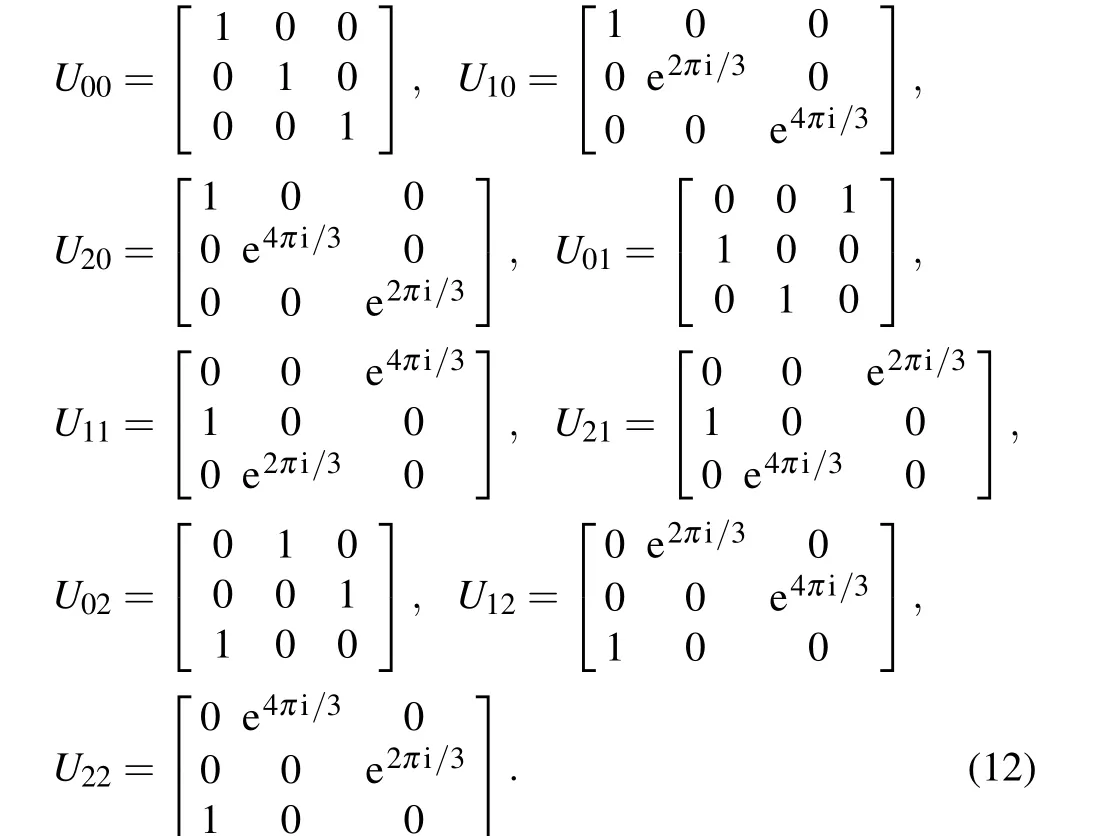
When influced byUnm, any 3D-Bell state can be derived from|ψ00〉by[44]

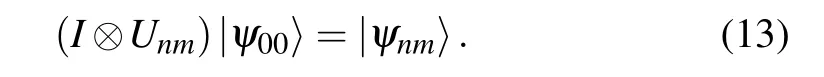
3. 3D-CQT scheme

In this section,we describe an ideal 3D controlled quantum teleportation (3D-CQT) scheme for an unknown singlequtrit state. The scheme involves three distant parties, Alice,Bob,and Charlie.Suppose that Alice(sender)intends to transmit an unknown single-qutrit state|?〉ato Bob(receiver). Bob can successfully receive the state only when the communication gets permission from Charlie(controller). The teleported state|?〉acan be expressed by

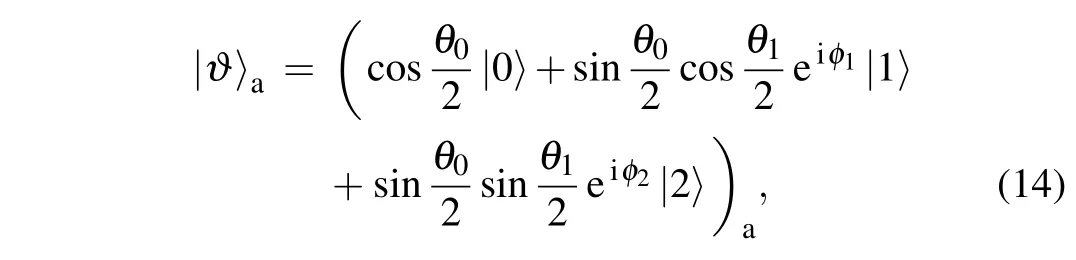
whereθ0,θ1∈[0,π]andφ1,φ2∈[0,2π].

To accomplish communication, Alice, Bob, and Charlie have to share an entangled state as the quantum channel. According to the principle of quantum teleportation,a three-qutrit entangled state is suitable for the scheme. Assume that the entangled state is a maximally entangled 3D-GHZ state described by

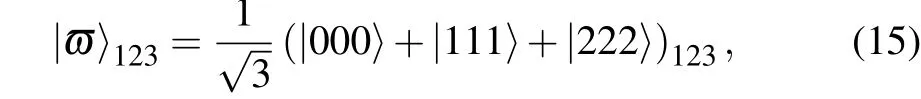
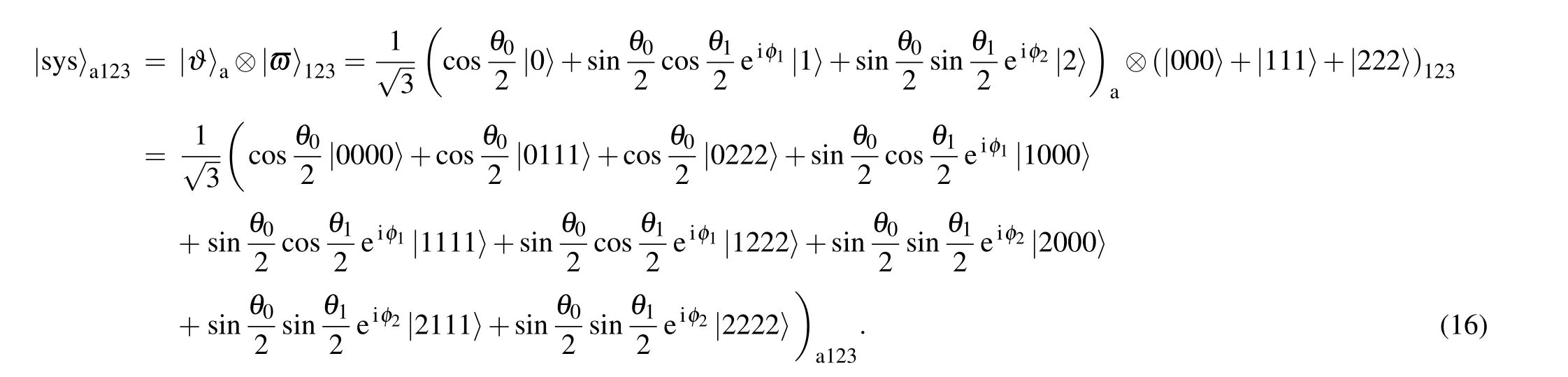
where qutrit 1 belongs to Alice, qutrit 2 to Bob, and qutrit 3 to Charlie. The entangled state|?〉123can be prepared using three qutrits with initial state|0〉?3and local unitary operationsH(3)and CNOT(3). The corresponding preparation circuit is shown in Fig.1.

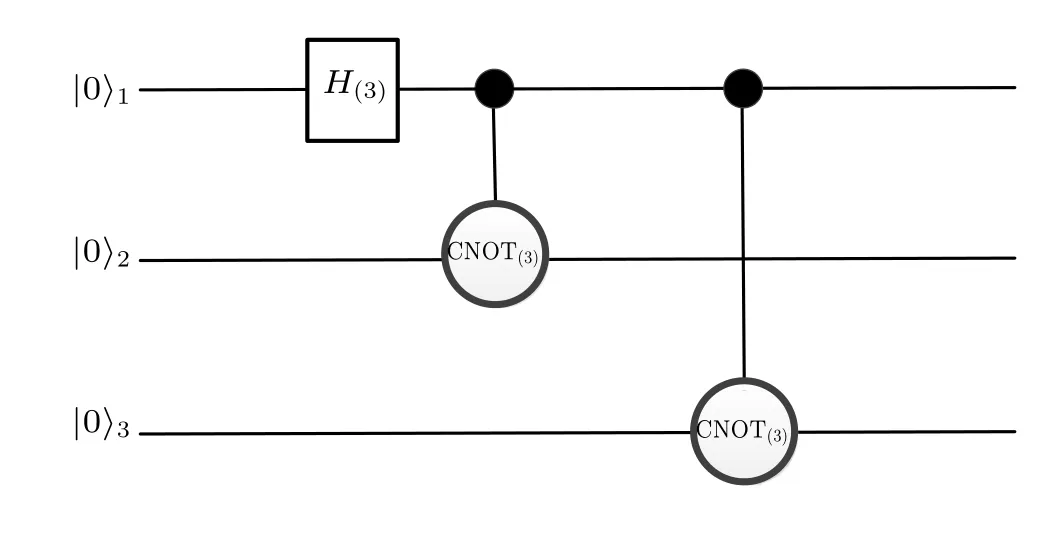
Fig.1. The quantum circuit for 3D-GHZ state preparation.

The state of the complete quantum system consisting of the teleported state|?〉aand the entangled state|?〉123is given by

Three steps in the scheme implementation are described as follows.

Step 1 Alice performs a joint 3D-Bell basis measurement on qutrits a and 1. The measurement result is one of the nine random 3D-Bell states with equal probability 1/9. There are similarly nine possibilities for the collapsed states of qutrits 2 and 3,which can be expressed as

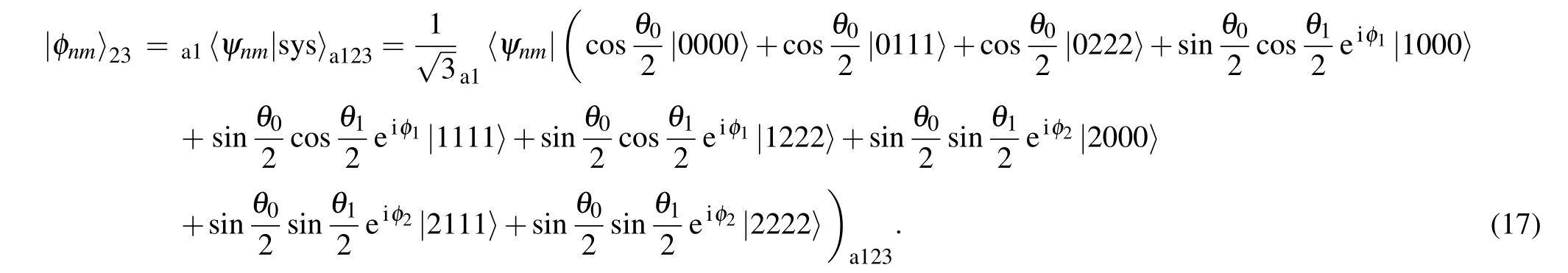
After the measurement,Alice encodes the result in classical bits and sends it to Bob via the classical channel.

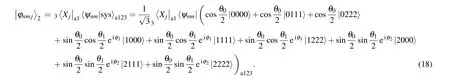
Similarly to Alice,Charlie also needs to send his measurement to Bob through the classical channel.

Step 3 Finally, based on the measurement results received from Alice and Charlie, Bob can construct the desired state|?〉aby applying the appropriate unitary transformation on qutrit 2. For example,if Alice and Charlie’s measurement results are|ψ10〉a1and|X1〉3,the collapsed state of qutrit 2 is given by(the global phase is omitted)

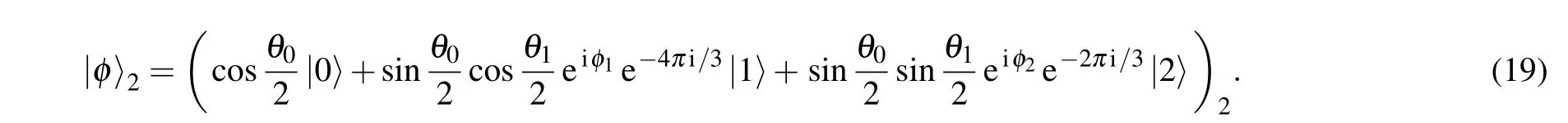
Bob can reconstruct the desired state|?〉aby performing the unitary transformationU20on qutrit 2.The three steps described above show that there are 27 possible measurements that Alice and Charlie can make. Table 1 shows all of these measurements,the collapsed states of qutrit 2,and corresponding unitary operations performed by Bob to reconstruct the teleported state|?〉a.

Table 1. Possible measurement results,collapsed states of qutrit 2,and unitary operations.

4. 3D-Pauli-like noise

Pauli noise is the most common type of quantum noise in a 2D quantum system. It can be bit-flip noise, phase-flip noise,bit-phase-flip noise,or depolarizing noise. The type of noise depends on the Pauli operator. In a 3D quantum system,the analogous Pauli noise,which we call 3D-Pauli-like noise,can be trit-flip noise,t-phase-flip noise,trit-phase-flip noise,or t-depolarizing noise. The type of noise depends on the Weyl operator(Eq.(12)). These types of noise are briefly described using Kraus operators.

4.1. Trit-flip

This type of noise is analogous to bit-flip for a qubit.Tritflip can be considered as an operator that causes the computation basis state|j〉(j=0,1,2)to flip either to one of the states|j+1 mod 3〉or|j+2 mod 3〉with probabilitypor remain unchanged with probability 1?p. The corresponding Kraus operators are given blow:

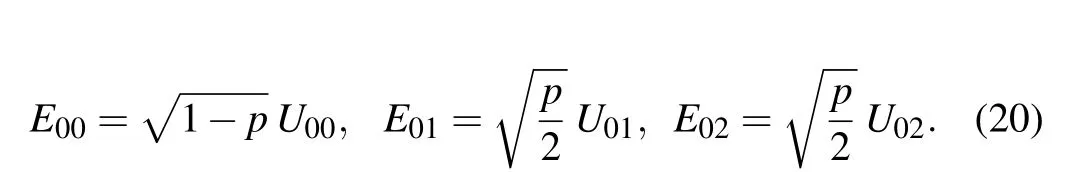
4.2. T-phase-flip

This type of noise is analogous to phase-flip for a qubit.It describes the loss of information in a qutrit without energy dissipation. In a t-phase-flip,the state|j〉(j=0,1,2)will either undergo one of the phase shifts e2πi/3|j〉or e4πi/3|j〉with probabilitypor remain unchanged with probability 1?p.The corresponding Kraus operators are

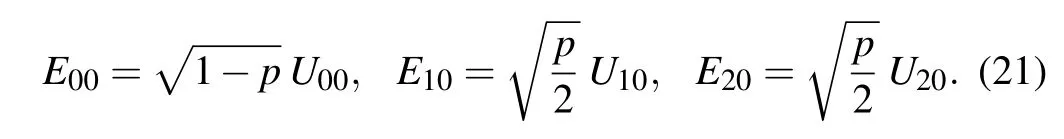
4.3. Trit-phase-flip

This type of noise is analogous to bit-phase-flip for a qubit.It is a compound noise consisting of trit-flip and t-phaseflip. In a trit-phase-flip,a qutrit may simultaneously undergo a flip and a phase shift. The corresponding Kraus operators are

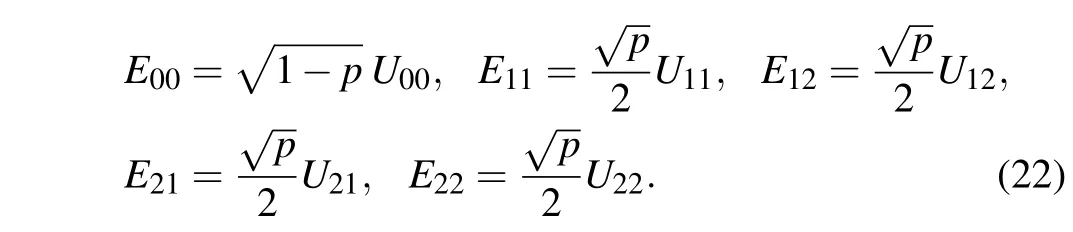
4.4. T-depolarizing

This type of noise is analogous to depolarizing for a qubit.T-depolarizing will change an arbitrary qutrit state to a maximally mixed stateI3/3. The corresponding Kraus operators are

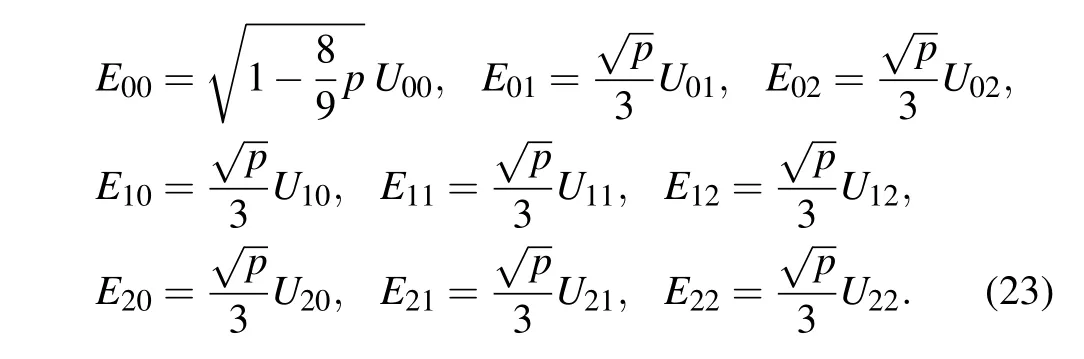
5. Scheme in 3D-Pauli-like noise channels with memory

In this section,it is assumed that the 3D-GHZ state|?〉123is the quantum channel and that it is prepared on Charlie’s side. Charlie keeps possession of qutrit 3,and sends qutrit 1 to Alice and qutrit 2 to Bob via quantum channels. It is also assumed that during transmissions, both qutrits are affected by 3D-Pauli-like noise. After the qutrits have been transmitted,the evolution of the state|?〉123under the influence of 3DPauli-like noise can be expressed by the density operator as

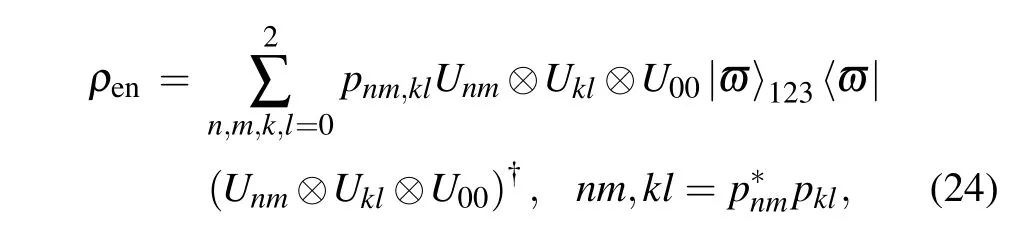
where noise parameterspnmandpklare interpreted as the probabilities of the operatorsUnmandUklacting on qutrits 1 and 2. Equation (24) shows that each qutrit passes independently through the 3D-Pauli-like noisy channel. This type of channel is often considered to be memoryless(an uncorrelated channel).However,in realistic communication,if qutrits 1 and 2 are transmitted with a very short time interval between them in a noisy channel,there is some degree of correlation between the two uses of the channel. Thus,the channel can be considered to be a channel with memory. In this work, we assume that the correlation is Markovian,which can be defined by

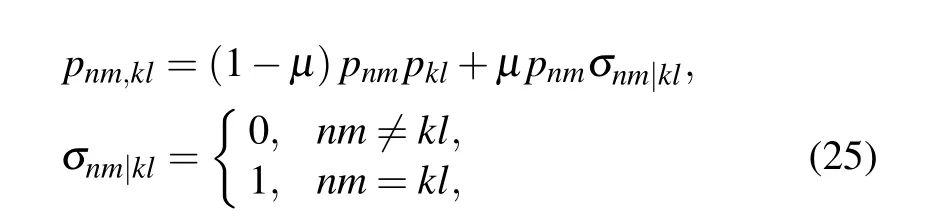
where the parameterμ(0≤μ ≤1) represents the degree of memory. Equation (25) shows that the same operator is applied to both qutrits with probabilityμ,and that the two operators are not correlated with probability(1?μ). The progress of qutrits 1 and 2 through the 3D-Pauli-like noise channel with memory is shown in Fig.2.

According to Eq.(25),ρencan be rewritten as

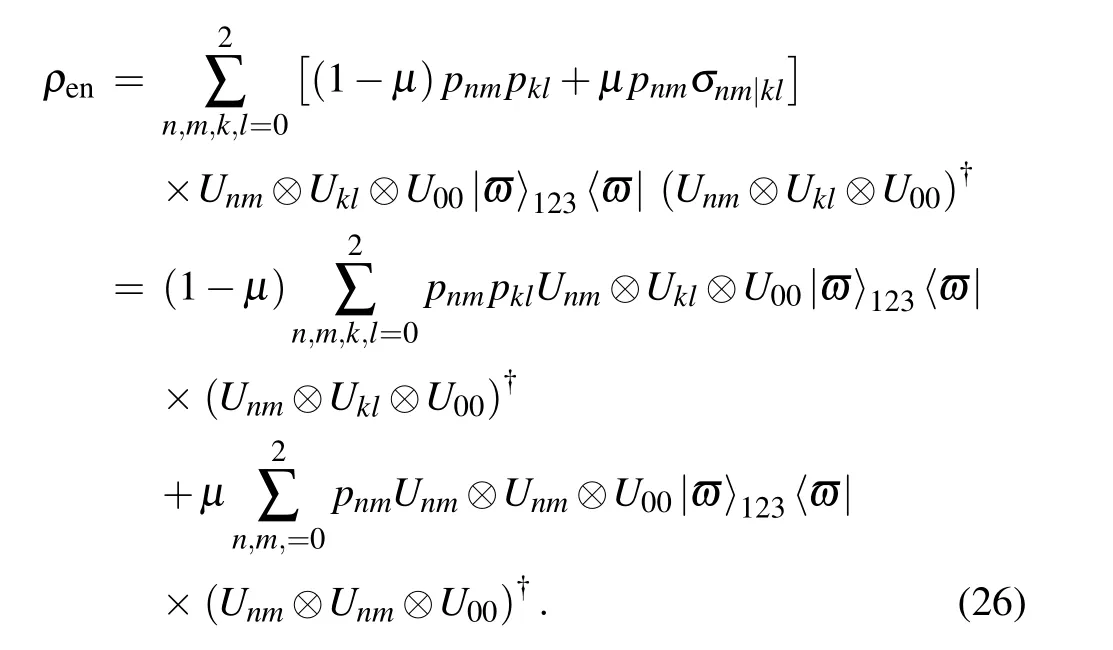
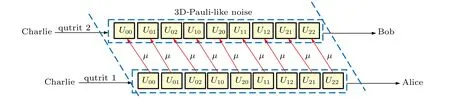
Fig.2. The progress of qutrits 1 and 2 through a 3D-Pauli-like noisy channel with memory,where Unm,(n,m=0,1,2)is the Weyl operator,and μ is the degree of memory.

Note that whenμ=0 the channel will become a memoryless channel,and whenμ=1 the channel will have perfect memory.

Using the implementation of quantum teleportation introduced in Section 3 through the channelρen,after the measurement operations and unitary transformations, Bob can obtain the output state given by the density operator

Mean fidelity is defined in terms of all possible measurement results as

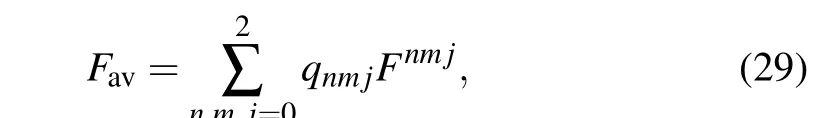
whereqnmjis the probability that the output stateρnmjoutoccurs.Favdepends mainly on the coefficients of the teleported state|?〉aand so it is more convenient to calculate the average fidelity over the set of input states[31,42]

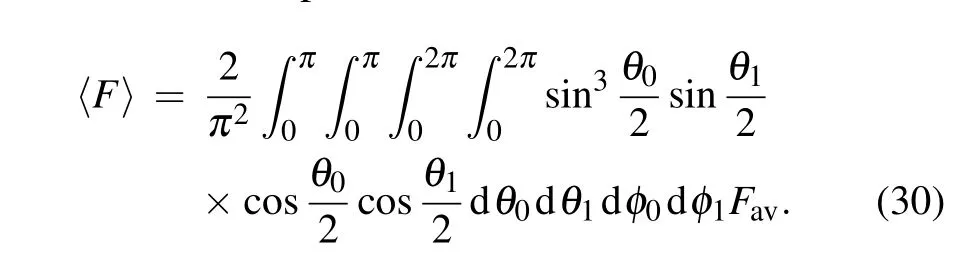
In the following subsection, we consider the 3D-CQT scheme for four types of 3D-Pauli-like noise(trit-flip,t-phaseflip,trit-phase-flip,and t-depolarizing)in channels with memory. For each type of memory in the noisy channel, the relationships between fidelity, memory and noise parameters, as well as classical fidelity,will be determined.

5.1. Calculation of fidelities

By using the Kraus operators for the four types of 3DPauli-like noise(Eqs.(20)–(23)), channel noise for each type of noise in a channel with memory can be defined by setting noise parameterspi j(i,j=0,1,2)in Eq.(26). Trit-flip noise in a memory channel is given by setting noise parametersp00=1?p,p01=p02=p/2, andp10=p11=p12=p20=p21=p22= 0. T-phase-flip noise in a memory channel is given by setting noise parametersp00= 1?p,p10=p20=p/2,andp01=p02=p11=p12=p21=p22=0. Trit-phase-flip noise in a memory channel is given by setting noise parametersp00=1?p,p11=p12=p21=p22=p/4, andp01=p02=p10=p20=0. T-depolarizing noise in a memory channel is given by setting noise parametersp00=1?8p/9 andp01=p02=p10=p20=p11=p12=p21=p22=p/9. The average fidelity is easily calculated using the equation given in Ref.[41]

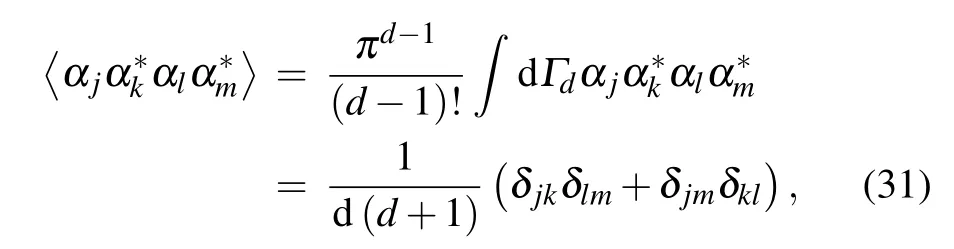
wheredis the dimension of the quantum system,αi(i=0,1,...,d ?1)is the coefficient of the teleported state,α?iis the complex conjugate ofαi,and dΓdis an invariant volume element given by

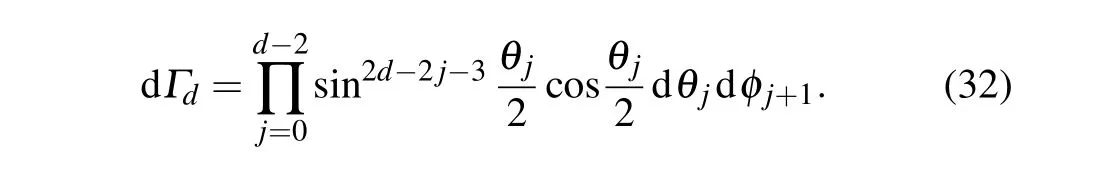
Whend=3,the three coefficients of the teleported state are

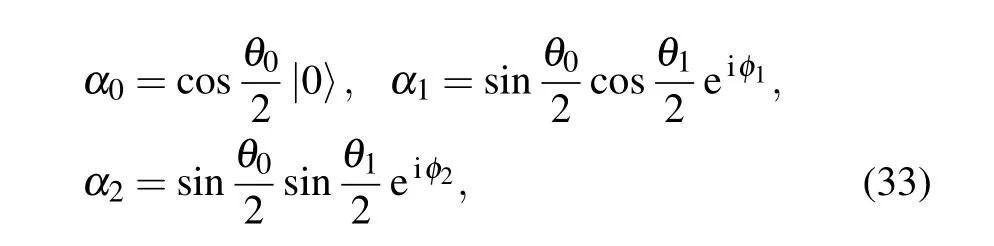
and,according to Eq.(32), dΓ3is given by

These results are used in calculating the average fidelity(Eq.(30)).Equations(26)–(30),with the help of Eq.(31),give the average fidelity of teleportation for each of the four types of noise in a channel with memory

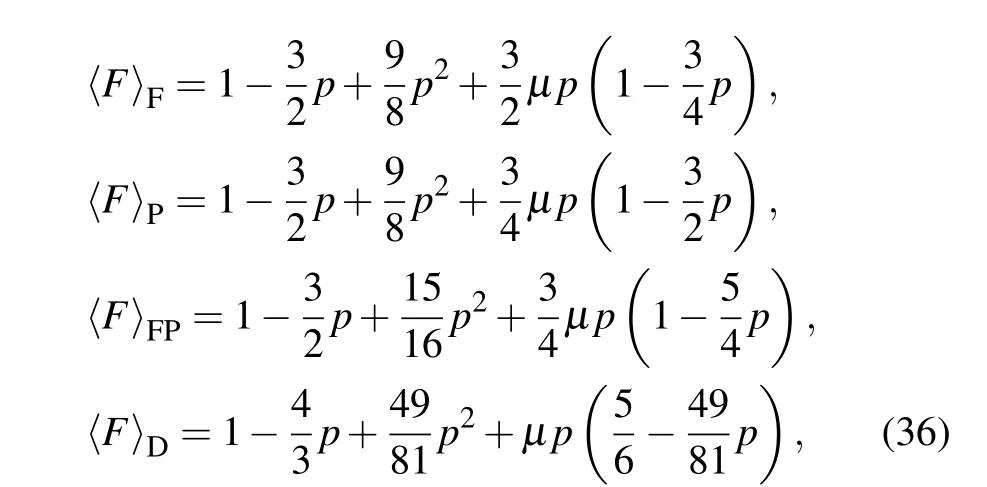
for 0≤u,p ≤1, where〈F〉Fis the average fidelity for the channel with trit-flip noise,〈F〉Pfor t-phase-flip noise,〈F〉FPfor trit-phase-flip noise,and〈F〉Dfor t-depolarizing noise.

5.2. Analysis of the effect of memory on the average fidelity

In this subsection, we examine the effect of memory on the average fidelity for each type of channel noise. Using the equations for〈F〉F,〈F〉P,〈F〉FP, and〈F〉Dgiven in Eq. (36),the corresponding partial derivatives over parameteruare

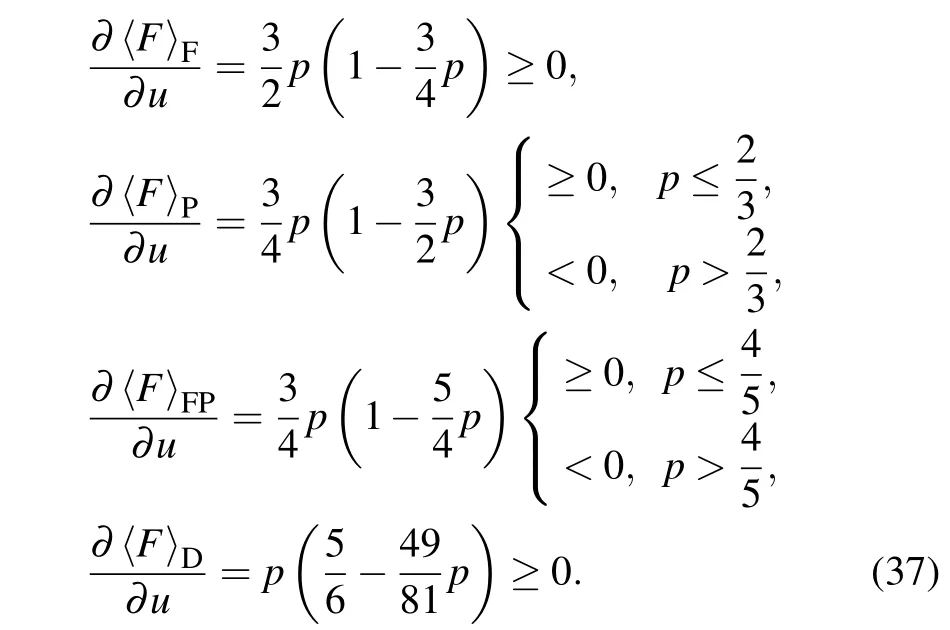
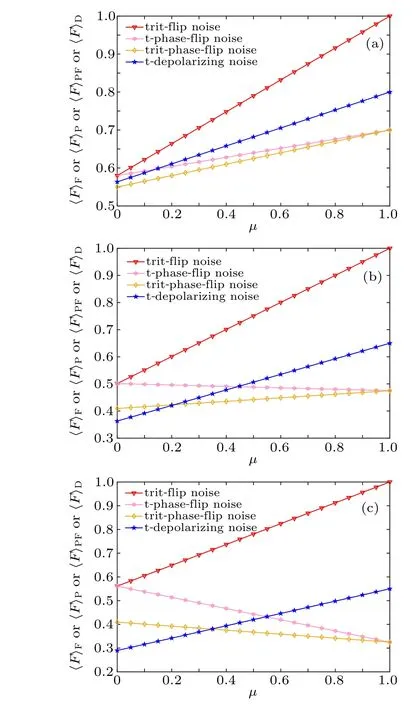
Fig. 3. The relationship between the average fidelity and the memory parameter(μ): (a) p=0.4,(b) p=0.7,and(c) p=0.9.

Equation (37) shows that average fidelities〈F〉Fand〈F〉Dincrease as the memory parameter increases regardless of the noise parameter. However,for average fidelities〈F〉Pand〈F〉FP, we observe respective threshold values (p=2/3 andp=4/5) derived from Eq. (32).〈F〉Pand〈F〉FPincrease as the memory parameter increases only when the noise parameter is below the corresponding threshold value.In other words,for trit-flip noise and t-depolarizing noise,teleportation accuracy can be improved by increasing the value of channel memory even for the strongest noise. However,for t-phase-flip and trit-phase-flip noise, the accuracy of teleportation can be improved by increasing the value of channel memory only if the noise parameter satisfies a certain condition. Figure 3 gives the relationship between the average fidelity and the memory parameter for the three casesp=0.4,p=0.7,andp=0.9.

Figure 3 shows that in all cases, the average fidelity increases as the memory parameter increases whenp= 0.4.However, the average fidelity〈F〉Pdecreases as the memory parameter increases whenp=0.7, and the average fidelities〈F〉Pand〈F〉FPdecrease as the memory parameter increases whenp=0.9.

Fidelityfc=1/2 is known in a 3D quantum system as classical fidelity.[46]It is interesting to make a comparison between 3D average fidelity and classical fidelity. The relationship between average fidelity, memory parameter, and noise parameter, together with classical fidelity for each type of noisy channel is shown in Fig.4.Figures 4(a)–4(d)show the trit-flip channel noise, t-phase-flip channel noise, trit-phaseflip channel noise, and t-depolarizing channel noise, respectively. The grey grid represents the classical fidelity,fc=1/2.

We derive the following conclusions from inspecting Fig.4

i)Trit-flip noise

Figure 4(a) shows that whenμ=0 (i.e., the channel is memoryless),the average fidelity〈F〉Finitially decreases and then increases as the noise parameterpincreases,and reaches the minimum value 1/2 (equal to classical fidelityfc) whenp ≈0.7. However, whenμ ＞0 (i.e., the channel has memory),〈F〉Fis always larger than 1/2. Whenμ=1,〈F〉Fis always at a maximum value 1,regardless ofp. This observation confirms that memory in the trit-flip noisy channel improves the efficiency of the teleportation scheme and that the scheme becomes immune to trit-flip noise when there is the strongest correlation between two successive uses of the channel.

ii) T-depolarizing noise

Figure 4(d)shows that in the case〈F〉D=1/2,the noise parameterpincreases as the memory parameterμincreases.Whenμ=1,〈F〉Dis not always less than 1/2. This observation shows that memory increases the robustness of the scheme for t-depolarizing noise.

iii) T-phase-flip noise and trit-phase-flip noise

Figures 4(b) and 4(c) show that there are some regions where〈F〉Pand〈F〉FPare belowfcand that the regions do not change significantly as the memory parameter increases. That is,an increase in memory does not increase resistance to these types of noise as it does for the other two types of noise.

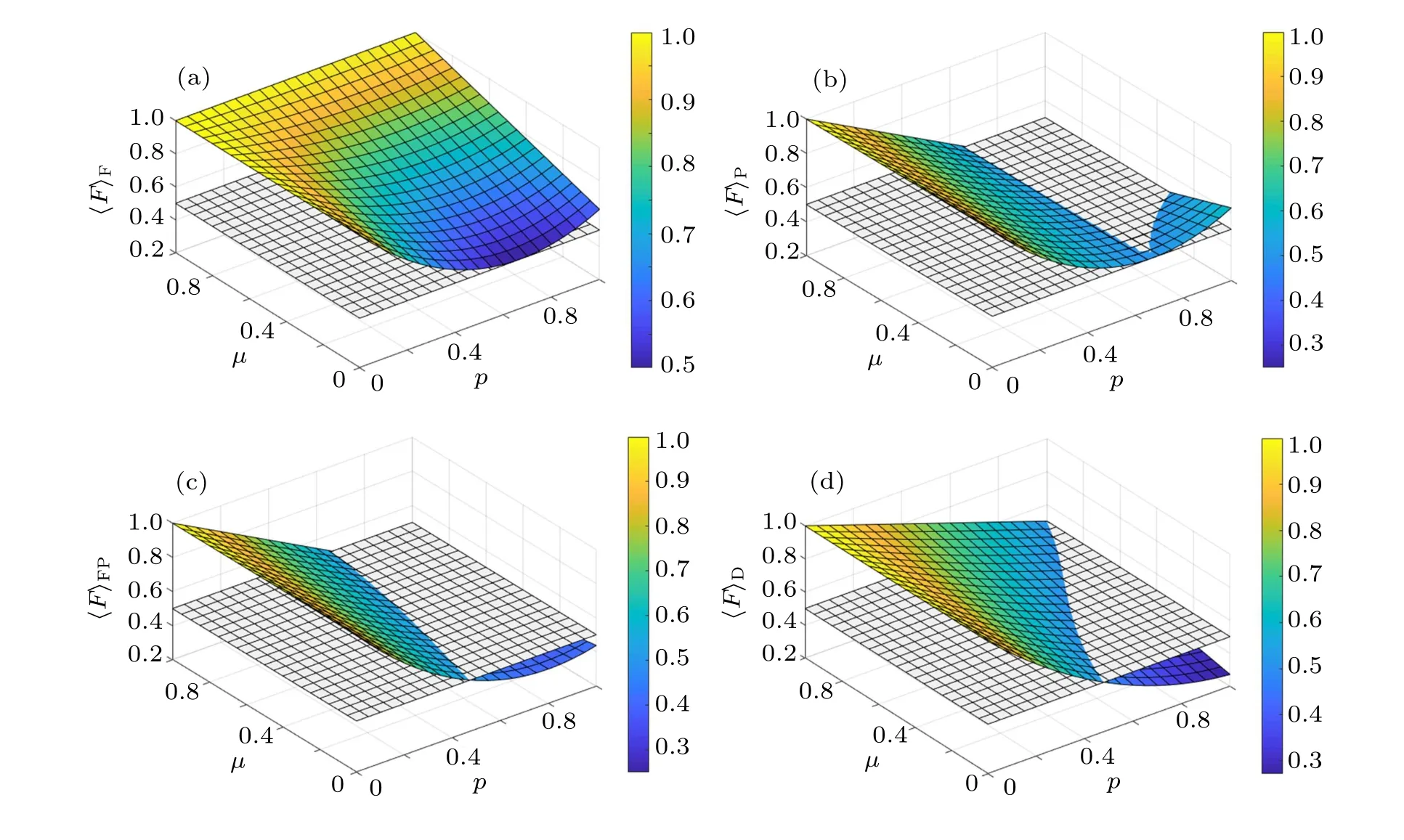
Fig.4. The relationship between 3D average fidelity and the parametersμ and p together with classical fidelity.

6. Conclusions

A controlled quantum teleportation scheme in a 3D quantum system was proposed.Alice transmits an unknown singlequtrit state to Bob under the control of Charlie in a pre-shared 3D GHZ state. An ideal implementation of the scheme was introduced. Noise is an unavoidable factor in a realistic implementation that reduces the fidelity of teleportation. The scheme was described in a realistic environment with noisy channels. Four types of 3D-Pauli noise(trit-flip, t-phase-flip,trit-phase-flip, and t-depolarizing) were introduced, respectively. Our work is different from other existing studies in introducing memory in channels. Relationships between the average fidelity of teleportation with memory and noise parameters were determined, and the values of average fidelity obtained were compared with classical qubit fidelity. The results showed that memory in a channel can increase the average fidelity for trit-flip and t-depolarizing noises but cannot for t-phase-flip and trit-phase-flip noises,above a certain noise threshold. This work introduces a novel approach to increasing the efficiency of high-dimensional teleportation.