INHERITANCE OF DIVISIBILITY FORMS A LARGE SUBALGEBRA?
Qingzhai FAN(范慶齋)
Department of Mathematics Shanghai Maritime University,Shanghai 201306,China E-mail:qzfan@shmtu.edu.cn
Xiaochun FANG(方小春)Xia ZHAO(趙霞)
Department of Mathematics Tongji University,Shanghai 200092,China E-mail:xfang@mail.#edu.cn;1710383@#edu.cn
Abstract Let A be an infinite dimensional stablyfinite unital simple separable C?-algebra.Let B?A be a stably(centrally)large subalgebra in A such that B is m-almost divisible(m-almost divisible,weakly(m,n)-divisible).Then A is 2(m+1)-almost divisible(weakly m-almost divisible,secondly weakly(m,n)-divisible).
Key words C?-algebras;large subalgebra;Cuntz semigroup
1 Introduction
Large and stably large subalgebra were introduced in[1]by Phillips as an abstraction of Putnam’s orbit breaking subalgebra of the crossed product C(X,Z,σ)of the Cantor set by a minimal homeomorphism in[2].The Putnam subalgebra played a key role in[3],in which it is proved that C(X,Z,σ)has tracial rank zero whenever this property is consistent with its K-theory and dim(X)<∞.Let X be a compact Hausdor ffspace and let h:X→X be a minimal homeomorphism.Let Y?X be a compact subset such that h(Y)∩Y=?for all positive integer n.Phillips showed that C(Z,X,h)is a stably large subalgebra of C(Z,X,h)in[1].In[1],Phillips also showed that for an infinite dimensional simple unital C-algebra A and a stably large subalgebra B?A,
(1)B is simple and infinite dimensional,
(2)If B is stablyfinite then so is A,and if B is purely infinite,then so is A,
(3)The restriction maps T(A)→T(B)and QT(A)→QT(B)(on tracial states and quasitraces)are bijective,
(4)When A is stablyfinite,the inclusion of B in A induces an isomorphism on the semigroups that remain after deleting from Cu(B)and Cu(A)all the classes of nonzero projections,
(5)When A is stablyfinite,B and A have the same radius of comparison.
In[4],Archey and Phillips defined centrally large subalgebras,and they proved that if B is centrally large in A and B has stable rank one,then so does A.In[5],Archey,Buck and Phillips proved that if A is a simple infinite dimensional stably finite unital C-algebra and B ?A is a centrally large subalgebra,then A is tracially Z-absorbing in the sense of [6]if and only if B is tracially Z-absorbing.Using the result of [5],Elliott and Niu in [7]showed that letting X be a compact metrizable space space and letting σ :X →X be a minimal homeomorphism,if we suppose that(X;σ)has a zero mean topological dimension,then the associated C-algebra C(Z,X,σ) is Z-absorbing.Elliott and Niu in [8]used large subalgebras to extended rotation algebras,and showed an application of large subalgebras beyond dynamical system setting.
In the quest to classify simple separable nuclear C-algebras,as suggested by Elliott,it has become necessary to invoke some regularity properties of the C-algebras.There are three regularity properties of particular interest:tensorial absorption of the Jiang-Su algebra Z,also called Z-stability;the finite nuclear dimension;and strict comparison of positive elements.The latter can be reformulated as an algebraic property of the Cuntz semigroup,which is referred to as almost unperforated.Winter and Toms have conjectured that these three fundamental properties are equivalent for all separable,simple,nuclear C-algebras.
In [9],we study the comparison properties of C-algebras.We show that if B is centrally large in A and B has a certain comparison property,then A has the same comparison property.
In this article,we study the divisible properties of C-algebras,and we demonstrate the following theorem:
Theorem 1.1
Let A be an infinite dimensional stably finite unital simple separable C-algebra.Let B ?A be a stably (centrally) large subalgebra in A such that B is m-almost divisible (m-almost divisible,weakly (m,n)-divisible).Then A is 2(m+1)-almost divisible(weakly m-almost divisible,secondly weakly (m,n)-divisible).2 Preliminaries and Definitions




Let A be a stably finite unital C-algebra.Recall that a positive element a ∈A is called purely positive if a is not Cuntz equivalent to a projection.This is equivalent to saying that 0 is an accumulation point of σ(a) (recalling that σ(a) denotes the spectrum of a).
Given a in M(A)and ε>0,we denote by (a ?ε)the element of C(a) corresponding(via the functional calculus) to the function f(t)=max(0,t ?ε),t ∈σ(a).By the functional calculus,it follows in a straightforward manner that ((a ?ε)?ε)=(a ?(ε+ε)).
The following theorem is well known:
Theorem 2.1
(see [11]) Let A be a stably finite C-algebra.Then,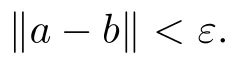
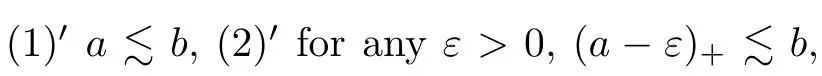

The property of m-almost divisible was introduced by Robert and Tikuisis in [12].
Definition 2.2
(see [12]) Let m ∈N.We say that A is m-almost divisible if for each a ∈W(A),k ∈N and ε>0,there exists b ∈W(A)such that kb ≤a and(a?ε)≤(k+1)(m+1)b.Definition 2.3
Let m ∈N.We say that A is weakly m-almost divisible if for each a ∈W(A),k ∈N and ε >0,there exists b ∈W(A) such that kb ≤a+a and (a ?ε)≤(k+1)(m+1)b.The property of weakly (m,n)-divisible was introduced by Kirchberg and Rordam in [13].
Definition 2.4
(see [13]) Let A be a unital C-algebra.Let m,n ≥1 be integers.A is said to be weakly (m,n)-divisible,if for every u in W(A) and any ε >0,there exist elements x,x,···,x∈W(A)such that mx≤u for all j=1,2,···,n and(u?ε)≤x+x+···+x.Definition 2.5
Let A be unital C-algebra.Let m,n ≥1 be integers.A is said to be secondly weakly (m,n)-divisible if for every u in W(A) and any ε >0,there exist elements x,x,···,x∈W(A) such that mx≤u+u for all j=1,2,···,n and (u ?ε)≤x+x+···+x.Large and stably large subalgebra were introduced in [1]by Phillips.

(1) 0 ≤g ≤1;

(3) For j=1,2,···,m we have (1 ?g)c∈B;


Definition 2.7
(see [1]) Let A be an infinite dimensional simple unital C-algebra.A unital subalgebra B ?A is said to be stably large in A if M(B) is large in M(A) for all integers n ∈N.Centrally large and stably centrally large subalgebras were introduced in[4]by Archey and Phillips.

(1) 0 ≤g ≤1;

(3) For j=1,2,···,m we have (1 ?g)c∈B;


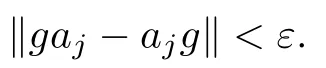
Definition 2.9
(see [4]) Let A be an infinite dimensional simple unital C-algebra.A unital subalgebra B ?A is said to be stably centrally large in A if M(B) is large in M(A)for all integer n ∈N.The following two Theorems are Lemma 1.7 and Lemma 2.7 in [1]:

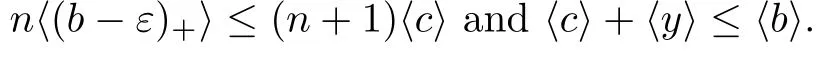
3 The Main Results
Theorem 3.1
Let A be an infinite dimensional stably finite unital simple separable C-algebra.Let B ?A be a stably large subalgebra in A such that B is m-almost divisible.Then A is 2(m+1)-almost divisible.
We may assume that a ∈A.By Theorem 2.11,there exist c ∈Aand a non-zero element y ∈Asuch that
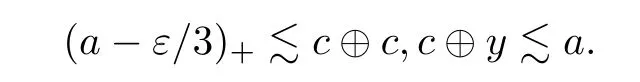

(1) 0 ≤g ≤1,

(2) (1 ?g)c(1 ?g)∈B,and
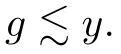
By Theorem 2.10,we have
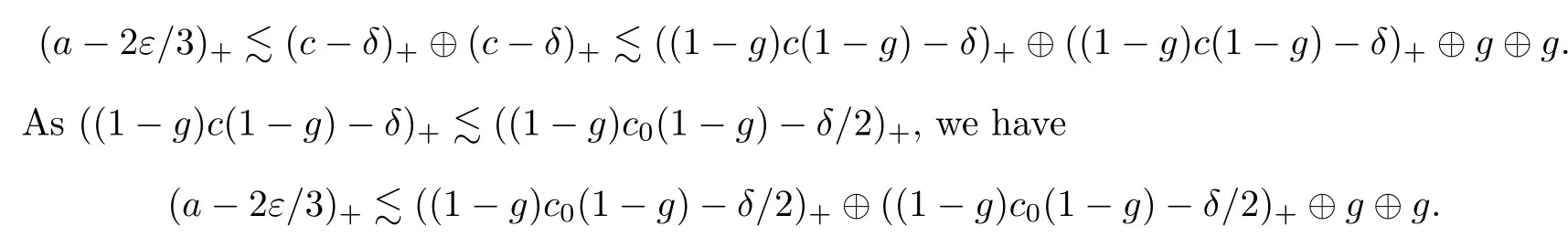

Theorem 3.2
Let A be an infinite dimensional stably finite unital simple separable C-algebra.Let B ?A be a stably centrally large subalgebra in A such that B is m-almost divisible.Then A is weakly m-almost divisible.
With F={a} and any ε>0,since B ?A is a stably centrally large subalgebra of A,there exists g ∈B such that
(1) 0 ≤g ≤1,
(2) (1 ?g)a(1 ?g)∈B,and


Case (1)
We assume that (a?3ε)is Cuntz equivalent to a projection.(1.1) We assume that (a?4ε)is Cuntz equivalent to a projection.

With F={a} and any ε>0,since B ?A is a stably centrally large subalgebra of A,there exists g∈B such that
(1)0 ≤g≤1,
(2)(1 ?g)a∈B,
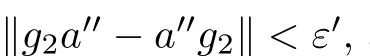
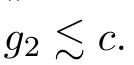



With F={a} and any ε>0,since B ?A is a stably centrally large subalgebra of A,there exists g∈B such that


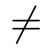

We may assume a ∈A.
With F={a} and any ε>0,since B ?A is a stably centrally large subalgebra of A,there exists g ∈B such that
(1) 0 ≤g ≤1,
(2) (1 ?g)a(1 ?g)∈B,and
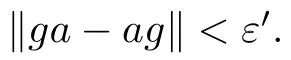



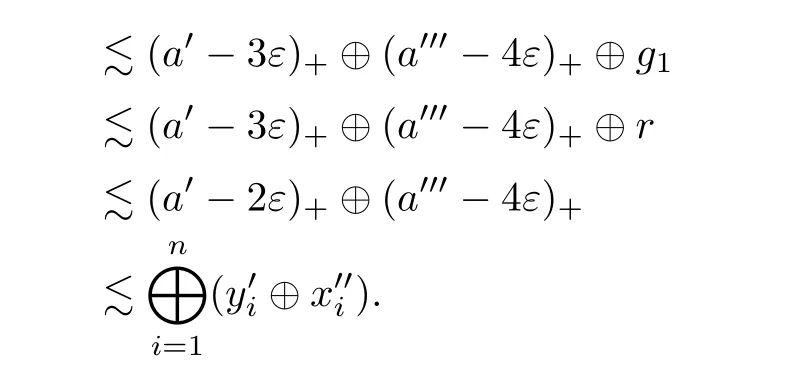
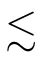
With F={a} and any ε>0,since B ?A is a stably centrally large subalgebra of A,there exists g∈B such that
(1)0 ≤g≤1,
(2)(1 ?g)a∈B,
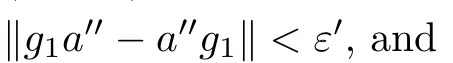



With F={a} and any ε>0,since B ?A is a stably centrally large subalgebra of A,there exists g∈B such that
(1)0 ≤g≤1,
(2)(1 ?g)a∈B,
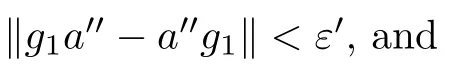



 Acta Mathematica Scientia(English Series)2021年1期
Acta Mathematica Scientia(English Series)2021年1期
- Acta Mathematica Scientia(English Series)的其它文章
- ON THE MIXED RADIAL-ANGULAR INTEGRABILITY OF MARCINKIEWICZ INTEGRALS WITH ROUGH KERNELS?
- THE LOCAL WELL-POSEDNESS OF A CHEMOTAXIS-SHALLOW WATER SYSTEM WITH VACUUM?
- UNDERSTANDING SCHUBERT’S BOOK(I)?
- GLEASON’S PROBLEM ON FOCK-SOBOLEV SPACES?
- THE EXISTENCE AND STABILITY OF STATIONARY SOLUTIONS OF THE INFLOW PROBLEM FOR FULL COMPRESSIBLE NAVIER-STOKES-POISSON SYSTEM?
- ON THE CAUCHY PROBLEM FOR AW-RASCLE SYSTEM WITH LINEAR DAMPING?
