CROSSED PRODUCTS BY FINITE GROUP ACTIONS WITH CERTAIN TRACIAL ROKHLIN PROPERTY?
Qingzhai Fan(范慶齋)
Department of Mathematics,Shanghai Maritime University,Shanghai 201306,China E-mail:fanqingzhai@fudan.edu.cn;qzfan@shmtu.edu.cn
Xiaochun Fang(方小春)
Department of Mathematics,Tongji University,Shanghai 200092,China E-mail:xfang@mail.#edu.cn
Abstract We introduce a special tracial Rokhlin property for unital C?-algebras.Let A be a unital tracial rank zero C?-algebra(or tracial rank no more than one C?-algebra).Suppose that α :G → Aut(A)is an action of a finite group G on A,which has this special tracial Rokhlin property,and suppose that A is a α-simple C?-algebra.Then,the crossed product C?-algebra C?(G,A,α)has tracia rank zero(or has tracial rank no more than one).In fact,we get a more general results.
Key words C?-algebras;Rokhlin property;crossed product C?-algebra
1 Introduction
The Elliott program for the classification of amenable C?-algebras might be said to have begun with the K-theoretical classification of AF-algebras in[1].Since then,many classes of C?-algebras have been classified by the Elliott invariant.Among them,one important class is the class of simple unital AH-algebras without dimension growth(the real rank zero case,cf[2],and general case cf[3]).To axiomatize Elliott-Gong’s decomposition theorem for real rank zero AH algebras(classified by Elliott-Gong in[2])and Gong’s decomposition theorem(cf[4])for simple AH algebras(classified by Elliott-Gong-Li in[3]),Huaxin Lin introduce the concept of TAF and TAI([5,6]).Instead of assuming inductive limit structure,he started with a certain abstract approximation property,and showed that C?-algebras with this abstract approximation property and certain additional properties are AH-algebras without dimension growth.More precisely,Lin introduced the class of tracially approximate interval algebras(also called C?-algebras of tracial topological rank one).
Inspired by Lin’s tracial approximation by interval algebras in[6],Elliott and Niu in[7]considered tracial notion of approximation by other classes of C?-algebras.Let ? be a class of unital C?-algebras.Then,the class of C?-algebras which can be tracially approximated by C?-algebras in ?,denoted by TA?,is defined as follows.A simple unital C?-algebra A is said to belong to the class TA? if for any ε>0,any finite subset F ? A,and any element a≥ 0,there exist a projection p∈A and a C?-subalgebra B of A with 1B=p and B ∈ ?,such that
(1)kxp?pxk<ε for all x∈F;
(2)pxp∈εB for all x∈F;
(3)1?p is Murray-von Neumann equivalent to a projection in
Also inspired by Lin’s non-simple tracial approximation C?-algebras in[5,6],the present author and Fang considered non-simple C?-algebras tracially approximated by certain C?-algebras in[8].Let ? be a class of unital C?-algebras.Then,the class of C?-algebras which can be tracially approximated by C?-algebras in ?,denoted still by TA?,is defined as follows.A unital C?-algebra A is said to belong to the class TA? if for any positive numbers 0< σ3<σ4< σ1< σ2<1,any ε>0,any finite subset F ? A containing a positive element b,and any integer n>0,there exist a projection p∈A,and a C?-subalgebra B of A with B ∈ ? and 1B=p,such that
(1)kxp?pxk<ε for all x∈F;
(2)pxp∈εB for all x∈F;
Recall that the definition given by Elliott and Niu and the definition given above and in[8]coincide in the simple case.
The Rokhlin property in ergodic theory was adapted to the context of von Neumann algebras by Connes in[9].It was adapted by Hermann and Ocneanu for UHF-algebras in[10].Rordam[11]and Kishimoto[12]considered the Rokhlin property in a much more general C?-algebra context.More recently,Phillips and Osaka studied finite group actions which satisfy a certain type of Rokhlin property on some simple C?-algebras in[13–16].
In this article,we introduce a special tracial Rokhlin property for unital C?-algebras,and this special Rokhlin property generalizes the Rokhlin property.This special Rokhlin property implies the weak tracial Rokhlin property defined by Wang in[17].The different between this special tracial Rokhlin property and weak tracial Rokhlin property is that we can study the properties of crossed product C?-algebra with a finite group G action on non-simple C?-algebra of tracial topological rank no more than k.
When C?-algebra is simple,this special tracial Rokhlin property is equivalent to the tracial Rokhlin property defined by Phillips.We also get the following two theorems.
(1)Let ? be a class of unital C?-subalgebras such that ? is closed under passing to unital hereditary C?-algebras,under passing to finite direct sums,and under passing to quotient C?-algebra.Let A ∈ TA? be an in finite dimensional unital C?-algebra.Suppose that α :G →Aut(A)is an action of a finite group G on A which has this special tracial Rokhlin property,and suppose that A is a α-simple C?-algebra.Then,the crossed product C?-algebra C?(G,A,α)belongs to TA?.
In particular,let A ∈ TA ? be an in finite dimensional unital C?-algebra.Suppose that α:G→Aut(A)is an action of a finite group G on A which has Rokhlin property,and suppose that A is a α-simple C?-algebra.Then,the crossed product C?-algebra C?(G,A,α)belongs to TA?.
As a consequence,let A be an in finite dimensional unital tracial rank zero C?-algebra(or tracial rank no more than one).Suppose that α :G → Aut(A)is an action of a finite group G on A which has the Rokhlin property,and suppose that A is a α-simple C?-algebra.Then,C?(G,A,α)has tracial topological rank zero(or tracial rank no more than one).
(2)Let ? be a class of unital C?-algebras such that ? is closed under passing to unital hereditary C?-subalgebra and tensoring matrix algebras.Let A ∈ TA? be an in finite dimensional simple unital C?-algebra.Suppose that α :G → Aut(A)is an action of a finite group G on A which has tracial Rokhlin property.Then,the crossed product C?-algebra C?(G,A,α)belongs to TA?.
As a consequence,let A be a unital simple isometrically rich C?-algebra(that is,the set of one-sided invertible elements is dense in A)and let α :G → Aut(A)be an action of a finite group G on A which has the tracial Rokhlin property.Then,C?(G,A,α)is an isometrically rich C?-algebra.
We also show that if A is a unital simple purely in finite C?-algebra(that is,A 6=C and if for any nonzero element a∈A,there are x,y∈A such that xay=1)and α:G→Aut(A)is an action of a finite group G on A which has the tracial Rokhlin property,then C?(G,A,α)is a unital simple purely in finite C?-algebra.
2 Preliminaries and Definitions
Recall that a C?-algebra A has the property SP,if every nonzero hereditary C?-subalgebra of A contains a nonzero projection.
A unital C?-algebra A is called isometrically rich C?-algebra,if the set of one-sided invertible elements is dense in A(cf.[18,19]).
A nonzero projection p is said to be in finite if p~q,where q≤p and
A unital simple C?-algebra A is said to be purely in finite,ifand if for any nonzero element a∈A,there are x,y∈A such that xay=1.
Let A be a C?-algebra and α ∈ Aut(A).We say A is α-simple if A does not have any non-trivial α-invariant closed two-sided ideals.
Let a and b be two positive elements in a C?-algebra A.We write[a]≤ [b](cf Definition 3.5.2 in[20]),if there exists a partial isometry v∈ A??such that,for every c∈ Her(a),v?c,cv∈A,vv?=P[a],where P[a]is the range projection of a in A??,and v?cv ∈ Her(b)(where Her(b)is the hereditary C?-algebra generated by b).We write[a]=[b]if v?Her(a)v=Her(b).Let n be a positive integer.We write n[a]≤[b],if there are n mutually orthogonal positive elements b1,b2, ···,bn∈ Her(b)such that[a]≤ [bi],i=1,2, ···,n.
Let 0< σ1< σ2≤ 1 be two positive numbers.Define
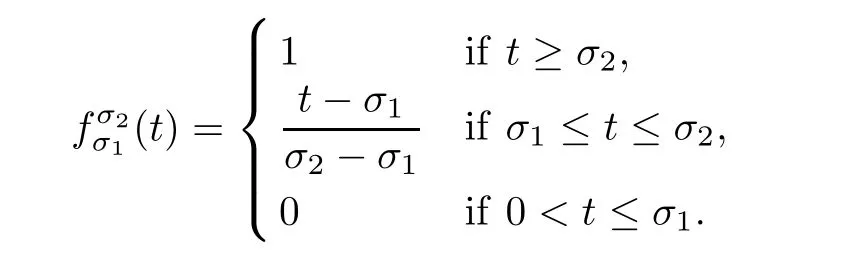
Let ? be a class of unital C?-algebras.Then,the class of C?-algebras which can be tracially approximated by C?-algebras in ?,denoted by TA?,is defined as follows.
Definition 2.1([6,7]) A unital simple C?-algebra A is said to belong to the class TA?if for any ε>0,any finite subset F ? A,and any nonzero element a ≥ 0,there exist a nonzero projection p∈A and a C?-subalgebra B of A with 1B=p and B ∈ ?,such that
(1)kxp?pxk<ε for all x∈F;
(2)pxp∈εB for all x∈F;
(3)[1?p]≤[a].
Definition 2.2([6,8]) A unital C?-algebra A is said to belong to the class TA? if for any positive numbers 0< σ3< σ4< σ1< σ2<1,any ε>0,any finite subset F ? A,any nonzero positive element a,and any integer n>0,there exist a nonzero projection p∈A and a C?-subalgebra B of A with B ∈ ? and 1B=p,such that
(1)kxp?pxk<ε for all x∈F;
(2)pxp∈εB for all x∈F;
By[21],if A is a unital simple C?-algebra and A∈TA?,then Definition 2.1 and Definition 2.2 are equivalent.
Let I1(I0)denote the class of all interval algebras(all finite dimensional C?-algebras).A is said to have tracial rank no more than one(tracial rank zero)if A∈TAI1(A∈TAI0),we will write TR(A)≤1(TR(A)=0).
Lemma 2.3([7,21–23]) If the class ? is closed under passing to tensoring matrix algebras,or closed under passing to unital hereditary C?-subalgebras,or closed under passing to unital quotient algebras,then TA? is closed under passing to matrix algebras or passing to unital hereditary C?-subalgebras or closed under passing to unital quotient algebras.
Theorem 2.4([22]) Let ? be a class of unital C?-algebras.Then,any simple unital C?-algebra A∈TA(TA?)belongs to TA?.
Definition 2.5([16]) Let A be an in finite dimensional unital separable C?-algebra,and let α :G → Aut(A)be an action of a finite group G on A.We say α has Rokhlin property if for any finite set F ?A,any ε>0,there are mutually orthogonal projections eg∈A for g∈G such that
(1)kαg(eh)?eghk< ε for all g,h ∈ G;
(2)kegd?degk<ε for all g∈G and all d∈F;
Definition 2.6([16]) Let A be an in finite dimensional simple unital separable C?-algebra,and let α :G → Aut(A)be an action of a finite group G on A.We say α has tracial Rokhlin property if for any finite set F ? A,any ε>0,and any nonzero positive element b∈ A,there are mutually orthogonal projections eg∈A for g∈G such that
(1)kαg(eh)?eghk< ε for all g,h ∈ G;
(2)kegd?degk<ε for all g∈G and all d∈F;
(4)kebek≥kbk?ε.
Theorem 2.7([16]) Let A be an in finite dimensional unital simple C?-algebra,and let α:G→Aut(A)be an action of a finite group G on A which has the tracial Rokhlin property.Then,C?(G,A,α)is a simple C?-algebra.
Theorem 2.8([16]) Let A be an in finite dimensional simple unital C?-algebra,and α:G→Aut(A)be an action of a finite group G on A which has the tracial Rokhlin property.Then,A has the SP property or has the Rokhlin property.
Theorem 2.9([14]) Let A be a unital C?-algebra,and let α :G → Aut(A)be an action with the Rokhlin property.Then,for every finite subset S ? C?(G,A,α)and any ε >0,there are n,a projection f ∈ A,and a unital homomorphismsuch thatfor all a∈S.
Theorem 2.10([16]) Let A be a unital C?-algebra with the property SP and let α :G →Aut(A)be an action of a finite group G on A which has the tracial Rokhlin property.Then,any non-zero hereditary C?-subalgebra of the crossed product algebra C?(G,A,α)has a nonzero projection which is equivalent to a projection in A.
Definition 2.11Let A be an in finite dimensional unital separable C?-algebra,and let α :G → Aut(A)be an action of a finite group G on A.We say α has a special tracial Rokhlin property if for any finite set F ? A,for any positive numbers 0< σ3< σ4< σ1< σ2<1,any integer n,any ε>0,and any nonzero positive element b∈ A,there are mutually orthogonal projections eg∈A for g∈G such that
(1)kαg(eh)?eghk< ε for all g,h ∈ G;
(2)kegd?degk<ε for all g∈G and all d∈F;
(4)kebek≥kbk?ε.
NoteIn Definition 2.11(3)can be replace bywith
Definition 2.12([17]) Let A be an in finite dimensional unital separable C?-algebra,and let α :G → Aut(A)be an action of a finite group G on A.We say α has weak tracial Rokhlin property if for any finite set F ? A,any ε>0,any every full positive element b,there are mutually orthogonal projections eg∈A for g∈G such that
(1)kαg(eh)?eghk< ε for all g,h ∈ G;
(2)kegd?degk<ε for all g∈G and all d∈F;
(4)kebek≥kbk?ε.
Theorem 2.13([16]) Let α :G → Aut(A)be an action of a finite group G on A with the tracial Rokhlin property,and let p be an invariant projection.Then,the induced action α on pAp has the tracial Rokhlin property.
Theorem 2.14([16]) Let A be an in finite dimensional simple unital C?-algebra,and α:G→Aut(A)be an action of a finite group G on A.Then,α has the tracial Rokhlin property if and only if for any finite set F ?A,any ε >0,and any nonzero positive element b∈A,there are mutually orthogonal projections eg∈A for g∈G such that
(1)kαg(eh)?eghk< ε for all g,h ∈ G;
(2)kegd?degk<ε for all g∈G and all d∈F;
(3)[1 ? e]≤ b,with e= Σg∈Geg,and e is α-invariant projection;
(4)kebek≥kbk?ε.
Theorem 2.15Let A be an in finite dimensional unital C?-algebra,and α :G → Aut(A)be an action of a finite group G on A which has the special tracial Rokhlin property.Then,α:G→Aut(A)is an action of a finite group G on A which has the weak tracial Rokhlin property.
ProofSuppose that G={g1,g2,···gm},where g1is the unit of G.We need to show that for any finite set F ? A,any integer n,any ε>0,and any full positive element b∈ A,there are mutually orthogonal projections egi∈A for gi∈G and 1≤i≤m such that
(4)kebek≥kbk?ε.
As b is a full element,there are xi∈ A(i=1,2, ···,k)such thatTake 0 Applying Definition 2.11 tothere are mutually orthogonal projections egi∈A for 1≤i≤m,such that (1′)for any 1≤ i,j≤ m; (2′)for any 1≤ i≤ m and any d∈ H; ( 3′)with (4′)kebek ≥ kbk? ε. By functional calculus,we have So,there are zi∈(1?e)A(1?e)such that We have Theorem 2.16([17]) Let A be an in finite dimensional unital C?-algebra with property SP,and α :G → Aut(A)be an action of a finite group G on A which has the weak tracial Rokhlin property.Then,every nonzero hereditary C?-algebra of C?(G,A,α)has a projection which is equivalent to some porjection in A in the sense of Murray-von Neumann. Corollary 2.17Let A be an in finite dimensional unital C?-algebra with property SP,and α :G → Aut(A)be an action of a finite group G on A which has the special tracial Rokhlin property.Then,every nonzero hereditary C?-algebra of C?(G,A,α)has a projection which is equivalent to some porjection in A in the sense of Murray-von Neumann. Theorem 2.18([17]) Let A be an in finite dimensional unital C?-algebra,and let α :G →Aut(A)be an action of a finite group G on A which has the weak tracial Rokhlin property.Suppose that A is α-simple,then C?(G,A,α)is a simple C?-algebra. Corollary 2.19Let A be an in finite dimensional unital C?-algebra,and let α :G →Aut(A)be an action of a finite group G on A which has the special tracial Rokhlin property.Suppose that A is α-simple,then C?(G,A,α)is a simple C?-algebra. Theorem 2.20Let A be an in finite dimensional unital simple separable C?-algebra,and let α :G → Aut(A)be an action of a finite group G on A.Then,Definition 2.6 and Definition 2.11 are equivalent. ProofFirst,we show that Definition 2.11 implies that Definition 2.6.We need to show that for any finite set F?A,any ε>0,and any a nonzero positive element b∈A,there are mutually orthogonal projections eg∈A for g∈G such that (1)kαg(eh)?eghk< ε for all g,h ∈ G; (2)kegd?degk<ε for all g∈G and all d∈F; (4)kebek≥kbk?ε. As Definition 2.11 holds,and as A is a simple unital C?-algebra,there are xi∈ A(i=1,2,···,k)such thatTakesuch that (1)kαg(eh)?eghk< ε for all g,h ∈ G; (2)kegd?degk<ε for all g∈G and all d∈H; (4)kebek≥kbk?ε. By functional calculus,we have There are zi∈(1?e)A(1?e)such that therefore we have We have Second,we show that Definition 2.6 implies Definition 2.11. By Theorem 2.8,we may assume that A has the property SP. We need to show that for any finite set F ? A,for any positive numbers 0< σ3< σ4<σ1< σ2<1,any ε>0,and any nonzero positive element b∈ A,there are mutually orthogonal projections eg∈A for g∈G such that (1)kαg(eh)?eghk< ε for all g,h ∈ G; (2)kegd?degk<ε for all g∈G and all d∈F; (4)kebek≥kbk?ε. As α :G → Aut(A)has tracial Rokhlin property,for finite set F ? A,any ε>0,any every positive element b,there are mutually orthogonal projectionsfor g ∈ G such that (1′)for all g,h ∈ G; (2′)for all g ∈ G and all d ∈ F; (3′) (4′) By Theorem 2.14,we may assume that e′is a α-invariant projection. As A has the property SP,there exist projectionssuch that[f]≤ [g].By Theorem 2.13,the induced action α on(1 ? e′)A(1 ? e′)has the tracial Rokhlin property,so for any ε>0,and any positive element f,there are mutually orthogonal projectionsfor g∈G such that (1′′)for all g,h ∈ G; (2′′)for all g ∈ G and all d ∈ F ∪ ; (3′′)with (4′′) (4)kebek≥kbk?ε. Theorem 2.21Let A be an in finite dimensional unital C?-algebra,and α :G → Aut(A)be an action of a finite group G on A which has the special tracial Rokhlin property.Then,A has the SP property or has Rokhlin property. ProofIf A does not have property SP,by Theorem 2.15,then there is a nonzero positive element a∈A which generates a hereditary subalgebra,which contains no nonzero projection.? Lemma 3.1([16]) Let n ∈ N,andbe a system of matrix units for Mn.For every ε>0,there is δ>0 such that,whenever B is a unital C?-algebra,and wj,k,for 1≤j,k≤n,are elements of B such that (2)kwj1,k1wj2,k2?δj2,k1wj1,k2k<δ for 1≤ j1,j2,k1,k2≤ n; (3)wj,jare orthogonal projections with,there exists a unital homomorphism ?:Mn→B such that ?(ej,j)=wj,jfor 1≤ j≤n and k?(ej,k)?wj,kk<ε for 1≤ j,k≤n. Theorem 3.2Let ? be a class of unital C?-algebras such that ? is closed under passing to unital hereditary C?-algebra,closed under passing to finite direct sums,and closed passing to unital quotient C?-algebra.Let A ∈ TA? be an in finite dimensional unital C?-algebra.Suppose that α :G → Aut(A)is an action of a finite group G on A which has the special tracial Rokhlin property,and suppose that A is a α-simple C?-algebra.Then,the crossed product C?-algebra C?(G,A,α)belongs to TA?. ProofBy Theorem 2.21,we prove this theorem by two steps. First,we assume that A has Rokhlin property. By Theorem 2.4,we need to show that for any finite subset S of the form S=F∪{ugi:1≤i≤ m},where F is a finite subset of the unit ball of A and ugi∈ C?(G,A,α)is the canonical unitary implementing the automorphism αgi,any ε>0,and any a nonzero positive element b∈ C?(G,A,α),there exist C?-subalgebra D ? C?(G,A,α)and a projection e∈ C?(G,A,α)with 1D=e and D∈TA?,such that (1)kex?xek<ε for any x∈S; (2)exe∈εD for any x∈S; (3)[1A?e]≤[b]. Second,we suppose that A has the property SP. By Corollary 2.19,C?(G,A,α)is a simple C?-algebra.Suppose that G={g1,g2,···gm},where g1is the unit of G.By Theorem 2.4,we need to show that for any finite subset S of the form S=F∪{ugi:1≤i≤m},where F is a finite subset of the unit ball of A and ugi∈ C?(G,A,α)is the canonical unitary implementing the automorphism αgi,any ε>0,and any a nonzero positive element b ∈ C?(G,A,α),there exist C?-subalgebra D ? C?(G,A,α)and a projection e∈ C?(G,A,α)with 1D=e and D ∈ TA?,such that (1)kex?xek<ε for any x∈S; (2)exe∈εD for any x∈S; (3)[1A?e]≤[b]. By Corollary 2.17,there exist nonzero projection r∈A such that[r]≤[b]. As C?(G,A,α)is a simple unital C?-algebra,there are xi∈ C?(G,A,α)(i=1,2, ···,k)such thatTakesuch thatPutthen we have Set δ= ε/(16m).Choose η >0 according to Lemma 3.1 for m given above and δ in place of ε.Moreover,we may require η < ε/[8m(m+1)].Applying Definition 2.11 to F ∪,η in place with ε,and p in place of r,there are gk∈ G and mutually orthogonal projections egi∈A for 1≤i≤m,such that (1′)for any 1 ≤ i,j≤ m; (2′)for any 1≤i≤ m and any d∈H; (3′)with By(1′)and(2′),we have By functional calculus,we have So,there are zi∈(1?e)A(1?e)such that We have Using the same methods as Theorem 2.2 in[16],we can provethat the(1≤i,j≤m)satisfy the conditions in Lemma 3.1. Let(fij)(1≤i,j≤m)be a system of matrix units for Mm.By Lemma 3.1,there exists a unital homomorphism ψ0:Mm→ eC?(G,A,α)e such thatfor all 1≤ i,j≤ m,andfor all 1≤ i≤ m.Now,we define a unital homomorphismby for all 1≤i,j≤m and a∈eg1Aeg1.Then, Let ki,jbe the integer such that gki,j=gigj.For 1≤i≤m,we have Now,let a∈F.Set Using the inequity above and the inequalities and we have (1)kae?eak≤mη<ε,for any a∈F. (2)exe ∈εD for any x ∈ S,by(?)and(??); Corollary 3.3Let A be an in finite dimensional unital tracial rank zero C?-algebra.Suppose that α :G → Aut(A)is an action of a finite group G on A which has the special tracial Rokhlin property,and suppose that A is a α-simple C?-algebra.Then,C?(G,A,α)has tracial topological rank zero. Corollary 3.4Let A be an in finite dimensional unital tracial topological rank one C?-algebra.Suppose that α :G → Aut(A)is an action of a finite group G on A which has the special tracial Rokhlin property,and suppose that A is a α-simple C?-algebra.Then,C?(G,A,α)has tracial topological rank no more than one. Corollary 3.5Let ? be a class of unital C?-algebras such that ? is closed under passing to unital hereditary C?-algebra and closed passing to finite direct sums.Let A ∈ TA? be an in finite dimensional unital C?-algebra.Suppose that α :G → Aut(A)is an action of a finite group G on A which has the Rokhlin property,and suppose that A is a α-simple C?-algebra.Then,the crossed product C?-algebra C?(G,A,α)belongs to TA?. Corollary 3.6Let A be an in finite dimensional unital tracial rank zero C?-algebra.Suppose that α :G → Aut(A)is an action of a finite group G on A which has the Rokhlin property,and suppose that A is a α-simple C?-algebra.Then,C?(G,A,α)has tracial topological rank zero. Corollary 3.7Let A be an in finite dimensional unital tracial topological rank one C?-algebra.Suppose that α :G → Aut(A)is an action of a finite group G on A which has the Rokhlin property,and suppose that A is a α-simple C?-algebra.Then,C?(G,A,α)has tracial topological rank no more than one. Theorem 4.1Let ? be a class of unital C?-algebras,which ? is closed under passing to unital hereditary C?-subalgebras and closed under passing to tensoring matrix algebras.Let A ∈ TA? be an in finite dimensional simple unital C?-algebra.Suppose that α :G → Aut(A)is an action of a finite group G on A which has tracial Rokhlin property.Then,the crossed product algebra C?(G,A,α)belongs to TA?. ProofBy Theorem 2.8,we prove this theorem by two steps. First,we suppose that α has Rokhlin property.We need to show that for any finite subset S,any ε>0,any nonzero positive element b ∈ C?(G,A,α),there exist a C?-subalgebra D ? C?(G,A,α)and a projection e∈ C?(G,A,α)with 1D=e and D ∈ TA?,such that (1)kex?xek<ε for any x∈S; (2)exe∈εD for any x∈S; (3)[1A?e]≤[b]. By Theorem 2.9,for S and ε >0,there exist n and a projection f ∈ A,and a unital homomorphismsuch thatfor all a ∈ S. Second,we suppose that A has the property SP. By Theorem 2.7,C?(G,A,α)is a simple C?-algebra.Suppose that G={g1,g2,···gm},where g1is the unit of G.By Theorem 2.4,we need to show that for any finite subset S of the form S=F∪{ugi:1≤i≤m},where F is a finite subset of the unit ball of A and ugi∈ C?(G,A,α)is the canonical unitary implementing the automorphism αgi,any ε >0,any nonzero positive element b∈ C?(G,A,α),there exist a C?-subalgebra D ? C?(G,A,α)and a projection e∈ C?(G,A,α)with 1D=e and D ∈ TA?,such that (1)kex?xek<ε for any x∈S; (2)exe∈εD for any x∈S; Set δ= ε/(16m).Choose η >0 according to Lemma 3.1 for m given above and δ in place of ε.Moreover,we may require η < ε/[8m(m+1)].Applying Definition 2.6 to α with F given above,η in place with ε,and p in place of b,there are gk∈ G and mutually orthogonal projections egi∈A for 1≤i≤m,such that (1′)kαgi(egj)?egigjk< η for any 1 ≤ i,j≤ m; (2′)kegia?aegik< η for any 1≤ i≤m and any a∈F; (3′)[1?e]≤ [p],with By(1′)and(2′),we have Using the same methods as Theorem 2.2 in[16],we can prove that the wgi,gj∈ eC?(G,A,α)e(1≤i,j≤m)satisfy the conditions in Lemma 3.1. Let(fij)(1≤i,j≤m)be a system of matrix units for Mm.By Lemma 3.1,there exists a unital homomorphism ψ0:(G,A,α)e such thatfor all 1≤ i,j≤ m,and ψ0(fii)=egifor all 1≤ i≤ m.Now,we define a unital homomorphismby for all 1≤i,j≤m and a∈eg1Aeg1.Then, Let ki,jbe the integer such that gki,j=gigj.For 1≤i≤m,we have Now,let a∈F.Set Using the inequity above and the inequalities and we have (1)kae?eak≤mη<ε,for any a∈F, for any ugi∈ C?(G,A,α)the canonical unitary implementing the automorphism αgi; (2)exe ∈εD for any x ∈ S,by(?)and(??); (3)[1A?e]≤[p]≤[b]. Theorem 4.2([24]) Let ? be a class of unital simple isometrically rich C?-algebras.Then,any simple unital C?-algebra in the class TA? is an isometrically rich C?-algebra. Corollary 4.3Let A be a unital simple isometrically rich C?-algebra.Suppose that α:G→Aut(A)is an action of a finite group G on A which has the tracial Rokhlin property.Then C?(G,A,α)is an isometrically rich C?-algebra. Theorem 4.4([24]) Let ? be a class of unital simple purely in finite C?-algebras.Then,any simple unital C?-algebra in the class of TA? is a simple purely in finite C?-algebra. Corollary 4.5([25,26]) Let A be a unital simple purely in finite C?-algebra.Suppose that α :G → Aut(A)is an action of a finite group G on A which has the tracial Rokhlin property.Then,C?(G,A,α)is a simple unital purely in finite C?-algebra. AcknowledgementsThe first author is grateful to George Elliott for helpful advice and suggestion.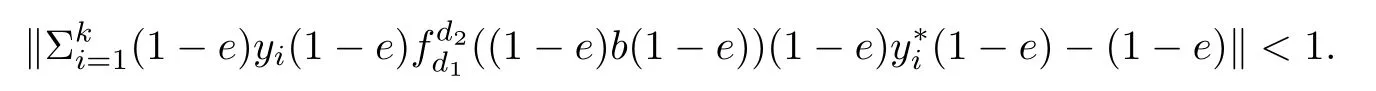


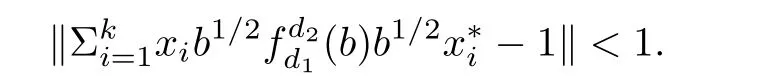




3 Crossed Products by Finite Group Actions With Special Tracial Rokhlin Property


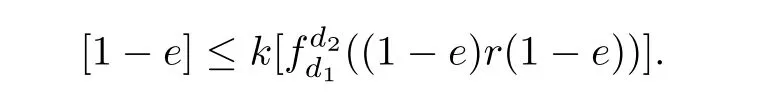
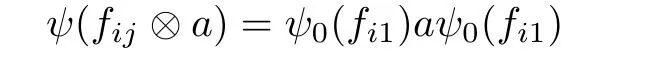

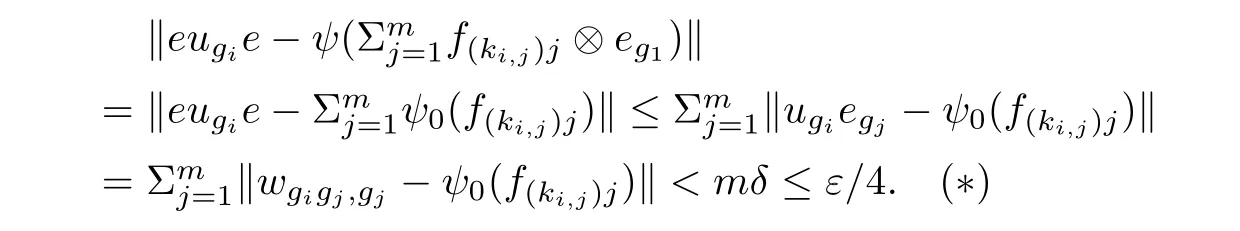
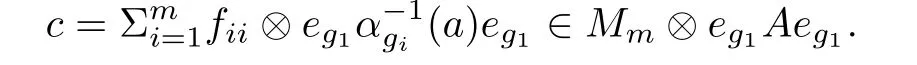




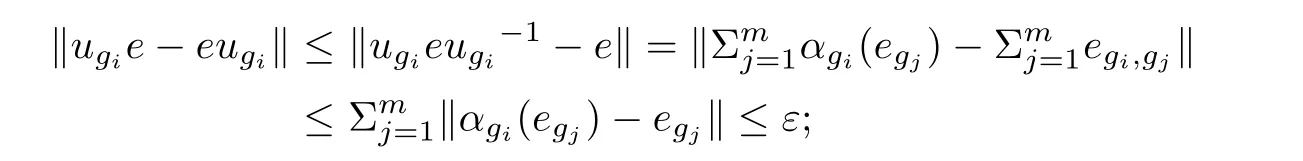
4 Crossed Products by Finite Group Actions with Tracial Rokhlin Property

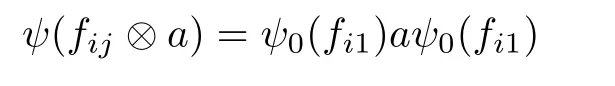



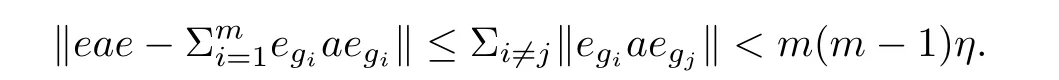
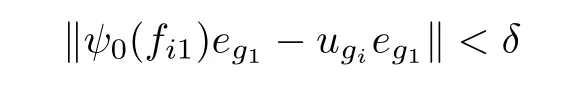



 Acta Mathematica Scientia(English Series)2018年3期
Acta Mathematica Scientia(English Series)2018年3期
- Acta Mathematica Scientia(English Series)的其它文章
- HELICAL SYMMETRIC SOLUTION OF 3D NAVIER-STOKES EQUATIONS ARISING FROM GEOMETRIC SHAPE OF THE BOUNDARY?
- INITIAL BOUNDARY VALUE PROBLEM FOR A NONCONSERVATIVE SYSTEM IN ELASTODYNAMICS?
- LONG-TIME DYNAMICS OF THE STRONGLY DAMPED SEMILINEAR PLATE EQUATION IN RN?
- STABILITY OF TRAVELING WAVES IN A POPULATION DYNAMIC MODEL WITH DELAY AND QUIESCENT STAGE?
- NONLINEAR STABILITY OF VISCOUS SHOCK WAVES FOR ONE-DIMENSIONAL NONISENTROPIC COMPRESSIBLE NAVIER–STOKES EQUATIONS WITH A CLASS OF LARGE INITIAL PERTURBATION?
- A GENERALIZATION OF GAUSS-KUZMIN-LéVY THEOREM?
