UNDERSTANDING SCHUBERT’S BOOK(I)?

Banghe LI(李邦河)

KLMM,Academy of Mathematics and Systems Science,Chinese Academy of Sciences,Beijing 100190,China E-mail:libh@amss.ac.cn

Abstract Hilbert Problem 15 required an understanding of Schubert’s book[1],both its methods and its results.In this paper,following his idea,we prove that the formulas in§6,§7,§10,about the incidence of points,lines and planes,are all correct.As an application,we prove formulas 8 and 9 in§12,which are frequently used in his book.

Key words Hilbert Problem 15;enumeration geometry;incidence formula

1 Introduction

Hilbert Problem 15 entitled the“rigorous foundation of Schubert’s enumerative calculus”,consists of this:

“To establish rigorously and with an exact determination of the limits of the validity of those geometrical numbers obtained in enumerative geometry,in particular,to study those geometrical numbers obtained by means of enumerative calculus developed by Schubert in his book on the basis of the so-called principle of special position,or conservative of number”.

This translation is based on the original German and is a bit different from the translation by Newson[2]repeated in[3].The difference is that in Newson’s translation,all the geometrical numbers to be studied are obtained in Schubert’s book.Our translation infers that Hilbert hopes to check the whole enumerative geometry before 1900,and Schubert’s work is needed‘in particular’to study.The reasons we translated it so are as follows:

First,and most importantly,we understand that the German origin was so.

Second,upon reading the whole book,we understand that Schubert’s work can be regarded as a summary of the achievement of the mathematicians of that era,e.g.,the whole of§21 is a summary of the method of the Chasles-Zeuthen reduction;the whole of§26 summarized the most important numbers about the planar curve of degree four from Zeuthen’s long paper[4].

Third,Schubert said in the preface of his book:“There is a chapter(Vol.VIII,5C)about enumerative geometry in Annals of the progress in mathematics···The pages of that chapter clearly indicate how rich achievements in this field have been obtained in the past almost 15 years···If this book can be regarded as a complement to some of the chapters of the huge books of Salmon-Fiedler and of Clebsch-Lindemann,the hard work that the author has devoted to this book has already gotten the best reward”.

In Schubert’s time,enumerative geometry was very prosperous,and enjoyed a very high reputation in the mathematical community,so much so that Chasles was awarded the Copley medal by the Royal Society of London for his famous number 3264,which concerned conics.Schubert received a gold medal from the Copenhagen academy of sciences for the huge number 5819539783680,which concerned twisted cubics.As mathematics gradually became more rigorous,the ε ?δ method replaced intuitive infinitesimals,and enumerative geometry suffered,because it is not rigorous neither method or argument.Thus,it gradually decayed.We believe that Hilbert must have appreciated and highly regarded the work of Schubert and his colleagues,and hope to revive and further develop this work under a rigorous foundation.

In §4,Schubert gave a proof of an important formula pertaining to example 4.His proof is very short but very difficult to understand.In [5],following his idea,we gave a rigorous proof by using nonstandard analysis.In §23,Schubert stated four theorems concerning planar cuspidal curves,and said that he obtained these by experience.By using the concept of generic points,developed by Van der Waerden [6]and Weil [7],and representing generic points by the triangular sequence of Ritt and Wu,we proved that these are all correct in [8,9],with the aid of computer.

In this paper,we strictly prove,following Schubert’s idea,that the formulas in §6,§7,§10 regarding incidence of points,lines and planes,are all correct.His proof is very beautiful.There are two places through where his proofs were not rigorous.The first regards multiplicity.The second concerns the simplicity of a homomorphism pull-back of the rings of numerical equivalence from one variety to another variety.Regarding the first,we overcome the lack of rigor by using the fact that multiplicity one is equivalent to transversality.In terms of the second,we prove the simplicity by using a concrete construction and the projection formula in a Chow ring.

Before reading this paper,we suggest that the reader be familiar with Kleiman’s papers [3,10],both of which are excellent papers that have historical meaning in terms of Hilbert Problem 15.

2 Equations Between the Basic Conditions of Three Principal Elements

In this section,we strictly prove all formulas of §6 in Schubert’s book,following his ideas.These formulas pertain to the relation between three principal elements:points,lines and planes in CP.For smooth variety,Schubert works on the ring of numerical equivalence,which is actually the quotient ring of the Chow ring modulo numerical equivalence.Let X be a nonsingular variety.We denote A(X) as the Chow ring of X and N(X) as the ring of numerical equivalence.

The conditions p,pand P are defined as follows:

? p:the condition that the points are on a given plane in CP;

? p:the condition that the points are on a given line in CP;

? P:the condition that the point is a given point in CP.

Schubert gave the following relations in N(CP):

1) p=p.

Schubert’s proof for 1)is that prepresents the number of points of a 2-dimensional system which is on the two given planes.Thus,these points are also on the intersection line of the planes.On the other hand,prepresents the number of the system on a given line.Hence,according to the principle of the conservation of numbers,p=pfor any 2-dimensional system.

In modern terminology,it is clear that 1) refers to the numerical equivalence of conditions explained as subvarieties or cycles.For rigorous proof of 1),we need to count the intersection points with multiplicities.For two planes in general position,it is clear that they intersect at a line with multiplicity 1,because of the transversality.Thus,p=pholds,even in the Chow ring of CP.Thus it holds after modulo numerical equivalence.

2) p=pp.

This is obtained by multiplying p on both sides of 1).

3) pp=P.

4) p=P.

The last two are due to the fact that a plane and a line in a general position,or three planes in a general position,intersect at a point with multiplicity 1,because of the transversality.

Denote by CPthe dual space of CPconsisting of all planes in CPas its points,and let e,eand E be the following conditions:

? e:the condition that the planes pass through a given point in CP;

? e:the condition that the planes pass through a given line in CP;

? E:the condition that the plane is a given plane in CP.

Then by duality,we have the following relations in N(CP):

5) e=e.

6) e=ee.

7) ee=E.

8) e=E.

For the space of lines in CPdenoted by G(3,1),the basic conditions g,g,g,gand G are given as follows:

? g:the condition that the lines intersect with a given line in CP;

? g:the condition that the lines are on a given plane in CP;

? g:the condition that the lines pass through a given point in CP;

? g:the condition that the lines are on a given plane and pass through a given point on it;

? G:the condition that the line is a given line.

Schubert proved that certain relations are in N(G(3,1)).The first of these is

9) g=g+g.

Schubert derived this in a way that is not completely rigorous,saying that for a 2-dimensional system of lines,grepresents the number of lines in the system which intersect with two given lines,letting the two given lines intersect themselves,so gcomes first from those passing through the intersection point,and second from those contained in the plane determined by the 2 lines;thus g=g+g.

According to modern requirements,Schubert had actually only proved that

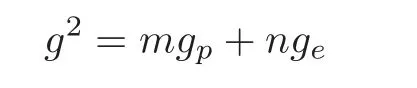
for a 2-dimensional cycle in G(3,1),where m and n are the multiplicities of gand g,respectively,as components of the intersection of two given varieties.

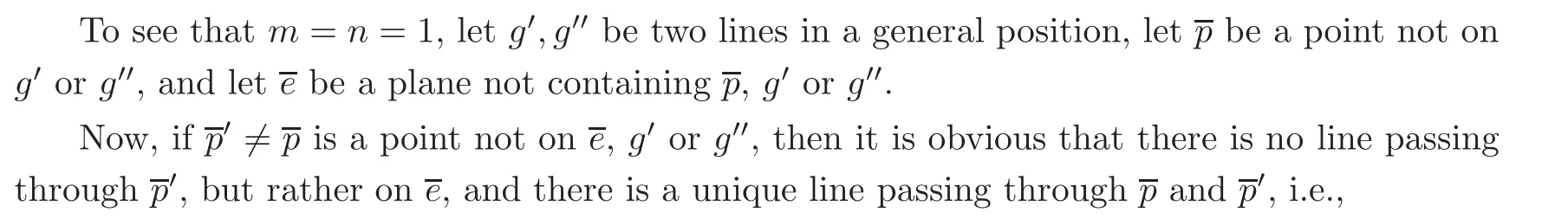
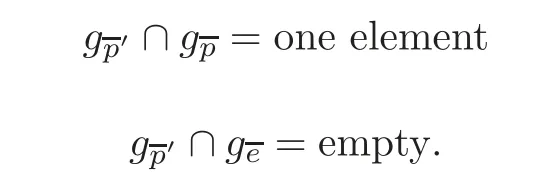
To see that the multiplicities of the two above elements are 1,we need some equations.

First,G(3,1) is a hypersurface in CP,as follows:

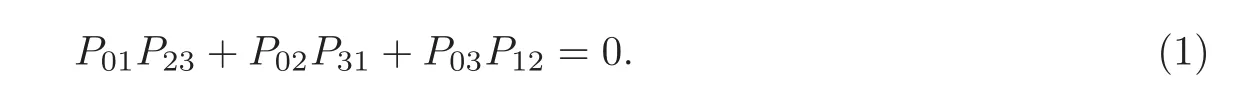
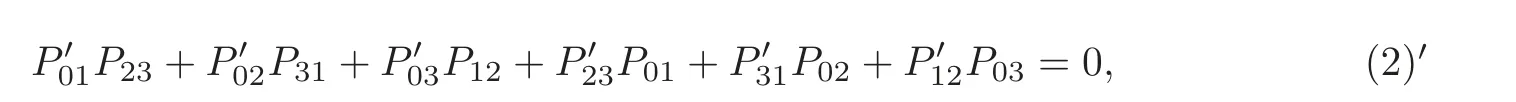
and those of gare (1) and (2),which is obviously defined.

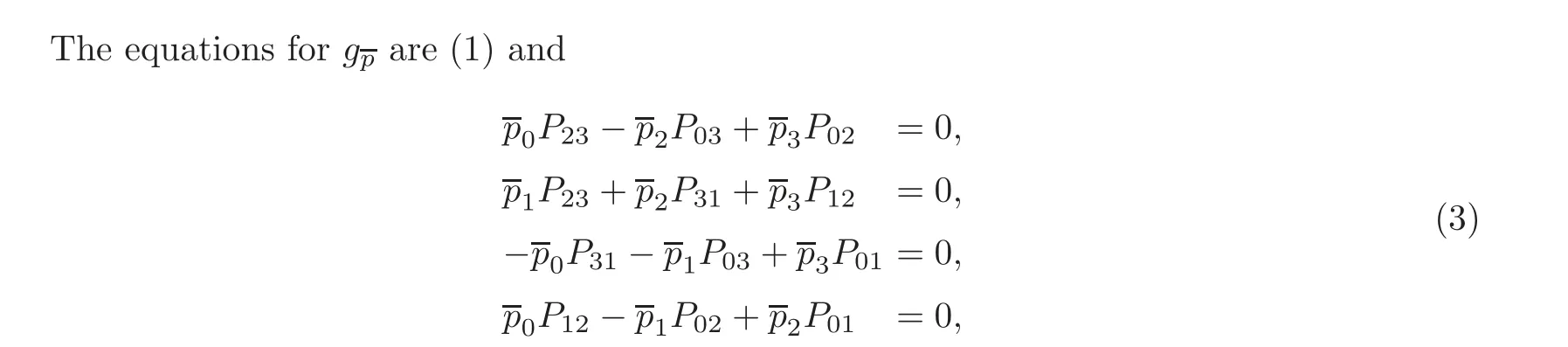
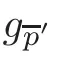
Take the affine open set of CPwith P=1.Then the point of G(3,1)in this set is given by

The same procedure as above gives n=1,so 9) is proved.

After 9),Schubert gave the following formulas:

10) gg=g;

11) gg=g;

12) gg=G;

13) gg=0.

Schubert said that these formulas can be obtained in a fashion similar as to that for 9),but his proof about 9) is not rigorous enough,so we give the proof here.

For 10),let p be a point not on g.Then the intersection of g and gis the set of lines passing through p and on the plane determined by p and g.Hence we have

10)gg=mg,m ∈Z.

For 11),let e be a plane not containing g.Then the intersection of g and gis the set of lines passing through the intersection point of g and e and contained in e.Hence we have

11)gg=ng,n ∈Z.

For 12),let g be a line intersecting with the plane of gat a unique point which differs from the point g.Then ggis the unique element given by the line connecting the two mentioned points.Thus,we have

12)gg=kG,k ∈Z.

For 13),take p not on e,so the intersection of gand gis empty,and hence is true.Recall that in the proof of 9),we proved that

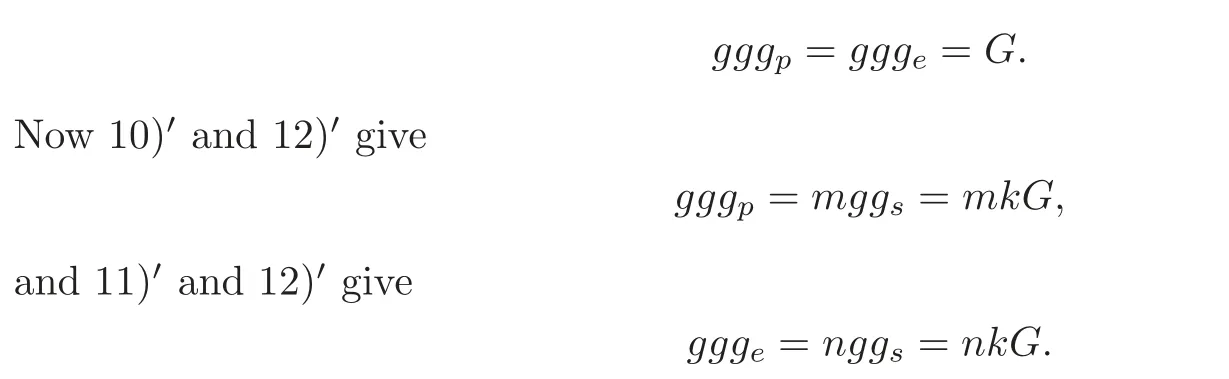
Hence m=n=k=1,and 10)–13) hold.Multiplying 9) by g yields

14) g=gg+gg.Furthermore,due to 10) and 11),we have

15) g=2g.

Finally,using 12) and 13),along with multiplication by symbols,we get

3 Incidence Formulas of Points and Lines

Denote the set of figures of a line in CPwith a point on it F(CP) (or F).Schubert gave conditions in Fand relations between these in §7 of his book.

There are four 2-fold conditions in F:

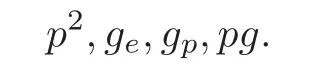
The basic relation is

I) pg=p+gor

I) pg=p+gfor the formula 1) in above section,p=p.

Schubert’s proof:pg represents those elements of Fwhose point is on a given plane e,and whose line intersects with a given line g.Let g be on e.Then the elements of Fin pg consist of those with points on g and those with line on e.Hence,according to the principle of conservation of number,I) holds.

This proof is only due to level of sets,so it says only that

for some m,n ≥1.To prove m=n=1,we need some equations.

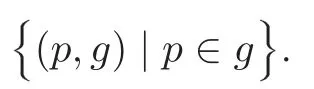
i.e.,in the affine open set of CP×CPwith p=1 and P=1,the subset of Fin this set is given by(?),which is an affine space with coordinates(p,P,P,P,P),and its imbedding in CP×CPis given by

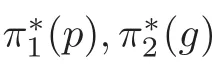
to get n=1.For this,we need some equations,and only have to prove that pG=pg=Pg=one point in Fwith multiplicity 1.

For pG,let p be given by the plane

with l,l,l,lbeing independent complex numbers over Q.After the substitutions given by(??),we get

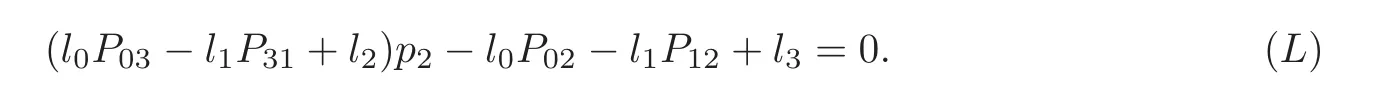
Letting G be given by the line with Plücker coordinates,we get that

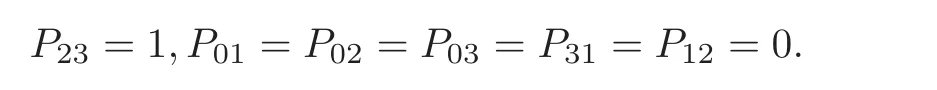
Then the equation (L),together with P=P=P=P=0,gives the unique solution for pG:

The multiplicity of this is obviously 1.

For pg,let pbe given by the planes

Thus,in the coordinate system (p,P,P,P,P),the equation (p),together with (3),becomes

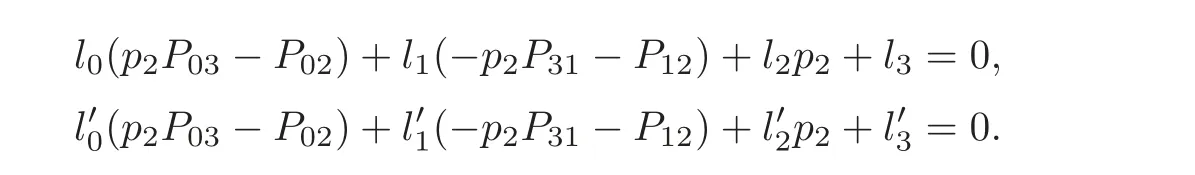
Substituting the equation (g) into the above yields

A Groebner basis for the two polynomials in above equations is

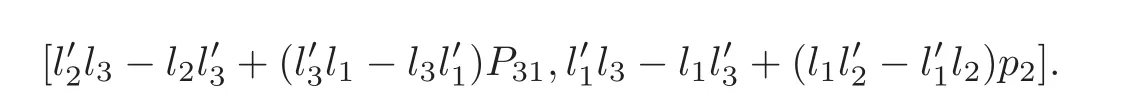
Thus the unique solution has multiplicity 1.

For Pg,let us take P given by [x,x,x,1]such that x,x,xare the complex numbers that are independent over Q,and let gbe given by the lines [P,P,P,P,P,P]=[1,0,1,0,0,0]and [1,0,0,0,1,0].Then the equations of P and gin CP×CPwith p=1 and P=1 are given by

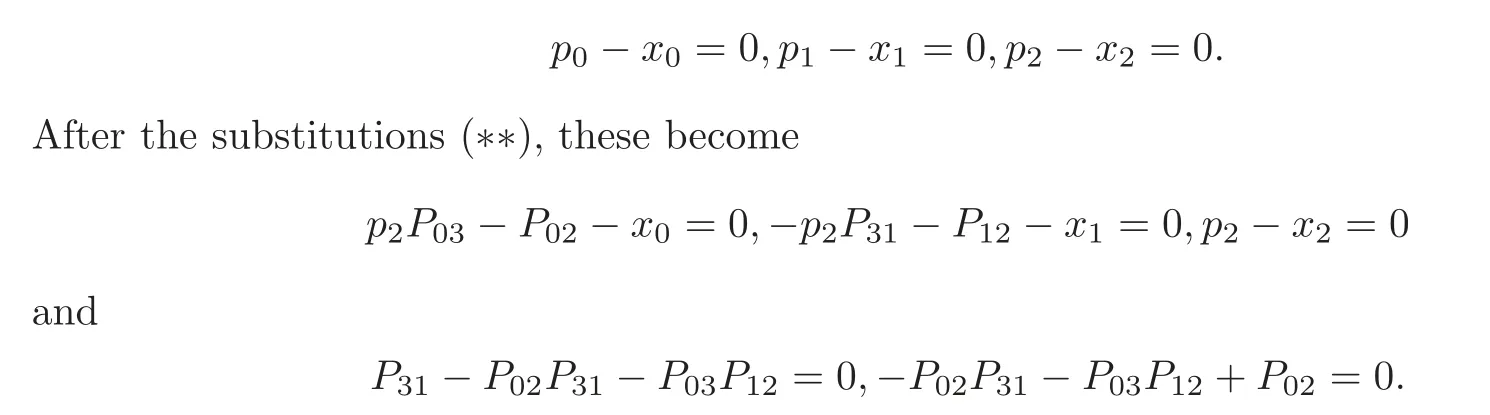
A Groebner basis of the above five polynomials is

Thus the unique solution has multiplicity 1,and the proof of I) is complete.

The formulas II) and III) are obtained by I) directly,so we omit the proofs,and only write them down:

II) pg=p+g;

III) pg=pg=G+pg=G+pg.

4 Other Incidence Formulas

In this section,we strictly prove all formulas of §10 of Schubert’s book.

Let F(CP) be the flag variety consisting of the pairs of (g,e) with a line g on a plane e in CP.Then,by duality,Schubert wrote down the formulas

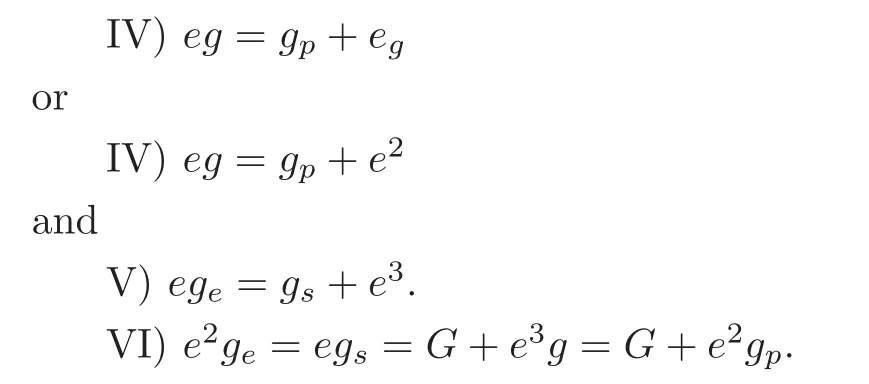
Another incidence figure is F(CP),which consists of the pairs (p,e) with a point p on a plane e in CP.

Formulas regarding the basic conditions of this incidence figure can be obtained by calculations including the 2-dimensional formulas derived so far.Schubert said:“It should be noticed while calculating that when a point p is on a line g,and g is on a plane e,p must be on e”.

From the above words of Schubert,we see that his idea was to drive formulas for Ffrom the formulas for Fand F,via the intermediate figures F,in order to combine F,Fand Ftogether,where

In N(F),he multiplies 1) by e and 2) by p,and notices the equality of the righthand sides of the so obtained two formulas to give

After substituting egand pgby the formulas II) and V),respectively,he obtains

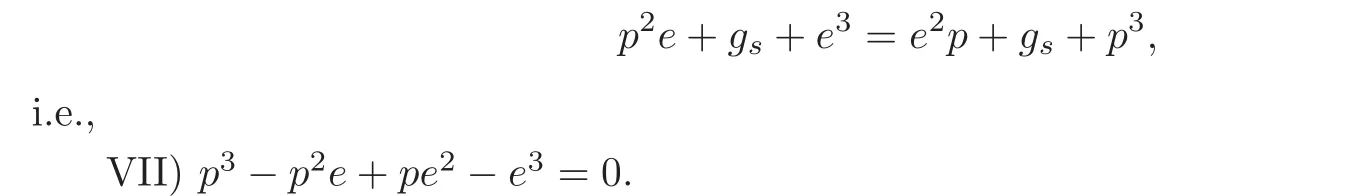
This is a formula in N(F),but Schubert regards this as a formula in N(F).To justify his understanding,we need the natural projection

and to prove that π:N(F)→N(F) is a monomorphism.

We will use the well-known projection formula for the Chow ring,

for all classes x ∈A(X),y ∈A(Y),where f :X →Y is a proper morphism of non-singular varieties.

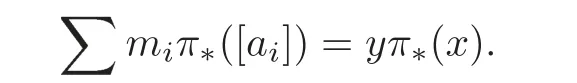
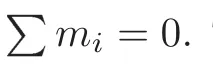
Lemma 4.2

π:N(F)→N(F) is a monomorphism.

“The fourth figure we introduced in §4 concerns the incidence figures consisting of two intersecting lines.We use g and h to denote these two lines,and p to denote their intersection point.Then,according to I,II and III,we have the following formulas:

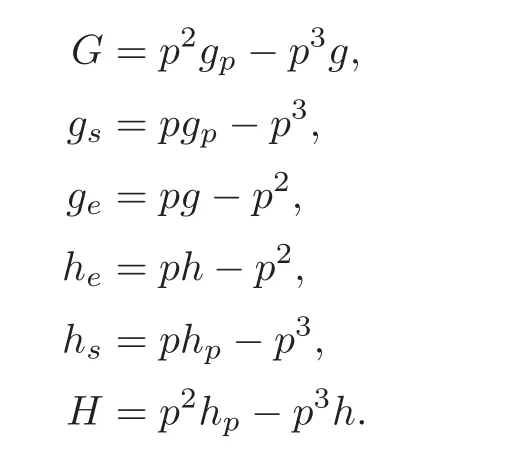
For these 6 equations,multiplying the first by 1,the second by ?h,the third by h,the fourth by g,the fifth by ?g and the sixth by ?g,yields

IX) G ?gh+gh+gh?gh+H=0.

This is the lowest dimensional formula between the basic conditions of the intersection pairs of lines.Multiplying this by h,hand hyields the 5-and 6-dimensional formulas:

X) Gh ?g(h+h)+(g+g)h?gH=0;

XI) Gh?gh+gH=0;

XII) Gh?gh+gH=0.

We have already seen Formula XII) in the example of §9.Multiplying IX) by hyields the obvious result

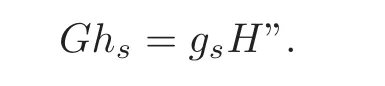
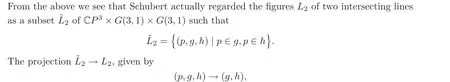
“Any above formula obtained by symbolic calculus can be also derived by the geometric method naturally.No doubt,this method would be much more complicated for most cases.As an example,we give a geometric derivation for the incidence formula VII.

For the figures consisting of the pairs of a plane e with a point p on it,there are the following basic 3-dimensional conditions:

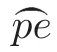
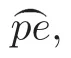
As before,Schubert’s geometric proof does not count the multiplicities,so for XIII),he has only proved that

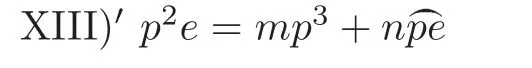
for some m,n ≥1.Again to determine m,n,we need some equations.First,Fis a hypersurface in CP×CP,given by the equation

Now,by using the routine procedure we have used,it is easy to show that m=n=1.Hence XIII) and XIV) hold.

5 Some Important Applications of Incidence Formula

In this section,we give rigorous proofs of the Applications 8 and 9 in §12 of Schubert’s book following his idea.All of these applications concern the systems of curves.

What are systems? For one dimensional planar systems,we have given a description in[5],but here,we are concerned with higher dimensional systems.According to Van der Waerden[6],§5.6,a system of curves is the algebraic set formed by Chow coordinates of the curves.In practice,however,it is more complicated than just using Chow coordinates.For example,all of the quadratic curves in space form two components by their Chow coordinates.One is the set of all pairs of lines,which is obviously an irreducible variety G(3,1)×G(3,1).Another component is the set of all of the planar quadratic curves.However,if we regard this set as a CPbundle over CP,any double line has been regarded as having infinite elements,since it stays on any plane containing it,while any double line is only one point in the relevant Chow variety.Thus,this Chow variety seems singular,and we have already blown up the Chow variety in some sense.

Use Cto denote the set of all planar curves of degree m in CP,which is a CPbundle over CP.Here a m-multiple line has already been regarded as consisting of many elements,as before.For a system of planar curves,the natural understanding should be a quasi-subvariety V of C,whose elements are irreducible curves.In actual fact,however,Schubert’s system is one of complete curves,i.e.,the curve and its dual curve are considered together.Thus,his system can be defined rigorously,as follows:

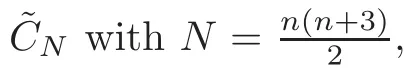
We don’t know whether all such systems are nonsingular.There are examples in which the principle of conservation of numbers,i.e.,where the intersection number of two subvarieties is unchanged under algebraic equivalence,is not correct on some singular varieties.Thus,we are not sure that this principle is always true for systems such as those of Schubert.

In the Chow ring,Fulton [11](p143.Example 8.3.13)defined A(X) as a subset of A(X)whose elements are a pull-back of A(Y) via a morphism from X to Y where Y is nonsingular.The intersection of elements in A(X) with elements in A(X) can be well defined.

Lemma 5.1

Let X be a complete variety.The subset of A(X) whose elements are numerically equivalent to 0 is an ideal in A(X).

Now we come to the Applications 8 and 9 in §12 of Schubert’s book.

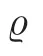
Let Σbe a subset of Σ×Fsuch that

Now,we define α:Σ →all the planes in CP.

There are three cases.

Case 1

The restriction of the morphism α on σ is surjective,so it is a branched covering.The number of sheets is μ[σ].

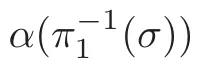
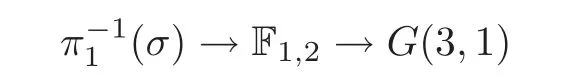
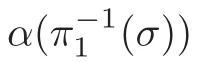
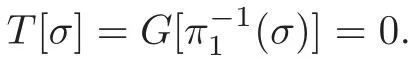
Now,our proof for Application 8 is complete.

For 9,we quote all of that which Schubert said about it:“Regarding a planar curve in the plane μ as the locus of points,we get a one-dimensional point system.Applying the incidence formula VII on this,we get a second important equation about planar curves.We use a to represent its degree,ν to represent the condition that it intersects with a given line,and P to represent the condition that it passes through a given point.Then the symbols p,pe and pecan be replaced by P,μν and a·μ,respectively,while the symbol eshould be set to 0,since a two dimensional system of curves cannot satisfy the condition that it stays in one given plane.Thus,for a two dimensional system of planar curves,we have

We give a rigorous proof following Schubert’s idea.First we emphasize that the two dimensional system defined by Schubert should again be the two dimensional subvariety in a larger system Σ as we defined before with m=a,and we should consider Σto be a subset of Σ×Fsuch that

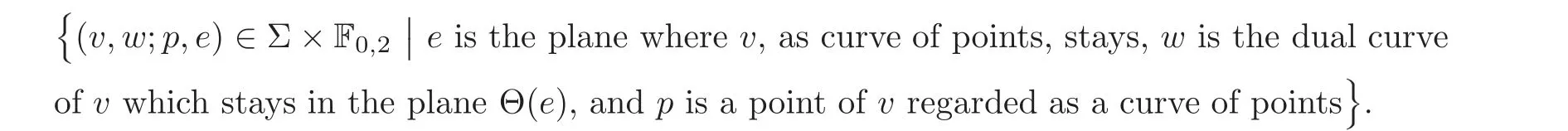
Let πand πbe the natural projections onto Σ and F,respectively.

Also,define α :Σ →all of the planes in CPsuch that α sends each element in σ to the plane in which it stays.

Case 2

If the image of α is of a dimension of two,there exists a line in the space of planes that intersects with it at finite points.Except for finite points,the inverse under α is finite;that is to say,except for finite planes,there are only finite elements in σ that stay in the same plane.Thus,we can find a line in the space of planes that intersects with the image of α at finite points and where the inverse of every intersection points under α is finite.Choose this line as e.This line corresponds to a line in the space of points such that erepresents all of the plane passing through this line.

Any plane in the space of points not passing through the above line intersects each plane passing through the line at a straight line.If this line intersects with curves in σ at infinite points,it must be a part of this curve.Since there are only finite planes passing through the line such that the curves in σ may stay and where for each plane there are at most finite curves that stay,we can find a plane not passing through the line satisfying that the intersecting line between this plane and any plane passing through the line intersects curves in σ at only finite points.

Note that each line intersects with curves at a points if they stay in the same plane.Thus we get

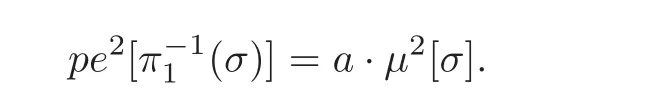
Now,our proof for Application 9 is complete.