一類差分多項(xiàng)式的零點(diǎn)和唯一性
王乙萍,黃志剛
(蘇州科技大學(xué) 數(shù)理學(xué)院, 江蘇 蘇州 215000)
0 引 言
本文假定讀者熟悉Nevanlinna值分布理論的一些基本概念和標(biāo)準(zhǔn)記號(hào)[1-4]. 設(shè)f(z) 是復(fù)平面上的亞純函數(shù), 用T(r,f)表示復(fù)平面上亞純函數(shù)f(z)的特征函數(shù),λ(f)表示復(fù)平面上亞純函數(shù)f(z) 的零點(diǎn)收斂指數(shù),σ(f)表示復(fù)平面上亞純函數(shù)f(z)的增長(zhǎng)級(jí). 如果亞純函數(shù)α(z)滿足T(r,α(z))=S(r,f), 則稱α(z)為關(guān)于f(z)的小函數(shù), 其中S(r,f)表示任意滿足S(r,f)=o(T(r,f)),r→∞, 的量, 最多有可能除去一個(gè)r的有限對(duì)數(shù)測(cè)度例外集. 假設(shè)f(z) 和g(z)為非常數(shù)亞純函數(shù),a為任意復(fù)數(shù). 如果f(z)?a和g(z)?a有相同的零點(diǎn), 且重?cái)?shù)也相同, 則稱a為f(z) 和g(z)的 CM 分擔(dān)值; 若不計(jì)零點(diǎn)的重?cái)?shù), 則稱a為f(z) 和g(z)的 IM分擔(dān)值. 另外, 設(shè)p是正整數(shù), 用表示關(guān)于f?a的零點(diǎn)的計(jì)數(shù)函數(shù), 假設(shè)z0是f?a的m重零點(diǎn). 若m≤p, 則f?a的零點(diǎn)記為m重; 若m>p, 則f?a的零點(diǎn)記為p重.
定義 1[5]令是非零多項(xiàng)式, 其中是復(fù)常數(shù),Γ0=m1+2m2, 這里的m1表示P(z)的單重零點(diǎn)的個(gè)數(shù),m2表示P(z) 的多重零點(diǎn)的個(gè)數(shù). 記d=gcd(λ0,λ1,···,λn), 其中

1959年, Hayman[6]在f(z) 是有限級(jí)亞純函數(shù)的條件下, 得出了兩種特殊形式的微分多項(xiàng)式和的值分布. 之后, 許多學(xué)者研究了一般形式的微分多項(xiàng)式的值分布, 并取得了一些重要成果. 近年來, Halburd-Korhonen[7]及蔣翼邁和馮紹繼[8]分別獨(dú)立地建立了差分Nevanlinna值分布理論, Laine-Yang[9]得到了涉及差分多項(xiàng)式的Clunie引理. 應(yīng)用這些理論, 許多學(xué)者對(duì)有限級(jí)超越整函數(shù)的差分多項(xiàng)式的值分布問題和唯一性問題進(jìn)行了深入研究[10-18], 推動(dòng)了復(fù)域差分值分布理論的發(fā)展.
2010年, 在文獻(xiàn)[11]中祁曉光等得到了如下唯一性結(jié)果.
定理 A[11]假設(shè)f(z),g(z)是兩個(gè)有限級(jí)超越整函數(shù), 并且c是非零復(fù)常數(shù). 若n≥6 ,fn(z)f(z+c)和gn(z)g(z+c)是 CM 分 擔(dān) 1的, 那么 有f(z)g(z)=t1或者f(z)=t2g(z), 其中t1,t2是常數(shù), 并且滿足.
2011年, 在文獻(xiàn)[5]中羅旭丹和林偉川得到了如下唯一性結(jié)果.
定理 B[5]假設(shè)f(z),g(z)是兩個(gè)有限級(jí)超越整函數(shù), 并且c是非零復(fù)常數(shù). 若n>2Γ0+1 ,P(f)f(z+η)和P(g)g(z+η)是 CM 分擔(dān) 1 的, 那么下列結(jié)果必有一個(gè)成立:
(i)f=tg, 其中t為常數(shù)且滿足td=1 ;
(ii)f和g滿足代數(shù)方程, 其中R(f,g)≡0R(w1,w2)=P(w1)w1(z+c)?P(w2)w2(z+c);
(iii)f(z)=eα(z),g(z)=eβ(z), 其中α(z),β(z)是多項(xiàng)式,b是使α(z)+β(z)=b成立的常數(shù), 且滿足.
定理 1假設(shè)f(z),g(z)是有限級(jí)超越整函數(shù), 令, 其中ci(i=1,2,···,k)是互不相同的非零復(fù)常數(shù),ti(i=1,2,···,k) 是非零常數(shù),P(z)是一個(gè)多項(xiàng)式,m是集合{z:P(z)=0}的勢(shì), 且滿足n≥4m+5. 如果H1(z)和G1(z)是 CM 分擔(dān)1的, 那么下列結(jié)果必有一個(gè)成立:
(i) ,f=tg其中t為常數(shù), 且滿足td=1;
(ii)f和g滿足代數(shù)方程R(f,g)≡0, 其中ci).
2019年, Laine在文獻(xiàn)[18]中考慮了一類差分多項(xiàng)式的零點(diǎn)分布情況, 得到下列定理C.
定理 C[18]假設(shè)f(z)是有限級(jí)超越整函數(shù), 記, 其中ci(i=1,2,···,k)是互不相同的非零復(fù)常數(shù),bi(z)(i=0,1,···,k)是關(guān)于f(z)的小函數(shù). 如果n≥2,s≥1,那么F(z)?b0(z) 有無窮多個(gè)零點(diǎn).
定理 2假設(shè)f(z)是有限級(jí)超越整函數(shù), 記, 其中ci(i=1,2,···,k)是互不相同的非零復(fù)常數(shù),bi(z)(i=0,1,···,k)是關(guān)于f(z)的小函數(shù),P(z) 是一個(gè)多項(xiàng)式,m是集合{z:P(z)=0}的勢(shì)且滿足n>m+1,s≥1, 那么Hn(z)?b0(z) 有無窮多個(gè)零點(diǎn).
1 引 理
引理 1[4]假設(shè)f(z)為亞純函數(shù), 且為函數(shù)f(z) 的小函數(shù), 則,其中
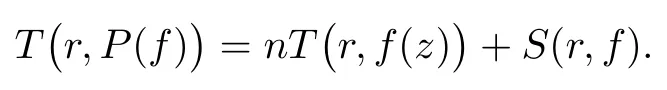
引理 2[8]設(shè)c1c2,f(z) 為不同復(fù)數(shù),為有限級(jí)亞純函數(shù), 且滿足σ(f)=ρ, 則對(duì)任意的ε>0, 有
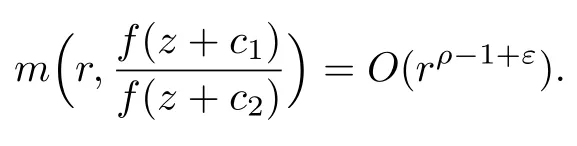
引理 3如果p(z) 是一個(gè)次數(shù)大于零的多項(xiàng)式函數(shù), 且存在某一復(fù)常數(shù)A, 使得

其中0, 那么一定有 degp(z)=1 .
證 明假設(shè), 其中an,an?1,···,a0是p(z)的系數(shù),an0, 因此有

由于p(z+c)?p(z)=A, 可得, 因此c=0 或an=0 , 矛盾.
引理 4[9]設(shè)f(x)是有限級(jí)超越亞純函數(shù), 其增長(zhǎng)級(jí)為ρ=ρ(f)<∞, 且滿足方程

其中U(z,f),P(z,f)和Q(z,f)是f(z)及其平移算子的差分多項(xiàng)式, 滿足 degU(z,f)=n(≥1) ,degQ(z,f)≤n. 若U(z,f)中具有f(z)及其平移算子的最高次數(shù)的項(xiàng)只有一項(xiàng), 則任給ε>0, 有
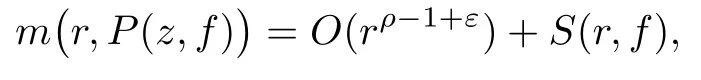
最多可能除去一個(gè)具有有限對(duì)數(shù)測(cè)度的例外集.
引理 5[19]設(shè)fj(j=1,2,3) 是亞純函數(shù), 并且滿足

如果f1不是常數(shù), 并且

其中 0≤λ<1, 并且T(r)=max1≤j≤3{T(r,fj(z))},I?為具有無窮線性測(cè)度的集合, 那么可以得到f2(z)≡1或f3(z)≡1.
引理 6[4]設(shè)fj(z)(j=1,···,n)(n≥2)是亞純函數(shù),gj(z)(j=1,···,n) 都是整函數(shù), 且滿足下面三個(gè)條件:
(ii)當(dāng) 1≤j 1≤j≤n1≤h (iii) 當(dāng),時(shí), 其中E?(1,∞), 且E的線性測(cè)度和對(duì)數(shù)測(cè)度都有窮. 那么fj(z)≡0(j=1,···,n). 由于H1(z),G1(z)是 CM 分擔(dān) 1 的, 故有 其中β(z) 為多項(xiàng)式. 將式(1)變形之后可得 由于 因而 同理可得,nT(r,g)+S(r,g)≤Tr,G1(z). 由式(2)和定理1的條件可得 由式(5)—(8)可得 因?yàn)閚≥4m+5, 所以根據(jù)引理5可得T2(z)≡1或T3(z)≡1. 下面分兩種情形討論. 情形一若T2(z)≡1, 則 eβ(z)≡1, 那么H1(z)≡G1(z), 即 假設(shè)an是式(12)中唯一的非零系數(shù), 因?yàn)間是超越整函數(shù), 所以hn+1=1. 假設(shè)an不是式(12)中唯一的非零系數(shù), 如果hn+11, 根據(jù)式(12)和引理1, 有T(r,g)=S(r,g), 矛盾, 因此hn+1=1. 同理,對(duì)任意的非零系數(shù)ak(k=0,1,···,n), 可以得到hk+1=1. 因此,f(z)=hg(z),h是常數(shù)且滿足hd=1 ,其中d由定義1給出. 若t(z)不是常數(shù), 那么由式(11)可知f和g滿足代數(shù)方程R(f,g)≡0, 其中R(w1,w2)= 情形二若, 則, 即G1(z)H1(z)≡1. 假設(shè)β1,β2,···,βm是P(z)=0的根, 并且對(duì)應(yīng)重?cái)?shù)為l1,l2,···,lm, 則有 由式(13)可以得到β1,β2,···,βm是Picard例外值. 如果m≥2,βj0(j=1,2,···,m), 根據(jù)整函數(shù)的Picard定理可知,f(z)的Picard例外值至少有2個(gè). 因此, 得出矛盾. 當(dāng)m=1,l1=n時(shí), 則存在復(fù)常數(shù)γ, 使得 那么 因?yàn)閒(z),g(z)是超越整函數(shù), 所以由Picard定理可知沒有零點(diǎn). 那么 其中μ(z),ν(z)是多項(xiàng)式. 于是 以下分兩種情況進(jìn)行證明. (a) 如果對(duì)I={c1,c2,···,ck}中的任意元素ci都有μ(z+ci)?ν(z) 不等于常數(shù), 那么根據(jù)引理6,可得t1=t2=···=tk≡0, 這顯然矛盾. (b) 如果I={c1,c2,···,ck}中存在有限多個(gè)元素ci, 使得μ(z+ci)?ν(z) 等于常數(shù), 事實(shí)上, 最多存在一項(xiàng)這樣的項(xiàng). 不妨設(shè)I中存在元素ci,cj滿足 其中C1,C2為常數(shù). 根據(jù)式(16), 有 C1?C2是一個(gè)常數(shù), 這與引理3矛盾. 因此必存在I={c1,c2,···,ck}中的某個(gè)元素cp, 使得 由式(15)和式(17)可得 先證Hn(z)?b0(z)0. 若Hn(z)?b0(z)0 , 即 對(duì)式(19)應(yīng)用引理4, 則任給ε>0 , 有 另外, 再由Valiron-Mokhon’ko定理可得 由n>m+1可知式(19)不可能成立. 因此 假設(shè)Hn(z)?b0(z)僅有有限多個(gè)零點(diǎn), 那么 由于 故得到 根據(jù)式(23)和Nevanlinna第二基本定理, 可得 由式(25)—(26), 有 與n>m+1矛盾. 因此Hn(z)?b0(z)有無窮多個(gè)零點(diǎn).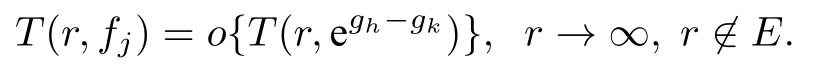
2 定理的證明
2.1 定理1的證明


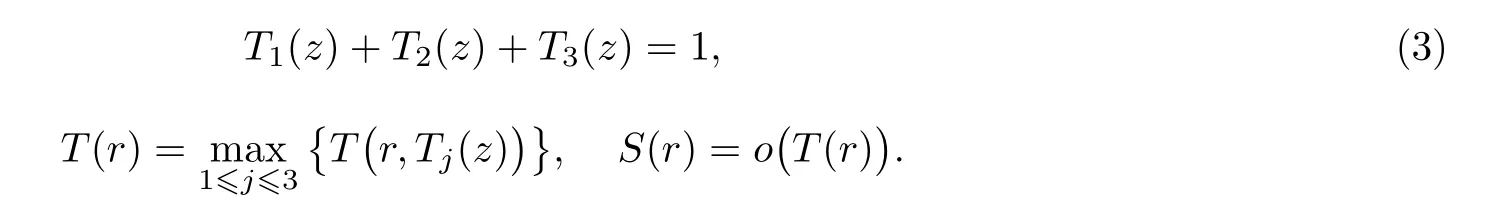
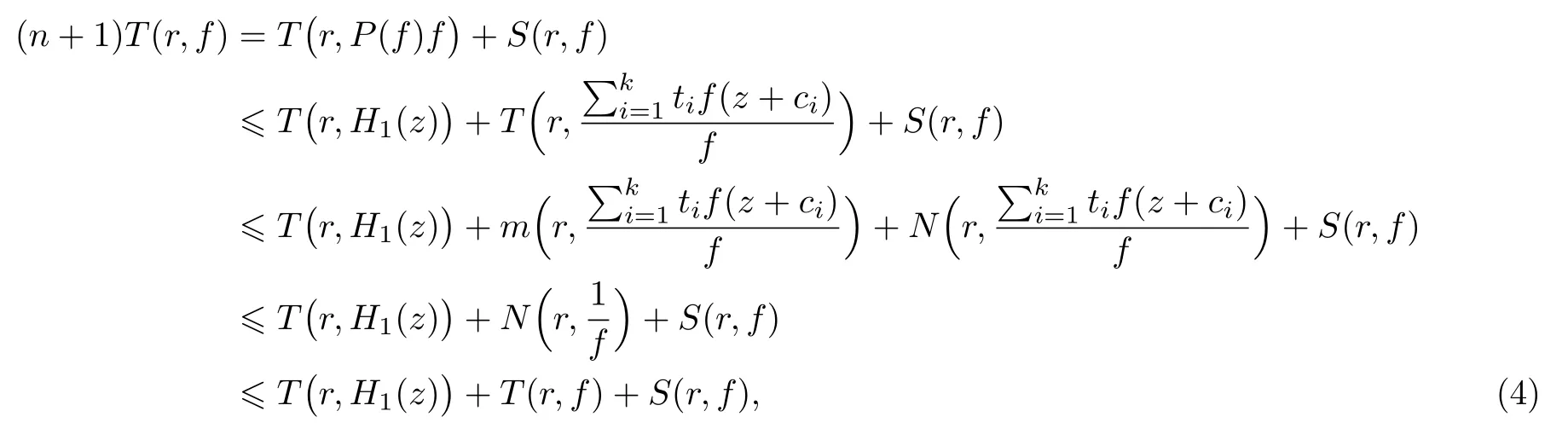
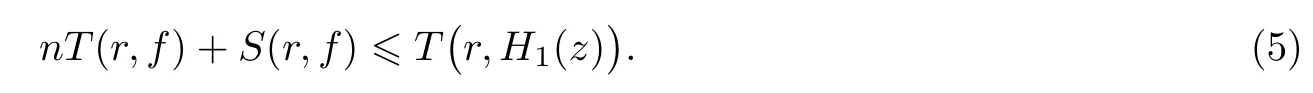

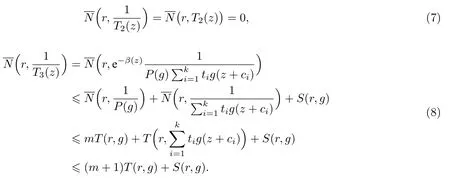
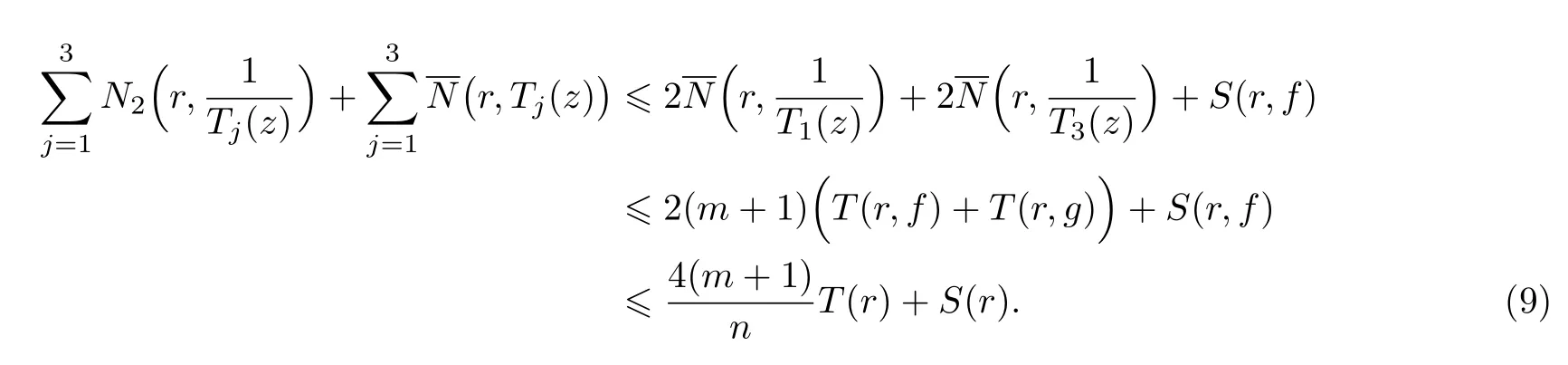
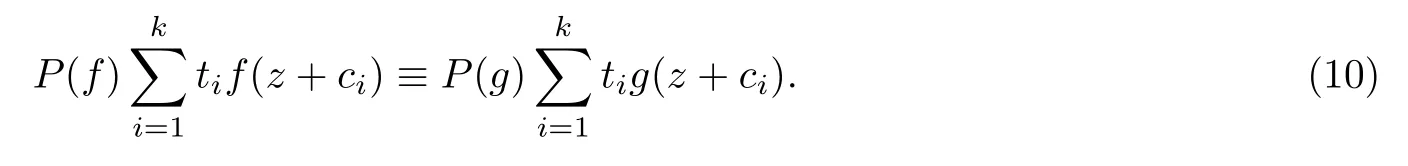
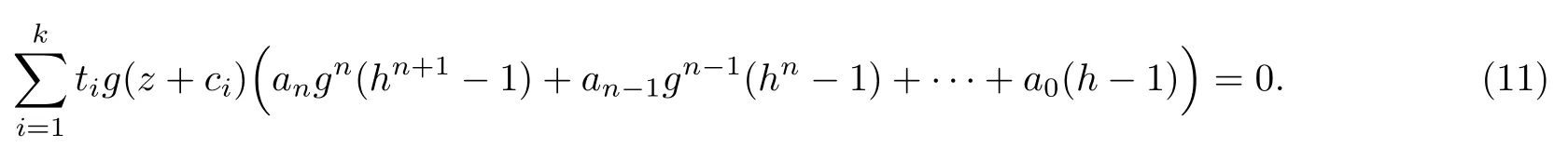

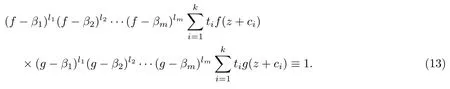
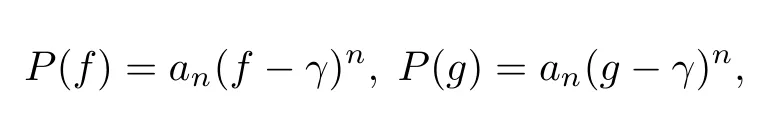
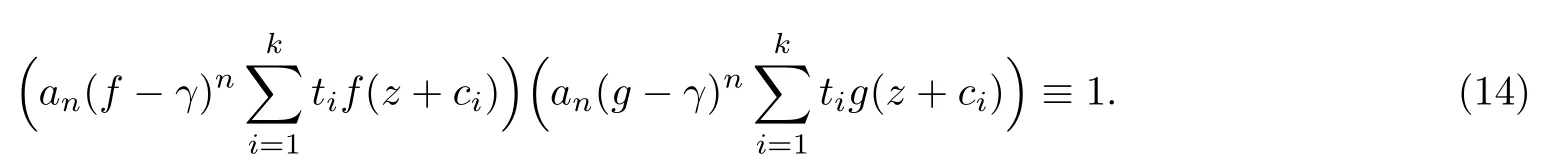
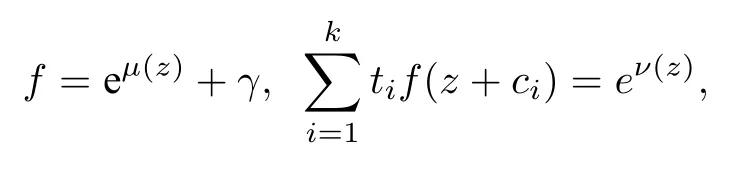
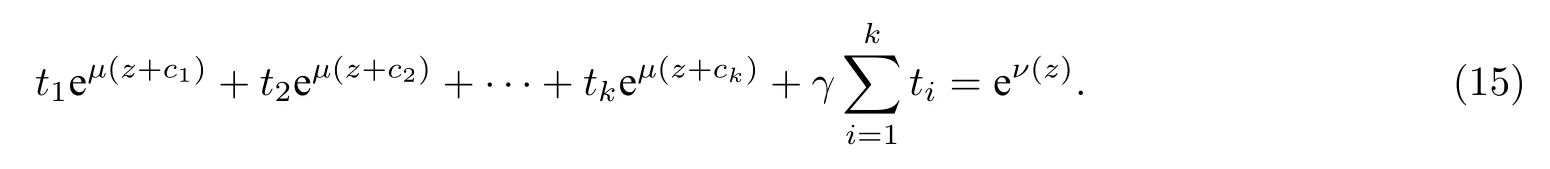
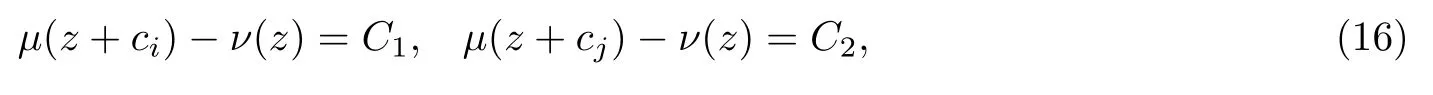
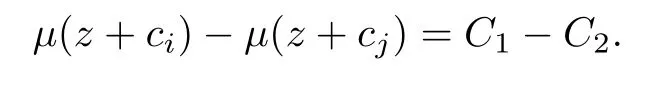

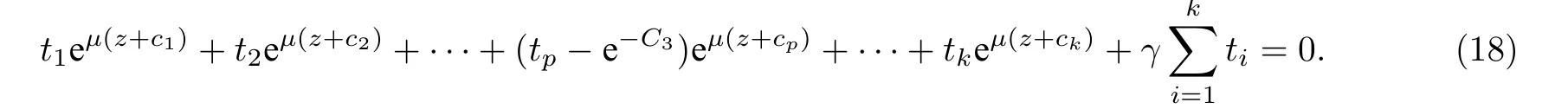
2.2 定理2的證明